Flood Control Optimization of Reservoir Group Based on Improved Sparrow Algorithm (ISSA)
Abstract
:1. Introduction
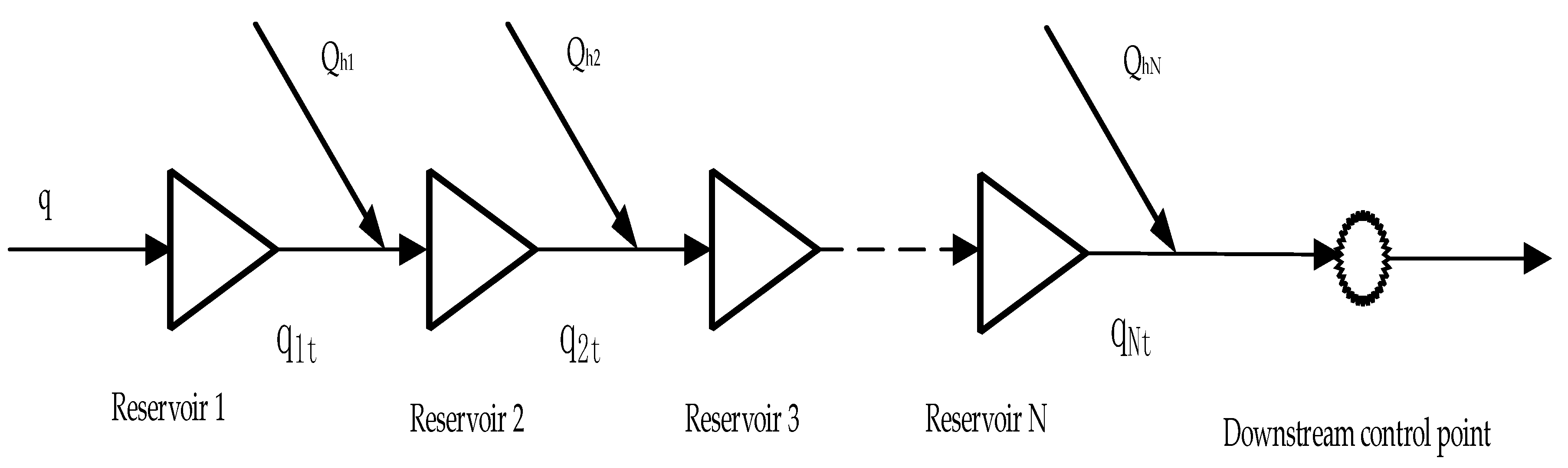
2. Reservoir Joint Flood Control Dispatching Model
2.1. Objective Function
2.2. Condition of Constraint
- (1)
- Water balance constraint:
- (2)
- Constraints on reservoir water level:where T represents the water level of the k reservoir during flood control operations (m); stands for the lowest allowable water level during flood control operations, which is the flood limit water level; T stands for the maximum allowable water level during flood control operations, which is the check water level;
- (3)
- Letdown flow constraint:where is the discharge of the kth reservoir; is the maximum discharge capacity of the kth reservoir.
- (4)
- Initial water level constraint:where is the initial water level; is the lowest allowable water level during flood control operation.
- (5)
- Terminal water level constraint:where is the water level of the reservoir at the end of flood control regulation; is the lowest allowable water level during flood control operation.
3. Sparrow Optimization Algorithm
3.1. Basic Sparrow Search Algorithm (SSA)
3.2. Improved Sparrow Algorithm (ISSA)
- (1)
- Sin chaos initialization population
- (2)
- Dynamic adaptive weight
- (3)
- An improved formula for updating the position of the watchman
- (4)
- Fusion of Cauchy Variation and Reverse Learning Strategy
4. Model Analysis
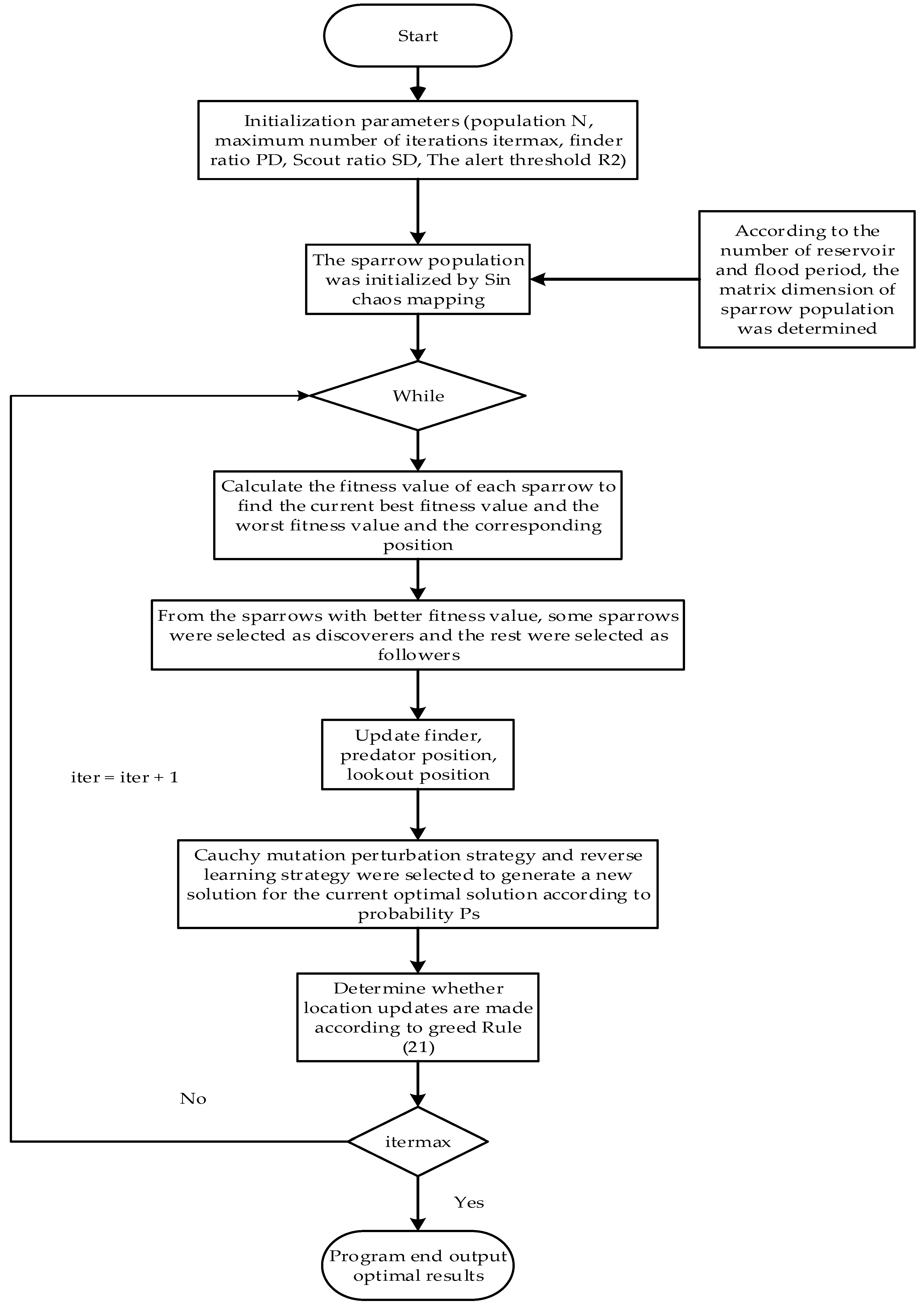
4.1. Solution Method of Flood Control Operation Model
- (1)
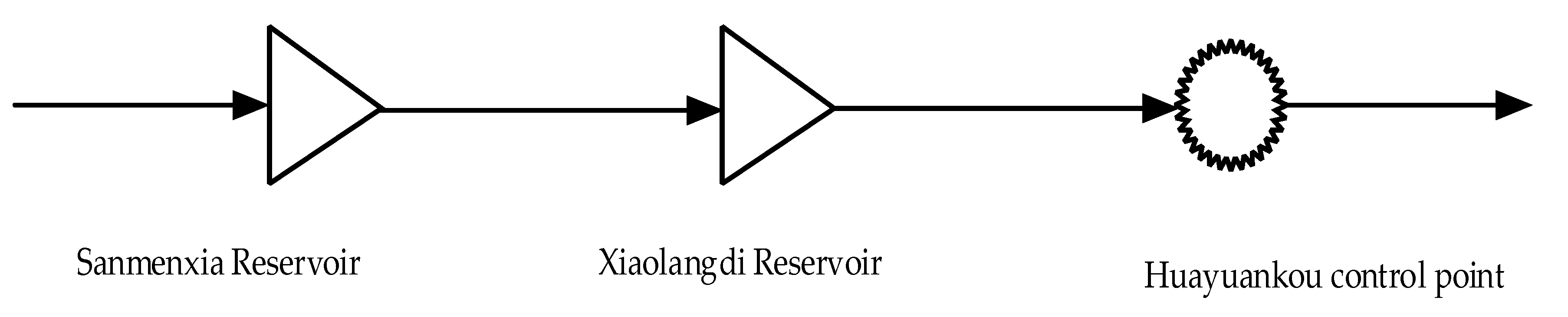
- Initialization parameters, such as population number N, maximum iteration number , discoverer proportion PD, joiner proportion SD, alert threshold R2 and initialization of sparrow population using the Sin chaotic map of Equation (12) according to the calculation period given by flood flow. The sparrow is constructed with the discharge of each reservoir at the end of each cycle as the control variable. The flood lasts 78 periods and has two reservoirs, so the vector dimension is 156. Then, the matrix form of sparrow population:is the ith initial sparrow, including 156 elements. 1~78 represents the reservoir water level at the end of the Sanmenxia Reservoir period, and 79~156 represents the end of the Xiaolangdi Reservoir period.
- (2)
- Calculate the fitness value of each sparrow and find out the current optimal fitness value, the worst fitness value, and the corresponding position.
- (3)
- From the sparrows with better fitness values, select some sparrows as the discoverers, and update their positions according to Formula (14).
- (4)
- The remaining sparrows will be the participants, and their positions will be updated in the original way.
- (5)
- Randomly select some sparrows from the sparrows as watchers and update their positions according to Formula (15).
- (6)
- According to probability , the Cauchy mutation perturbation strategy and reverse learning strategy are selected to perturb the current optimal solution to generate a new solution.
- (7)
- Determine whether to update the location according to the greedy rule (21).
- (8)
- Judge whether the end conditions are met. If the end conditions are met, proceed to the next step; otherwise, skip to step (2).
- (9)
- The program ends and the optimal result is output.
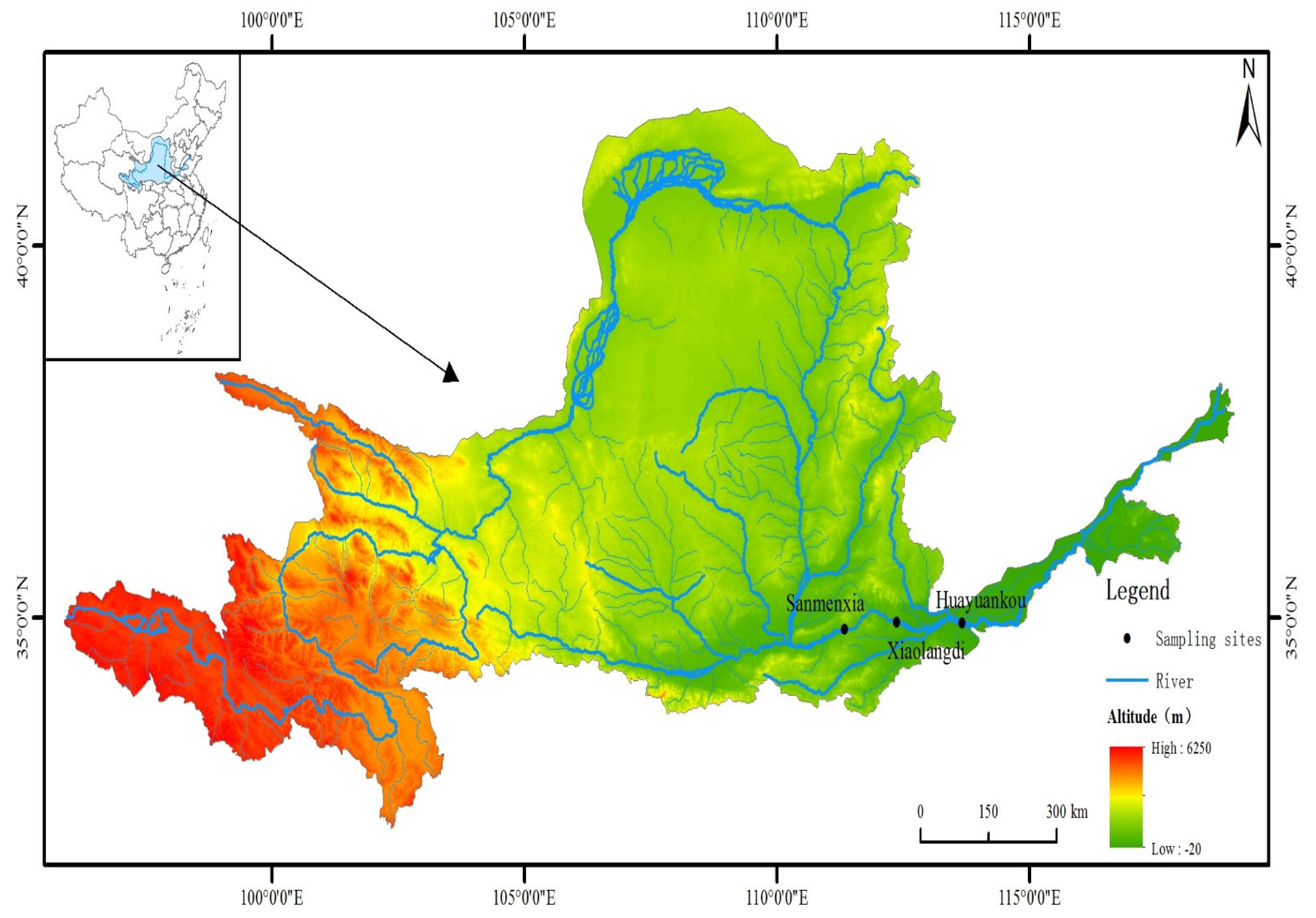
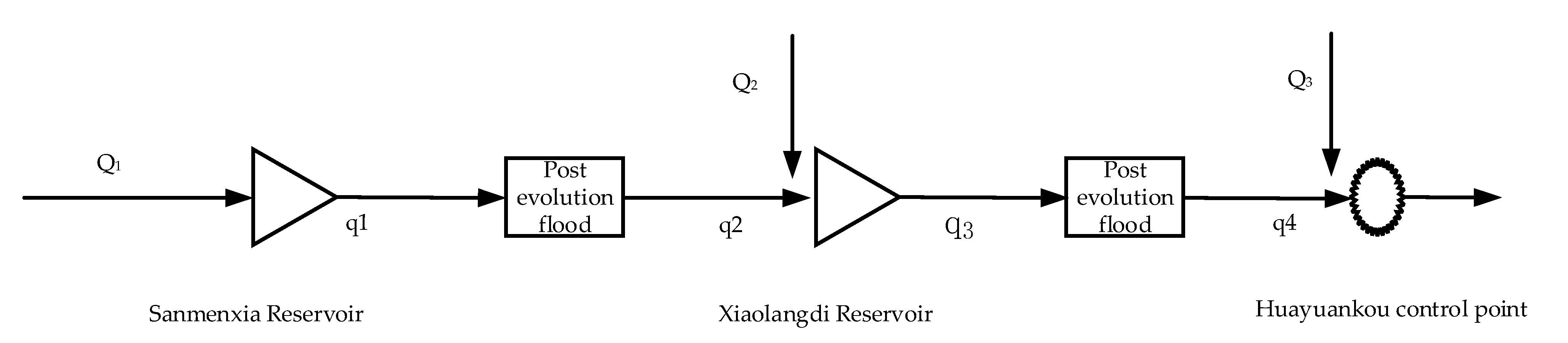
4.2. Study Area of Flood Control Operation Model
4.3. Interval Water Supply Analysis of Flood Control Operation Model
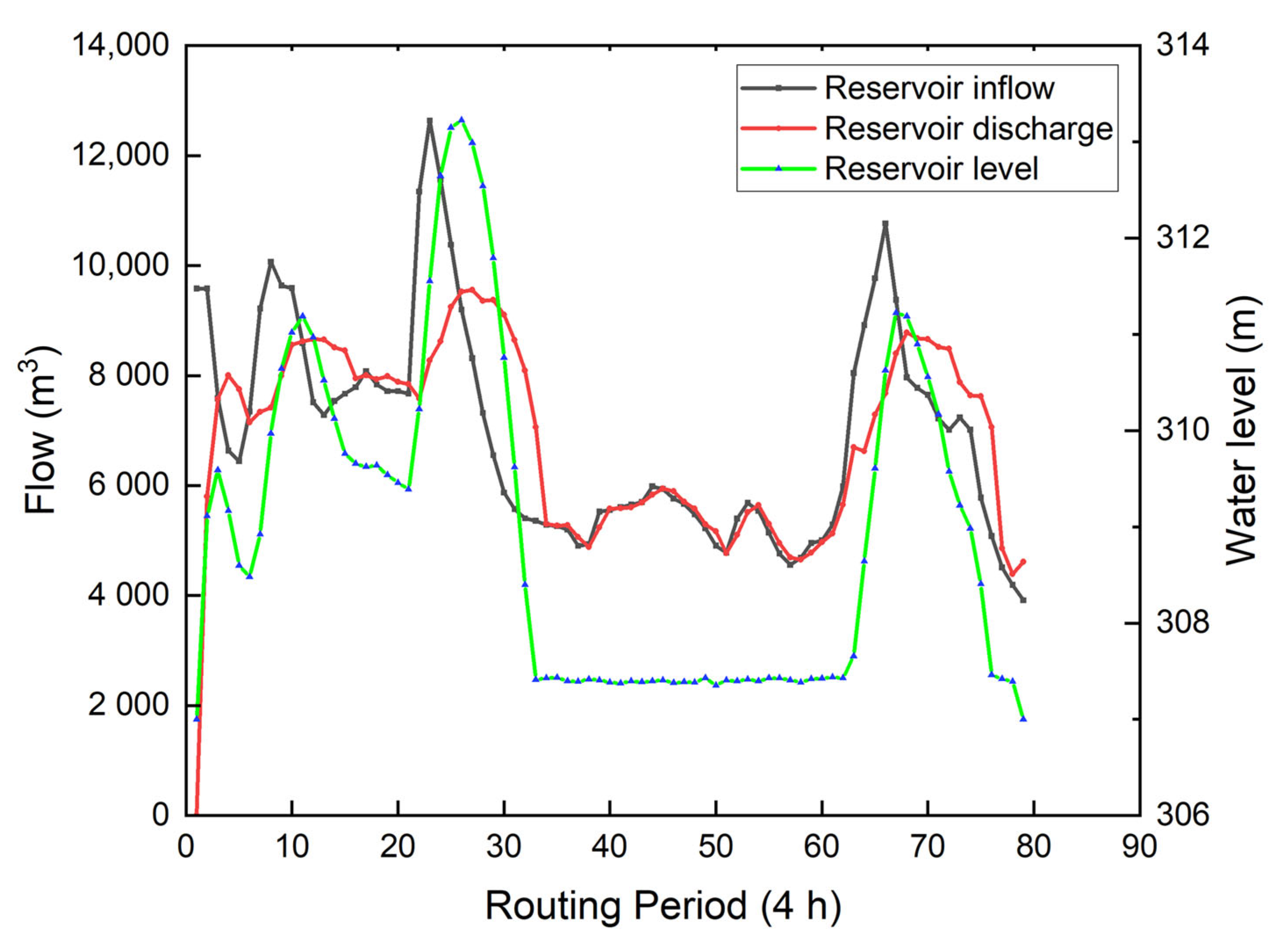
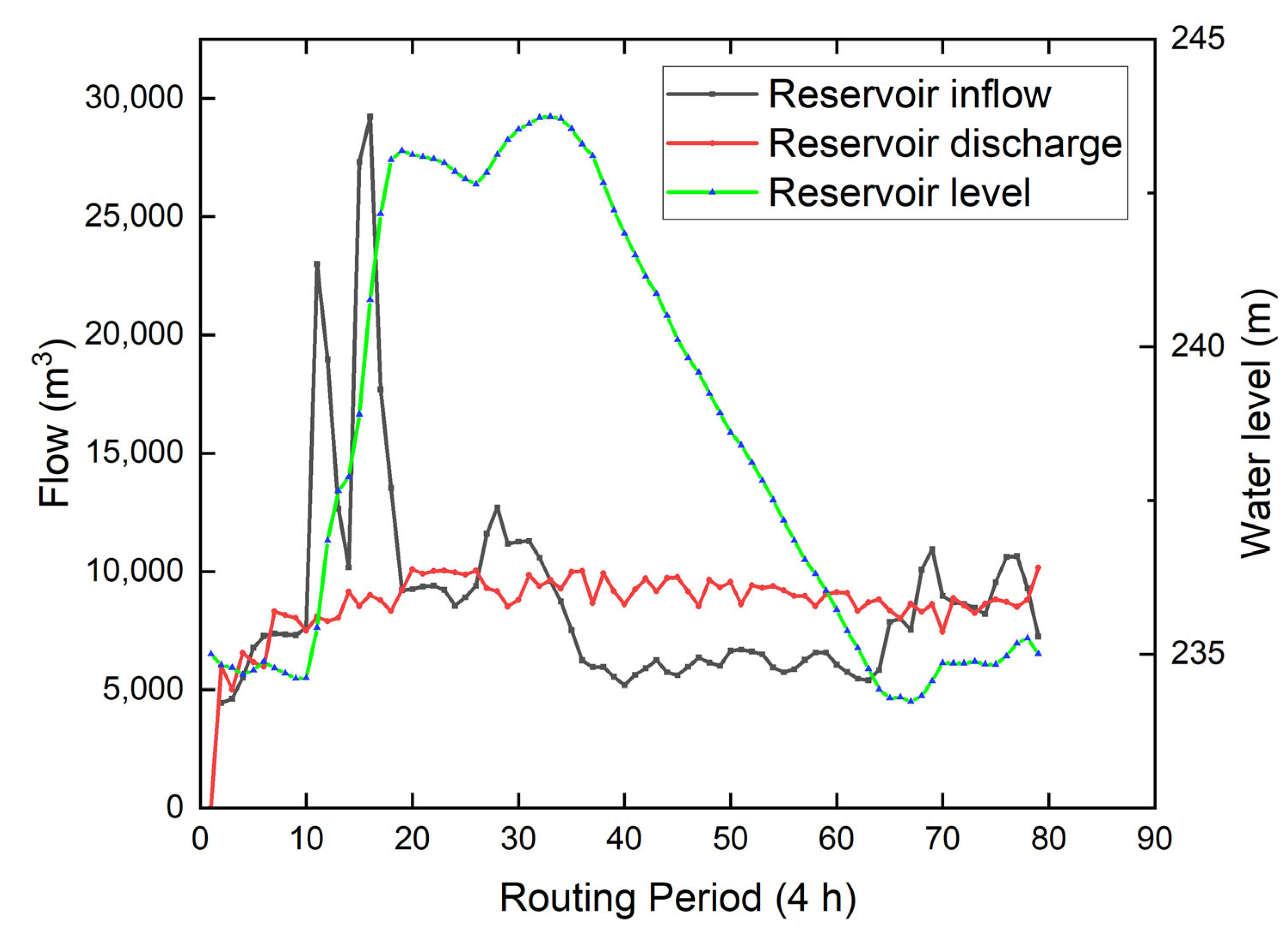
5. Results and Discussion
6. Conclusions
- (1)
- From the solution results of the model, it can be seen that the construction of this model not only guarantees the flood control safety of the reservoir itself when encountering the flood with the return period of 1000 years, but also guarantees the flood control safety of the downstream, indicating the rationality and applicability of the model.
- (2)
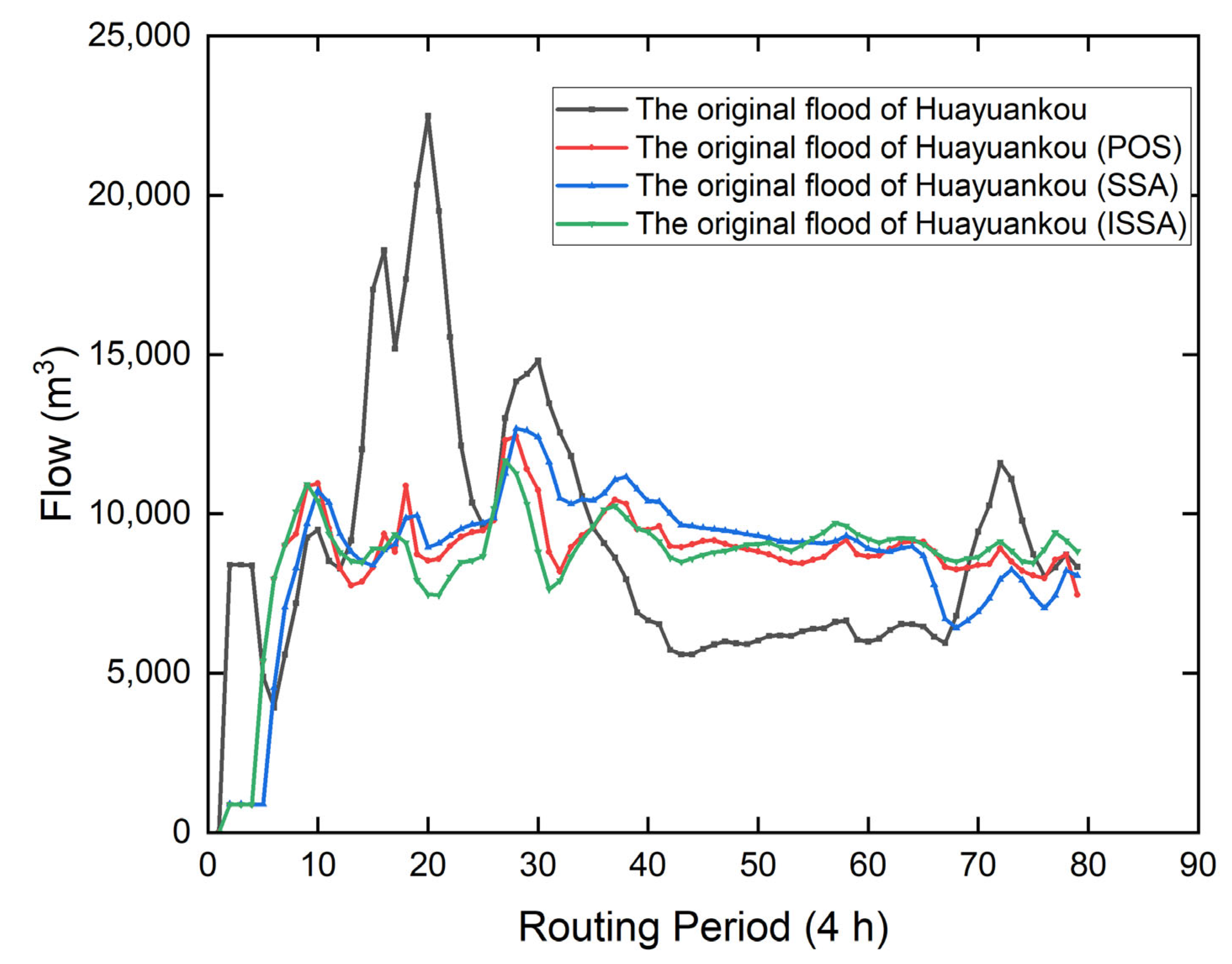
- In this paper, ISSA, SSA and POS algorithms are used to study the flood control operation of tandem cascade reservoirs including Sanmenxia Reservoir and Xiaolangdi Reservoir on the Yellow River mainstream. The comparison of the solution results of the three optimization algorithms shows that the ISSA algorithm is more efficient than the conventional SSA algorithm and POS algorithm and can fully play the role of reservoir capacity compensation to achieve the best flood control effect. The results show that the ISSA algorithm can effectively solve the flood control optimal operation problem of cascade reservoirs. It provides a new method to solve the problem of joint flood control operation of cascade reservoirs. It also provides a reference for the ISSA algorithm to be applied to other research fields.
- (3)
- Without the regulation of Sanmenxia Reservoir and Xiaolangdi Reservoir, the maximum flood peak flow at the Huayuankou control point is 24,325 m3/s, far exceeding the flood control requirement of 22,000 m3/s at the Huayuankou control point section. Through the joint flood control operation of Sanmenxia Reservoir and Xiaolangdi Reservoir, the flood peak of the Huayuankou control point is reduced, making the maximum peak flow of the Huayuankou control point 11,676.3 m3/s, ensuring the flood control safety of the Huayuankou control point when encountering the millennium flood. This shows that it is necessary to study the joint flood control operation of Sanmenxia Reservoir and Xiaolangdi Reservoir, and further explains the significance of this study.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Chen, W.; Guo, X.; Law, T.; Cui, Z. Flood risk analysis in protective areas in Yellow River downstream. China Water Resour. 2017, 68, 56–58. [Google Scholar] [CrossRef]
- Su, C.; Wang, P.; Yuan, W.; Cheng, C.; Data, T.Z.; Yan, D.; Wu, Z. An MILP based optimization model for reservoir flood control operation considering spillway gate scheduling. J. Hydrol. 2022, 613, 128483. [Google Scholar] [CrossRef]
- Li, J.; Zhong, P.-A.; Wang, Y.; Yang, M.; Fu, J.; Liu, W.; Xu, B. Risk analysis for the multi-reservoir flood control operation considering model structure and hydrological uncertainties. J. Hydrol. 2022, 612, 128263. [Google Scholar] [CrossRef]
- Zhang, Z.; He, X.; Geng, S.; Zhuang, S.; Li, H.; Tian, Y. Study on flood control projects joint flood control operation of The Daqing river basin. IOP Conf. Ser.: Earth Environ. Sci. 2021, 826, 012007. [Google Scholar] [CrossRef]
- Zhang, J.; Cai, X.; Lei, X.; Liu, P.; Wang, H. Real-time reservoir flood control operation enhanced by data assimilation. J. Hydrol. 2021, 598, 126426. [Google Scholar] [CrossRef]
- Li, H.; Liu, J. The Application of Dynamic Programming Algorithm in the Optimal Dispatching of the Xiaolangdi Reservoir. Henan Sci. 2011, 29, 461–465. [Google Scholar] [CrossRef]
- Wang, S.; Jiang, Z.; Liu, Y. Dimensionality Reduction Method of Dynamic Programming under Hourly Scale and Its Application in Optimal Scheduling of Reservoir Flood Control. Energies 2022, 15, 676. [Google Scholar] [CrossRef]
- Xin, Y.; Zhou, Y.; Gu, Q.; Zhang, T. Optimal Scheduling of Day-ahead Considering the Safety Difference of Energy Storage Device Capacity. Sci. Technol. Eng. 2022, 22, 2291–2297. [Google Scholar]
- Lee, S.-Y.; Hamlet, A.F.; Fitzgerald, C.J.; Burges, S.J. Optimized Flood Control in the Columbia River Basin for a Global Warming Scenario. J. Water Resour. Plann. Manag. 2009, 135, 440–450. [Google Scholar] [CrossRef] [Green Version]
- Cuevas-Velásquez, V.; Sordo-Ward, A.; García-Palacios, J.H.; Bianucci, P.; Garrote, L. Probabilistic Model for Real-Time Flood Operation of a Dam Based on a Deterministic Optimization Model. Water 2020, 12, 3206. [Google Scholar] [CrossRef]
- Sumi, T.; Mitsunari, M.; Hamaguchi, T. Challenges in Flood Control Operation and dissemination of Related Information-Lessons from the record-breaking heavy rain in July 2018, Japan. Water Energy Int. 2021, 64, 14–21. [Google Scholar]
- Huang, K.; Ye, L.; Chen, L.; Wang, Q.; Dai, L.; Zhou, J.; Singh, V.P.; Huang, M.; Zhang, J. Risk analysis of flood control reservoir operation considering multiple uncertainties. J. Hydrol. 2018, 565, 672–684. [Google Scholar] [CrossRef]
- Ren, M.; Zhang, Q.; Yang, Y.; Wang, G.; Xu, W.; Zhao, L. Research and application of joint optimal operation for flood defense of reservoir group based on improved genetic algorithm. China Flood Drought Manag. 2022, 32, 21–26. [Google Scholar] [CrossRef]
- Wu, Z.; Zhou, J.; Yang, J. Flood Dispatching Optimization of Three Gorges Region Based on Ant Colony Algorithms. Water Power 2008, 55, 5–7. [Google Scholar] [CrossRef]
- Lin, Z. Research on optimal operation of cascade reservoirs based on improved ant colony algorithm. Telecom World 2016, 23, 162–163. [Google Scholar]
- Qin, H.; Zhou, J.; Wang, G.; Zhang, Y. Multi-objective optimization of reservoir flood dispatch based on multi-objective differential evolution algorithm. J. Hydraul. Eng. 2009, 40, 513–519. [Google Scholar] [CrossRef]
- Chen, H.-T.; He, J.; Wang, W.-C.; Chen, X.-N. Simulation of maize drought degree in Xi’an City based on cusp catastrophe model. Water Sci. Eng. 2021, 14, 28–35. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, Y. Research on optimal joint operation of cascade reservoirs based on improved PSO parallel algorithm. Techenical Superv. Water Resour. 2018, 26, 147–149+182. [Google Scholar] [CrossRef]
- Chen, J.; Zhong, P.-A.; Liu, W.; Wan, X.-Y.; Yeh, W.W.-G. A multi-objective risk management model for real-time flood control optimal operation of a parallel reservoir system. J. Hydrol. 2020, 590, 125264. [Google Scholar] [CrossRef]
- Malinowski, K.; Karbowski, A.; Salewicz, K.A. Hierarchical Control Structures for Real Time Scheduling of Releases in a Multireservoir System During Floods. IFAC Proc. Vol. 1987, 20, 405–412. [Google Scholar] [CrossRef]
- Nan, L.; Jiankai, X.; Huisheng, S. A sparrow search algorithm with adaptive t distribution mutation-based path planning of unmanned aerial vehicles. J. Donghua Univ. (Nat. Sci.) 2022, 48, 69–74. [Google Scholar] [CrossRef]
- Mao, Q.; Qiang, Z. Improved Sparrow Algorithm Combining Cauchy Mutation and Opposition-Based Learning. J. Front. Comput. Sci. Technol. 2021, 15, 1155–1164. [Google Scholar] [CrossRef]
| Reservoir | Sanmenxia Reservoir | Xiaolangdi Reservoir |
|---|---|---|
| Control watershed area | 688,400 km2 | 694,000 km2 |
| Flood control limited water level | 305 m | 220 m |
| Flood control high water level | 335 m | 275 m |
| Total reservoir capacity | 16,200,000,000 m3 | 12,650,000,000 m3 |
| Name of River Section | Flood Propagation Time | Number of Flood Routing Sections | K | x | Δt |
|---|---|---|---|---|---|
| Sanmenxia–Xiaolangdi | 8 h | 2 | 3.875 | 0.2 | 4 h |
| Xiaolangdi–Huayuankou | 12 h | 3 | 4.576 | 0.3 | 4 h |
| Algorithm | Population Quantity (N) | Maximum Iterations (Itemax) | Maximum Peak Flood Discharge | Peak Clipping Rate |
|---|---|---|---|---|
| ISSA | 50 | 1000 | 11,676.3 m3/s | 48% |
| SSA | 100 | 1000 | 12,673.65 m3/s | 45% |
| POS | 80 | 1000 | 12,408.23 m3/s | 44% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, J.; Liu, S.-M.; Chen, H.-T.; Wang, S.-L.; Guo, X.-Q.; Wan, Y.-R. Flood Control Optimization of Reservoir Group Based on Improved Sparrow Algorithm (ISSA). Water 2023, 15, 132. https://doi.org/10.3390/w15010132
He J, Liu S-M, Chen H-T, Wang S-L, Guo X-Q, Wan Y-R. Flood Control Optimization of Reservoir Group Based on Improved Sparrow Algorithm (ISSA). Water. 2023; 15(1):132. https://doi.org/10.3390/w15010132
Chicago/Turabian StyleHe, Ji, Sheng-Ming Liu, Hai-Tao Chen, Song-Lin Wang, Xiao-Qi Guo, and Yu-Rong Wan. 2023. "Flood Control Optimization of Reservoir Group Based on Improved Sparrow Algorithm (ISSA)" Water 15, no. 1: 132. https://doi.org/10.3390/w15010132
APA StyleHe, J., Liu, S.-M., Chen, H.-T., Wang, S.-L., Guo, X.-Q., & Wan, Y.-R. (2023). Flood Control Optimization of Reservoir Group Based on Improved Sparrow Algorithm (ISSA). Water, 15(1), 132. https://doi.org/10.3390/w15010132







