An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in the Wave Motion over Sloped Bed
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Investigations
2.1.1. Description of the Flow
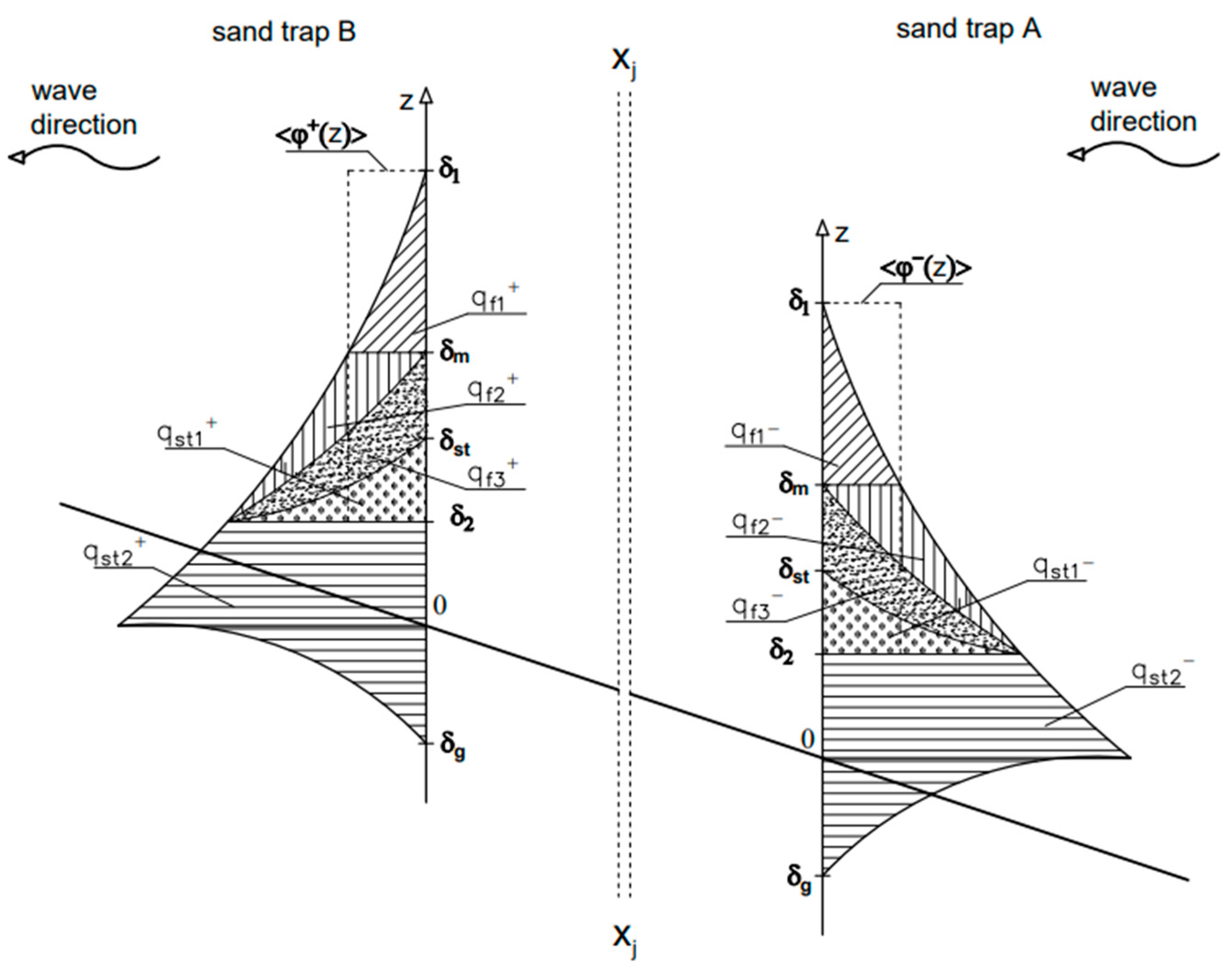
2.1.2. Sediment Transport during the Wave Crest and Trough Phase
2.1.3. Grain Size Distributions of Transported Sediments
2.2. Experimental Investigations
2.2.1. Experimental Set-Up
2.2.2. Scope of the Measurement
- sandy with a very high proportion of fine fractions (d50 < 0.20 mm; sand D: grain content di < 0.20 mm = 97%);
- sandy with low content of fine fractions (d50 ≥ 0.20 mm; grain content di < 0.20 mm equal to sand A: = 6%, B: = 10.5%, C: = 26%, respectively).
3. Results and Discussion
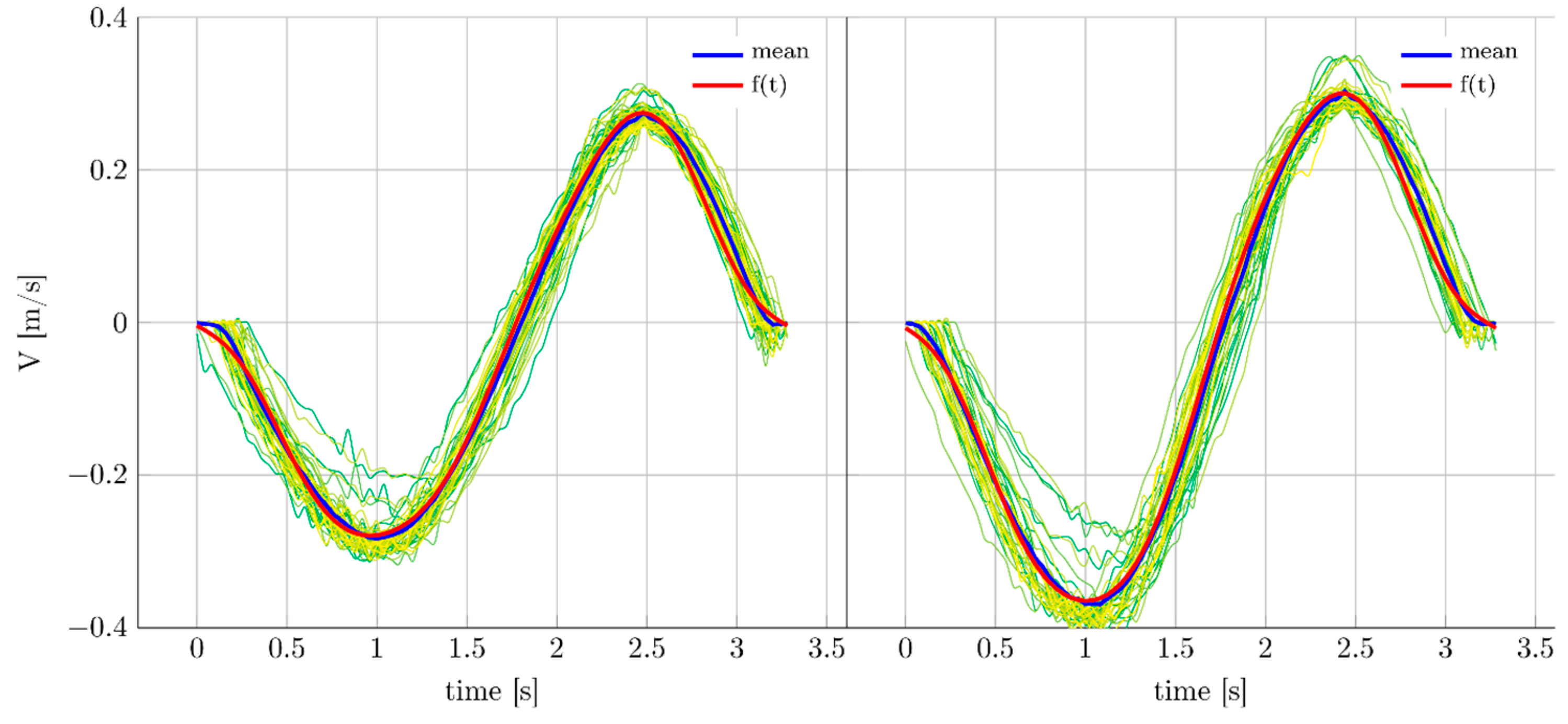
3.1. Free Stream Velocity Measurements
3.2. PIV Measurements
- As can be assumed, in the situation of a sloping bed, the flux inside the near-wall layer (thickness , where is the thickness of the boundary layer as determined by the Kaczmarek et al. 2022 model) from the computational area and directed to the trap (positive values) reaches values clearly greater than the absolute values of flux returning to the computational area (Table 4). This is understandable, as the effect of a negative pressure gradient becomes apparent, which causes an increase in hydrodynamic forcing and an increase in flux values . For a flat bed, in the lack of a negative pressure gradient, the magnitudes of fluxes leaving and returning to the computational area are much smaller. Under the conditions of a sloping bed, only in case of sand D, i.e., in the situation of presence of a very large number of fine fractions in the bed, the fluxes returning are larger than those leaving. This is because the large number of very fine fractions in the fluxes , and means a larger (after they are mixed) and closer to the bed averaged by depth return fluxes , at the boundary of near-wall layer.In case of sediments A, B, C, the returning fluxes high above the bed () are balanced with the fluxes leaving the control area. Only in the case of sediment D, the returning fluxes are larger than the outgoing fluxes, as the proportion of suspended fine and very fine fractions in this flux is dominant. In case of a flat bed, the returning fluxes (Table 4) are slightly larger, while in the case of a sloping bed, the negative pressure gradient causes more material (including fluxes ) falls into the trap. As a result, the return fluxes are slightly smaller.In summary, it can be expected that higher hydrodynamic forcing caused by a negative pressure gradient will cause the fluxes measured over a sloping bed to be closer to those calculated by the Kaczmarek et al. model of fluxes , than in the flat bed situation;
- Under sloping bed conditions, the fluxes both outgoing and entering the trap (with a minus sign) in the wave trough phase are smaller than the fluxes under flat bed conditions. This is due to weaker hydrodynamic conditions caused by the effect of a positive pressure gradient, which reduces transport. In addition, at the bed the flux outgoing towards the trap in the area of positive pressure gradient additionally feeds the flux As a result, the fluxes entering traps will be significantly larger than those outgoing.It is also worth noting, that in case of a sloping bed, the fluxes directed to traps (for sediments A, B, C) in the trough phase of the wave reach absolute values smaller than the fluxes in the crest phase of the wave (Table 4). The above observation seems to be understandable due to the effects occurring over the sloping bed, which increase fluxes and decreasing the fluxes . In turn, the fluxes outgoing from the trap (with a minus sign) are similar in value to the fluxes entering the trap on the opposite side (with a minus sign). This represents the opposite situation to that on a flat bed (Table 4), where fluxes entering the trap are clearly larger than the fluxes outgoing on the opposite side from the trap. Furthermore, taking into account the fact that under sloping bed conditions the flux in the trough phase directed to the trap is smaller than the flux under flat bed conditions, it can be expected that the effect of fine fractions in the trough of the wave on the acceleration of coarse fractions will be much smaller. On the other hand, the increased amount of material flowing into the trap (including very fine fractions) in the wave crest leads to expect that the effect of flushing very fine fractions from the bed occurring in the case of a flat bed will not take place in the situation of a sloping bed. Finally, it is worth noting that the effects caused by positive pressure gradient are so strong (Table 4) that even in areas higher up the bed (for all types of sediments, the absolute values of flux from the calculation area and directed to the trap remain greater than the flux returning. This is because the latter is formed only by the fluxes and . This is the opposite situation from that on a flat bed, where the fluxes were balanced.
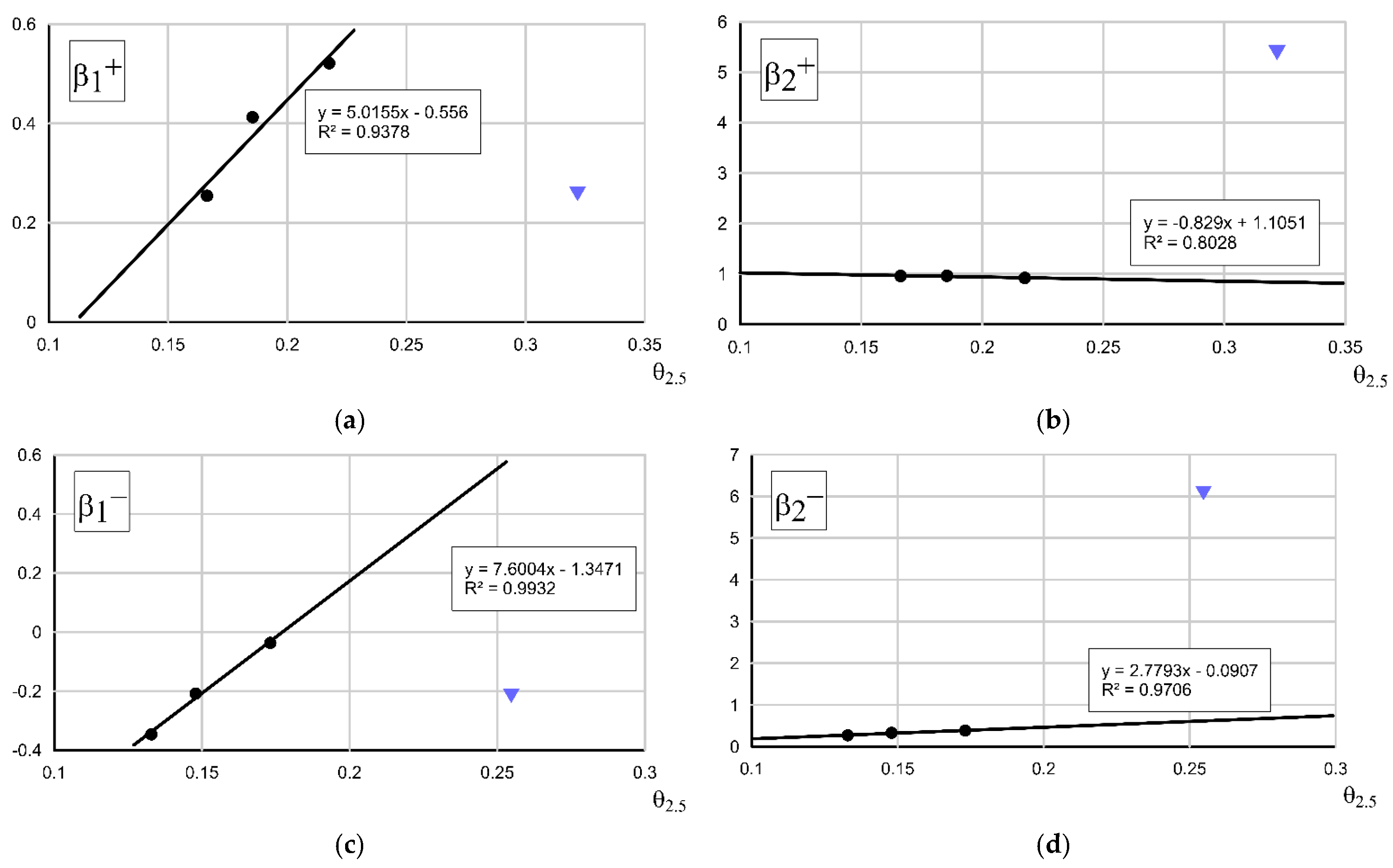
3.3. Correction Factors for Sediment Fluxes
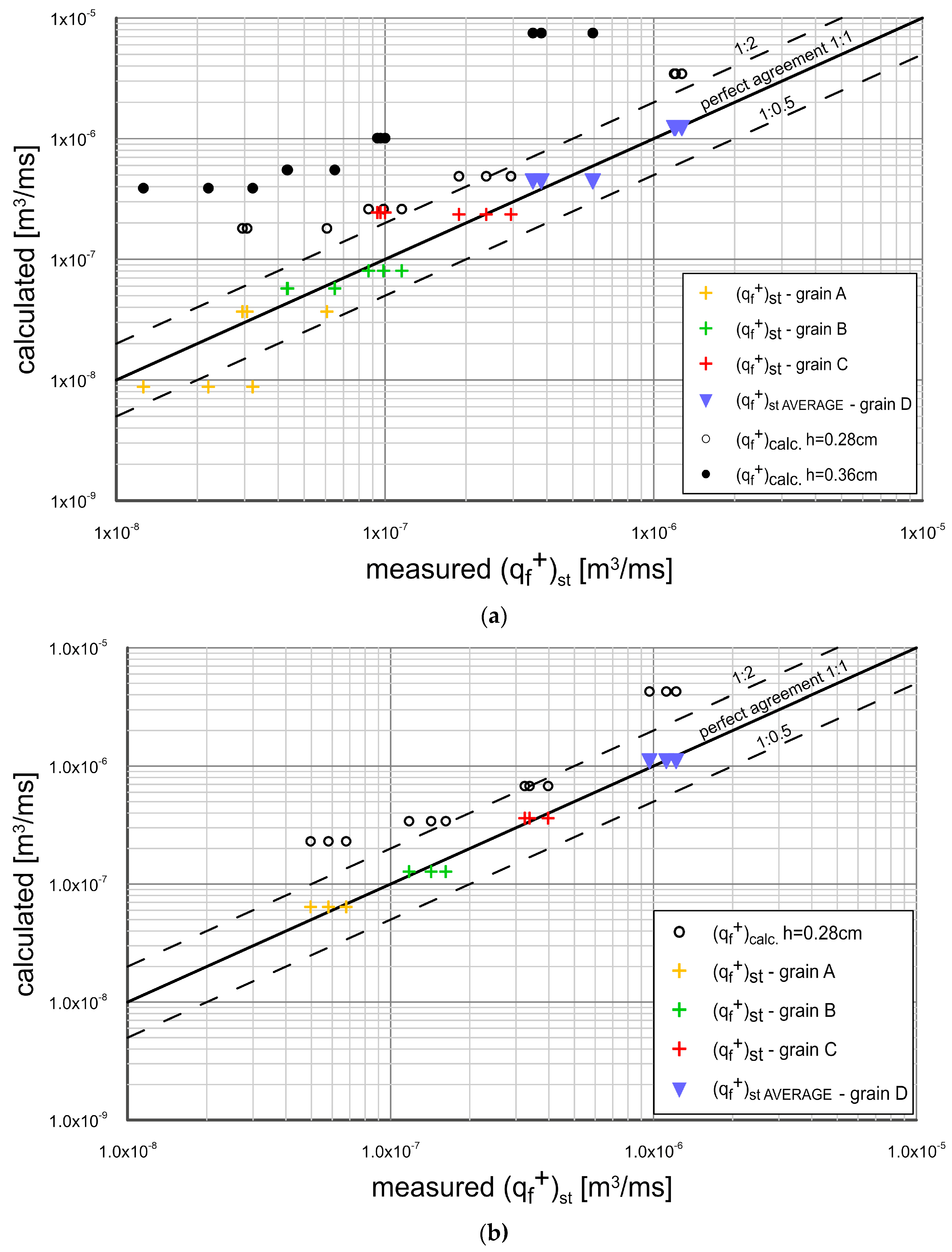
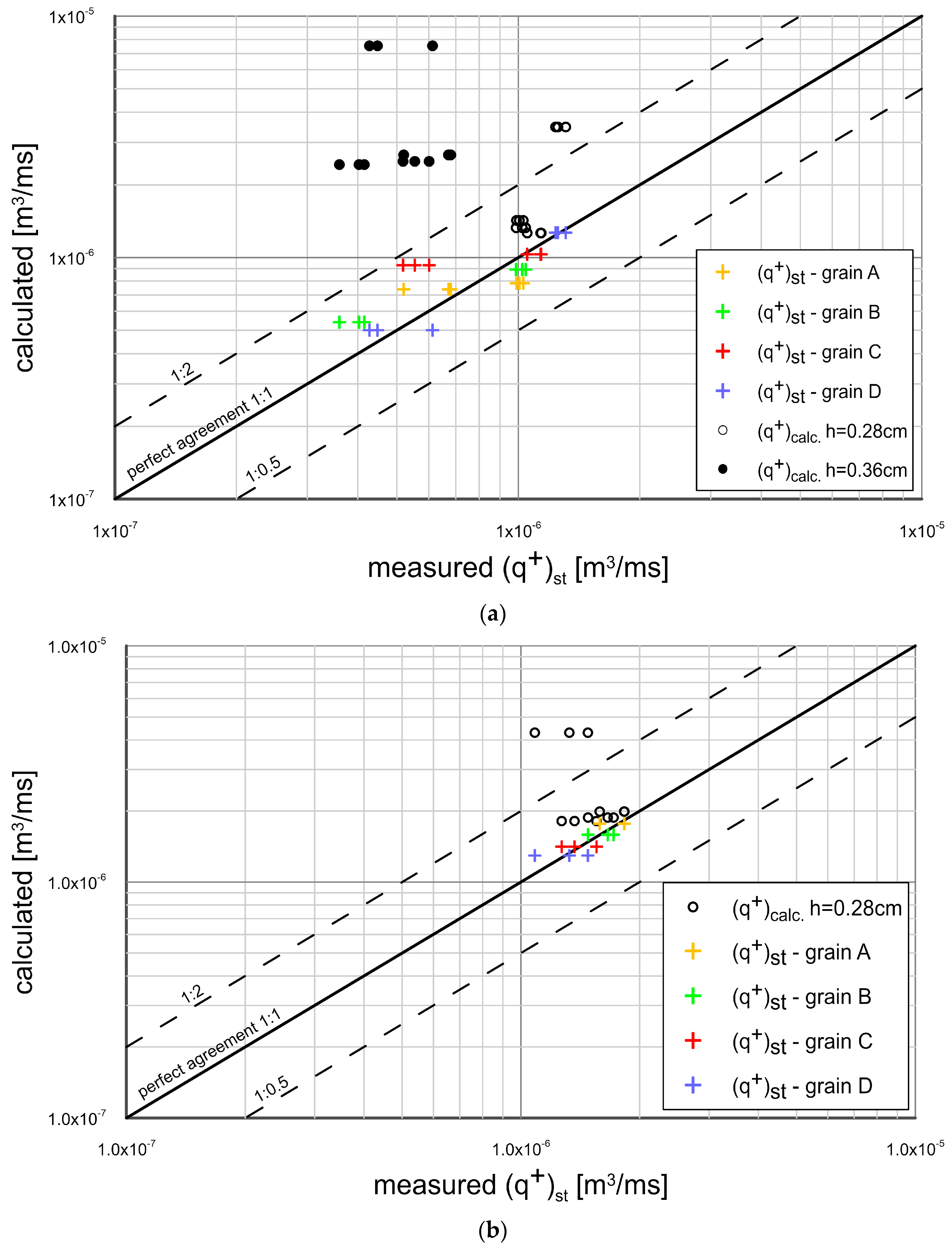
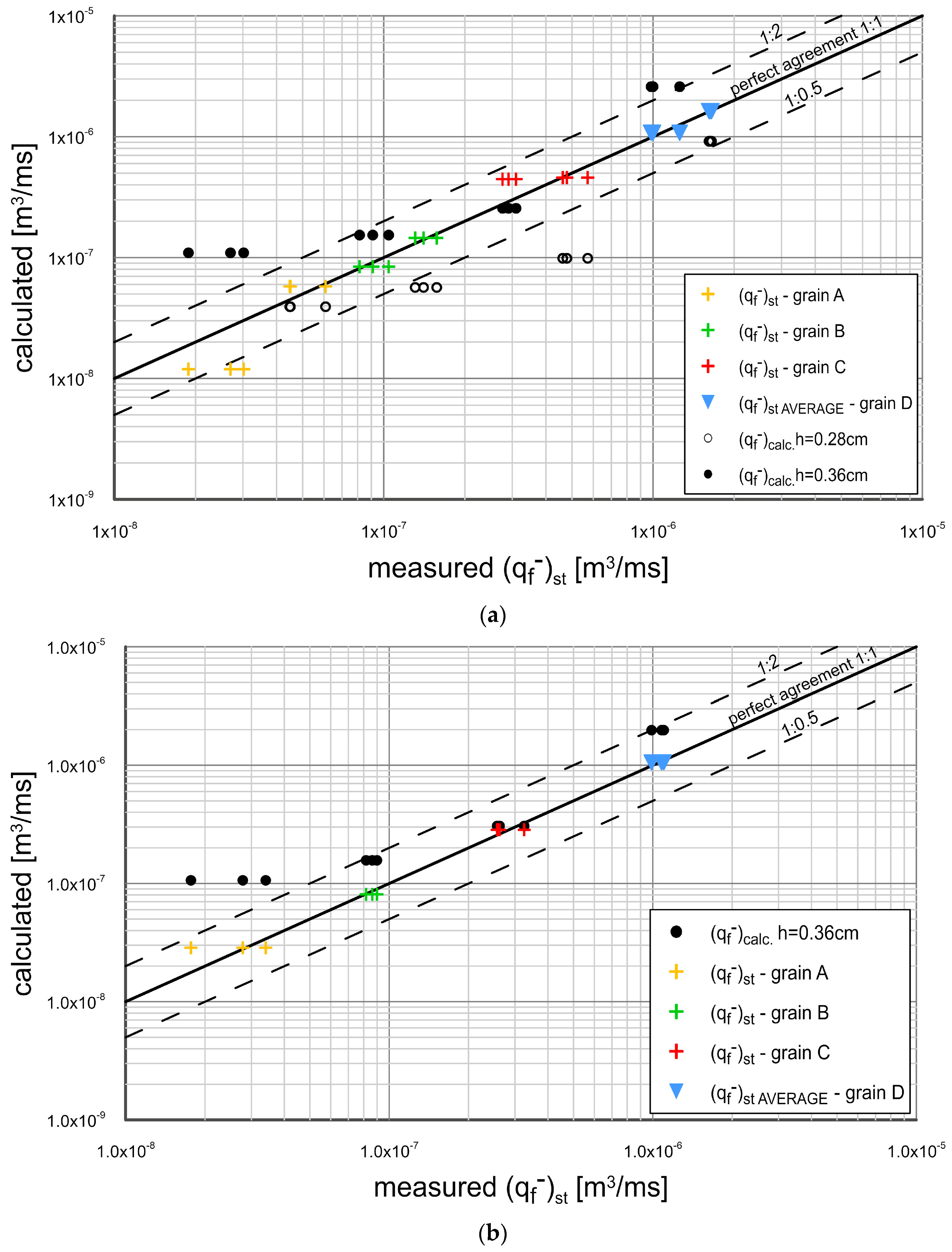
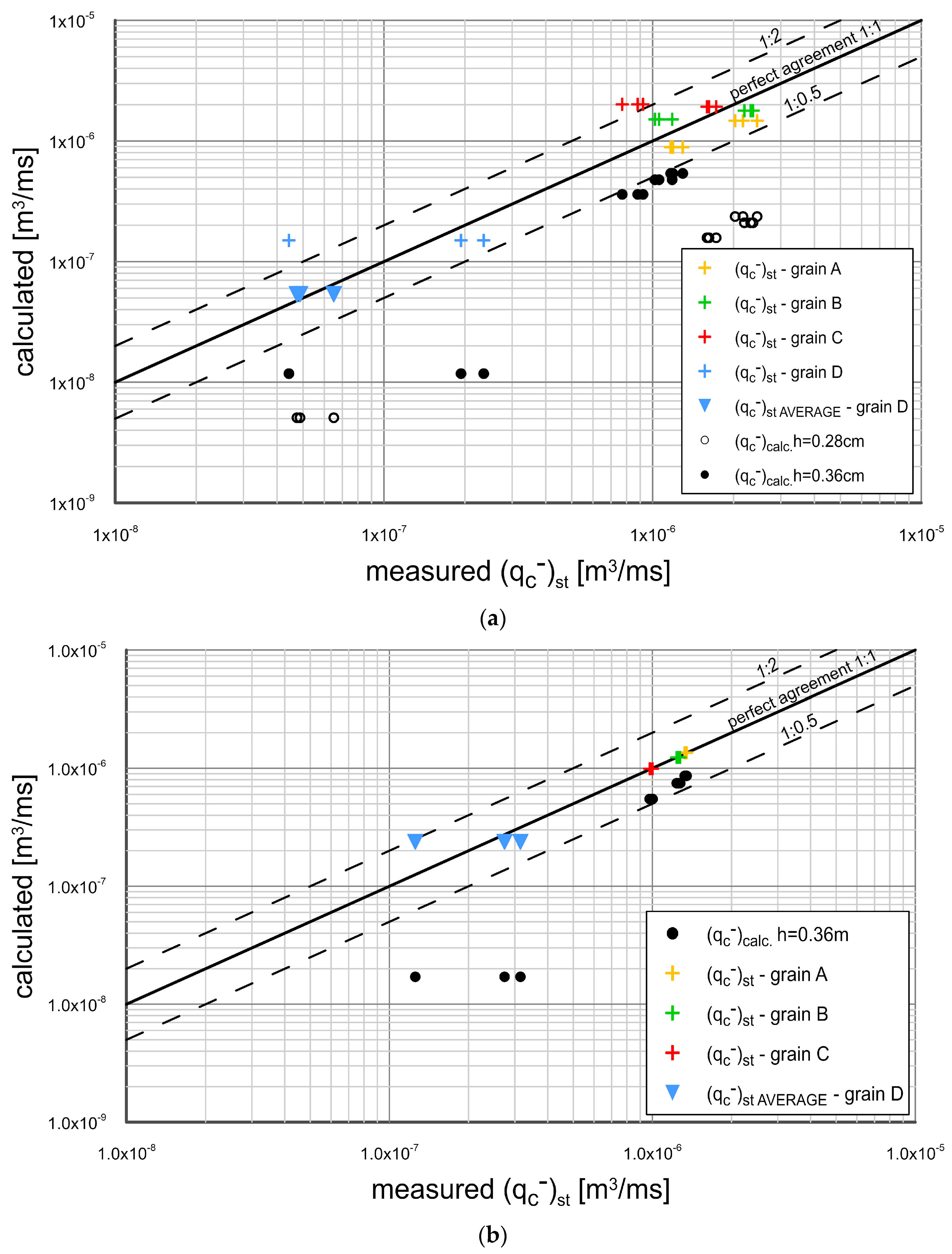
3.4. Comparison of Transport Calculations with Mesurement Results
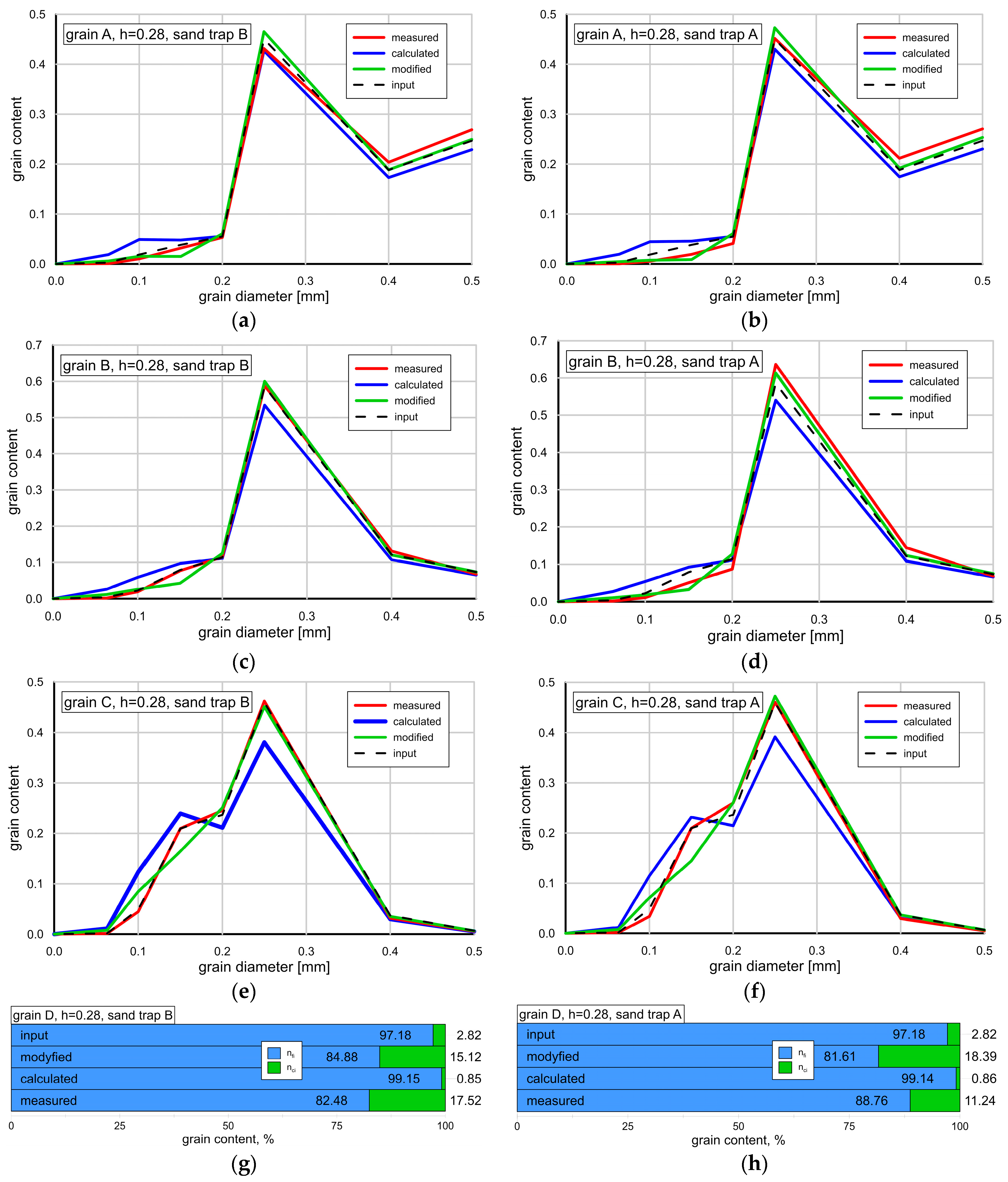
3.5. Comparison of Grain Size Distributions Calculations with Mesurement Results
4. Conclusions
- The vertical structure of total sediment transport with the content of very fine and fine (di < 0.20 mm) and coarse (di ≥ 0.20 mm) fractions, both in the crest and trough of the wave, consists of components:
- transport of outgoing sediment fluxes from the control area, which are deposited in adjacent control areas in both directions;
- transport of fine and very fine sediment fluxes returning to the initial area in a suspended state;
- Experimental results were compared with the results of theoretical analysis, based on the three-layer model of Kaczmarek et al. 2022. This model does not take into account the effects of additional vertical sorting of very fine sediment fractions and neglects the effects of phase lags of fine fractions, as well as does not take into account the effects related to the bed slope, i.e., effect of gravitational forces acting on grains, and the effect of pressure gradients when changing the flow cross section. Therefore, it was proposed to modify this model with the above-mentioned effects. Subsequently, calculations of the transport of fluxes of very fine and fine fractions, coarse fractions and total fractions outgoing in the crest and trough phases from the initial area and deposited in adjacent control areas were carried out and compared with the measurement results. The agreement of calculation results with measurements within +/− a factor two of the measurements was obtained. Calculations of granulometric distributions of sediments retained in adjacent areas from the crest and trough of the wave were also carried out. The calculated granulometric compositions were compared with the measurements and satisfactory agreement of the results was obtained for fine, very fine and coarse fractions;
- Modification of the Kaczmarek et al. 2022 model was carried out based on four coefficients that correct the fluxes of fine and very fine fractions and coarse fractions that feed adjacent control areas on the crest and trough side of the wave. For sands with a relatively low content of fine fractions with d50 ≥ 0.20 mm, it was possible to find a functional relationship of these coefficients with a determination coefficient R2 > 0.80. For sands with a dominant amount of fine and very fine fractions (d50 < 0.20 mm), such a relationship could not be obtained, suggesting the need for further experimental research in this area.
- Sediment transport over the sloping bed in the wave crest increases compared to the flat bed, due to the zone of negative pressure gradient. In the wave crest phase, due to higher hydrodynamic forcing, the fluxes deposited in the adjacent control area (falling into the trap) are larger than those in the flat bed situation. This results in better agreement between the results of calculations by the Kaczmarek et al. 2022 model and the results of measurements compared to those from a flat bed. This agreement deteriorates in case of sediments with a high content of fine and very fine grains, when the fluxes of coarse fractions falling into the trap and the fluxes of fine fractions returning to the initial area are increased;
- In the trough, the situation is reversed—the intensity of sediment transport decreases due to the zone of positive pressure gradient. Due to lower hydrodynamic forcing, the outgoing fluxes toward the adjacent area, as well as the return fluxes in the wave crest are smaller than the fluxes in a flat bed situation. Virtually all of the outgoing flux feeds into the adjacent area (trap), and only a relatively small flux of the finest fractions returns in the wave crest to the initial area. This results in almost perfect agreement between calculations by the Kaczmarek et al. 2022 model and measurements. However, in case of sediment with a large number of fine and very fine fractions, their increased amount in suspension has a decisive influence on the transport of coarse fractions and finally results in an underestimation of the measured transport of coarse fractions by the Kaczmarek et al. 2022 model;
- The influence of gravity forces reveals itself very strongly only in the trough phase when sediment is composed of coarse fractions and a small amount of fine and very fine fractions. However, in case of the greater amount of fine and very fine fractions in the bed, they have a decisive influence on the transport of coarse fractions in the trough phase, far exceeding the influence of gravity forces.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wilson, K.C. Analysis of bed-load motion at high shear stress. J. Hydraul. Eng. 1987, 115, 825–830. [Google Scholar] [CrossRef]
- Sumer, B.M.; Kozakiewicz, A.; Fredsøe, J.; Deigaard, R. Velocity and concentration profiles in sheet-flow layer of movable bed. J. Hydraul. Eng. 1996, 11, 549–558. [Google Scholar] [CrossRef]
- Samaga, B.R.; Garde, R.J.; Ranga Raju, K.G. Total load transport of sediment mixtures. Irrig. Power J. 1985, 42, 345–353. [Google Scholar]
- Karim, F. Bed material discharge prediction for nonuniform bed sediments. J. Hydraul. Eng. 1998, 124, 597–604. [Google Scholar] [CrossRef]
- Wu, W.; Wang, S.S.Y.; Jia, Y. Nonuniform sediment transport in alluvial rivers. J. Hydraul. Res. 2000, 38, 427–434. [Google Scholar] [CrossRef]
- Blom, A.; Ribberink, J.; Parker, G. Vertical sorting and the morphodynamics of bed form-dominated rivers: A sorting evolution model. J. Geophys. Res. 2008, 113, F01019. [Google Scholar] [CrossRef]
- Khosravi, K.; Chegini, A.H.N.; Mao, L.; Rodriguez, J.F.; Saco, P.M.; Binns, A.D. Experimental Analysis of Incipient Motion for Uniform and Graded Sediments. Water 2021, 13, 1874. [Google Scholar] [CrossRef]
- Sun, Z.; Zheng, H.; Xu, D.; Hu, C.; Zhang, C. Vertical concentration profile of nonuniform sediment. Int. J. Sediment Res. 2021, 36, 12–126. [Google Scholar] [CrossRef]
- Ribberink, J.S. Bed-load transport for steady flows and unsteady oscillatory flows. Coast. Eng. 1998, 34, 59–82. [Google Scholar] [CrossRef]
- Dohmen-Janssen, M.C. Grain Size Influence on Sediment Transport in Oscillatory Flow; Febodruk BV: Enschede, The Netherlands, 1999; ISBN 90-9012929-4. [Google Scholar]
- Hassan, W.N. Transport of Size-Graded and Uniform Sediments under Oscillatory Sheet-Flow Conditions. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 2003. [Google Scholar]
- Bailard, J.A. An energetics total load sediment transport model for a plane sloping beach. J. Geophys. Res. 1981, 86, 10938–10954. [Google Scholar] [CrossRef]
- Shields, A. Anwendung der Aehnlichkeitsmechanik und der Turbulenzforschung auf die Geschiebebewegung; Erschienen im Eigenveriage der Preusischen Versuchsanstalt fur Wasserbau und Schiffbau: Berlin, Germany, 1936. [Google Scholar]
- Smart, G.M. Sediment transport formula for steep channels. J. Hydraul. Eng. 1984, 110, 267. [Google Scholar] [CrossRef]
- Wong, M.; Parker, G. Reanalysis and correction of bed-load relation of Meyer-Peter and Müller using their own database. J. Hydraul. Eng. 2006, 132, 1159–1168. [Google Scholar] [CrossRef]
- Damgaard, J.S.; Whitehouse, R.J.S.; Soulsby, R.L. Bed-load sediment transport on steep longitudinal slopes. J. Hydraul. Eng. 1997, 123, 1130–1138. [Google Scholar] [CrossRef]
- Cheng, N.S.; Chen, X. Slope Correction for Calculation of Bedload Sediment Transport Rates in Steep Channels. J. Hydraul. Eng. 2014, 140, 843. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Müller, R. Formulas for bed-load transport. In Proceedings of the 2nd Meeting of the International Association for Hydraulic Structures Research, Delft, The Netherlands, 7 June 1948; pp. 39–64. [Google Scholar]
- Lamb, M.P.; Dietrich, W.E.; Venditti, J.G. Is the critical Shields stress for incipient sediment motion dependent on channel-bed slope? J. Geophys. Res. 2008, 113, F02008. [Google Scholar] [CrossRef]
- Recking, A.; Frey, P.; Paquier, A.; Belleudy, P.; Champagne, J.Y. Bed-load transport flume experiments on steep slopes. J. Hydraul. Eng. 2008, 134, 9. [Google Scholar] [CrossRef]
- Parker, C.; Clifford, N.J.; Thorne, C.R. Understanding the influence of slope on the threshold of coarse grain motion: Revisiting critical stream power. Geomorphology 2011, 126, 51–65. [Google Scholar] [CrossRef]
- Maurin, R.; Chauchat, J.; Frey, P. Revisiting slope influence in turbulent bedload transport: Consequences for vertical flow structure and transport rate scaling. J. Fluid Mech. 2018, 839, 135–156. [Google Scholar] [CrossRef]
- King, D.B. Studies in Oscillatory Flow Bedload Sediment Transport. Ph.D. Thesis, University of California, San Diego, CA, USA, 1991. [Google Scholar]
- Tan, W.; Yuan, J. Modeling net sheet-flow sediment transport rate under skewed and asymmetric oscillatory flows over a sloping bed. Coast. Eng. 2018, 136, 65–80. [Google Scholar] [CrossRef]
- Tan, W.; Yuan, J. Experimental study of sheet-flow sediment transport under nonlinear oscillatory flow over a sloping bed. Coast. Eng. 2019, 147, 1–11. [Google Scholar] [CrossRef]
- Tan, W.; Yuan, J. Net sheet-flow sediment transport rate: Additivity of wave propagation and nonlinear waveshape effects. Cont. Shelf Res. 2020, 240, 104724. [Google Scholar] [CrossRef]
- Box, W.; Järvelä, J.; Västilä, K. Flow resistance of floodplain vegetation mixtures for modelling river flows. J. Hydrol. 2021, 601, 126593. [Google Scholar] [CrossRef]
- Khan, M.A.; Sharma, N.; Lama, G.F.C.; Hasan, M.; Garg, R.; Busico, G.; Alharbi, R.S. Three-Dimensional Hole Size (3DHS) Approach for Water Flow Turbulence Analysis over Emerging Sand Bars: Flume-Scale Experiments. Water 2022, 14, 1889. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Rillo Migliorini Giovannini, M.; Errico, A.; Mirzaei, S.; Padulano, R.; Chirico, G.B.; Preti, F. Hydraulic Efficiency of Green-Blue Flood Control Scenarios for Vegetated Rivers: 1D and 2D Unsteady Simulations. Water 2021, 13, 2620. [Google Scholar] [CrossRef]
- Lama, G.F.C.; Errico, A.; Francalanci, S.; Solari, L.; Chirico, G.B.; Preti, F. Hydraulic Modeling of Field Experiments in a Drainage Channel Under Different Riparian Vegetation Scenarios. In Innovative Biosystems Engineering for Sustainable Agriculture, Forestry and Food Production; Coppola, A., Di Renzo, G., Altieri, G., D’Antonio, P., Eds.; Springer: Cham, Switzerland, 2020; pp. 69–77. [Google Scholar] [CrossRef]
- Radosz, I.; Zawisza, J.; Biegowski, J.; Paprota, M.; Majewski, D.; Kaczmarek, L.M. An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in Wave Motion. Water 2022, 14, 2397. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Biegowski, J.; Sobczak, Ł. Modeling of Sediment Transport with a Mobile Mixed-Sand Bed in Wave Motion. J. Hydraul. Eng. 2022, 148, 04021054. [Google Scholar] [CrossRef]
- Kaczmarek, L.M. Moveable Sea Bed Boundary Layer and Mechanics of Sediment Transport; IBW PAN: Gdańsk, Poland, 1999; ISBN 83-85708-35-9. [Google Scholar]
- Kaczmarek, L.M.; Ostrowski, R. Modelling intensive near–bed sand transport under wave–current flow versus laboratory and field data. Coast. Eng. 2002, 45, 1–18. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Biegowski, J.; Ostrowski, R. Modelling cross–shore intensive sand transport and changes of grain size distribution versus field data. Coast. Eng. 2004, 51, 501–529. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Sawczyński, S.; Biegowski, J. Hydrodynamic Equilibrium for Sediment Transport and Bed Response to Wave Motion. Acta Geophys. 2015, 63, 486–513. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Sawczyński, S.; Biegowski, J. An Equilibrium Transport Formula for Modeling Sedimentation of Dredged Channels. Coast. Eng. 2017, 59, 1750015-1–1750015-35. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Biegowski, J.; Sobczak, Ł. Modeling of Sediment Transport in Steady Flow over Mobile Granular Bed. J. Hydraul. Eng. 2019, 145, 04019009. [Google Scholar] [CrossRef]
- Kaczmarek, L.M.; Radosz, I.; Zawisza, J. Numerical Calculations with a Multi-layer Model of Mixed Sand Transport Against Measurements in Wave Motion and Steady Flow. Annu. Set Environ. Prot. 2021, 23, 629–641. [Google Scholar] [CrossRef]
- Malarkey, J.; Davies, A. Free-stream velocity descriptions under waves with skewness and asymmetry. Coast. Eng. 2012, 68, 78–95. [Google Scholar] [CrossRef]
- Elfrink, B.; Hanes, D.M.; Ruessink, B.G. Parameterization and simulation of near bed orbital velocities under irregular waves in shallow water. Coast. Eng. 2006, 53, 915–927. [Google Scholar] [CrossRef]
- Zou, Q.; Hay, A.E. The Vertical Structure of the Wave Bottom Boundary Layer over a Sloping Bed: Theory and Field Measurements. J. Phys. Oceanogr. 2003, 33, 1380–1400. [Google Scholar] [CrossRef]
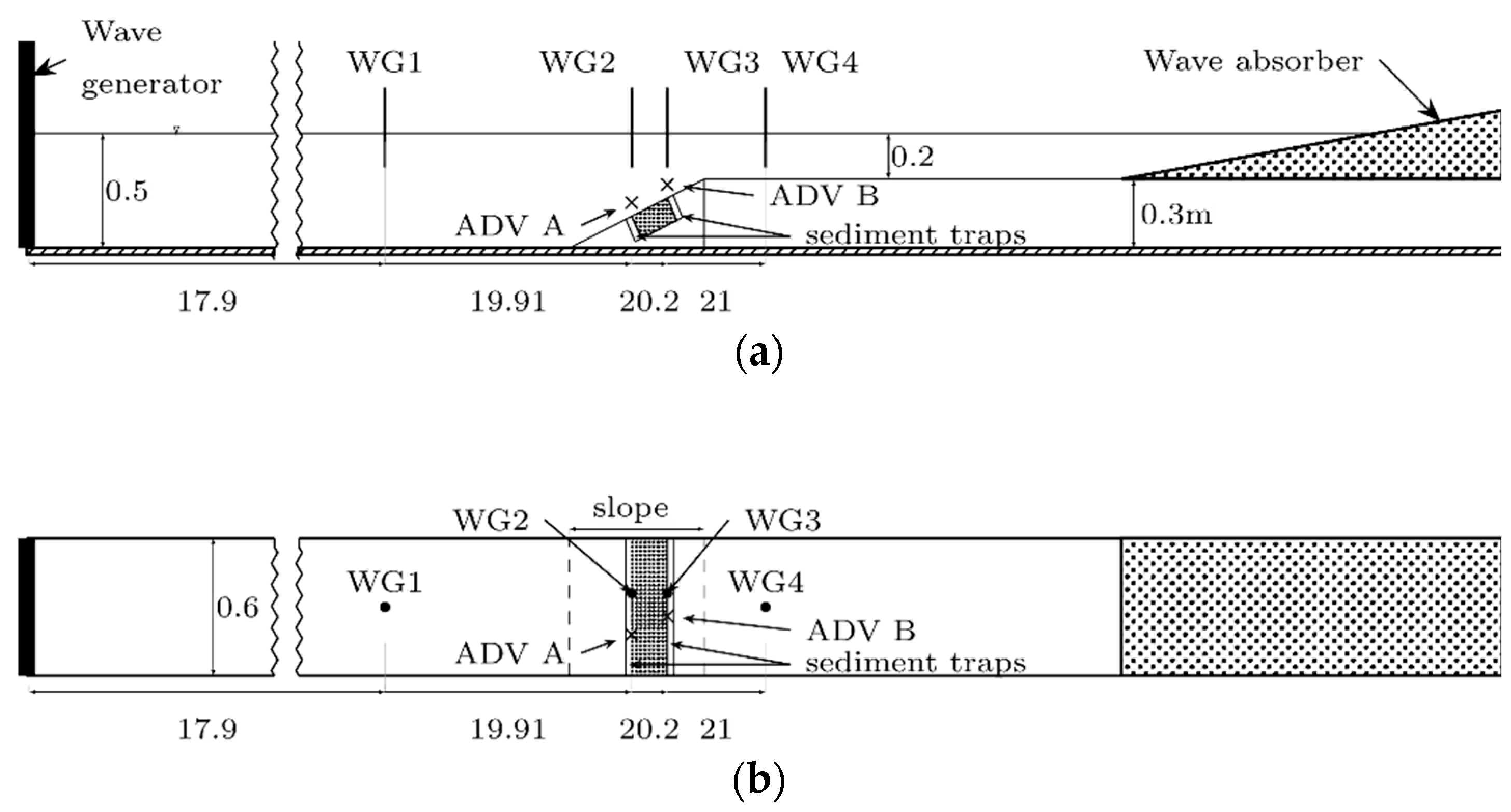




| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Water depth | h0 | 0.50 | m |
| Wave height | Hw | 0.12 | m |
| Test duration | Tw | 10 | min |
| Wave peak period | Tp | 3.0 | s |
| Representative diameter of bottom-building sediment grains | d50 | A: 0.38 B: 0.32 C: 0.25 D: 0.14 | mm |
| Sediment density | ρs | 2.62 | g/cm3 |
| Liquid density | ρw | 1.00 | g/cm3 |
| Sediment porosity | np | 0.4 | – |
| Type of Sand | d90/d50/d10 |
|---|---|
| A. Coarse quartz sand | 0.58/0.38/0.24 |
| B. Medium quartz sand | 0.48/0.32/0.20 |
| C. Fine quartz sand | 0.38/0.25/0.16 |
| D. Very fine quartz sand | 0.19/0.14/0.08 |
| 0.5*a0 | a1 | b1 | a2 | b2 | a3 | b3 | a4 | b4 | ADV |
|---|---|---|---|---|---|---|---|---|---|
| −0.0216 | 0.0389 | −0.2504 | −0.0216 | 0.0358 | −0.0022 | 0.0216 | 0.0025 | 0.0107 | A |
| −0.0395 | 0.0396 | −0.3023 | −0.0121 | 0.0611 | 0.0003 | 0.0198 | 0.0045 | 0.0116 | B |
| δ = 0.5 cm—Flat Bed | ||||
| Case | Trough h = 0.36 cm | Crest h = 0.28 cm | ||
| from Sand Trap | to Sand Trap | to Sand Trap | from Sand Trap | |
| Sand A | 0.00012 | −0.00020 | 0.00014 | −0.00009 |
| (8.6%) | (4.5%) | (11.1%) | (6.8%) | |
| Sand B | 0.00018 | −0.00025 | 0.00008 | −0.00009 |
| (3.7%) | (5.6%) | (21.2%) | (8.7%) | |
| Sand C | 0.00022 | −0.00025 | 0.00006 | −0.00007 |
| (5.2%) | (3.9%) | (16.4%) | (5.3%) | |
| δ = 2.0 cm—Flat Bed | ||||
| Case | Trough h = 0.36 cm | Crest h = 0.28 cm | ||
| from Sand Trap | to Sand Trap | to Sand Trap | from Sand Trap | |
| Sand A | 0.00067 | −0.00061 | 0.00042 | −0.00049 |
| (7.2%) | (7.0%) | (17.0%) | (8.6%) | |
| Sand B | 0.00094 | −0.00091 | 0.00024 | −0.00038 |
| (2.5%) | (8.1%) | (24.5%) | (11.4%) | |
| Sand C | 0.00105 | −0.00091 | 0.00016 | −0.00035 |
| (3.1%) | (5.2%) | (12.6%) | (6.4%) | |
| δ = 0.5 cm—Sloped Bed | ||||
| Case | Trough h = 0.36 cm | Crest h = 0.28 cm | ||
| from Sand Trap | to Sand Trap | to Sand Trap | from Sand Trap | |
| Sand A | 0.00004 | −0.00018 | 0.00033 | −0.00017 |
| (8.0%) | (5.9%) | (4.0%) | (4.9%) | |
| Sand B | 0.00004 | −0.00021 | 0.00039 | −0.00015 |
| (7.7%) | (7.0%) | (3.5%) | (8.4%) | |
| Sand C | 0.00004 | −0.00017 | 0.00033 | −0.00015 |
| (7.5%) | (8.3%) | (4.2%) | (8.4%) | |
| Sand D | 0.00005 | −0.00015 | 0.00010 | −0.00013 |
| (6.3%) | (4.5%) | (9.6%) | (5.5%) | |
| δ = 2.0 cm—Sloped Bed | ||||
| Case | Trough h = 0.36 cm | Crest h = 0.28 cm | ||
| from Sand Trap | to Sand Trap | to Sand Trap | from Sand Trap | |
| Sand A | 0.00049 | −0.00044 | 0.00075 | −0.00078 |
| (7.5%) | (8.4%) | (6.2%) | (4.3%) | |
| Sand B | 0.00068 | −0.00085 | 0.00106 | −0.00098 |
| (3.8%) | (8.7%) | (5.2%) | (7.0%) | |
| Sand C | 0.00061 | −0.00076 | 0.00107 | −0.00094 |
| (4.2%) | (8.8%) | (6.2%) | (7.0%) | |
| Sand D | 0.00037 | −0.00073 | 0.00049 | −0.00085 |
| (6.1%) | (5.3%) | (8.3%) | (4.3%) | |
| Crest | ||||
| Type of Sand | —Sloped Bed Case | —Flat Bed Case | —Sloped Bed Case | —Flat Bed Case |
| Sand A | 0.278185 | 0.204274 | 0.96722 | 0.600155 |
| Sand B | 0.374075 | 0.308164 | 0.95137 | 0.759586 |
| Sand C | 0.535349 | 0.482891 | 0.924714 | 1.027727 |
| Sand D | 0.258206 | 1.049027 | 5.387826 | 1.896533 |
| Trough | ||||
| Type of Sand | —Sloped Bed Case | —Flat Bed Case | —Sloped Bed Case | —Flat Bed Case |
| Sand A | −0.33714 | −0.31215 | 0.278621 | 0.153719 |
| Sand B | −0.22297 | −0.12580 | 0.320369 | 0.531003 |
| Sand C | −0.03117 | 0.187276 | 0.390508 | 1.164859 |
| Sand D | −0.21587 | 1.199482 | 6.076916 | 3.214157 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Radosz, I.; Zawisza, J.; Biegowski, J.; Paprota, M.; Majewski, D.; Kaczmarek, L.M. An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in the Wave Motion over Sloped Bed. Water 2023, 15, 125. https://doi.org/10.3390/w15010125
Radosz I, Zawisza J, Biegowski J, Paprota M, Majewski D, Kaczmarek LM. An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in the Wave Motion over Sloped Bed. Water. 2023; 15(1):125. https://doi.org/10.3390/w15010125
Chicago/Turabian StyleRadosz, Iwona, Jerzy Zawisza, Jarosław Biegowski, Maciej Paprota, Dawid Majewski, and Leszek M. Kaczmarek. 2023. "An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in the Wave Motion over Sloped Bed" Water 15, no. 1: 125. https://doi.org/10.3390/w15010125
APA StyleRadosz, I., Zawisza, J., Biegowski, J., Paprota, M., Majewski, D., & Kaczmarek, L. M. (2023). An Experimental Study on Progressive and Reverse Fluxes of Sediments with Fine Fractions in the Wave Motion over Sloped Bed. Water, 15(1), 125. https://doi.org/10.3390/w15010125







