Early Forecasting Hydrological and Agricultural Droughts in the Bouregreg Basin Using a Machine Learning Approach
Abstract
:1. Introduction
2. Materials and Methods
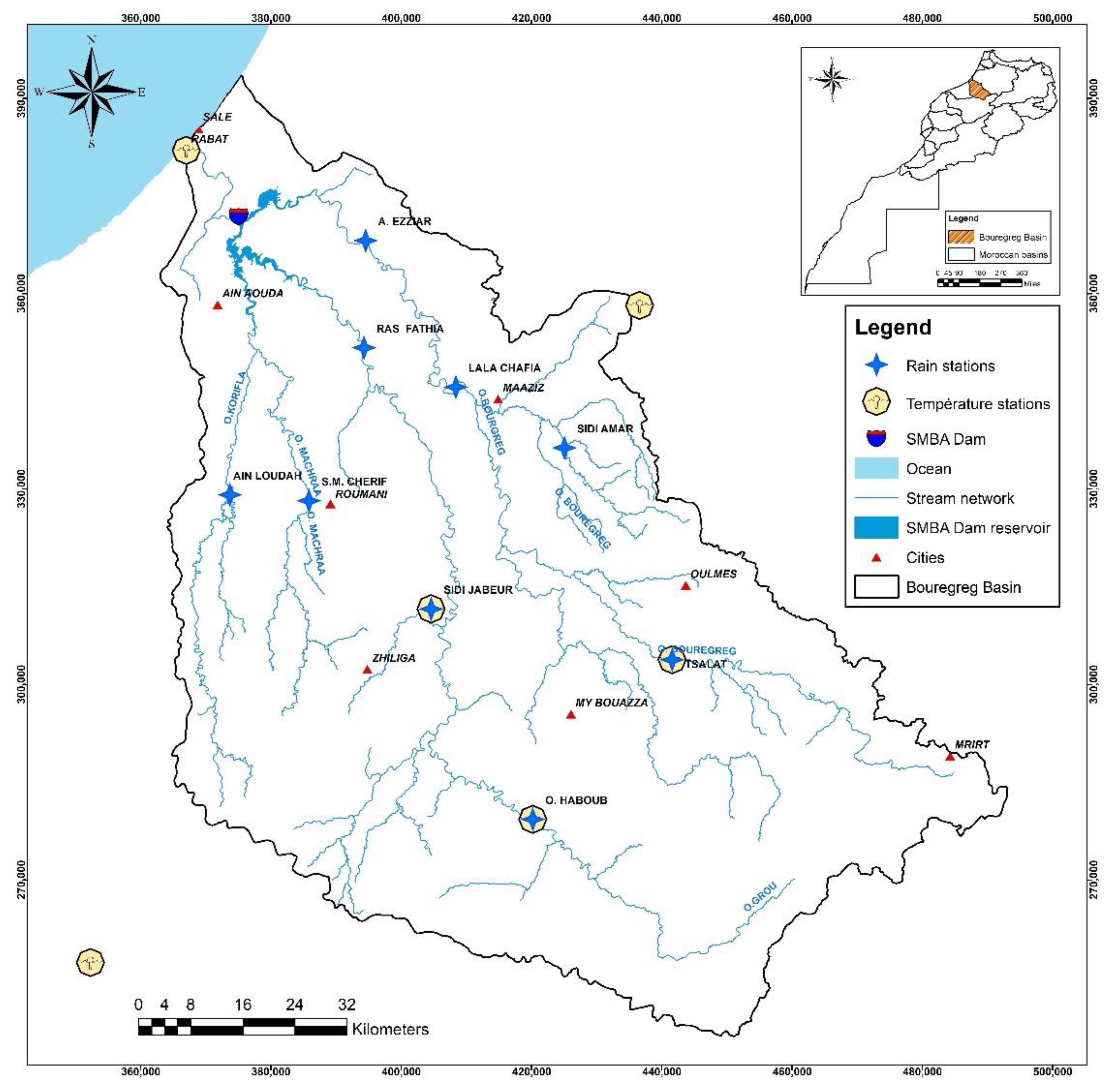
2.1. Study Area
2.2. Datasets
2.2.1. Precipitation and Temperature
2.2.2. Runoff Data
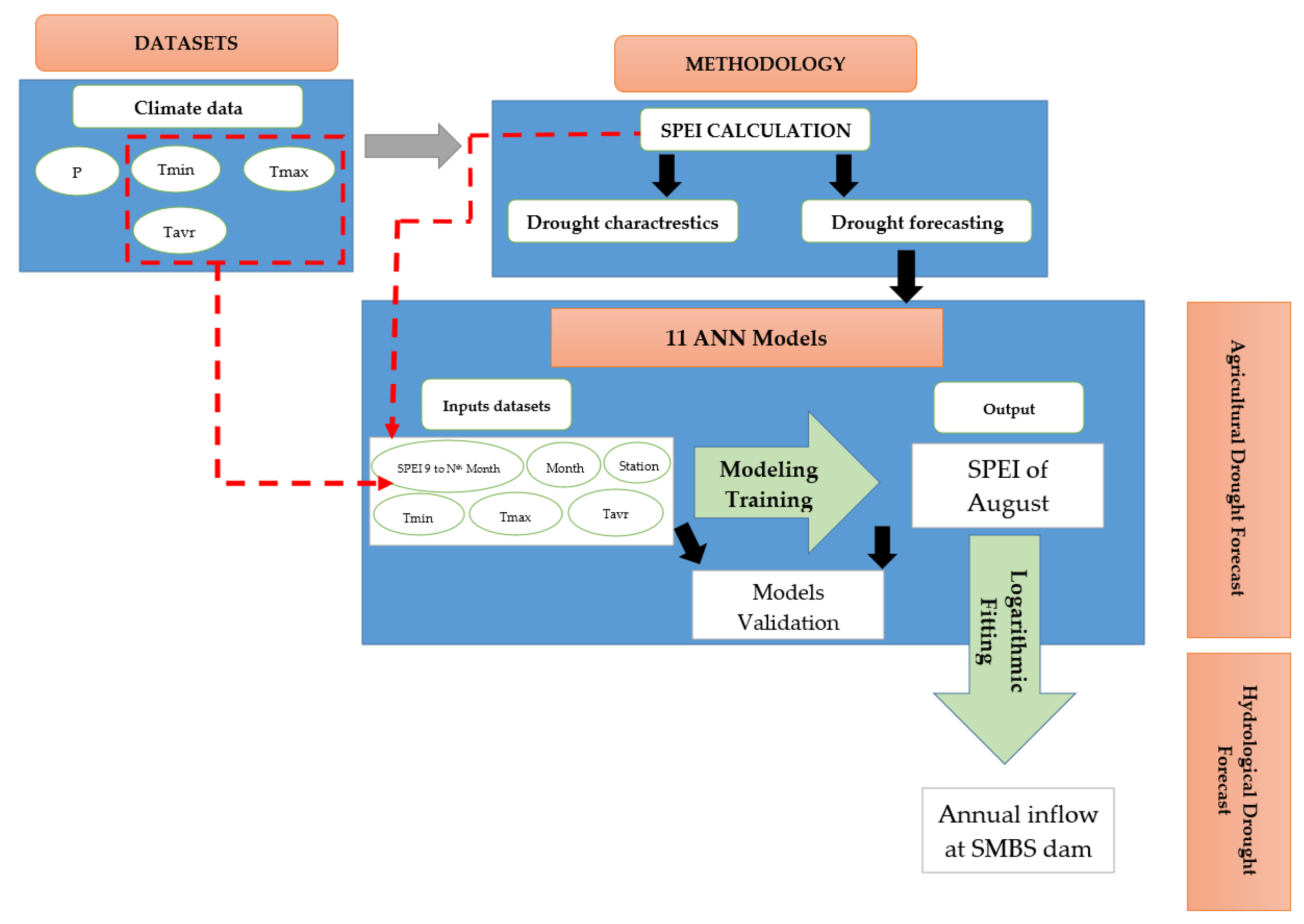
2.3. Methodology
2.3.1. Standard Precipitation Evapotranspiration Index (SPEI)
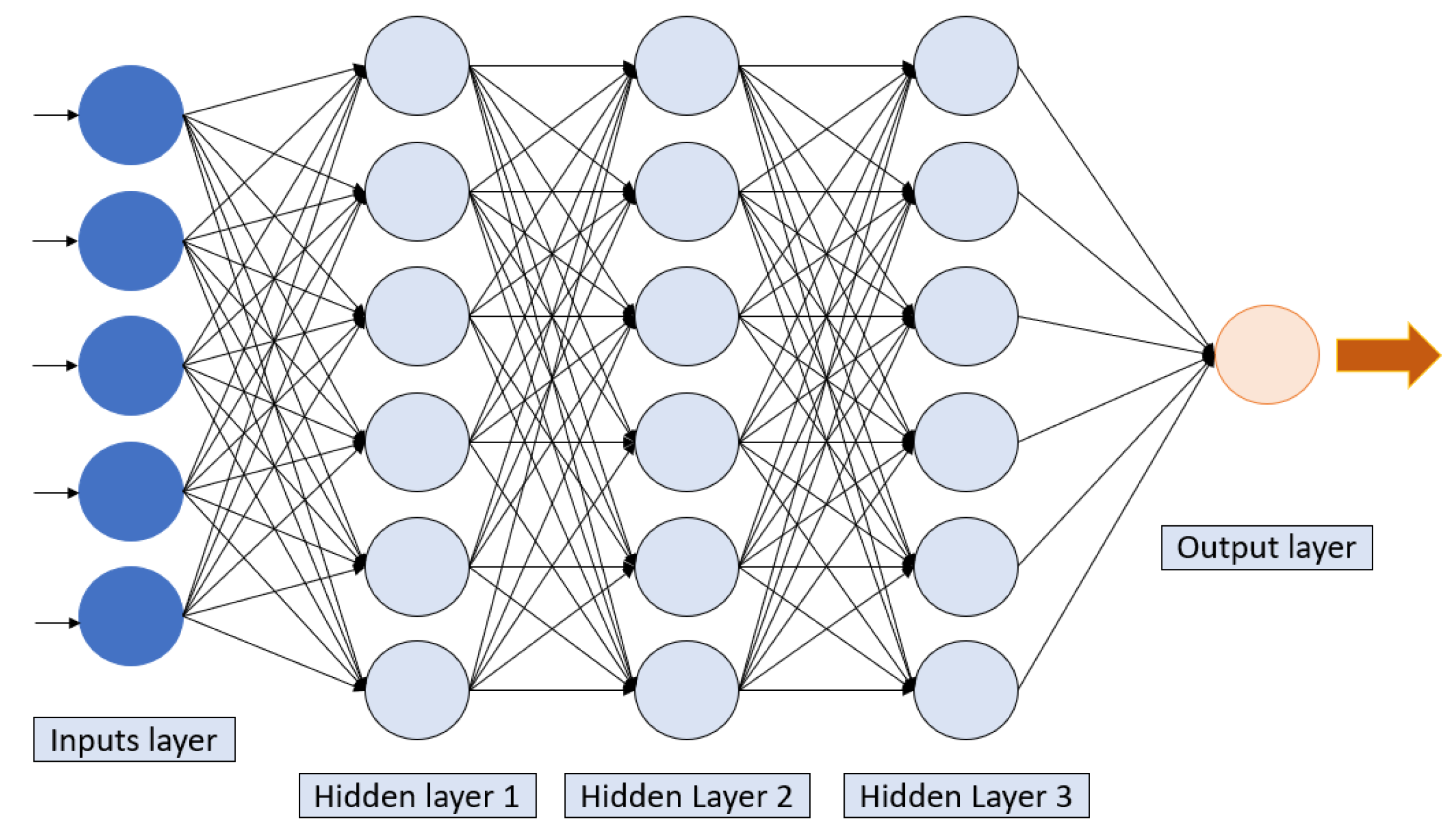
2.3.2. Artificial Neural Network (ANN)
2.3.3. Performances of the Models
3. Results
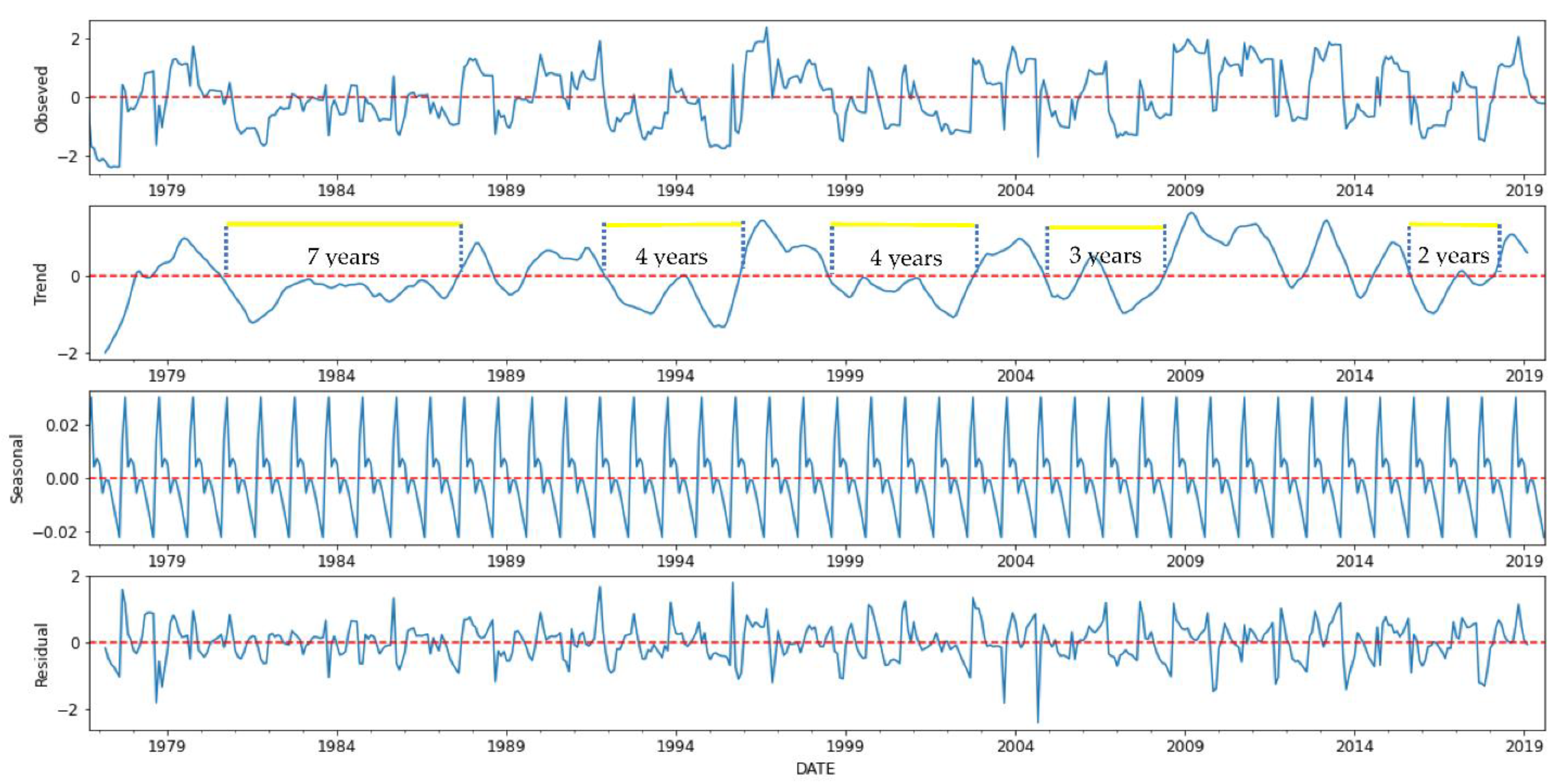
3.1. Analysis of the Drought Events and Characteristics during 1970–2021
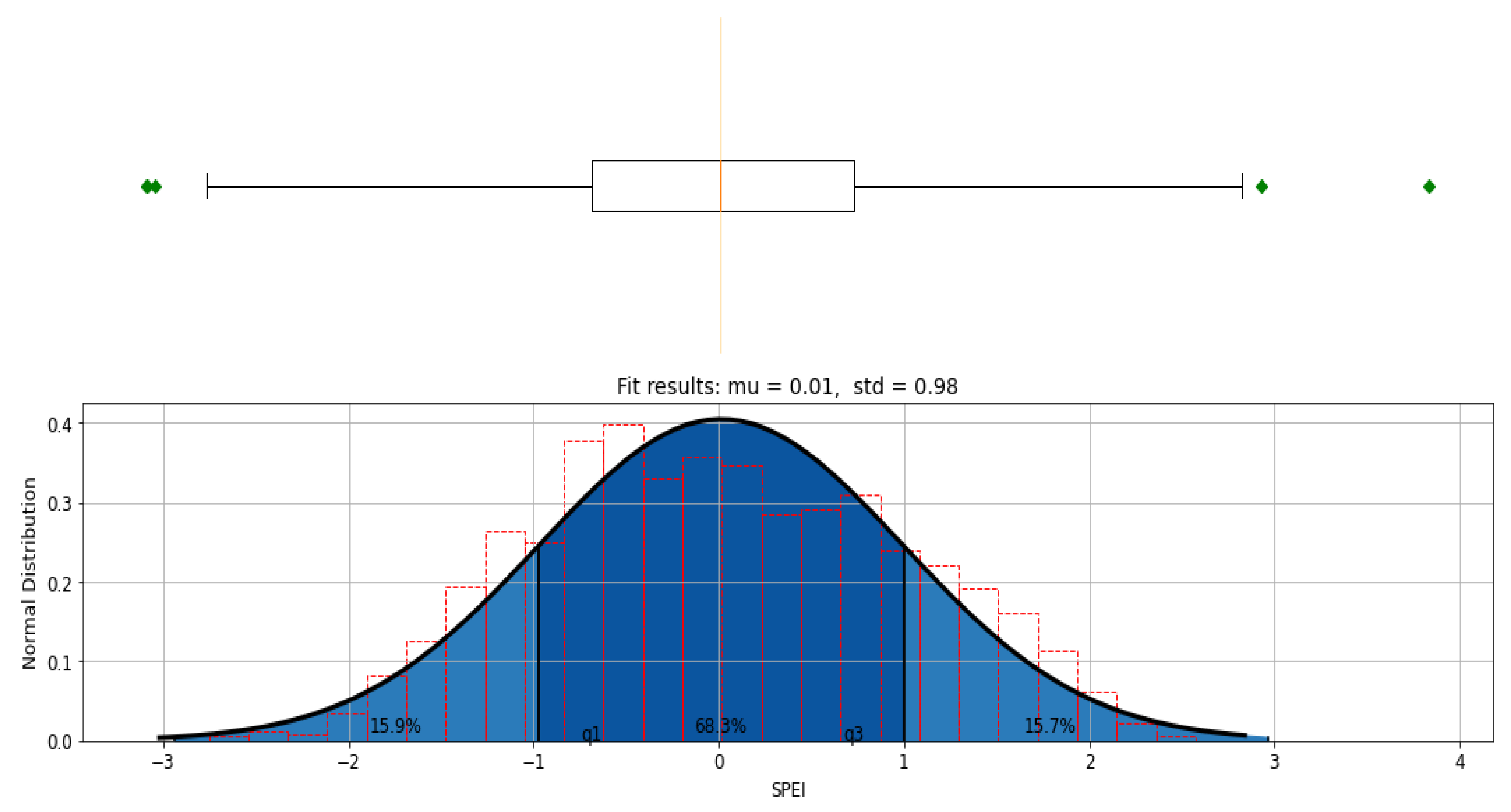
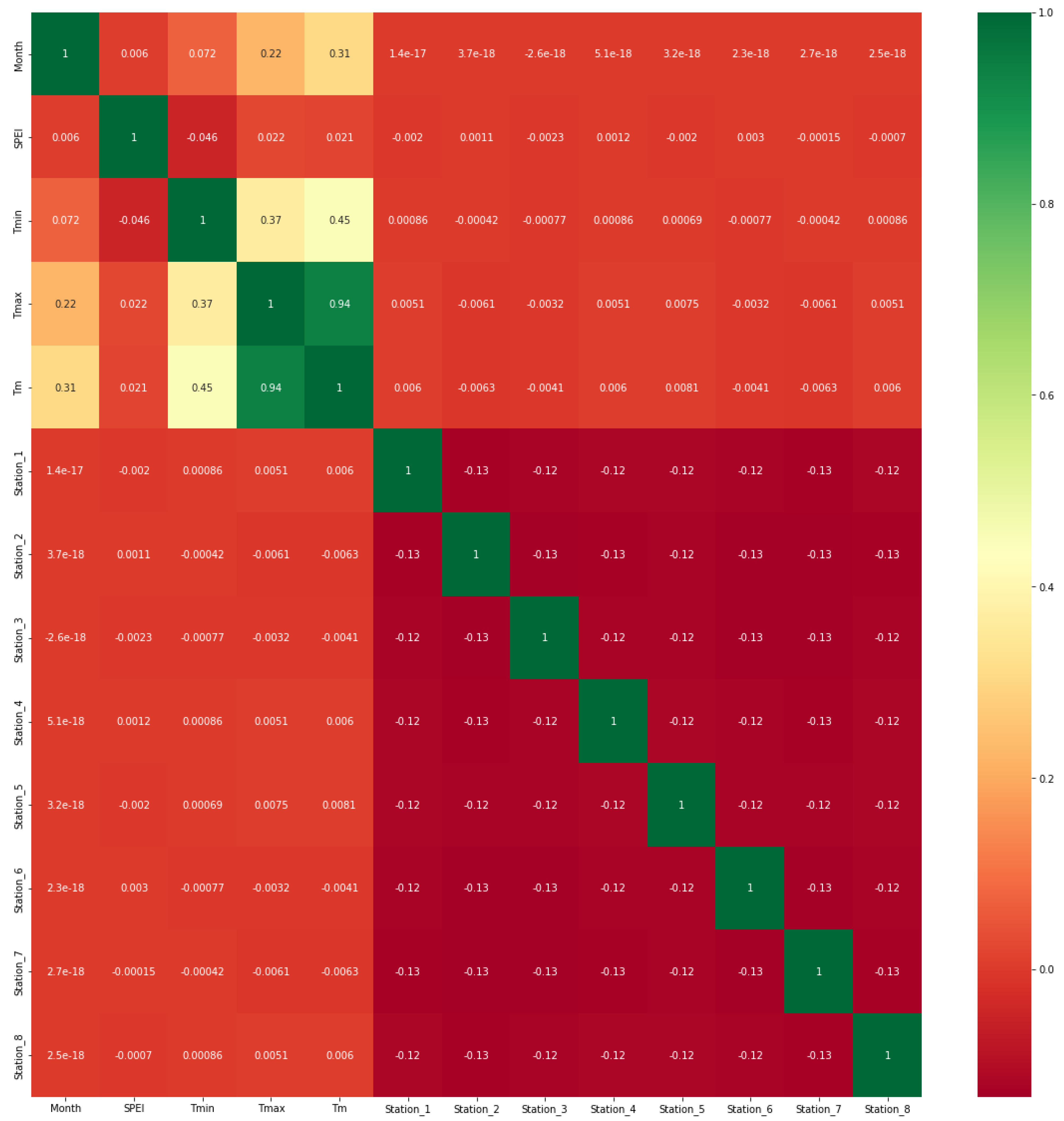
3.2. Data Analysis
3.3. Training Process of the Machine Learning Models
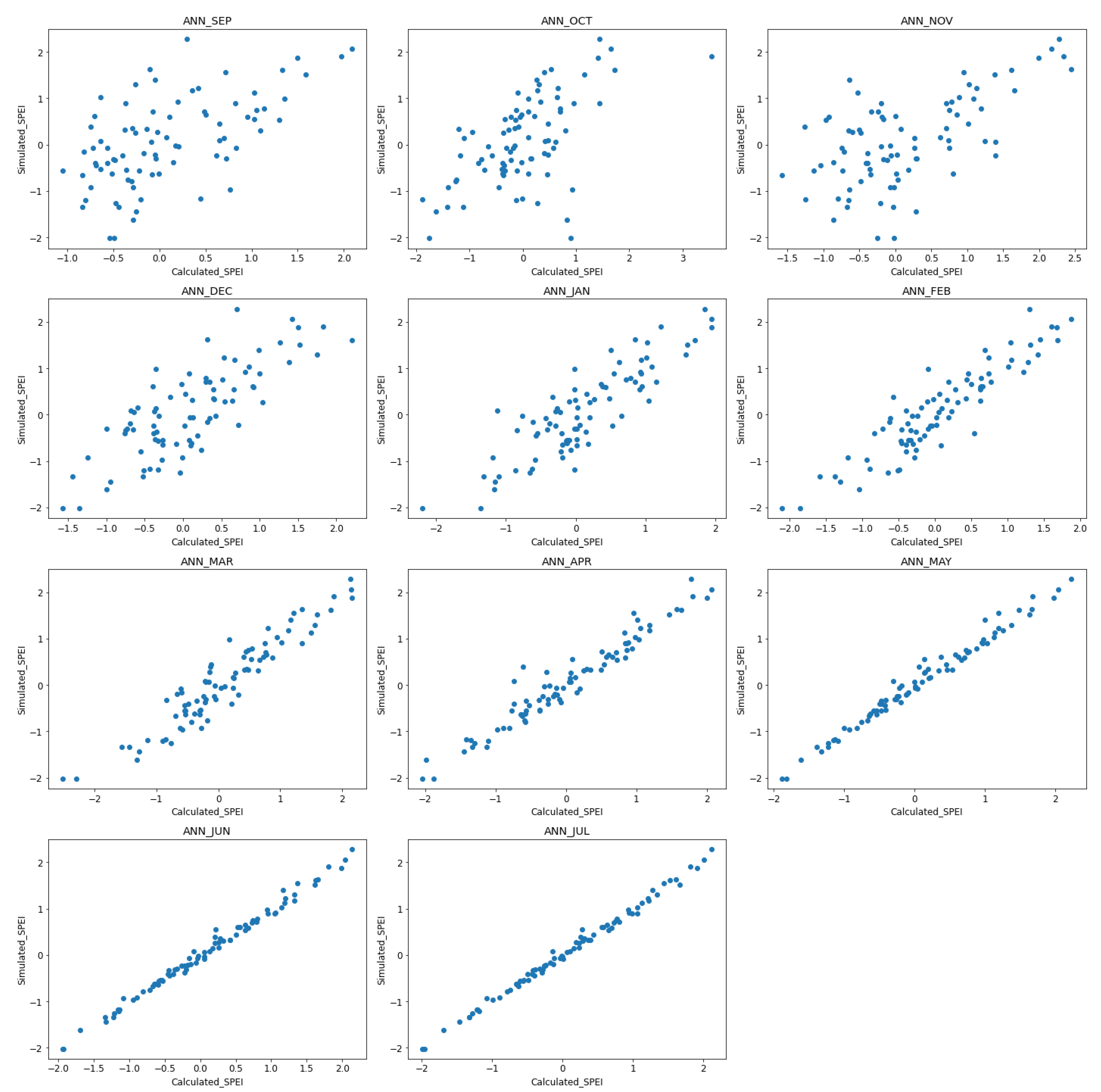
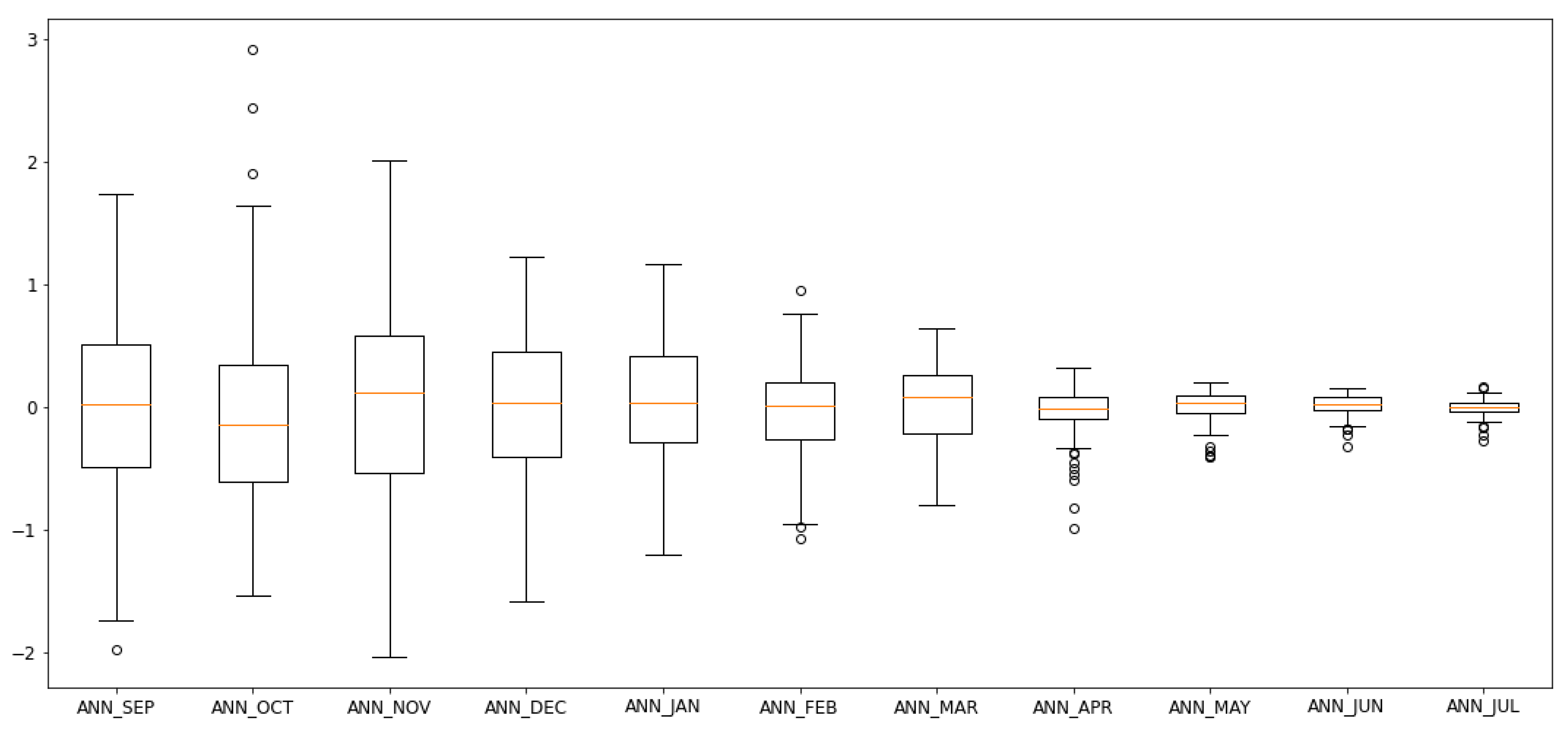
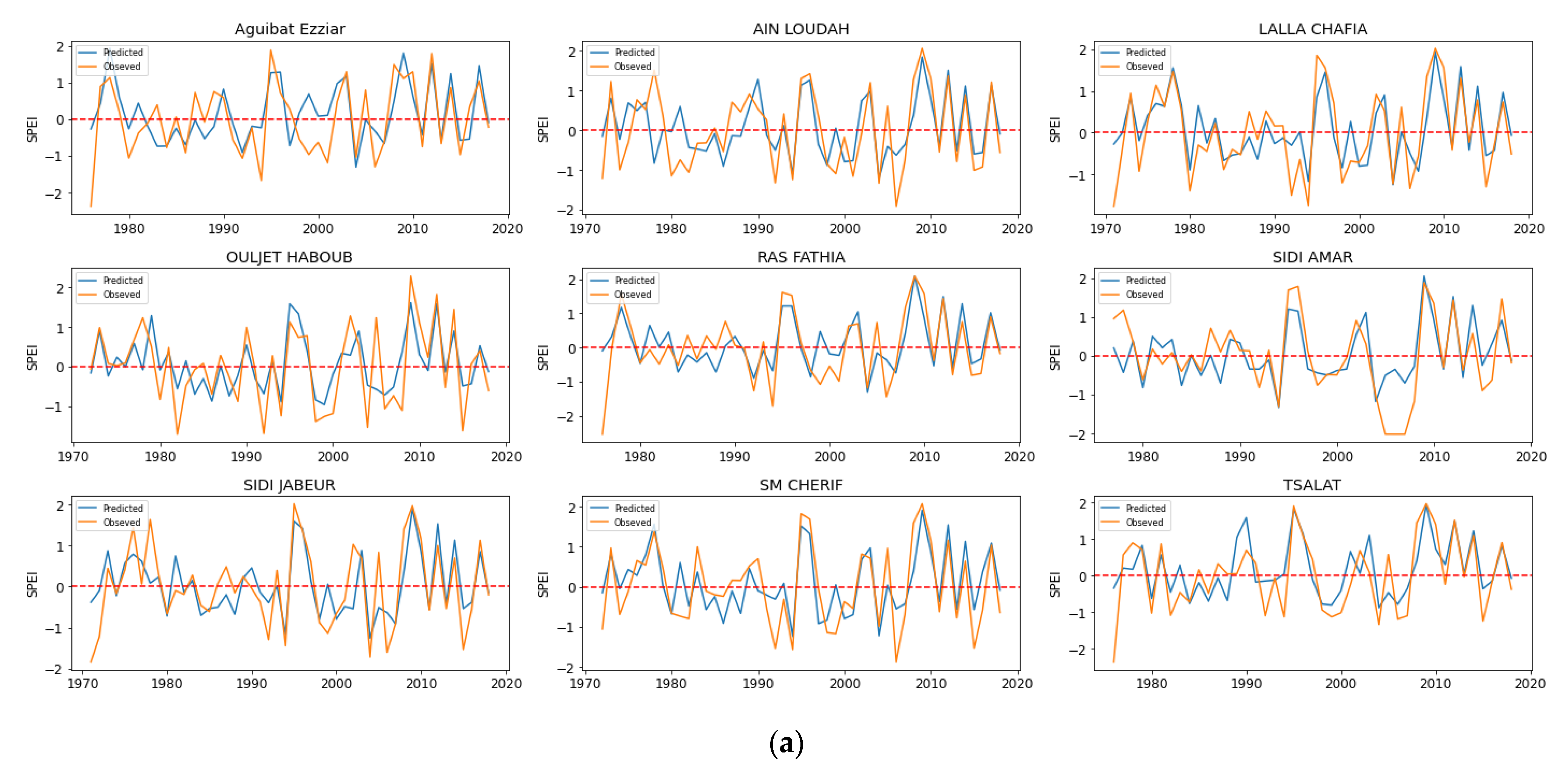
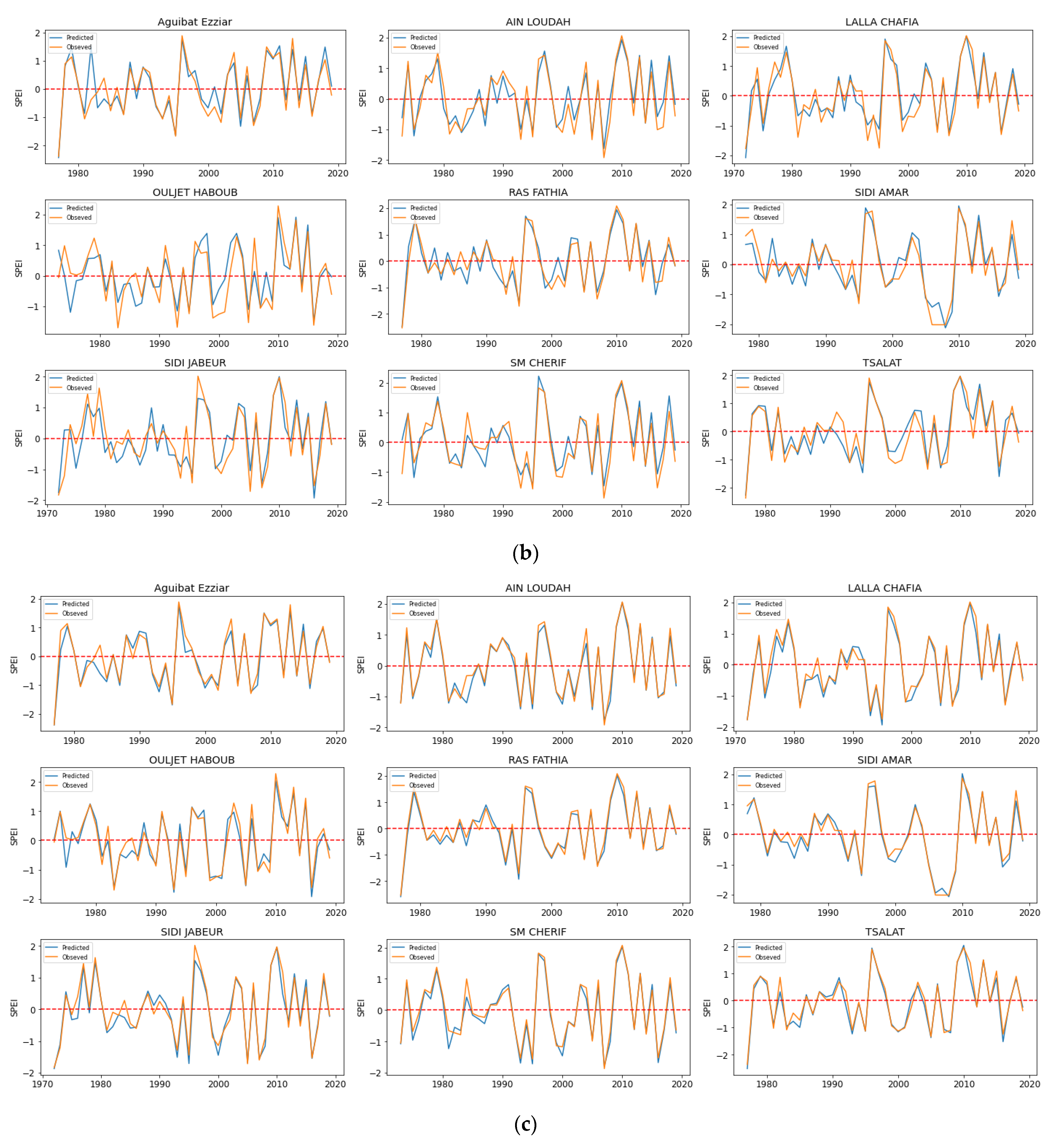
3.4. Validation of the ML Models
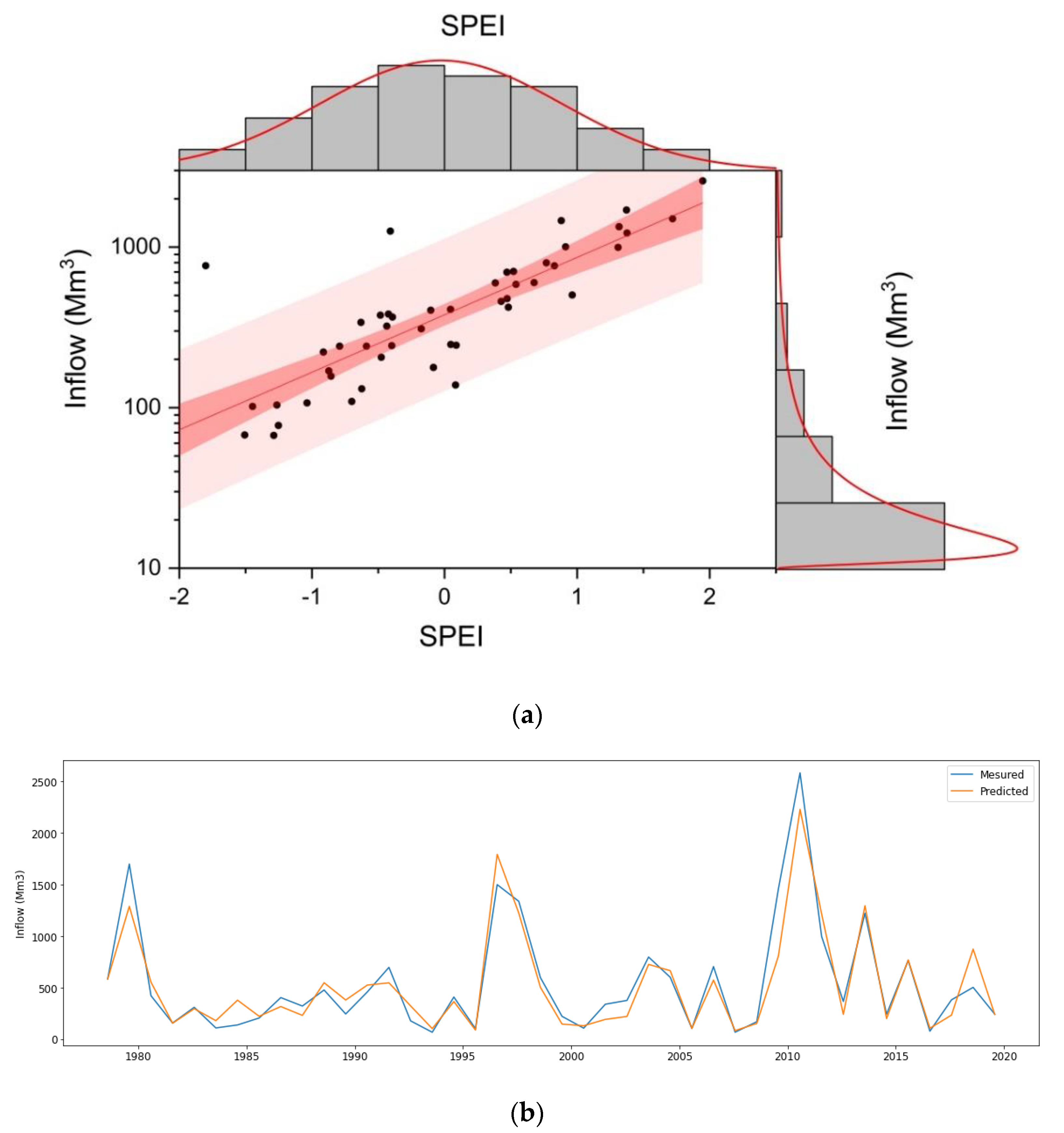
3.5. Hydrological Drought Prediction
4. Conclusions
- Developed ANN models presented good prediction accuracy in forecasting drought using SPEI, with an NSE ranging from 0.62 to 0.99, an R2 ranging from 0.62 to 0.99, and an RMSE ranging from 0.07 to 0.58. Thus, the generalization ability through the validation process demonstrated the stability of the applied models in predicting the annual SPEI;
- From December, the models are fairly accurate in predicting the annual SPEI at the end of the hydrological year;
- Hydrological drought is exponentially linked to agricultural drought.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Maughan, N.; Camenisch, C.; Brázdil, R.; White, S. Societal impacts of historical droughts in a warming world. Reg. Environ. Chang. 2022, 22, 74. [Google Scholar] [CrossRef]
- Mohammed, S.; Alsafadi, K.; Enaruvbe, G.O.; Bashir, B.; Elbeltagi, A.; Széles, A.; Alsalman, A.; Harsanyi, E. Assessing the impacts of agricultural drought (SPI/SPEI) on maize and wheat yields across Hungary. Sci. Rep. 2022, 12, 8838. [Google Scholar] [CrossRef] [PubMed]
- Manzano, A.; Clemente, M.A.; Morata, A.; Luna, M.Y.; Beguería, S.; Vicente-Serrano, S.M.; Martín, M.L. Analysis of the atmospheric circulation pattern effects over SPEI drought index in Spain. Atmos. Res. 2019, 230, 104630. [Google Scholar] [CrossRef]
- Wilhite, D.A.; Svoboda, M.D.; Hayes, M.J. Understanding the complex impacts of drought: A key to enhancing drought mitigation and preparedness. Water Resour. Manag. 2007, 21, 763–774. [Google Scholar] [CrossRef] [Green Version]
- Mohammed, S.; Alsafadi, K.; Al-Awadhi, T.; Sherief, Y.; Harsanyie, E.; El Kenawy, A.M. Space and time variability of meteorological drought in Syria. Acta Geophys. 2020, 68, 1877–1898. [Google Scholar] [CrossRef]
- Ahmed, K.; Shahid, S.; Harun, S.B.; Wang, X.-J. Characterization of seasonal droughts in Balochistan Province, Pakistan. Stoch. Environ. Res. Risk Assess. 2016, 30, 747–762. [Google Scholar] [CrossRef]
- Van Dijk, A.I.J.M.; Beck, H.E.; Crosbie, R.S.; de Jeu, R.A.M.; Liu, Y.Y.; Podger, G.M.; Timbal, B.; Viney, N.R. The Millennium Drought in southeast Australia (2001–2009): Natural and human causes and implications for water resources, ecosystems, economy, and society. Water Resour. Res. 2013, 49, 1040–1057. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P.; Xia, Y. Seasonal Drought Prediction: Advances, Challenges, and Future Prospects. Rev. Geophys. 2018, 56, 108–141. [Google Scholar] [CrossRef] [Green Version]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relationship of drough frequency and duration to time scale. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 17–22. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A Multiscalar Drought Index Sensitive to Global Warming: The Standardized Precipitation Evapotranspiration Index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Morsy, M.; Moursy, F.I.; Sayad, T.; Shaban, S. Climatological Study of SPEI Drought Index Using Observed and CRU Gridded Dataset over Ethiopia. Pure Appl. Geophys. 2022, 179, 3055–3073. [Google Scholar] [CrossRef]
- Hou, M.; Yao, N.; Li, Y.; Liu, F.; Biswas, A.; Pulatov, A.; Hassan, I. Better Drought Index between SPEI and SMDI and the Key Parameters in Denoting Drought Impacts on Spring Wheat Yields in Qinghai, China. Agronomy 2022, 12, 1552. [Google Scholar] [CrossRef]
- Tirivarombo, S.; Osupile, D.; Eliasson, P. Drought monitoring and analysis: Standardised Precipitation Evapotranspiration Index (SPEI) and Standardised Precipitation Index (SPI). Phys. Chem. Earth. 2018, 106, 1–10. [Google Scholar] [CrossRef]
- Elbeltagi, A.; AlThobiani, F.; Kamruzzaman, M.; Shaid, S.; Roy, D.K.; Deb, L.; Islam, M.; Kundu, P.K.; Rahman, M. Estimating the Standardized Precipitation Evapotranspiration Index Using Data-Driven Techniques: A Regional Study of Bangladesh. Water 2022, 14, 1764. [Google Scholar] [CrossRef]
- Nejadrekabi, M.; Eslamian, S.; Zareian, M.J. Spatial statistics techniques for SPEI and NDVI drought indices: A case study of Khuzestan Province. Int. J. Environ. Sci. Technol. 2022, 19, 6573–6594. [Google Scholar] [CrossRef]
- Liu, C.; Yang, C.; Yang, Q.; Wang, J. Spatiotemporal drought analysis by the standardized precipitation index (SPI) and standardized precipitation evapotranspiration index (SPEI) in Sichuan Province, China. Sci. Rep. 2021, 11, 1280. [Google Scholar] [CrossRef]
- Jamro, S.; Dars, G.H.; Ansari, K.; Krakauer, N.Y. Spatio-Temporal Variability of Drought in Pakistan Using Standardized Precipitation Evapotranspiration Index. Appl. Sci. 2019, 9, 4588. [Google Scholar] [CrossRef] [Green Version]
- Mehraein, M.; Mohanavelu, A.; Naganna, S.R.; Kulls, C.; Kisi, O. Monthly Streamflow Prediction by Metaheuristic Regression Approaches Considering Satellite Precipitation Data. Water 2022, 14, 3636. [Google Scholar] [CrossRef]
- Ezzaouini, M.A.; Mahé, G.; Kacimi, I.; El Bilali, A.; Zerouali, A.; Nafii, A. Predicting Daily Suspended Sediment Load Using Machine Learning and NARX Hydro-Climatic Inputs in Semi-Arid Environment. Water 2022, 14, 862. [Google Scholar] [CrossRef]
- El Bilali, A.; Moukhliss, M.; Taleb, A.; Nafii, A.; Alabjah, B.; Brouziyne, Y.; Mazigh, N.; Teznine, K.; Mhamed, M. Predicting daily pore water pressure in embankment dam: Empowering Machine Learning-based modeling. Environ. Sci. Pollut. Res. 2022, 29, 47382–47398. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumari, N.; Dharpure, J.; Mokhtar, A.; Alsafadi, K.; Kumar, M.; Mehdinejadiani, B.; Etedali, H.R.; Brouziyne, Y.; Islam, A.T.; et al. Prediction of Combined Terrestrial Evapotranspiration Index (CTEI) over Large River Basin Based on Machine Learning Approaches. Water 2021, 13, 547. [Google Scholar] [CrossRef]
- Shamshirband, S.; Hashemi, S.; Salimi, H.; Samadianfard, S.; Asadi, E.; Shadkani, S.; Kargar, K.; Mosavi, A.; Nabipour, N.; Chau, K.W. Predicting Standardized Streamflow index for hydrological drought using machine learning models. Eng. Appl. Comput. Fluid Mech. 2020, 14, 339–350. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Huete, A. An improved SPEI drought forecasting approach using the long short-term memory neural network. J. Environ. Manag. 2021, 283, 111979. [Google Scholar] [CrossRef] [PubMed]
- Ghasemi, P.; Karbasi, M.; Nouri, A.Z.; Tabrizi, M.S.; Azamathulla, H.M. Application of Gaussian process regression to forecast multi-step ahead SPEI drought index. Alex. Eng. J. 2021, 60, 5375–5392. [Google Scholar] [CrossRef]
- Kisi, O.; Gorgij, A.D.; Zounemat-Kermani, M.; Mahdavi-Meymand, A.; Kim, S. Drought forecasting using novel heuristic methods in a semi-arid environment. J. Hydrol. 2019, 578, 124053. [Google Scholar] [CrossRef]
- Park, S.; Im, J.; Jang, E.; Rhee, J. Drought assessment and monitoring through blending of multi-sensor indices using machine learning approaches for different climate regions. Agric. For. Meteorol. 2016, 216, 157–169. [Google Scholar] [CrossRef]
- Mokhtar, A.; Jalali, M.; He, H.; Al-Ansari, N.; Elbeltagi, A.; Alsafadi, K.; Abdo, H.G.; Sammen, S.S.; Gyasi-Agyei, Y.; Rodrigo-Comino, J. Estimation of SPEI Meteorological Drought Using Machine Learning Algorithms. IEEE Access 2021, 9, 65503–65523. [Google Scholar] [CrossRef]
- El Bilali, A.; Lamane, H.; Taleb, A.; Nafii, A. A framework based on multivariate distribution-based virtual sample generation and DNN for predicting water quality with small data. J. Clean. Prod. 2022, 368, 133227. [Google Scholar] [CrossRef]
- El Bilali, A.; Abdeslam, T.; Mazigh, N.; Moukhliss, M. Prediction of chemical water quality used for drinking purposes based on artificial neural networks. Moroc. J. Chem. 2020, 3, 665–672. [Google Scholar]
- Rajaee, T.; Ebrahimi, H.; Nourani, V. A review of the artificial intelligence methods in groundwater level modeling. J. Hydrol. 2019, 572, 336–351. [Google Scholar] [CrossRef]
- Kaur, A.; Sood, S.K. Deep learning based drought assessment and prediction framework. Ecol. Informatics 2020, 57, 101067. [Google Scholar] [CrossRef]
- Mohammed, S.; Elbeltagi, A.; Bashir, B.; Alsafadi, K.; Alsilibe, F.; Alsalman, A.; Zeraatpisheh, M.; Széles, A.; Harsányi, E. A comparative analysis of data mining techniques for agricultural and hydrological drought prediction in the eastern Mediterranean. Comput. Electron. Agric. 2022, 197, 106925. [Google Scholar] [CrossRef]
- Dost, R.; Kasiviswanathan, K. Quantification of Water Resource Sustainability in Response to Drought Risk Assessment for Afghanistan River Basins. Nat. Resour. Res. 2022; in press. [Google Scholar] [CrossRef]
- Achite, M.; Jehanzaib, M.; Elshaboury, N.; Kim, T.-W. Evaluation of Machine Learning Techniques for Hydrological Drought Modeling: A Case Study of the Wadi Ouahrane Basin in Algeria. Water 2022, 14, 431. [Google Scholar] [CrossRef]
- Almikaeel, W.; Čubanová, L.; Šoltész, A. Hydrological Drought Forecasting Using Machine Learning—Gidra River Case Study. Water 2022, 14, 387. [Google Scholar] [CrossRef]
- Brouziyne, Y.; Belaqziz, S.; BenaabidateAboubdillah, L.; Aboubdillah, A.; El Bilali, A.; Elbeltagi, A.; Tzoraki, O.; Chehbouni, A. Modeling long term response of environmental flow attributes to future climate change in a North African watershed (Bouregreg watershed, Morocco). Ecohydrol. Hydrobiol. 2021, 22, 155–167. [Google Scholar] [CrossRef]
- El Bilali, A.; Taleb, A.; El Idrissi, B.; Brouziyne, Y.; Mazigh, N. Comparison of a data-based model and a soil erosion model coupled with multiple linear regression for the prediction of reservoir sedimentation in a semi-arid environment. Euro-Mediterranean J. Environ. Integr. 2020, 5, 64. [Google Scholar] [CrossRef]
- El Bilali, A.; Taleb, A. Prediction of irrigation water quality parameters using machine learning models in a semi-arid environment. J. Saudi Soc. Agric. Sci. 2020, 19, 439–451. [Google Scholar] [CrossRef]
- Abramowitz, M.; Stegun, I. Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables; U.S. Government Printing Office: Washington, DC, USA, 1964.
- Yin, J.; Zhao, P.; Zhang, Y.; Han, Y.; Wang, S. A Data Augmentation Method for War Trauma Using the War Trauma Severity Score and Deep Neural Networks. Electronics 2021, 10, 2657. [Google Scholar] [CrossRef]
- Liu, P.; Wang, J.; Sangaiah, A.K.; Xie, Y.; Yin, X. Analysis and Prediction of Water Quality Using LSTM Deep Neural Networks in IoT Environment. Sustainability 2019, 11, 2058. [Google Scholar] [CrossRef] [Green Version]
- Aggarwal, C.C. Data Mining; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bonaccorso, G. Machine Learning Algorithms: Popular Algorithms for Data Science and Machine Learning; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: Berlin, Germany, 2009. [Google Scholar]
- Kubat, M. An Introduction to Machine Learning; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Dawson, C.; Wilby, R. Une approche de la modélisation pluie-deblt par ies réseaux neuronaux artificiels. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Schalkoff, R. Artificial Neural Networks; McGraw-Hill Higher Education: New York, NY, USA, 1997. [Google Scholar]
- Nash, J.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Brouziyne, Y.; Abouabdillah, A.; Chehbouni, A.; Hanich, L.; Bergaoui, K.; McDonnell, R.; Benaabidate, L. Assessing Hydrological Vulnerability to Future Droughts in a Mediterranean Watershed: Combined Indices-Based and Distributed Modeling Approaches. Water 2020, 12, 2333. [Google Scholar] [CrossRef]
- Banerjee, O.; Bark, R.; Connor, J.; Crossman, N.D. An ecosystem services approach to estimating economic losses associated with drought. Ecol. Econ. 2013, 91, 19–27. [Google Scholar] [CrossRef]
- Musolino, D.A.; Massarutto, A.; de Carli, A. Does drought always cause economic losses in agriculture? An empirical investigation on the distributive effects of drought events in some areas of Southern Europe. Sci. Total. Environ. 2018, 633, 1560–1570. [Google Scholar] [CrossRef]
- Abedin, A.; Habiba, U.; Shaw, R. Community Perception and Adaptation to Safe Drinking Water Scarcity: Salinity, Arsenic, and Drought Risks in Coastal Bangladesh. Int. J. Disaster Risk Sci. 2014, 5, 110–124. [Google Scholar] [CrossRef] [Green Version]
- Ahmed, S.M. Impacts of drought, food security policy and climate change on performance of irrigation schemes in Sub-saharan Africa: The case of Sudan. Agric. Water Manag. 2020, 232, 106064. [Google Scholar] [CrossRef]
- El Bilali, A.; Abdeslam, T.; Ayoub, N.; Lamane, H.; Ezzaouini, M.A.; Elbeltagi, A. An interpretable machine learning approach based on DNN, SVR, Extra Tree, and XGBoost models for predicting daily pan evaporation. J. Environ. Manag. 2023, 327, 116890. [Google Scholar] [CrossRef]
- Yadav, A.; Joshi, D.; Kumar, V.; Mohapatra, H.; Iwendi, C.; Gadekallu, T.R. Capability and Robustness of Novel Hybridized Artificial Intelligence Technique for Sediment Yield Modeling in Godavari River, India. Water 2022, 14, 1917. [Google Scholar] [CrossRef]
| Reference | Model/Method | Drought Index | Performances | Country |
|---|---|---|---|---|
| [32] | Bagging, Random Forest, Random Subspace, Random Tree | SPI | Radom Tree outperformed other models | Syria |
| [33] | Spatial and temporal variation of sustainability in response to meteorological droughts | SPI | *** | Afghanistan |
| [24] | Three machine learning, MLP, GRNN, and Gaussian process regression (GPR) | SPEI | GPR outperformed other models | Iran |
| [34] | ANN, SVM, ANFIS, Decision Tree, | SRI | SVM outperformed other models | Algeria |
| [35] | ANN, SVM | SHMI | Both models showed accurate results | Slovakia |
| Hydrological Station | River | Period | Mean (mm) | Max (mm) | Min (mm) | Standard Deviation |
|---|---|---|---|---|---|---|
| Aguibat Ziar | Bouregreg | 1976–2021 | 269.5 | 725 | 0 | 198.9 |
| Ras Fathia | Grou | 1976–2021 | 245.2 | 780.7 | 0 | 185.2 |
| S.M. Cherif | Mechraa | 1972–2021 | 232.3 | 785.7 | 0 | 175.5 |
| Ain Loudah | Korifla | 1972–2021 | 225.7 | 671 | 0 | 162.8 |
| Lalla Chafia | Bouregreg | 1971–2021 | 225.5 | 689 | 0 | 166.1 |
| Sidi Amar | Tabahart | 1977–2021 | 225.4 | 657.7 | 0 | 180.1 |
| Sidi Jabeur | Grou | 1971–2021 | 195.5 | 592.1 | 0 | 142.9 |
| Tsalat | Guennour | 1976–2021 | 284.8 | 868.7 | 0 | 212.3 |
| Ouljet Haboub | Grou | 1972–2021 | 184.6 | 563.4 | 0 | 133.7 |
| Climatological Station | Period of Observation | Mean (°C) | Max (°C) | Min (°C) |
|---|---|---|---|---|
| Rabat | 1960–2021 | 17.5 | 31.6 | 3.9 |
| Khémisset | 1971–2021 | 20.2 | 39 | 2 |
| Khouribga | 1972–2021 | 19.7 | 41 | −1 |
| Ain Loudah | 1971–2021 | 19.6 | 38.3 | 2 |
| Sidi Jabeur | 1971–2021 | 19.7 | 38 | 2 |
| Ouljet Haboub | 1972–2021 | 19.8 | 39 | 1 |
| Inflow Station | Max Annual Inflow (Mm3) | Min Annual Inflow (Mm3) | Mean Annual Inflow (Mm3) | Standard Deviation |
|---|---|---|---|---|
| SMBA’s Dam | 2583.9 | 67.2 | 541.9 | 530.6 |
| Models | Parameters/Functions/Algorithm |
|---|---|
| ANN_Sep, ANN_Oct, ANN_Nov, ANN_Dec, ANN_Jan, ANN_Feb, ANN_Mar, ANN_Apr, ANN_May, ANN_Jun, ANN_Jul | 6 layers (including input and output layers) 310 neurons in hidden layers (10, 100, 100, 100) Algorithm: Adam Function activation: Softmax Epoch number: 1000 Learning rate: 0.01 |
| R2 | RMSE | NSE | Performance Rank | |
|---|---|---|---|---|
| ANN_Sep | 0.65 | 0.59 | 0.64 | Good fit |
| ANN_Oct | 0.73 | 0.51 | 0.73 | Good fit |
| ANN_Nov | 0.82 | 0.41 | 0.82 | Good fit |
| ANN_Dec | 0.81 | 0.43 | 0.81 | Good fit |
| ANN_Jan | 0.87 | 0.35 | 0.81 | Very good fit |
| ANN_Feb | 0.90 | 0.31 | 0.87 | Very good fit |
| ANN_Mar | 0.96 | 0.19 | 0.90 | Very good fit |
| ANN_Apr | 0.96 | 0.18 | 0.96 | Very good fit |
| ANN_May | 0.98 | 0.12 | 0.96 | Very good fit |
| ANN_Jun | 0.99 | 0.08 | 0.98 | Very good fit |
| ANN_Jul | 0.99 | 0.06 | 0.99 | Very good fit |
| R2 | RMSE | NSE | Performance | |
|---|---|---|---|---|
| ANN_Sep | 0.35 | 0.77 | 0.32 | Unsatisfactory fit |
| ANN_Oct | 0.36 | 0.81 | 0.25 | Unsatisfactory fit |
| ANN_Nov | 0.37 | 0.81 | 0.25 | Unsatisfactory fit |
| ANN_Dec | 0.62 | 0.58 | 0.62 | Good fit |
| ANN_Jan | 0.75 | 0.46 | 0.75 | Very good fit |
| ANN_Feb | 0.84 | 0.38 | 0.83 | Very good fit |
| ANN_Mar | 0.90 | 0.3 | 0.89 | Very good fit |
| ANN_Apr | 0.94 | 0.23 | 0.93 | Very good fit |
| ANN_May | 0.98 | 0.13 | 0.98 | Very good fit |
| ANN_Jun | 0.99 | 0.09 | 0.99 | Very good fit |
| ANN_Jul | 0.99 | 0.07 | 0.99 | Very good fit |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nafii, A.; Taleb, A.; El Mesbahi, M.; Ezzaouini, M.A.; El Bilali, A. Early Forecasting Hydrological and Agricultural Droughts in the Bouregreg Basin Using a Machine Learning Approach. Water 2023, 15, 122. https://doi.org/10.3390/w15010122
Nafii A, Taleb A, El Mesbahi M, Ezzaouini MA, El Bilali A. Early Forecasting Hydrological and Agricultural Droughts in the Bouregreg Basin Using a Machine Learning Approach. Water. 2023; 15(1):122. https://doi.org/10.3390/w15010122
Chicago/Turabian StyleNafii, Ayoub, Abdeslam Taleb, Mourad El Mesbahi, Mohamed Abdellah Ezzaouini, and Ali El Bilali. 2023. "Early Forecasting Hydrological and Agricultural Droughts in the Bouregreg Basin Using a Machine Learning Approach" Water 15, no. 1: 122. https://doi.org/10.3390/w15010122







