Risk-Informed Design of RCC Dams under Extreme Seismic Loading
Abstract
:1. Introduction
2. A Review of Seismic Design and Dam Safety Risk Analysis of Concrete Dams
2.1. Seismic Design Philosophies
2.2. Risk-Informed Decision-Making (RIDM) in Dam Engineering
2.3. Objectives and Contributions
3. The Proposed Concept of Risk-Informed Design for New RCC Dams
4. Regional Seismic Hazards
4.1. Probabilistic Seismic Hazards
4.2. Representative Time Histories
5. Risk-Informed Design Criteria
5.1. #1 Elastic Response for 500- to 1000-Year Seismic Events
- No cracking of the concrete;
- No sliding of the RCC dam.
5.2. #2 Linear-Elastic Transitioning to Possible Localized Non-Linear Response with Limited Damage Beginning to Occur between the 1000- and 5000-Year Seismic Events
- Limited cracking of the concrete permitted, but not permitted to crack through the section for the 1000-year event;
- No sliding of the RCC dam for the 1000-year event.
5.3. #3 Non-Linear Response, Moderate Damage, and Post-Earthquake Stability for Events Larger Than 5000-Year Return Periods—Earthquake Events with Estimated Recurrence Intervals of up to 1 in 50,000 Years Were Evaluated
- Cracking through the section allowed with the estimated extent and location of damage within the dam being judged acceptable;
- Sliding of any section of the dam limited to less than about 2 to 4 feet of estimated displacement;
- Sensitivity analysis for higher and lower friction angles on any identified planes of sliding to inform risk analysis.
5.4. #4 Post-Seismic Stability Factor of Safety (FOS) > 1.0
- Predicted for all loading conditions, including the damage from the 10,000- and 50,000-year events when a reasonable lower bound residual friction angle of 35 degrees is assumed for the planes of sliding, and full uplift (drains assumed inoperable) is applied linearly along the sliding plane as a full normal operating reservoir at the upstream heel of the dam and tailwater at the toe of the dam.
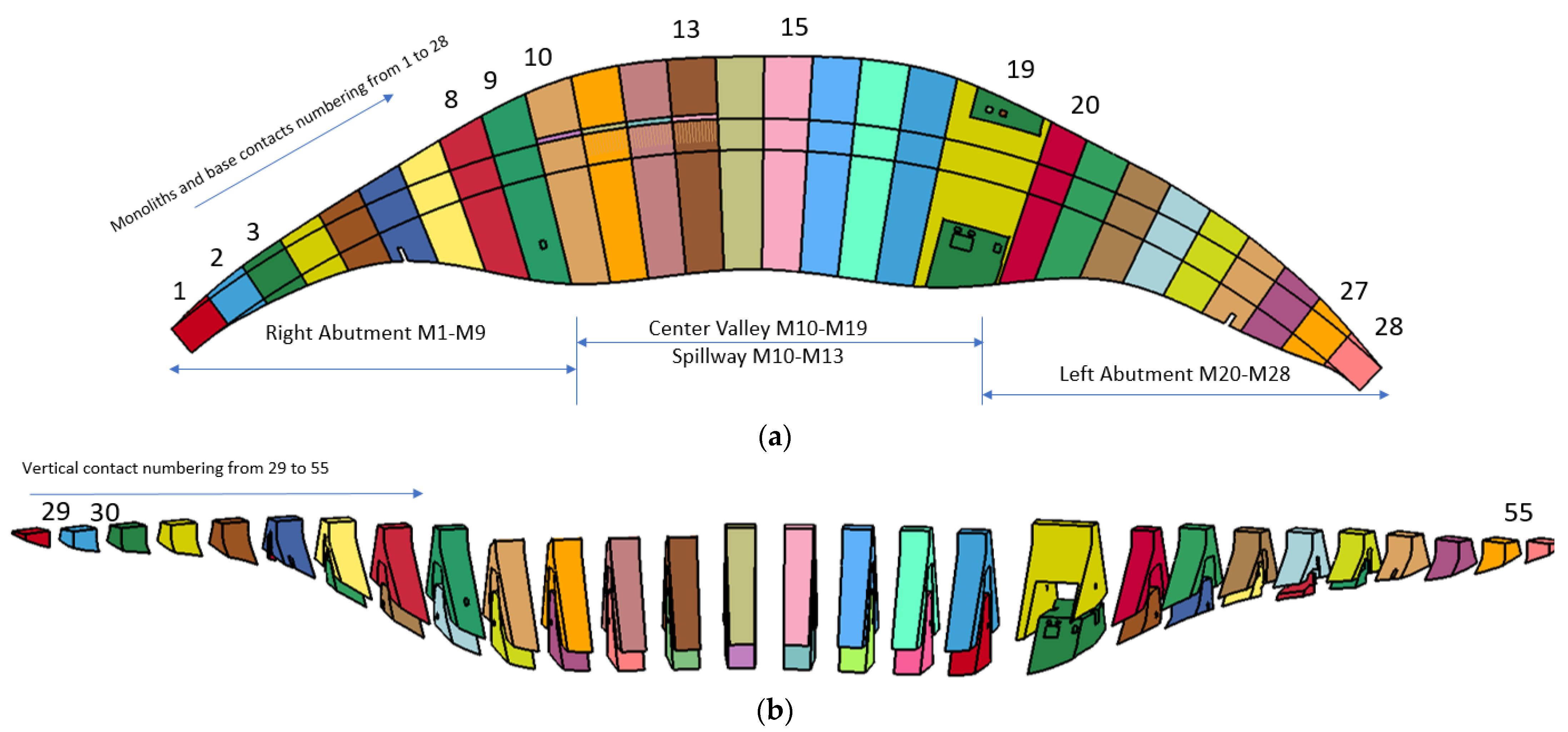
6. Structural Model and Modeling Approach
6.1. Model Descriptions including Provisions for Non-Linear Response
6.2. Material Properties
- Outer Zone: 2400 psi (16.55 MPa)
- Inner Zone: 1800 psi (12.41 MPa)
- Dam/foundation contact tensile strength: 150 psi;
- Basal joint shear strength (prior to cracking): ϕ (friction angle) = 55 deg., c (cohesion) = 150 psi [1.03 MPa].
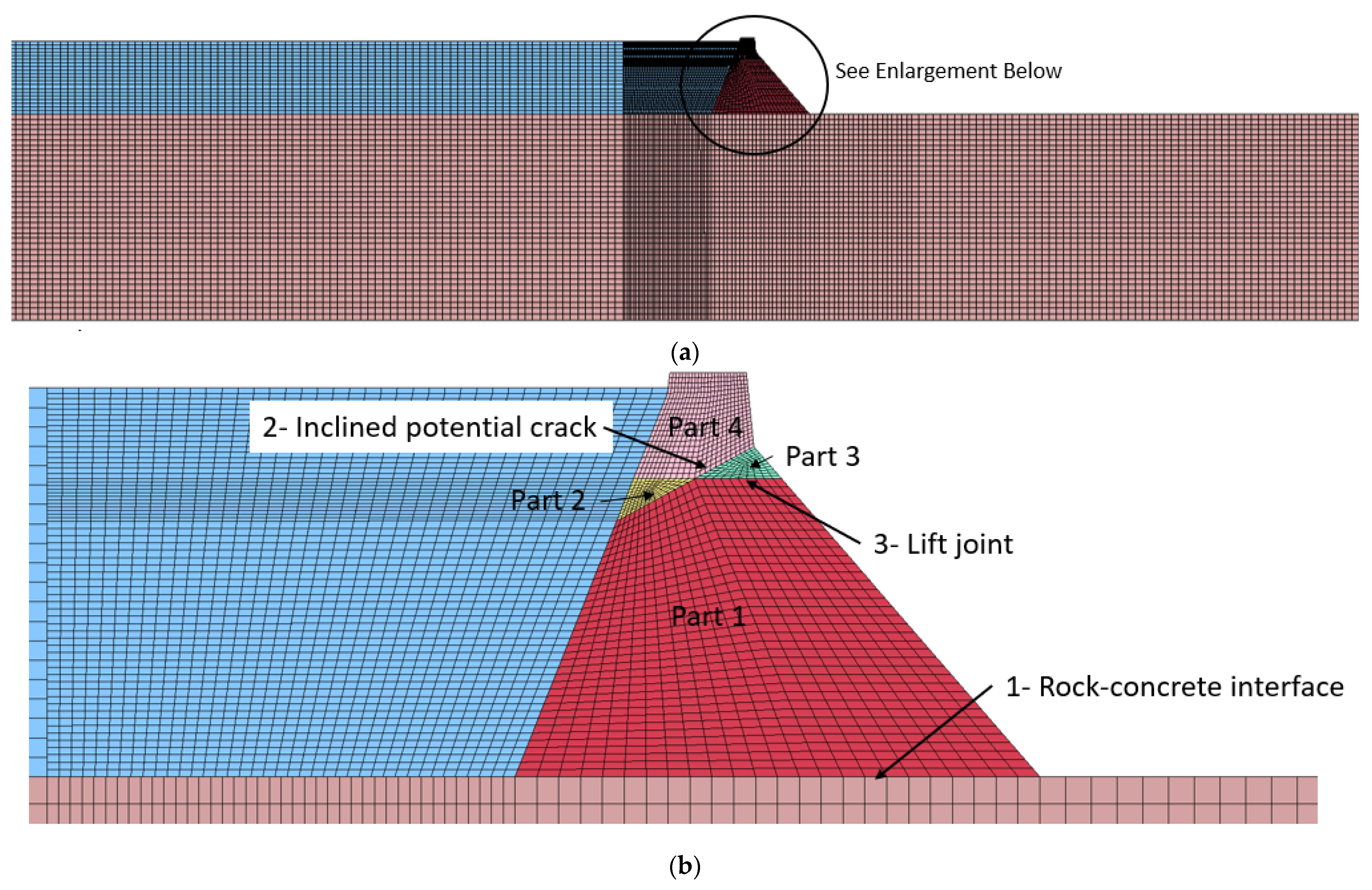
6.3. Cracking Potential in the Upper Portion of the Dam
6.4. Model Setup and Calibration
6.5. Model Study Cases
7. Model Results
7.1. Static Analyses
7.2. 3D Seismic Response Analyses
- Sliding of the dam at the dam to foundation interface or along a lower lift (just above the foundation contact) that yields to a large displacement between adjacent monoliths or instability of one or more monoliths;
- Overstressing during the earthquake leading to cracking and sliding in the upper part of the dam with significant degradation (rubbilizing) of the concrete along vertical monolith joints.
- Up to what level of earthquake will the structure behavior be linear, and when/where will the onset of cracking/damage and non-linear behavior begin with no large overstressing or significant damage to the dam?
- What and where are the maximum stresses and the potential for damage within the structure for larger earthquakes? The evaluation results lead to the decision to develop a simple 2D model for capturing the cracking/displacement failure mode within the RCC dam structure.
- What are the maximum estimated non-linear displacement and expected relative monolith displacements at the end of larger earthquakes?
- Post-earthquake performance and stability of the dam.
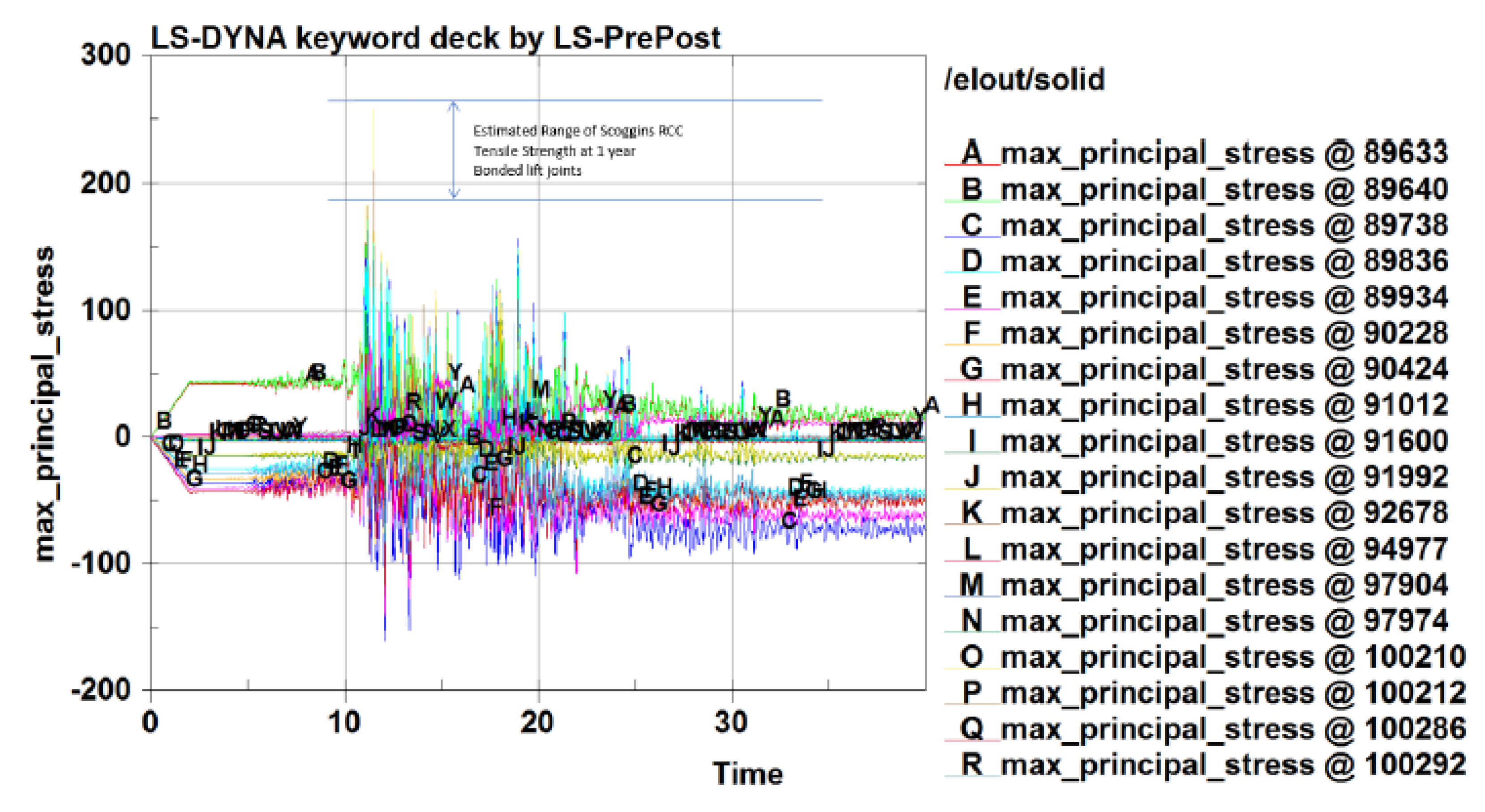
7.3. Cracking in the Upper Portion of the Dam
- Cracking along a continuous horizontal lift surface (Contact 3 on Figure 4);
- Cracking along a bi-modal surface, including a lifting surface from the upstream face to the center of the dam and an inclined crack from the downstream face to the center of the dam (a combination of cracking on the upstream half of Contact 3 and the downstream half of Contact 2 forming the tan colored block shown on Figure 4).
8. Risk Analysis Results
9. Conclusions and Recommendations
9.1. #1 Elastic (Linear) Response for 500- to 1000-Year Seismic Events
- No cracking of the concrete;
- No sliding of the RCC dam.
Structural Analysis Results
9.2. #2 Linear-Elastic Transitioning to Possible Localized Non-Linear Response with Limited Damage Beginning to Occur between the 1000- and 5000-Year Seismic Events
- Limited cracking of the concrete permitted, but not permitted to crack through the section for the 1000-year event;
- No sliding of the RCC dam for the 1000-year event.
Structural Analysis Results
9.3. #3 Non-Linear Response, Moderate Damage, and Post-Earthquake Stability for Events Larger Than 5000-Year Return Periods
- Cracking through the section may be allowed depending on analysis results and the estimated extent and location of damage within the dam;
- Sliding resultant of any section of the dam limited to less than about 2 to 4 feet of estimated displacement;
- Sensitivity analysis for higher and lower friction angles on any identified planes of sliding to inform risk analysis.
Structural Analysis Results
9.4. #4 Post-Seismic Stability FOS > 1.0
- Predicted for all loading conditions, including the 10,000- and 50,000-year events, when a reasonable lower bound residual friction angle of 35 degrees is assumed for the planes of sliding, and full uplift is applied linearly along the sliding plane as a full reservoir at the upstream heel of the dam and tailwater at the toe of the dam.
Post-Seismic Stability Analysis Results
Funding
Data Availability Statement
Acknowledgments
- Clean Water Services: Tom VanderPlaat and John Dummer.
- U.S. Bureau of Reclamation: Roman Koltuniuk, Randall Kuzniakowski, Derek Wittwer, Jason Schneider, Jennifer Huggins, Walt Heyder, Bryan Simpson, Dom Galic, Dave Gillette, Lindy Johnson, Tara Schenk McFarland.
- HDR Contributors: John Charlton, Andrew Little, and John Ballegeer for site characterization; Andrew Little, Jeff Allen, and Tatro and Hines for RCC Mix Designs; Farzad Abedzadeh, Phoebe Purcell, and Kevin Gribble for Structural Modeling; Dan Osmun, Bill Fiedler, Elena Sossenkina, and Stephanie Williams for Risk Analyses.
Conflicts of Interest
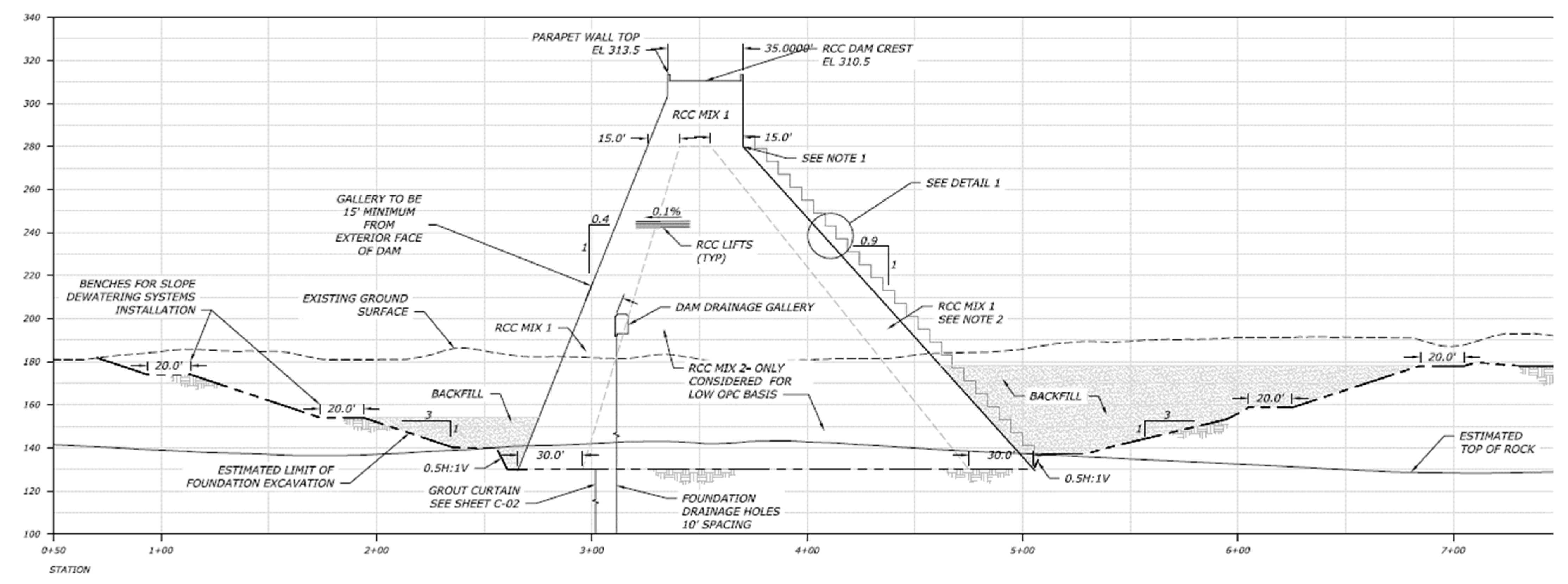
Appendix A
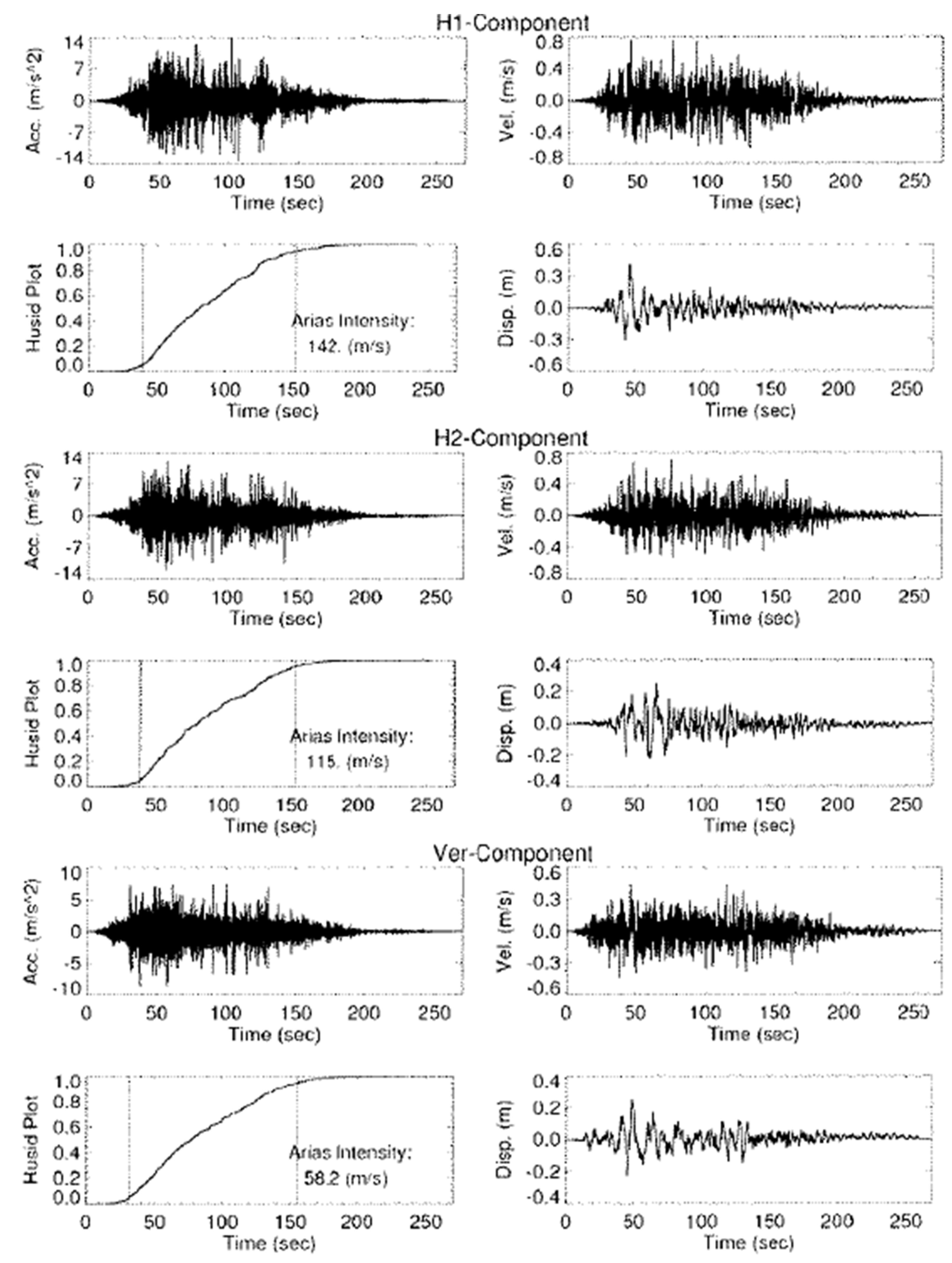
Appendix B
Appendix C
| No. | Load Case Name | RCC Strength Parameters | Loading Conditions | Foundation Drain Efficiency | Comments | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Base Case 3 | Long-Term 4 | Post Earthquake 5 | Abutment Contact Strength Adjustment 6 | Gravity | Earthquake Recurrence Interval (yr.) | S.D. Motion MYG008 7 | L.D. Motion SRCH10 (SP) 8 | Post-Earthquake | Fully Operational, 65% | Non-Operational, Full Uplift 9 | |||
| 1 | Static—maximum normal reservoir | X | X | N/A | X | Model used to check damping response. Model also runs to failure by increasing fluid weight to inform risk analysis and failure mode description. Uplift pressure distribution based on 65% drain efficiency. | |||||||
| 2 | Static—PMF reservoir | X | X | N/A | X | ||||||||
| 3 | Static—PMF with degraded contact strength and uplift | X | N/A | X | Foundation/ RCC contact joint strength set at 40 degrees. Study case performed shows results of post-earthquake evaluations, indicating potential for dam movement for events with less than 1000-year return period. | ||||||||
| 4 | Seismic | X | 10,000 | X | X | Study case helped identify problems with the shape of the dam/foundation contact. All model runs subsequently completed with adjusted abutment contact strength. | |||||||
| 5 | Seismic | X | X | 10,000 | X | X | |||||||
| 6 | Seismic | X | X | 10,000 | X | X | Simulation performed to test an alternative non-linear concrete strength model. Not part of risk analysis simulations until further evaluation of study case 5 results is completed. | ||||||
| 7 | Seismic | X | X | 10,000 | X | X | |||||||
| 8 | Seismic/Post Earthquake | See Comment | X | X | 10,000 | X | X | X—during EQ | X—following EQ | Running model with phi = 35 and c = 100 as concrete shear strength degrading to phi = 35 and c = 0 once basal crack develops. These parameters used for full duration of EQ. Represents worst-case deformations for assumed loading conditions. Cracked monoliths at end of EQ represent post-EQ stability, with contact strength of 35 degrees and modified uplift with drains non-operational. | |||
| 9 | Seismic | X | X | 10,000 | X | X | Model run completed in 144 s, capturing majority of estimated deformations. Running with elastic element adjusted to have water properties for the reservoir portion of the model mesh. | ||||||
| 10 | Seismic | X | X | 50,000 | X | X | |||||||
| 11 | Seismic | X | X | 50,000 | X | X | |||||||
| 12 | Seismic/Post Earthquake | See Comment | X | X | X | 50,000 | X | X | X—during EQ | X-following EQ | Running model with phi = 35 and c = 100 as concrete shear strength degrading to phi = 35 and c = 0 once basal crack develops. These parameters used for full duration of EQ. Represents worst-case deformations for assumed loading conditions. Cracked monoliths at end of EQ represent post-EQ stability, with contact strength of 35 degrees and modified uplift with drains non-operational. | ||
| 14 | Seismic | X | X | 50,000 | X | X | |||||||
| 15 | Seismic | X | X | 5000 | X | X | |||||||
| 16 | Seismic | X | X | 5000 | X | X | |||||||
| 17 | Seismic/Post Earthquake | See Comment | X | X | 5000 | X | X | X—during EQ | X-following EQ | Running model with phi = 35 and c = 100 as concrete shear strength degrading to phi = 35 and c = 0 once basal crack develops. These parameters used for full duration of EQ. Represents worst-case deformations for assumed loading conditions. Cracked monoliths at end of EQ represent post-EQ stability, with contact strength of 35 degrees and modified uplift with drains non-operational. | |||
| 18 | Seismic | X | X | 5000 | X | X | |||||||
| 19 | Seismic | X | X | 1000 | X | X | |||||||
| 20 | Seismic | X | 1000 | X | X | ||||||||
| Study Case No. | Base Contact Properties | Inclined Contact Properties | Lift Joint Properties | Comments on Contacts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tensile Strength (Psi) | Shear Strength—Cohesion (psi) | Shear Strength—Friction Coefficient | Tensile Strength (psi) | Shear Strength—Cohesion (psi) | Shear Strength—Friction Coefficient | Tensile Strength (psi) | Shear Strength—Cohesion (psi) | Shear Strength—Friction Coefficient | ||
| 1 | 1 × 1020 (tied) | 1 × 1020 (tied) | 10.0 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | All bonded |
| 2 | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 250 | 250 | 1.0 | 150 | 150 | 1.0 | Bonded at the base |
| 3 | 100 | 100 | 1.0 | 250 | 250 | 1.0 | 150 | 150 | 1.0 | Typical strength, low |
| 4 | 150 | 150 | 1.43 | 250 | 250 | 1.0 | 250 | 250 | 1.0 | All high |
| 5 | 150 | 150 | 1.43 | 150 | 150 | 1.43 | 150 | 150 | 1.43 | Typical, long term |
| 6 | 100 | 100 | 1.00 | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | Sliding base only |
| 7 | 100 | 100 | 1.00 | 150 | 150 | 1.43 | 150 | 150 | 1.43 | Crest contacts high |
| 8 | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 150 | 150 | 1.0 | Horizontal joint only |
| 9 | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 150 | 150 | 1.43 | 150 | 150 | 1.0 | Cracked intact concrete friction on inclined joint |
| 10 | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | 150 | 150 | 1.0 | 1 × 1020 (tied) | 1 × 1020 (tied) | 1 × 1020 (tied) | Bilinear crack strength at upstream |
| Representative Ground Motion Return Period | Applicable Load Partition Range (Years) | Study Case No. | Notes | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Left Monoliths | Central Monoliths | Right Monoliths | Post-Earthquake | ||||||
| Base Material Properties | Long-Term Material Properties | Base Material Properties | Long-Term Material Properties | Base Material Properties | Long-Term Material Properties | Base Material Properties | |||
| 1000—year | 800 to 3000 | 0 (0) | 0 (0) | 0 (0) | FOS > 1.0 | Model behaves linearly, no base cracking or sliding. | |||
| 5000—year | 3000 to 8000 | 3–4 (0.25–0.33) | 0 (0) | 1–3 (0.08–0.25) | 0 (0) | 0 (0) | 0 (0) | ||
| 5000—year | 3000 to 8000 | 6–9 (0.5–0.75) 1 | 4–6 (0.33 to 0.5) 1 | 0–2.5 (0–0.21) 1 | FOS > 1.0 | Model base cracks with sliding in center valley and left abutment areas. Right abutment Monoliths 1–4 remained uncracked and undeformed, suggesting linear behavior. Worst case deformation estimate for residual friction angle of 35 degrees once contact is cracked. Post-EQ FOS > 1.0. | |||
| 10,000—year | 8000 to 25,000 | 6–9 (0.5–0.75) | 0 (0) | 3–5 (0.25–0.42) | 0 (0) | 1–3 (0.08–0.25) | 0 (0) | Results for Base Material Properties. | |
| 10,000—year | 8000 to 25,000 | 11–20 (0.92–1.67) | 12–15 (1–1.25) | 11–13 (0.92–1.08) | FOS > 1.0 | Model base cracks with sliding in center valley and left abutment areas. Right abutment Monoliths 1–4 remained uncracked and undeformed, suggesting linear behavior. Worst case deformation estimate for residual friction angle of 35 degrees once contact is cracked. Post-EQ FOS > 1.0. | |||
| 50,000—year | >25,000 | 11–14 (0.92–1.12) | 2.5–6 (0.2–0.5) | 7.5–10 (0.63–0.83) | −1–3 (−0.08–0.25) | 8–10 (0.67–0.83) | 0 (0) | Note Monolith M19 (outlet works) in lower left abutment moves total of 2.5 inches downstream. Differential movement between M19 and M20 < 9 inches. | |
| 50,000—year | >25,000 | 15–40 (1.25–3.33) | 18–26 (1.5–2.17) | 24–26 (2–2.17) | FOS > 1.0 | Model base cracks with sliding in center valley and left abutment areas. Right abutment Monoliths 1–4 remained uncracked and undeformed, suggesting linear behavior. Worst case deformation estimate for residual friction angle of 35 degrees once contact is cracked. Post-EQ FOS > 1.0. | |||
| Representative Ground Motion Return Period | Applicable Load Partition Range (Years) | Study Case No. | Notes | ||||||
|---|---|---|---|---|---|---|---|---|---|
| Left Monoliths | Central Monoliths | Right Monoliths | Post-Earthquake FOS | ||||||
| Base Material Properties | Long-Term Material Properties | Base Material Properties | Long-Term Material Properties | Base Material Properties | Long-Term Material Properties | Base Material Properties | |||
| 1000—year | 800 to 3000 | 0 (0) | 0 (0) | 0 (0) | |||||
| 5000—year | 3000 to 8000 | +15 (1.25) | 5–9 (0.42–0.75) | 5–6 (0.42–0.5) | |||||
| 10,000—year | 8000 to 25,000 | 19–22 (1.58–1.83) | 10–24 (0.83–2) | 17–25 (1.42–2.08) | Model run to 144 sections of total 200-s duration. Deformations for time > 144 s expected to be minimal. Moreover, for this initial case, the foundation strength parameters at the contact were not adjusted to account for adverse (downstream sloping) excavation surface, so deformations in abutments are higher than expected when strong abutment adjustment is made. | ||||
| 50,000—year | >25,000 | 18–30 (1.5–2.5) | 18–51 (1.5–4.25) | 35 (2.92) | Displacements are at time = 144 s. | ||||
| Representative Ground Motion Return Period | Applicable Load Partition Range (Years) | Strength Assumptions 1 | Base Cracking Through | Representative Maximum Stress Condition—Monoliths | Monolith Contraction Joint Conditions Following Earthquake | Other Comments | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Left Monoliths | Central Monoliths | Right Monoliths | Monolith Number(s) | Estimated Maximum Tensile Stress Excursion Range (psi) 2 | Number of Excursions | Estimated Damage Condition through Monolith 3 | Monolith Contraction Joint Numbers 4 | Estimated Maximum Tensile Stress Adjacent to TCJ (psi) | Estimated Maximum Differential Movement (Inches) 5 | Estimated Damage to Monolith Contraction Joints | ||||
| 1000 | 800–3000 | BC | N | N | N | 19–20 | 190–210 (Z) 180–240 (P) | 2 3 | ND ND | 19–20 | 210 | 0 | ND | Dam in linear elastic range, monolith joints remaining in contact. |
| 5000 | 3000–8000 | BC | Y | Y | N | 24–25 | 190–380 (P) | 3 | OC | 22–23 | >242 | <2 inches (M21–M22) | LCI | |
| LT | N | N | N | 9 | 260–400 (P) | 3 | OC | 7–8, 8–9, 9–10 | 390–410 | 0 | LCI | |||
| PEQ | Y | Y | N | 15 | 125–150 (P) | 4 | ND | <5 inches (M21–M22) | LCI | |||||
| 10,000 | 8000–25,000 | BC | Y | Y | Y | 14 | 210–230 (P) | 3 | ND | 14–15, 15–16, | 200–230 | <5 inches (M21–M22) | ND | |
| LT | N | N | N | 14, 15 | 240–415 (P) | 3 | OC | 13–14, 14–15, 15–16, 16–17, 17–18 | 200–415 | 0 | LCI–MCI | |||
| PEQ | Y | Y | Y | 14, 15, 16 | 200–224 (P) | 1 | ND | 13–14, 14–15, 15–16, 20–21 | <240 | <8 inches (M21–M22) | ND | |||
| 50,000 | >25,000 | BC | Y | Y | Y | 4, 5, 6, 7, 20 | 240–500 (P) | 6 | LCI | 5–6, 6–7, 15–16, 16–17 | 250–500 | <9 inches (M19–25) and (M4–M9) | LCI—MCI | |
| LT | Y | Y | N | 14, 15, 16, 17 | 240–500 (P) | 9 | LCI-MCI | 15–16, 16–17, 17–18 | 240–500 | <3 inches (M4–M5) | LCI—MCI | |||
| PEQ | Y | Y | Y | 15, 16, 17 | 240–280 (P) | 3 | OC | 15–16, 16–17, 17–18 | 240–310 | <7 inches (M19–M25) | OC—LCI | |||
| Representative Ground Motion Return Period | Applicable Load Partition Range (Years) | Strength Assumptions 1 | Base Cracking Through | Representative Maximum Stress Condition—Monoliths | Monolith Contraction Joint Conditions Following Earthquake | Other Comments | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Left Monoliths | Central Monoliths | Right Monoliths | Monolith Number(s) | Estimated Maximum Tensile Stress Excursion Range (psi) 2 | Number of Excursions | Estimated Damage Condition through Monolith 3 | Monolith Contraction Joint Numbers 4 | Estimated Maximum Tensile Stress Adjacent to TCJ (psi) | Estimated Maximum Differential Movement (Inches) 5 | Estimated Damage to Monolith Contraction Joints | ||||
| 1000 | 800–3000 | BC | N | N | N | 15 | 100–115 (P) | 4 (P) | ND | 12-13 | 0 | ND | ||
| 5000 | 3000–8000 | BC | Y | Y | Y | 15, 16 | 190–295 (P) | 3 (P) | ND—OC | 19-20 | 480–780 (P) | <8 inches (M21–M22) | LCI—MCI | |
| LT | ||||||||||||||
| PEQ | ||||||||||||||
| 10,000 | 8000–25,000 | BC | Y | Y | Y | 11, 12, 18, 19, 23, 24 | 200–380 (Z) 290–410 (P) | 1–5 (Z) 12 (P) | OC—LCI | 290–410 (P) | <10 inches (M21–M22) | LCI—MCI | ||
| LT | ||||||||||||||
| PEQ | ||||||||||||||
| 50,000 | >25,000 | BC | Y | Y | Y | 15 | 250–450 (P) | 13 | MCI | 6-7, 7-8 | 300–390 (P) | <10 inches (M6–M7, or M7–M8) | MCLL—MCI | |
| LT | ||||||||||||||
| PEQ | ||||||||||||||
References
- U.S. Bureau of Reclamation. FAC 09-01 Directives and Standards for Cost Estimating. 15 October 2007. Available online: https://www.usbr.gov/recman/fac/fac09-01.pdf (accessed on 19 December 2022).
- Chopra, A. Earthquake analysis of arch dams: Factors to be considered. J. Struct. Eng. 2012, 138, 205–214. [Google Scholar] [CrossRef] [Green Version]
- Saouma, V.E.; Hariri-Ardebili, M.A. Aging, Shaking, and Cracking of Infrastructures: From Mechanics to Concrete Dams and Nuclear Structures; Springer-Nature: Cham, Switzerland, 2021. [Google Scholar]
- U.S. Bureau of Reclamation. Design of Gravity Dams; Technical Report; U.S. Bureau of Reclamation: Denver, CO, USA, 1976.
- U.S. Army Corps of Engineers. Gravity Dam Design; Technical Report EM 1110-2-2200; Department of the Army: Washington, DC, USA, 1995. [Google Scholar]
- Chopra, A.K. Earthquake Engineering for Concrete Dams: Analysis, Design, and Evaluation; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Priestly, M. Performance based seismic design. Bull. N. Z. Soc. Earthq. Eng. 2000, 33, 325–346. [Google Scholar] [CrossRef] [Green Version]
- Collins, K.R.; Wen, Y.K.; Foutch, D.A. Dual-level seismic design: A reliability-based methodology. Earthq. Eng. Struct. Dyn. 2016, 45, 1451–1471. [Google Scholar] [CrossRef]
- Sinković, N.L.; Brozovič, M.; Dolšek, M. Risk-based seismic design for collapse safety. Earthq. Eng. Struct. Dyn. 1996, 25, 1433–1467. [Google Scholar] [CrossRef]
- Cimellaro, G.P.; Renschler, C.; Bruneau, M. Introduction to resilience-based design (rbd). In Computational Methods, Seismic Protection, Hybrid Testing and Resilience in Earthquake Engineering; Springer International Publishing: Cham, Switzerland, 2015; pp. 151–183. [Google Scholar]
- Ramakrishnan, C.; Francavilla, A. Structural shape optimization using penalty functions. J. Struct. Mech. 1974, 3, 403–422. [Google Scholar] [CrossRef]
- Akbari, A. Sadoughi. Shape optimization of structures under earthquake loadings. Struct. Multidiscip. Optim. 2013, 47, 855–866. [Google Scholar] [CrossRef] [Green Version]
- Zhang, M.; Li, M.; Ma, X. Isogeometric shape optimization of high RCC gravity dams with functionally graded partition structure considering hydraulic fracturing. Eng. Struct. 2019, 179, 341–352. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Ma, X. Updated kriging-assisted shape optimization of a gravity dam. Water 2021, 13, 87. [Google Scholar] [CrossRef]
- Abdollahi, A.; Amini, A.; Hariri-Ardebili, M. An uncertainty–aware dynamic shape optimization framework: Gravity dam design. Reliab. Eng. Syst. Saf. 2022, 222, 108402. [Google Scholar] [CrossRef]
- Altarejos-Garcia, L.; Escuder-Bueno, I.; Serrano-Lombillo, A.; de Membrillera-Ortuno, M. Methodology for estimating the probability of failure by sliding in concrete gravity dams in the context of risk analysis. Struct. Saf. 2012, 36–37, 1–13. [Google Scholar] [CrossRef]
- Gardoni, P.; Murphy, C. A scale of risk. Risk Anal. 2014, 34, 1208–1227. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, K.A. The History of Dam Safety Governance including Risk Analysis in the US. In Proceedings of the FEMA National Dam Safety Program Technical Webinar, Online, 16–19 February 2021. [Google Scholar]
- Casagrande, A. Role of the “Calculated Risk” in Earthwork and Foundation Engineering, The Terzaghi Lecture. J. Soil Mech. Found. Div. Proc. Am. Soc. Civ. Eng. 1965, 4, 1–40. [Google Scholar]
- Jimmy Carter, Memorandum to the Heads of Certain Federal Agencies on Dam Safety, 23 April 1977, Online by Gerhard Peters and John T. Woolley, The American Presidency Project. Available online: https://www.presidency.ucsb.edu/node/243672 (accessed on 19 December 2022).
- Public Law 95-578 Reclamation Dam Safety Act. 2 November 1978. Available online: https://www.usbr.gov/ssle/sodactasamended.pdf (accessed on 19 December 2022).
- Executive Order 12148, FEMA and the National Dam Safety Program. Available online: https://fas.org/agency/dhs/fema/EO12148.htm (accessed on 19 December 2022).
- Association of State Dam Safety Officials. FEMA P-93, Federal Guidelines for Dam Safety; ASDSO: Lexington, KY, USA, 1979. [Google Scholar]
- Whitman, R.V. Evaluating Calculated Risk in Geotechnical Engineering. ASCE J. Geotech. Eng. 1984, 110, 143–188. [Google Scholar] [CrossRef]
- U.S. Bureau of Reclamation. Guidelines for Achieving Public Protection in Dam Safety Decision Making; U.S. Department of Interior, Bureau of Reclamation: Denver, Colorado, USA, 1997.
- Department of the Army, U.S. Army Corps of Engineering. Safety of Dams—Policy and Procedures; ER 1110-2-1156; Department of the Army: Washington, DC, USA, 2011. [Google Scholar]
- Tennessee Valley Authority. TVA-SPP-27.0 Dam Safety; Tennessee Valley Authority: Knoxville, TN, USA, 2011. [Google Scholar]
- Federal Emergency Management Agency. Federal Guidelines for Dam Safety Risk Management; P-1025; FEMA: Washington, DC, USA, 2015. [Google Scholar]
- Federal Energy Regulatory Commission. Dam Safety Regulations; Federal Energy Regulatory Commission: Washington, DC, USA, 2021. [Google Scholar]
- Hariri-Ardebili, M. Risk, reliability, resilience (R3) and beyond in dam engineering: A state-of-the-art review. Int. J. Disaster Risk Reduct. 2018, 31, 806–831. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.; Nuss, L. Seismic risk prioritization of a large portfolio of dams: Revisited. Adv. Mech. Eng. 2018, 10, 1687814018802531. [Google Scholar] [CrossRef] [Green Version]
- Stedinger, J.; Heath, D.C.; Thompson, K. Risk Analysis for Dam Safety Evaluation: Hydrologic Risk; Technical Report; Army Engineer Institute for Water Resources: Fort Belvoir, VA, USA, 1996. [Google Scholar]
- Bowles, D.S.; Anderson, L.R.; Glover, T.F. A role for risk assessment in dam safety management. In Proceedings of the 3rd International Conference Hydropower, Trondheim, Norway, 30 June–2 July 1997; Volume 97. [Google Scholar]
- Bowles, D. Advances in the practice and use of portfolio risk assessment. In Proceedings of the ANCOLD 2000 Conference on Dams, Melbourne, Australia, 12–17 March 2001; pp. 21–32. [Google Scholar]
- Chauhan, S.S.; Bowles, D.S. Dam safety risk assessment with uncertainty analysis. In Proceedings of the Australian Committee on Large Dams Risk Workshop, Launceston, Australia, 13–15 October 2003. [Google Scholar]
- Peyras, L.; Royet, P.; Boissier, D. Dam ageing diagnosis and risk analysis: Development of methods to support expert judgment. Can. Geotech. J. 2006, 43, 169–186. [Google Scholar] [CrossRef]
- Smith, M. Dam risk analysis using Bayesian networks. In Proceedings of the Engineering Conferences International, Lillehammer, Norway, 18–21 June 2006. ECI Symposium Series. [Google Scholar]
- Serrano-Lombillo, A.; Escuder-Bueno, I.; de Membrillera-Ortuño, M.G.; Altarejos-Garcia, L. Methodology for the calculation of annualized incremental risks in systems of dams. Risk Anal. 2011, 31, 1000–1015. [Google Scholar] [CrossRef]
- Castillo-Rodriguez, J.T.; Needham, J.T.; Morales-Torres, A.; Escuder-Bueno, I. A combined risk analysis approach for complex dam-levee systems. Struct. Infrastruct. Eng. 2017, 13, 1624–1638. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A. Living in a multi-risk chaotic condition: Pandemic, natural hazards and complex emergencies. Int. J. Environ. Res. Public Health 2020, 17, 5635. [Google Scholar] [CrossRef]
- Hariri-Ardebili, M.A.; Lall, U. Superposed natural hazards and pandemics: Breaking dams, Foods, and COVID-19. Sustainability 2021, 13, 8713. [Google Scholar] [CrossRef]
- U.S. Army Corps of Engineers. Interim Approach for Risk-Informed Designs for Dam and Levee Projects. Engineering and Construction Bulletin No. 2019-15. 8 October 2019. Available online: https://www.wbdg.org/ffc/dod/engineering-and-construction-bulletins-ecb/usace-ecb-2019-15 (accessed on 19 December 2022).
- U.S. Army Corp of Engineers. ER 1110-2-1156, Safety of Dams—Policy and Procedures. 31 March 2014. Available online: https://www.publications.usace.army.mil/Portals/76/Publications/EngineerRegulations/er_1110-2-1156.pdf (accessed on 19 December 2022).
- U.S. Bureau of Reclamation. Updated Ground Motions for Scoggins Dam, Technical Memorandum 86-68330-2012-26; U.S. Bureau of Reclamation: Washington, DC, USA, 2013.
- Ferguson, K.A.; Osmun, D.W.; Abedzadeh, F.; Anderson, S.; Moen, K. Risk Informed Design of Large Concrete (RCC) Dams in High Seismic Hazard Regions. In Proceedings of the United States Society on Dams (USSD) Annual Conference, Miami, FL, USA, 30 April–4 May 2018. [Google Scholar]
- U.S. Bureau of Reclamation. State-of-Practice for the Nonlinear Analysis of Concrete Dams; Technical Service Center: Denver, CO, USA, 2013.
- Weiland, M.; (Chair of the International Commission On Large Dams [ICOLD] Committee on Seismic Aspects of Dam Design, Zurich, Switzerland); Ferguson, K.A.; (HDR Engineering, Inc, Senior Technical Advisor for Dams and Hydraulic Structures, Denver, CO, USA). Personal communication, 2021.
- Chopra, A.K.; Chakrabarti, P. The Koyna Earthquake and the Damage to Koyna Dam. Bull. Seismol. Soc. Am. 1973, 63, 381–397. [Google Scholar] [CrossRef]
- Nuss, L.K.; Matsumoto, N.; Hansen, K.D. Shaken but not Stirred, Earthquake Performance of Concrete Dams. In Proceedings of the 2012 Annual Conference, United States Society on Dams, New Orleans, LA, USA, 23–27 April 2012. [Google Scholar]
- Mridha, S.; Maity, D. Experimental Investigation on Nonlinear Dynamic Response of Concrete Gravity Dam-Reservoir System. Eng. Struct. 2014, 80, 289–297. [Google Scholar] [CrossRef]
- Wang, G.; Lu, W.; Zhou, C.; Zhou, W. The Influence of Initial Crack on the Crock Propagation Process of Concrete Gravity Dam-Reservoir-Foundation Systems. J. Earthq. Eng. 2015, 19, 991–1011. [Google Scholar] [CrossRef]
- U.S. Bureau of Reclamation; U.S. Army Corps of Engineers. Best Practices in Dam and Levee Safety Risk Analysis. 2019. Available online: https://usbr.gov/ssle/damsafety/risk/BestPractices/Chapters/1-BestPracticesCover.pdf (accessed on 19 December 2022).
- U.S. Bureau of Reclamation. Interim Dam Safety Public Protection Guidelines, A Risk Framework to Support Dam Safety Decision-Making; Bureau of Reclamation: Denver, CO, USA, 2011.
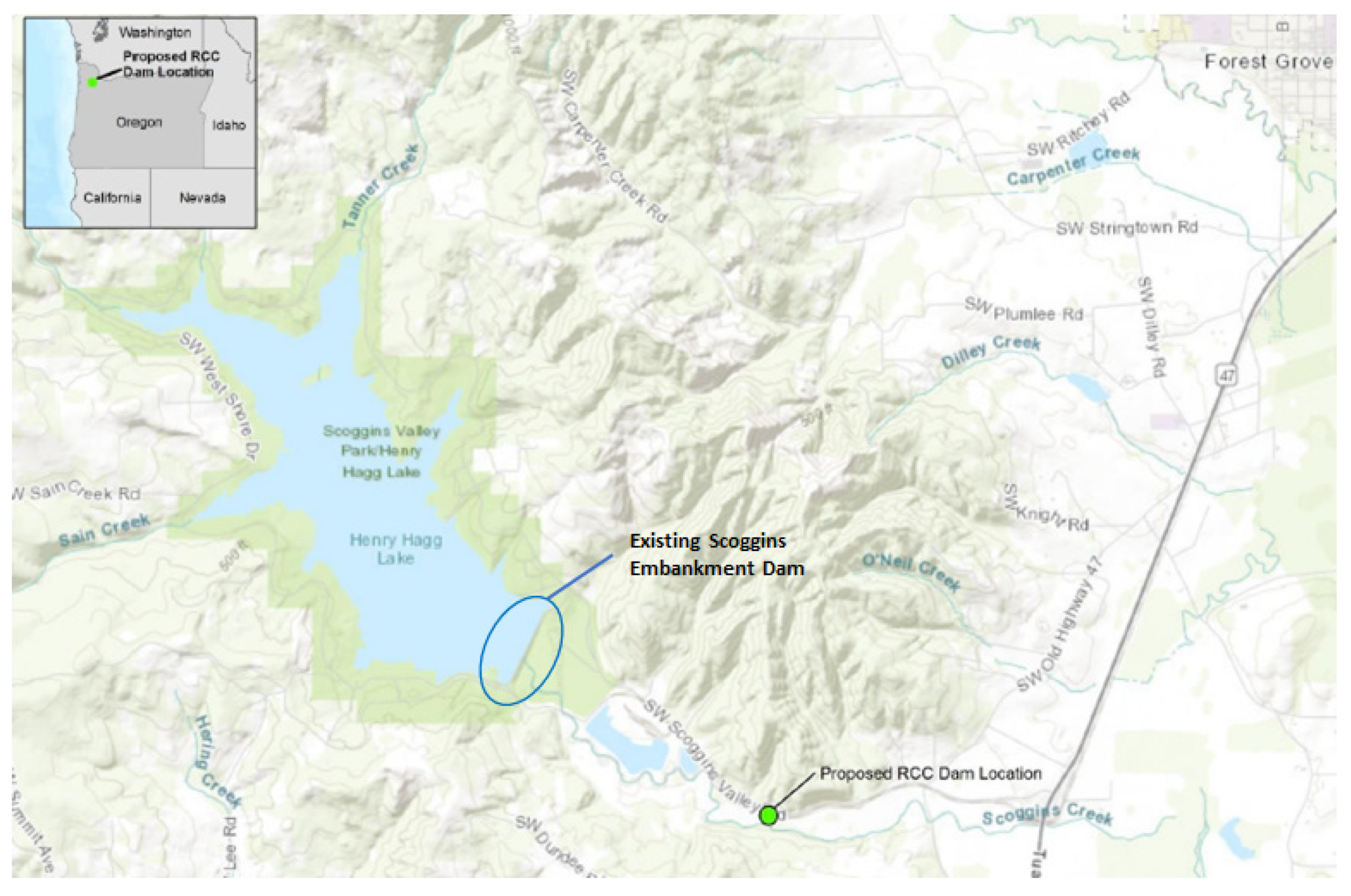
- Ferguson, K.A.; Vanderplaat, T.; Dummer, J. Risk Informed Design of a New Scoggins RCC Dam, Oregon Under Extreme Seismic Loading. In Proceedings of the United States Society on Dams Annual Conference, San Diego, CA, USA, 10–14 April 2022. [Google Scholar]



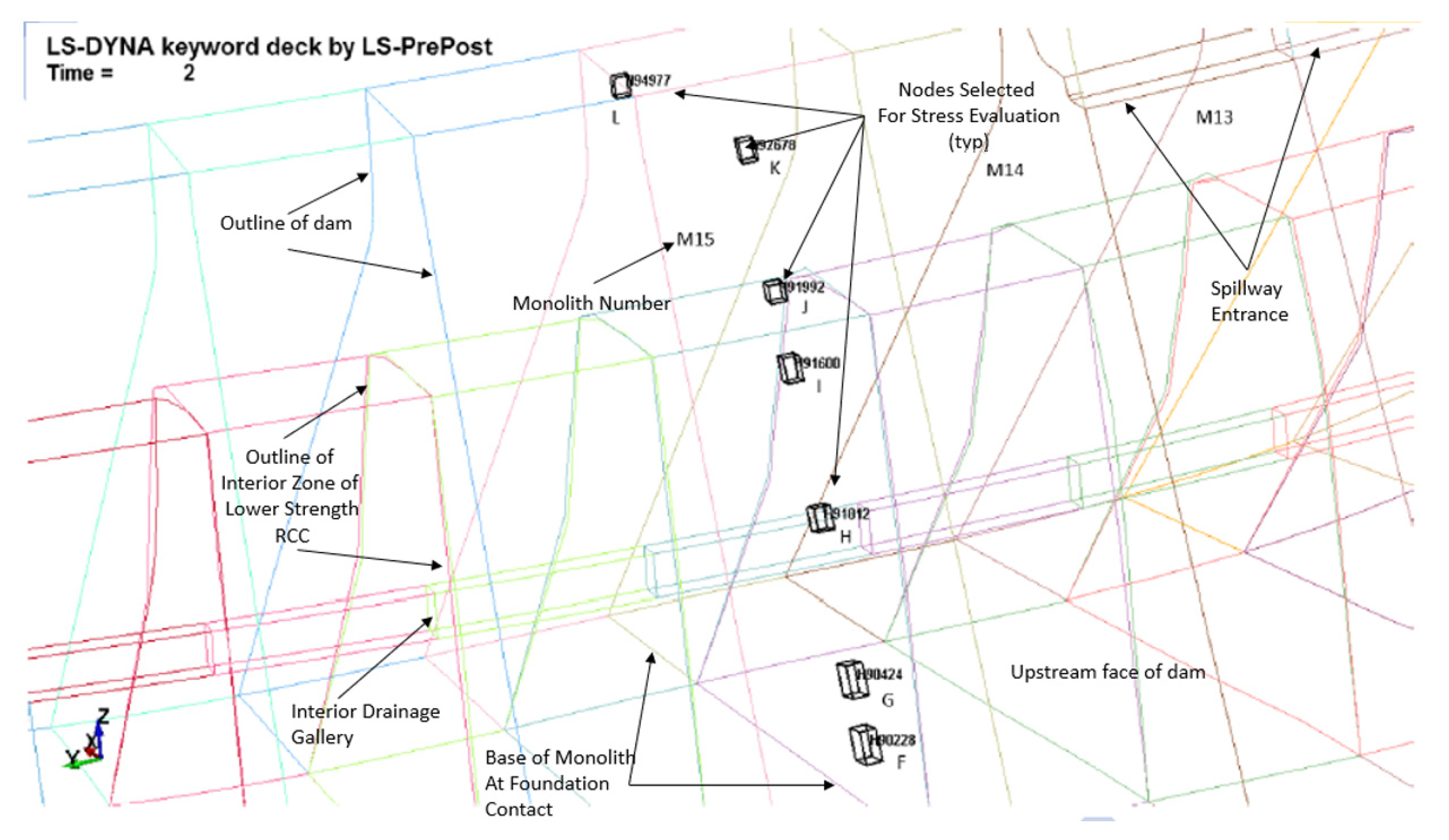
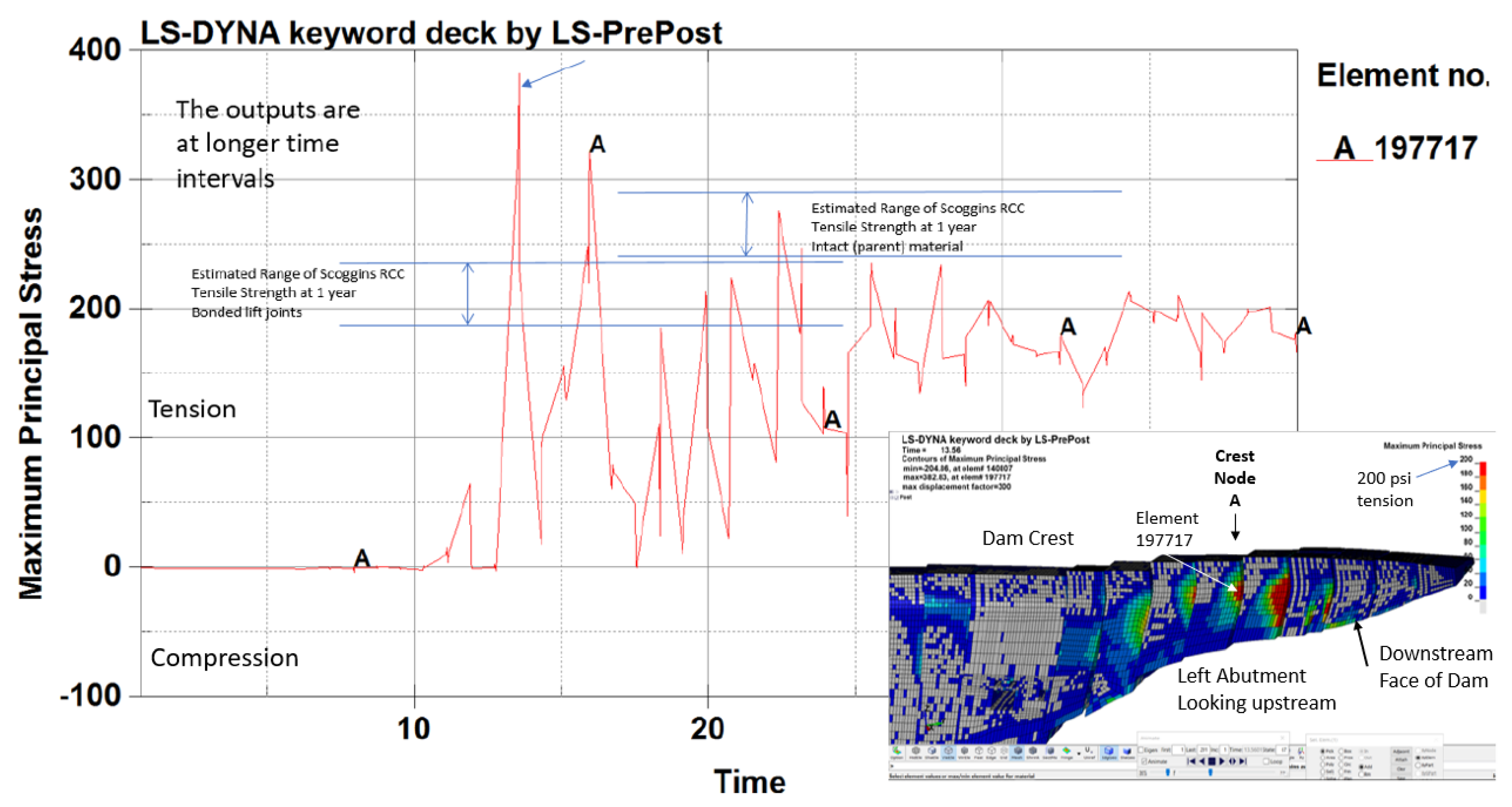
| Return Period (Years) | CSZ Events (g) | Total Hazard PGA (g) |
|---|---|---|
| 500 | 0.16 | 0.37 |
| 1000 | 0.40 | 0.55 |
| 5000 | 0.95 | 1.08 |
| 10,000 | 1.25 | 1.36 |
| 50,000 | 2.00 | 2.08 |
| Material Properties | Assigned Value |
|---|---|
| Average Bedrock Density (y) | 145 lb/ft3 (6.94 kpa) |
| Rock Mass Deformation Modulus (E) | 1.00 × 106 lb/in2 (6895 MPa) |
| Poisson’s Ratio (v) | 0.32 |
| Shear Wave Velocity (Vs) | 3500 ft/s (1067 m/s) |
| P-Wave Velocity (Vp) | 6800 ft/s (2073 m/s) |
| Type of Concrete | SS | SB | BB |
|---|---|---|---|
| (Pounds per Cubic Foot—lb/ft3 [kpa]) | |||
| RCC Outer Zone (2400) | 138 [6.61] | 145 [6.94] | 150 [7.18] |
| RCC Inner Zone (1800) | 137 [6.56] | 145 [6.94] | 150 [7.18] |
| Structural Concrete | N/A | 145 [6.94] | 150 [7.18] |
| Type of Concrete | Young’s Modulus (E) | Poisson’s Ratio (v) |
|---|---|---|
| RCC Outer Zone (2400) | 2.61 × 106 lb/in2 (17,995 MPa) | 0.20 |
| RCC Inner Zone (1800) | 2.32 × 106 lb/in2 (15,996 MPa) | 0.20 |
| Structural Concrete | 4.07 × 106 lb/in2 (28,062 MPa) | 0.20 |
| Name | Lower Bound Psi (MPa) | Upper Bound Psi (MPa) |
|---|---|---|
| Static Tensile Strength (Intact RCC) | 160 [1.103] | 195 [1.344] |
| Dynamic Tensile Strength (Intact RCC) | 242 [1.668] | 292 [2.013] |
| Static Tensile Strength (Principal stresses oriented perpendicular to RCC lift surfaces—80% of intact) | 128 [0.882] | 156 [1.076] 1 |
| Dynamic Tensile Strength (Principal stresses oriented perpendicular to RCC lift surfaces—150% of static adjusted for lift joints) | 192 [1.324] | 234 [1.613] 2 |
| Feature | Intact Shear Strength—Base Case | Intact Shear Strength—Long-Term Case | Cracked but Undeformed Shear Strength | Residual Shear Strength |
|---|---|---|---|---|
| Intact RCC | Phi = 45 deg., c = 100 psi [0.69 Mpa] | Phi = 55 deg., c = 150 psi [1.03 MPa] | ||
| Bonded Lift Joint | Phi = 45 deg., c = 100 psi | Phi = 55 deg., c = 150 psi | ||
| Un-bonded Lift Joint | Phi = 45 deg. | Phi = 35 deg. |
| Name of Contact Surface | Type of LS-DYNA Contact Used | Shear Bond Strength (Cohesion) (lb/in2) | Normal Bond (Tensile) Strength (lb/in2) | Initial (Intact) Friction Angle (Degrees) | Residual Friction Angle after Sliding Initiates (Degrees) |
|---|---|---|---|---|---|
| Dam/Foundation | Tiebreak with Friction | 100 to 250 3 | 100 to 250 3 | 45 (long-term of 55 also used) 2 | 35 |
| Dam/Water | Tied | Tied | Tied | N/A | |
| Foundation/Water | Tied | Tied | Tied | N/A | |
| TCJs 4 | Sliding with Friction | N/A | N/A | 45 1 |
| Case | Reservoir (Feet [m]) | Tailwater (Feet) | Drain Efficiency | Compression at Base | Friction (deg.) | Cohesion (psi [MPa]) | Sliding FOS |
|---|---|---|---|---|---|---|---|
| Normal | 303.5 [92.5] | 160 | 0% | 100% | 45 | 0 | 2.09 |
| 35 | 0 | 1.46 | |||||
| 45 | 25 [0.17] | 3.0 | |||||
| 35 | 42 [0.29] | 3.0 | |||||
| 35 | 70 [0.48] | 4.0 | |||||
| PMF | 310.5 [94.6] | 192 | 0% | 100% | 45 | 0 | 1.7 |
| 35 | 0 | 1.19 | |||||
| 45 | 9 [0.06] | 2.0 | |||||
| 35 | 24 [0.17] | 2.0 | |||||
| 35 | 45 [0.31] | 2.7 |
| Side Shear Stress (psi) | Base Displacement (Inches [cm]) | Crest Displacement (Inches [cm]) | Relative Crest Displacement (Inches [cm]) |
|---|---|---|---|
| 0 | 19 [48.26] | 42 [106.68] | 42 − 19 = 23 [58.42] |
| 0.25 [0.002 MPa] | 12 [30.48] | 26 [66.04] | 26 − 12 = 14 [35.56] |
| 3D analysis (left, center, right) | 14, 6, 10 [35.6, 15.2, 25.4] | — | 0 |
| Side Shear Stress (psi) | Base Displacement (Inches [cm]) | Crest Displacement (Inches [cm]) | Relative Crest Displacement (Inches [cm]) |
|---|---|---|---|
| 0 | 13 [33] | 28 [71.1] | 28 − 13 = 15 [38.1] |
| 0.25 [0.002 MPa] | 8 [20.3] | 12 [30.5] | 12 − 8 = 4 [10.2] |
| 3D analysis (left, center, right) | 6, 3, 0 [15.2, 7.6, 0] | — | 0 |
| Side Shear Stress (psi) | Base Displacement (Inches [m]) | Crest Displacement (Inches [m]) | Relative Crest Displacement (Inches [m]) |
|---|---|---|---|
| 0, Case 3 | 147 [3.73] | 280 [7.11] | 280 − 147 = 133 [3.38] |
| 0, Case 6 | 186 [4.72] | — | 0 |
| 0.25, Case 5 [0.002 MPa] | 33 [0.84] | 46 [1.17] | 46 − 33 = 13 [0.33] |
| 3D analysis (left, center, right) | 38, 51, 85 [0.97, 1.3, 2.16] | — | 0 |
| Potential Failure Mode | AFP (Annual Failure Probability) | Estimated Mean Loss of Life | ALL (Annualized Life Loss Risk) |
|---|---|---|---|
| PFM 5—Seismic sliding and instability at the RCC/foundation contact: limited release failure, short duration | 3.05 × 10−7 | 1 | 3.05 × 10−7 |
| PFM 5—Seismic sliding and instability at the RCC/foundation contact: catastrophic failure, short duration | 1.80 × 10−7 | 12 | 2.07 × 10−6 |
| PFM 5—Seismic sliding and instability at the RCC/foundation contact: limited release failure, long duration | 5.22 × 10−6 | 1 | 5.22 × 10−6 |
| PFM 5—Seismic sliding and instability at the RCC/foundation contact: catastrophic failure, long duration | 2.42 × 10−7 | 12 | 2.78 × 10−6 |
| PFM 6—Seismic sliding and instability at the base of the chimney section: catastrophic failure, short duration | 3.52 × 10−6 | 12 | 4.04 × 10−5 |
| PFM 6—Seismic sliding and instability at the base of the chimney section: catastrophic failure, long duration | 7.33 × 10−6 | 12 | 8.43 × 10−5 |
| PFM 11—Left abutment rock block instability: limited release failure | 2.33 × 10−8 | 1 | 2.33 × 10−8 |
| PFM 11—Left abutment rock block instability: catastrophic failure | 1.60 × 10−8 | 11 | 1.84 × 10−7 |
| Total Risk | 1.68 × 10−5 | 8 (weighted loss of life) | 1.35 × 10−4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ferguson, K.A. Risk-Informed Design of RCC Dams under Extreme Seismic Loading. Water 2023, 15, 116. https://doi.org/10.3390/w15010116
Ferguson KA. Risk-Informed Design of RCC Dams under Extreme Seismic Loading. Water. 2023; 15(1):116. https://doi.org/10.3390/w15010116
Chicago/Turabian StyleFerguson, Keith A. 2023. "Risk-Informed Design of RCC Dams under Extreme Seismic Loading" Water 15, no. 1: 116. https://doi.org/10.3390/w15010116





