Development and Application of a Rainfall Temporal Disaggregation Method to Project Design Rainfalls
Abstract
1. Introduction
2. Materials and Methods
2.1. Study Area and Observation
2.2. Climate Models
2.3. Bias Correction for Climate Model Data
2.4. Neyman–Scott Rectangular Pulse Model (NSRPM)
- (1)
- Calculate the mean of 1 h rainfall, , the variance of 24 h rainfall, , the transition probability from wet to wet, in 24 h (daily) rainfall, the transition probability from dry to dry, in 24 h (daily) rainfall, and the probability of zero depth, . can be easily obtained by dividing the mean of input data by the temporal scale of input data. For example, if the input data is a 3 h scale rainfall, the 1 h mean rainfall is the input rainfall mean that is divided by 3.
- (2)
- Estimate the variance of 1, 3, 6, and 12 h rainfall, , , , and . It is known that it is desirable to construct a regression model with the variance of input data and the variance of the 1, 3, 6, and 12 h rainfall calculated from the observations for parameter estimation [21,23]. This assumes regional normality on a monthly scale and it is considered realistic to utilize empirical relationships rather than arbitrary distributions.
- (3)
- Ninety statistics, , , , , , , , and are used to estimate parameters to minimize the following objective function (Equation (12)), and genetic algorithms are used.where is the statistic obtained from the observations, is the statistic derived from the corresponding NSRPM results, and is the weight of statistic . Since all statistics of the synthetic time series produced by the NSRPM are important in the rainfall disaggregation process, parameters are estimated by giving the same weight ( = 1) for all statistics.
2.5. Rainfall Temporal Disaggregation Based on the NSRPM (RTD-NSRPM)
- Identification of the sequence of target rainfall events (wet = 0, dry = 1);
- Exploration of a synthetic time series with the same rainfall sequence; and
- Determination of the optimal time series that minimizes the following objective () among the explored synthetic time series.
2.6. Evaluation Strategy
3. Results and Discussion
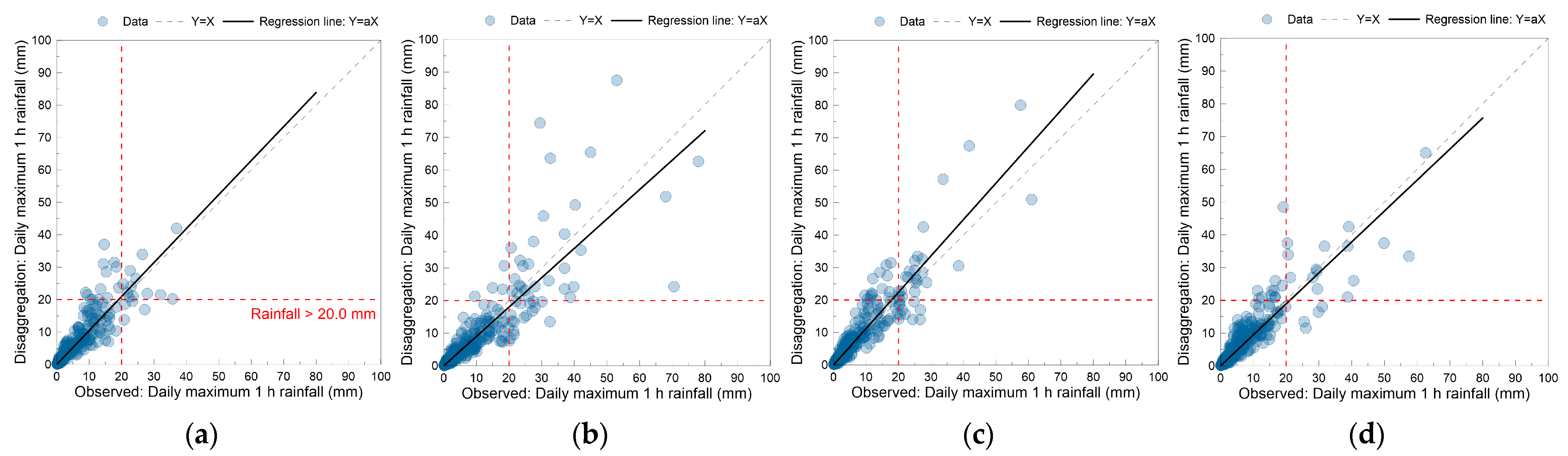
3.1. Verification of the RTD-NSRPM
3.2. Comparison with the NSRPM
3.3. Projection of 1 h Maximum Rainfall
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Y.; Li, H.; Reggiani, P. Climate Variability and Climate Change Impacts on Land Surface, Hydrological Processes and Water Management. Water 2019, 11, 1492. [Google Scholar] [CrossRef]
- IPCC. 2014: Climate Change 2014: Synthesis Report. In Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Core Writing Team, Pachauri, R.K., Meyer, L.A., Eds.; IPCC: Geneva, Switzerland, 2014; p. 151. [Google Scholar]
- Maraun, D.; Wetterhall, F.; Ireson, A.M.; Chandler, R.E.; Kendon, E.J.; Widmann, M.; Brienen, S.; Rust, H.W.; Sauter, T.; Themeßl, M.; et al. Precipitation downscaling under climate change: Recent developments to bridge the gap between dynamical models and the end user. Rev. Geophys. 2010, 48. [Google Scholar] [CrossRef]
- Eden, J.M.; Widmann, M.; Maraun, D.; Vrac, M. Comparison of GCM- and RCM-simulated precipitation following stochastic postprocessing. J. Geophys. Res. Atmos. 2014, 119, 11040–11053. [Google Scholar] [CrossRef]
- Tabari, H. Statistical Analysis and Stochastic Modelling of Hydrological Extremes. Water 2019, 11, 1681. [Google Scholar] [CrossRef]
- Taylor, K.E.; Stouffer, R.J.; Meehl, G.A. An overview of CMIP5 and the experiment design. Bull. Am. Meteorol. Soc. 2012, 93, 485–498. [Google Scholar] [CrossRef]
- Lee, J.; Jang, J.; Kim, S. Performance Evaluation of Rainfall Disaggregation according to Temporal Scale of Rainfall Data. J. Wetl. Res. 2018, 20, 345–352. [Google Scholar]
- Jalota, S.K.; Vashisht, B.B.; Sharma, S.; Kaur, S. Chapter 2—Climate Change Projections. In Understanding Climate Change Impacts on Crop Productivity and Water Balance; Academic Press: Cambridge, MA, USA, 2018; pp. 55–86. [Google Scholar]
- Lombardo, F.; Volpi, E.; Koutsoyiannis, D. Rainfall downscaling in time: Theoretical and empirical comparison between multifractal and Hurst-Kolmogorov discrete random cascades. Hydrol. Sci. J. 2012, 57, 1052–1066. [Google Scholar] [CrossRef][Green Version]
- Debele, B.; Srinivasan, R.; Parlange, J.Y. Accuracy evaluation of weather data generation and disaggregation methods at finer timescales. Adv. Water Res. 2007, 30, 1286–1300. [Google Scholar] [CrossRef]
- Abdellatif, M.; Atherton, W.; Alkhaddar, R. Application of the Stochastic Model for Temporal Rainfall Disaggregation for Hydrological Studies in North Western England. J. Hydroinform. 2013, 15, 555–567. [Google Scholar] [CrossRef]
- Nourani, V.; Farboudfam, N. Rainfall time series disaggregation in mountainous regions using hybrid wavelet-artificial intelligence methods. Environ. Res. 2019, 168, 306–318. [Google Scholar] [CrossRef]
- Rafatnejad, A.; Tavakolifar, H.; Nazif, S. Evaluation of the climate change impact on the extreme rainfall amounts using modified method of fragments for sub-daily rainfall disaggregation. Int. J. Climatol. 2022, 42, 908–927. [Google Scholar] [CrossRef]
- Burton, A.; Fowler, H.J.; Blenkinsop, S.; Kilsby, C.G. Downscaling transient climate change using a Neyman–Scott Rectangular Pulses stochastic rainfall model. J. Hydrol. 2010, 381, 18–32. [Google Scholar] [CrossRef]
- Olsson, J.; Burlando, P. Reproduction of temporal scaling by a rectangular pulses rainfall model. Hydrol. Processes 2002, 16, 611–630. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P.; Xie, G.; Isham, V.; Onof, C.; Walsh, D.C.I. A fine-scale point process model of rainfall with dependent pulse depths within cells. Hydrol. Sci. J. 2011, 56, 1110–1117. [Google Scholar] [CrossRef]
- Velghe, T.; Troch, P.A.; De Troch, F.P.; Van de Velde, J. Evaluation of cluster-based rectangular pulses point process models for rainfall. Water Resour. Res. 1994, 30, 2847–2857. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; De Power, B.F.; Valdes, J.B. Rectangular pulses point process models for rainfall: Analysis of empirical data. J. Geophys. Res. Atmos. 1987, 92, 9645–9656. [Google Scholar] [CrossRef]
- Entekhabi, D.; Rodriguez-Iturbe, I.; Eagleson, P.S. Probabilistic representation of the temporal rainfall process by a modified Neyman-Scott rectangular pulses model: Parameter estimation and validation. Water Resour. Res. 1989, 25, 295–302. [Google Scholar] [CrossRef]
- Cowpertwait, P.S. Further developments of the Neyman-Scott clustered point process for modeling rainfall. Water Resour. Res. 1991, 27, 1431–1438. [Google Scholar] [CrossRef]
- Cowpertwait, P.S. A generalized point process model for rainfall. Proc. R. Soc. London Ser. A Math. Phys. Sci. 1994, 447, 23–37. [Google Scholar]
- Onof, C.; Chandler, R.E.; Kakou, A.; Northrop, P.; Wheater, H.S.; Isham, V. Rainfall modelling using Poisson-cluster processes: A review of developments. Stoch. Environ. Res. Risk Assess. 2000, 14, 384–411. [Google Scholar] [CrossRef]
- Burton, A.; Kilsby, C.G.; Fowler, H.J.; Cowpertwait, P.S.P.; O’connell, P.E. RainSim: A spatial–temporal stochastic rainfall modelling system. Environ. Model. Softw. 2008, 23, 1356–1369. [Google Scholar] [CrossRef]
- Haddad, K.; Rahman, A. Derivation of short-duration design rainfalls using daily rainfall statistics. Nat. Hazards 2014, 74, 1391–1401. [Google Scholar] [CrossRef]
- Nguyen, V.T.V.; Nguyen, T.D.; Wang, H. Regional estimation of short duration rainfall extremes. Water Sci. Technol. 1998, 37, 15–19. [Google Scholar] [CrossRef]
- Kim, J.; Park, M.; Joo, J. Comparison of characteristics and spatial distribution tendency of daily precipitation based on the regional climate models for the Korean Peninsula. J. Korean Soc. Hazard Mitig. 2015, 15, 59–70. [Google Scholar] [CrossRef][Green Version]
- Kim, J.; Joo, J. Characteristics of daily precipitation data based on the detailed climate change ensemble scenario depending on the regional climate models and the calibration. J. Korean Soc. Hazard Mitig. 2015, 15, 261–272. [Google Scholar] [CrossRef][Green Version]
- Joo, J.; Kim, S.; Park, M.; Kim, J. Evaluation and calibration method proposal of RCP daily precipitation data. J. Korean Soc. Hazard Mitig. 2015, 15, 79–91. [Google Scholar] [CrossRef][Green Version]
- Lee, J.; Kim, U.; Kim, L.H.; Kim, E.S.; Kim, S. Management of organic matter in watersheds with insufficient observation data: The Nakdong River basin. Desalinat. Water Treat. 2019, 152, 44. [Google Scholar] [CrossRef]
- Kim, K.; Choi, J.; Lee, O.; Cha, D.H.; Kim, S. Uncertainty quantification of future design rainfall depths in Korea. Atmosphere 2020, 11, 22. [Google Scholar] [CrossRef]
- Boé, J.; Terray, L.; Habets, F.; Martin, E. Statistical and dynamical downscaling of the Seine basin climate for hydro-meteorological studies. Int. J. Climatol. J. R. Meteorol. Soc. 2007, 27, 1643–1655. [Google Scholar] [CrossRef]
- Cannon, A.J.; Sobie, S.R.; Murdock, T.Q. Bias correction of GCM precipitation by quantile mapping: How well do methods preserve changes in quantiles and extremes? J. Clim. 2015, 28, 6938–6959. [Google Scholar] [CrossRef]
- Kim, S.; Han, S. Urban Stormwater Capture Curve Using Three-Parameter Mixed Exponential Probability Density Function and NRCS Runoff Curve Number Method. Water Environ. Res. 2010, 82, 43–50. [Google Scholar] [PubMed]
- Choi, C.H.; Cho, S.; Park, M.J.; Kim, S. Overflow risk analysis for designing a nonpoint sources control detention. Water Environ. Res. 2012, 84, 434–440. [Google Scholar] [CrossRef] [PubMed]
- Lee, O.; Choi, J.; Jang, S.; Kim, S. Application of Stochastic Point Rainfall Model for Temporal Downscaling of Daily Precipitation Data. J. Korean Soc. Hazard Mitig. 2017, 17, 323–337. [Google Scholar] [CrossRef]
- Lee, J.; Kim, S. Temporal Disaggregation of Daily Rainfall data using Stochastic Point Rainfall Model. J. Korean Soc. Hazard Mitig. 2018, 18, 493–503. [Google Scholar] [CrossRef][Green Version]
- Rodríguez-Iturbe, I. Scale of fluctuation of rainfall models. Water Resour. Res. 1986, 22, 15S–37S. [Google Scholar] [CrossRef]
- Cowpertwait, P.S.P.; O’Connel, P.E.; Metcalfe, A.V.; Mawdsley, J.A. Stochastic point process modeling of rainfall: 1. Single-site fitting and validation. J. Hydrol. 1996, 175, 17–46. [Google Scholar] [CrossRef]
- Joo, J.; Lee, J.; Kim, J.H.; Jun, H.; Jo, D. Inter-event time definition setting procedure for urban drainage systems. Water 2014, 6, 45–58. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Onof, C. Rainfall disaggregation using adjusting procedures on a Poisson cluster model. J. Hydrol. 2001, 246, 109–122. [Google Scholar] [CrossRef]










| Acronym | GCM | RCM | Period | Scale (Temporal, Spatial, Year) | Scenario |
|---|---|---|---|---|---|
| RRD 1 | MPI_ESM_LR | MM5 | Present 1981–2010 | 3 h, 12.5 km, 365 days | RCP 4.5 |
| RRD 2 | MPI_ESM_LR | WRF | 3 h, 12.5 km, 365 days | RCP 4.5 | |
| RRD 3 | MPI_ESM_LR | RegCM | 3 h, 12.5 km, 365 days | RCP 4.5 | |
| RRD 4 | MPI_ESM_LR | RSM | 3 h, 12.5 km, 365 days | RCP 4.5 | |
| RRD 5 | HadGEM2-AO | MM5 | Future 2021–2050 | 3 h, 12.5 km, 365 days | RCP 4.5 |
| RRD 6 | HadGEM2-AO | WRF | 3 h, 12.5 km, 365 days | RCP 4.5 | |
| RRD 7 | HadGEM2-AO | RegCM | 3 h, 12.5 km, 360 days | RCP 4.5 | |
| RRD 8 | HadGEM2-AO | RSM | 3 h, 12.5 km, 360 days | RCP 4.5 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Kim, U.; Kim, S.; Kim, J. Development and Application of a Rainfall Temporal Disaggregation Method to Project Design Rainfalls. Water 2022, 14, 1401. https://doi.org/10.3390/w14091401
Lee J, Kim U, Kim S, Kim J. Development and Application of a Rainfall Temporal Disaggregation Method to Project Design Rainfalls. Water. 2022; 14(9):1401. https://doi.org/10.3390/w14091401
Chicago/Turabian StyleLee, Jeonghoon, Ungtae Kim, Sangdan Kim, and Jungho Kim. 2022. "Development and Application of a Rainfall Temporal Disaggregation Method to Project Design Rainfalls" Water 14, no. 9: 1401. https://doi.org/10.3390/w14091401
APA StyleLee, J., Kim, U., Kim, S., & Kim, J. (2022). Development and Application of a Rainfall Temporal Disaggregation Method to Project Design Rainfalls. Water, 14(9), 1401. https://doi.org/10.3390/w14091401








