Numerical Analysis of the Groundwater Flow System and Heat Transport for Sustainable Water Management in a Regional Semi-Arid Basin in Central Mexico
Abstract
1. Introduction
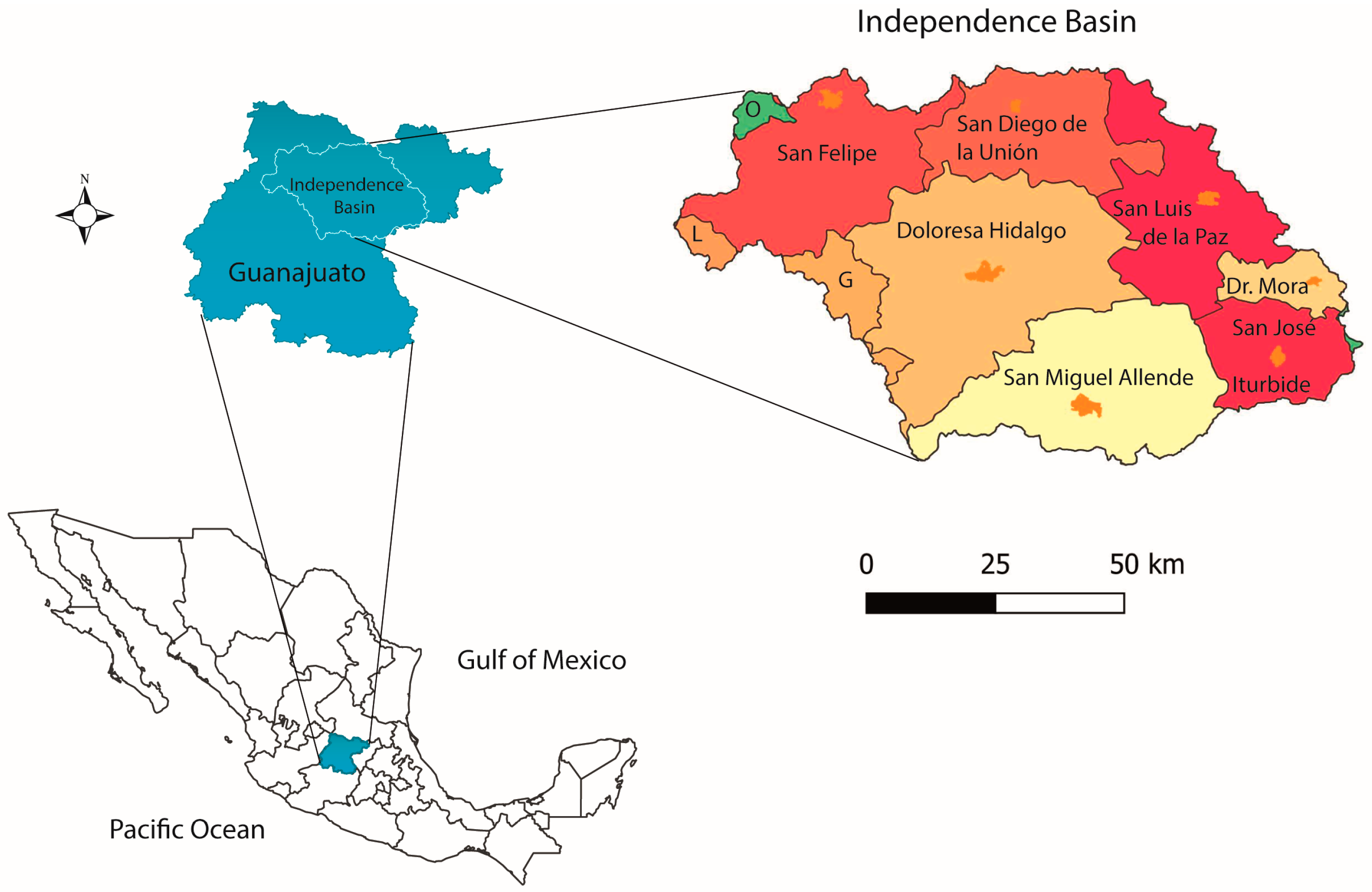
Description of the Study Basin
2. Hydrogeology of the Basin
2.1. Geology
2.2. Hydrostratigraphy
2.3. Natural Manifestations of Groundwater Conditions
2.4. Historical and Current Manifestations of Groundwater Conditions
2.5. Preliminary Water Budget
2.6. Previous Modeling
3. Materials and Methods
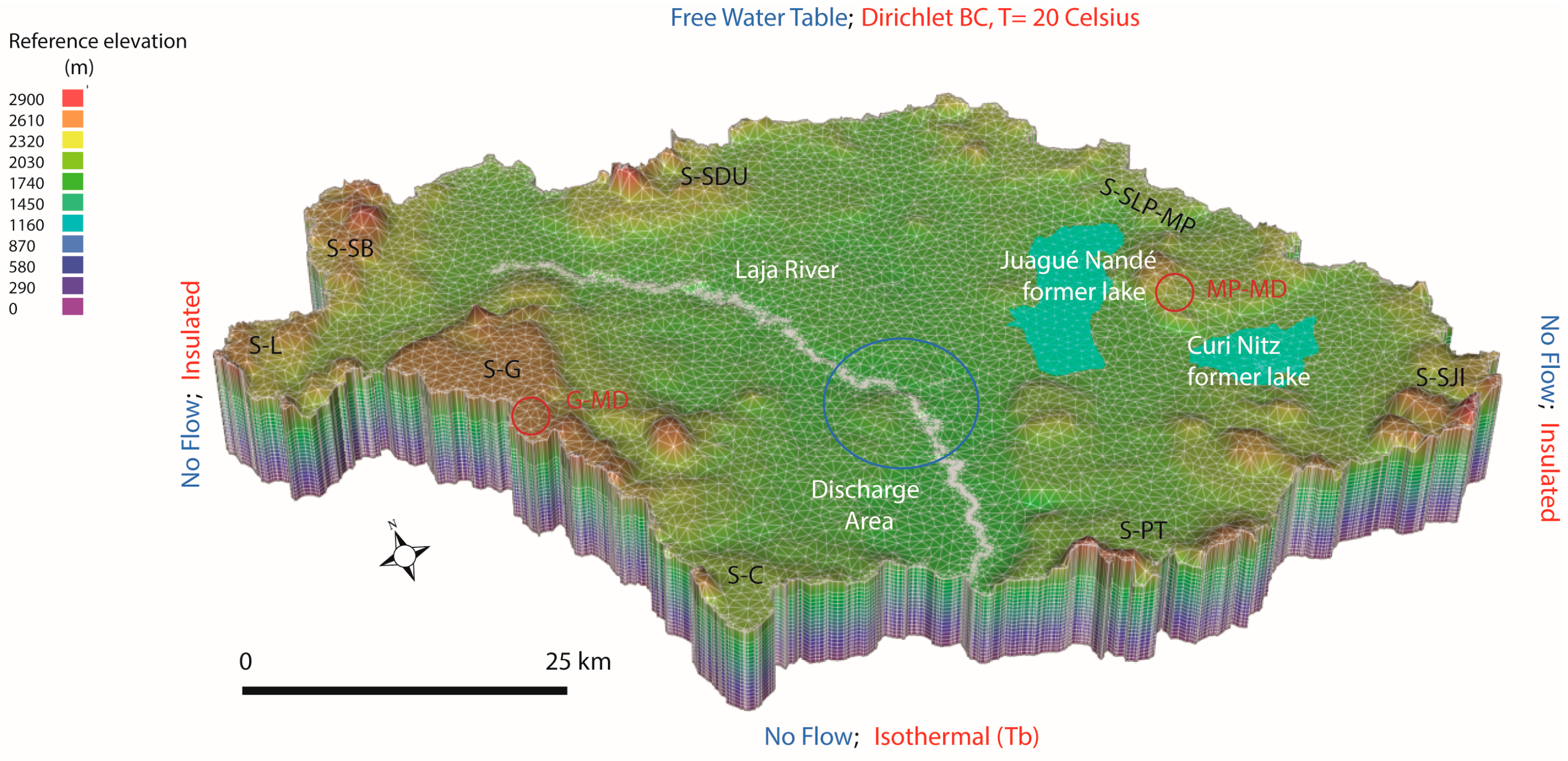
3.1. Conceptual Model of Flow
3.2. Modeling of the Flow System and Heat Transport
3.2.1. Description of the Numerical Model
3.2.2. Boundary Conditions
3.2.3. Modeling Strategy
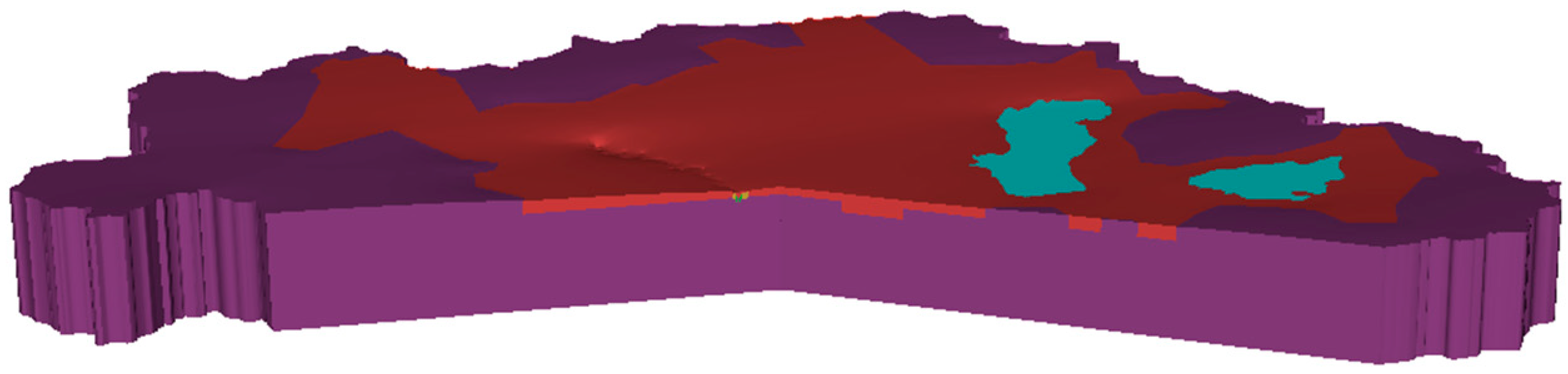
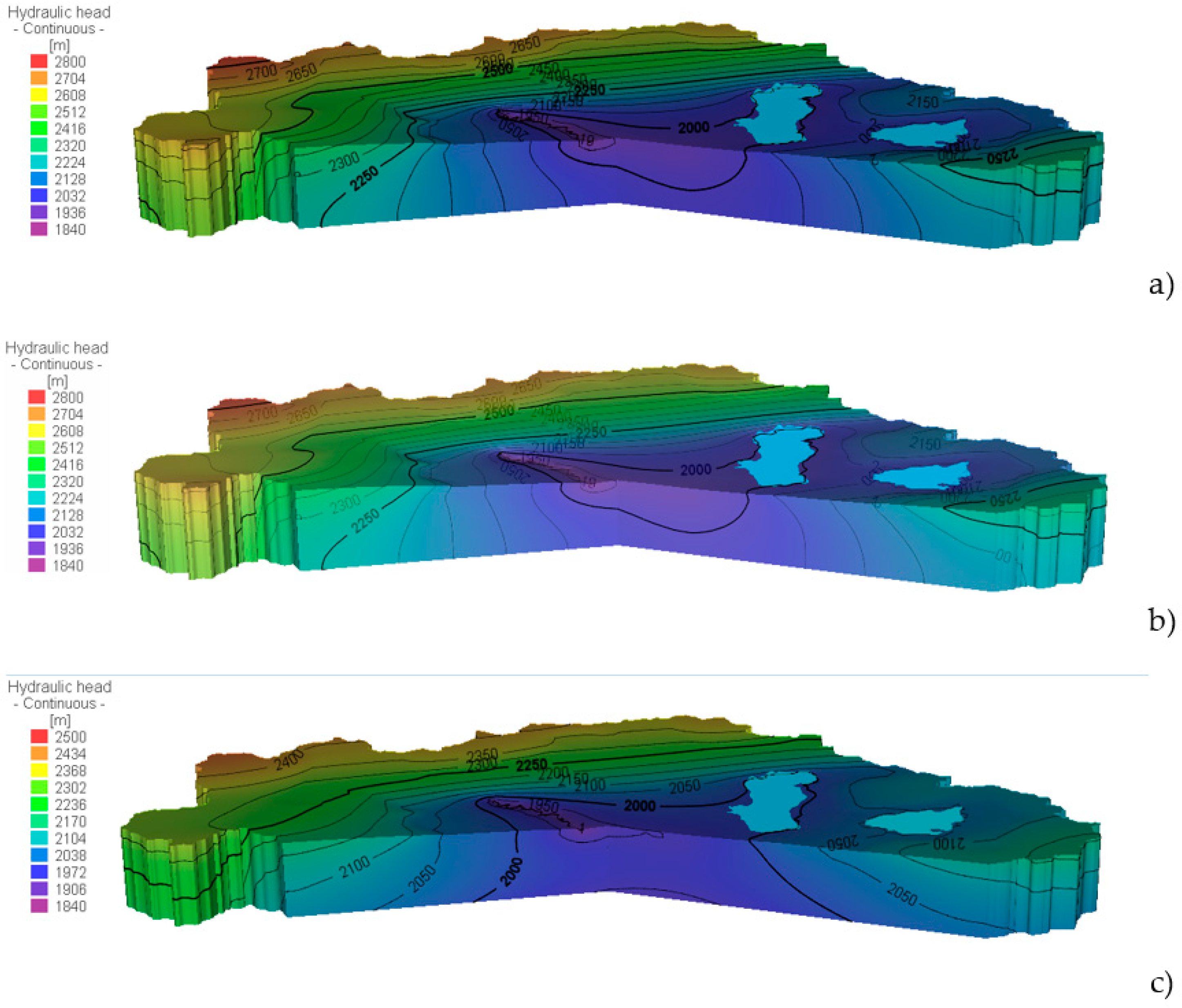
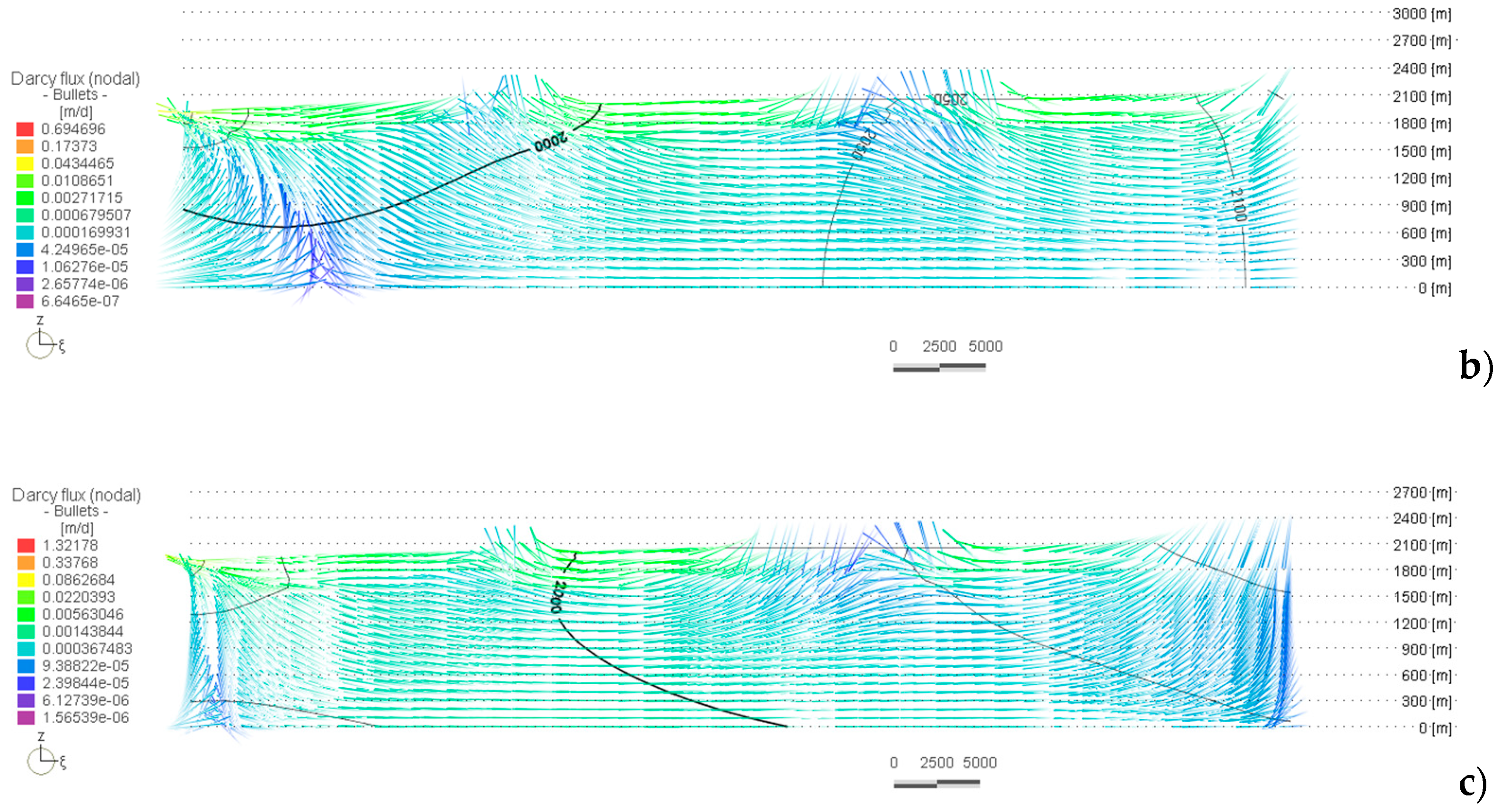
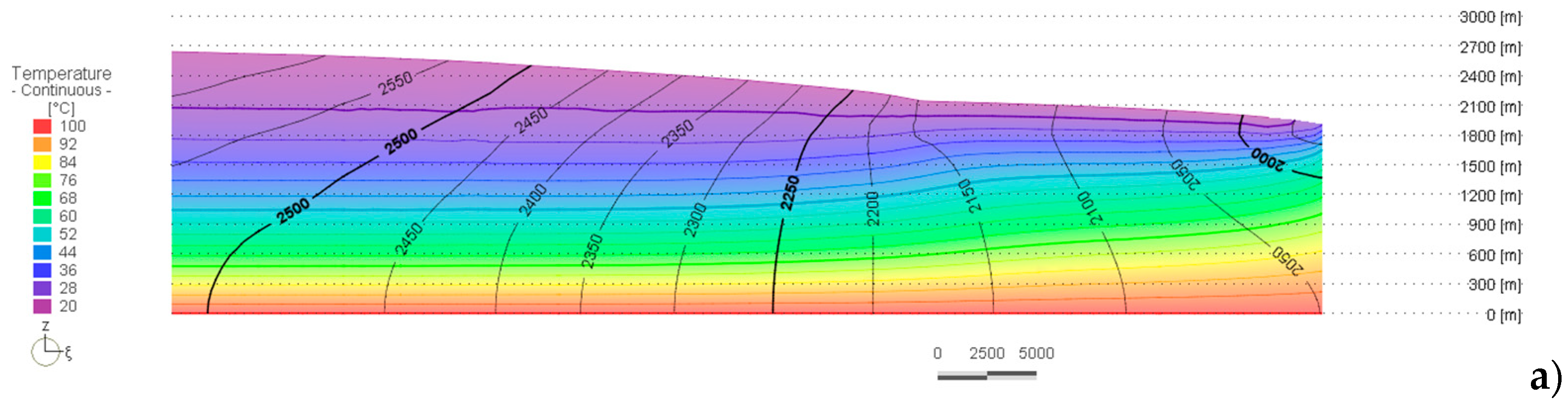
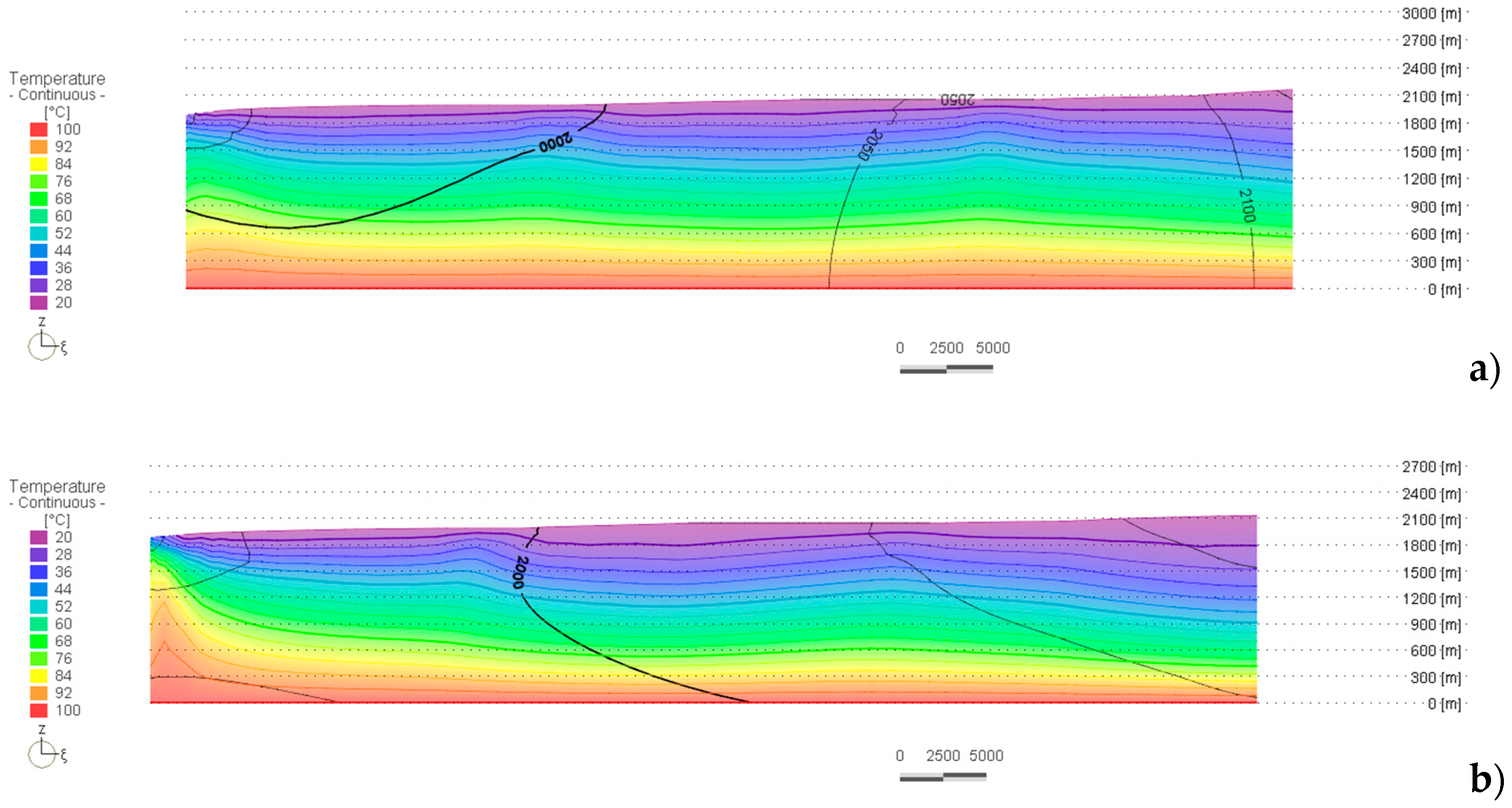
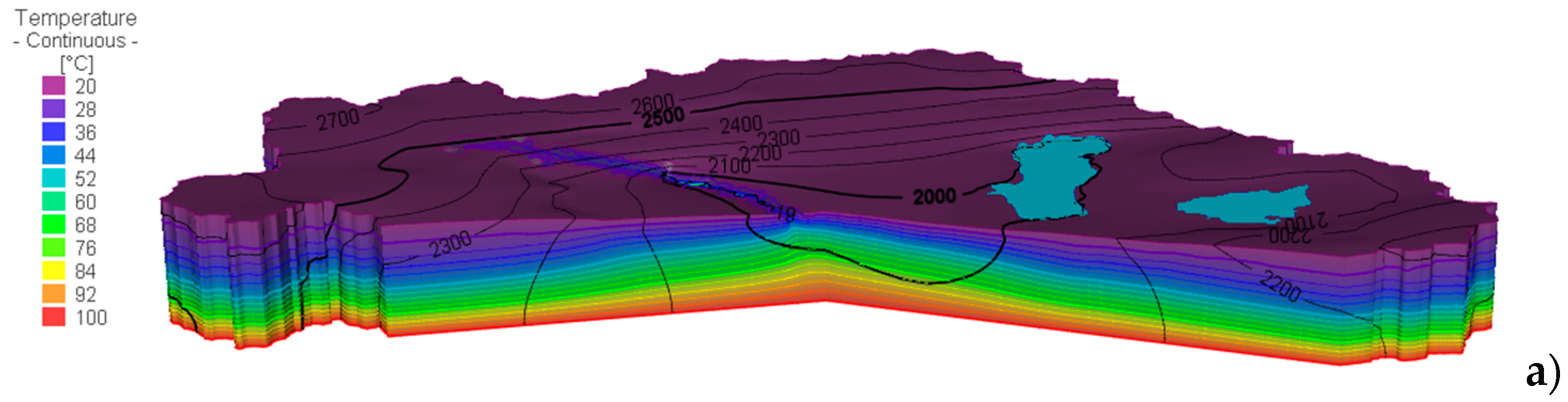
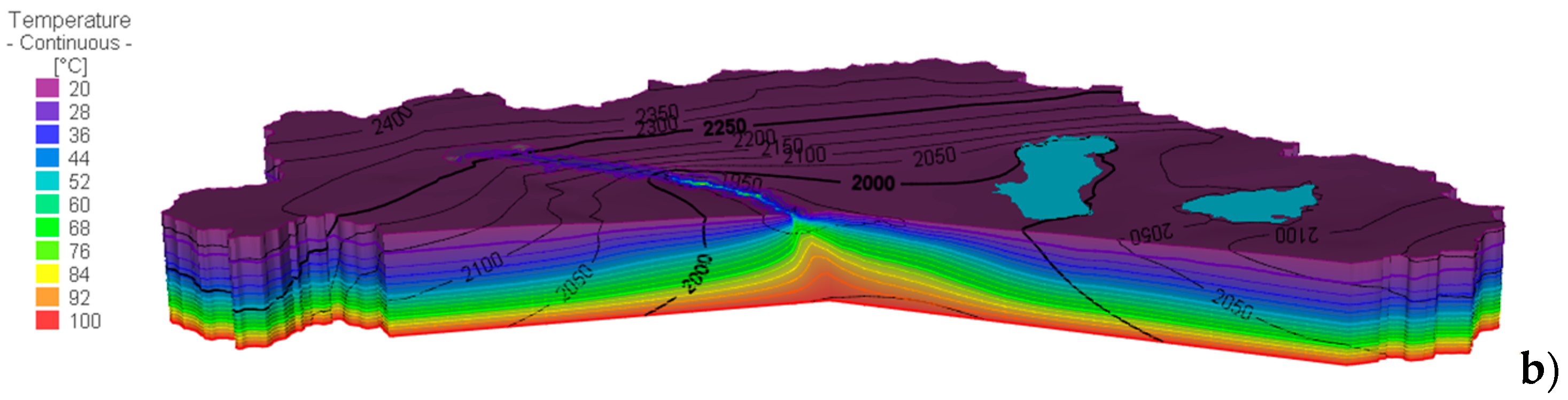
4. Results
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ortega-Guerrero, M.A.; Castellanos, J.Z.; Aguilar, G.R.; Vázquez-Alarcón, A.; Alanis, R.E.; Vargas, C.C.; Urrutia, E.F. A Conceptual Model for Increases of Sodium, Sar, Alkalinity and ph at the Independence Aquifer in Guanajuato, Mexico; TERRA Latinoamericana: Mexico City, Mexico, 2002; Volume 20, pp. 199–207. Available online: https://www.redalyc.org/articulo.oa?id=57320213 (accessed on 10 September 2021).
- Ortega-Guerrero, M.A. Occurrence, distribution, hydrochemistry and origin of arsenic, fluoride and other trace elements dissolved in groundwater at basin scale in central Mexico. Rev. Mex. Ciencias Geol. 2009, 26, 143–161. [Google Scholar] [CrossRef]
- González, P. Geografía Local del Estado de Guanajuato, 1st ed.; Ediciones La Rana: Guanajuato, Mexico, 1904; p. 691. [Google Scholar]
- Tarquín, A.G. Leyendas y Tradiciones de la Tribu Chichimeca; Ediciones del Gobierno de Guanajuato: Guanajuato, Mexico, 1963; p. 135. [Google Scholar]
- Nieto-Samaniego, A.F.; Macias-Romo, C.; Alaníz-Álvarez, S.A. Nuevas Edades Isotópicas de la Cubierta Volcánica Cenozoica de la Parte Meridional de la Mesa Central; Revista Mexicana de Ciencias Geológicas: Guanajuato, Mexico, 1996; Volume Voume 13, pp. 117–122. [Google Scholar]
- Pérez-Venzor, J.A.; Aranda-Gómez, J.J.; McDowell, F.W.; Solorio-Munguia, J.G. Bosquejo de la Evolución Geológica del Volcán Palo Huérfano; Revista Mexicana de Ciencias Geológicas: Guanajuato, Mexico, 1996; Volume 13, pp. 174–183. [Google Scholar]
- Chiodi, M.; Monod, O.; Busnardo, R.; Gaspard, D.; Sánchez, A.; Yta, M. Une discordance ante albienne datée par une faune d’ammonites at brachiopodes de type Tèthysien au Mexique Central. Geobios 1988, 21, 125–135. [Google Scholar] [CrossRef]
- Elías–Herera, M.; Ortega-Gutierrez, F. The Early Cretaceous Arperos oceanic basin (western Mexico). Geochemical evidence for an aseismic ridge formed near a spreading center. Tectonophysics 1998, 292, 321–326. [Google Scholar] [CrossRef]
- Nieto-Samaniego, A.F.; García-Dobargones Bueno, J.E.; Aguirre-Maese, A.L. Interpretación Estructural de Los Rasgos Geomorfológicos Principales de la Sierra de Guanajuato: Universidad Nacional Autónoma de México. Rev. Inst. de Geol. 1992, 10, 1–5. [Google Scholar]
- Aranda-Gómez, J.J.; Aranda-Gómez, J.M.; Nieto-Samaniego, A.F. Consideraciones acerca de la evolución tectónica durante el Cenozoico de la Sierra de Guanajuato y la parte meridional de la Mesa Central. Rev. Inst. Geol. 1989, 8, 33–56. [Google Scholar]
- Aranda-Gómez, J.J.; McDowell, F.W. Paleogene extension in the southern Basin and Range Province of Mexico: Syn-depositional tilting of the Eocene red beds and Oligocene volcanic rocks in the Guanajuato mining district. Int. Geol. Rev. 1998, 40, 116–134. [Google Scholar] [CrossRef]
- Labarthe-Hernández, G.; Tristán-González, M.; Aranda-Gómez, J.J. Revisión Estratigráfica del Cenozoico en la Parte Central del Estado de San Luis Potosí; Universidad Autónoma de San Luis Potosí, Instituto Geológico y Metalúrgico: Folleto Técnico, Mexico, 1982; Volume 85, p. 208. [Google Scholar]
- Prol-Ledesma, R.M.; Morán-Centeno, D. Heat flow and geothermal provinces in Mexico. Geothermics 2019, 78, 183–200. [Google Scholar] [CrossRef]
- Martínez-Roldán, N.; Goytia-Goyenechea, L. Mining trace in the city of Guanajuato (México) between the XVI-XIX centuries: Urban morphology and planimetry in the archive of Indias in Sevilla (Spain). Rev. Contexto. Sept. 2020, XIV, 35–49. [Google Scholar]
- Consejo de Recursos Minerales. Ficha de Inventario de Yacimientos Minerales, Estado de Guanajuato. 2002. Available online: https://mapserver.sgm.gob.mx/InformesTecnicos/InventariosMinerosWeb/A1103PAPJ0003_01.pdf (accessed on 12 November 2021).
- Aguilar-García, R.; Ortega-Guerrero, M.A. Analysis of the dynamics of water in the unsaturated zone in a soil subject to conservation practices: Implications for aquifer management and adaptation to climate change. Rev. Mex. De Cienc. Geológicas 2017, 34, 91–104. [Google Scholar] [CrossRef][Green Version]
- Martínez-Arredondo, J.C.; Jofre Meléndez, R.; Ortega Chávez, V.M.; Ramos Arroyo, Y.R. Descripción de la variabilidad climática normal (1951–2010) en la cuenca del río Guanajuato, centro de México. Acta Univ. 2015, 25, 31–47. [Google Scholar] [CrossRef][Green Version]
- Palacios-Vélez, E.; López-López, C. La Sobreexplotación de Las Cuencas Hidrológicas: El Caso De La Cuenca Del Río de La Laja, Guanajuato; En Cotler, H., Ed.; El Manejo Integral de Cuencas en México; México, Secretaría del Medio Ambiente y Recursos Naturales, Instituto Nacional de Ecología: Mexico City, Mexico, 2004; pp. 117–131. [Google Scholar]
- Ortega, A.; Farvolden, R.N. Computer analysis of regional groundwater flow and boundary conditions in the Basin of Mexico. J. Hydrol. 1989, 110, 271–294. [Google Scholar]
- Morales-Casique, E.; Guinzberg-Belmont, J.; Ortega-Guerrero, A. Regional groundwater flow and geochemical evolution in the Amacuzac River Basin, Mexico. Hydrogeol. J. 2016, 24, 1873–1890. [Google Scholar] [CrossRef]
- Toth, J. A theory of groundwater motion in small drainage basins in central Alberta, Canada. J. Geophys. Res. 1962, 67, 4375–4387. [Google Scholar] [CrossRef]
- Toth, J. A theoretical analysis of groundwater flow in small basins. J. Geophys. Res. 1963, 68, 4795–4812. [Google Scholar] [CrossRef]
- Freeze, R.A.; Witherspoon, P.A. Theoretical analysis of regional analysis flow: 1. Analytical and numerical solutions to the mathematical model. Water Resour. Res. 1966, 2, 641–656. [Google Scholar] [CrossRef]
- Freeze, R.A.; Witherspoon, P.A. Theoretical analysis of regional analysis flow: 2. Effect of water table configuration and subsurface permeability variations. Water Resour. Res. 1967, 3, 623–634. [Google Scholar] [CrossRef]
- Freeze, R.A.; Witherspoon, P.A. Theoretical analysis of regional analysis flow: 3. Quantitative interpretations. Water Resour. Res. 1968, 4, 581–590. [Google Scholar] [CrossRef]
- Freeze, R.A. Quantitative interpretation of regional groundwater patterns as an aid to wáter balancee studies. Int. Assoc. Sci. Hydrol. Gen. Assem. Berne Publ. 1967, 78, 154–173. [Google Scholar]
- Freeze, R.A. Three dimensional, transient, saturated-unsaturated flow in a groundwater basin. Water Resour. Res. 1971, 7, 929–941. [Google Scholar] [CrossRef]
- Jamieson, G.R.; Freeze, R.A. Determining hydraulic conductivity distributions in a mountainous area using mathematical modeling. Groundwater 1983, 21, 168–177. [Google Scholar] [CrossRef]
- Forster, C.B.; Smith, L. Groundwater flow systems in mountainous terrain: 1. Numerical modeling technique. Water Resour. Res. 1988, 24, 999–1010. [Google Scholar] [CrossRef]
- Forster, C.B.; Smith, L. Groundwater flow systems in mountainous terrain: 2. Controlling factors. Water Resour. Res. 1988, 24, 1011–1023. [Google Scholar] [CrossRef]
- Long, A.J.; Valder, J.F. Multivariate analyses with end-member mixing to characterize groundwater flow: Wind cave and associated aquifers. J. Hydrol. 2011, 409, 315–327. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Mace, R.E.; Barrett, M.E.; Smith, B.B. Can we simulate regional groundwater flow in a karst system using equivalent porous media models? Case study, Barton Springs Edwards aquifer, USA. J. Hydrol. 2003, 276, 137–158. [Google Scholar] [CrossRef]
- Ghasemizadeh, R.; Yu, X.; Butscher, C.; Hellweger, F.; Padilla, I.; Alshawabkeh, A. Equivalent porous media (EPM) simulation of groundwater hydraulics and contaminant transport in karst aquifers. PLoS ONE 2015, 10, e0138954. [Google Scholar] [CrossRef] [PubMed]
- Domenico, P.A.; Palciauskas, V.V. Theoretical analysis of forced convective heat transfer in regional ground-water flow. GSA Bull. 1973, 84, 3803–3814. [Google Scholar] [CrossRef]
- An, R.; Jiang, X.-W.; Wang, J.-Z.; Wan, L.; Wang, X.-S.; Li, H. A theoretical analysis of basin-scale groundwater temperature distribution. Hydrogeol. J. 2015, 23, 397–404. [Google Scholar] [CrossRef]
- Szijártó, M.; Galsa, A.; Tóth, A.; Mádl-Szónyi, J. Numerical analysis of the potential for mixed thermal convection in the Buda Thermal Karst, Hungary. J. Hydrol. Reg. Stud. 2021, 34, 100783. [Google Scholar] [CrossRef]
- Szijártó, M.; Galsa, A.; Tóth, A.; Mádl-Szónyi, J. Numerical investigation of the combined effect of forced and free termal convection in synthetic groundwater basins. J. Hydrol. 2019, 572, 364–379. [Google Scholar] [CrossRef]
- Diersch, H.J. FEFLOW Finete Element Modeling of Flow, Mass and Heat Transport in Porous and Fractured Media; Springer: New York, NY, USA, 2014; p. 996. ISBN 978-3-642-38739-5. [Google Scholar] [CrossRef]
- Saar, M.O. Review: Geothermal heat as a tracer of large-scale groundwater flow and as a means to determine permeability fields. Hydrogeol. J. 2011, 19, 31–52. [Google Scholar] [CrossRef]
- Tóth, J. Gravitational Systems of Groundwater Flow: Theory, Evaluation, Utilization; Cambridge University Press: Cambridge, UK, 2009; p. 297. ISBN 978-0-521-88638-3. [Google Scholar]
- Jiang, X.W.; Wan, L.; Wang, X.S.; Wang, D.; Wang, H.; Wang, J.Z.; Zhang, H.; Zhang, Z.Y.; Zhao, K.Y. A multi-method study of regional groundwater circulation in the Ordos Plateau, NW China. Hydrogeol. J. 2018, 26, 1657–1668. [Google Scholar] [CrossRef]
- López, T.; Antoine, R.; Kerr, Y.; Darrozes, J.; Rabinowicz, M.; Ramillien, G.; Cazenave, A.; Genthon, P. Subsurface hydrology of the Lake Chad Basin from convection modelling and observations. Surv. Geophys. 2016, 37, 471–502. [Google Scholar] [CrossRef]
- Smith, L.; Chapman, D.S. On the thermal effects of groundwater flow: I. Regional scale systems. J. Geophys. Rcs. 1983, 88, 593–608. [Google Scholar] [CrossRef]
- Parsons, M.L. Groundwater thermal regime in a glacial complex. Water Resour. Res. 1970, 6, 1701–1720. [Google Scholar] [CrossRef]
- Woodbury, A.D.; Smith, L. On the thermal effects of three dimensional groundwater flow. J. Geophy. Res. 1985, 90, 759–767. [Google Scholar] [CrossRef]
- Manning, C.E.; Ingebritsen, S.E. Permeability of the continental crust: Implications of geothermal data and metamorphic systems. Rev. Geophys. 1999, 37, 127–150. [Google Scholar] [CrossRef]
- Garven, G.; Freeze, R.A. Theoretical analysis of the role of groundwater flow in the genesis of stratabound ore deposits. I. Mathematical and numerical model. Am. J. Sci. 1984, 284, 1085–1124. [Google Scholar] [CrossRef]
- Garven, G.; Freeze, R.A. Theoretical analysis of the role of groundwater flow in the genesis of stratabound ore deposits. 11. Quantitative results. Am. J. Sci. 1984, 284, 1125–1174. [Google Scholar] [CrossRef]
- Anderson, M.P. Heat as a ground water tracer. Ground Water 2005, 43, 951–968. [Google Scholar] [CrossRef]
- Tóth, A.; Galsa, A.; Mádl-Szónyi, J. Significance of basin asymmetry and regional groundwater flow conditions in preliminary geothermal potential assessment—Implications on extensional geothermal plays. Glob. Planet. Change 2020, 195, 103344. [Google Scholar] [CrossRef]
- de la Fuente-Hernández, J.; Aguilar-Díaz, F.C.; Cintra-Viveiro, C.A. Fluorosis Dental y Factores Asociados en Estudiantes Residentes de Comunidades del Estado de Guanajuato; Universidad Nacional Autónoma de México, Entreciencias, diálogos en la Sociedad del Conocimiento: Mexico City, Mexico, 2016; Volume 4, Available online: http://www.redalyc.org/articulo.oa?id=457647810005 (accessed on 3 February 2022).
- Farías, P.; Estevez-García, J.A.; Onofre-Pardo, E.N.; Pérez-Humara, M.L.; Rojas-Lima, E.; Álamo-Hernández, U.; Rocha-Amador, D.O. Fluoride Exposure through Different Drinking Water Sources in a Contaminated Basin in Guanajuato, Mexico: A Deterministic Human Health Risk Assessment. Int. J. Environ. Res. Public Health 2021, 18, 11490. [Google Scholar] [CrossRef] [PubMed]
- Ortega-Guerrero, M.A. Situación del Agua Subterránea en México: Una Experiencia Científico-Legislativa y Sus Implicaciones; Revista Punto de Acuerdo, Fundación Humanismo Político, diciembre-febrero: Mexico City, Mexico, 2011; pp. 30–40. [Google Scholar]
- Carmona-Lara, C.; Carrillo-Rivera, J.J.; Hatch-Kuru, G.; Huizar-Alvarez, R.; Ortega-Guerrero, M.A. Ley del Agua Subterránea: Una Propuesta; Universidad Nacional Autónoma de México: Mexico City, Mexico, 2017; p. 87. ISBN 978-607-02-8997-2. [Google Scholar] [CrossRef]
- Consejo Nacional de Ciencia y Tecnología; Ciencias y Humanidades: México City, Mexico, 2021; p. 60. Available online: https://conacyt.mx/evento/presentacion-de-la-revista-ciencias-y-humanidades/ (accessed on 3 February 2022).



| Scenario | Density | Viscosity |
|---|---|---|
| I. Isothermal | Constant | Constant |
| II. Convective 1 | Linear dependency on T 1 | Constant |
| III. Convective 2 | Nonlinear dependency on T | Variable-dependent on T |
| Definition | Symbol | Value | Unit |
|---|---|---|---|
| Hydraulic conductivity Granular Porosity | Kxx | 1 | m/d |
| Kyy | 0.1 | m/d | |
| Kzz | 0.01 | m/d | |
| ε | 0.3 | Vol/vol | |
| Hydraulic conductivity Fractured Porosity | Kxx | 0.1 | m/d |
| Kyy | 0.01 | m/d | |
| Kzz | 0.001 | m/d | |
| ε | 0.1 | Vol/vol | |
| Hydraulic-head BC Fluid-flux BC | Elevation Laja River | m | |
| Infiltration rate with elevation | m/d | ||
| Surface temperature BC Bottom temperature BC Porosity Volumetric head capacity of fluid Volumetric head capacity of solid Thermal conductivity of fluid Thermal conductivity of solid Anisotropy of solid thermal conductivity Longitudinal dispersivity Transverse dispersivity | T Tb ε ρs cs ρc Λ Λs βd βd | 20 100 0.1 4.2 2.56 0.65 3 1 5 0.5 | Celsius Celsius Vol/vol MJ/m3/K MJ/m3/K J/m/s/K J/m/s/K m m |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ortega Guerrero, M.A. Numerical Analysis of the Groundwater Flow System and Heat Transport for Sustainable Water Management in a Regional Semi-Arid Basin in Central Mexico. Water 2022, 14, 1377. https://doi.org/10.3390/w14091377
Ortega Guerrero MA. Numerical Analysis of the Groundwater Flow System and Heat Transport for Sustainable Water Management in a Regional Semi-Arid Basin in Central Mexico. Water. 2022; 14(9):1377. https://doi.org/10.3390/w14091377
Chicago/Turabian StyleOrtega Guerrero, Marcos Adrián. 2022. "Numerical Analysis of the Groundwater Flow System and Heat Transport for Sustainable Water Management in a Regional Semi-Arid Basin in Central Mexico" Water 14, no. 9: 1377. https://doi.org/10.3390/w14091377
APA StyleOrtega Guerrero, M. A. (2022). Numerical Analysis of the Groundwater Flow System and Heat Transport for Sustainable Water Management in a Regional Semi-Arid Basin in Central Mexico. Water, 14(9), 1377. https://doi.org/10.3390/w14091377






