1. Introduction
The coastline of Thailand is approximately 2600 km long and has more than 11 million people living in this area. At present, Thailand’s coast is experiencing a severe erosion problem, resulting in the loss of property of the people and the government spoiling the scenery, which affects the economy such as the tourism business and causes damage to coastal resources. Moreover, coastal erosion in many areas is likely to extend in terms of land and severity. Therefore, corrective plans and solutions are urgently and essentially desired.
When waves swash the beach, they transfer energy to the sand, causing dispersed sediment. Every time waves come in and out of the beach, sediment will also blow in both directions. As a result, coastal erosion emerged on the beach, losing more sediment from erosion than acquired. In most areas of Thailand facing coastal erosion, efforts have been made to protect shorelines with breakwaters, especially, rock dams. The most significant advantage of this method is its durability, but there is a massive disadvantage of causing severe erosion at the end next to the rock dam, the so-called “end effect.” It occurs because the wave energy is diverted from every part of the rock dam to its end. Moreover, another disadvantage of rock dams is that they cannot cause sediment deposition.
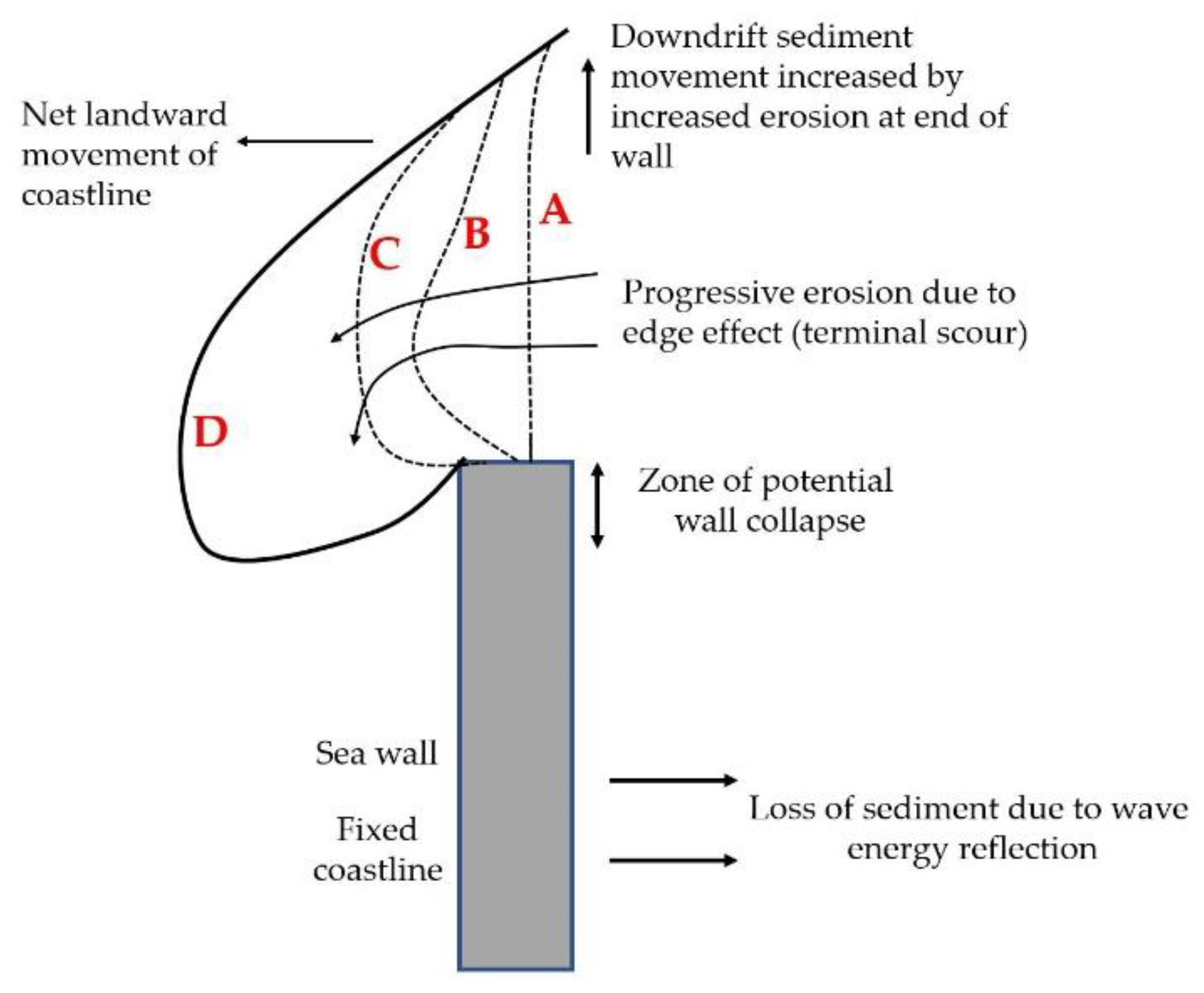
Figure 1 shows an explanatory diagram and overview of the end effect occurrence [
1]. The rock dam acted as a fixed coastline, so the end effect causes intensified corrosion starting from state A to D, depending on the time.
Khao Rup Chang is one of several beaches that have been greatly affected by the end effect, as seen in
Figure 2. The state
C end effect was so severe that trees fell, and the coast collapsed, as shown in
Figure 2. Accordingly, it was appropriate to be employed as a case study for this research. In the past, for adjacent areas, relevant agencies solved this problem by extending the rock dam’s length more, which is an indirect solution. However, the end effect still existed and expanded in wider areas, so building or extending additional rock dams was not a suitable solution. The disadvantages of the rock dam and the beach damage mentioned above, as well as the explanation of the end effect presented in
Figure 1, necessitate a search for new solutions.
The derosion lattice (DL) is a highly flexible strength-net device, a novel type of breakwater. Its advantages are that it can reduce the incoming wave energy due to friction and vibration of polyamide strands and dissipate to a broader area [
2]. It has been successfully installed to prevent coastal erosion in Shuang-Chun [
3] and Kimen beaches [
4] in Taiwan. However, it is well known that the DL performance depends on the beach’s installing condition, terrain, and climate. Moreover, it has never been used to solve the end effect before. Therefore, these conditions must be considered if installed for solving the end effect in Thailand, and its performance should be assessed. In order to find a properly installed condition, trial and error is not the right process to perform because it will waste a lot of budget and time, resulting in more corrosion at the beach while waiting for an appropriate solution; therefore, computational fluid dynamics (CFD) is a suitable tool to find a proper solution to avoid the mentioned disadvantages. Computer capability and CFD software have developed rapidly today. Thus, they were applied to effectively solve this problem by assessing the environment to determine maintenance guidelines [
5,
6,
7] and optimizing breakwater design [
8,
9,
10].
Therefore, this research aims to employ CFD to assess the DL performance by using the actual environment of Khao Rup Chang beach before deciding whether actually to install it or not. First, the simulation results were validated and analyzed to determine the root cause of the end effect. Next, the optimal condition for installing the DL at the actual site would be determined if the DL performance was compelling. Finally, the DL performance was assessed after employing the optimal condition to install the DL on-site. This research highlights the reality and completeness of the simulation conditions, as the research includes the views of experts from related fields as consultants for accurate, reliable, and practical results.
2. Theoretical Background
This section presents a brief overview of governing equations required to perform the CFD calculation, including conservation, turbulence, the volume of fluid equations, and assessment parameters.
2.1. Conservation Equations
The incompressible flow and Newtonian fluid can be calculated by solving Reynolds-averaged Navier–Strokes (RANS) conservation and turbulence equations. In a transient state, the mass and momentum conservation are given as (1) and (2), respectively.
where
is the mean velocity vector,
ρ is the fluid density,
p is the static pressure,
is the porous media source term,
is the gravitational acceleration, and
is the stress tensor related to the strain rate as follows:
where
I is a unit tensor,
μ is a molecular viscosity, and
T is matrix transposition.
2.2. Turbulence Equations
Since wave behavior swashing the beach can be considered a turbulent, swirling flow, with the occurrence of a collision between fluid and obstruction, the shear stress transport (SST)
k–
ω turbulence model was employed. It is a suitable turbulence model for monitoring the complex flow, particularly swirls, because it consists of
k, representing the amount of energy produced due to turbulent flow, and
ω referring to the ability of the turbulence distribution, including the possibility of many small swirls. Therefore, it has been employed in many applications [
11,
12,
13,
14]. The SST
k–
ω equations can be written as
where
μt is the eddy viscosity, and
Pk is the shear production of turbulence.
ω is the specific dissipation rate,
k is the turbulent kinetic energy, and
F1 is the blending function.
α3,
β3, and
σω3 are the specific coefficients for the SST
k–
ω turbulence model.
represent the components of the cartesian velocities, and
is a model constant.
2.3. Volume of Fluid Equations
The movement of the water waves through the beach and the DL relies on a principle of free-surface flow. Therefore, researchers in [
5,
6,
7,
8,
9,
10] used the volume of fluid (VOF), one of the models in multiphase flows. The VOF for a constant mass transfer between phases can be expressed according to [
15] as follows:
where the index
designates a fluid phase,
is a volume fraction of fluid, and
is fluid velocity. The notation
means the empty cell of
qth fluid,
the full cell of
qth fluid, and
the cell interface contained between the
qth fluid and one or more other fluids.
Equation (5) cannot be solved to determine the primary phase; the primary phase volume fraction is computed based on the constraint given by
Since the wave motion changes with time, the explicit formulation of the finite volume method can be written as
where
and
are indices for the current and previous time step, respectively.
V is a cell volume.
is volume flux through the face, based on a normal velocity.
is a face value of the
volume fraction.
After defining boundary conditions, the CFD calculates and then displays the numerical results in shade color for analysis.
2.4. Assessment Parameters
In this research, ANSYS Fluent, a well-known CFD software, was employed to solve (1–7) to present the behavior of waves swashing through the beach with and without the DL. After the calculation is complete, many valuable indicators resulting from CFD can be presented as assessment parameters of the DL performance. After analyzing all the available data and suggestions from the consultants, the water velocity (v) and bottom shear stress (τ) were assigned to be assessment parameters because they could be used to reasonably describe the behavior of waves and the occurrence of the end effect accordingly. High performance is based on the following principle: low v and small τ. The theory behind the two assessment parameters is briefly explained in the next sections.
2.4.1. Water Velocity (v)
A suspension velocity is the most negligible fluid velocity supporting tiny particles to remain afloat. It depends on the density of the fluid, the density of the particle, and the shape of the particles [
16,
17]. Therefore, when
v is lower than the suspension velocity, particles such as sediment, sand, etc. will fall onto the beach floor. This description implies that the installing condition provides a broad region with a lower
v is more likely to sediment than a higher
v. Since we do not precisely know the density, size, shape, and type of sediment on the beach, we cannot determine suspension velocity accurately. We, therefore, reasonably used the
v to assess the DL performance instead. The lower the value of
v, the greater the beach’s tendency to be uneroded with sediment deposition at that position.
2.4.2. The Bottom Shear Stress (τ)
This is defined similarly to the wall shear stress of Newtonian fluid, which is directly proportional to the viscosity and velocity gradient [
12,
14]. Since the water is a Newtonian fluid,
τ is the bottom shear stress acting on the beach floor. The higher the value of
τ, the greater the beach’s tendency to be eroded at that position.
3. Methodology
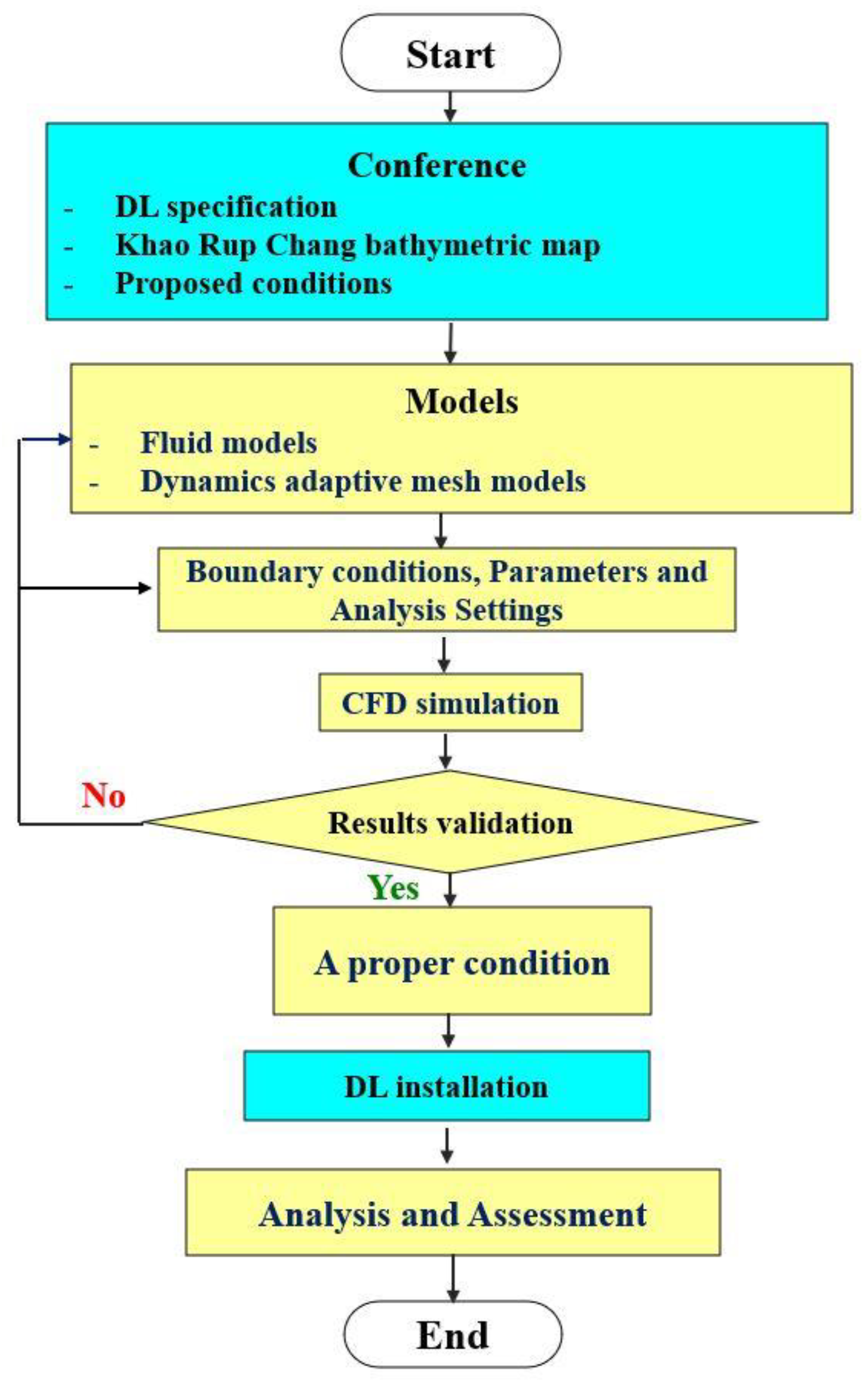
The research methodology used can be described as a flowchart shown in
Figure 3. It is divided into two parts: the blue part is practical actions, and the yellow part is the CFD simulation.
3.1. Conference
As mentioned in
Section 1, the DL method was expected to solve the end effect in Thailand. Previously, it has been installed and successfully protected the coastal erosion in Taiwan.
Figure 4 shows the actual DL when (a) installed completely and (b) being used on Taiwan beach [
2]. From (a) to (b), it can be seen that the DL can reduce coastal erosion and increase sedimentation. However, the two countries, Thailand and Taiwan, have beaches with different geographies and environments, and it was not used to solve the end effect before. Therefore, to achieve accurate results consistently as close to those of the actual installed site as possible, this research had a conference to listen to advice from consultants from many fields. For example, a team of inventors from ReShore Technologies, Taiwan, provided suggestions on the DL specification and possible conditions for installation. A team of marine specialists from the Aquatic Resource Research Institute, Chulalongkorn University, Thailand, supported the overview information of the geography and climate of the beach. An expert on the sea and breakwater from the Marine Department, Ministry of Transport, explained his experience gained from the field trips to several beaches. Thai Wiring System Ltd. accommodated miscellaneous facilities and instruments for the experiment.
The conference results gave us detailed information on the DL, geography, climate, etc., which can be applied to further proposed conditions and simulation settings to assess the DL performance as close to the actual situation as possible.
3.1.1. Derosion Lattice (DL)
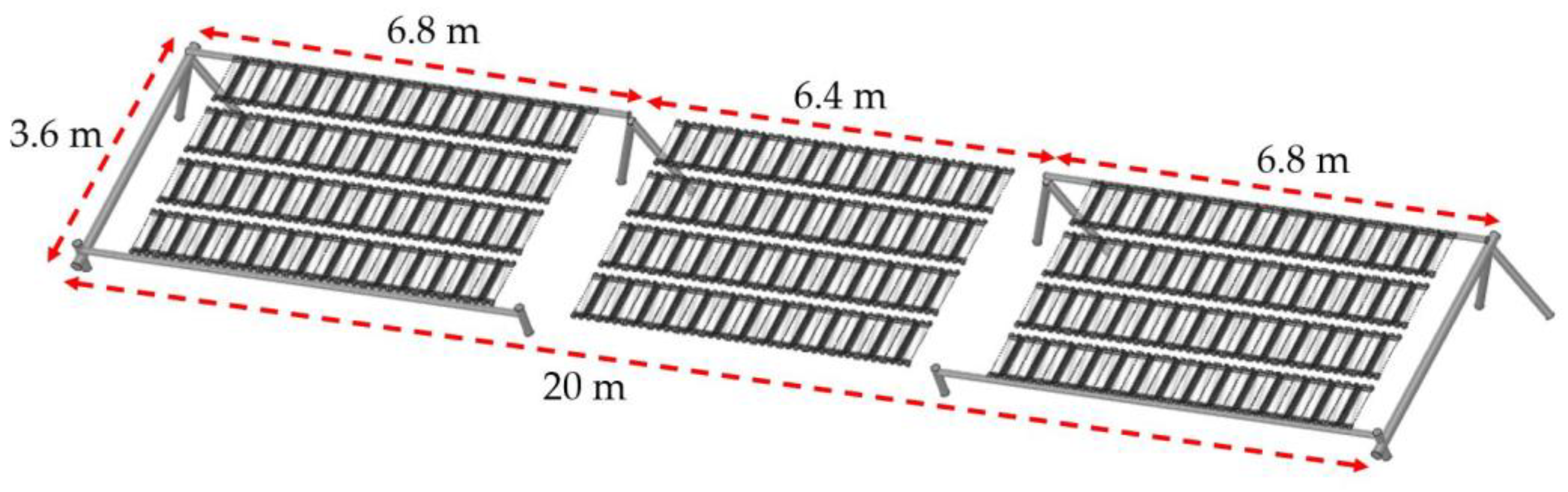
Since the number of DL, lengths, and installation locations must be evaluated to suit the operating conditions and be consistent with the actual terrain and climate,
Figure 5 reveals a simplified model and dimension of the DL suggested by the consultants suitable for a case study beach. In addition, the DL was modified to leave only parts essentially required for the simulation.
3.1.2. Khao Rup Chang Beach
The location is 7°08′34.6″ N, 100°38′48.3″ E in Songkhla Province, southern Thailand.
Figure 6 shows an aerial photograph of the beach as (a) an overview with a marked area enlarged the end effect area and (b) a zoom-in of the end effect. According to
Figure 2 and
Figure 6, the beach was eroded, causing a concave area of about 300 × 10 m
2 to creep into the shoreline. As expected, it was the most eroded area next to the rock dam structure. From the information from an expert of the Marine Department, Ministry of Transport, who is concerned and responsible for this problem, the end effect is severe during the northeast monsoon season, between October and December, when the water level, wind, and wave speed are high. To obtain accurate CFD-assessed results consistent with the actual beach profile, the necessary geological and climatic data, such as wind direction, bathymetric map, etc., were gathered from the consultants mentioned in
Section 3.1 and analyzed to create the CAD models, mesh models, and the proposed conditions for simulation. In addition, the bathymetric map is included in a
Supplementary Material File entitled Bathymetric_map.pdf.
3.1.3. Proposed Conditions
According to suggestions from consultants in the conference, we concluded that the placement position (P) and an angle of attack (
θ), the angle between the DL and wavefront, affect the DL performance. Therefore, the CFD simulation was divided into eight cases to find a proper condition for the DL installation, as reported in
Table 1. For example, the symbols can be described as follows:
P0 is a case without the DL, used as a controlled case for comparison;
P1/15° is a case with the DL placed at a position P1 with
θ of 15°. This case is the recommended condition successful in preventing coastal erosion in Taiwan [
3,
4];
P2/10° is a case with the DL placed at a position P2 with θ of 10°, etc.
Other symbols in
Table 1 are described in the same way. In addition, the position P1–P4 of DL placed at the beach is explained further in the next section.
3.2. Models
3.2.1. Fluid Model
The modified solid model of DL in
Figure 5 was adjusted and merged in the beach model of 60 × 76 × 10 m
3 (W × L × H) following the proposed conditions in
Table 1. Compared with the dimension of the DL, we were confident that the scale of the fluid model we created was large enough to accurately monitor the waves’ flow behavior passing through the DL and the beach.
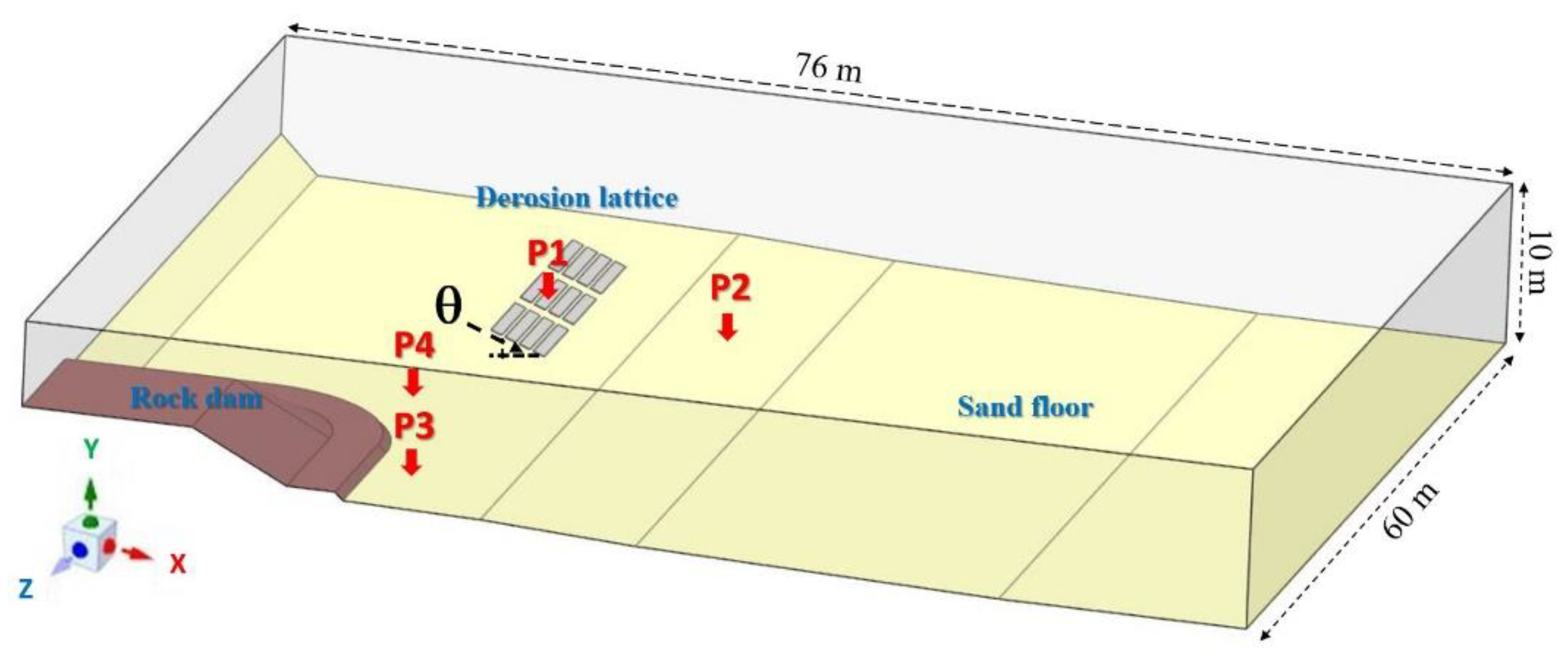
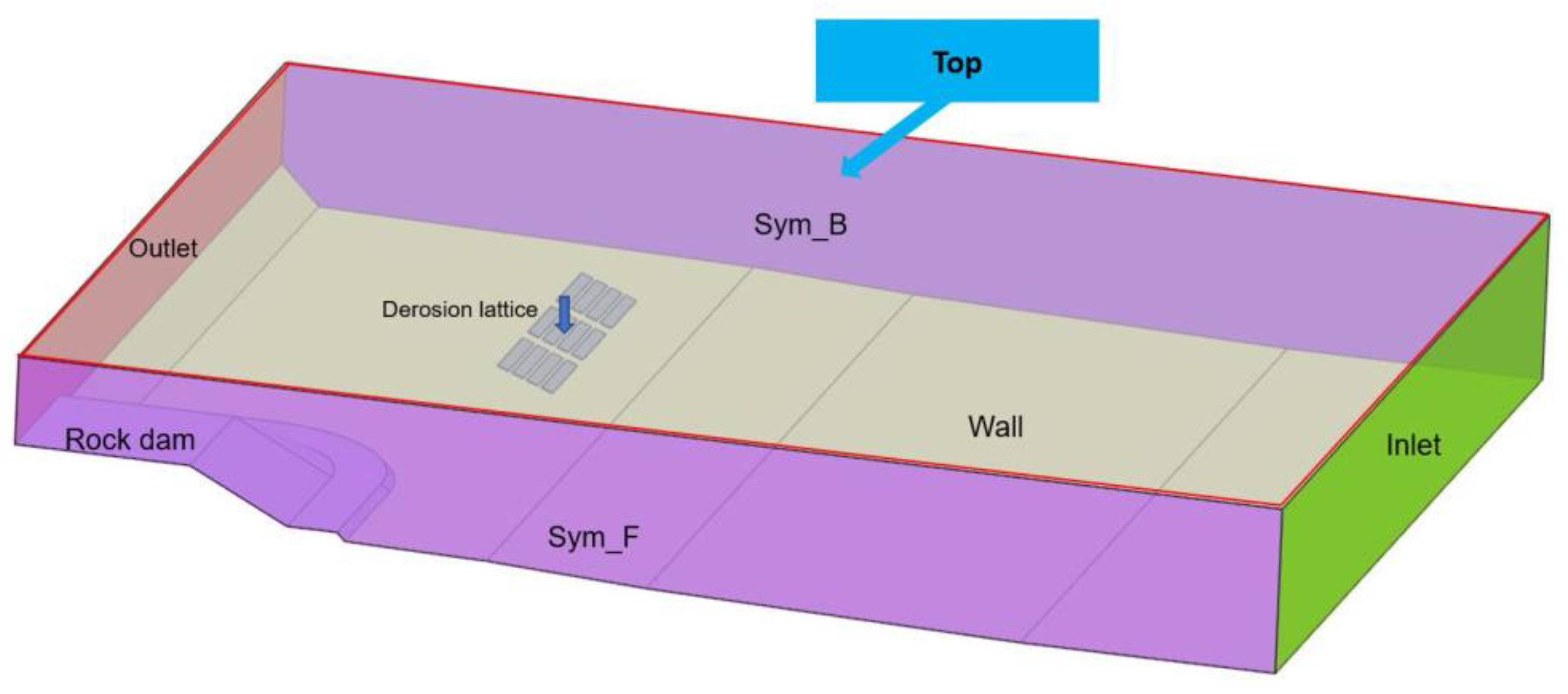
Figure 7 reveals an example of a fluid model with dimensions consisting of the rock dam, sand floor, and adjustable angle of attack (
θ). Lines in the sand floor represent the different depths created according to the bathymetric map. The further to the right, the deeper the water level. Accordingly, P1–P4 are the placement of positions mentioned earlier. P1 is 20 m away from the rock dam, P2 is toward the sea, P3 is overlapped with the rock dam, and P4 is adjacent to the rock dam.
3.2.2. Dynamic Adaptive Mesh Model
Due to the flow of sea waves when swashing into the beach, the water surface ripples up and down all the time, so the mesh model requires smaller, more delicate meshes of high quality in that area. For this reason, the fluid model in
Figure 7 was used as a prototype and converted to a dynamic adaptive mesh (DAM) model [
18]. The benefit of this type of DAM model is that we do not have to create a large number of small meshes, which would cause the mesh model to have too many elements and nodes that could exceed the computational resource capability. Therefore, instead, we created a polyhedral mesh model to achieve accurate results by coding it into a DAM model on the interface between water and air, allowing the mesh to vary in shape, size, type, and number according to the wave swashing behavior.
Figure 8 shows a sample of the polyhedral mesh model of
P0 viewed from (a) the outside and (b) the inside. In (a), the DAM model had the smallest size of 5 mm and the largest of 100 mm. It had a total of 760,000 elements and 2,200,000 nodes. It should be borne in mind that the mentioned DAM model in (a) is the roughest model to use when wave behavior is uncomplicated. However, when the wave behavior is complicated, the dynamic adaptive meshes at the interface shown in the marked area of (b) are adjusted automatically to capture the physics of waves. Therefore, the more complicated the waves’ behavior, the greater the number and the finer the mesh model.
3.3. Boundary Conditions, Parameters Setting, and Analysis Setting
After listening to all advice from the consultants, all data were analyzed and modified to the boundary conditions, parameters, and analysis settings.
Figure 9 shows the boundary conditions defined in the fluid model. The parameters and analysis settings required for the boundary conditions are reported in
Table 2 and
Table 3, respectively. The wave properties are statistically average values in the monsoon season collected by Marine Department. The wavefront direction was assigned perpendicular to the beach because of a lack of information in a survey report during a simulation process. Moreover, the DL properties were obtained from the experimental data and mathematical modeling suggested by the DL inventors. In ANSYS Fluent software, all parameters and settings were assigned to the volume-of-fluid (VOF) model. The open channel wave with the third-order Stokes wave theories was applied since the wave began to blow from a depth of 2 m toward the beach. The third-order Stoke wave theories were used for finite-amplitude waves in intermediate to deep liquid depth ranges and nonlinear [
15]. Therefore, this depth could be considered moderate and, thus, correspond to this research. The computational resource was high-performance computing (HPC) 512 cores of an Intel Xenon Gold 6148 with a 2.40 GHz processor with 2688 GB RAM. The HPC automatically optimized the calculation, which required 3–8 h depending on each case. Upon completing the calculation, the software displayed the free surface flow between the air and water wave in the first 20 s. The proposed conditions in
Table 1 were calculated in all cases.
4. Results and Discussion
First, the simulation results were validated, the occurrence of the end effect was confirmed, and the possibility to employ solving the end effect was investigated. Next, the DL performance was assessed by comparing the simulation results with and without the DL. Then, a proper condition for the DL installation was determined. Finally, after installing the DL on-site in the proper condition, installation outcomes were analyzed to assure the DL’s effectiveness and its suitability for use in Thailand.
4.1. Validation
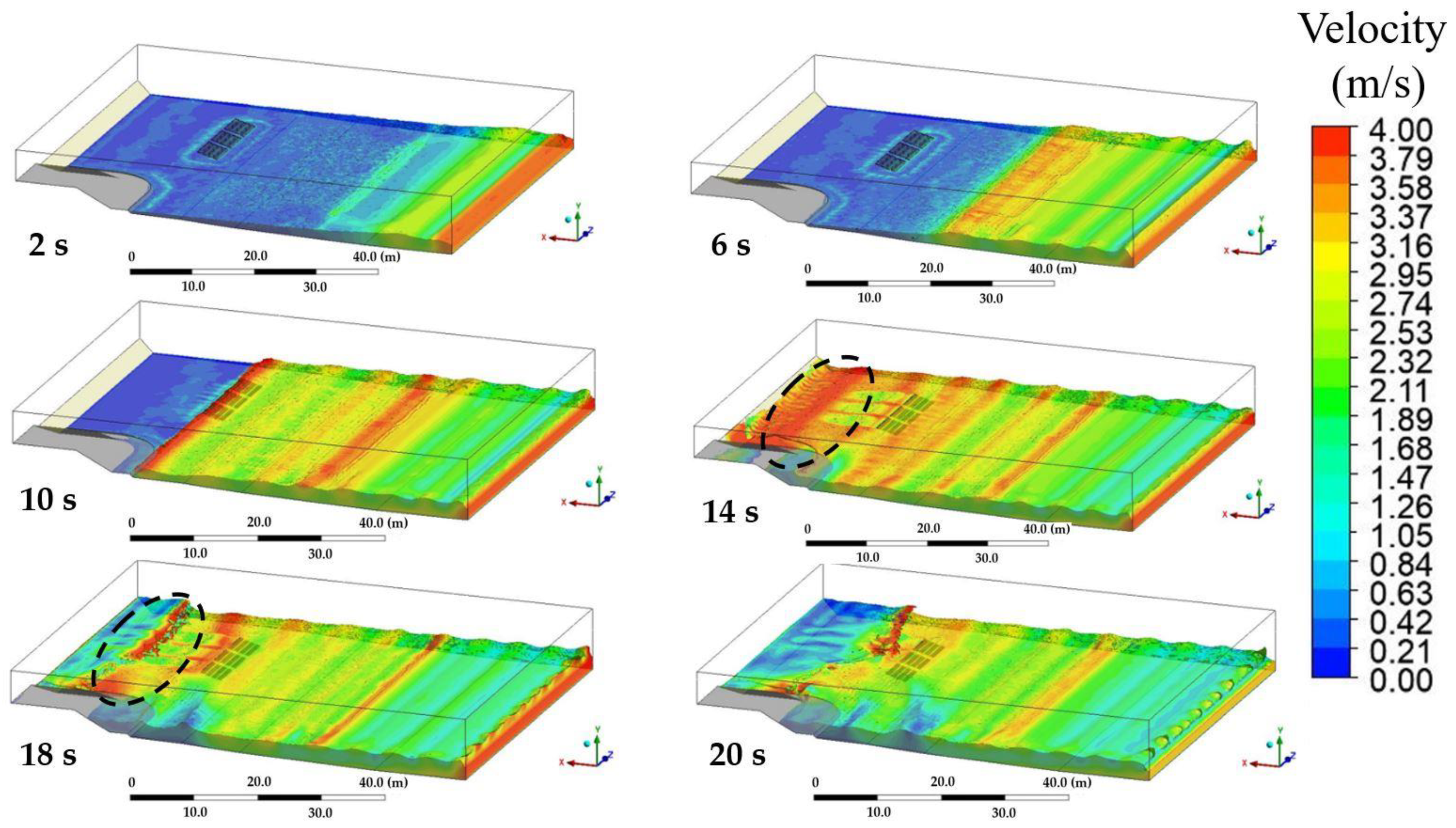
Using a monsoon as a climatic condition,
Figure 10 reveals the water velocity for the different times of
P1/10°, where the red indicates a higher value than the blue. Waves increase in velocity as they approach the beach due to the slope change. As a result, the bottom of the wave moves beneath the sand and rubs against the sand floor, causing the wave to lose balance. The wave’s crest then lifts and breaks, increasing the velocity, consistent with the physics of waves, as expected. To validate the behavior of waves passing the DL, the results between 10 and 14 s were considered. The results showed that the waves moved into the DL with a
v of 3.8 m/s. After impact,
v decreased to a minimum of 1.0 m/s. It means that the DL reduced the
v, as expected. At 14–18 s, in the marked areas, waves refracted after impacting the rock dam and collided with an adjacent beach at a higher velocity, resulting in corrosion; therefore, this confirmed the end effect occurrence. Readers who need more information about this figure can investigate the results using an animation clip attached in a
Supplementary Material File entitled P1_15.mp4.
Since
Figure 10 corresponds to the physics of waves and can reasonably explain the end effect occurrence, we believe the research methodology and the simulation results are validated. Additionally, when the conditions changed according to
Table 1, the obtained results were also reliable. In addition, the DL decreased wave velocity; therefore, initially, the DL may be a solution to the end effect. The DL performance was assessed in detail, and its results are presented in the next section.
4.2. DL Performance Assessment
The DL performance was assessed by the water velocity (
v) and the bottom shear stress (
τ) using the criteria mentioned in
Section 2.4. In addition, all cases were presented in two dimensions as a top view at 12 s, 0.25 m above mean sea level. The authors confirming the presentation with this setting helped in the analysis to achieve accurate results.
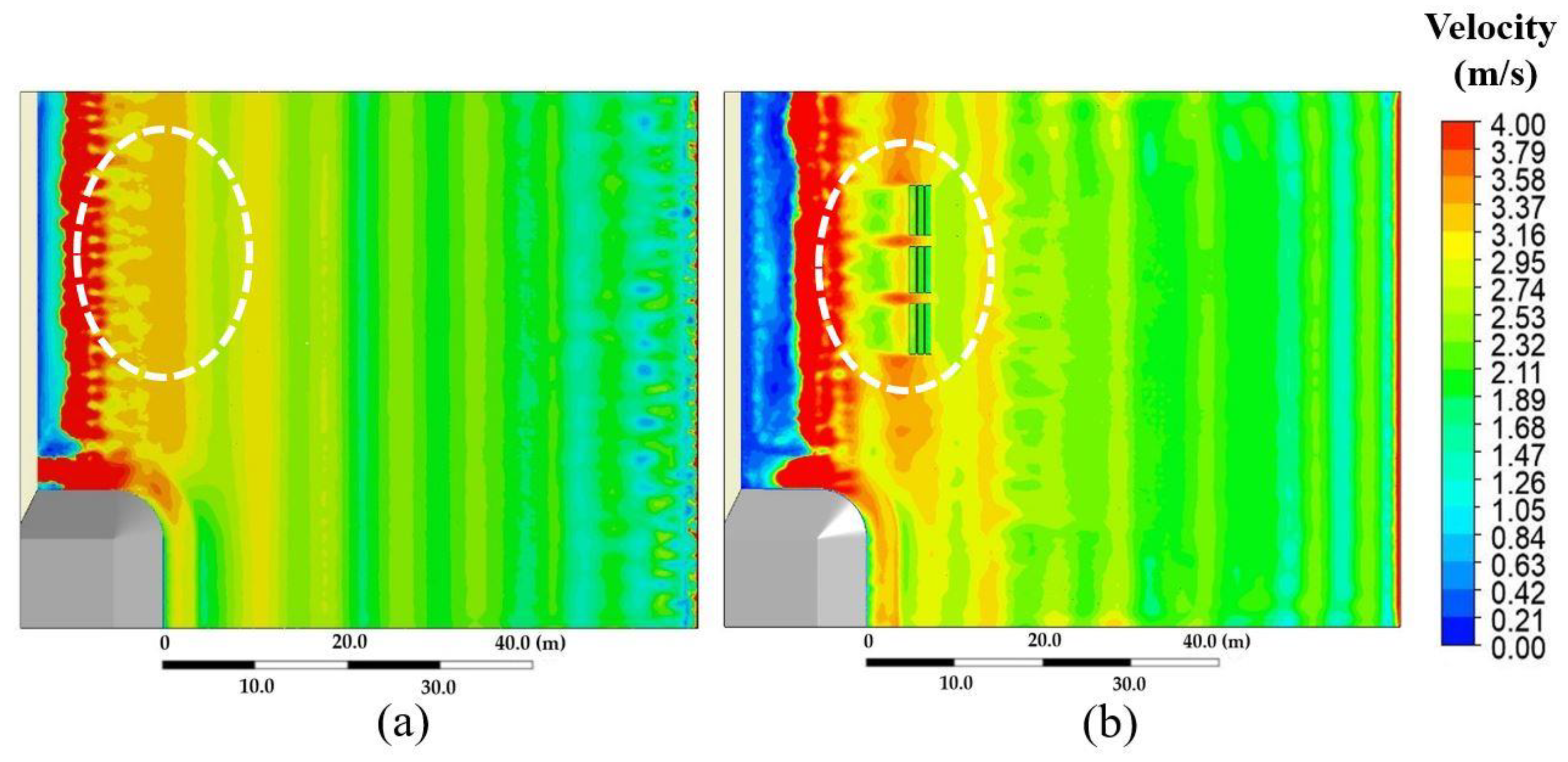
Figure 11 shows the
v of (a)
P0 and (b)
P1/15°. Consider the marked white area. It can be seen that when installing the DL, the
v of waves moving through the DL decreased, as it changed from 2.5–3.0 m/s in
P0 to 1.5–2.5 m/s in
P1/15°, especially behind the DL.
Similarly,
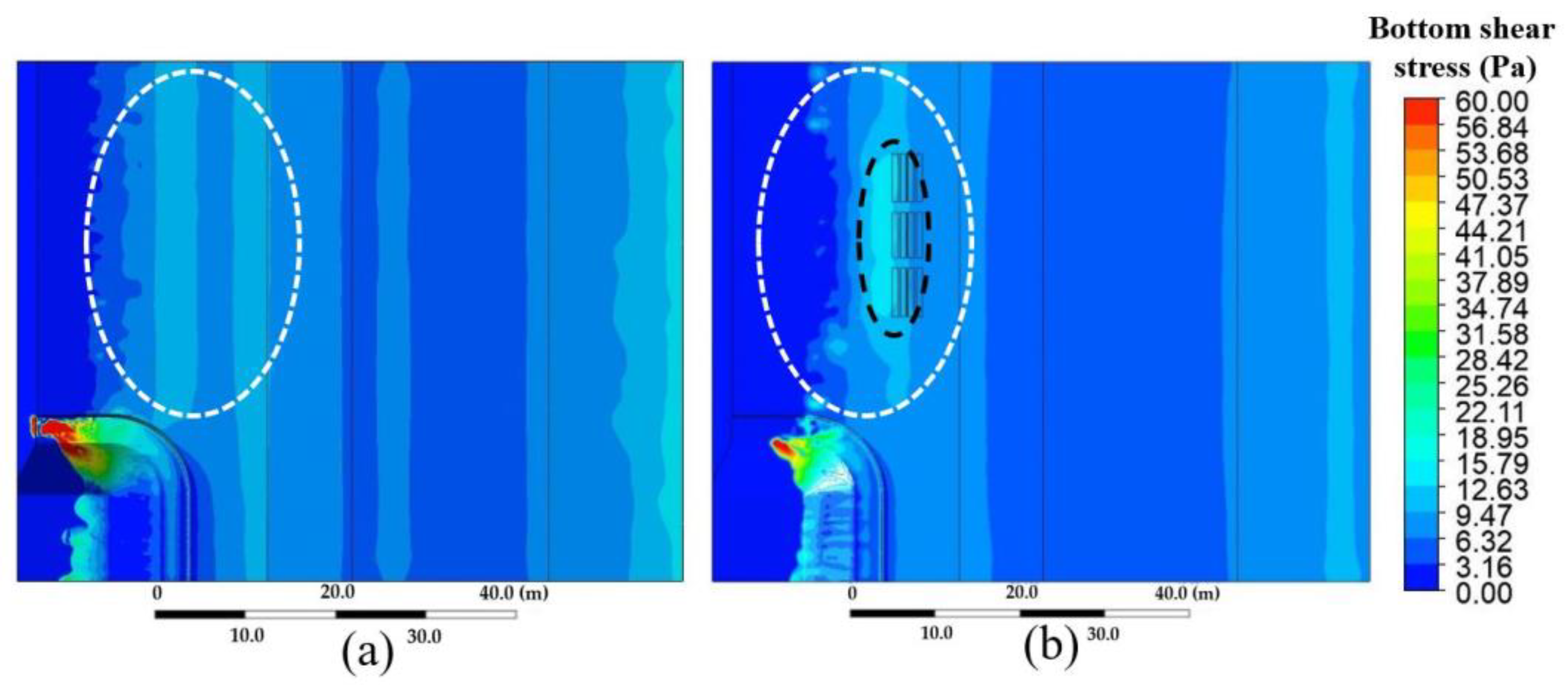
Figure 12 reveals the
τ of (a)
P0 and (b)
P1/15°. Again, a comparison between (a) and (b) in marked white areas showed that
P1/15° gave the lower
τ with a broader area than
P0. However, in a marked black area of (b), this region exhibited
τ about 20% greater than
P0. This is because many waves impacted the DL and collided with the sand floor. The higher the number of waves, the greater the
τ on the sand floor. However, these waves, after impact, had low
v, proved by
Figure 11b, so their suspension velocity is also low. As mentioned in
Section 2.4.2, this figure implies that DL installation had a high chance of sand and sediment blown by waves from other locations settling in this area for sedimentation. Moreover, the comparison results for other mean sea levels reported a similar trend of
v and
τ as explained in
Figure 11 and
Figure 12. Animation clips can be downloaded from the following
Supplementary Files for more information: P0.mp4 and P1_15.mp4.
From all results reported in this section, it can be confirmed that the DL can reasonably reduce erosion and enhance sedimentation. Therefore, it is an alternative solution to solve the end effect. However, optimal performance must be derived from a proper condition for the DL installation, which is reported in the next section.
4.3. A Proper Condition for the DL Installation
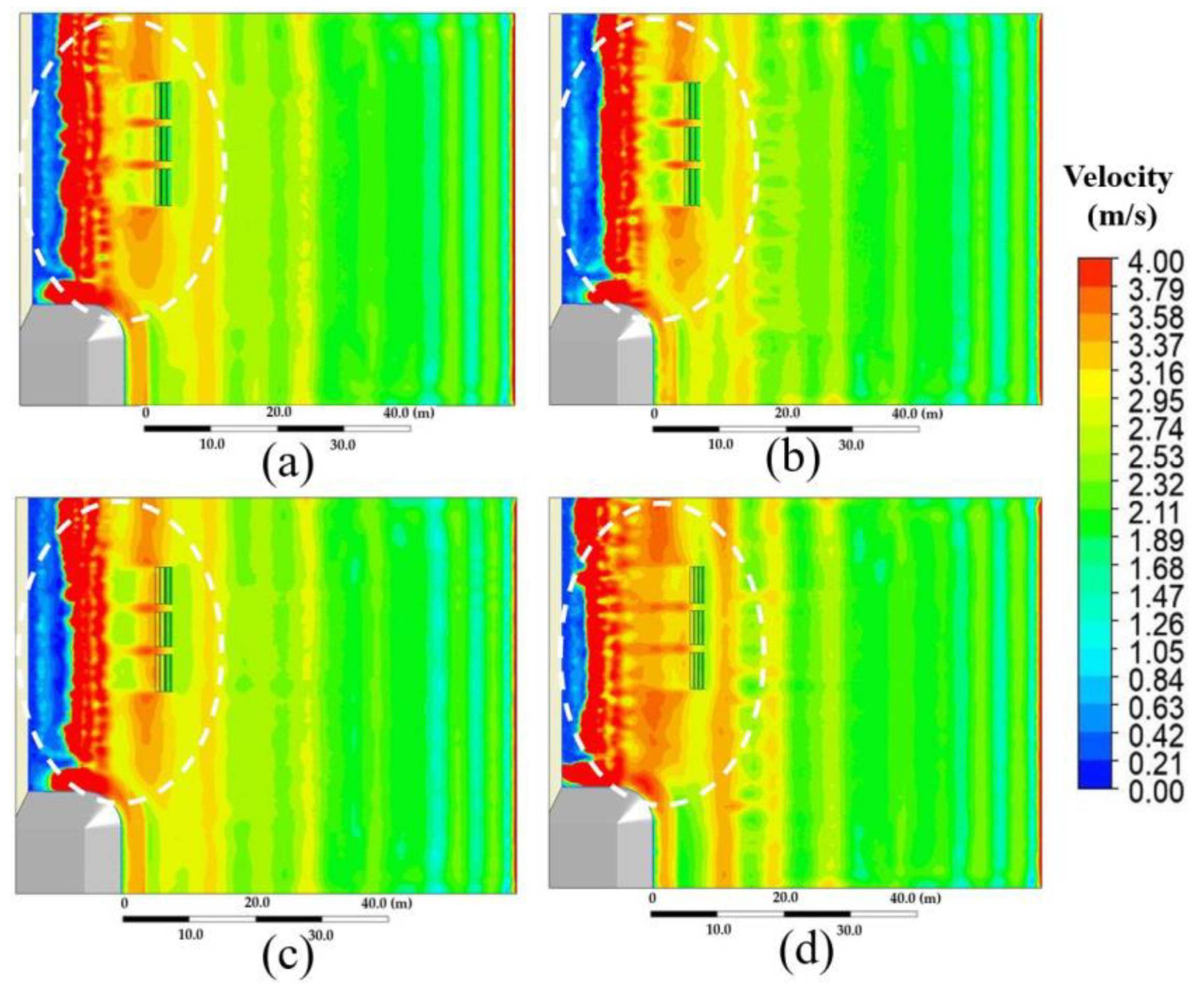
The conditions were divided into a proper θ and suitable placement position (P). The same conditions as assigned previously were applied with different values of θ and P.
4.3.1. A Proper θ
Similarly,
Figure 13 and
Figure 14 reveal the
v and
τ, respectively, for (a)
P1/10°, (b)
P1/15°, (c)
P1/30°, and (d)
P1/45°. In
Figure 13, when installing the DL with different values of
θ, the contour of the
v region was also varied. In the marked areas, the DL installation using
P1/15° and
P1/30° had similar velocity reduction capability. On the contrary,
v of
P1/45° was also faster than that of the other cases; therefore, this is the worst case.
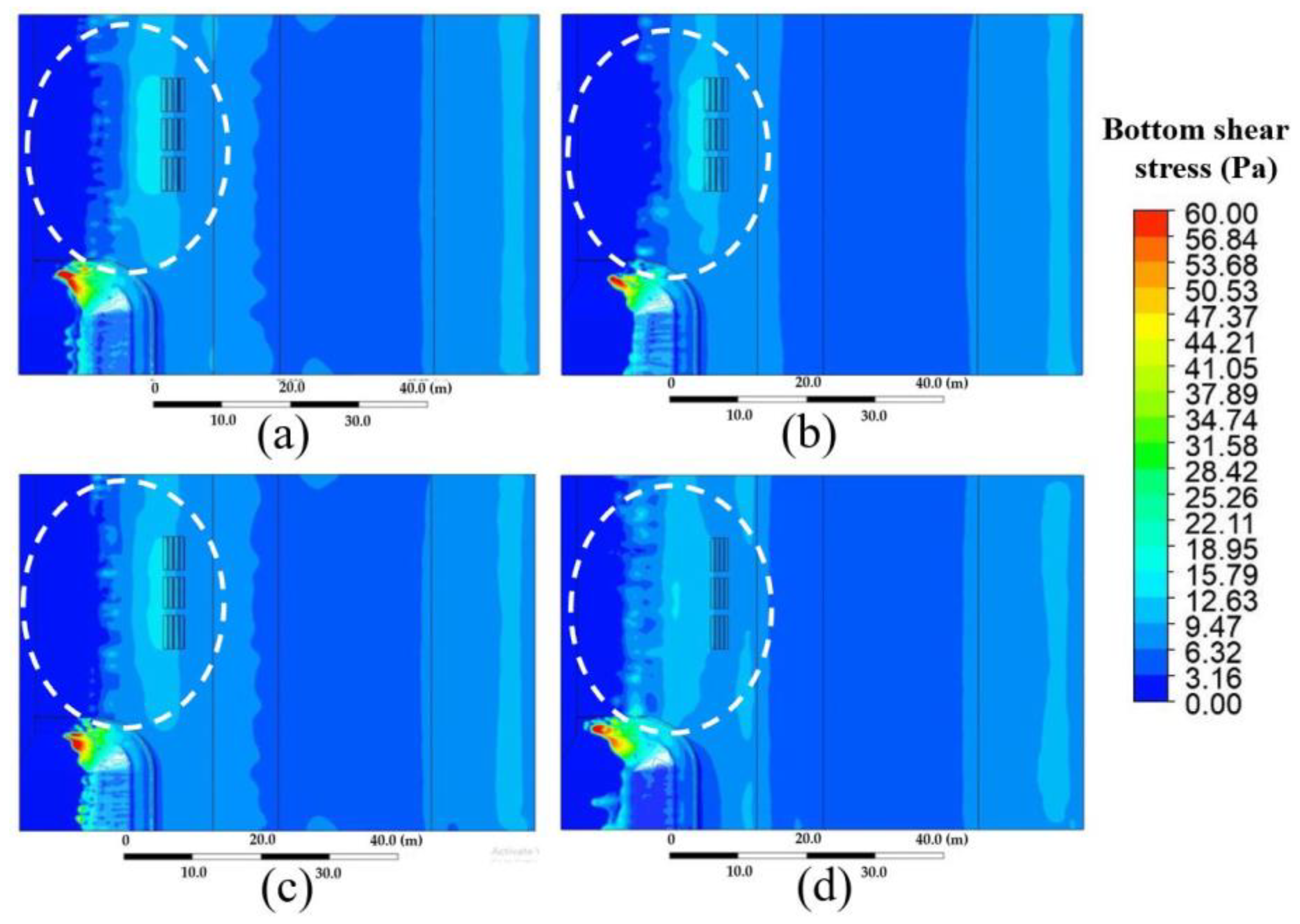
As shown in
Figure 14, the analysis results of
τ were consistent with the
v of
Figure 13. In conclusion,
P1/45° yielded the worst results. However,
P1/15° and
P1/30° presented similar results, so both cases were candidate options that should be considered for further structural analysis.
When considering structural analysis,
P1/30° had less stability and strength than
P1/15°. Since
P1/30° was subjected to incoming wavefront at
θ of 30°, causing higher stress at the DL than
P1/15°, using
P1/30° may require frequent maintenance and shortened lifetime. The more the angle of attack is, the less the stability and strength become. According to all reported results, we believe that the DL installation at
θ at 15° was a proper condition. This angle agreed with the
θ recommended by the inventors’ successful installation at the beaches in Taiwan [
2,
3,
4], also confirming the reliability of this research.
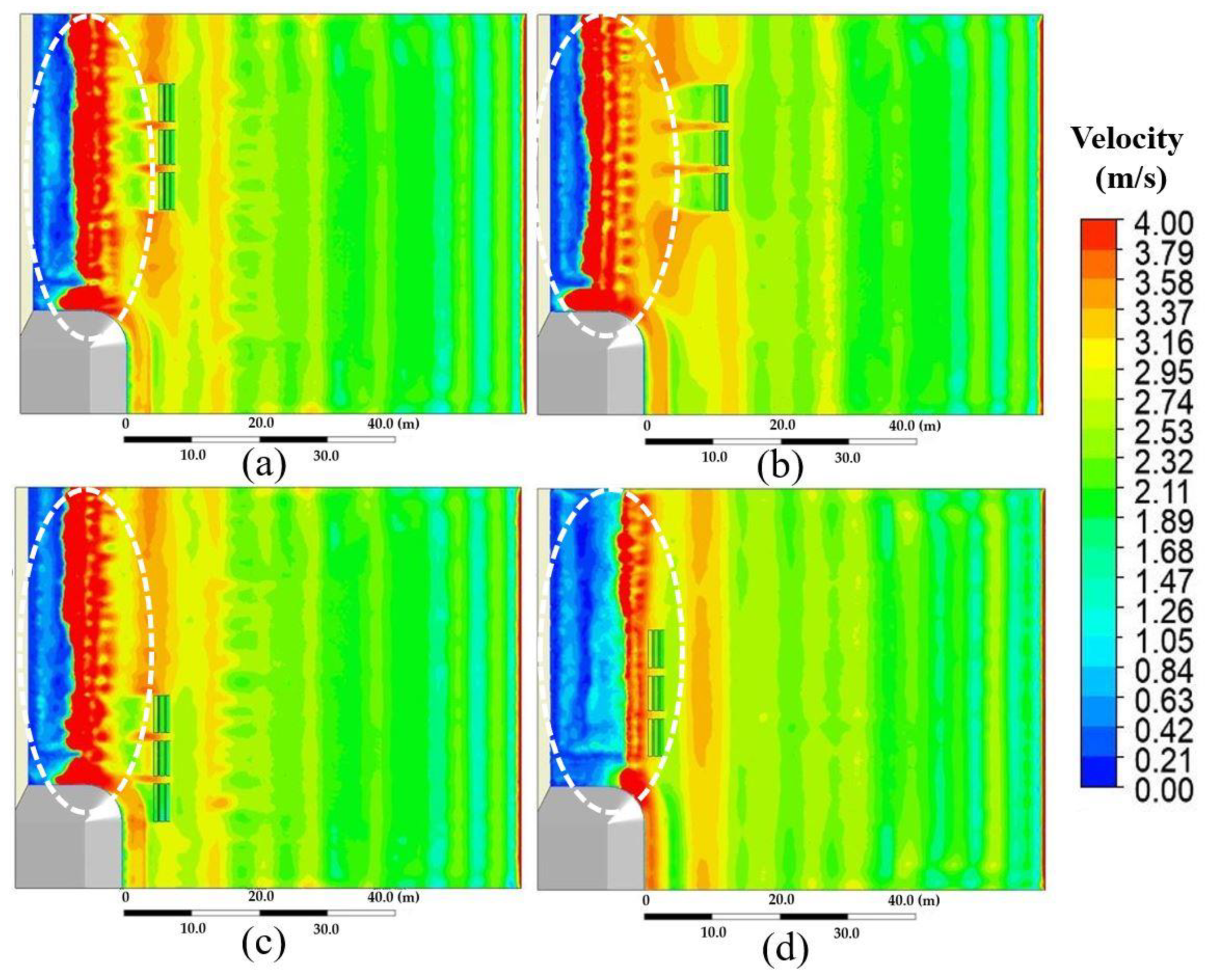
4.3.2. A Suitable Placement Position
Based on the same boundary conditions defined previously and fixed
θ at 15° as a proper angle of attack,
Figure 15 and
Figure 16 show the
v and
τ for (a)
P1/15°, (b)
P2/15°, (c)
P3/15°, and (d)
P4/15°. In a similar analysis to that performed in the previous figures, the simulation results in the marked areas show that when the DL was installed at different locations, it could prevent erosion and enhance sedimentation differently. Moreover, both figures reveal that installing DL at P4 was a suitable position placement.
Finally, all results indicated that P4/15° is the optimum condition for installing the DL on-site. Next, installation outcomes are discussed and presented.
4.4. Installation Outcomes
At the beginning of the monsoon season, the optimum condition of
P4/15° was employed as strict information for installing the DL at Khao Rup Chang beach. It has served its function throughout the monsoon season. The installation outcomes were observed about two months later after the complete installation.
Figure 17 reports the installation outcomes: (a) the first day of installation, (b) viewed from the back, and (c) viewed from the side, two months later. In (a), the beach was prepared for a field test. Comparing (a) and (b) revealed that the beach’s concavity decreased because of less erosion and more sedimentation. In (c), an overview of the beach is observed, showing less concavity from the end effect. In addition,
Figure 18 shows the images by Google Earth two months later installation related to
Figure 17b,c to confirm the discussion. As observed with the naked eye for 300 m away from the rock dam in the marked area, compared with
Figure 6b, the DL affected the beach erosion and sedimentation in a wide area, consistent with the CFD discussion in
Figure 10,
Figure 11,
Figure 12,
Figure 13,
Figure 14,
Figure 15 and
Figure 16. In addition, compared with
Figure 2, the environment was clearly better. Therefore, from the authors’ point of view, the DL can effectively solve the end effect in Khao Rup Chang beach with excellent performance, and the CFD assessment was also successful.
5. Conclusions and Suggestions
To solve the end effect, the CFD method was employed to assess the DL performance and find the optimal installation condition for Khao Rup Chang beach, Thailand, as a case study, using actual terrain and climatic conditions of the monsoon season. The simulation results of the water velocity and the bottom shear stress showed the behavior of water waves passing the DL and the beach, which is reasonably consistent with the physics of waves, as expected. Furthermore, by changing both angles of attack and placement positions, the simulation results showed the optimal condition—namely, installation with the angle of attack at 15° with the placement position adjacent to the rock dam—in which case the DL provided the optimum performance. After applying the optimal condition to install the DL at the actual site, installation outcomes from a field test during the monsoon season also confirmed that the DL could effectively decrease erosion and enhance beach sedimentation in Thailand. Therefore, the construction of rock dams and installation with the DL at its tails is the most suitable solution for the long-term prevention of coastal erosion, increasing sedimentation, and solving the end effect.
Although this study is an urgent attempt to implement the DL to solve the end effect, it should be noted that information on terrain and climate are averages for a beach in a southern region of Thailand. In fact, each region has its own characteristic environment. Furthermore, preliminary field reports indicated that the actual data for this beach slightly differ from those we used in the simulation. For example, in this study, the wavefront was assigned perpendicular to impact the beach with equal water and air velocities, but in reality, it is 40–50° with a different velocity. Additionally, water was generally absorbed by the sand beach to reduce the amount of water and speed, which was not considered in this research due to the lack of related variables. However, the slight difference mentioned above did not affect the conclusion. Finally, this research reports the installation outcomes as a qualitative overview. However, a quantitative estimate of erosion and sedimentation was not made. In other words, equations and mathematical modeling with sediment variables were not given due to a survey report’s lack of information on related variables. Therefore, if the simulation is merged with the entire field report from the oceanological survey, the DL performance will absolutely increase, and quantitative overview results such as volume of increasing sediment, size of the enhanced area, etc., resulting from the DL, will be presented. These data will help Thai agencies concerned about the environmental estimation of DL’s worthiness in particular.
Author Contributions
Conceptualization, J.T., M.K. and W.B.; methodology, J.T., M.K. and W.B.; software, W.T. and M.P.; validation, J.T., M.K. and W.B.; formal analysis, J.T.; investigation, J.T.; resources, J.T. and W.T.; data curation, J.T. and W.T.; writing—original draft preparation, J.T., W.T., M.K. and W.B.; writing—review and editing, J.T.; visualization, W.T.; supervision, J.T.; project administration, J.T.; funding acquisition, J.T. and W.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research was sponsored by the Innovation and Technology Assistance Program (ITAP) grant number PI640897. The APC was partially funded by the College of Advanced Manufacturing Innovation (AMI), King Mongkut’s Institute of Technology Ladkrabang (KMITL).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
No additional data are available.
Acknowledgments
Consultations were provided by Ta-Hsiung Peng from ReShore Technologies of Taiwan, Pramot Sojisuporn from the Chulalongkorn University of Thailand, and Bunlung Meangbua from the Marine Department of Thailand. Facilities were contributed by Thai Wiring System Ltd., AMI and KMITL.
Conflicts of Interest
The authors declare no conflict of interest for this research.
References
- Boateng, I.; Bray, M. Comparative Merits of Adaptation Policies of Sea Level Rise and Their Potential Impacts on Coastal Settlement in Developing Countries. In Proceedings of the XXX FIG Working Week and General Assembly: Strategic Integration of Surveying Services, Hong Kong, China, 13–17 May 2007; Available online: https://www.oicrf.org/-/comparative-merits-of-adaptation-policies-of-sea-level-rise-and-their-potential-impacts-on-coastal-settlements-in-developing-countries (accessed on 10 January 2022).
- Tech, R. Successful Demonstration Project-Taiwan. Available online: https://reshore.tech/successful-demonstration-projects/ (accessed on 10 January 2022).
- Chyan-Deng, J.; Ta-Hsiung, P.; Shih-Jen, H.; Hung-Chu, H. An Experimental Field Study Using A Flexible High-Strengh Net Breakwater for Shore Protection. J. Mar. Sci. Technol. 2015, 23, 117–126. [Google Scholar] [CrossRef]
- Zhang, Z.; Ta-Hsiung, P. Coastal Erosion Protection by Derosion Lattice at Beimen Cliff of Kinmen. In Proceedings of the 41th Ocean Engineering Conference in Taiwan, Taiwan, China, 1 November 2019; National Cheng Kung University: Taiwan, China, 2019. [Google Scholar]
- Dabelow, S.; Zhang, N. Evaluation of The Effectiveness of a Coastal Wave Reduction and Sediment Retention Structure Using CFD Simulations. In Proceedings of the ASME 2017 Fluids Engineering Division Summer Meeting, Waikoloa, HI, USA, 3 August 2017. [Google Scholar]
- Ouyang, H.; Hantz, J.; Nguyen, T.; Harrington, A.; Zhang, N. Numerical Analysis of Breakwaters Turbulence Under Coastal Wave Actions. In Proceedings of the ASME 2018 International Mechanical Engineering Congress and Exposition, Pittsburgh, PA, USA, 9–15 September 2018. [Google Scholar]
- Osorio-Cano, J.D.; Alcérreca-Huerta, J.C.; Osorio, A.F.; Oumeraci, H. CFD modelling of wave damping over a fringing reef in the Colombian Caribbean. Coral Reefs 2018, 37, 1093–1108. [Google Scholar] [CrossRef]
- Gomes, A.; Pinho, J.L.S.; Valente, T.; Antunes do Carmo, J.S.; V Hegde, A. Performance Assessment of a Semi-Circular Breakwater through CFD Modelling. J. Mar. Sci. Eng. 2020, 8, 226. [Google Scholar] [CrossRef]
- Romya, A.A.; Moghazy, H.M.; Iskander, M.M.; Abdelrazek, A.M. Performance assessment of corrugated semi-circular breakwaters for coastal protection. Alex. Eng. J. 2022, 61, 3587–3598. [Google Scholar] [CrossRef]
- Sakib, S.; Besse, G.; Yin, P.; Gang, D.; Hayes, D. Sediment transport simulation and design optimization of a novel marsh shoreline protection technology using computational fluid dynamics (CFD) modeling. Int. J. Sediment Res. 2022, 37, 14–25. [Google Scholar] [CrossRef]
- Kaewbumrung, M.; Tangsopa, W.; Thongsri, J. Investigation of the Trailing Edge Modification Effect on Compressor Blade Aerodynamics Using SST k-ω Turbulence Model. Aerospace 2019, 6, 48. [Google Scholar] [CrossRef]
- Jansaengsuk, T.; Kaewbumrung, M.; Busayaporn, W.; Thongsri, J. A Proper Shape of the Trailing Edge Modification to Solve a Housing Damage Problem in a Gas Turbine Power Plant. Processes 2021, 9, 705. [Google Scholar] [CrossRef]
- Puangburee, L.; Busayaporn, W.; Kaewbumrung, M.; Thongsri, J. Evaluation and Improvement of Ventilation System Inside Low-Cost Automation Line to Reduce Particle Contamination. ECTI Trans. Electr. Eng. Electron. Commun. 2020, 18, 35–44. [Google Scholar] [CrossRef][Green Version]
- Ansys, I. Turbulence, Fluent Theory Guide 17.1. In Fluent Theory Guide 17.1; ANSYS, Inc.: Canonsburg, PA, USA, 2016. [Google Scholar]
- Ansys, I. Multiphase Flows, Fluent Theory Guide 2020 R1. In Fluent Theory Guide 2020 R1; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
- Khongsin, J.; Thongsri, J. Numerical Investigation on the Performance of Suction Head in a Cleaning Process of Hard Disk Drive Factory. ECTI Trans. Electr. Eng. Electron. Commun. 2020, 18, 28–34. [Google Scholar] [CrossRef]
- Thongsri, J.; Tangsopa, W.; Khongsin, J. A Suitable Shape of the Suction Head for a Cleaning Process in a Factory Developed by Computational Fluid Dynamics. Processes 2021, 9, 1902. [Google Scholar] [CrossRef]
- Ansys, I. Adapting the Mesh, Fluent Theory Guide 2020 R1. In Fluent Theory Guide 2020 R1; ANSYS, Inc.: Canonsburg, PA, USA, 2020. [Google Scholar]
Figure 1.
An explanatory diagram and overview of the end effect occurrence [
1].
Figure 1.
An explanatory diagram and overview of the end effect occurrence [
1].
Figure 2.
The end effect at Khao Rup Chang beach, Thailand.
Figure 2.
The end effect at Khao Rup Chang beach, Thailand.
Figure 3.
A flowchart of research methodology.
Figure 3.
A flowchart of research methodology.
Figure 4.
The derosion lattice when (
a) installed completely and (
b) being used in Taiwan [
2].
Figure 4.
The derosion lattice when (
a) installed completely and (
b) being used in Taiwan [
2].
Figure 5.
A modified solid model of DL for simulation.
Figure 5.
A modified solid model of DL for simulation.
Figure 6.
Khao Rup Chang Beach: (a) an overview and (b) the enlarged end effect.
Figure 6.
Khao Rup Chang Beach: (a) an overview and (b) the enlarged end effect.
Figure 7.
An example of fluid model.
Figure 7.
An example of fluid model.
Figure 8.
A sample of mesh model viewed from (a) outside and (b) inside.
Figure 8.
A sample of mesh model viewed from (a) outside and (b) inside.
Figure 9.
The boundary conditions.
Figure 9.
The boundary conditions.
Figure 10.
The water velocity for the different times of P1/15°.
Figure 10.
The water velocity for the different times of P1/15°.
Figure 11.
The water velocity of (a) P0 and (b) P1/15°.
Figure 11.
The water velocity of (a) P0 and (b) P1/15°.
Figure 12.
The bottom shear stress of (a) P0 and (b) P1/15°.
Figure 12.
The bottom shear stress of (a) P0 and (b) P1/15°.
Figure 13.
The water velocity of (a) P1/10°, (b) P1/15°, (c) P1/30°, and (d) P1/45°.
Figure 13.
The water velocity of (a) P1/10°, (b) P1/15°, (c) P1/30°, and (d) P1/45°.
Figure 14.
The bottom shear stress of (a) P1/10°, (b) P1/15°, (c) P1/30°, and (d) P1/45°.
Figure 14.
The bottom shear stress of (a) P1/10°, (b) P1/15°, (c) P1/30°, and (d) P1/45°.
Figure 15.
The water velocity of (a) P1/15°, (b) P2/15°, (c) P3/15°, and (d) P4/15°.
Figure 15.
The water velocity of (a) P1/15°, (b) P2/15°, (c) P3/15°, and (d) P4/15°.
Figure 16.
The bottom shear stress of (a) P1/15°, (b) P2/15°, (c) P3/15°, and (d) P4/15°.
Figure 16.
The bottom shear stress of (a) P1/15°, (b) P2/15°, (c) P3/15°, and (d) P4/15°.
Figure 17.
The installation outcomes: (a) the first day of installation, (b) viewed from the back, and (c) viewed from the side, two months later after installation.
Figure 17.
The installation outcomes: (a) the first day of installation, (b) viewed from the back, and (c) viewed from the side, two months later after installation.
Figure 18.
The images by Google Earth: two months later after the DL installation.
Figure 18.
The images by Google Earth: two months later after the DL installation.
Table 1.
The proposed conditions for simulation.
Table 1.
The proposed conditions for simulation.
| Case | Position | θ | Symbol |
|---|
| 1 | P0 | - | P0 |
| 2 | P1 | 10° | P1/10° |
| 3 | P1 | 15° | P1/15° |
| 4 | P1 | 30° | P1/30° |
| 5 | P1 | 45° | P1/45° |
| 6 | P2 | 15° | P2/15° |
| 7 | P3 | 15° | P3/15° |
| 8 | P4 | 15° | P4/15° |
Table 2.
The essential parameters setting for boundary conditions.
Table 2.
The essential parameters setting for boundary conditions.
| Name | Type | Value |
|---|
| Inlet | - -
Velocity inlet - -
Open channel wave BC - -
Wave theory: third order Stokes
| Wave velocity = 3.496 m/s
Water depth = 0 m (from MSL)
Wave height = 0.5 m
Wave length = 10 m |
| Outlet | Pressure outlet | 0 Pa |
| Top | Pressure outlet | 0 Pa |
| Rock dam | Wall | - |
| Wall | Wall | - |
| Sym_F | Symmetry | - |
| Sym_B | Symmetry | - |
| Derosion Lattice | Porous media | Porosity = 0.68
Viscous resistance (inverse permeability) = 21,869.53 m−2
Inertial resistance = 7.8335 m−1 |
Table 3.
The analysis setting.
Table 3.
The analysis setting.
| List | Setting |
|---|
| The pressure-velocity coupling method | SIMPLE |
| Pressure spatial discretization | Body force weighted |
| The gradient discretization | Least squares cell-based scheme |
| The momentum | The second-order upwind |
| The volume fraction | Compressive |
| The turbulent kinetic energy | The second-order upwind |
| Specific dissipation rate | The second-order upwind |
| Transient formulation | Bounded second-order implicit |
| Time advancement type | Adaptive: multiphase-specific |
| Total time | 20 s |
| Time step size | Initial: 0.006 s, Max: 0.006 s and Min: 0.00001 s |
| Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).