Deep Learning for Streamflow Regionalization for Ungauged Basins: Application of Long-Short-Term-Memory Cells in Semiarid Regions
Abstract
:1. Introduction
- Can the LSTM be used as a hydrological and/or streamflow regionalization model in a semiarid region? Does it outperform a conceptual hydrological model and the FFNN? How does their performance change with the amount of data in each catchment?
- Can simple alterations in FFNN be done to include short-term memory results in a model that outperforms the LSTM in hydrological modeling and streamflow regionalization in a semiarid region with shallow soils and intermittent rivers?
2. Materials and Methods
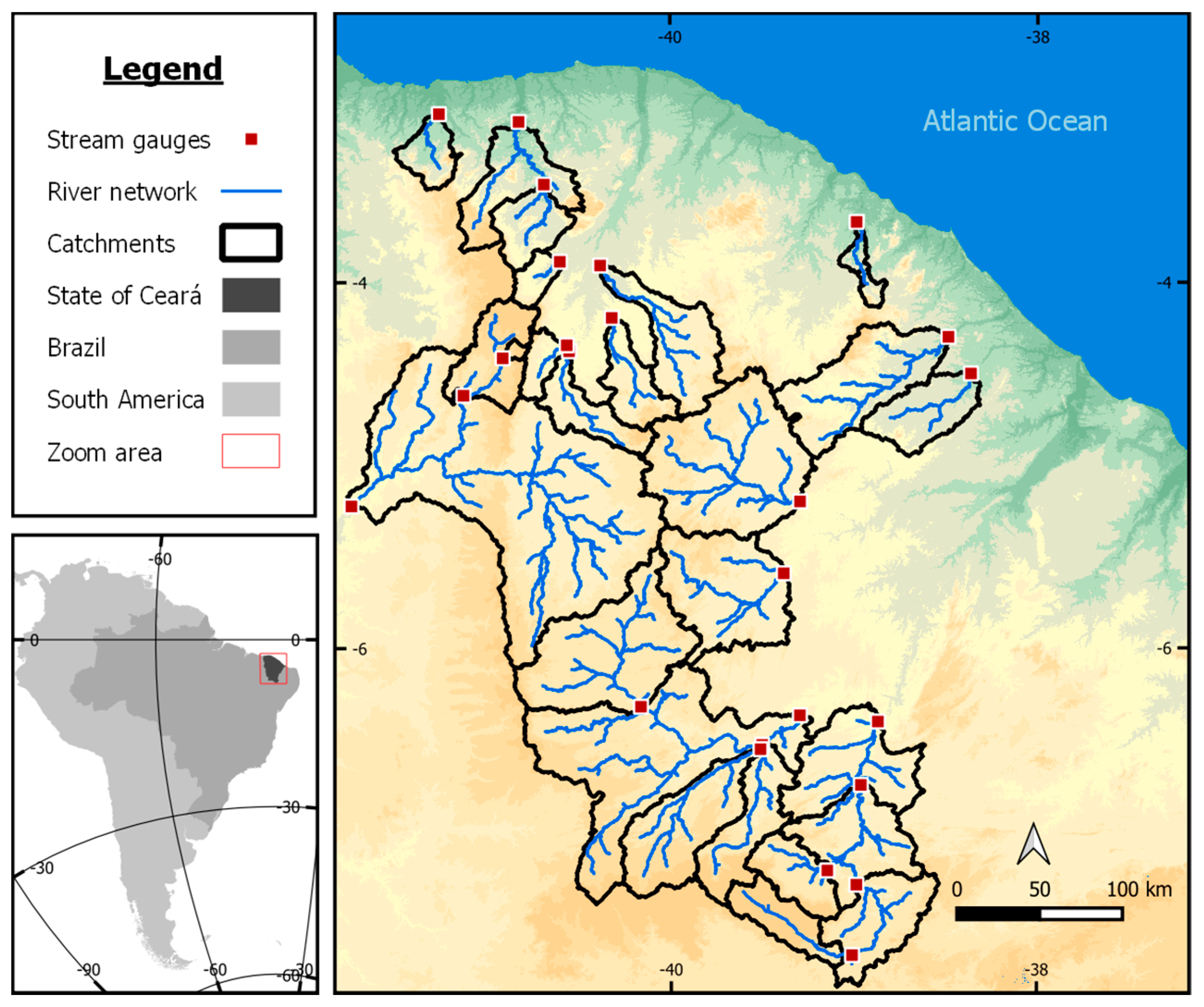
2.1. Case Study and Data
2.2. Methodology
2.3. Rainfall Runoff and Streamflow Regionalization Models
2.3.1. Soil Moisture Account Modeling (SMAP)
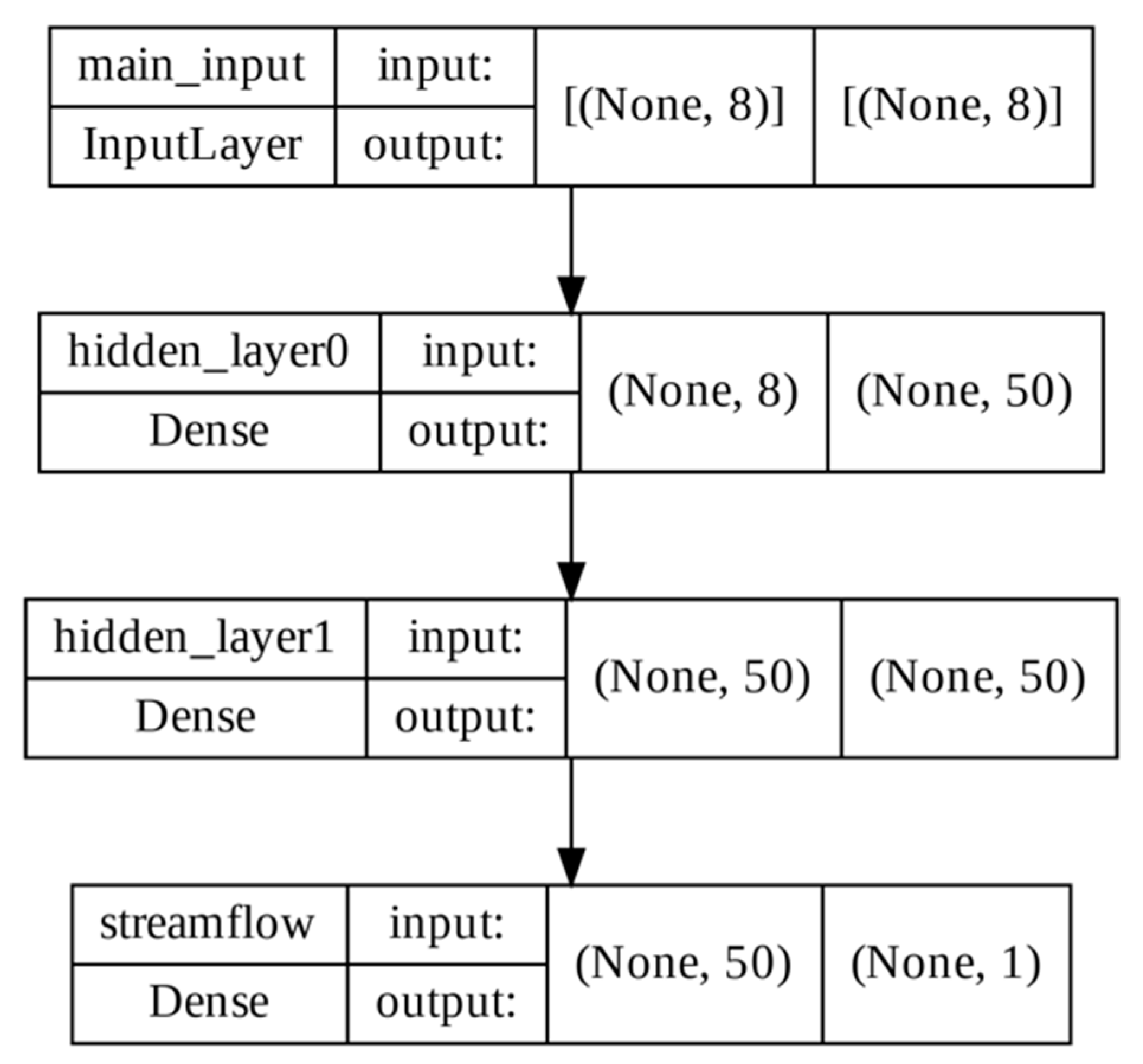
2.3.2. Feedforward Neural Network (FFNN)
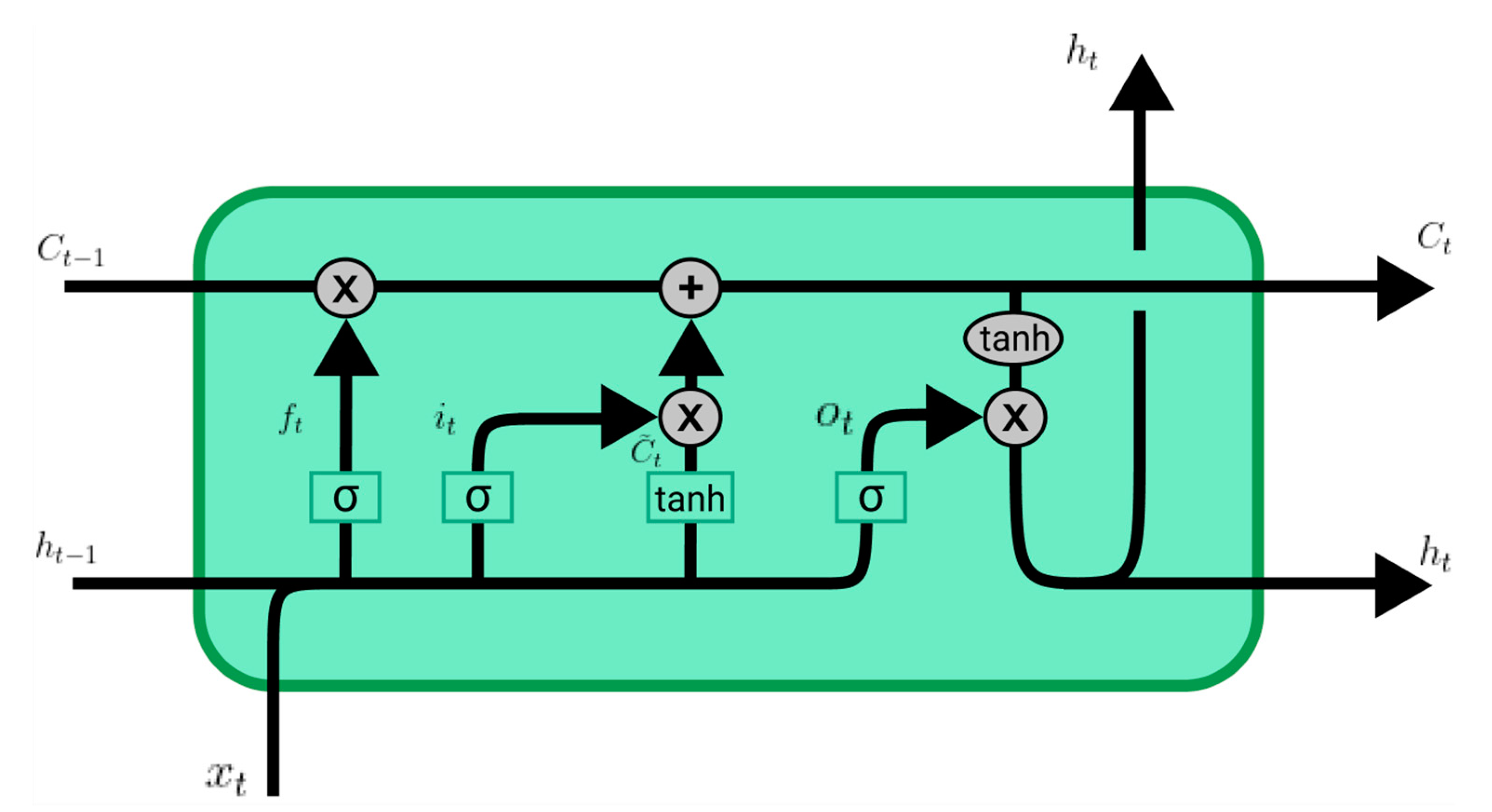
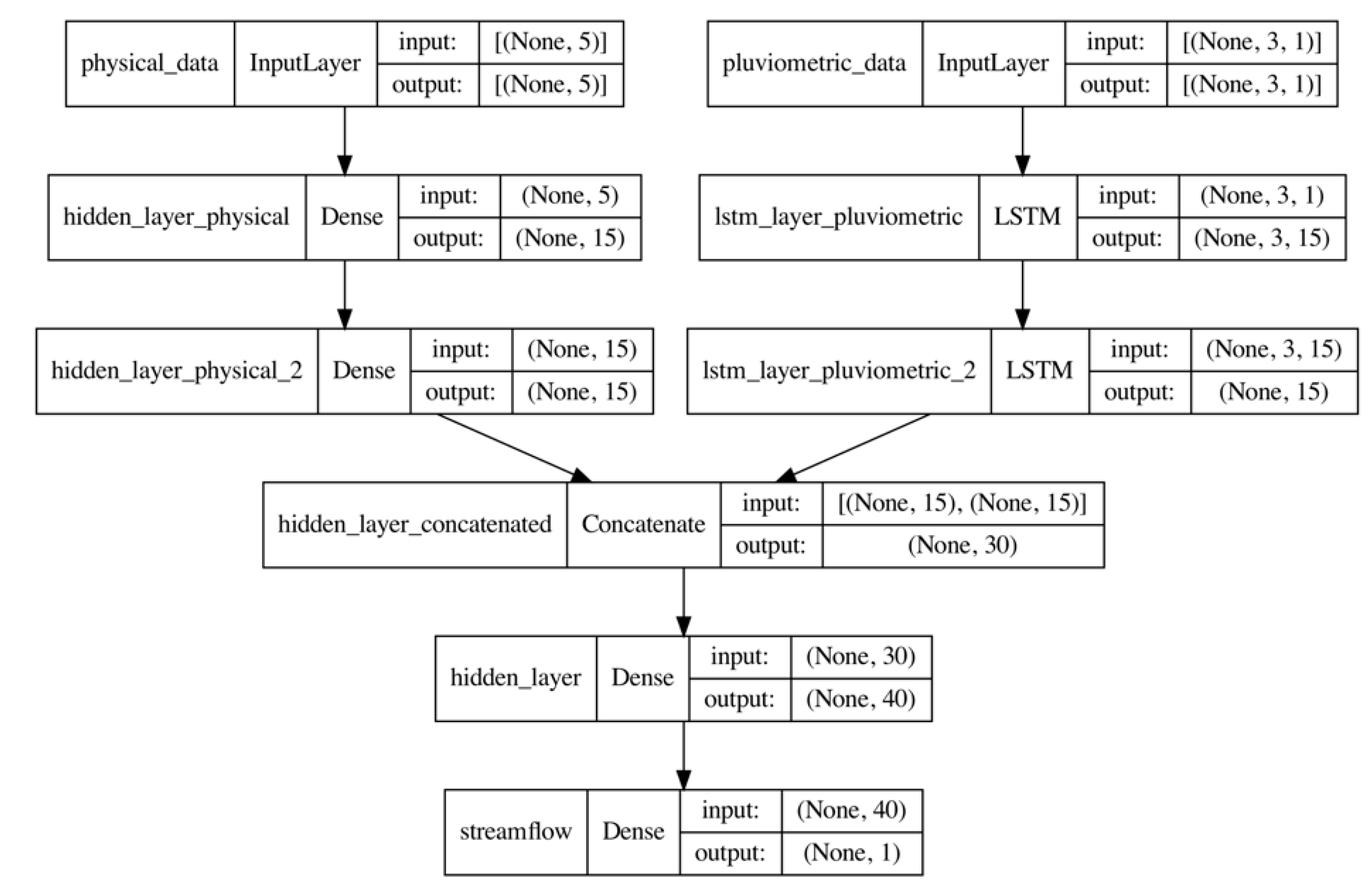
2.3.3. Long-Short-Term Memory Neural Network (LSTM)
2.3.4. LSTM Model Explanation
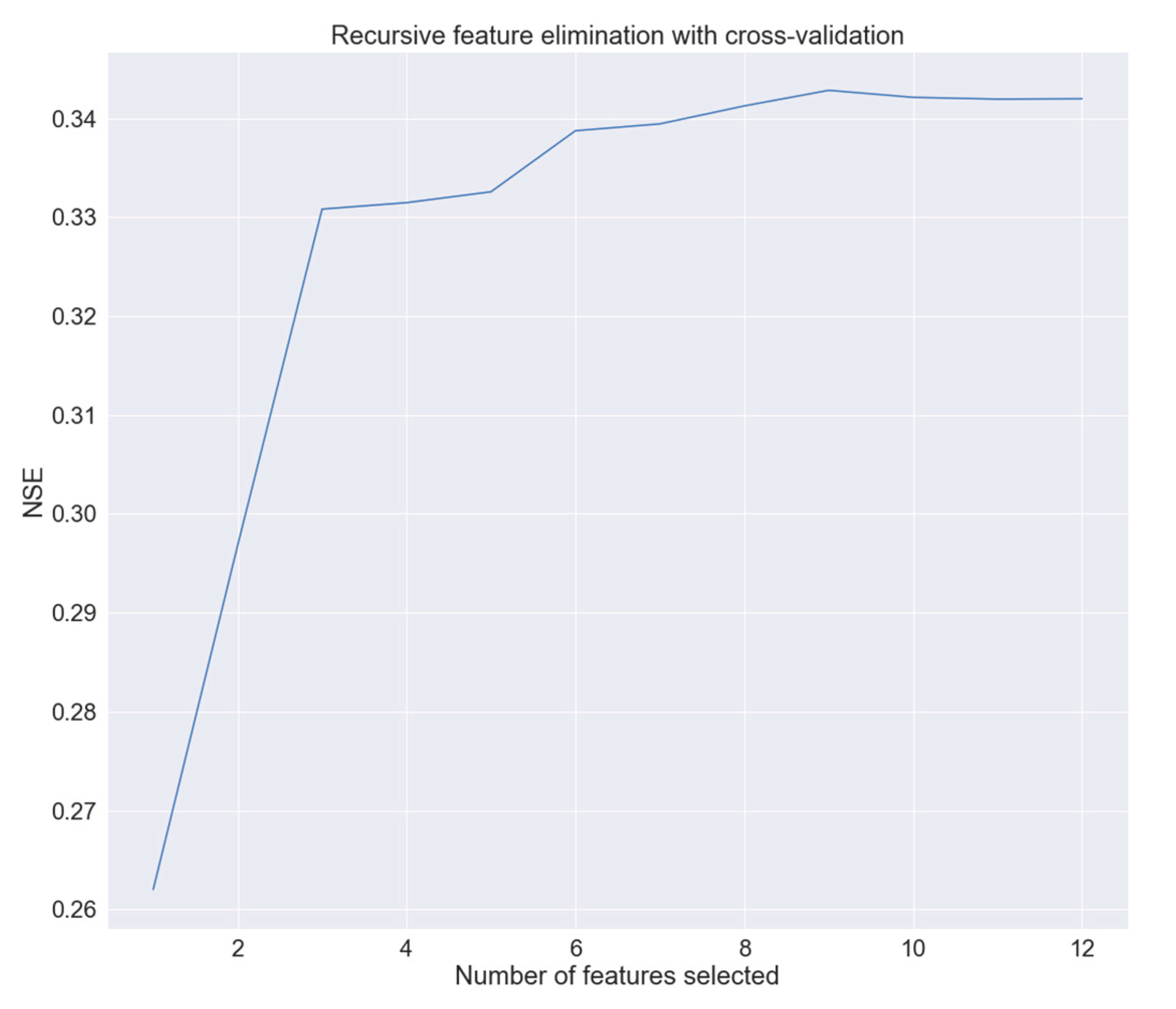
2.4. Feature Selection for the Streamflow Regionalization Models
2.5. Experimental Design
2.5.1. Experiment 1: LSTM and FFNN as Rainfall-Runoff Models
2.5.2. Experiment 2: LSTM and FFNN as Streamflow Regionalization Models for Ungauged Basins
2.6. Model Calibration and Evaluation
2.7. Performance Evaluation and Objective Function
- 1.
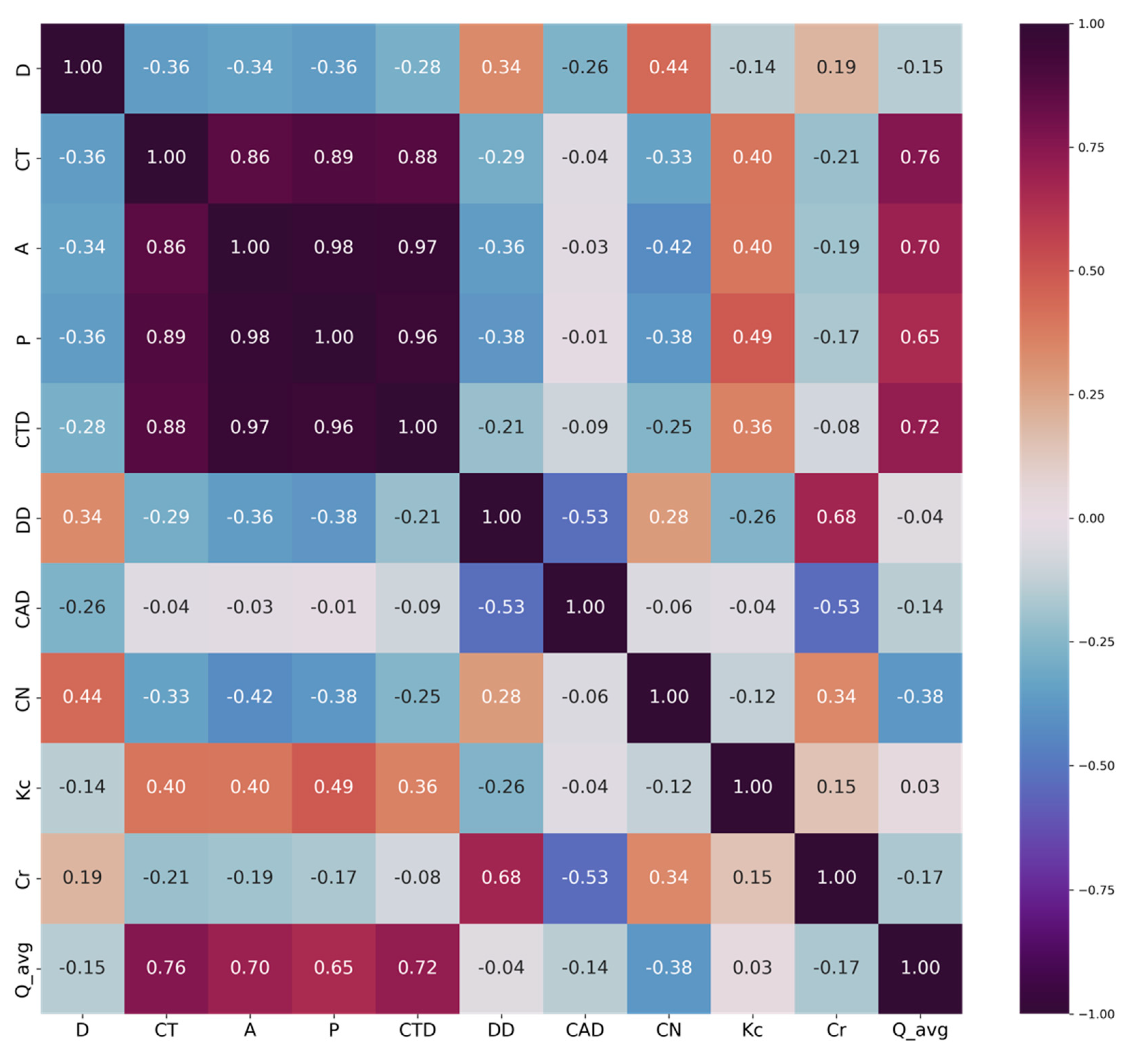
- Pearson Correlation Coefficient—Represents the intensity of linear dependency of two variables, it will indicate how similar some of the features are and if they are strongly linear dependent; one of these variables with two features does not need to be included in the model:
- : Variable 1
- : Variable 2
- 2.
- Nash-Sutcliffe Efficiency Coefficient—the index varies from (−∞, 1], values close to 1 indicate that the model fits perfectly with historical series, while values close to 0 would indicate that the model is as representative as the mean. Negative values indicate that the mean is more representative than the model. Its mathematical representation is given by:
- : Modeled discharge at time t
- : Observed discharge at time t
- : Mean of observed discharges
- 3.
- Root Mean Squared Error—used to indicate the magnitude of the error, and its value represents the average vertical distance between observed and predicted values.
- : Observed value at time i
- : Predicted value at time i
- n: Number of predictions
- 4.
- Relative Absolute Error—used to indicate a relative measure of the performance of the model with a naïve model that uses only the mean of the observed variable. It is similar to NSE, in a way. If , it would be better to use only the mean to describe the target variable:
- : Observed value at time i
- : Predicted value at time i
- : Average of observed value
- n: Number of pr edictions
3. Results
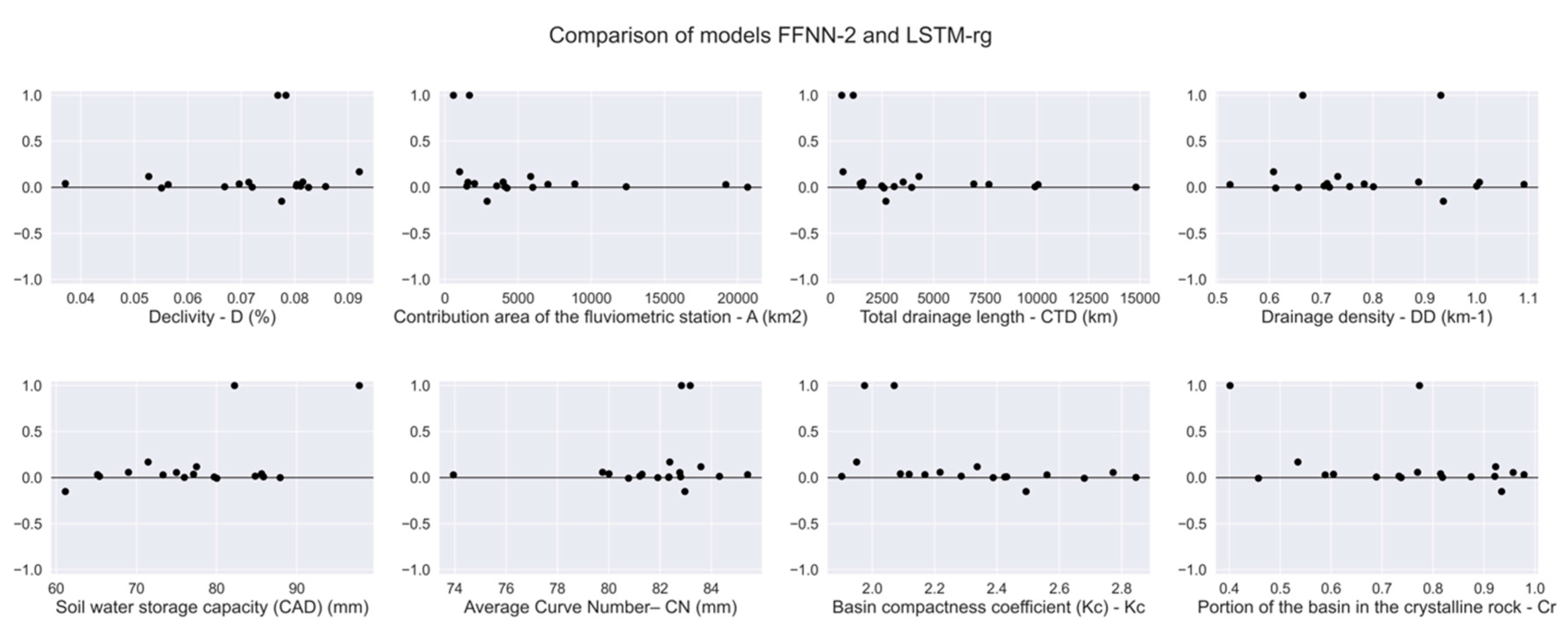
3.1. Selected Features
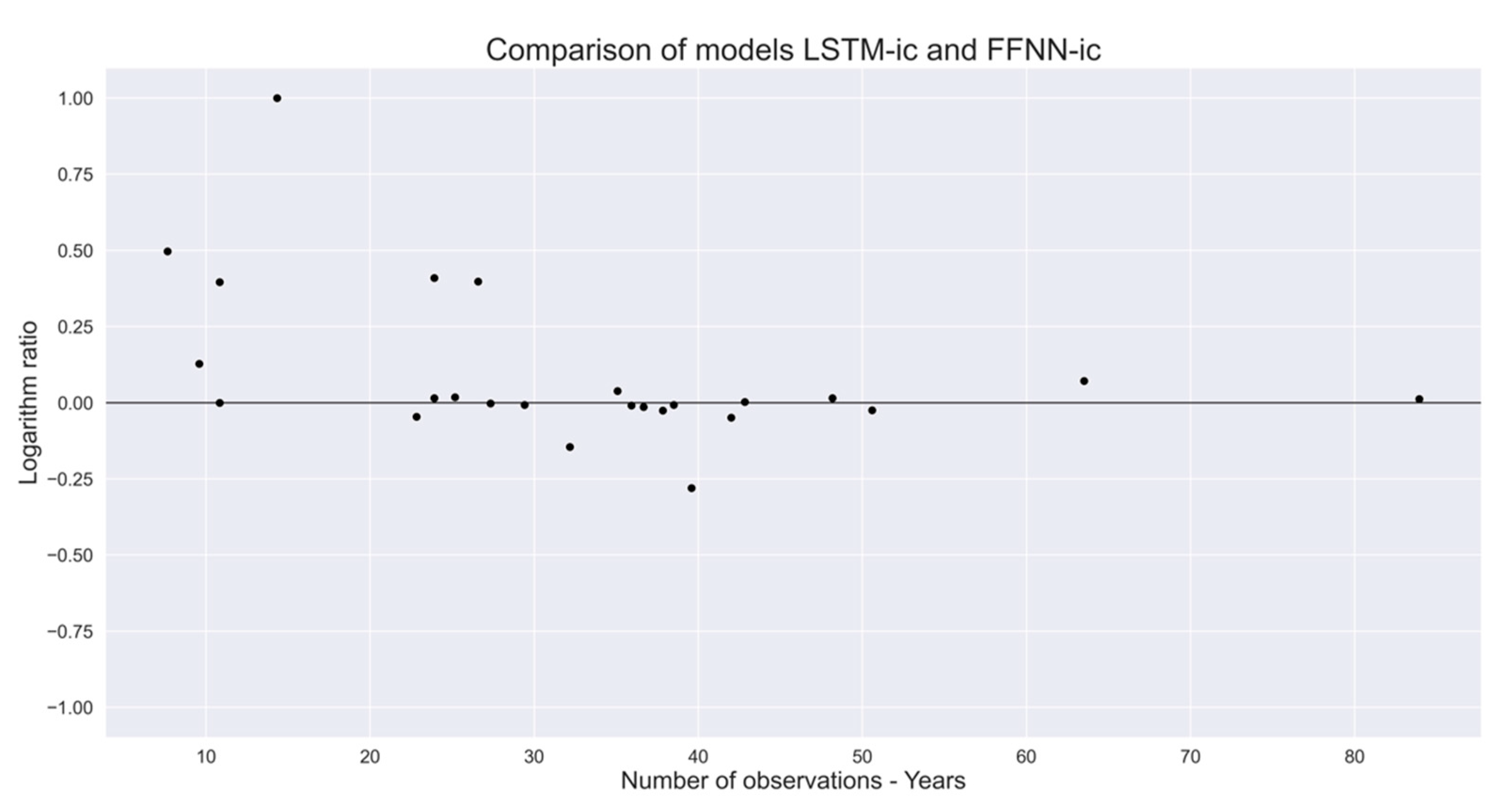
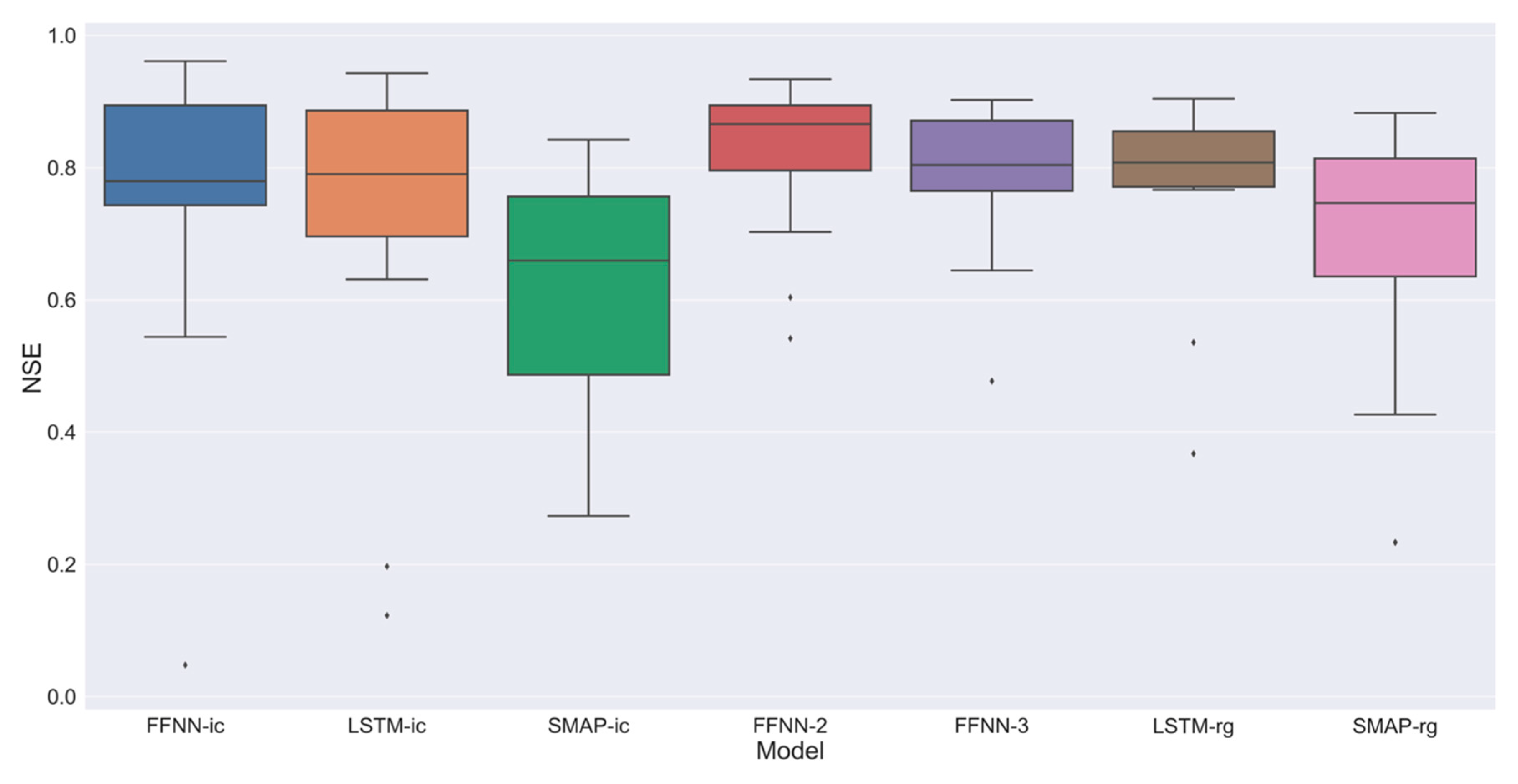
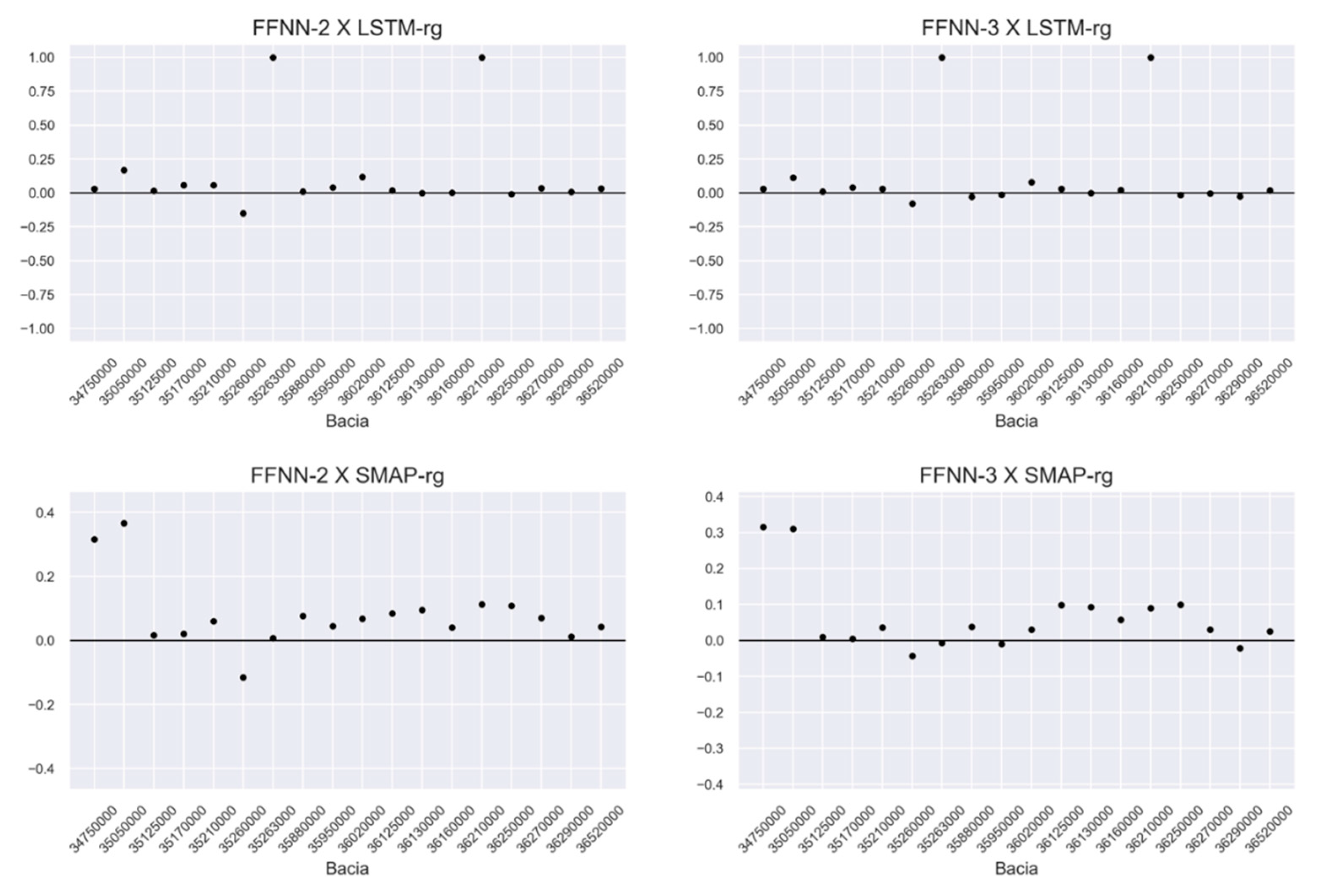
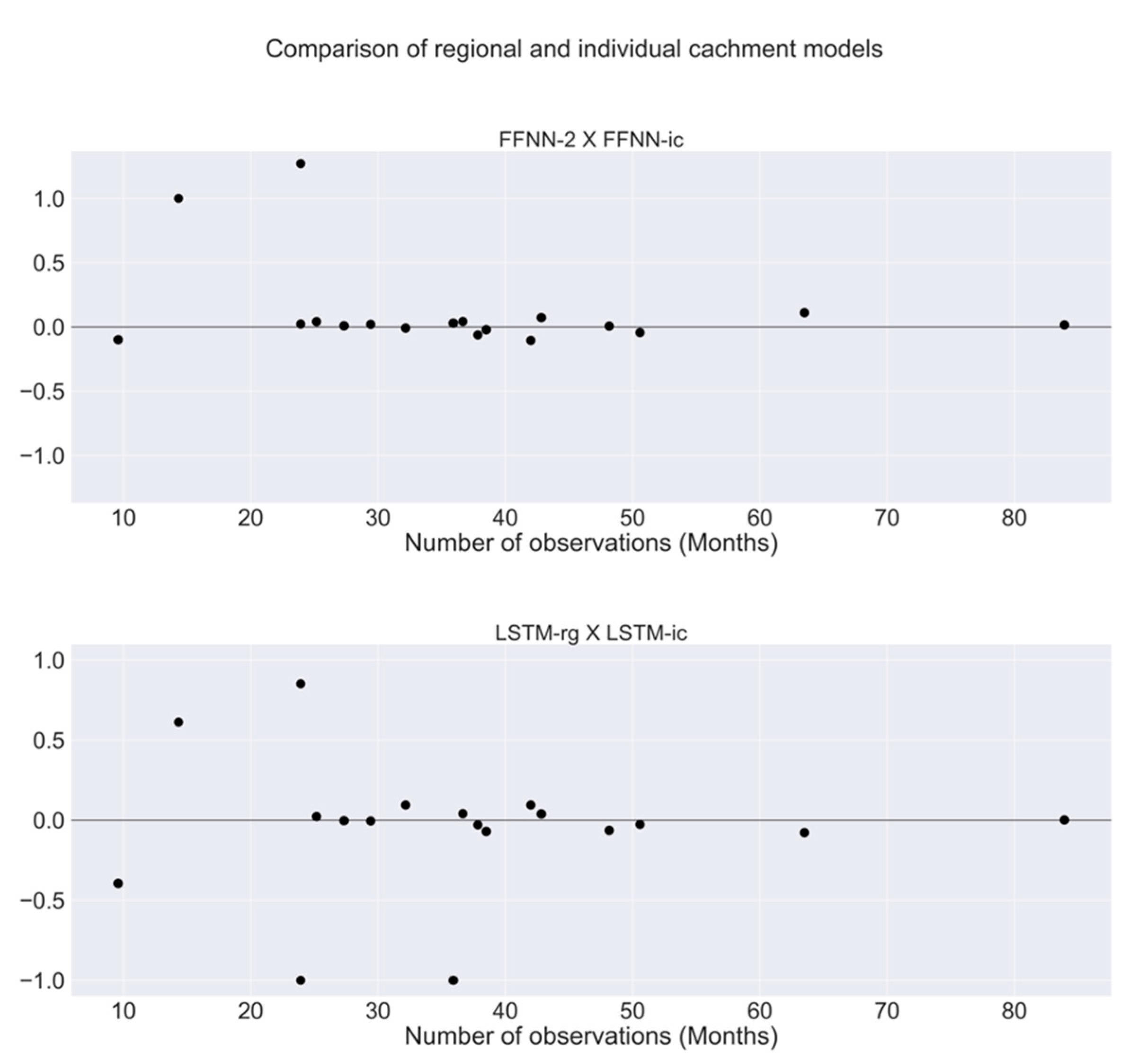
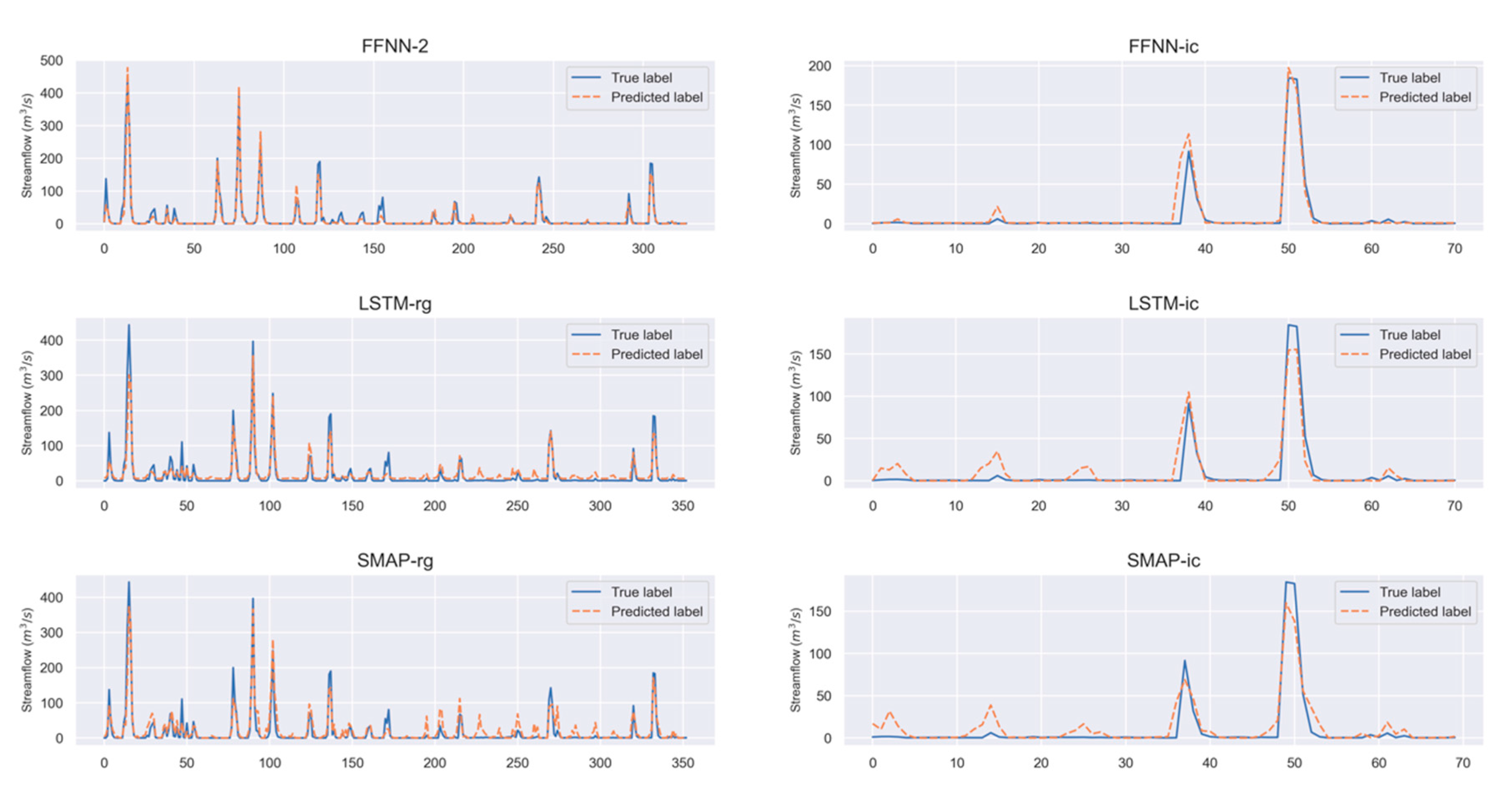
3.2. Results of Models
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Freire-González, J.; Decker, C.; Hall, J.W. The Economic Impacts of Droughts: A Framework for Analysis. Ecol. Econ. 2017, 132, 196–204. [Google Scholar] [CrossRef]
- Mosley, L.M. Drought Impacts on the Water Quality of Freshwater Systems; Review and Integration. Earth-Science Rev. 2015, 140, 203–214. [Google Scholar] [CrossRef]
- Clark, J.S.; Iverson, L.; Woodall, C.W.; Allen, C.D.; Bell, D.M.; Bragg, D.C.; D’Amato, A.W.; Davis, F.W.; Hersh, M.H.; Ibanez, I.; et al. The Impacts of Increasing Drought on Forest Dynamics, Structure, and Biodiversity in the United States. Glob. Chang. Biol. 2016, 22, 2329–2352. [Google Scholar] [CrossRef] [Green Version]
- Kirchner, J.W. Getting the Right Answers for the Right Reasons: Linking Measurements, Analyses, and Models to Advance the Science of Hydrology. Water Resour. Res. 2006, 42, 1–5. [Google Scholar] [CrossRef]
- Wood, E.F.; Roundy, J.K.; Troy, T.J.; Van Beek, L.P.H.; Bierkens, M.F.; Blyth, E.; De Roo, A.; Döll, P.; Ek, M.; Famiglietti, J.; et al. Hyperresolution global land surface modeling: Meeting a grand challenge for monitoring Earth’s terrestrial water. Water Resour. Res. 2011, 47, W05301. [Google Scholar] [CrossRef]
- Clark, M.P.; Bierkens, M.F.P.; Samaniego, L.; Woods, R.A.; Uijenhoet, R.; Bennet, K.E.; Pauwels, V.R.N.; Cai, X.; Wood, A.W.; Peters-Lidard, C.D. The Evolution of Process-Based Hydrologic Models: Historical Challenges and the Collective Quest for Physical Realism. Hydrol. Earth Syst. Sci. 2017, 21, 3427–3440. [Google Scholar] [CrossRef] [Green Version]
- Fowler, K.J.A.; Peel, M.C.; Western, A.W.; Zhang, L.; Peterson, T.J. Simulating Runoff under Changing Climatic Conditions: Revisiting an Apparent Deficiency of Conceptual Rainfall-Runoff Models. Water Resour. Res. 2016, 52, 1820–1846. [Google Scholar] [CrossRef] [Green Version]
- Herrnegger, M.; Senoner, T.; Nachtnebel, H.P. Adjustment of Spatio-Temporal Precipitation Patterns in a High Alpine Environment. J. Hydrol. 2018, 556, 913–921. [Google Scholar] [CrossRef]
- Govindaraju, R.S.; Rao, A.R. Artificial Neural Networks in Hydrology; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013; Volume 36. [Google Scholar]
- Her, Y.; Yoo, S.H.; Cho, J.; Hwang, S.; Jeong, J.; Seong, C. Uncertainty in Hydrological Analysis of Climate Change: Multi-Parameter vs. Multi-GCM Ensemble Predictions. Sci. Rep. 2019, 9, 4974. [Google Scholar] [CrossRef] [Green Version]
- Sivapalan, M.; Takeuchi, K.; Franks, S.W.; Gupta, V.K.; Karambiri, H.; Lakshmi, V.; Liang, X.; McDonnell, J.J.; Mendiondo, E.M.; O’Connell, P.E.; et al. IAHS Decade on Predictions in Ungauged Basins (PUB), 2003-2012: Shaping an Exciting Future for the Hydrological Sciences. Hydrol. Sci. J. 2003, 48, 857–880. [Google Scholar] [CrossRef] [Green Version]
- Croke, B.F.W.; Merritt, W.S.; Jakeman, A.J. A Dynamic Model for Predicting Hydrologic Response to Land Cover Changes in Gauged and Ungauged Catchments. J. Hydrol. 2004, 291, 115–131. [Google Scholar] [CrossRef]
- Götzinger, J.; Bárdossy, A. Comparison of Four Regionalisation Methods for a Distributed Hydrological Model. J. Hydrol. 2007, 333, 374–384. [Google Scholar] [CrossRef]
- Oudin, L.; Andréassian, V.; Perrin, C.; Michel, C.; Le Moine, N. Spatial Proximity, Physical Similarity, Regression and Ungaged Catchments: A Comparison of Regionalization Approaches Based on 913 French Catchments. Water Resour. Res. 2008, 44, 1–15. [Google Scholar] [CrossRef]
- Merz, R.; Blöschl, G. Regionalisation of Catchment Model Parameters. J. Hydrol. 2004, 287, 95–123. [Google Scholar] [CrossRef] [Green Version]
- Post, D.A. Regionalizing Rainfall-Runoff Model Parameters to Predict the Daily Streamflow of Ungauged Catchments in the Dry Tropics. Hydrol. Res. 2009, 40, 433–444. [Google Scholar] [CrossRef]
- Li, H.; Zhang, Y.; Chiew, F.H.S.; Xu, S. Predicting Runoff in Ungauged Catchments by Using Xinanjiang Model with MODIS Leaf Area Index. J. Hydrol. 2009, 370, 155–162. [Google Scholar] [CrossRef]
- Samuel, J.; Coulibaly, P.; Metcalfe, R.A. Estimation of Continuous Streamflow in Ontario Ungauged Basins: Comparison of Regionalization Methods. J. Hydrol. Eng. 2011, 16, 447–459. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiew, F.H.S. Relative Merits of Different Methods for Runoff Predictions in Ungauged Catchments. Water Resour. Res. 2009, 45, W07412. [Google Scholar] [CrossRef]
- McCabe, M.F.; Franks, S.W.; Kalma, J.D. Calibration of a Land Surface Model Using Multiple Data Sets. J. Hydrol. 2005, 302, 209–222. [Google Scholar] [CrossRef]
- Sefton, C.E.M.; Howarth, S.M. Relationships between Dynamic Response Characteristics and Physical Descriptors of Catchments in England and Wales. J. Hydrol. 1998, 211, 1–16. [Google Scholar] [CrossRef]
- Lee, H.; McIntyre, N.R.; Wheater, H.S.; Young, A.R. Predicting Runoff in Ungauged UK Catchments. Proc. Inst. Civ. Eng. Water Manag. 2006, 159, 129–138. [Google Scholar] [CrossRef] [Green Version]
- Besaw, L.E.; Rizzo, D.M.; Bierman, P.R.; Hackett, W.R. Advances in Ungauged Streamflow Prediction Using Artificial Neural Networks. J. Hydrol. 2010, 386, 27–37. [Google Scholar] [CrossRef]
- Heuvelmans, G.; Muys, B.; Feyen, J. Regionalisation of the Parameters of a Hydrological Model: Comparison of Linear Regression Models with Artificial Neural Nets. J. Hydrol. 2006, 319, 245–265. [Google Scholar] [CrossRef]
- Fathian, F.; Mehdizadeh, S.; Kozekalani Sales, A.; Safari, M.J.S. Hybrid Models to Improve the Monthly River Flow Prediction: Integrating Artificial Intelligence and Non-Linear Time Series Models. J. Hydrol. 2019, 575, 1200–1213. [Google Scholar] [CrossRef]
- Safari, M.J.S.; Rahimzadeh Arashloo, S.; Danandeh Mehr, A. Rainfall-Runoff Modeling through Regression in the Reproducing Kernel Hilbert Space Algorithm. J. Hydrol. 2020, 587, 125014. [Google Scholar] [CrossRef]
- Shen, C. A Transdisciplinary Review of Deep Learning Research and Its Relevance for Water Resources Scientists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Kratzert, F.; Klotz, D.; Brenner, C.; Schulz, K.; Herrnegger, M. Rainfall-Runoff Modelling Using Long Short-Term Memory (LSTM) Networks. Hydrol. Earth Syst. Sci. 2018, 22, 6005–6022. [Google Scholar] [CrossRef] [Green Version]
- Hu, C.; Wu, Q.; Li, H.; Jian, S.; Li, N.; Lou, Z. Deep Learning with a Long Short-Term Memory Networks Approach for Rainfall-Runoff Simulation. Water 2018, 10, 1543. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Z.; Yan, J.; Demir, I. A Rainfall-Runoff Model with LSTM-Based Sequence-to-Sequence Learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Fan, H.; Jiang, M.; Xu, L.; Zhu, H.; Cheng, J.; Jiang, J. Comparison of Long Short Term Memory Networks and the Hydrological Model in Runoff Simulation. Water 2020, 12, 175. [Google Scholar] [CrossRef] [Green Version]
- Addor, N.; Newman, A.J.; Mizukami, N.; Clark, M.P. The CAMELS data set: Catchment attributes and meteorology for large-sample studies. Hydrol. Earth Syst. Sci. 2017, 21, 5293–5313. [Google Scholar] [CrossRef] [Green Version]
- Barros, F.; Martins, E.; Souza Filho, F.A. Regionalização de parâmetros do modelo chuva-vazão SMAP das bacias hidrográficas do Ceará. In Gerenciamento de Recursos Hídricos no Semiárido; Expressão Gráfica e Editora: Fortaleza, Brazil, 2013. [Google Scholar]
- Abadi, M.; Agarwal, A.; Barham, P.; Brevdo, E.; Chen, Z.; Citro, C.; Zheng, X. Tensorflow: Large-scale machine learning on heterogeneous distributed systems. arXiv Prepr. 2016, arXiv:1603.04467. [Google Scholar]
- Lopes, J.E.G.; Braga, B.P.F., Jr.; Conejo, J.G.L. SMAP—A Simplified Hydrologic Model. Appl. Modeling Catchment Hydrol. 1982, 167–176. Available online: https://agris.fao.org/agris-search/search.do?request_locale=ar&recordID=US201302608054&query=&sourceQuery=&sortField=&sortOrder=&agrovocString=&advQuery=¢erString=&enableField= (accessed on 16 March 2022).
- Companhia de Gestão dos Recursos Hídricos (COGERH). Estudos de Regionalização de Parâmetros de Modelo Hidrológico Chuva-Vazão, Para as Bacias Totais e Incrementais dos Reservatórios Monitorados Pela COGERH; COGERH: Fortaleza, Brazil, 2013. [Google Scholar]
- Alexandre, A.M.B.; Martins, E.S.; Clarke, R.T.; Reis, D.S., Jr. Regionalização de parâmetros de modelos hidrológicos. In Anais do XVI Simpósio Brasileiro de Recursos Hídricos; ABRH, João Pessoa–PB, 2005; Available online: http://www.funceme.br/produtos/manual/acudes_e_rios/Regionalizacao/textos/RegSMAP_PaperABRH.pdf (accessed on 16 March 2022).
- Nascimento, L.S.V.; Reis, D.S., Jr.; Martins, E.S.P. Avaliação do algoritmo evolutivo Mopso na calibração multiobjetivo do modelo SMAP no estado do Ceará. Diretoria da ABRH 2009, 14, 85–97. [Google Scholar] [CrossRef]
- Block, P.J.; Souza Filho, F.A.; Sun, L.; Kwon, H.H. A Streamflow Forecasting Framework Using Multiple Climate and Hydrological Models. J. Am. Water Resour. Assoc. 2009, 45, 828–843. [Google Scholar] [CrossRef]
- Barros, M.T.L.; Lopes, J.E.G.; Zambon, R.C.; Francato, A.L.; Barbosa, P.S.F.; Zanfelice, F.R. Climate Flow Forecast Model for the Brazilian Hydropower System. In Proceedings of the World Environmental and Water Resources Congress 2009: Great Rivers, Kansas City, MO, USA, 17–21 May 2009; Volume 342, pp. 4727–4735. [Google Scholar] [CrossRef]
- Da Silva, F.D.N.R.; Alves, J.L.D.; Cataldi, M. Climate Downscaling over South America for 1971–2000: Application in SMAP Rainfall-Runoff Model for Grande River Basin. Clim. Dyn. 2019, 52, 681–696. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Maemillan: New York, NY, USA, 1994; p. 696. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Elman, J.L. Finding Structure in Time. Cogn. Sci. 1990, 14, 179–211. [Google Scholar] [CrossRef]
- Hochreiter, S. The Vanishing Gradient Problem during Learning Recurrent Neural Nets and Problem Solutions. Int. J. Uncertain. Fuzziness Knowl.-Based Syst. 1998, 6, 107–116. [Google Scholar] [CrossRef] [Green Version]
- Guyon, I.; Weston, J.; Barnhill, S.; Vapnik, V. Gene selection for cancer classification using support vector machines. Mach. Learn. 2002, 46, 389–422. [Google Scholar] [CrossRef]
- Parajka, J.; Merz, R.; Blöschl, G. A Comparison of Regionalisation Methods for Catchment Model Parameters. Hydrol. Earth Syst. Sci. 2005, 9, 157–171. [Google Scholar] [CrossRef] [Green Version]
- Laaha, G.; Blöschl, G. A Comparison of Low Flow Regionalisation Methods-Catchment Grouping. J. Hydrol. 2006, 323, 193–214. [Google Scholar] [CrossRef]
- Leclerc, M.; Ouarda, T.B.M.J. Non-Stationary Regional Flood Frequency Analysis at Ungauged Sites. J. Hydrol. 2007, 343, 254–265. [Google Scholar] [CrossRef]
- Hinton, G.; Srivastava, N.; Swersky, K. Neural networks for machine learning lecture 6a overview of mini-batch gradient descent. Cited 2012, 14, 2. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Granata, F.; Di Nunno, F. Forecasting Evapotranspiration in Different Climates Using Ensembles of Recurrent Neural Networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Yin, J.; Deng, Z.; Ines, A.V.M.; Wu, J.; Rasu, E. Forecast of Short-Term Daily Reference Evapotranspiration under Limited Meteorological Variables Using a Hybrid Bi-Directional Long Short-Term Memory Model (Bi-LSTM). Agric. Water Manag. 2020, 242, 106386. [Google Scholar] [CrossRef]
- Docheshmeh Gorgij, A.; Alizamir, M.; Kisi, O.; Elshafie, A. Drought Modelling by Standard Precipitation Index (SPI) in a Semi-Arid Climate Using Deep Learning Method: Long Short-Term Memory. Neural Comput. Appl. 2022, 34, 2425–2442. [Google Scholar] [CrossRef]
| Stream-flow Station | Declivity—D (%) | Contribution Area of the Fluviometric Station—A (km2) | Total Drainage Length—CTD (km) | Drainage Density—DD (km−1) | Soil Water Storage Capacity (CAD) (mm) | Average Curve Number—CN (mm) | Basin Compact-ness Coefficient (Kc)—Kc | Portion of the Basin in the Crystalline Rock—Cr |
|---|---|---|---|---|---|---|---|---|
| 34730000 | 0.069 | 897.372 | 528.790 | 0.589 | 59.483 | 56.774 | 1.990 | 0.000 |
| 34740000 | 0.065 | 2221.989 | 356.001 | 0.160 | 51.100 | 59.941 | 1.085 | 0.000 |
| 34750000 | 0.056 | 19,185.920 | 10,051.126 | 0.524 | 73.315 | 73.945 | 2.560 | 0.588 |
| 35050000 | 0.092 | 997.264 | 606.451 | 0.608 | 71.461 | 82.375 | 1.950 | 0.534 |
| 35125000 | 0.081 | 1501.237 | 1501.190 | 1.000 | 65.377 | 84.315 | 1.902 | 0.921 |
| 35170000 | 0.081 | 3967.244 | 3523.080 | 0.888 | 69.009 | 79.753 | 2.217 | 0.770 |
| 35210000 | 0.071 | 1566.680 | 1574.683 | 1.005 | 74.984 | 82.767 | 2.772 | 0.957 |
| 35223000 | 0.082 | 693.135 | 636.738 | 0.919 | 82.157 | 84.314 | 2.178 | 0.763 |
| 35240000 | 0.100 | 1532.777 | 1309.706 | 0.854 | 66.220 | 85.743 | 2.467 | 0.913 |
| 35260000 | 0.078 | 2875.183 | 2690.396 | 0.936 | 61.125 | 82.961 | 2.493 | 0.934 |
| 35263000 | 0.077 | 587.889 | 547.171 | 0.931 | 82.225 | 83.172 | 1.975 | 0.773 |
| 35668000 | 0.082 | 495.859 | 364.205 | 0.734 | 76.364 | 82.358 | 2.876 | 0.926 |
| 35880000 | 0.086 | 4085.575 | 3084.452 | 0.755 | 85.831 | 82.799 | 2.431 | 0.875 |
| 35950000 | 0.037 | 2027.716 | 1442.687 | 0.711 | 85.603 | 80.000 | 2.090 | 0.815 |
| 36020000 | 0.053 | 5852.006 | 4284.214 | 0.732 | 77.478 | 83.589 | 2.336 | 0.923 |
| 36125000 | 0.080 | 3533.321 | 2492.858 | 0.706 | 84.805 | 81.209 | 2.285 | 0.733 |
| 36130000 | 0.083 | 5996.827 | 3935.060 | 0.656 | 87.925 | 81.907 | 2.388 | 0.737 |
| 36160000 | 0.072 | 20,664.322 | 14,792.266 | 0.716 | 75.959 | 82.330 | 2.845 | 0.818 |
| 36210000 | 0.078 | 1665.995 | 1106.796 | 0.664 | 97.794 | 82.833 | 2.070 | 0.401 |
| 36220000 | 0.028 | 1564.877 | 355.644 | 0.227 | 88.639 | 84.871 | 2.588 | 0.153 |
| 36250000 | 0.055 | 4240.717 | 2596.731 | 0.612 | 80.005 | 80.765 | 2.680 | 0.457 |
| 36270000 | 0.070 | 8869.966 | 6943.068 | 0.783 | 77.104 | 81.294 | 2.118 | 0.605 |
| 36290000 | 0.067 | 12,381.522 | 9914.359 | 0.801 | 79.707 | 82.338 | 2.424 | 0.689 |
| 36470000 | 0.085 | 998.024 | 1332.280 | 1.335 | 66.302 | 78.687 | 2.102 | 0.988 |
| 36520000 | 0.080 | 7035.737 | 7678.188 | 1.091 | 65.151 | 85.408 | 2.169 | 0.978 |
| Experiment | Model | D | CT | A | P | CTD | DD | CAD | CN | Kc | Cr | E | Precipitation Lags | Streamflow Lags |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | FFNN-ic | |||||||||||||
| LSTM-ic | ||||||||||||||
| SMAP-ic | ||||||||||||||
| 2 | FFNN-2 | |||||||||||||
| FFNN-3 | ||||||||||||||
| LSTM-rg | ||||||||||||||
| SMAP |
| Basin | n obs | Experiment 1 | Experiment 2 | |||||
|---|---|---|---|---|---|---|---|---|
| FFNN-ic | LSTM-ic | SMAP-ic | FFNN-2 | FFNN-3 | LSTM-rg | SMAP-rg | ||
| 34730000 | 475 | 0.192 | 0.101 | −0.304 | −3.559 | −4.854 | −3.216 | |
| 34740000 | 92 | 0.199 | 0.624 | −31.361 | 0.505 | 0.440 | 0.564 | |
| 34750000 | 514 | 0.747 | 0.751 | 0.653 | 0.883 | 0.881 | 0.823 | 0.427 |
| 35050000 | 115 | 0.680 | 0.912 | 0.760 | 0.542 | 0.477 | 0.367 | 0.233 |
| 35125000 | 328 | 0.896 | 0.890 | 0.814 | 0.915 | 0.903 | 0.885 | 0.883 |
| 35170000 | 462 | 0.939 | 0.923 | 0.617 | 0.895 | 0.863 | 0.785 | 0.854 |
| 35210000 | 578 | 0.910 | 0.943 | 0.503 | 0.925 | 0.874 | 0.814 | 0.806 |
| 35223000 | 130 | 0.069 | 0.172 | 0.230 | 0.278 | 0.100 | 0.182 | |
| 35240000 | 421 | 0.455 | 0.496 | 0.538 | 0.739 | 0.509 | 0.615 | |
| 35260000 | 504 | 0.770 | 0.687 | 0.666 | 0.604 | 0.714 | 0.855 | 0.788 |
| 35263000 | 287 | 0.790 | 0.817 | 0.817 | 0.832 | 0.805 | −0.564 | 0.817 |
| 35668000 | 319 | 0.335 | 0.835 | 0.019 | −0.750 | 0.151 | −1.522 | |
| 35880000 | 287 | 0.048 | 0.123 | 0.435 | 0.893 | 0.816 | 0.873 | 0.748 |
| 35950000 | 386 | 0.881 | 0.631 | −0.413 | 0.863 | 0.760 | 0.786 | 0.778 |
| 36020000 | 762 | 0.544 | 0.641 | 0.274 | 0.703 | 0.644 | 0.536 | 0.602 |
| 36125000 | 440 | 0.748 | 0.724 | 0.481 | 0.825 | 0.854 | 0.795 | 0.680 |
| 36130000 | 302 | 0.823 | 0.858 | 0.697 | 0.905 | 0.901 | 0.904 | 0.728 |
| 36160000 | 1007 | 0.743 | 0.764 | 0.686 | 0.771 | 0.802 | 0.767 | 0.703 |
| 36210000 | 431 | 0.744 | 0.728 | 0.769 | 0.796 | 0.755 | −0.070 | 0.613 |
| 36250000 | 454 | 0.918 | 0.866 | 0.281 | 0.796 | 0.780 | 0.810 | 0.620 |
| 36270000 | 172 | −0.871 | 0.197 | 0.747 | 0.875 | 0.798 | 0.806 | 0.745 |
| 36290000 | 607 | 0.961 | 0.908 | 0.843 | 0.869 | 0.804 | 0.854 | 0.845 |
| 36470000 | 274 | 0.878 | 0.790 | 0.070 | 0.767 | 0.432 | 0.574 | |
| 36520000 | 353 | 0.891 | 0.875 | 0.617 | 0.934 | 0.898 | 0.865 | 0.847 |
| Metrics | FFNN-ic | LSTM-ic | SMAP-ic | FFNN-2 | FFNN-3 | LSTM-rg | SMAP-rg |
|---|---|---|---|---|---|---|---|
| NSE | 0.780 ± 0.091 | 0.790 ± 0.105 | 0.659 ± 0.103 | 0.866 ± 0.045 | 0.804 ± 0.045 | 0.808 ± 0.055 | 0.747 ± 0.07 |
| RMSE (m3/s) | 10.197 ± 3.548 | 9.706 ± 4.692 | 11.282 ± 3.990 | 10.765 ± 6.243 | 12.541 ± 6.617 | 11.730 ± 6.532 | 14.670 ± 7.213 |
| RAE (%) | 0.325 ± 0.088 | 0.350 ± 0.057 | 0.466 ± 0.071 | 0.306 ± 0.050 | 0.344 ± 0.040 | 0.374 ± 0.091 | 0.414 ± 0.046 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nogueira Filho, F.J.M.; Souza Filho, F.d.A.; Porto, V.C.; Vieira Rocha, R.; Sousa Estácio, Á.B.; Martins, E.S.P.R. Deep Learning for Streamflow Regionalization for Ungauged Basins: Application of Long-Short-Term-Memory Cells in Semiarid Regions. Water 2022, 14, 1318. https://doi.org/10.3390/w14091318
Nogueira Filho FJM, Souza Filho FdA, Porto VC, Vieira Rocha R, Sousa Estácio ÁB, Martins ESPR. Deep Learning for Streamflow Regionalization for Ungauged Basins: Application of Long-Short-Term-Memory Cells in Semiarid Regions. Water. 2022; 14(9):1318. https://doi.org/10.3390/w14091318
Chicago/Turabian StyleNogueira Filho, Francisco José Matos, Francisco de Assis Souza Filho, Victor Costa Porto, Renan Vieira Rocha, Ályson Brayner Sousa Estácio, and Eduardo Sávio Passos Rodrigues Martins. 2022. "Deep Learning for Streamflow Regionalization for Ungauged Basins: Application of Long-Short-Term-Memory Cells in Semiarid Regions" Water 14, no. 9: 1318. https://doi.org/10.3390/w14091318
APA StyleNogueira Filho, F. J. M., Souza Filho, F. d. A., Porto, V. C., Vieira Rocha, R., Sousa Estácio, Á. B., & Martins, E. S. P. R. (2022). Deep Learning for Streamflow Regionalization for Ungauged Basins: Application of Long-Short-Term-Memory Cells in Semiarid Regions. Water, 14(9), 1318. https://doi.org/10.3390/w14091318






