Compost Amendment Impact on Soil Physical Quality Estimated from Hysteretic Water Retention Curve
Abstract
:1. Introduction
2. Materials and Methods
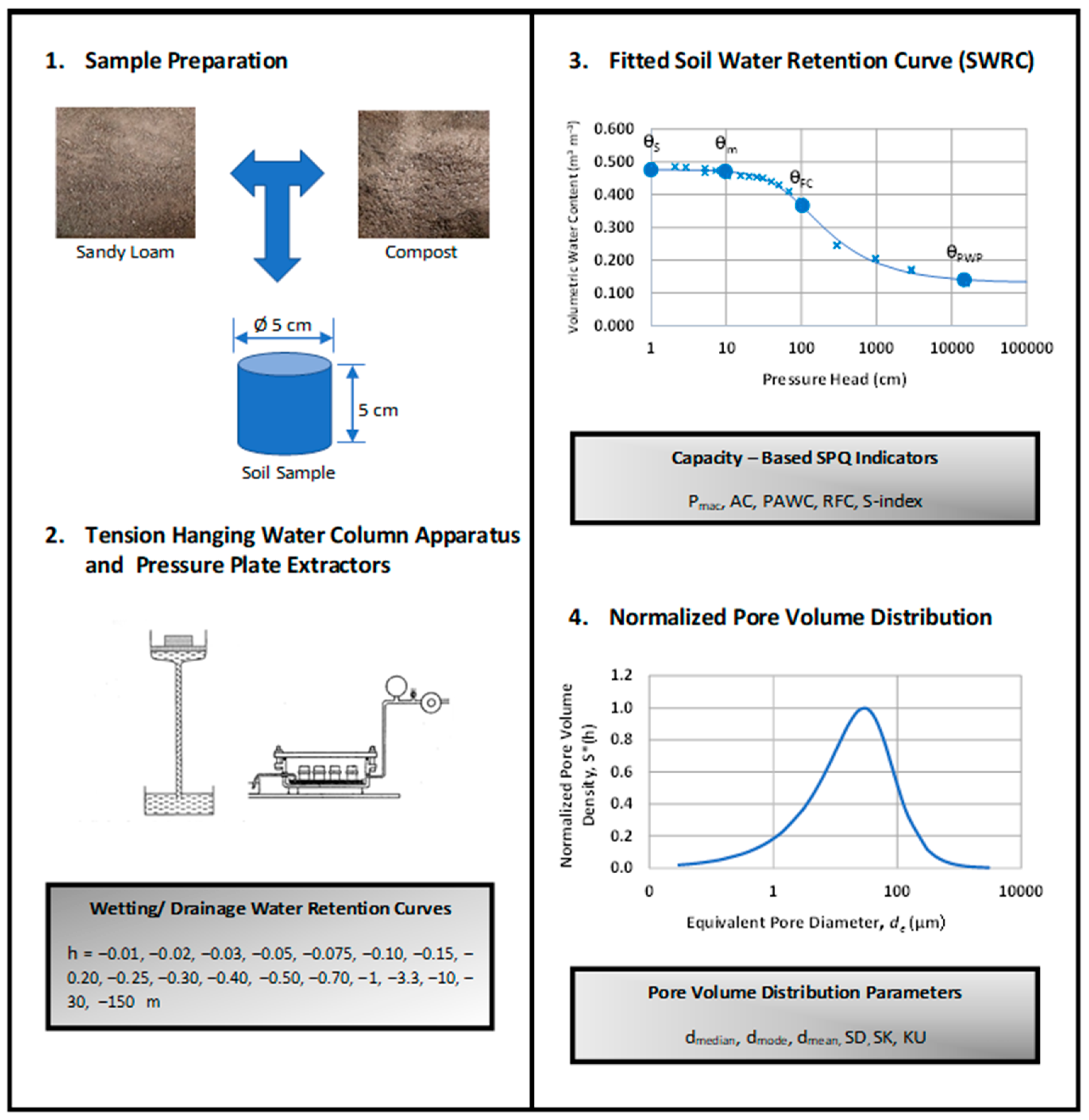
2.1. Sample Preparation and SWRC Measurement
2.2. SWRC Parameterization
2.3. Estimation of Soil Physical Quality
2.4. Data Analisys
3. Results and Discussion
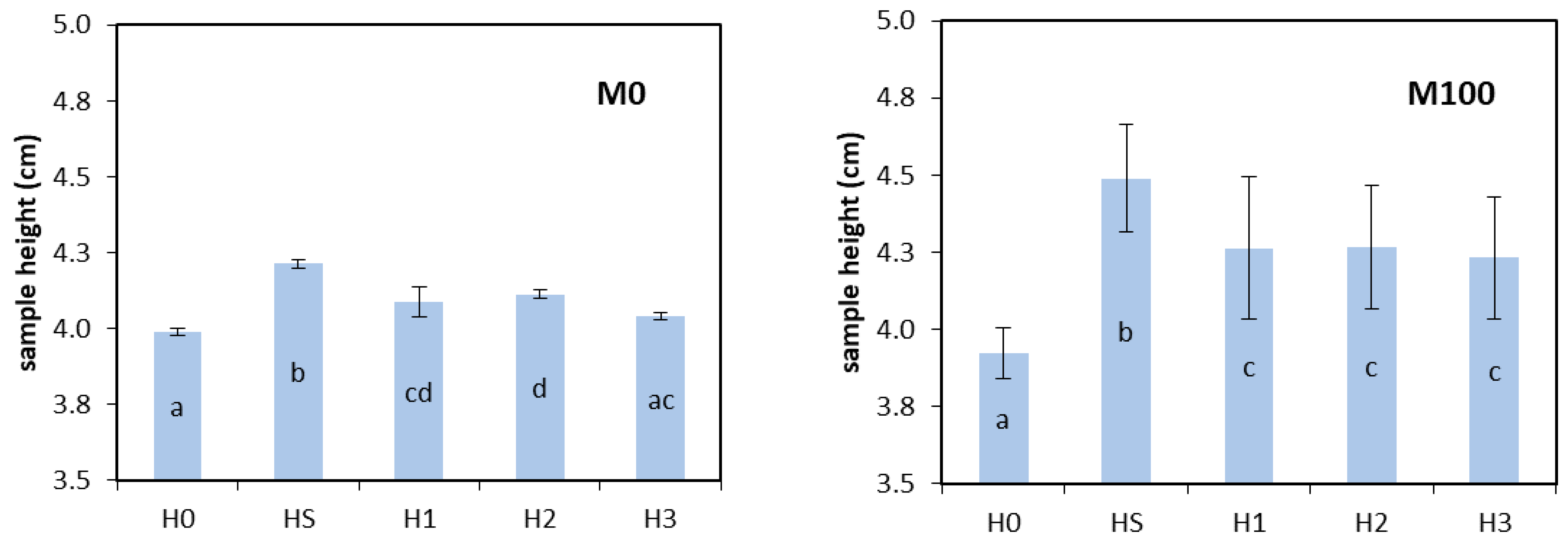
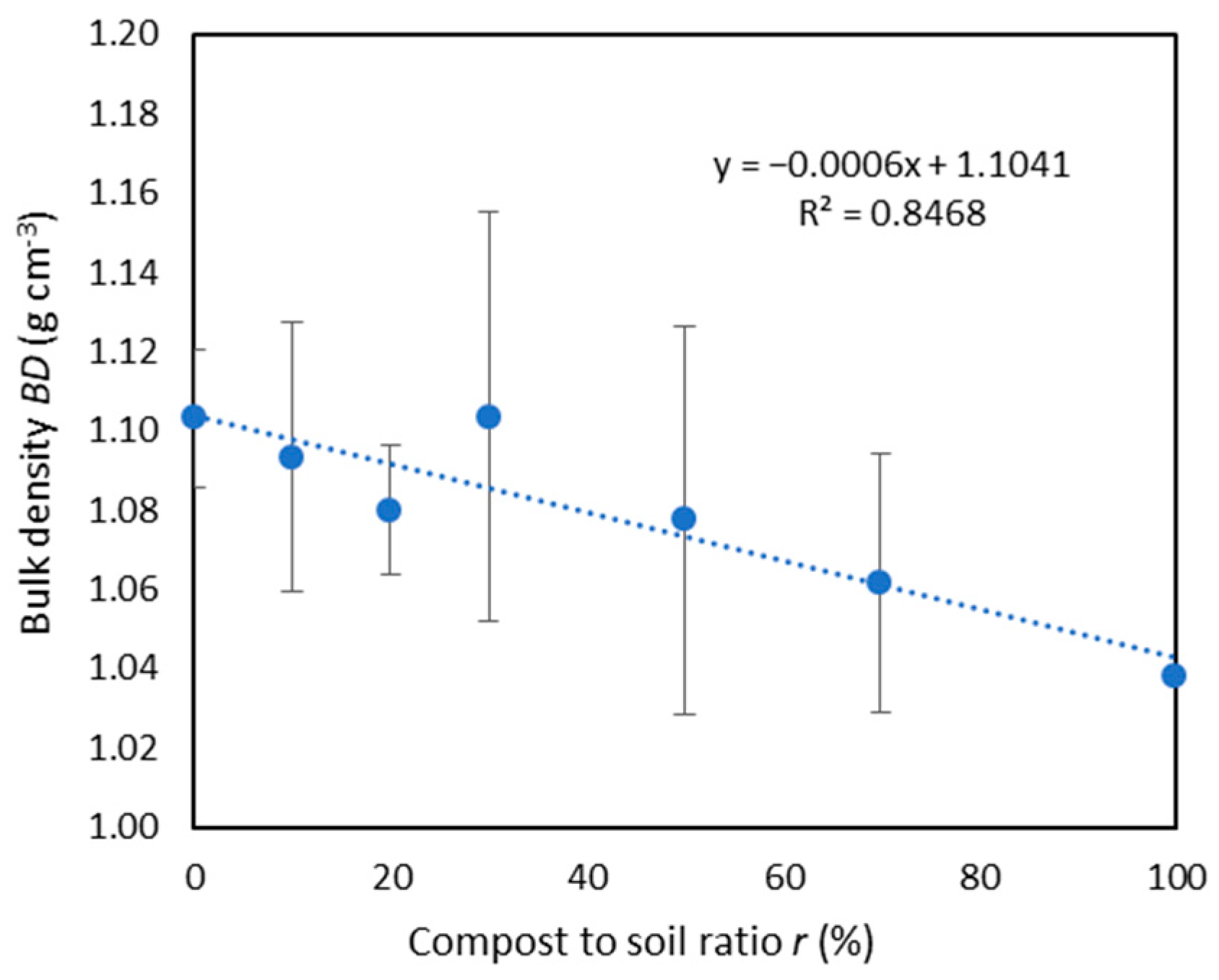
3.1. Soil Bulk Density
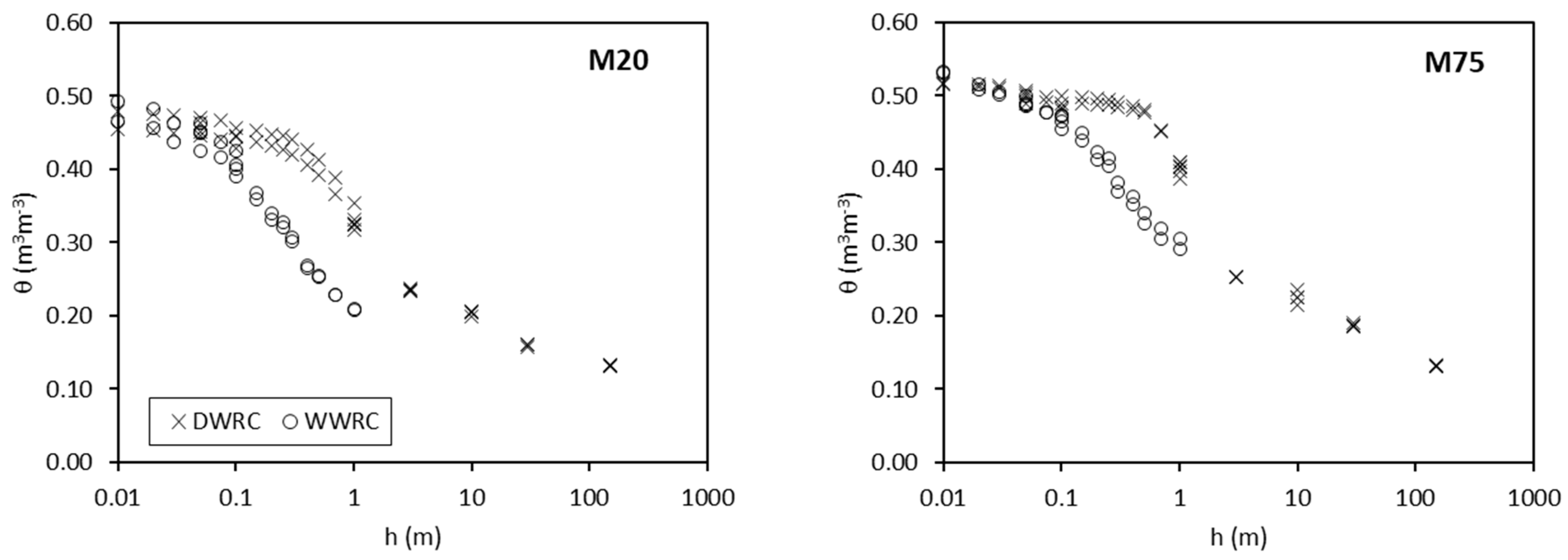
3.2. Soil Water Retention and Pore Volume Distribution
3.3. Influence of Hysteresis on Soil Physical Quality
3.4. Influence of Compost Amendment on Soil Water Retention and Physical Quality
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Dong, L.; Zhang, W.; Xiong, Y.; Zou, J.; Huang, Q.; Xu, X.; Ren, P.; Huang, G. Impact of short-term organic amendments incorporation on soil structure and hydrology in semiarid agricultural lands. Int. Soil Water Conserv. Res. 2021, in press. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Drury, C.F.; Yang, X.M.; Fox, C.A.; Tan, C.S.; Zhang, T.Q. Land management effects on the near-surface physical quality of a clay loam soil. Soil Tillage Res. 2007, 96, 316–330. [Google Scholar] [CrossRef]
- Arthur, E.; Cornelis, W.M.; Vermang, J.; de Rocker, E. Amending a loamy sand with three compost types: Impact on soil quality. Soil Use Manag. 2011, 27, 116–123. [Google Scholar] [CrossRef]
- Mandal, M.; Chandran, R.; Sencindiver, J. Amending Subsoil with Composted Poultry Litter-I: Effects on Soil Physical and Chemical Properties. Agronomy 2013, 3, 657–669. [Google Scholar] [CrossRef] [Green Version]
- Negiş, H.; Şeker, C.; Gümüş, I.; Manirakiza, N.; Mücevher, O. Effects of Biochar and Compost Applications on Penetration Resistance and Physical Quality of a Sandy Clay Loam Soil. Commun. Soil Sci. Plant Anal. 2020, 51, 38–44. [Google Scholar] [CrossRef]
- Aggelides, S.M.; Londra, P.A. Effects of compost produced from town wastes and sewage sludge on the physical properties of a loamy and a clay soil. Bioresour. Technol. 2000, 71, 253–259. [Google Scholar] [CrossRef]
- Annabi, M.; Houot, S.; Francou, C.; Poitrenaud, M.; Bissonnais, Y.L. Soil Aggregate Stability Improvement with Urban Composts of Different Maturities. Soil Sci. Soc. Am. J. 2007, 71, 413–423. [Google Scholar] [CrossRef]
- Ibrahim, A.; Marie, H.A.M.E.; Elfaki, J. Impact of biochar and compost on aggregate stability in loamy sand soil. Agric. Res. J. 2021, 58, 34–44. [Google Scholar] [CrossRef]
- Głąb, T.; Żabiński, A.; Sadowska, U.; Gondek, K.; Kopeć, M.; Mierzwa-Hersztek, M.; Tabor, S.; Stanek-Tarkowska, J. Fertilization effects of compost produced from maize, sewage sludge and biochar on soil water retention and chemical properties. Soil Tillage Res. 2020, 197, 104493. [Google Scholar] [CrossRef]
- Zemánek, P. Evaluation of compost influence on soil water retention. Acta Univ. Agric. Silvic. Mendel. Brun. LIX 2011, 3, 227–232. [Google Scholar] [CrossRef] [Green Version]
- Schneider, S.; Coquet, Y.; Vachier, P.; Labat, C.; Roger-Estrade, J.; Benoit, P.; Pot, V.; Houot, S. Effect of Urban Waste Compost Application on Soil Near-Saturated Hydraulic Conductivity. J. Environ. Qual. 2009, 38, 772–781. [Google Scholar] [CrossRef] [PubMed]
- Whelan, A.; Kechavarzi, C.; Coulon, F.; Sakrabani, R.; Lord, R. Influence of compost amendments on the hydraulic functioning of brownfield soils. Soil Use Manag. 2013, 29, 260–270. [Google Scholar] [CrossRef] [Green Version]
- Şeker, C.; Manirakiza, N. Effectiveness of compost and biochar in improving water retention characteristics and aggregation of a sandy clay loam soil under wind erosion. Carpathian J. Earth Environ. Sci. 2020, 15, 5–18. [Google Scholar] [CrossRef]
- Kranz, C.N.; McLaughlin, R.A.; Johnson, A.; Miller, G.; Heitman, J.L. The effects of compost incorporation on soil physical properties in urban soils—A concise review. J. Environ. Manag. 2020, 261, 110209. [Google Scholar] [CrossRef] [PubMed]
- Sadeghi, S.; Ebrahimi, S.; Zakerinia, M. The Study of the Parametric Changes in Water Potential Points by Using Waste Manuciple Compost in Three Kinds of Soils. Int. J. Basic Sci. Appl. Res. 2014, 3, 254–260. Available online: http://www.isicenter.org (accessed on 22 February 2022).
- Paradelo, R.; Basanta, R.; Barral, M.T. Water-holding capacity and plant growth in compost-based substrates modified with polyacrylamide, guar gum or bentonite. Sci. Hortic. 2019, 243, 344–349. [Google Scholar] [CrossRef]
- Benito, M.; Masaguer, A.; Moliner, A.; de Antonio, R. Chemical and physical properties of pruning waste compost and their seasonal variability. Bioresour. Technol. 2006, 97, 2071–2076. [Google Scholar] [CrossRef]
- Ibrahim, A.; Horton, R. Biochar and compost amendment impacts on soil water and pore size distribution of a loamy sand soil. Soil Sci. Soc. Am. J. 2021, 85, 1021–1036. [Google Scholar] [CrossRef]
- Curtis, M.J.; Claassen, V.P. Regenerating topsoil functionality in four drastically disturbed soil types by compost incorporation. Restor. Ecol. 2009, 17, 24–32. [Google Scholar] [CrossRef]
- Palazzolo, E.; Laudicina, V.A.; Roccuzzo, G.; Allegra, M.; Torrisi, B.; Micalizzi, A.; Badalucco, L. Bioindicators and nutrient availability through whole soil profile under orange groves after long-term different organic fertilizations. SN Appl. Sci. 2019, 1, 468. [Google Scholar] [CrossRef] [Green Version]
- Glab, T.; Zabinski, A.; Sadowska, U.; Gondek, K.; Kopec, M.; Mierzwa-Hersztek, M.; Tabor, S. Effects of co-composted maize, sewage sludge, and biochar mixtures on hydrological and physical qualities of sandy soil. Geoderma 2018, 315, 27–35. [Google Scholar] [CrossRef]
- Rivier, P.-A.; Jamniczky, D.; Nemes, A.; Makó, A.; Barna, G.; Uzinger, N.; Rékási, M.; Farkas, C. Short-term effects of compost amendments to soil on soil structure, hydraulic properties, and water regime. J. Hydrol. Hydromech. 2022, 70, 74–88. [Google Scholar] [CrossRef]
- Dexter, A.R. Soil physical quality Part I. Theory, effects of soil texture, density, and organic matter, and effects on root growth. Geoderma 2004, 120, 201–214. [Google Scholar] [CrossRef]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, W.D.; Drury, C.F.; Tan, C.S.; Fox, C.A.; Yang, X.M. Use of indicators and pore volume-function characteristics to quantify soil physical quality. Geoderma 2009, 152, 252–263. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Drury, C.F.; Tan, C.S.; Yang, X.M. Temporal effects of food waste compost on soil physical quality and productivity. Can. J. Soil Sci. 2015, 95, 251–268. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, W.D.; Bowman, B.T.; Drury, C.F.; Tan, C.S.; Lu, X. Indicators of good soil physical quality: Density and storage parameters. Geoderma 2002, 110, 131–146. [Google Scholar] [CrossRef]
- Topp, G.C.; Reynolds, W.D.; Cook, F.J.; Kirby, J.M.; Carter, M.R. Physical attributes of soil quality. In Development in Soil Science; Soil Quality for Crop Production and Ecosystem Health; Gregorich, E.G., Carter, M.R., Eds.; Elsevier: New York, NY, USA, 1997; Volume 25, pp. 21–58. [Google Scholar]
- Manici, L.M.; Castellini, M.; Caputo, F. Soil-inhabiting fungi can integrate soil physical indicators in multivariate analysis of Mediterranean agroecosystem dominated by old olive groves. Ecol. Indic. 2019, 106, 105490. [Google Scholar] [CrossRef]
- Stellacci, A.M.; Castellini, M.; Diacono, M.; Rossi, R.; Gattullo, C.E. Assessment of soil quality under different soil management strategies: Combined use of statistical approaches to select the most informative soil physico-chemical indicators. Appl. Sci. 2021, 11, 5099. [Google Scholar] [CrossRef]
- Agnese, C.; Bagarello, V.; Baiamonte, G.; Iovino, M. Comparing physical quality of forest and pasture soils in a Sicilian watershed. Soil Sci. Soc. Am. J. 2011, 75, 1958–1970. [Google Scholar] [CrossRef]
- Iovino, M.; Castellini, M.; Bagarello, V.; Giordano, G. Using static and dynamic indicators to evaluate soil physical quality in a Sicilian area. Land Degrad. Dev. 2016, 27, 200–210. [Google Scholar] [CrossRef]
- Cullotta, S.; Bagarello, V.; Baiamonte, G.; Gugliuzza, G.; Iovino, M.; La Mela Veca, D.S.; Maetzke, F.; Palmeri, V.; Sferlazza, S. Comparing Different Methods to Determine Soil Physical Quality in a Mediterranean Forest and Pasture Land. Soil Sci. Soc. Am. J. 2016, 80, 1038–1056. [Google Scholar] [CrossRef]
- Shahab, H.; Emami, H.; Haghnia, G.H.; Karimi, A. Pore Size Distribution as a Soil Physical Quality Index for Agricultural and Pasture Soils in Northeastern Iran. Pedosphere 2013, 23, 312–320. [Google Scholar] [CrossRef]
- Kutilek, M.; Nielsen, D.R. Soil Hydrology. In GeoEcology Textbook; Catena Verlag: Cremlingen, Germany, 1994; 370p, ISBN 3-923381-26-3. [Google Scholar]
- Zhao, Y.; Wen, T.; Shao, L.; Chen, R.; Sun, X.; Huang, L.; Chen, X. Predicting hysteresis loops of the soil water characteristic curve from initial drying. Soil Sci. Soc. Am. J. 2020, 84, 1642–1649. [Google Scholar] [CrossRef]
- Haverkamp, R.; Reggiani, P.; Ross, P.J.; Parlange, J.Y. Soil Water Hysteresis Prediction Model Based on Theory and Geometric Scaling. Environ. Mech. 2002, 129, 213–246. [Google Scholar]
- Alagna, V.; Bagarello, V.; Cecere, N.; Concialdi, P.; Iovino, M. A test of water pouring height and run intermittence effects on single-ring infiltration rates. Hydrol. Processes 2018, 32, 3793–3804. [Google Scholar] [CrossRef]
- Eden, M.; Gerke, H.H.; Houot, S. Organic waste recycling in agriculture and related effects on soil water retention and plant available water: A review. Agron. Sustain. Dev. 2017, 37, 11. [Google Scholar] [CrossRef] [Green Version]
- Gugliuzza, G.; Verduci, A.; Iovino, M. Water retention characteristics of substrates containing biochar and compost as peat and perlite replacements for ornamental plant production. Acta Hortic. 2021, 1305, 507–511. [Google Scholar] [CrossRef]
- Dane, J.H.; Hopmans, J.W. 3.3.2.2 Hanging water column. In Methods of Soil Analysis, Part 4, Physical Methods, Number 5 in the Soil Science Society of America Book Series; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America, Inc.: Madison, WI, USA, 2002; pp. 680–683. [Google Scholar]
- Dane, J.H.; Hopmans, J.W. 3.3.2.4 Pressure plate extractor. In Methods of Soil Analysis, Part 4, Physical Methods, Number 5 in the Soil Science Society of America Book Series; Dane, J.H., Topp, G.C., Eds.; Soil Science Society of America, Inc.: Madison, WI, USA, 2002; pp. 688–690. [Google Scholar]
- Reynolds, W.D.; Drury, C.F.; Yang, X.M.; Tan, C.S. Optimal soil physical quality inferred through structural regression and parameter interactions. Geoderma 2008, 146, 466–474. [Google Scholar] [CrossRef]
- Seki, K. SWRC fit—A nonlinear fitting program with a water retention curve for soils having unimodal and bimodal pore structure. Hydrol. Earth Syst. Sci. 2007, 4, 407–437. [Google Scholar]
- Castellini, M.; Iovino, M. Pedotransfer functions for estimating soil water retention curve of Sicilian soils. Arch. Agron. Soil Sci. 2019, 65, 1401–1416. [Google Scholar] [CrossRef]
- Reynolds, W.D.; Yang, X.M.; Drury, C.F.; Zhang, T.Q.; Tan, C.S. Effects of selected conditioners and tillage on the physical quality of a clay of a clay loam soil. Can. J. Soil Sci. 2003, 83, 381–393. [Google Scholar] [CrossRef]
- Dexter, A.R.; Czyz, E.A. Applications of s-theory in the study of soil physical degradation and its consequences. Land Degrad. Dev. 2007, 18, 369–381. [Google Scholar] [CrossRef]
- Warrick, A.W. Appendix 1: Spatial variability. In Environmental Soil Physics; Hillel, D., Ed.; Academic Press: San Diego, USA, 1998; pp. 655–675. [Google Scholar]
- Khaleel, R.; Reddy, R.; Overcash, M.R. Changes in Soil Physical Properties Due to Organic Waste Applications: A Review. J. Environ. Qual. 1981, 10, 133–141. [Google Scholar] [CrossRef]
- Brown, S.; Cotton, M. Changes in soil properties and carbon content following compost application: Results of on-farm sampling. Compost Sci. Util. 2011, 19, 88–97. [Google Scholar] [CrossRef]
- Carsel, R.F.; Parrish, R.S. Developing Joint Probability-Distributions of Soil-Water Retention Characteristics. Water Resour. Res. 1988, 24, 755–769. [Google Scholar] [CrossRef] [Green Version]
- Haverkamp, R.; Leij, F.J.; Fuentes, C.; Sciortino, A.; Ross, P.J. Soil water retention: I. Introduction of a shape index. Soil Sci. Soc. Am. J. 2005, 69, 1881–1890. [Google Scholar] [CrossRef]
- Al-Omran, A.; Ibrahim, A.; Alharbi, A. Effects of Biochar and Compost on Soil Physical Quality Indices. Commun. Soil Sci. Plant Anal. 2021, 52, 2482–2499. [Google Scholar] [CrossRef]
- Doerr, S.H.; Shakesby, R.A.; Walsh, R.P.D. Soil water repellency: Its causes, characteristics and hydro-geomorphological significance. Earth Sci. Rev. 2000, 51, 33–65. [Google Scholar] [CrossRef]
- Kaluarachchi, J.J.; Parker, J.C. Effects of hysteresis with air entrapment on water flow in the unsaturated zone. Water Resour. Res. 1987, 23, 1967–1976. [Google Scholar] [CrossRef]
- DeBano, L.F. Water Repellent Soils: A State-of-the-Art; General Technical Report, PSW-46; United States Department of Agriculture, Forest Service: Berkeley, CA, USA, 1981; 21p.
- Castellini, M.; Ventrella, D. Impact of conventional and minimum tillage on soil hydraulic conductivity in typical cropping system in southern Italy. Soil Tillage Res. 2012, 124, 47–56. [Google Scholar] [CrossRef]
- Bagarello, V.; Castellini, M.; Iovino, M. Influence of the pressure head sequence on the soil hydraulic conductivity determined with the tension infiltrometer. Appl. Eng. Agric. 2005, 21, 383–391. [Google Scholar] [CrossRef]
- Bagarello, V.; Castellini, M.; Iovino, M. Comparison of unconfined and confined unsaturated hydraulic conductivity. Geoderma 2007, 137, 394–400. [Google Scholar] [CrossRef]
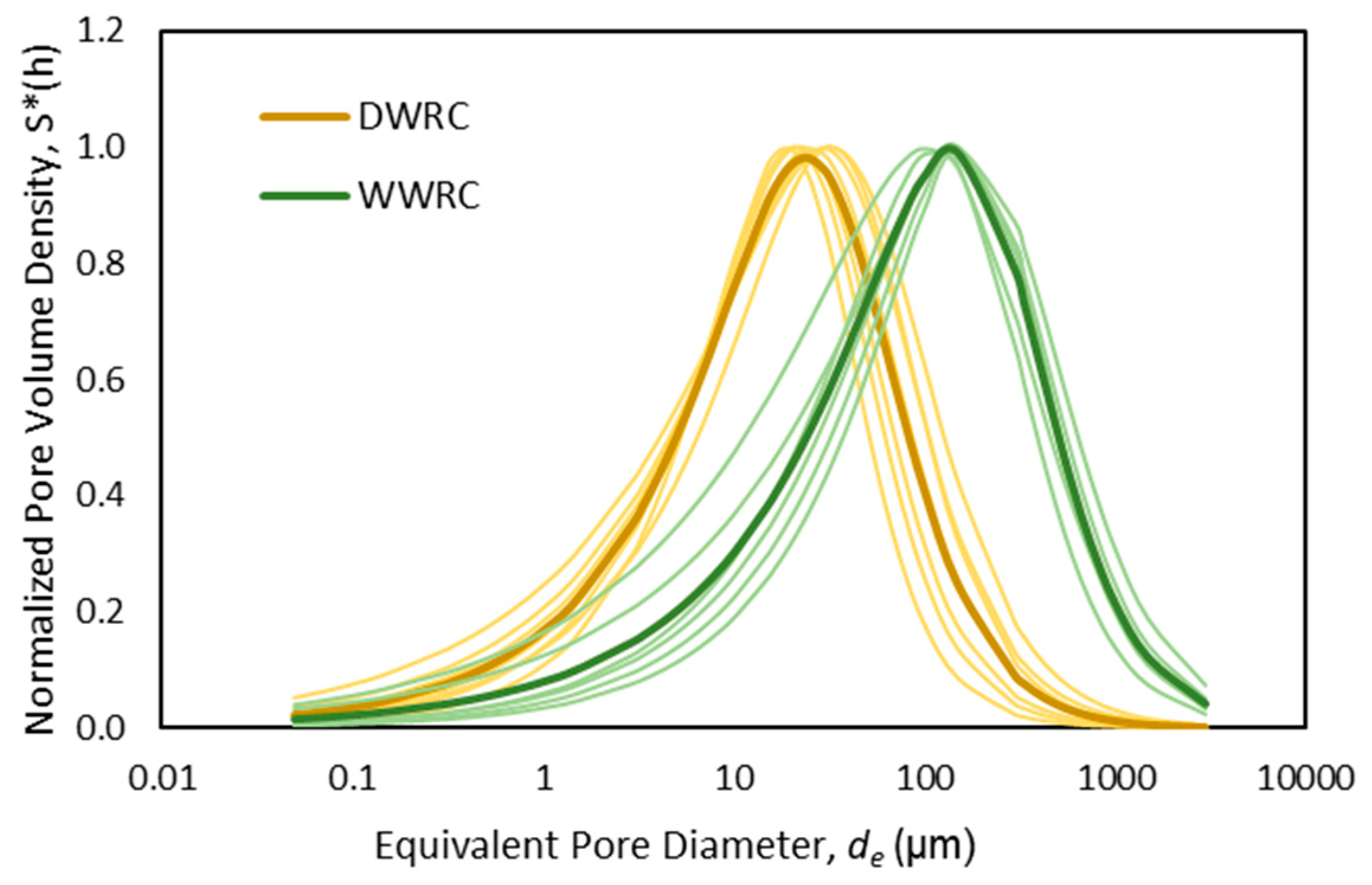
| Soil | Compost | ||
|---|---|---|---|
| Clay (%) | 17.6 | pH | 7.2 |
| Silt (%) | 29.8 | EC (dS/m) | 0.54 |
| Sand (%) | 52.6 | C (%) | 9.91 |
| OM (%) | 2.1 | N (%) | 0.64 |
| pH | 7.8 | P (%) | 0.45 |
| EC (dS/m) | 0.48 | Ash (%) | 82.5 |
| CEC (cmol Kg−1) | 25.31 | C/N ratio | 15:1 |
| α | n | θs | θr | R | ME | RMSE | |
|---|---|---|---|---|---|---|---|
| Wetting water retention curve WWRC | |||||||
| Min | 0.0613 | 1.406 | 0.457 | 0.110 | 0.9954 | −6.54 × 10−4 | 6.00 × 10−3 |
| Max | 0.1203 | 1.894 | 0.536 | 0.161 | 0.9976 | 3.83 × 10−4 | 9.00 × 10−3 |
| Mean | 0.0871 | 1.639 | 0.500 | 0.138 | 0.9962 | −3.14 × 10-6 | 7.57 × 10−3 |
| Draining water retention curve DWRC | |||||||
| Min | 0.0088 | 1.458 | 0.443 | 0.110 | 0.9931 | −4.70 × 10−5 | 5.90 × 10−3 |
| Max | 0.0231 | 1.998 | 0.508 | 0.161 | 0.9985 | 1.13 × 10−4 | 1.58 × 10−2 |
| Mean | 0.0149 | 1.726 | 0.479 | 0.138 | 0.9959 | 2.62 × 10−5 | 1.11 × 10−2 |
| SPQ | Units | Wetting Water Retention Curve | Draning Water Retention Curve | Optimal Range | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | R | Min | Max | Mean | R | |||
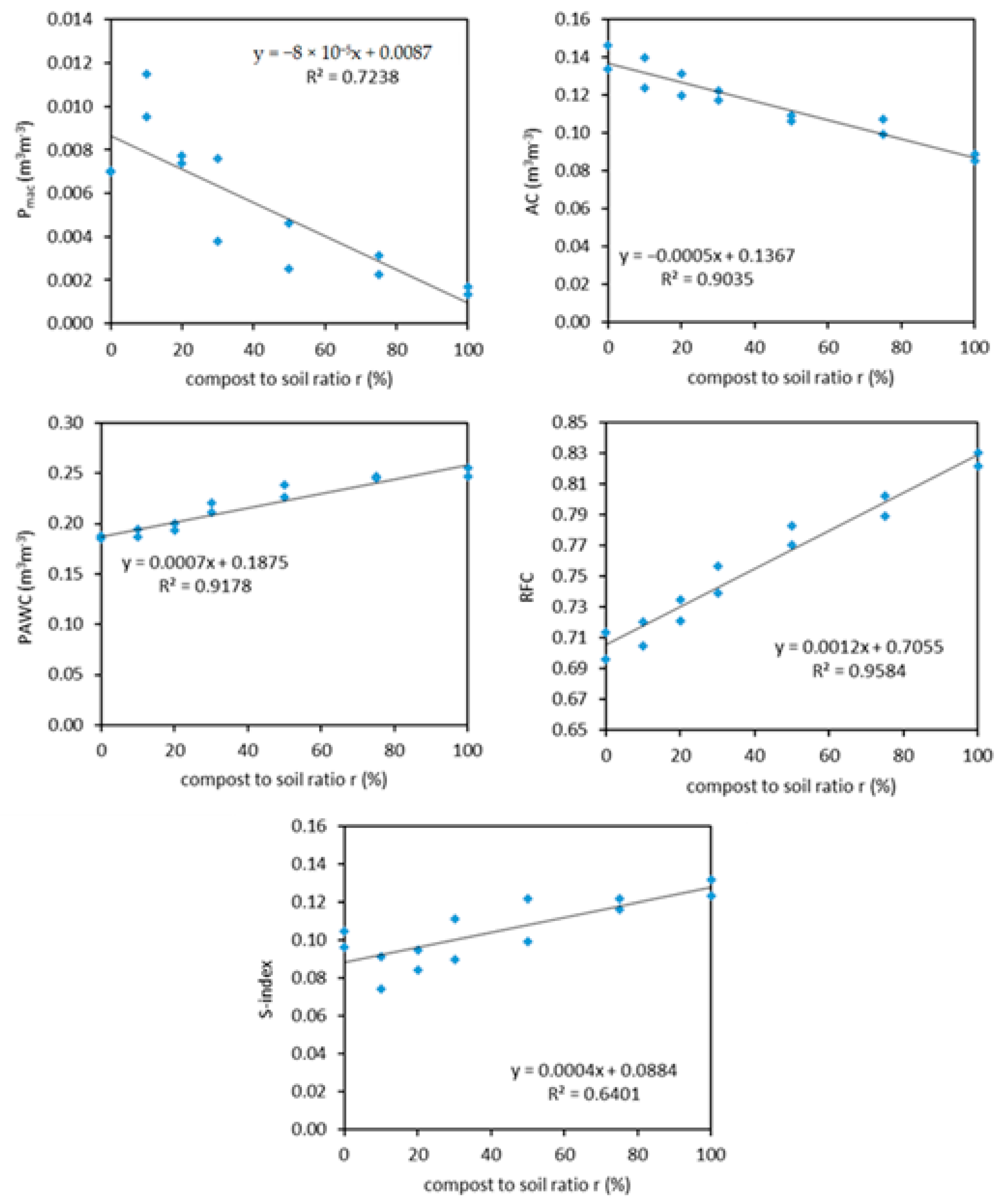
| Pmac | m3m−3 | 0.047 | 0.087 | 0.072 | 0.1439 | 0.001 | 0.012 | 0.006 | −0.8508 | ≥0.07 |
| AC | m3m−3 | 0.224 | 0.306 | 0.267 | −0.2528 | 0.085 | 0.146 | 0.116 | −0.9505 | ≥0.14 |
| PAWC | m3m−3 | 0.051 | 0.272 | 0.102 | 0.6419 | 0.185 | 0.255 | 0.216 | 0.9580 | ≥0.20 |
| RFC | - | 0.354 | 0.571 | 0.464 | 0.5322 | 0.696 | 0.831 | 0.756 | 0.9790 | 0.60–0.70 |
| S-index | - | 0.077 | 0.125 | 0.101 | −0.4651 | 0.074 | 0.132 | 0.104 | 0.8001 | ≥0.05 |
| dmedian | μm | 51.4 | 130.9 | 94.7 | −0.3660 | 15.1 | 24.1 | 17.8 | −0.7754 | 3–7 |
| dmode | μm | 102.3 | 168.4 | 142.8 | −0.1191 | 18.5 | 33.1 | 25.7 | −0.9523 | 60–140 |
| dmean | μm | 36.8 | 116.9 | 78.3 | −0.4141 | 12.1 | 20.7 | 15.0 | −0.5329 | 0.7–2 |
| SD | - | 3.7 | 11.7 | 6.1 | 0.5079 | 3.3 | 9.2 | 5.1 | −0.6303 | 400–1000 |
| SK | - | −0.29 | −0.17 | −0.22 | −0.5725 | −0.27 | −0.16 | −0.21 | 0.7285 | −0.43 to −0.41 |
| KU | - | 1.14 | 1.16 | 1.15 | 0.5919 | 1.14 | 1.16 | 1.15 | −0.7699 | 1.13–1.14 |
| α | n | θs | θr | |
|---|---|---|---|---|
| WWRC | 0.3376 | −0.5773 | 0.8188 | n.d. |
| DWRC | −0.8909 | 0.7785 | 0.7905 | 0.7367 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bondì, C.; Castellini, M.; Iovino, M. Compost Amendment Impact on Soil Physical Quality Estimated from Hysteretic Water Retention Curve. Water 2022, 14, 1002. https://doi.org/10.3390/w14071002
Bondì C, Castellini M, Iovino M. Compost Amendment Impact on Soil Physical Quality Estimated from Hysteretic Water Retention Curve. Water. 2022; 14(7):1002. https://doi.org/10.3390/w14071002
Chicago/Turabian StyleBondì, Cristina, Mirko Castellini, and Massimo Iovino. 2022. "Compost Amendment Impact on Soil Physical Quality Estimated from Hysteretic Water Retention Curve" Water 14, no. 7: 1002. https://doi.org/10.3390/w14071002
APA StyleBondì, C., Castellini, M., & Iovino, M. (2022). Compost Amendment Impact on Soil Physical Quality Estimated from Hysteretic Water Retention Curve. Water, 14(7), 1002. https://doi.org/10.3390/w14071002








