Modeling Cyanobacteria Vertical Migration
Abstract
:1. Introduction
1.1. Background
1.2. Models of Vertical Migration
| Equations | Parameters and Definitions | ||
|---|---|---|---|
| Kromkamp and Walsby [8] | |||
| (1) | , density of cyanobacteria colony , time , irradiance at depth of colony , previous irradiance , half-saturation irradiance settling velocity | , acceleration due to gravity cyanobacteria colony radius , density of water viscosity of water ratio of cell volume to colony volume form resistance depth at current timestep depth at previous timestep time interval | |
| (2) | |||
| (3) | |||
| SCUM96 [21] | |||
| (4) | cyanobacteria photosynthetic rate respiration rate , maximum rate of carbon used for growth growth ballast density of a cell mucilage density , ratio of cell volume to colony volume | , number of cells in a colony cell carbon content cell volume as defined above | |
| (5) | |||
| (6) | |||
| (7) | |||
| (8) | |||
| Visser et al. [13] | |||
| (9) | irradiance at depth of colony compensation irradiance | cell density at end of preceding light period | |
| (10) | , light intensity at maximum density rate of density change when | as defined above | |
| Wallace and Hamilton [14] | |||
| (11) | half-saturation irradiance | , response time | |
| (12) | , as defined above | ||
| Belov and Giles [4] | |||
| (13) | depth of colony , maximum colony velocity , light attenuation coefficien | depth of waterbody , frequency of daily light cycle , as defined above | |
| Serizawa et al. [39] | |||
| (14) | ballast factor , velocity scale factor , neutral buoyancy ballast factor growth rate | , reciprocol of decay time time before present , as defined above | |
| (15) | |||
| CAEDYM [43] | |||
| (16) | a a | as defined above | |
| (17) | a, half saturation constant for light-dependent density change | ||
2. Modeling Framework and Available Field Data
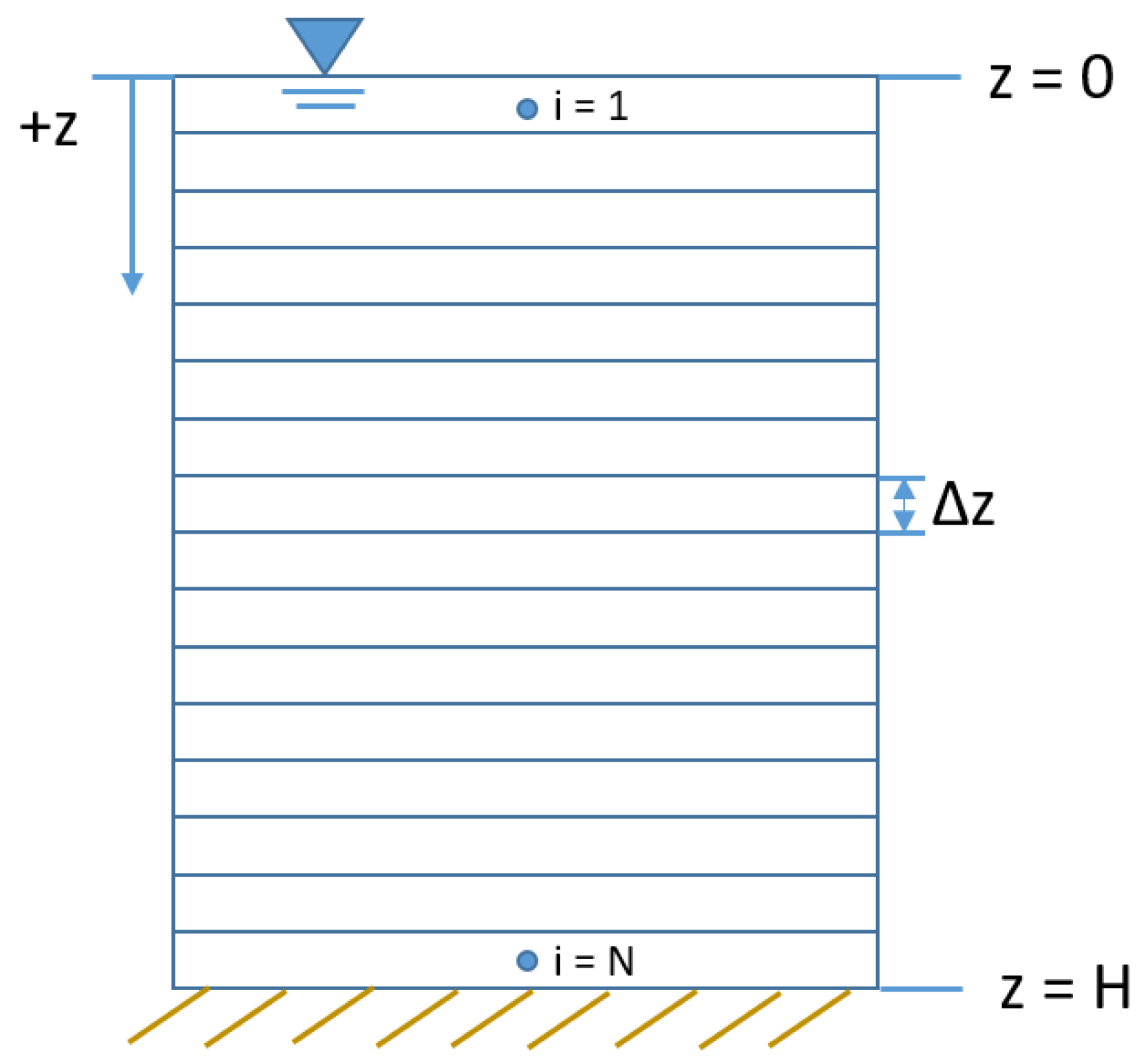
2.1. Continuum and Particle Transport Models
2.1.1. Predefined Velocity
2.1.2. Dynamic Velocity
2.2. Field Data
2.3. Model Setup
3. Modeling Results
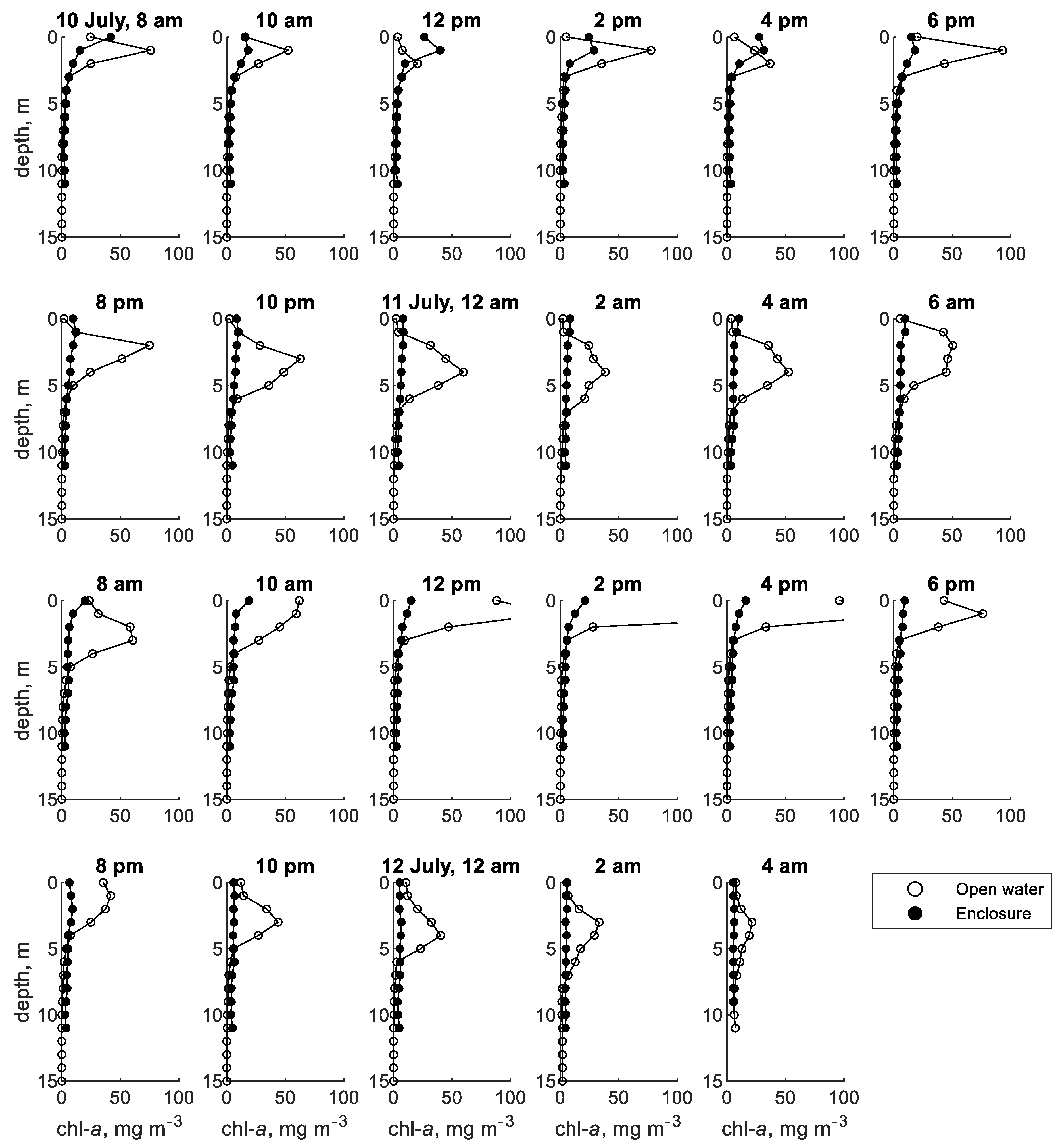
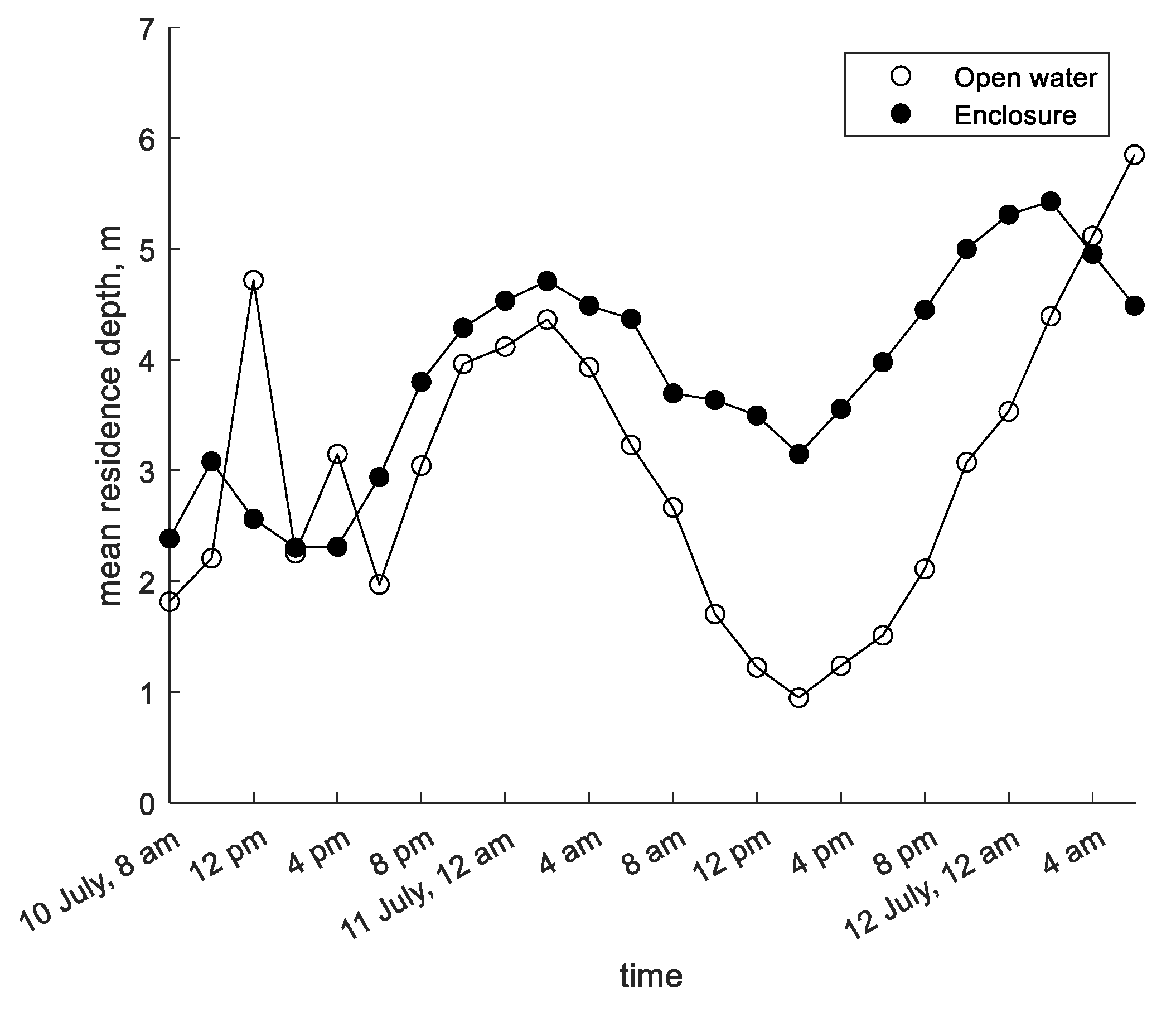
3.1. Shennong Stream Enclosure
3.2. Shennong Stream Open Water
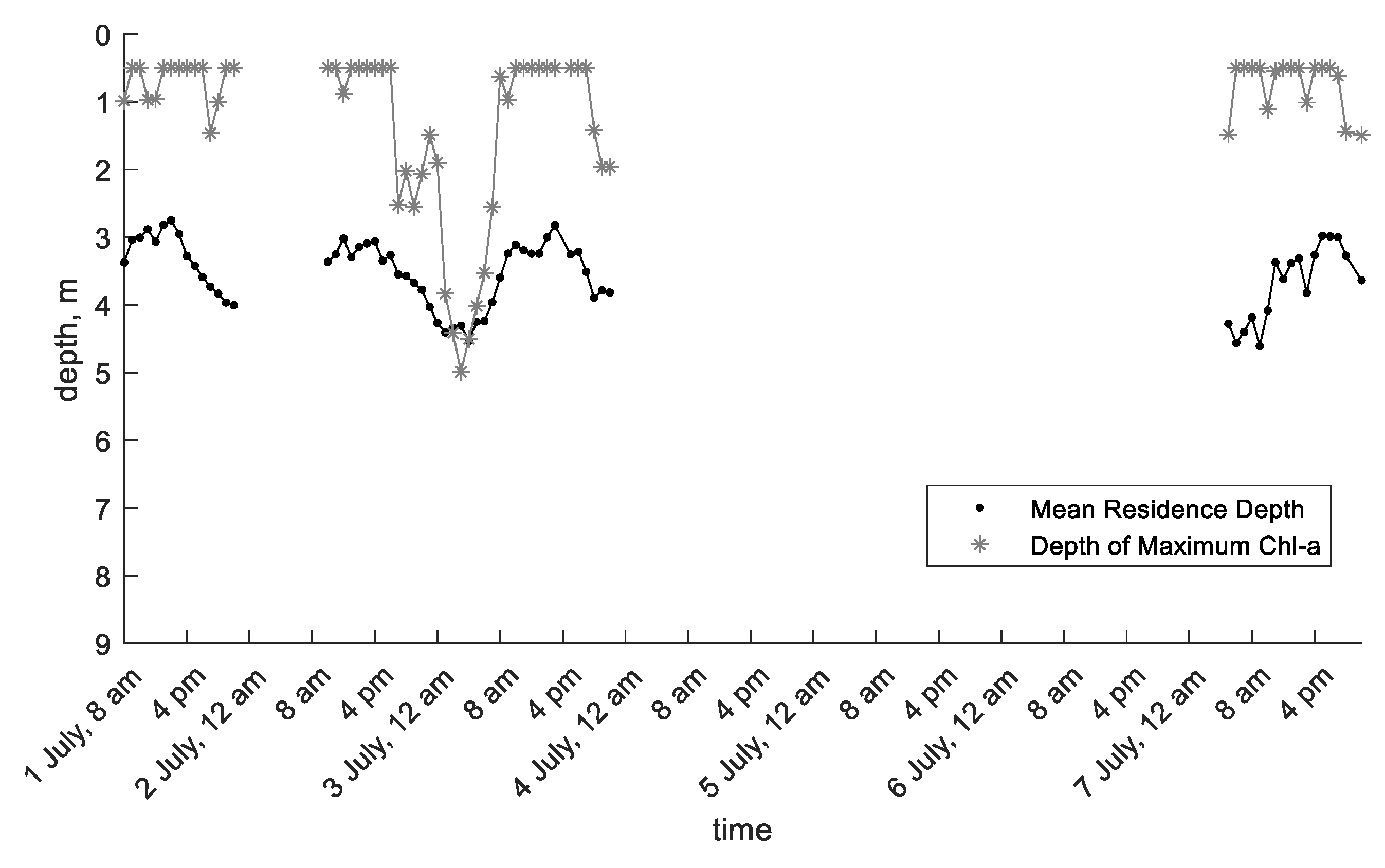
3.3. Xiangxi Bay
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Howard, A. Problem Cyanobacterial Blooms: Explanation and Simulation Modelling. Trans. Inst. Br. Geogr. 1994, 19, 213–224. [Google Scholar] [CrossRef]
- Lopez, C.B.; Jewett, E.B.; Dortch, Q.; Walton, B.T.; Hudnell, H.K. Scientific Assessment of Freshwater Harmful Algal Blooms; Interagency Working Group on Harmful Algal Blooms, Hypoxia, and Human Health of the Joint Subcommittee on Ocean Science and Technology: Washington, DC, USA, 2008.
- Visser, P.M.; Ibelings, B.W.; Bormans, M.; Huisman, J. Artificial mixing to control cyanobacterial blooms: A review. Aquat. Ecol. 2016, 50, 423–441. [Google Scholar] [CrossRef] [Green Version]
- Belov, A.P.; Giles, J.D. Dynamical model of buoyant cyanobacteria. Hydrobiologia 1997, 349, 87–97. [Google Scholar] [CrossRef]
- Brookes, J.D.; Ganf, G.G. Variations in the buoyancy response of Microcystis aeruginosa to nitrogen, phosphorus and light. J. Plankton Res. 2001, 23, 1399–1411. [Google Scholar] [CrossRef]
- Ganf, G.G.; Oliver, R.L. Vertical separation of light and available nutrients as a factor causing replacement of green algae by bluegreen algae in the plankton of a stratified lake. J. Ecol. 1982, 70, 829–844. [Google Scholar] [CrossRef]
- Bormans, M.; Sherman, B.S.; Webster, I.T. Is buoyancy regulation in cyanobacteria an adaptation to exploit separation of light and nutrients? Mar. Freshw. Res. 1999, 50, 897–906. [Google Scholar] [CrossRef]
- Kromkamp, J.; Walsby, A.E. A computer model of buoyancy and vertical migration in cyanobacteria. J. Plankton Res. 1990, 12, 161–183. [Google Scholar] [CrossRef]
- Kromkamp, J.C.; Mur, L.R. Buoyant density changes in the cyanobacterium Microcystis aeruginosa due to changes in the cellular carbohydrate content. FEMS Microbiol. Lett. 1984, 25, 105–109. [Google Scholar] [CrossRef]
- Kromkamp, J.; Konopka, A.; Mur, L.R. Buoyancy regulation in light-limited continuous cultures of Microcystis aeruginosa. J. Plankton Res. 1988, 10, 171–183. [Google Scholar] [CrossRef]
- Ibelings, B.W.; Mur, L.R.; Walsby, A.E. Diurnal changes in buoyancy and vertical distribution in populations of Microcystis in two shallow lakes. J. Plankton Res. 1991, 13, 419–436. [Google Scholar] [CrossRef]
- Cui, Y.J.; Liu, D.F.; Zhang, J.; Yang, Z.J.; Khu, S.T.; Ji, D.B.; Song, L.X.; Long, L.H. Diel migration of Microcystis during an algal bloom event in the Three Gorges Reservoir, China. Environ. Earth Sci. 2016, 75, 616. [Google Scholar] [CrossRef]
- Visser, P.M.; Passarge, J.; Mur, L.R. Modelling vertical migration of the cyanobacterium Microcystis. Hydrobiologia 1997, 349, 99–109. [Google Scholar] [CrossRef]
- Wallace, B.B.; Hamilton, D.P. The effect of variations in irradiance on buoyancy regulation in Microcystis aeruginosa. Limnol. Oceanogr. 1999, 44, 273–281. [Google Scholar] [CrossRef] [Green Version]
- Cao, H.S.; Kong, F.X.; Luo, L.C.; Shi, X.L.; Yang, Z.; Zhang, X.F.; Tao, Y. Effects of wind and wind-induced waves on vertical phytoplankton distribution and surface blooms of Microcystis aeruginosa in Lake Taihu. J. Freshw. Ecol. 2006, 21, 231–238. [Google Scholar] [CrossRef]
- Zhao, H.; Zhu, W.; Chen, H.; Zhou, X.; Wang, R.; Li, M. Numerical simulation of the vertical migration of Microcystis (cyanobacteria) colonies based on turbulence drag. J. Limnol. 2017, 76, 190–198. [Google Scholar] [CrossRef] [Green Version]
- Zhu, W.; Feng, G.; Chen, H.; Wang, R.; Tan, Y.; Zhao, H. Modelling the vertical migration of different-sized Microcystis colonies: Coupling turbulent mixing and buoyancy regulation. Environ. Sci. Pollut. Res. 2018, 25, 30339–30347. [Google Scholar] [CrossRef] [PubMed]
- Hudnell, H.K. The state of U.S. freshwater harmful algal blooms assessments, policy and legislation. Toxicon 2010, 55, 1024–1034. [Google Scholar] [CrossRef] [PubMed]
- Okada, M.; Aiba, S. Simulation of water-bloom in a eutrophic lake: III. Modeling the vertical migration and growth of Microcystis aeruginosa. Water Res. 1983, 17, 883–893. [Google Scholar] [CrossRef]
- Okada, M.; Aiba, S. Simulation of water-bloom in a eutrophic lake—II. Reassessment of buoyancy, gas vacuole and Turgor pressure of Microcystis aeruginosa. Water Res. 1983, 17, 877–882. [Google Scholar] [CrossRef]
- Howard, A.; Irish, A.E.; Reynolds, C.S. A new simulation of cyanobacterial underwater movement (SCUM’96). J. Plankton Res. 1996, 18, 1375–1385. [Google Scholar] [CrossRef] [Green Version]
- Easthope, M.P.; Howard, A. Simulating cyanobacterial growth in a lowland reservoir. Sci. Total Environ. 1999, 241, 17–25. [Google Scholar] [CrossRef]
- Walsby, A.E. Stratification by cyanobacteria in lakes: A dynamic buoyancy model indicates size limitations met by Planktothrix rubescens filaments. New Phytol. 2005, 168, 365–376. [Google Scholar] [CrossRef]
- Chien, Y.C.; Wu, S.C.; Chen, W.C.; Chou, C.C. Model simulation of diurnal vertical migration patterns of different-sized colonies of Microcystis employing a particle trajectory approach. Environ. Eng. Sci. 2013, 30, 179–186. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yao, B.; Liu, Q.; Gao, Y.; Cao, Z. Characterizing vertical migration of Microcystis aeruginosa and conditions for algal bloom development based on a light-driven migration model. Ecol. Res. 2017, 32, 961–969. [Google Scholar] [CrossRef] [Green Version]
- Olsen, N.R.B.; Hedger, R.D.; George, D.G. 3D Numerical modeling of Microcystis distribution in a water reservoir. J. Environ. Eng. 2000, 126, 949–953. [Google Scholar] [CrossRef]
- Wallace, B.B.; Hamilton, D.P. Simulation of water-bloom formation in the cyanobacterium Microcystis aeruginosa. J. Plankton Res. 2000, 22, 1127–1138. [Google Scholar] [CrossRef] [Green Version]
- Wallace, B.B.; Bailey, M.C.; Hamilton, D.P. Simulation of vertical position of buoyancy regulating Microcystis aeruginosa in a shallow eutrophic lake. Aquat. Sci. 2000, 62, 320–333. [Google Scholar] [CrossRef]
- Bonnet, M.P.; Poulin, M. Numerical modelling of the planktonic succession in a nutrient-rich reservoir: Environmental and physiological factors leading to Microcystis aeruginosa dominance. Ecol. Model. 2002, 156, 93–112. [Google Scholar] [CrossRef]
- Rabouille, S.; Thébault, J.M.; Salençon, M.J. Simulation of carbon reserve dynamics in Microcystis and its influence on vertical migration with Yoyo model. Comptes Rendus Biol. 2003, 326, 349–361. [Google Scholar] [CrossRef]
- Hedger, R.D.; Olsen, N.R.B.; George, D.G.; Malthus, T.J.; Atkinson, P.M. Modelling spatial distributions of Ceratium hirundnella and Microcystis spp. in a small productive British lake. Hydrobiologia 2004, 528, 217–227. [Google Scholar] [CrossRef]
- Rabouille, S.; Salençon, M. Functional analysis of Microcystis vertical migration: A dynamic model as a prospecting tool. II. Influence of mixing, thermal stratification and colony diameter on biomass production. Aquat. Microb. Ecol. 2005, 39, 281–292. [Google Scholar] [CrossRef]
- Rabouille, S.; Salençon, M.J.; Thébault, J.M. Functional analysis of Microcystis vertical migration: A dynamic model as a prospecting tool. Ecol. Model. 2005, 188, 386–403. [Google Scholar] [CrossRef]
- Guven, B.; Howard, A. Modelling the growth and movement of cyanobacteria in river systems. Sci. Total Environ. 2006, 368, 898–908. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Qian, X.; Zhang, Y. Modelling turbulent dispersion of buoyancy regulating cyanobacteria in wind-driven currents. In Proceedings of the 2009 3rd International Conference on Bioinformatics and Biomedical Engineering, Beijing, China, 11–13 June 2009; pp. 1–4. [Google Scholar]
- Aparicio Medrano, E.; Uittenbogaard, R.E.; Dionisio Pires, L.M.; van de Wiel, B.J.H.; Clercx, H.J.H. Coupling hydrodynamics and buoyancy regulation in Microcystis aeruginosa for its vertical distribution in lakes. Ecol. Model. 2013, 248, 41–56. [Google Scholar] [CrossRef]
- Ndong, M.; Bird, D.; Nguyen Quang, T.; Kahawita, R.; Hamilton, D.; de Boutray, M.L.; Prévost, M.; Dorner, S. A novel Eulerian approach for modelling cyanobacteria movement: Thin layer formation and recurrent risk to drinking water intakes. Water Res. 2017, 127, 191–203. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.; Feng, T.; Wang, P.; Hou, J.; Qian, J. Understanding the transport feature of bloom-forming Microcystis in a large shallow lake: A new combined hydrodynamic and spatially explicit agent-based modelling approach. Ecol. Model. 2017, 343, 25–38. [Google Scholar] [CrossRef]
- Serizawa, H.; Amemiya, T.; Rossberg, A.G.; Itoh, K. Computer simulations of seasonal outbreak and diurnal vertical migration of cyanobacteria. Limnology 2008, 9, 185–194. [Google Scholar] [CrossRef]
- Trolle, D.; Hamilton, D.P.; Hipsey, M.R.; Bolding, K.; Bruggeman, J.; Mooij, W.M.; Janse, J.H.; Nielsen, A.; Jeppesen, E.; Elliott, J.A.; et al. A community-based framework for aquatic ecosystem models. Hydrobiologia 2012, 683, 25–34. [Google Scholar] [CrossRef]
- Mooij, W.M.; Trolle, D.; Jeppesen, E.; Arhonditsis, G.; Belolipetsky, P.V.; Chitamwebwa, D.B.R.; Degermendzhy, A.G.; DeAngelis, D.L.; De Senerpont Domis, L.N.; Downing, A.S.; et al. Challenges and opportunities for integrating lake ecosystem modelling approaches. Aquat. Ecol. 2010, 44, 633–667. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, C.S.; Irish, A.E.; Elliott, J.A. The ecological basis for simulating phytoplankton responses to environmental change (PROTECH). Ecol. Model. 2001, 140, 271–291. [Google Scholar] [CrossRef]
- Hipsey, M.R.; Antenucci, J.P.; Romero, J.R.; Hamilton, D. Computational Aquatic Ecosystem Dynamics Model: CAEDYM v3; Centre for Water Research, University of Western Australia: Perth, Australia, 2007. [Google Scholar]
- Chung, S.W.; Imberger, J.; Hipsey, M.R.; Lee, H.S. The influence of physical and physiological processes on the spatial heterogeneity of a Microcystis bloom in a stratified reservoir. Ecol. Model. 2014, 289, 133–149. [Google Scholar] [CrossRef]
- Mascarenhas, F.C.B.; Trento, A.E. Particle-tracking method applied to transport problems in water bodies. WIT Trans. Ecol. Environ. 2006, 99, 503–513. [Google Scholar] [CrossRef]
- Chapra, S.C. Surface Water-Quality Modeling; Waveland Press: Long Grove, IL, USA, 2008. [Google Scholar]
- Tennessee Valley Authority. Heat and Mass Transfer between a Water Surface and the Atmosphere; Water Resources Report 0-6803; Lab Report #14; Division of Water Control Planning, Engineering Laboratory: Norris, TN, USA, 1972.
- Jacovides, C.P.; Timvios, F.S.; Papaioannou, G.; Asimakopoulos, D.N.; Theofilou, C.M. Ratio of PAR to broadband solar radiation measured in Cyprus. Agric. For. Meteorol. 2004, 121, 135–140. [Google Scholar] [CrossRef]
- Wang, L.; Cai, Q.; Zhang, M.; Xu, Y.; Kong, L.; Tan, L. Vertical distribution patterns of phytoplankton in summer Microcystis bloom period of Xiangxi Bay, Three Gorges Reservoir, China. Fresenius Environ. Bull. 2011, 20, 553–560. [Google Scholar]
- Reynolds, C.S. The Ecology of Freshwater Phytoplankton; Cambridge University Press: Cambridge, UK, 1984. [Google Scholar]
- Reynolds, C.S.; Oliver, R.L.; Walsby, A.E. Cyanobacterial dominance: The role of buoyancy regulation in dynamic lake environments. N. Z. J. Mar. Freshw. Res. 1987, 21, 379–390. [Google Scholar] [CrossRef]
- Nakamura, T.; Adachi, Y.; Suzuki, M. Flotation and sedimentation of a single Microcystis floc collected from surface bloom. Water Res. 1993, 27, 979–983. [Google Scholar] [CrossRef]
- Long, B.M.; Jones, G.J.; Orr, P.T. Cellular microcystin content in N-limited Microcystis aeruginosa can be predicted from growth rate. Appl. Environ. Microbiol. 2001, 67, 278–283. [Google Scholar] [CrossRef] [Green Version]
- Wu, Z.; Song, L. Physiological comparison between colonial and unicellular forms of Microcystis aeruginosa Kütz (cyanobacteria). Phycologia 2008, 47, 98–104. [Google Scholar] [CrossRef]
- Wu, Z.; Shi, J.; Li, R. Comparative studies on photosynthesis and phosphate metabolism of Cylindrospermopsis raciborskii with Microcystis aeruginosa and Aphanizomenon flos-aquae. Harmful Algae 2009, 8, 910–915. [Google Scholar] [CrossRef]
- Zhang, M.; Shi, X.; Yu, Y.; Kong, F. The acclimative changes in photochemistry after colony formation of the cyanobacteria Microcystis aeruginosa 1: Photoadaptive changes of M. Aeruginosa. J. Phycol. 2011, 47, 524–532. [Google Scholar] [CrossRef]
- Zhu, W.; Li, M.; Luo, Y.; Dai, X.; Guo, L.; Xiao, M.; Huang, J.; Tan, X. Vertical distribution of Microcystis colony size in Lake Taihu: Its role in algal blooms. J. Great Lakes Res. 2014, 40, 949–955. [Google Scholar] [CrossRef] [Green Version]
- Rowe, M.D.; Anderson, E.J.; Wynne, T.T.; Stumpf, R.P.; Fanslow, D.L.; Kijanka, K.; Vanderploeg, H.A.; Strickler, J.R.; Davis, T.W. Vertical distribution of buoyant Microcystis blooms in a Lagrangian particle tracking model for short-term forecasts in Lake Erie. J. Geophys. Res. Oceans 2016, 121, 5296–5314. [Google Scholar] [CrossRef]
- Reynolds, C.S. The Ecology of Phytoplankton; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]


| Study | Identifier | Minimum Density, | Maximum Density, | Colony Radius, | Saturating Light Intensity, | Maximum Growth Rate, |
|---|---|---|---|---|---|---|
| Reynolds [50] | - | - | - | 25–1000 | - | - |
| Reynolds et al. [51] | cyanobacteria | - | - | - | - | 0.6–0.8 |
| M. aeruginosa | 985 | 1005 | 120–3200 | - | - | |
| A. flos-aqua | 920 | 1030 | 28–100 | - | - | |
| P. agardhii | 985 | 1085 | 13.7–18.3 | - | - | |
| Nakamura et al. [52] | Microcystis sp. | - | - | 10–300 | - | - |
| Visser et al. [13] | Microcystis sp. | - | - | - | 139 | - |
| Long et al. [53] | M. aeruginosa | - | - | - | - | 1.2 |
| Wu and Song [54] | M. aeruginosa | - | - | - | 119–244 | - |
| Wu et al. [55] | M. aeruginosa | - | - | - | 65–119 | - |
| Zhang et al. [56] | M. aeruginosa | - | - | - | 75–392 | - |
| Zhu et al. [17,57] | Microcystis sp. | 967 | 997 | 10–350 | - | - |
| Rowe et al. [58] | Microcystis sp. | - | - | 12.5–370, median: 58.5 | - | - |
| Variable | Description | Value Range |
|---|---|---|
| A, m | Migration amplitude | 0.2–1.23 |
| , rad | Phase offset | |
| Light attenuation calibration coefficient | 0.05–0.13 | |
| Maximum growth rate | 0.7–1.0 | |
| Mortality rate | 0.06–0.25 | |
| Excretion rate | 0.04 | |
| Respiration rate | 0.04 | |
| Saturating light intensity | 100–150 | |
| Coefficient of density increase for light function model | 0.00545–0.02 | |
| Coefficient of density decrease for light function model | 0.00145–0.00518 | |
| Colony radius | 15–64 | |
| Minimum colony density | 920–980 | |
| Maximum colony density | 140–185 | |
| Initial colony density at surface | 930–1080 (continuum) 920–980 (particles) | |
| Initial colony density at bed | 930–980 (continuum) 995–1010 (particles) | |
| Minimum initial colony density at surface for Visser et al. [13] model | 980–1080 | |
| Minimum initial colony density at bed for Visser et al. [13] model | 975–980 | |
| Correction for density decrease equation for Visser et al. [13] model | 67 | |
| Time decay constant for averaging past densities | 5 |
| Mean Residence Depth AME, m | Chlorophyll a Concentration (Profile Average) AME, mg m3 | |||
|---|---|---|---|---|
| Model | Continuum | Particle Tracking | Continuum | Particle Tracking |
| Time-varying velocity | 1.074 | 1.127 | 2.871 | 3.176 |
| Belov and Giles [4] | 0.799 | 0.795 | 2.549 | 2.796 |
| Growth kinetics | 1.348 | 0.613 | 3.446 | 3.925 |
| Growth kinetics with time decay | 1.318 | - | 3.271 | - |
| Visser et al. [13] | 1.338 | 0.772 | 3.378 | 3.205 |
| Light function | 1.359 | 0.599 | 3.522 | 3.273 |
| Light function with time decay | 1.252 | - | 3.201 | - |
| Mean Residence Depth AME, m | Chlorophyll a Concentration (Profile Average) AME, mg m3 | |||
|---|---|---|---|---|
| Model | Continuum | Particle Tracking | Continuum | Particle Tracking |
| Time-varying velocity | 1.129 | 1.097 | 8.589 | 8.654 |
| Belov and Giles [4] | 1.113 | 1.100 | 8.645 | 8.716 |
| Growth kinetics | 1.096 | 0.986 | 7.735 | 8.498 |
| Growth kinetics with time decay | 1.064 | - | 7.193 | - |
| Visser et al. [13] | 1.093 | 0.993 | 7.589 | 8.670 |
| Light function | 1.087 | 0.964 | 7.425 | 8.654 |
| Light function with time decay | 1.087 | - | 7.253 | - |
| Mean Residence Depth AME, m | Depth of Maximum Chlorophyll a Concentration AME, m | |||||||
|---|---|---|---|---|---|---|---|---|
| Dz = 10−5 m2 s−1 | Dz = 10−4 m2 s−1 | Dz = 10−5 m2 s−1 | Dz = 10−4 m2 s−1 | |||||
| Model | Continuum | Particle Tracking | Continuum | Particle Tracking | Continuum | Particle Tracking | Continuum | Particle Tracking |
| Time-varying velocity | 0.351 | 0.509 | 0.422 | 0.415 | 0.557 | 0.609 | 0.696 | 0.846 |
| Belov and Giles [4] | 0.380 | 0.585 | 0.409 | 0.413 | 0.561 | 0.554 | 0.680 | 0.844 |
| Growth kinetics | 1.201 | 0.595 | 0.672 | 0.461 | 0.641 | 1.598 | 0.744 | 1.373 |
| Growth kinetics with time decay | 1.299 | - | 0.395 | - | 0.730 | - | 0.667 | - |
| Visser et al. [13] | 1.287 | 1.001 | 0.374 | 0.392 | 0.877 | 2.800 | 0.754 | 1.598 |
| Light function | 1.410 | 0.887 | 0.629 | 0.371 | 0.693 | 1.837 | 0.802 | 1.454 |
| Light function with time decay | 1.650 | - | 0.426 | - | 0.725 | - | 0.687 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Overman, C.; Wells, S. Modeling Cyanobacteria Vertical Migration. Water 2022, 14, 953. https://doi.org/10.3390/w14060953
Overman C, Wells S. Modeling Cyanobacteria Vertical Migration. Water. 2022; 14(6):953. https://doi.org/10.3390/w14060953
Chicago/Turabian StyleOverman, Corina, and Scott Wells. 2022. "Modeling Cyanobacteria Vertical Migration" Water 14, no. 6: 953. https://doi.org/10.3390/w14060953







