Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis
Abstract
:1. Introduction
2. Methodology
- Population: time series of groundwater resources’ quantity or quality characteristics
- Intervention: regression ML algorithms
- Comparator: observation and measurement
- Outcome: predictive capabilities (through quantitative measures of performance like the coefficient of determination)
- The article should present original research on one or more case studies (i.e., aquifers) that employ a regression ML algorithm to predict a specific and measurable aquifer characteristic in different time steps.
- The article should use a time series of input data to train its algorithm.
- The article should evaluate the accuracy of the prediction by comparing the ML algorithm outputs with observation.
- The article should report its goodness of prediction with quantitative measures of performance (i.e., statistical indices).
3. Results and Discussion
3.1. Statistical Analysis
3.2. Meta-Analysis
4. Opportunities
5. Summary and Conclusions
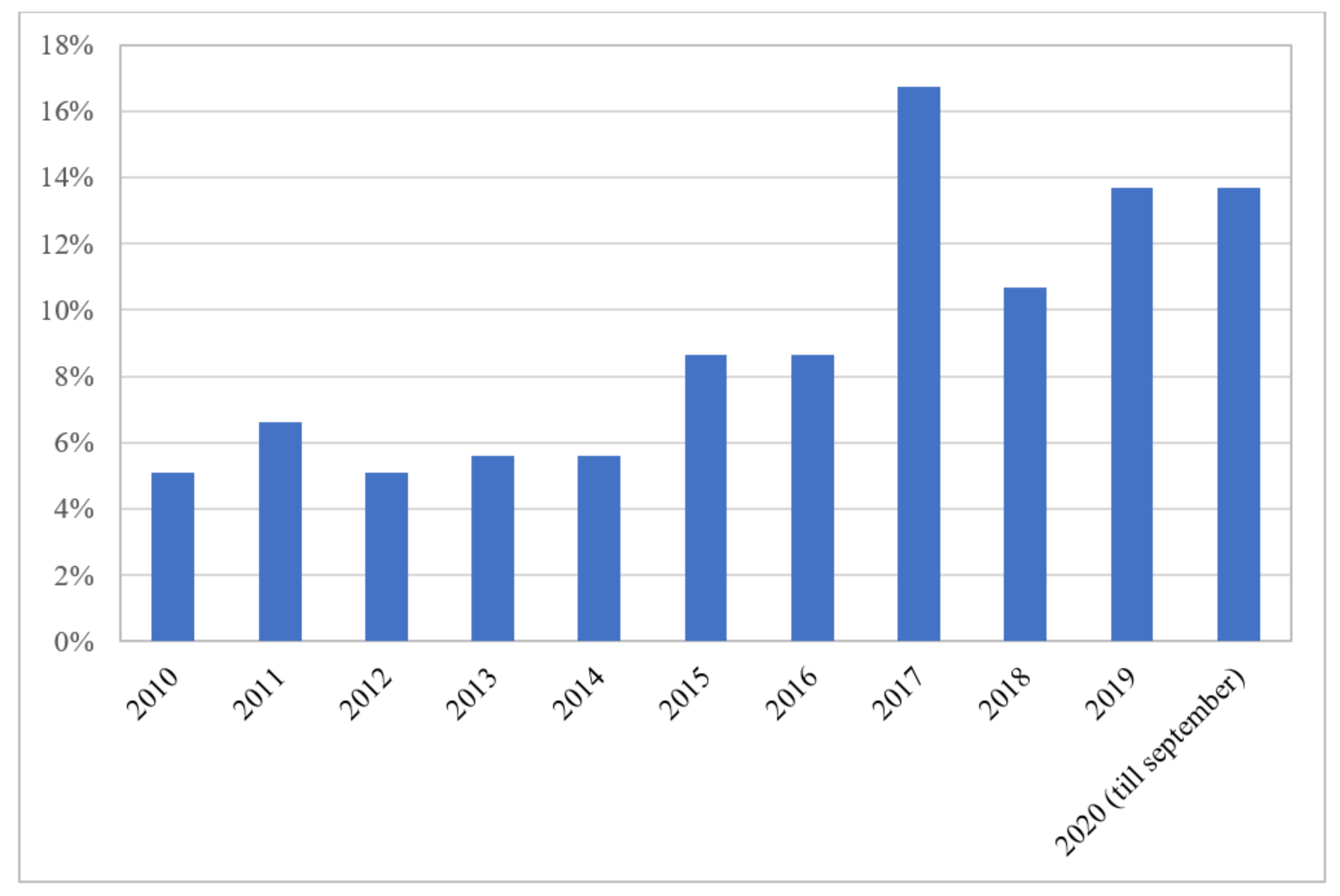
- Groundwater level modeling and forecasting is the most popular use of ML in the literature.
- Groundwater level at the previous time step and precipitation were the most employed input variables to feed groundwater models.
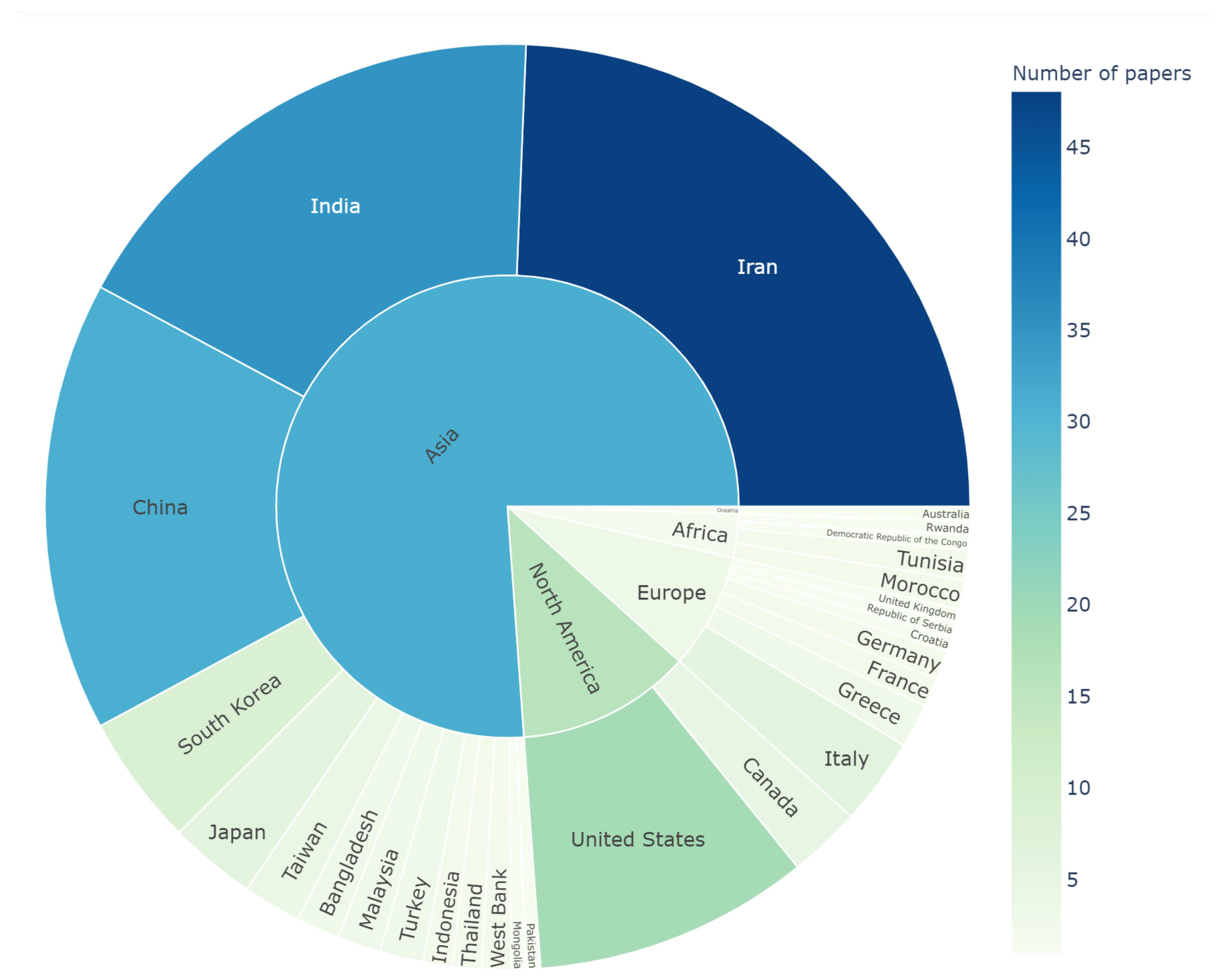
- Countries with more dependence on groundwater as a freshwater source produced the majority of studies on the application of ML in groundwater modeling.
- Feed-forward ANN with gradient descent as the optimization algorithm is the most employed and effective ML model to predict quantitative characteristics of groundwater. This might be due to the simplicity of this architecture and according to the availability of models and codes.
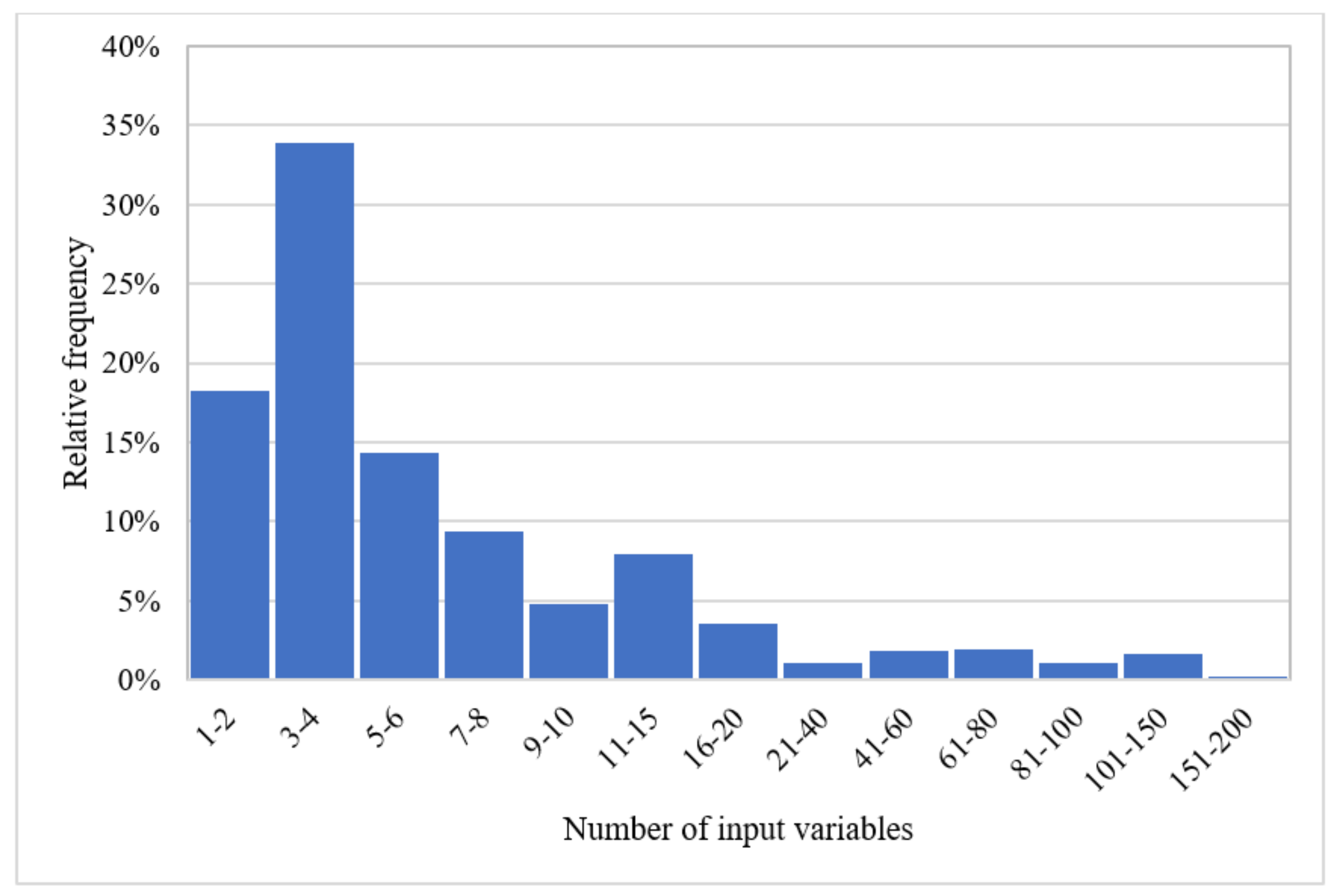
- A considerable portion of reports used only 3 to 4 input variables to train the ML models. The acceptable accuracy reported from these models can imply the capability of data-driven models to simulate the complicated nature of groundwater resources efficiently and effectively, even in the case of few input parameters.
- The monthly scale is the most employed temporal resolution in time series and, generally, finer temporal resolutions result in higher accuracy.
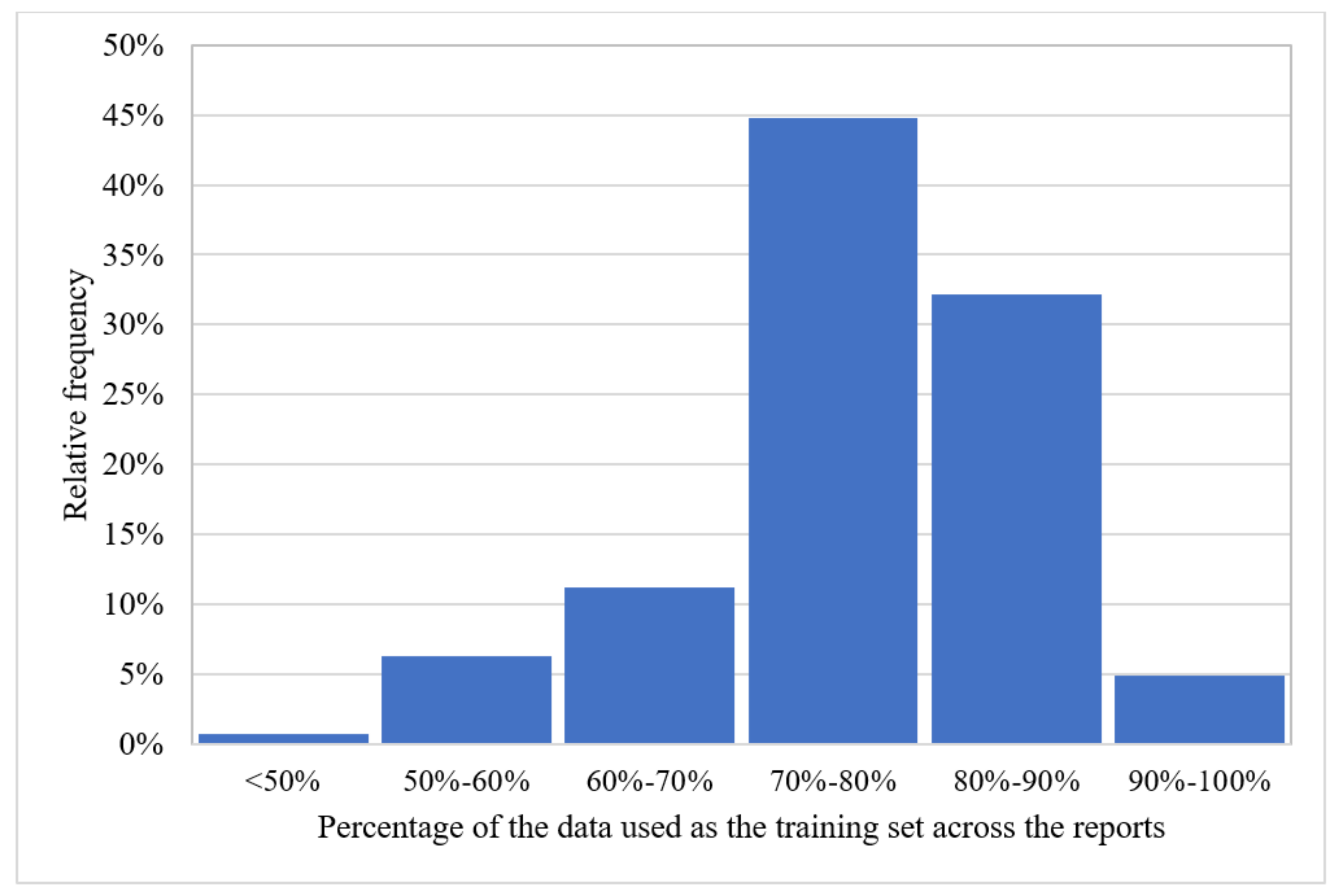
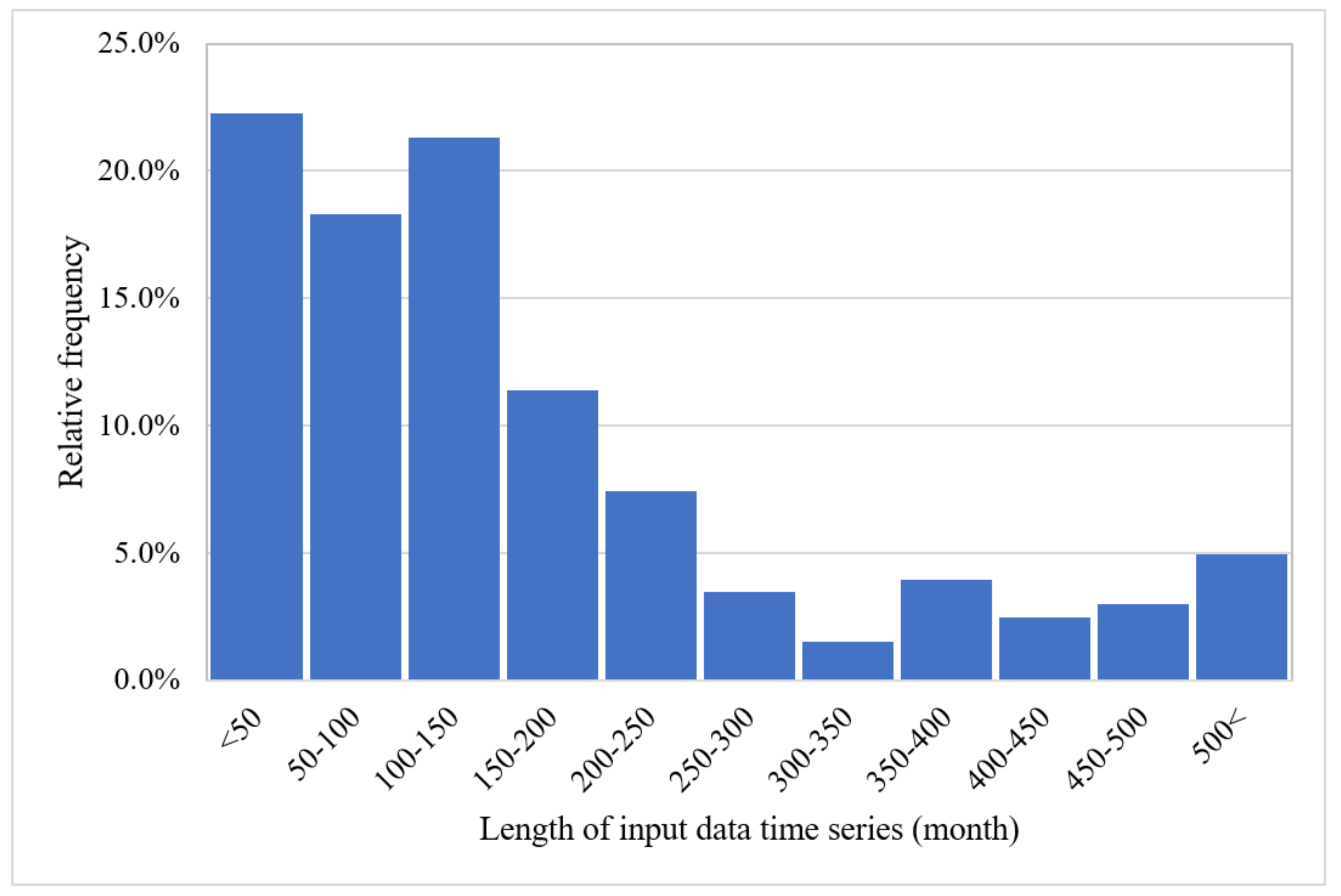
- Around 10–12 years of data are required to develop an acceptable ML model with monthly temporal resolution.
- Input variable selection is a highly used technique to choose the most appropriate input variables to train the models, and studies that used these techniques outperformed those that did not.
- A high portion of studies use their data-driven model to forecast the future states of groundwater resources.
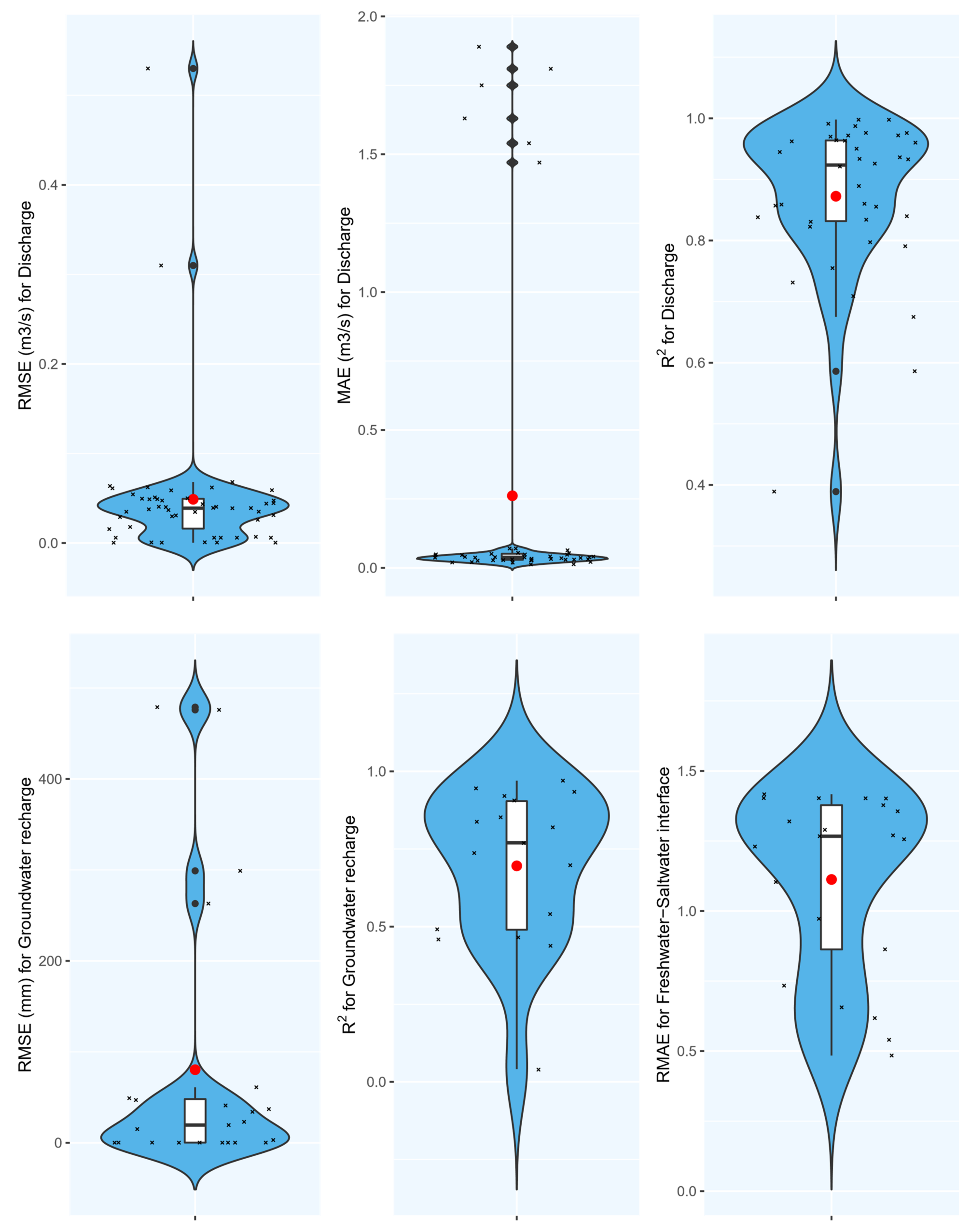
- RMSE is the most employed measure of performance between different studies and for various characteristics.
- While different ML methods have a similar accuracy in predicting groundwater characteristics, ANN is slightly superior to other methods.
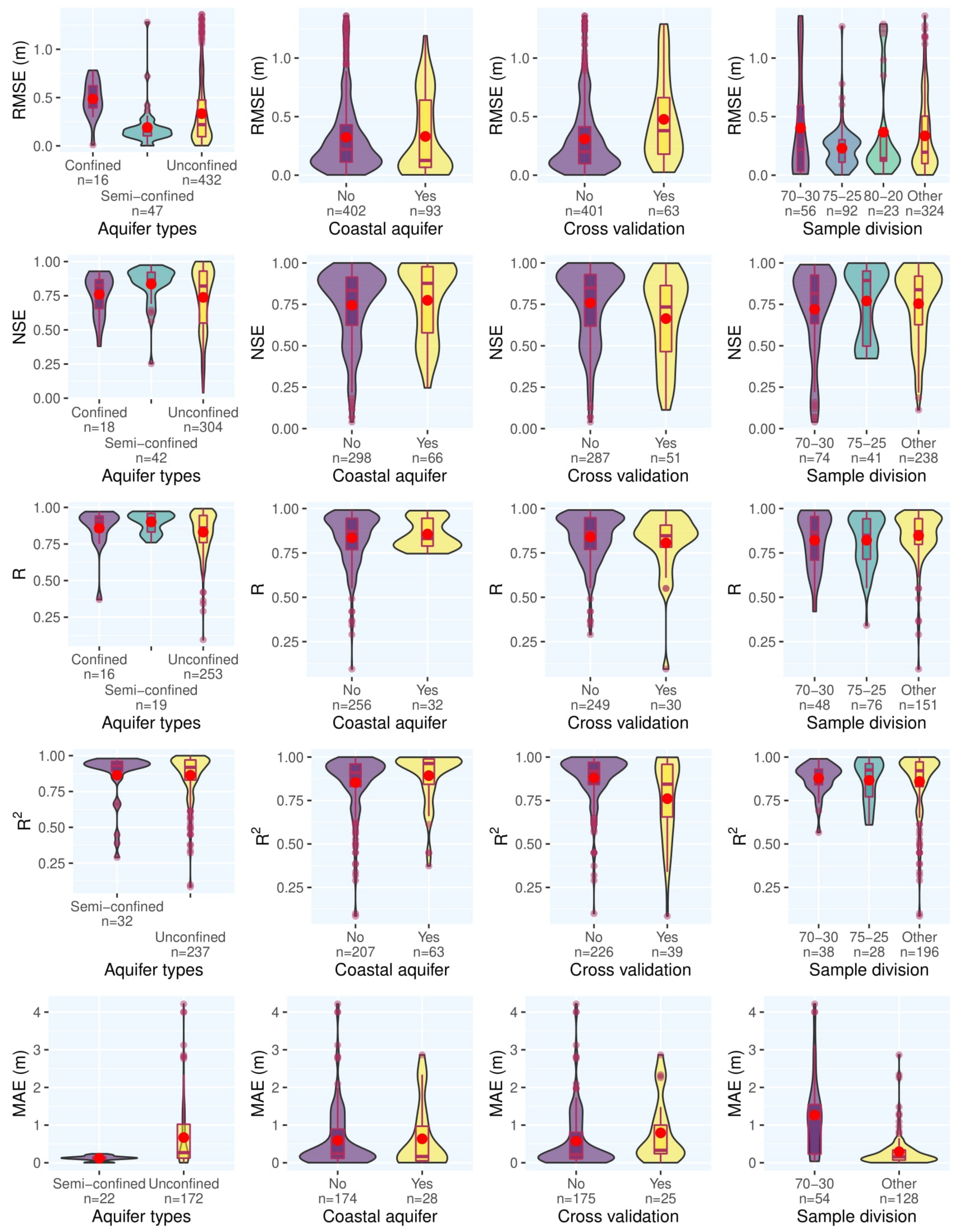
- When using traditional sample division without cross-validation, models generally result in higher quantitative measures of performance. However, results of cross-validation are generally expected to be a more accurate estimate of the true performance of the model since cross-validation reduces the risk of overfitting and increases the model generality.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AIC | Akaike information criterion |
| ANFIS | adaptive network-based fuzzy inference system |
| ANN | artificial neural network |
| CEBC | Center for Evidence-Based Conservation |
| FFNN | feed-forward neural networks |
| GEP | gene expression programming |
| GP | genetic programming |
| GA | genetic algorithm |
| LMA | Levenberg–Marquardt |
| LR | linear regression |
| MAE | mean absolute error |
| MAPE | mean absolute percentage error |
| MSE | mean squared error |
| ML | machine learning |
| MLR | multiple linear regression |
| NARX | nonlinear autoregressive network with exogenous inputs |
| NRMSE | normalized root mean square error |
| NSE | Nash–Sutcliffe efficiency |
| RF | random forest |
| RMAE | relative mean absolute error |
| RMSE | root mean square error |
| PSO | particle swarm optimization |
| SST | sea surface temperature |
| SVM | support vector machine |
| SWAT | soil and water assessment tool |
References
- McDonough, L.; Santos, I.R.; Andersen, M.S.; O’Carroll, D.; Rutlidge, H.; Meredith, K.; Oudone, P.; Bridgeman, J.; Gooddy, D.C.; Sorensen, J.P.R.; et al. Changes in global groundwater organic carbon driven by climate change and urbanization. Nat. Commun. 2020, 11, 1279. [Google Scholar] [CrossRef] [Green Version]
- Famiglietti, J.S. The global groundwater crisis. Nat. Clim. Chang. 2014, 4, 945–948. [Google Scholar] [CrossRef]
- Taylor, R.G.; Scanlon, B.; Döll, P.; Rodell, M.; Van Beek, R.; Wada, Y.; Longuevergne, L.; Leblanc, M.; Famiglietti, J.S.; Edmunds, M.; et al. Ground water and climate change. Nat. Clim. Chang. 2013, 3, 322–329. [Google Scholar] [CrossRef] [Green Version]
- Siebert, S.; Burke, J.; Faures, J.M.; Frenken, K.; Hoogeveen, J.; Döll, P.; Portmann, F.T. Groundwater use for irrigation–a global inventory. Hydrol. Earth Syst. Sci. 2010, 14, 1863–1880. [Google Scholar] [CrossRef] [Green Version]
- Alley, W.M.; Healy, R.W.; LaBaugh, J.W.; Reilly, T.E. Flow and storage in groundwater systems. Science 2002, 296, 1985–1990. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in In-dia. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [Green Version]
- Zaki, N.A.; Haghighi, A.T.; Rossi, P.M.; Tourian, M.J.; Kløve, B. Monitoring Groundwater Storage Depletion Using Gravity Recovery and Climate Experiment (GRACE) Data in Bakhtegan Catchment, Iran. Water 2019, 11, 1456. [Google Scholar] [CrossRef] [Green Version]
- Narasimhan, T.N.; Witherspoon, P.A. An integrated finite difference method for analyzing fluid flow in porous media. Water Resour. Res. 1976, 12, 57–64. [Google Scholar] [CrossRef] [Green Version]
- Huyakorn, P.S.; Lester, B.H.; Faust, C.R. Finite element techniques for modeling groundwater flow in fractured aquifers. Water Resour. Res. 1983, 19, 1019–1035. [Google Scholar] [CrossRef]
- Mosé, R.; Siegel, P.; Ackerer, P.; Chavent, G. Application of the mixed hybrid finite element ap-proximation in a groundwater flow model: Luxury or necessity? Water Resour. Res. 1994, 30, 3001–3012. [Google Scholar] [CrossRef]
- Wang, H.F.; Anderson, M.P. Introduction to Groundwater Modeling: Finite Difference and Finite Element Methods; Academic Press: Cambridge, CA, USA, 1995. [Google Scholar]
- Harbaugh, A.W.; Banta, E.R.; Hill, M.C.; McDonald, M.G. Modflow-2000, the U.S. geological survey modular ground-water model-user guide to modularization concepts and the ground-water flow process. Open-file Report. U.S. Geol. Surv. 2000, 92, 134. [Google Scholar]
- McDonald, M.G.; Harbaugh, A.W.; Original authors of MODFLOW. The history of MOD-FLOW. Groundwater 2003, 41, 280–283. [Google Scholar] [CrossRef] [PubMed]
- Singh, A. Groundwater resources management through the applications of simulation modeling: A re-view. Sci. Total Environ. 2014, 499, 414–423. [Google Scholar] [CrossRef] [PubMed]
- Jalalkamali, A.; Jalalkamali, N. Groundwater modeling using hybrid of artificial neural network with genetic algorithm. Afr. J. Agric. Res. 2011, 6, 5775–5784. [Google Scholar] [CrossRef]
- Fallah-Mehdipour, E.; Haddad, O.B.; Mariño, M.A. Prediction and simulation of monthly ground-water levels by genetic programming. J. Hydro. Environ. Res. 2013, 7, 253–260. [Google Scholar] [CrossRef]
- Sivapragasam, C.; Kannabiran, K.; Karthik, G.; Raja, S. Assessing Suitability of GP Modeling for Groundwater Level. Aquat. Procedia 2015, 4, 693–699. [Google Scholar] [CrossRef]
- Nayak, P.C.; Rao, Y.S.; Sudheer, K.P. Groundwater level forecasting in a shallow aquifer using artificial neural network approach. Water Resour. Manag. 2006, 20, 77–90. [Google Scholar] [CrossRef]
- Dash, N.B.; Panda, S.N.; Remesan, R.; Sahoo, N. Hybrid neural modeling for groundwater level prediction. Neural Comput. Appl. 2010, 19, 1251–1263. [Google Scholar] [CrossRef]
- Seyam, M.; Mogheir, Y. Application of Artificial Neural Networks Model as Analytical Tool for Groundwater Salinity. J. Environ. Prot. 2011, 2, 56–71. [Google Scholar] [CrossRef]
- Yoon, H.; Jun, S.-C.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- Shiri, J.; Kisi, O. Comparison of genetic programming with neuro-fuzzy systems for predicting short-term water table depth fluctuations. Comput. Geosci. 2011, 37, 1692–1701. [Google Scholar] [CrossRef]
- Moosavi, V.; Vafakhah, M.; Shirmohammadi, B.; Behnia, N. A Wavelet-ANFIS Hybrid Model for Groundwater Level Forecasting for Different Prediction Periods. Water Resour. Manag. 2013, 27, 1301–1321. [Google Scholar] [CrossRef]
- Sahoo, S.; Jha, M.K. Groundwater-level prediction using multiple linear regression and artificial neural network techniques: A comparative assessment. Appl. Hydrogeol. 2013, 21, 1865–1887. [Google Scholar] [CrossRef]
- Shiri, J.; Kisi, O.; Yoon, H.; Lee, K.-K.; Nazemi, A.H. Predicting groundwater level fluctuations with meteorological effect implications—A comparative study among soft computing techniques. Comput. Geosci. 2013, 56, 32–44. [Google Scholar] [CrossRef]
- Nourani, V.; Alami, M.T.; Vousoughi, F.D. Hybrid of SOM-Clustering Method and Wavelet-ANFIS Approach to Model and Infill Missing Groundwater Level Data. J. Hydrol. Eng. 2016, 21, 5016018. [Google Scholar] [CrossRef]
- Azari, A.; Zeynoddin, M.; Ebtehaj, I.; Sattar, A.; Gharabaghi, B.; Bonakdari, H. Integrated prepro-cessing techniques with linear stochastic approaches in groundwater level forecasting. Acta Geophys. 2021, 69, 1395–1411. [Google Scholar] [CrossRef]
- Osman, A.I.A.; Ahmed, A.N.; Huang, Y.F.; Kumar, P.; Birima, A.H.; Sherif, M.; Sefelnasr, A.; Ebraheemand, A.A.; El-Shafie, A. Past, Present and Perspective Methodology for Groundwater Modeling-Based Machine Learning Approaches. Arch. Comput. Methods Eng. 2022, 1–17. [Google Scholar] [CrossRef]
- Banerjee, P.; Singh, V.S.; Chatttopadhyay, K.; Chandra, P.; Singh, B. Artificial neural network model as a potential alternative for groundwater salinity forecasting. J. Hydrol. 2011, 398, 212–220. [Google Scholar] [CrossRef]
- Taormina, R.; Chau, K.W.; Sethi, R. Artificial neural network simulation of hourly groundwater lev-els in a coastal aquifer system of the Venice lagoon. Eng. Appl. Artif. Intell. 2012, 25, 1670–1676. [Google Scholar] [CrossRef] [Green Version]
- Hosseini, F.S.; Malekian, A.; Choubin, B.; Rahmati, O.; Cipullo, S.; Coulon, F.; Pradhan, B. A novel machine learning-based approach for the risk assessment of nitrate groundwater contamination. Sci. Total Environ. 2018, 644, 954–962. [Google Scholar] [CrossRef] [Green Version]
- Barzegar, R.; Moghaddam, A.A.; Deo, R.; Fijani, E.; Tziritis, E. Mapping groundwater contamination risk of multiple aquifers using multi-model ensemble of machine learning algorithms. Sci. Total Environ. 2018, 621, 697–712. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Moghaddam, D.D.; Rahmati, O.; Panahi, M.; Tiefenbacher, J.; Darabi, H.; Haghizadeh, A.; Haghighi, A.T.; Nalivan, O.A.; Tien Bui, D. The effect of sample size on different machine learning models for groundwater potential mapping in mountain bedrock aquifers. CATENA 2020, 187, 104421. [Google Scholar] [CrossRef]
- Rahman, A.S.; Hosono, T.; Quilty, J.M.; Das, J.; Basak, A. Multiscale groundwater level forecasting: Coupling new machine learning approaches with wavelet transforms. Adv. Water Resour. 2020, 141, 103595. [Google Scholar] [CrossRef]
- Mosavi, A.; Hosseini, F.S.; Choubin, B.; Abdolshahnejad, M.; Gharechaee, H.; Lahijanzadeh, A.; Dineva, A.A. Susceptibility prediction of groundwater hardness using ensemble machine learning models. Water 2020, 12, 2770. [Google Scholar] [CrossRef]
- Hussein, E.A.; Thron, C.; Ghaziasgar, M.; Bagula, A.; Vaccari, M. Groundwater Prediction Using Machine-Learning Tools. Algorithms 2020, 13, 300. [Google Scholar] [CrossRef]
- Farzin, M.; Avand, M.; Ahmadzadeh, H.; Zelenakova, M.; Tiefenbacher, J.P. Assessment of Ensemble Models for Groundwater Potential Modeling and Prediction in a Karst Watershed. Water 2021, 13, 2540. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Christensen, S.; Sonnenborg, O.T.; Seifert, D.; Højberg, A.L.; Troldborg, L. Review of strategies for handling geological uncertainty in groundwater flow and transport modeling. Adv. Water Resour. 2012, 36, 36–50. [Google Scholar] [CrossRef]
- Sahoo, S.; Russo, T.A.; Elliott, J.; Foster, I. Machine learning algorithms for modeling groundwater level changes in agricultural regions of the U.S. Water Resour. Res. 2017, 53, 3878–3895. [Google Scholar] [CrossRef]
- Adamowski, J.; Chan, H.F. A wavelet neural network conjunction model for groundwater level forecasting. J. Hydrol. 2011, 407, 28–40. [Google Scholar] [CrossRef]
- Gholami, V.; Chau, K.W.; Fadaee, F.; Torkaman, J.; Ghaffari, A. Modeling of groundwater level fluctuations using dendrochronology in alluvial aquifers. J. Hydrol. 2015, 529, 1060–1069. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, Y.; Zhang, X.; Ye, M.; Yang, J. Developing a Long Short-Term Memory (LSTM) based model for predicting water table depth in agricultural areas. J. Hydrol. 2018, 561, 918–929. [Google Scholar] [CrossRef]
- Raghavendra, N.S.; Deka, P.C. Support vector machine applications in the field of hydrology: A review. Appl. Soft Comput. 2014, 19, 372–386. [Google Scholar] [CrossRef]
- Shen, C. A transdisciplinary review of deep learning research and its relevance for water resources sci-entists. Water Resour. Res. 2018, 54, 8558–8593. [Google Scholar] [CrossRef]
- Sit, M.A.; Demiray, B.Z.; Xiang, Z.; Ewing, G.; Sermet, Y.; Demir, I. A comprehensive review of deep learning applications in hydrology and water resources. Water Sci. Technol. 2020, 82, 2635–2670. [Google Scholar] [CrossRef] [PubMed]
- Zounemat-Kermani, M.; Matta, E.; Cominola, A.; Xia, X.; Zhang, Q.; Liang, Q.; Hinkelmann, R. Neurocomputing in surface water hydrology and hydraulics: A review of two decades retrospective, current status and future prospects. J. Hydrol. 2020, 588, 125085. [Google Scholar] [CrossRef]
- Garg, A.X.; Hackam, D.; Tonelli, M. Systematic review and meta-analysis: When one study is just not enough. Clin. J. Am. Soc. Nephrol. 2008, 3, 253–260. [Google Scholar] [CrossRef]
- Collaboration for Environmental Evidence. Guidelines and Standards for Evidence Synthesis in Environmental Management; Version 5.0; Pullin, A.S., Frampton, G.K., Livoreil, B., Petrokofsky, G., Eds.; Collaboration for Environmental Evidence: Johannesburg, South Africa, 2018; Available online: https://environmentalevidence.org/ (accessed on 3 January 2021).
- Margat, J.; Van der Gun, J. Groundwater around the World: A Geographic Synopsis; CRC Press: Boca Raton, FL, USA, 2013. [Google Scholar]
- Dalin, C.; Wada, Y.; Kastner, T.; Puma, Y.W.M.J. Groundwater depletion embedded in international food trade. Nature 2017, 543, 700–704. [Google Scholar] [CrossRef] [Green Version]
- Döll, P.; Mueller Schmied, H.; Schuh, C.; Portmann, F.T.; Eicker, A. Global-scale assessment of groundwater depletion and related groundwater abstractions: Combining hydrological modeling with information from well observations and GRACE satellites. Water Resour. Res. 2014, 50, 5698–5720. [Google Scholar] [CrossRef]
- Sahour, H.; Gholami, V.; Vazifedan, M. A comparative analysis of statistical and machine learning techniques for mapping the spatial distribution of groundwater salinity in a coastal aquifer. J. Hydrol. 2020, 591, 125321. [Google Scholar] [CrossRef]
- Alagha, J.S.; Seyam, M.; Said, M.A.M.; Mogheir, Y. Integrating an artificial intelligence approach with k-means clustering to model groundwater salinity: The case of Gaza coastal aquifer (Pales-tine). Hydrogeol. J. 2017, 25, 2347–2361. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Keese, K.E.; Flint, A.L.; Flint, L.E.; Gaye, C.B.; Edmunds, W.M.; Simmers, I. Global synthesis of groundwater recharge in semiarid and arid regions. Hydrol. Process. 2006, 20, 3335–3370. [Google Scholar] [CrossRef]
- Suryanarayana, C.; Sudheer, C.; Mahammood, V.; Panigrahi, B. An integrated wavelet-support vector machine for groundwater level prediction in Visakhapatnam, India. Neurocomputing 2014, 145, 324–335. [Google Scholar] [CrossRef]
- Ebrahimi, H.; Rajaee, T. Simulation of groundwater level variations using wavelet combined with neural network, linear regression and support vector machine. Glob. Planet. Chang. 2017, 148, 181–191. [Google Scholar] [CrossRef]
- Hintze, J.L.; Nelson, R.D. Violin plots: A box plot-density trace synergism. Am. Stat. 1998, 52, 181–184. [Google Scholar]
- Ahmadi, A.; Emami, M.; Daccache, A.; He, L. Soil Properties Prediction for Precision Agriculture Using Visible and Near-Infrared Spectroscopy: A Systematic Review and Meta-Analysis. Agronomy 2021, 11, 433. [Google Scholar] [CrossRef]
- Pan, S.; Pan, N.; Tian, H.; Friedlingstein, P.; Sitch, S.; Shi, H.; Arora, V.K.; Haverd, V.; Jain, A.K.; Kato, E.; et al. Evaluation of global terrestrial evapotranspiration using state-of-the-art approaches in re-mote sensing, machine learning and land surface modeling. Hydrol. Earth Syst. Sci. 2020, 24, 1485–1509. [Google Scholar] [CrossRef] [Green Version]
- AghaKouchak, A.; Chiang, F.; Huning, L.S.; Love, C.A.; Mallakpour, I.; Mazdiyasni, O.; Moftakhari, H.; Papalexiou, S.M.; Ragno, E.; Sadegh, M. Climate Extremes and Compound Hazards in a Warming World. Annu. Rev. Earth Planet. Sci. 2020, 48, 519–548. [Google Scholar] [CrossRef] [Green Version]
- Mokhtari, A.; Ahmadi, A.; Daccache, A.; Drechsler, K. Actual Evapotranspiration from UAV Images: A Multi-Sensor Data Fusion Approach. Remote Sens. 2021, 13, 2315. [Google Scholar] [CrossRef]
- Ahmadi, A.; Nasseri, M.; Solomatine, D.P. Parametric uncertainty assessment of hydrological models: Coupling UNEEC-P and a fuzzy general regression neural network. Hydrol. Sci. J. 2019, 64, 1080–1094. [Google Scholar] [CrossRef]
- Ahmadi, A.; Nasseri, M. Do direct and inverse uncertainty assessment methods present the same results? J. Hydroinformatics 2020, 22, 842–855. [Google Scholar] [CrossRef]
- Saberi-Movahed, F.; Najafzadeh, M.; Mehrpooya, A. Receiving more accurate predictions for longi-tudinal dispersion coefficients in water pipelines: Training group method of data handling using extreme learning machine conceptions. Water Resour. Manag. 2020, 34, 529–561. [Google Scholar] [CrossRef]








| Predicted Variable | Percentage of Reports |
|---|---|
| Groundwater level | 82.5% |
| Discharge | 6.1% |
| Groundwater recharge | 2.7% |
| Freshwater–saltwater interface level | 2.5% |
| Salinity | 1.3% |
| Groundwater level fluctuation | 1.4% |
| Total dissolved solids | 0.6% |
| Electrical conductivity | 0.6% |
| Aquifer loss coefficient | 0.5% |
| Fluoride | 0.5% |
| Sodium adsorption ratio | 0.4% |
| Nitrate nitrogen (NO3-N) | 0.2% |
| Contamination level | 0.2% |
| Sulfate (SO4) | 0.2% |
| Hydraulic head change | 0.1% |
| Dissolved oxygen | 0.1% |
| Groundwater storage variation | 0.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ahmadi, A.; Olyaei, M.; Heydari, Z.; Emami, M.; Zeynolabedin, A.; Ghomlaghi, A.; Daccache, A.; Fogg, G.E.; Sadegh, M. Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis. Water 2022, 14, 949. https://doi.org/10.3390/w14060949
Ahmadi A, Olyaei M, Heydari Z, Emami M, Zeynolabedin A, Ghomlaghi A, Daccache A, Fogg GE, Sadegh M. Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis. Water. 2022; 14(6):949. https://doi.org/10.3390/w14060949
Chicago/Turabian StyleAhmadi, Arman, Mohammadali Olyaei, Zahra Heydari, Mohammad Emami, Amin Zeynolabedin, Arash Ghomlaghi, Andre Daccache, Graham E. Fogg, and Mojtaba Sadegh. 2022. "Groundwater Level Modeling with Machine Learning: A Systematic Review and Meta-Analysis" Water 14, no. 6: 949. https://doi.org/10.3390/w14060949








