A Geospatial Approach for Analysis of Drought Impacts on Vegetation Cover and Land Surface Temperature in the Kurdistan Region of Iraq
Abstract
:1. Introduction
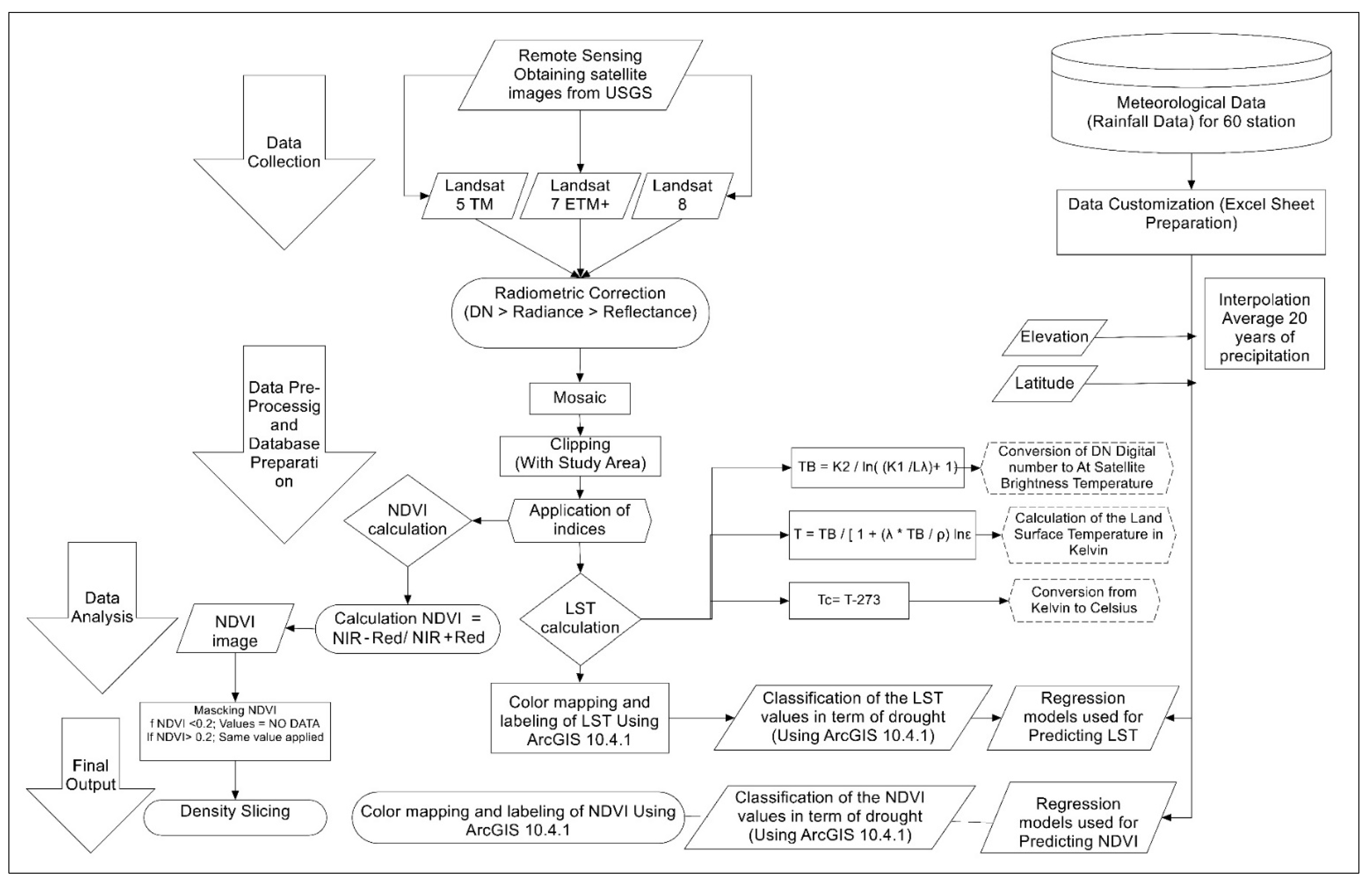
2. Materials and Methods
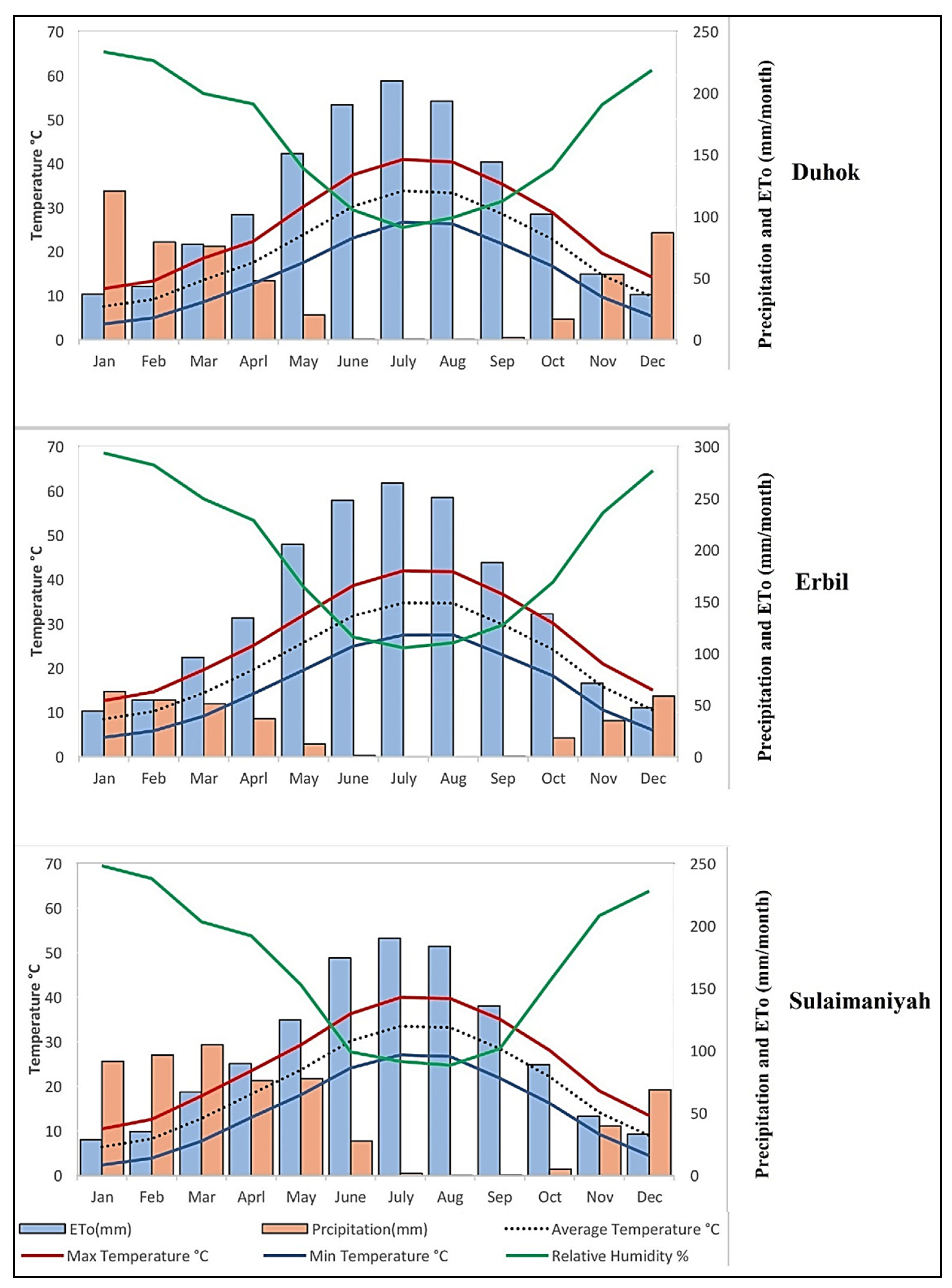
2.1. Study Area
2.2. Data
2.2.1. Landsat Datasets
2.2.2. Landsat Images Preprocessing
2.2.3. Image Processing
NDVI
LST
2.3. Statistical Analysis for Time Series
2.3.1. Trend Detection (Mann–Kendall Test)
2.3.2. Magnitude of Trend (Sen’s Slope)
2.3.3. Pearson Correlation between Indices and Ecological Parameters
2.3.4. Root Mean Square Error (RMSE) and Coefficient of Residual Mass (CRM)
3. Results
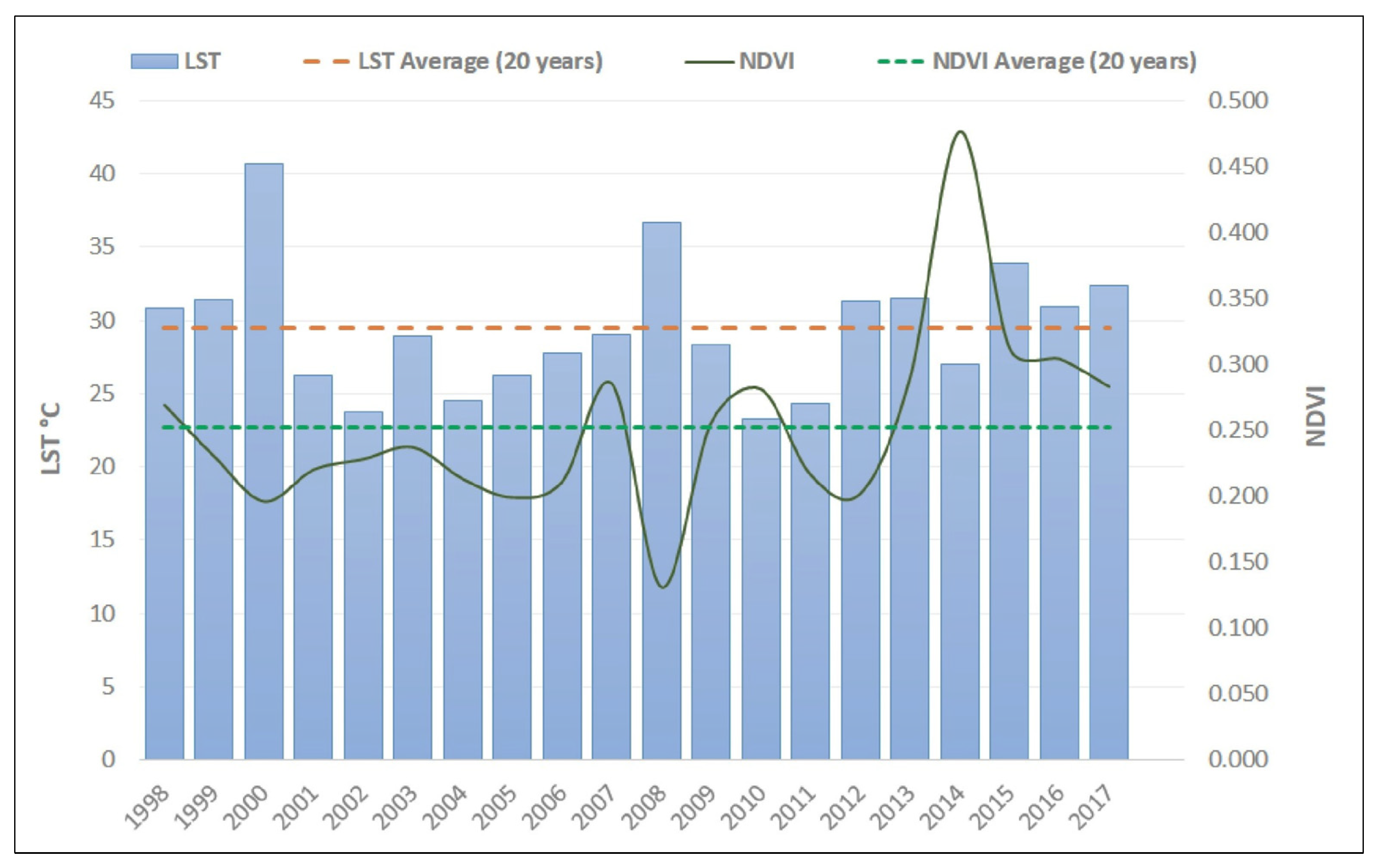
3.1. NDVI
3.2. LST
3.3. Pearson Correlation Matrix between Indices and Ecological Parameters
3.4. Trend Analysis of NDVI and LST by Mann–Kendall and Sen’s Slope
3.4.1. NDVI
3.4.2. LST
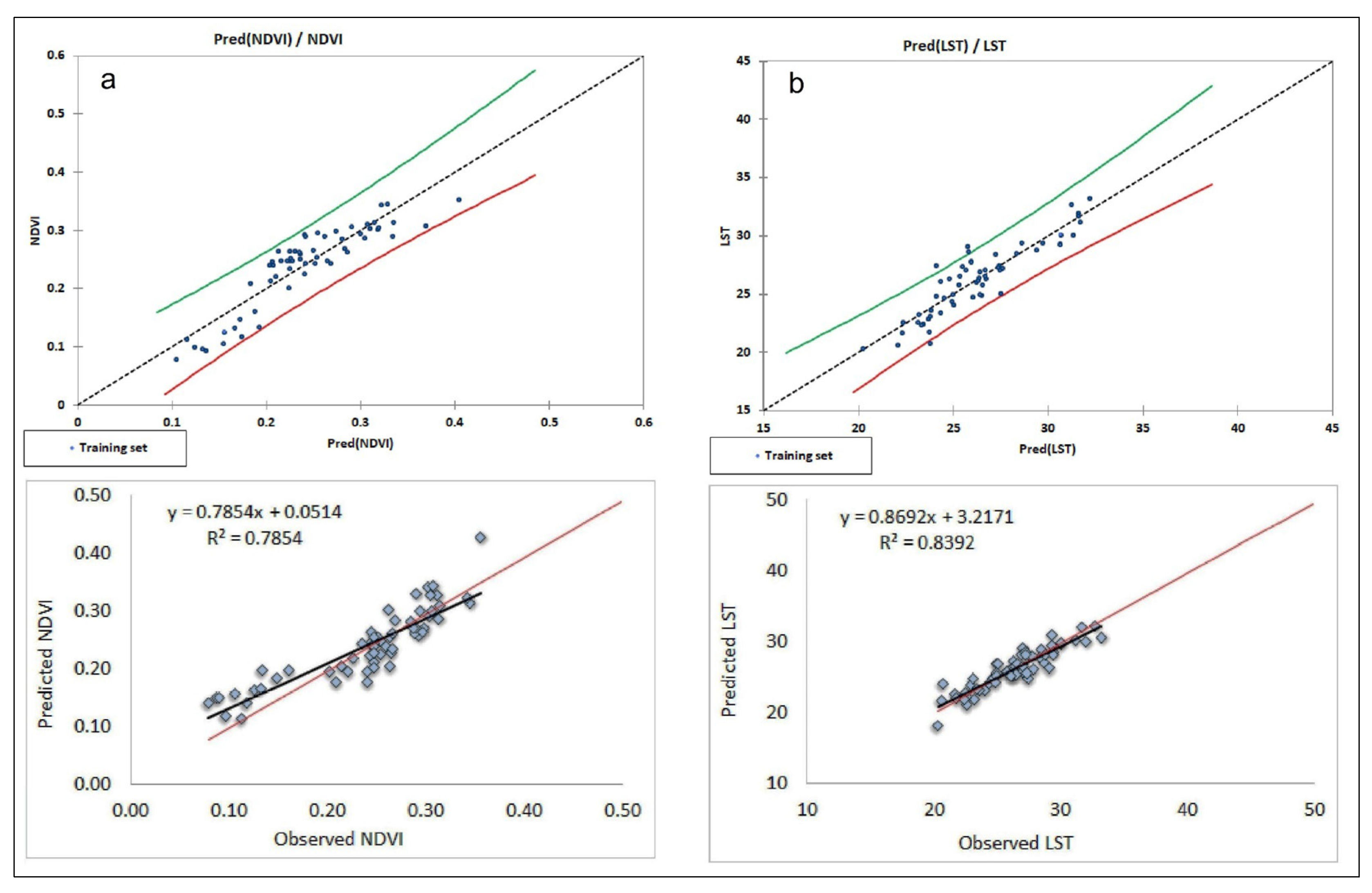
3.5. Multiple Regression Statistics, RMSE, and CRM
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aadhar, S.; Mishra, V. Data Descriptor: High-resolution near real-time drought monitoring in South Asia. Sci. Data 2017, 4, 170145. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dubovyk, O. The role of Remote Sensing in land degradation assessments: Opportunities and challenges. Eur. J. Remote Sens. 2017, 50, 601–613. [Google Scholar] [CrossRef]
- Rajsekhar, D.; Singh, V.P.; Mishra, A.K. Multivariate drought index: An information theory based approach for integrated drought assessment. J. Hydrol. 2015, 526, 164–182. [Google Scholar] [CrossRef]
- Lloyd-Hughes, B. The impracticality of a universal drought definition. Theor. Appl. Climatol. 2014, 117, 607–611. [Google Scholar] [CrossRef] [Green Version]
- Yan, G.; Liu, Y.; Chen, X. Evaluating satellite-based precipitation products in monitoring drought events in southwest China. Int. J. Remote Sens. 2018, 39, 3186–3214. [Google Scholar] [CrossRef]
- Al-Quraishi, A.M.F.; Negm, A.M. Environmental Remote Sensing and GIS in Iraq; Springer Water; Springer: Cham, Switzerland, 2019; ISBN 9783030213435. [Google Scholar]
- Schucknecht, A.; Erasmi, S.; Niemeyer, I.; Matschullat, J. Assessing vegetation variability and trends in north-eastern Brazil using AVHRR and MODIS NDVI time series. Eur. J. Remote Sens. 2013, 46, 40–59. [Google Scholar] [CrossRef] [Green Version]
- Van Loon, A.F.; Gleeson, T.; Clark, J.; Van Dijk, A.I.J.M.; Stahl, K.; Hannaford, J.; Di Baldassarre, G.; Teuling, A.J.; Tallaksen, L.M.; Uijlenhoet, R.; et al. Drought in the Anthropocene. Nat. Geosci. 2016, 9, 89. [Google Scholar] [CrossRef] [Green Version]
- Keyantash, J.A.; Dracup, J.A. An aggregate drought index: Assessing drought severity based on fluctuations in the hydrologic cycle and surface water storage. Water Resour. Res. 2004, 40, 1–14. [Google Scholar] [CrossRef] [Green Version]
- Wilhite, D.A.; Pulwarty, R.S. Drought and Water Crises; Routledge: London, UK, 2017; ISBN 9781138035645. [Google Scholar]
- UNESCO (United Nations Educational, Scientific and Cultural Organization). Integrated Drought Risk Management; UNESCO: Paris, France, 2014. [Google Scholar]
- Fadhil, A.M. Drought mapping using Geoinformation technology for some sites in the Iraqi Kurdistan region. Int. J. Digit. Earth 2011, 4, 239–257. [Google Scholar] [CrossRef]
- Andrieu, J. Phenological analysis of the savanna–forest transition from 1981 to 2006 from Côte d’Ivoire to Benin with NDVI NOAA time series. Eur. J. Remote Sens. 2017, 50, 588–600. [Google Scholar] [CrossRef] [Green Version]
- IdRC. Capacity Assessment for Drought Risk Management in Iraq; Final Report; Submitted to: United Nations Development Programme (UNDP); Interdisciplinary Research Consultants (IdRC): Amman, Jordan, 2012. [Google Scholar]
- Al-Quraishi, A.M.F.; Gaznayee, H.A.A.; Messina, J. Drought severity trend analysis based on the Landsat time-series dataset of 1998–2017 in the Iraqi Kurdistan Region. IOP Conf. Ser. Earth Environ. Sci. 2021, 779, 012083. [Google Scholar] [CrossRef]
- Wu, W.; Muhaimeed, A.S.; Al-Shafie, W.M.; Al-Quraishi, A.M.F. Using L-band radar data for soil salinity mapping—A case study in Central Iraq. Environ. Res. Commun. 2019. [Google Scholar] [CrossRef] [Green Version]
- Haktanir, K. Environmental Challenges in the Mediterranean 2000–2050; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar] [CrossRef]
- Harun, R.; Muresan, I.C.; Arion, F.H.; Dumitras, D.E.; Lile, R. Analysis of factors that influence the willingness to pay for irrigation water in the Kurdistan Regional Government, Iraq. Sustainablity 2015, 7, 9574–9586. [Google Scholar] [CrossRef] [Green Version]
- Fadhil, A.M. Sand dunes monitoring using remote sensing and GIS techniques for some sites in Iraq. In Proceedings of the 3rd International Conference on Photonics and Image in Agriculture Engineering (PIAGENG 2013), Sanya, China, 27–28 January 2013. [Google Scholar] [CrossRef]
- Awchi, T.A.; Jasim, A.I. Rainfall Data Analysis and Study of Meteorological Draught in Iraq for the Period 1970–2010. TKRIit J. Eng. Sci. 2017, 24, 110–121. [Google Scholar] [CrossRef]
- Hameed, H. Water Harvesting in Erbil Governorate, Kurdistan Region, Iraq Detection of Suitable Sites Using Geographic Information System and Remote Sensing. Master’s Thesis, Lund University, Lund, Sweden, 2013. [Google Scholar]
- Mohammed, R.; Scholz, M. Adaptation Strategy to Mitigate the Impact of Climate Change on Water Resources in Arid and Semi-Arid Regions: A Case Study. Water Resour. Manag. 2017, 31, 3557–3573. [Google Scholar] [CrossRef] [Green Version]
- Yao, Y.; Qin, Q.; Fadhil, A.M.; Li, Y.; Zhao, S.; Liu, S.; Sui, X.; Dong, H. Evaluation of EDI derived from the exponential evapotranspiration model for monitoring China’s surface drought. Environ. Earth Sci. 2011, 63, 425–436. [Google Scholar] [CrossRef]
- Zewdie, W.; Csaplovics, E. Remote sensing-based multi-temporal land cover classification and change detection in northwestern Ethiopia. Eur. J. Remote Sens. 2015, 48, 121–139. [Google Scholar] [CrossRef] [Green Version]
- Al-Quraishi, A.M.F.; Gaznayee, H.A.A.; Crespi, M. Drought Trend Analysis in Sulaimaniyah (Iraqi Kurdistan Region) for the Period 1998–2017 using Remote Sensing and GIS. J. Arid. Land 2020, 3, 413–430. [Google Scholar]
- Dabrowska-Zielinska, K.; Kogan, F.; Ciolkosz, A.; Gruszczynska, M.; Kowalik, W. Modelling of crop growth conditions and crop yield in Poland using AVHRR-based indices. Int. J. Remote Sens. 2002, 23, 1109–1123. [Google Scholar] [CrossRef]
- Abdel-Hamid, A.; Dubovyk, O.; Graw, V.; Greve, K. Assessing the impact of drought stress on grasslands using multi-temporal SAR data of Sentinel-1: A case study in Eastern Cape, South Africa. Eur. J. Remote Sens. 2020, 53, 1–14. [Google Scholar] [CrossRef]
- Alqasemi, A.S.; Hereher, M.E.; Al-Quraishi, A.M.F.; Saibi, H.; Aldahan, A.; Abuelgasim, A. Retrieval of monthly maximum and minimum air temperature using MODIS aqua land surface temperature data over the United Arab Emirates. Geocarto Int. 2021. ahead of print. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef] [Green Version]
- Owrangi, M.A.; Adamowski, J.; Rahnemaei, M.; Mohammadzadeh, A.; Sharifan, R.A. Drought Monitoring Methodology Based on AVHRR Images and SPOT Vegetation Maps. J. Water Resour. Prot. 2011, 3, 325–334. [Google Scholar] [CrossRef] [Green Version]
- Wan, Z.; Wang, P. International Journal of Remote Using MODIS Land Surface Temperature and Normalized Difference Vegetation Index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 37–41. [Google Scholar] [CrossRef]
- Heydari, H.; Zoej, M.J.V.; Maghsoudi, Y.; Dehnavi, S. An investigation of drought prediction using various remote-sensing vegetation indices for different time spans. Int. J. Remote Sens. 2018, 39, 1871–1889. [Google Scholar] [CrossRef]
- Karim, T.H.; Keya, D.R.; Amin, Z.A. Temporal and spatial variations in annual rainfall distribution in erbil province. Outlook Agric. 2018, 47, 59–67. [Google Scholar] [CrossRef]
- Eklund, L.; Persson, A.; Pilesjö, P. Cropland changes in times of conflict, reconstruction, and economic development in Iraqi Kurdistan. Ambio 2016, 45, 78–88. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Eklund, L.; Abdi, A.; Islar, M. From Producers to Consumers: The Challenges and Opportunities of Agricultural Development in Iraqi Kurdistan. Land 2017, 6, 44. [Google Scholar] [CrossRef] [Green Version]
- Saeed, M.A. Analysis of Climate and Drought Conditions in the Fedral. J. Int. Sci. Environ. 2012, 2, 953. [Google Scholar]
- Ministry of Planning-KRG. Regional Development Strategy for Kurdistan Region. 2012–2016 Final report 2017; Ministry of Planning-KRG: Erbil, Iraq, 2017.
- Module ENVI Atmospheric Correction Module: QUAC and FLAASH User’s Guide; Module Version; ITT Visual Information Solutions: Boulder, CO, USA, 2009; 44p.
- Sun, Q.; Tan, J.; Xu, Y. An ERDAS image processing method for retrieving LST and describing urban heat evolution: A case study in the Pearl River Delta Region in South China. Environ. Earth Sci. 2009, 59, 1047–1055. [Google Scholar] [CrossRef]
- Rouse, W.; Haas, H.; Deering, W. Monitoring Vegetation Systems in the Great Plains With Erts. In Proceedings of the 3rd Earth Resource Technology Satellite (ERTS) Symposium, Washington, DC, USA, 10–14 December 1973; Volume 1, pp. 48–62. [Google Scholar]
- Aquino, D.d.N.; Neto, O.C.d.R.; Moreira, M.A.; dos S. Teixeira, A.; de Andrade, E.M. Use of remote sensing to identify areas at risk of degradation in the semi-arid region. Rev. Cienc. Agron. 2018, 49, 420–429. [Google Scholar] [CrossRef]
- Nath, B.; Acharjee, S. Forest Cover Change Detection using Normalized Difference Vegetation Index (NDVI): A Study of Reingkhyongkine Lake’s, Adjoining Areas. Indian Cartogr. 2013, XXXIII, 348–403. [Google Scholar]
- Di Gregorio, A. Land Cover Classification System; FAO: Rome, Italy, 2005; ISBN 9251053278. [Google Scholar]
- Dash, P.; Göttsche, F.M.; Olesen, F.S.; Fischer, H. Land surface temperature and emissivity estimation from passive sensor data: Theory and practice-current trends. Int. J. Remote Sens. 2002, 23, 2563–2594. [Google Scholar] [CrossRef]
- Sun, D.; Kafatos, M. Note on the NDVI-LST relationship and the use of temperature-related drought indices over North America. Geophys. Res. Lett. 2007, 34, 1–4. [Google Scholar] [CrossRef] [Green Version]
- Qutbudin, I.; Shiru, M.S.; Sharafati, A.; Ahmed, K.; Al-Ansari, N.; Yaseen, Z.M.; Shahid, S.; Wang, X. Seasonal Drought Pattern Changes Due to Climate Variability: Case Study in Afghanistan. Water 2019, 11, 1096. [Google Scholar] [CrossRef] [Green Version]
- Pohlert, T. Package ‘trend’: Non-Parametric Trend Tests and Change-Point Detection. R Packag. 2016, 26. [Google Scholar] [CrossRef]
- Lu, Y.; Jiang, S.; Ren, L.; Zhang, L.; Wang, M.; Liu, R.; Wei, L. Spatial and Temporal Variability in Precipitation Concentration over Mainland China, 1961–2017. Water 2019, 11, 881. [Google Scholar] [CrossRef] [Green Version]
- U.S. Army Corps of Engineers. Mann-Kendall Analysis Mann-Kendall Analysis for the Fort Ord Site; HydroGeoLogic, Inc.—OU-1 Annual Groundwater Monitoring Report—Former Fort Ord, California; HydroGeoLogic, Inc.: Herndon, VA, USA, 2005.
- Gilbert, R.O. Statistical Methods for Environmental Pollution Monitoring. Stat. Methods Environ. Pollut. Monit. 1987, 204–224. [Google Scholar]
- Partal, T.; Kahya, E. Trend analysis in Turkish precipitation data. Hydrol. Process. 2006, 20, 2011–2026. [Google Scholar] [CrossRef]
- Batool, N.; Shah, S.A.; Dar, S.N.; Skinder, S. Rainfall variability and dynamics of cropping pattern in Kashmir Himalayas: A case study of climate change and agriculture. SN Appl. Sci. 2019, 1, 606. [Google Scholar] [CrossRef] [Green Version]
- Jiao, W.; Tian, C.; Chang, Q.; Novick, K.A.; Wang, L. A new multi-sensor integrated index for drought monitoring. Agric. For. Meteorol. 2019, 268, 74–85. [Google Scholar] [CrossRef] [Green Version]
- Yao, X.; Yao, X.; Jia, W.; Tian, Y.; Ni, J.; Cao, W.; Zhu, Y. Comparison and intercalibration of vegetation indices from different sensors for monitoring above-ground plant nitrogen uptake in winter wheat. Sensors 2013, 13, 3109–3130. [Google Scholar] [CrossRef] [PubMed]
- Dutta, D.; Kundu, A.; Patel, N.R. Predicting agricultural drought in eastern Rajasthan of India using NDVI and standardized precipitation index. Geocarto Int. 2013, 28, 192–209. [Google Scholar] [CrossRef]
- Gessner, U.; Machwitz, M.; Conrad, C.; Dech, S. Estimating the fractional cover of growth forms and bare surface in savannas. A multi-resolution approach based on regression tree ensembles. Remote Sens. Environ. 2013, 129, 90–102. [Google Scholar] [CrossRef] [Green Version]
- Lehnert, L.W.; Meyer, H.; Wang, Y.; Miehe, G.; Thies, B.; Reudenbach, C.; Bendix, J. Retrieval of grassland plant coverage on the Tibetan Plateau based on a multi-scale, multi-sensor and multi-method approach. Remote Sens. Environ. 2015, 164, 197–207. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Bao, Y.; Luo, J.; Jin, X.; Xu, X.; Song, X.; Yang, G. Exploring the best hyperspectral features for LAI estimation using partial least squares regression. Remote Sens. 2014, 6, 6221–6241. [Google Scholar] [CrossRef] [Green Version]
- Peres, L.F.; DaCamara, C.C. Land surface temperature and emissivity estimation based on the two-temperature method: Sensitivity analysis using simulated MSG/SEVIRI data. Remote Sens. Environ. 2004, 91, 377–389. [Google Scholar] [CrossRef]
- Gutman, G.G. Towards Monitoring Droughts from Space. J. Clim. 2002, 3, 282–295. [Google Scholar] [CrossRef] [Green Version]
- Lambin, E.F.; Ehrlich, D. The surface temperature-vegetation index space for land cover and land-cover change analysis. Int. J. Remote Sens. 1996, 17, 463–487. [Google Scholar] [CrossRef]
- Aliyu, S.; Bello, S. Performance Assessment of Hargreaves Model in Estimating Global Solar Radiation in Sokoto, Nigeria. Int. J. Adv. Sci. Res. Eng. 2018, 3, 6–15. [Google Scholar] [CrossRef]
- Park, H.; Kim, K.; Lee, D.K. Prediction of severe drought area based on random forest: Using satellite image and topography data. Water 2019, 11, 705. [Google Scholar] [CrossRef] [Green Version]
- Population, N. Quantile-Quantile Plot (QQ-plot) and the Normal Probability Plot Section 6-6. Norm. Probab. Plot. 2012, 2377, 1–8. [Google Scholar]
- Almamalachy, Y. Utilization of Remote Sensing in Drought Monitoring Over Iraq. Master’s Thesis, Portland State University, Portland, OR, USA, 2017. Paper 3996. [Google Scholar] [CrossRef] [Green Version]
- Mustafa, Y.T. Spatiotemporal Analysis of Vegetation Cover in Kurdistan Region-Iraq using MODIS Image Data. J. Appl. Sci. Technol. Trends 2020, 1, 1–6. [Google Scholar] [CrossRef] [Green Version]
- Al-timimi, Y.K.; George, L.E.; Al-jiboori, M.H. Drought Risk Assessment in Iraq using Remote Sensing and GIS Techniques. Iraqi J. Sci. 2012, 53, 1078–1082. [Google Scholar]
- Mustafa, Y.T. Mapping and Estimating Vegetation Coverage in Iraqi Kurdistan Region using Remote Sensing and GIS; Iraq-Final Report; Prepared and Implemented by Applied Remote Sensing & Gis (Ars&Gis) Center, University Of Zakho, Salahaddin University, University of Garmian, and Directorate of Forests and Range in Duhok; General Directorate of Horticulture, Forestry and Rangeland, Ministry of Agriculture and Water Resources: Erbil, Kurdistan Region, Iraq, 2015; pp. 1–136.
- Anyamba, A.; Tucker, C.J. Historical perspectives on AVHRR NDVI and vegetation drought monitoring. Remote Sens. Drought Innov. Monit. Approaches. 2012, 23–49. [Google Scholar] [CrossRef]
- Wang, J.; Wang, J.; Rich, P.M.; Price, K.P. Temporal responses of NDVI to precipitation and temperature in the central Great Plains, USA. Int. J. Remote Sens. 2003, 24, 2345–2364. [Google Scholar] [CrossRef]
- AlJawa, S.B.; Al-Ansari, N. Open Access Online Journal of the International Association for Environmental. Hydrol. Assess. Groundw. Qual. Using 2017, 26, 1–14. [Google Scholar]
- Oku, Y.; Ishikawa, H.; Haginoya, S.; Ma, Y. Recent trends in land surface temperature on the Tibetan Plateau. J. Clim. 2006, 19, 2995–3003. [Google Scholar] [CrossRef] [Green Version]
- Koundouri, P.; Karousakis, K.; Assimacopoulos, D.; Jeffrey, P.; Lange, M. Water Management in Arid and Semi-Arid Regions. In Water Management in Arid and Semi-Arid Regions; Northampton, Mass Edward Elgar: Cheltenham, UK, 2006; ISBN 9781845429973. [Google Scholar]
- Zhang, Y.; Wang, X.; Li, C.; Cai, Y.; Yang, Z.; Yi, Y. NDVI dynamics under changing meteorological factors in a shallow lake in future metropolitan, semi-arid area in North China. Sci. Rep. 2018, 8, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Robaa, S.M.; Zhian, J. AL-Barazanji Trends of Annual Mean Surface Air Temperature over Iraq. Nat. Sci. 2013, 11, 138–145. [Google Scholar]
- Yang, J.; Wang, Y.Q.; Sun, Z.; Wang, Q.Q.; Batkhishig, O.; Ouyang, Z.; Cammalleri, C.; Sepulcre-Cantó, G.; Vogt, J.; Mavi, H.S. Mapping Drought Hazard Using SPI index And GIS (A Case study: Fars province, Iran). Remote Sens. Environ. 2017, 7, 1–4. [Google Scholar] [CrossRef]
- Kogan, F.N. Global drought watch from space. Bull. Am. Meteorol. Soc. 1997, 78, 621. [Google Scholar] [CrossRef]
- Lambin, E.F. Change detection at multiple temporal scales: Seasonal and annual variations in landscape variables. Photogramm. Eng. Remote Sensing 1996, 62, 931–938. [Google Scholar]
- Julien, Y.; Sobrino, J.A. Comparison of cloud-reconstruction methods for time series of composite NDVI data. Remote Sens. Environ. 2010, 114, 618–625. [Google Scholar] [CrossRef]
- Friedl, M.A.; Davis, F.W. Sources of variation in radiometric surface temperature over a tallgrass prairie. Remote Sens. Environ. 1994, 48, 1–17. [Google Scholar] [CrossRef]
- Goward, S.N.; Xue, Y.; Czajkowski, K.P. Evaluating land surface moisture conditions from the remotely sensed temperature/vegetation index measurements: An exploration with the simplified simple biosphere model. Remote Sens. Environ. 2002, 79, 225–242. [Google Scholar] [CrossRef]
- Gupta, R.K.; Prasad, T.S.; Vijayan, D. Estimation of roughness length and sensible heat flux from wiFS and NOAA AVHRR data. Adv. Sp. Res. 2002, 29, 33–38. [Google Scholar] [CrossRef]
- Gaikwad, S.V.; Kale, K.V.; Kulkarni, S.B.; Varpe, A.B.; Pathare, G.N. Agricultural Drought Severity Assessment using Remotely Sensed Data: A Review. Int. J. Adv. Remote Sens. GIS. 2015, 4, 1195–1203. [Google Scholar] [CrossRef]
- Nemani, R.R.; Running, S.W. Estimation of Regional Surface Resistance to Evapotranspiration from NDVI and Thermal-IR AVHRR Data. J. Appl. Meteorol. 1989, 28, 276–284. [Google Scholar] [CrossRef]
- Karnieli, A.; Bayasgalan, M.; Bayarjargal, Y.; Agam, N.; Khudulmur, S.; Tucker, C.J. Comments on the use of the Vegetation Health Index over Mongolia. Int. J. Remote Sens. 2006, 27, 2017–2024. [Google Scholar] [CrossRef]
- Al-Quraishi, A.M.F.; Sadiq, H.A.; Messina, J.P. Characterization and Modeling Surface Soil Physicochemical Properties Using Landsat Images: A Case Study in the Iraqi Kurdistan Region. Int. Arch. Photogramm. Remote Sens. Spatial Inf. Sci. 2019, XLII-2/W16, 21–28. [Google Scholar] [CrossRef]
- Gaznayee, H.A.A.; Al-Quraishi, A.M.F. Analysis of agricultural drought, rainfall, and crop yield relationships in Erbil province, the Kurdistan region of Iraq based on Landsat time-series MSAVI2. J. Adv. Res. Dyn. Control Syst. 2019, 11, 536–545. [Google Scholar] [CrossRef]
- Gaznayee, H.A.A.; Al-Quraishi, A.M.F. Analysis of Agricultural Drought’s Severity and Impacts in Erbil Province, the Iraqi Kurdistan Region based on Time Series NDVI and TCI Indices for 1998 through 2017. J. Adv. Res. Dyn. Control Syst. 2019, 11, 287–297. [Google Scholar] [CrossRef]


| MT No. | Station Name | Lat | Long | DEM (m) | AP (mm) | MT No. | Station Name | Lat | Long | DEM (m) | AP (mm) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | (ER) | 36.19111 | 44.00917 | 412.7 | 326.2 | 31 | Mangish | 37.03513 | 43.09252 | 1030.2 | 645.0 |
| 2 | Qushtapa | 36.00085 | 44.02848 | 390.8 | 280.6 | 32 | Deraluke | 37.05859 | 43.64925 | 706.8 | 759.5 |
| 3 | Khabat | 36.27278 | 43.67389 | 285.9 | 290.9 | 33 | Akre | 36.74139 | 43.89333 | 683.1 | 600.0 |
| 4 | Bnaslawa | 36.1538 | 44.13999 | 540.7 | 320.2 | 34 | Amadia | 37.0925 | 43.48722 | 1148.5 | 745.7 |
| 5 | Harir | 36.5511 | 44.3648 | 837.3 | 552.2 | 35 | Sarsink | 37.05028 | 43.35028 | 957.1 | 841.6 |
| 6 | Soran | 36.63846 | 44.56136 | 701.6 | 625.7 | 36 | Bamarni | 37.11512 | 43.2693 | 1203.0 | 722.3 |
| 7 | Shaqlawa | 36.19111 | 44.00917 | 966.5 | 750.0 | 37 | Barda | 36.50822 | 43.58941 | 363.6 | 391.4 |
| 8 | Khalifan | 36.5986 | 44.4038 | 697.1 | 670.8 | 38 | Qasrok | 36.7009 | 43.59795 | 414.8 | 500.5 |
| 9 | Choman | 36.6374 | 44.8893 | 1178.4 | 732.2 | 39 | (SU) | 35.55722 | 45.43556 | 870.8 | 595.0 |
| 10 | Sidakan | 36.79736 | 44.6714 | 1011.3 | 822.5 | 40 | Bazian | 35.58902 | 45.13952 | 943.7 | 596.1 |
| 11 | Rwanduz | 36.61194 | 44.52472 | 801.6 | 712.3 | 41 | Halabja | 35.18639 | 45.97389 | 716.6 | 648.8 |
| 12 | Mergasur | 36.8382 | 44.3062 | 1108.9 | 1356.0 | 42 | Penjwen | 35.61972 | 45.94139 | 1442.9 | 968.7 |
| 13 | Dibaga | 35.87303 | 43.80496 | 328.3 | 246.2 | 43 | Chwarta | 35.71972 | 45.57472 | 1011.6 | 694.8 |
| 14 | Gwer | 36.04486 | 43.4808 | 309.7 | 235.3 | 44 | Dukan | 35.95417 | 44.95278 | 700.4 | 576.4 |
| 15 | Barzewa | 36.6268 | 44.6333 | 798.3 | 721.1 | 45 | Qaladiza | 36.1755 | 45.1333 | 628.2 | 681.9 |
| 16 | Bastora | 36.33888 | 44.16049 | 630.0 | 412.4 | 46 | Rania | 36.2391 | 44.8855 | 607.8 | 713.9 |
| 17 | Makhmoor | 35.7833 | 43.5833 | 287.7 | 228.2 | 47 | S-sadiq | 35.34369 | 45.85344 | 544.1 | 550.2 |
| 18 | Koya | 36.09944 | 44.64806 | 724.5 | 472.2 | 48 | Qaradagh | 35.30933 | 45.38961 | 887.9 | 721.7 |
| 19 | Taqtaq | 35.88737 | 44.58561 | 397.5 | 371.1 | 49 | Arbat | 35.42462 | 45.58683 | 701.6 | 492.5 |
| 20 | Shamamk | 36.0400 | 43.84669 | 310.6 | 276.2 | 50 | Kani | 35.38498 | 45.70458 | 685.8 | 498.7 |
| 21 | (DU) | 36.8679 | 42.97900 | 588.3 | 495.1 | 51 | Byara | 35.22507 | 46.11625 | 1333.5 | 656.3 |
| 22 | Semel | 36.87333 | 42.85400 | 491.6 | 414.4 | 52 | Mawat | 35.90074 | 45.4105 | 1063.8 | 712.0 |
| 23 | Zakho | 37.14361 | 42.68191 | 501.4 | 528.7 | 53 | Darband | 35.11626 | 45.68625 | 534.6 | 557.9 |
| 24 | Batel | 36.95946 | 42.72165 | 531.0 | 435.5 | 54 | Chamcha | 35.53333 | 44.83333 | 726.6 | 427.0 |
| 25 | Dam-DU | 36.87576 | 43.0029 | 605.6 | 514.2 | 55 | Kalar | 34.6411 | 45.32927 | 243.2 | 304.7 |
| 26 | Dar. Hajam | 37.19878 | 42.82273 | 649.8 | 509.5 | 56 | Agjalar | 35.74827 | 44.89741 | 702.3 | 390.0 |
| 27 | zaxo-farh | 37.15991 | 42.65873 | 447.1 | 525.2 | 57 | Bngrd | 36.06601 | 45.02989 | 841.2 | 666.7 |
| 28 | Batifa | 37.18404 | 37.18404 | 930.2 | 670.3 | 58 | Sangaw | 35.28623 | 45.1825 | 704.4 | 470.8 |
| 29 | kanimasi | 37.22906 | 37.22906 | 1332.3 | 736.2 | 59 | Bawanor | 34.82332 | 45.5087 | 358.4 | 364.3 |
| 30 | Zaweta | 36.90583 | 36.90583 | 1006.4 | 723.4 | 60 | Kifri | 34.68333 | 44.96639 | 238.7 | 279.2 |
| Class | Class Classification Criterion |
|---|---|
| Bare soil and/or water (no vegetation) | NDVI ≤ 0 |
| Very Low NDVI | ≤0.2 |
| Low to Moderately Low NDVI | 0.2 < NDVI ≤ 0.6 |
| Moderately High to High NDVI | 0.6 < NDVI ≤ 1 |
| Class 1 | Class 2 | Class 3 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Values < 0.2 | 0.2 < Values ≤ 0.6 | 0.2 < Values < 1 | ||||||||||||
| Years | Max. | Min. | Mean | Std. Dev. | Very Low NDVI | Low to Moderately Low NDVI | Moderately High to High NDVI | Total Vegetative Cover | ||||||
| Area (km²) | Area (%) | Area (km²) | Area (%) | Area (km²) | Area (%) | (km²) | (%) | (±%) | Total Study Area (km²) | |||||
| 1998 | 0.99 | 0.10 | 0.27 | 0.13 | 9890.0 | 37.5 | 16,075.4 | 60.9 | 417.8 | 1.6 | 26,383.2 | 52.4 | −1.6 | 53,000 |
| 1999 | 0.98 | 0.10 | 0.23 | 0.10 | 12,881.7 | 46.1 | 14,994.2 | 53.7 | 70.2 | 0.3 | 27,946.0 | 55.5 | 1.5 | 53,000 |
| 2000 | 0.99 | 0.02 | 0.20 | 0.13 | 6050.0 | 83.7 | 1175.1 | 16.3 | 0 | 0.0 | 7225.1 | 14.4 | −39 | 53,000 |
| 2001 | 0.73 | 0.03 | 0.22 | 0.13 | 14,859.6 | 50.0 | 14,707.5 | 49.5 | 169.3 | 0.6 | 29,736.4 | 59.1 | 5 | 53,000 |
| 2002 | 0.73 | 0.06 | 0.23 | 0.12 | 14,320.6 | 47.6 | 15,741.6 | 52.3 | 51.3 | 0.2 | 30,113.5 | 59.8 | 5.8 | 53,000 |
| 2003 | 0.72 | 0.05 | 0.24 | 0.12 | 12,635.4 | 43.6 | 16,319.1 | 56.3 | 49.4 | 0.2 | 29,003.9 | 57.6 | 3.6 | 53,000 |
| 2004 | 0.72 | 0.04 | 0.21 | 0.12 | 15,076.6 | 49.9 | 15,109.7 | 50.0 | 11.3 | 0.0 | 30,197.6 | 60 | 6 | 53,000 |
| 2005 | 0.73 | 0.06 | 0.20 | 0.10 | 14,704.7 | 55.7 | 11,702.8 | 44.3 | 10.9 | 0.0 | 26,418.4 | 52.5 | −1.5 | 53,000 |
| 2006 | 0.78 | 0.02 | 0.21 | 0.14 | 14,744.0 | 51.7 | 13,699.3 | 48.1 | 67.8 | 0.2 | 28,511.1 | 56.7 | 2.6 | 53,000 |
| 2007 | 0.73 | 0.11 | 0.29 | 0.11 | 7802.9 | 25.7 | 22,419.1 | 73.9 | 110.2 | 0.4 | 30,332.3 | 60.3 | 6.2 | 53,000 |
| 2008 | 0.64 | 0.02 | 0.13 | 0.09 | 16,453.7 | 79.8 | 4156.1 | 20.2 | 0.1 | 0.0 | 20,609.9 | 41 | −13 | 53,000 |
| 2009 | 0.85 | 0.08 | 0.26 | 0.11 | 9091.2 | 36.3 | 15,910.7 | 63.6 | 35.4 | 0.1 | 25,037.3 | 49.7 | −4.3 | 53,000 |
| 2010 | 0.72 | 0.13 | 0.28 | 0.11 | 7873.5 | 27.3 | 20,994.2 | 72.7 | 27 | 0.1 | 28,894.7 | 57.4 | 3.4 | 53,000 |
| 2011 | 0.76 | 0.06 | 0.22 | 0.13 | 15,185.5 | 56.4 | 11,670.7 | 43.4 | 61.3 | 0.2 | 26,917.5 | 53.5 | −0.6 | 53,000 |
| 2012 | 0.72 | 0.01 | 0.20 | 0.13 | 14,024.1 | 53.1 | 12,340.4 | 46.7 | 36.9 | 0.1 | 26,401.4 | 52.5 | −1.6 | 53,000 |
| 2013 | 0.63 | 0.16 | 0.29 | 0.09 | 4636.1 | 16.5 | 23,491.1 | 83.5 | 0.3 | 0.0 | 28,127.6 | 55.9 | 1.8 | 53,000 |
| 2014 | 1.00 | 0.29 | 0.48 | 0.12 | 5674.20 | 18.4 | 25,152.7 | 81.6 | 0.0 | 0.0 | 30,826.8 | 61.3 | 7.2 | 53,000 |
| 2015 | 0.64 | 0.18 | 0.31 | 0.08 | 2076.6 | 6.5 | 29,782.4 | 93.5 | 2.2 | 0.0 | 31,861.2 | 63.3 | 9.3 | 53,000 |
| 2016 | 0.72 | 0.18 | 0.30 | 0.08 | 2984.6 | 9.2 | 29,325.5 | 90.8 | 5.1 | 0.0 | 32,315.2 | 64.2 | 10.2 | 53,000 |
| 2017 | 0.64 | 0.18 | 0.28 | 0.07 | 21.4 | 0.1 | 26,111.7 | 96.4 | 963.6 | 3.6 | 27,096.8 | 53.8 | −0.2 | 53,000 |
| Year | Class 1 <10 °C | Class 2 10–20 °C | Class 3 20–30 °C | Class 4 30–40 °C | Class 5 > 40 °C | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Area (km²) | Area (%) | Area (km²) | Area (%) | Area (km²) | Area (%) | Area (km²) | Area (%) | Area (km²) | Area (%) | |
| 1998 | 864.3 | 1.7 | 2914.5 | 5.8 | 19,465.7 | 38.7 | 23,901.7 | 47.5 | 3181.5 | 6.3 |
| 1999 | 972.8 | 1.9 | 4379.3 | 8.7 | 15,646.5 | 31.1 | 23,061.8 | 45.8 | 6267.1 | 12.5 |
| 2000 | 424.9 | 0.8 | 321.0 | 0.6 | 3135.3 | 6.2 | 18,785.7 | 37.3 | 27,660.7 | 55.0 |
| 2001 | 589.6 | 1.2 | 8546.9 | 17.0 | 26,527.3 | 52.7 | 14,639.5 | 29.1 | 24.2 | 0.0 |
| 2002 | 1892.9 | 3.8 | 14,647.2 | 29.1 | 25,793.2 | 51.3 | 7,968.2 | 15.8 | 26.0 | 0.1 |
| 2003 | 424.9 | 0.8 | 3509.7 | 7.0 | 26,701.8 | 53.1 | 19,629.0 | 39.0 | 62.2 | 0.1 |
| 2004 | 2106.9 | 4.2 | 10,379.9 | 20.6 | 31,040.3 | 61.7 | 6,588.5 | 13.1 | 211.9 | 0.4 |
| 2005 | 1208.7 | 2.4 | 6545.3 | 13.0 | 32,586.4 | 64.7 | 9,785.2 | 19.4 | 202.0 | 0.4 |
| 2006 | 291.9 | 0.6 | 3702.6 | 7.4 | 32,097.4 | 63.8 | 14,184.1 | 28.2 | 51.6 | 0.1 |
| 2007 | 388.6 | 0.8 | 4378.6 | 8.7 | 28,483.9 | 56.6 | 13,110.3 | 26.0 | 3966.2 | 7.9 |
| 2008 | 881.4 | 1.8 | 1547.2 | 3.1 | 8150.3 | 16.2 | 20,487.5 | 40.7 | 19,261.1 | 38.3 |
| 2009 | 530.7 | 1.1 | 6669.1 | 13.3 | 25,221.3 | 50.1 | 15,938.3 | 31.7 | 1968.1 | 3.9 |
| 2010 | 1471.7 | 2.9 | 14,943.1 | 29.7 | 29,135.4 | 57.9 | 4,642.8 | 9.2 | 134.6 | 0.3 |
| 2011 | 1021.7 | 2.0 | 11,501.9 | 22.9 | 31,743.5 | 63.1 | 6,038.5 | 12.0 | 22.0 | 0.0 |
| 2012 | 223.7 | 0.4 | 1737.1 | 3.5 | 19,951.8 | 39.6 | 22,213.8 | 44.1 | 6201.3 | 12.3 |
| 2013 | 219.6 | 0.4 | 1692.6 | 3.4 | 17,799.6 | 35.4 | 30,154.3 | 59.9 | 461.5 | 0.9 |
| 2014 | 1148.9 | 2.3 | 4866.5 | 9.7 | 27,964.0 | 55.6 | 16,251.3 | 32.3 | 96.8 | 0.2 |
| 2015 | 478.2 | 1.0 | 1213.3 | 2.4 | 14,941.8 | 29.7 | 25,203.0 | 50.1 | 8491.2 | 16.9 |
| 2016 | 810.0 | 1.6 | 1483.8 | 2.9 | 22,040.9 | 43.8 | 21,873.4 | 43.5 | 4119.5 | 8.2 |
| 2017 | 1895.0 | 3.8 | 3650.5 | 7.3 | 15,964.2 | 31.7 | 20,770.0 | 41.3 | 8048.0 | 16.0 |
| Longitude | Latitude | Elevation | Rainfall | LST | NDVI | |
|---|---|---|---|---|---|---|
| Longitude | 1 | |||||
| Latitude | −0.81 ** | 1 | ||||
| Elevation | 0.2 | 0.25 | 1 | |||
| Rainfall | 0.14 | 0.34 ** | 0.80 ** | 1 | ||
| LST | 0.14 | −0.59 ** | −0.78 ** | −0.83 ** | 1 | |
| NDVI | −0.03 | 0.53 ** | 0.76 ** | 0.83 ** | −0.89 ** | 1 |
| Mann–Kendall Trends | Sen’s Slope | ||||||
|---|---|---|---|---|---|---|---|
| Time Series Location Name | First Year | Last Year | N | Test Z | Sen’s Slope (Q) | Prop. | Trend (at 95% Level of Significance) |
| Erbil | 1998 | 2017 | 20 | 0.68 | 0.002 | 0.7522 | no trend |
| Qushtapa | 1998 | 2017 | 20 | 1.52 | 0.005 | 0.9364 | no trend |
| Khabat | 1998 | 2017 | 20 | 2.34 | 0.008 | 0.9903 | increasing |
| Bnaslawa | 1998 | 2017 | 20 | 1.91 | 0.006 | 0.9722 | no trend |
| harir | 1998 | 2017 | 20 | 1.65 | 0.006 | 0.9510 | no trend |
| Soran | 1998 | 2017 | 20 | 1.52 | 0.006 | 0.9364 | no trend |
| Shaqlawa | 1998 | 2017 | 20 | 1.72 | 0.005 | 0.9572 | no trend |
| Khalifan | 1998 | 2017 | 20 | 1.65 | 0.006 | 0.9510 | no trend |
| choman | 1998 | 2017 | 20 | 1.36 | 0.003 | 0.9135 | no trend |
| Sidakan | 1998 | 2017 | 20 | 1.40 | 0.004 | 0.9185 | no trend |
| Rwanduz | 1998 | 2017 | 20 | 1.56 | 0.005 | 0.9403 | no trend |
| Mergasur | 1998 | 2017 | 20 | 2.08 | 0.007 | 0.9811 | increasing |
| Dibaga | 1998 | 2017 | 20 | 1.20 | 0.004 | 0.8850 | no trend |
| Gwer | 1998 | 2017 | 20 | 1.04 | 0.003 | 0.8504 | no trend |
| barzewa | 1998 | 2017 | 20 | 2.21 | 0.006 | 0.9863 | increasing |
| Bastora | 1998 | 2017 | 20 | 0.97 | 0.002 | 0.8348 | no trend |
| Makhmoor | 1998 | 2017 | 20 | 1.23 | 0.004 | 0.8912 | no trend |
| Koya | 1998 | 2017 | 20 | 1.49 | 0.004 | 0.9322 | no trend |
| Taqtaq | 1998 | 2017 | 20 | 1.91 | 0.006 | 0.9722 | no trend |
| Shamamk | 1998 | 2017 | 20 | 0.78 | 0.003 | 0.7819 | no trend |
| Duhok | 1998 | 2017 | 20 | 1.91 | 0.004 | 0.9722 | no trend |
| semel | 1998 | 2017 | 20 | 1.30 | 0.005 | 0.9028 | no trend |
| Zakho | 1998 | 2017 | 20 | 1.20 | 0.003 | 0.8850 | no trend |
| Batel | 1998 | 2017 | 20 | 2.24 | 0.004 | 0.9874 | increasing |
| Duhok | 1998 | 2017 | 20 | 1.56 | 0.005 | 0.9403 | no trend |
| Darkar | 1998 | 2017 | 20 | 1.69 | 0.005 | 0.9542 | no trend |
| zaxo-farh | 1998 | 2017 | 20 | 0.42 | 0.002 | 0.6634 | no trend |
| Batifa | 1998 | 2017 | 20 | 1.82 | 0.006 | 0.9654 | no trend |
| kani masi | 1998 | 2017 | 20 | 3.47 | 0.012 | 0.9997 | no trend |
| Zaweta | 1998 | 2017 | 20 | 2.66 | 0.007 | 0.9961 | increasing |
| Mangish | 1998 | 2017 | 20 | 2.24 | 0.008 | 0.9874 | increasing |
| Deraluke | 1998 | 2017 | 20 | 1.98 | 0.008 | 0.9761 | no trend |
| Akre | 1998 | 2017 | 20 | 1.46 | 0.004 | 0.9279 | no trend |
| Amadia | 1998 | 2017 | 20 | 2.08 | 0.005 | 0.9811 | increasing |
| Sarsink | 1998 | 2017 | 20 | 1.20 | 0.003 | 0.8850 | no trend |
| Bamarni | 1998 | 2017 | 20 | 2.17 | 0.008 | 0.9851 | increasing |
| Bardarash | 1998 | 2017 | 20 | 0.94 | 0.003 | 0.8266 | no trend |
| Qasrok | 1998 | 2017 | 20 | 1.78 | 0.005 | 0.9628 | no trend |
| SUL | 1998 | 2017 | 20 | 1.98 | 0.005 | 0.9761 | no trend |
| Bazian | 1998 | 2017 | 20 | 2.11 | 0.005 | 0.9825 | increasing |
| Halabja | 1998 | 2017 | 20 | 2.11 | 0.005 | 0.9825 | increasing |
| Penjwen | 1998 | 2017 | 20 | 1.91 | 0.008 | 0.9722 | no trend |
| Chwarta | 1998 | 2017 | 20 | 1.40 | 0.006 | 0.9185 | no trend |
| Dukan | 1998 | 2017 | 20 | 1.40 | 0.004 | 0.9185 | no trend |
| Qaladiza | 1998 | 2017 | 20 | 1.27 | 0.003 | 0.8971 | no trend |
| Rania | 1998 | 2017 | 20 | 1.36 | 0.003 | 0.9135 | no trend |
| Said sadiq | 1998 | 2017 | 20 | 1.59 | 0.005 | 0.9441 | no trend |
| Qaradagh | 1998 | 2017 | 20 | 1.33 | 0.003 | 0.9083 | no trend |
| Arbat | 1998 | 2017 | 20 | 0.91 | 0.003 | 0.8182 | no trend |
| mwan | 1998 | 2017 | 20 | 1.65 | 0.004 | 0.9510 | no trend |
| Byara | 1998 | 2017 | 20 | 2.50 | 0.008 | 0.9938 | increasing |
| Mawat | 1998 | 2017 | 20 | 2.17 | 0.004 | 0.9851 | increasing |
| Darbandik | 1998 | 2017 | 20 | 1.91 | 0.005 | 0.9722 | no trend |
| Chamcha | 1998 | 2017 | 20 | 1.20 | 0.004 | 0.8850 | no trend |
| Kalar | 1998 | 2017 | 20 | 0.97 | 0.001 | 0.8348 | no trend |
| Agjalar | 1998 | 2017 | 20 | 0.55 | 0.002 | 0.7094 | no trend |
| bngrd | 1998 | 2017 | 20 | 1.62 | 0.004 | 0.9476 | no trend |
| Sangaw | 1998 | 2017 | 20 | 1.46 | 0.005 | 0.9279 | no trend |
| Bawanor | 1998 | 2017 | 20 | 1.49 | 0.003 | 0.9322 | no trend |
| Kifri | 1998 | 2017 | 20 | 0.71 | 0.002 | 0.7623 | no trend |
| Mann–Kendall Trends | Sen’s Slope | ||||||
|---|---|---|---|---|---|---|---|
| Time Series Location Name | First Year | Last Year | N | Test Z | Sen’s Slope (Q) | Prop. | Trend (At 95% Level of Significance) |
| Erbil | 1998 | 2017 | 20 | 2.04 | 0.456 | 0.9795 | increasing |
| Qushtapa | 1998 | 2017 | 20 | 2.08 | 0.492 | 0.9811 | increasing |
| Khabat | 1998 | 2017 | 20 | 1.10 | 0.203 | 0.8650 | no trend |
| Bnaslawa | 1998 | 2017 | 20 | 0.71 | 0.114 | 0.7623 | no trend |
| harir | 1998 | 2017 | 20 | 0.68 | 0.125 | 0.7522 | no trend |
| Soran | 1998 | 2017 | 20 | 1.07 | 0.150 | 0.8578 | no trend |
| Shaqlawa | 1998 | 2017 | 20 | 0.58 | 0.066 | 0.7204 | no trend |
| Khalifan | 1998 | 2017 | 20 | −0.06 | 0.000 | 0.4741 | no trend |
| choman | 1998 | 2017 | 20 | −1.75 | −0.242 | 0.0399 | no trend |
| Sidakan | 1998 | 2017 | 20 | −0.39 | −0.051 | 0.3485 | no trend |
| Rwanduz | 1998 | 2017 | 20 | −0.58 | −0.100 | 0.2796 | no trend |
| Mergasur | 1998 | 2017 | 20 | −1.82 | −0.698 | 0.0346 | no trend |
| Dibaga | 1998 | 2017 | 20 | 2.17 | 0.450 | 0.9851 | increasing |
| Gwer | 1998 | 2017 | 20 | 2.01 | 0.172 | 0.9779 | increasing |
| barzewa | 1998 | 2017 | 20 | −1.01 | −0.114 | 0.1573 | no trend |
| Bastora | 1998 | 2017 | 20 | 1.85 | 0.366 | 0.9678 | no trend |
| Makhmoor | 1998 | 2017 | 20 | 2.37 | 0.264 | 0.9911 | no trend |
| Koya | 1998 | 2017 | 20 | −1.40 | −0.260 | 0.0815 | no trend |
| Taqtaq | 1998 | 2017 | 20 | 0.06 | 0.010 | 0.5259 | no trend |
| Shamamk | 1998 | 2017 | 20 | 1.98 | 0.179 | 0.9761 | increasing |
| Duhok | 1998 | 2017 | 20 | −0.13 | −0.025 | 0.4484 | no trend |
| semel | 1998 | 2017 | 20 | 0.13 | 0.009 | 0.5516 | no trend |
| Zakho | 1998 | 2017 | 20 | 0.10 | 0.020 | 0.5388 | no trend |
| Batel | 1998 | 2017 | 20 | −0.03 | −0.001 | 0.4871 | no trend |
| Duhok Dam | 1998 | 2017 | 20 | 0.06 | 0.014 | 0.5259 | no trend |
| Darkar hajam | 1998 | 2017 | 20 | 0.94 | 0.183 | 0.8266 | no trend |
| zaxo−farh | 1998 | 2017 | 20 | −1.75 | −0.375 | 0.0399 | no trend |
| Batifa | 1998 | 2017 | 20 | −0.52 | −0.087 | 0.3018 | no trend |
| kani masi | 1998 | 2017 | 20 | −1.52 | −0.563 | 0.0636 | no trend |
| Zaweta | 1998 | 2017 | 20 | −1.33 | −0.400 | 0.0917 | no trend |
| Mangish | 1998 | 2017 | 20 | −2.08 | −0.470 | 0.0189 | Decreasing |
| Deraluke | 1998 | 2017 | 20 | −0.42 | −0.065 | 0.3366 | no trend |
| Akre | 1998 | 2017 | 20 | −1.69 | −0.375 | 0.0458 | no trend |
| Amadia | 1998 | 2017 | 20 | −1.07 | −0.240 | 0.1422 | no trend |
| Sarsink | 1998 | 2017 | 20 | −1.10 | −0.285 | 0.1350 | no trend |
| Bamarni | 1998 | 2017 | 20 | −2.11 | −0.717 | 0.0175 | Decreasing |
| Bardarash | 1998 | 2017 | 20 | 0.23 | 0.031 | 0.5898 | no trend |
| Qasrok | 1998 | 2017 | 20 | 0.29 | 0.056 | 0.6149 | no trend |
| Sulaymaniyah | 1998 | 2017 | 20 | 0.29 | 0.045 | 0.6149 | no trend |
| Bazian | 1998 | 2017 | 20 | −0.78 | −0.192 | 0.2181 | no trend |
| Halabja | 1998 | 2017 | 20 | 0.84 | 0.183 | 0.8005 | no trend |
| Penjwen | 1998 | 2017 | 20 | −2.95 | −0.662 | 0.0016 | Decreasing |
| Chwarta | 1998 | 2017 | 20 | −2.21 | −0.540 | 0.0137 | Decreasing |
| Dukan | 1998 | 2017 | 20 | 0.52 | 0.065 | 0.6982 | no trend |
| Qaladiza | 1998 | 2017 | 20 | −1.52 | −0.342 | 0.0636 | no trend |
| Rania | 1998 | 2017 | 20 | −0.32 | −0.087 | 0.3728 | no trend |
| Said sadiq | 1998 | 2017 | 20 | 0.42 | 0.120 | 0.6634 | no trend |
| Qaradagh | 1998 | 2017 | 20 | −0.23 | −0.023 | 0.4102 | no trend |
| Arbat | 1998 | 2017 | 20 | 0.42 | 0.111 | 0.6634 | no trend |
| mwan | 1998 | 2017 | 20 | −0.13 | −0.034 | 0.4484 | no trend |
| Byara | 1998 | 2017 | 20 | −2.30 | −0.502 | 0.0106 | Decreasing |
| Mawat | 1998 | 2017 | 20 | −1.85 | −0.468 | 0.0322 | no trend |
| Darbandikhan | 1998 | 2017 | 20 | 0.06 | 0.010 | 0.5259 | no trend |
| Chamchamal | 1998 | 2017 | 20 | 1.98 | 0.562 | 0.9761 | Increasing |
| Kalar | 1998 | 2017 | 20 | 2.01 | 0.366 | 0.9779 | Increasing |
| Agjalar | 1998 | 2017 | 20 | 1.43 | 0.324 | 0.9233 | no trend |
| bngrd | 1998 | 2017 | 20 | 1.27 | 0.211 | 0.8971 | no trend |
| Sangaw | 1998 | 2017 | 20 | 0.84 | 0.239 | 0.8005 | no trend |
| Bawanor | 1998 | 2017 | 20 | 2.01 | 0.454 | 0.9779 | Increasing |
| Kifri | 1998 | 2017 | 20 | 2.50 | 0.237 | 0.9938 | Increasing |
| y = β0 + β1 x1 + β2 x2 + β3 x3 | |||||||
|---|---|---|---|---|---|---|---|
| β0 | β1 | β2 | β3 | ||||
| Year | R | Intercept | x1 Coefficients | x2 Coefficients | x3 Coefficients | RMSE | CRM |
| 1998 | 0.77 | −2.19 | 6.4 × 10−2 | −9.9 × 10−7 | 1.6931 × 10−4 | 0.090 | 0.284 |
| 1999 | 0.80 | −1.02 | 3.0 × 10−2 | 9.790 × 10−5 | 3.0739 × 10−4 | 0.047 | 0.002 |
| 2000 | 0.80 | −1.27 | 3.5 × 10−2 | 5.872 × 10−5 | 2.4785 × 10−4 | 0.039 | 0.031 |
| 2001 | 0.72 | −0.06 | 3 × 10−3 | 1.0642 × 10−4 | 2.1147 × 10−4 | 0.062 | 0.002 |
| 2002 | 0.77 | −0.79 | 2.6 × 10−2 | 3.402 × 10−5 | 2.0132 × 10−4 | 0.056 | 0.009 |
| 2003 | 0.75 | −0.89 | 2.8 × 10−2 | 8.010 × 10−5 | 8.339 × 10−5 | 0.046 | 0.000 |
| 2004 | 0.77 | −0.94 | 2.8 × 10−2 | 2.258 × 10−5 | 2.0384 × 10−4 | 0.054 | −0.004 |
| 2005 | 0.74 | −1.03 | 2.9 × 10−2 | 7.895 × 10−5 | 1.7897 × 10−4 | 0.068 | 0.088 |
| 2006 | 0.81 | −1.35 | 4.0 × 10−2 | 1.4746 × 10−4 | 5.234 × 10−5 | 0.050 | −0.005 |
| 2007 | 0.76 | 0.26 | −5 × 10−3 | 1.1165 × 10−4 | 1.6574 × 10−4 | 0.056 | 0.011 |
| 2008 | 0.78 | −1.40 | 3.9 × 10−2 | 8.544 × 10−5 | 1.2644 × 10−4 | 0.043 | 0.016 |
| 2009 | 0.77 | −1.67 | 4.9 × 10−2 | 7.641 × 10−5 | 1.7644 × 10−4 | 0.057 | 0.000 |
| 2010 | 0.76 | −1.93 | 5.8 × 10−2 | 5.352 × 10−5 | 7.833 × 10−5 | 0.051 | 0.006 |
| 2011 | 0.84 | −2.12 | 6.1 × 10−2 | 4.172 × 10−5 | 1.9596 × 10−4 | 0.054 | −0.004 |
| 2012 | 0.74 | −0.97 | 2.9 × 10−2 | 9.920 × 10−5 | 9.931 × 10−5 | 0.050 | 0.004 |
| 2013 | 0.81 | −1.84 | 5.6 × 10−2 | 9.731 × 10−5 | 4.716 × 10−5 | 0.049 | 0.003 |
| 2014 | 0.73 | 0.86 | −1.9 × 10−2 | 1.0719 × 10−4 | 2.6338 × 10−4 | 0.065 | −0.006 |
| 2015 | 0.78 | −0.15 | 8 × 10−3 | 9.893 × 10−5 | 1.3360 × 10−4 | 0.049 | 0.005 |
| 2016 | 0.84 | −0.79 | 2.7 × 10−2 | 1.6592 × 10−4 | 4.533 × 10−5 | 0.043 | 0.007 |
| 2017 | 0.87 | −0.85 | 2.6 × 10−2 | 1.6069 × 10−4 | 1.3260 × 10−4 | 0.044 | −0.001 |
| y = β0 + β1 x1 + β2 x2 + β3 x3 | |||||||
|---|---|---|---|---|---|---|---|
| β0 | β1 | β2 | β3 | ||||
| Years | R | Intercept | x1 Coefficients | x2 Coefficients | x3 Coefficients | RMSE | CRM |
| 1998 | 0.50 | 200.326 | −4.5090 × 100 | 3.79 × 10−3 | −7.70 × 10−3 | 3.366 | −0.0019 |
| 1999 | 0.74 | 162.592 | −3.6067 × 100 | −2.98 × 10−3 | −4.37 × 10−3 | 2.736 | 0.0000 |
| 2000 | 0.63 | 115.233 | −1.8216 × 100 | −1.62 × 10−3 | −2.774 × 10−2 | 7.026 | −0.0271 |
| 2001 | 0.47 | −92.048 | 3.2245 × 100 | 3.73 × 10−3 | −2.01 × 10−3 | 4.823 | −0.0374 |
| 2002 | 0.75 | 161.735 | −3.8018 × 100 | −3.39 × 10−3 | 5.0 × 10−4 | 2.709 | 0.0158 |
| 2003 | 0.59 | −8.567 | 1.0771 × 100 | −1.60 × 10−3 | −4.29 × 10−3 | 3.745 | −0.1117 |
| 2004 | 0.68 | 42.094 | −3.318 × 10−1 | −4.21 × 10−3 | −8.13 × 10−3 | 3.456 | −2.95 × 10−5 |
| 2005 | 0.67 | −51.024 | 5.825 × 10−1 | 1.403 × 10−2 | 6.25 × 10−3 | 5.988 | 0.0121 |
| 2006 | 0.58 | 73.968 | −1.1655 × 100 | −5.41 × 10−3 | −2.93 × 10−3 | 3.709 | −0.0001 |
| 2007 | 0.66 | 137.659 | −2.9794 × 100 | 1.17 × 10−3 | −7.40 × 10−3 | 3.568 | 0.0001 |
| 2008 | 0.52 | −71.482 | 3.0436 × 100 | 1.90 × 10−3 | −2.42 × 10−3 | 3.626 | −1.17 × 10−5 |
| 2009 | 0.55 | 168.828 | −3.8644 × 100 | 4.77 × 10−3 | −9.94 × 10−3 | 4.759 | 0.0003 |
| 2010 | 0.75 | 61.496 | −7.443 × 10−1 | −1.6 × 10−4 | −1.737 × 10−2 | 4.132 | −0.0002 |
| 2011 | 0.65 | 110.496 | −2.2353 × 100 | −5.50 × 10−3 | −1.06 × 10−3 | 3.189 | −0.0001 |
| 2012 | 0.75 | 88.654 | −1.4965 × 100 | −6.09 × 10−3 | −5.20 × 10−3 | 2.774 | 0.0031 |
| 2013 | 0.85 | 36.517 | 1.13 × 10−2 | 1.11 × 10−3 | −1.716 × 10−2 | 3.840 | −0.0109 |
| 2014 | 0.83 | 130.942 | −2.6048 × 100 | −6.98 × 10−3 | −1.367 × 10−2 | 3.522 | 0.0026 |
| 2015 | 0.80 | 169.176 | −3.6726 × 100 | −1.752 × 10−2 | 3.63 × 10−3 | 4.159 | −6.24 × 10−5 |
| 2016 | 0.82 | 109.215 | −1.9879 × 100 | −5.89 × 10−3 | −1.167 × 10−2 | 3.797 | −0.0090 |
| 2017 | 0.79 | 200.224 | 4.4465 × 100 | −1.164 × 10−2 | −4.23 × 10−3 | 4.413 | 0.0008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gaznayee, H.A.A.; Al-Quraishi, A.M.F.; Mahdi, K.; Ritsema, C. A Geospatial Approach for Analysis of Drought Impacts on Vegetation Cover and Land Surface Temperature in the Kurdistan Region of Iraq. Water 2022, 14, 927. https://doi.org/10.3390/w14060927
Gaznayee HAA, Al-Quraishi AMF, Mahdi K, Ritsema C. A Geospatial Approach for Analysis of Drought Impacts on Vegetation Cover and Land Surface Temperature in the Kurdistan Region of Iraq. Water. 2022; 14(6):927. https://doi.org/10.3390/w14060927
Chicago/Turabian StyleGaznayee, Heman Abdulkhaleq A., Ayad M. Fadhil Al-Quraishi, Karrar Mahdi, and Coen Ritsema. 2022. "A Geospatial Approach for Analysis of Drought Impacts on Vegetation Cover and Land Surface Temperature in the Kurdistan Region of Iraq" Water 14, no. 6: 927. https://doi.org/10.3390/w14060927









