Combined Modeling of Multivariate Analysis and Geostatistics in Assessing Groundwater Irrigation Sustenance in the Middle Cheliff Plain (North Africa)
Abstract
:1. Introduction
2. Materials and Methods
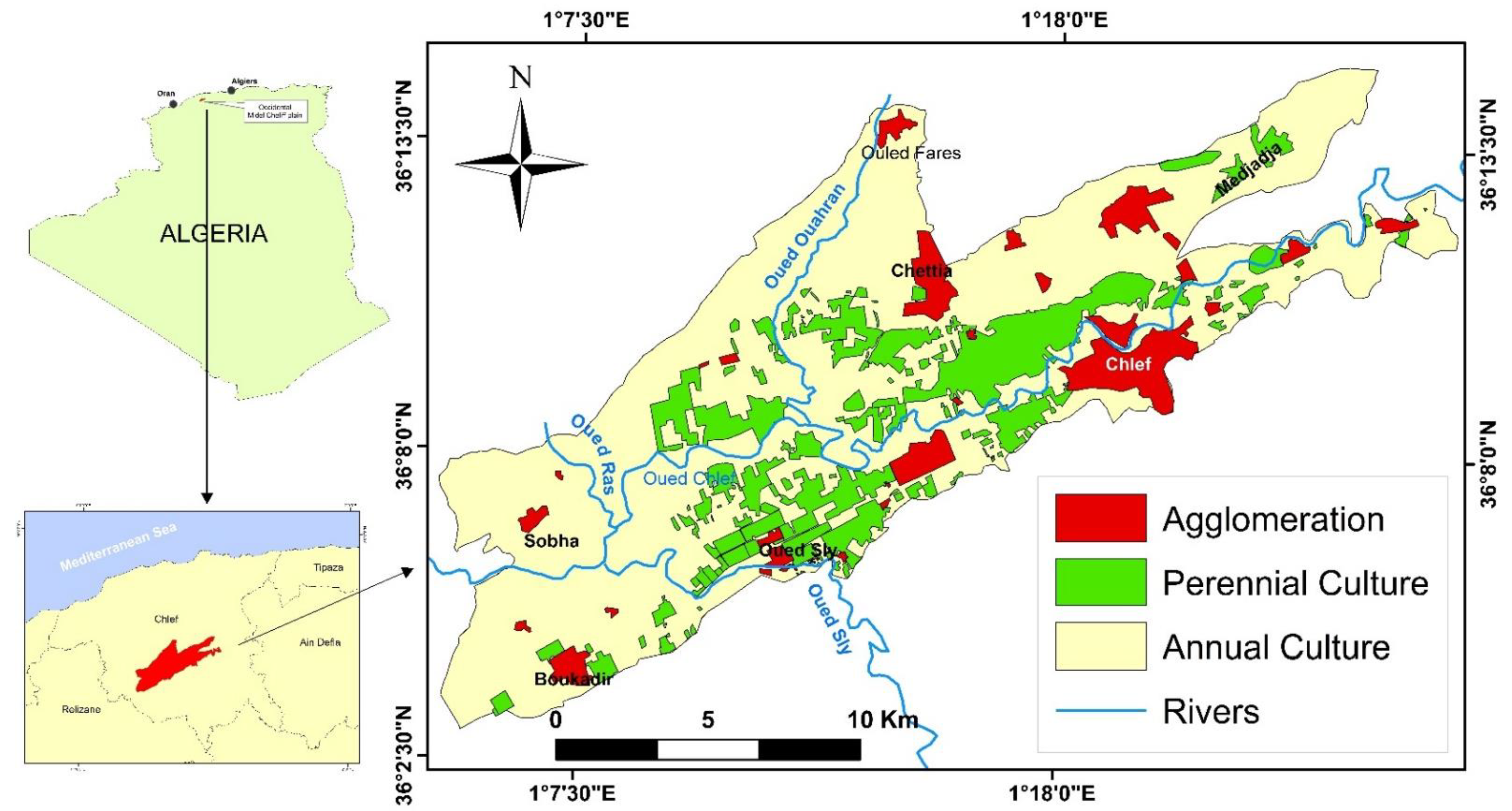
2.1. Study Area
2.2. Geological and Hydrogeological Contexts
2.3. Sampling Collecting and Analysis
2.4. Statistical Analysis Approaches
2.5. Geochemical Modelling
2.6. Geostatistical Modelling
3. Results and Discussion
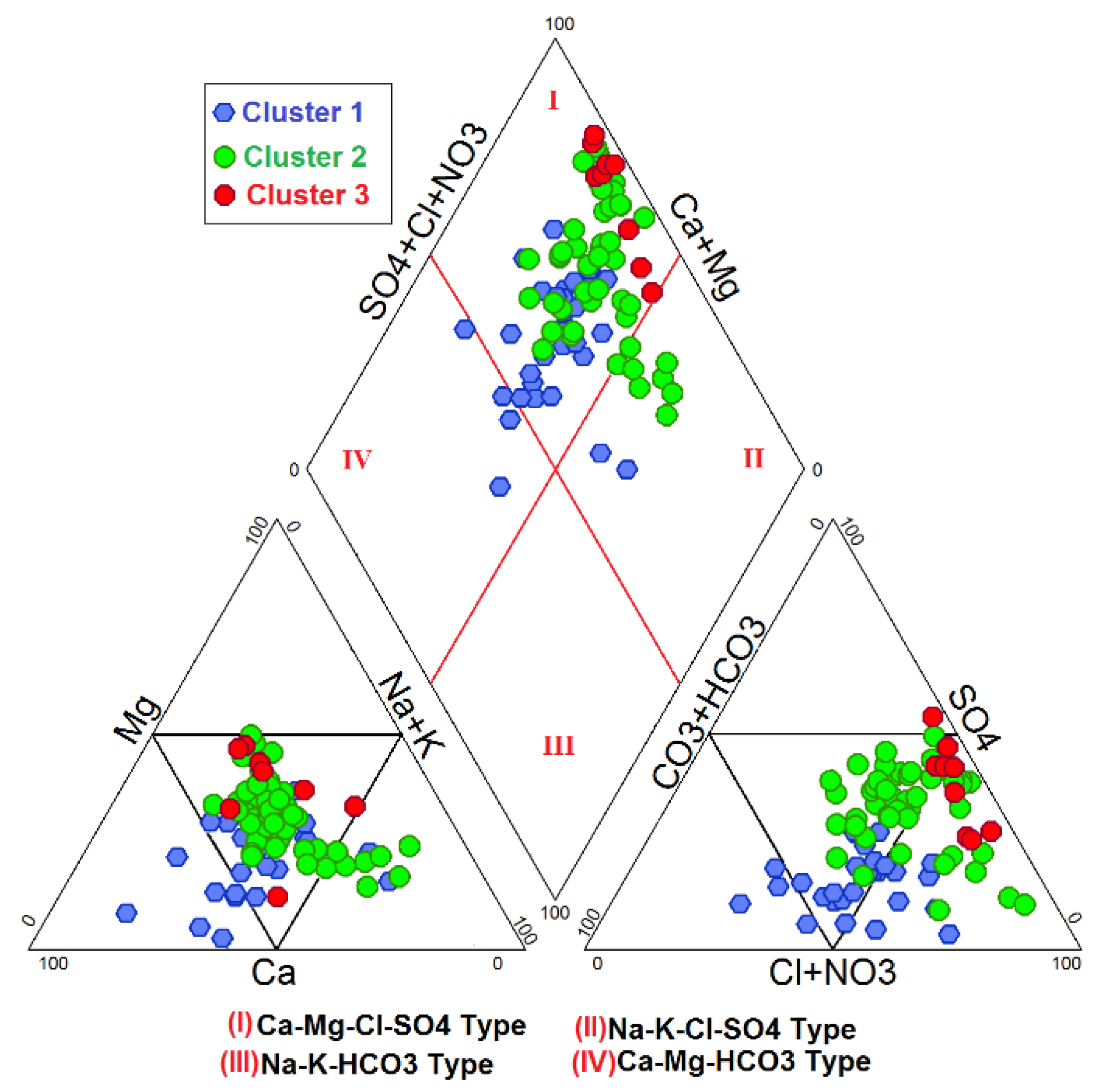
3.1. Hydrochemical Characterics of Groundwater
3.2. The Principal Component Analysis (PCA)
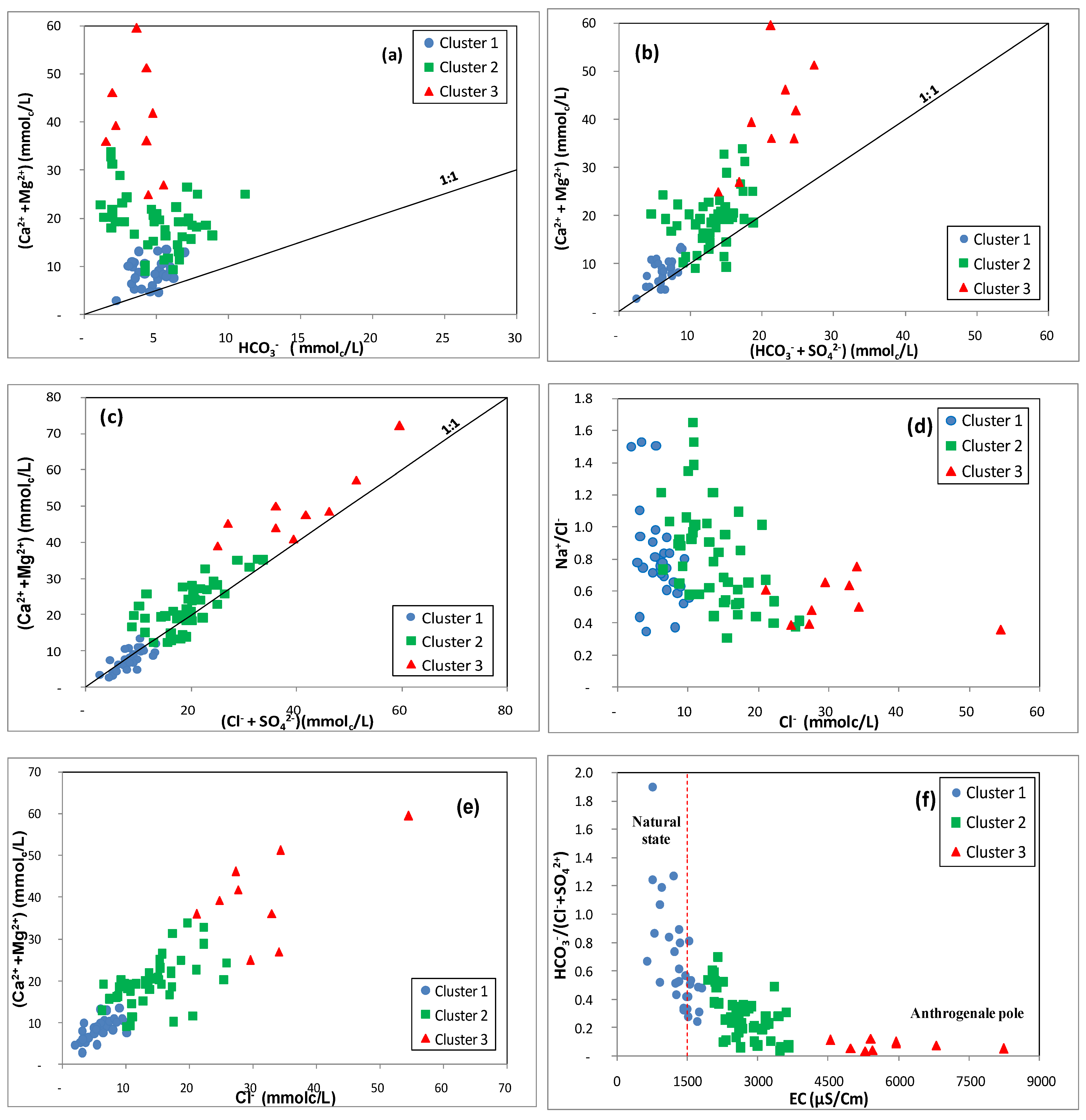
3.3. Hydrogeochemical Process
3.3.1. Evaporation
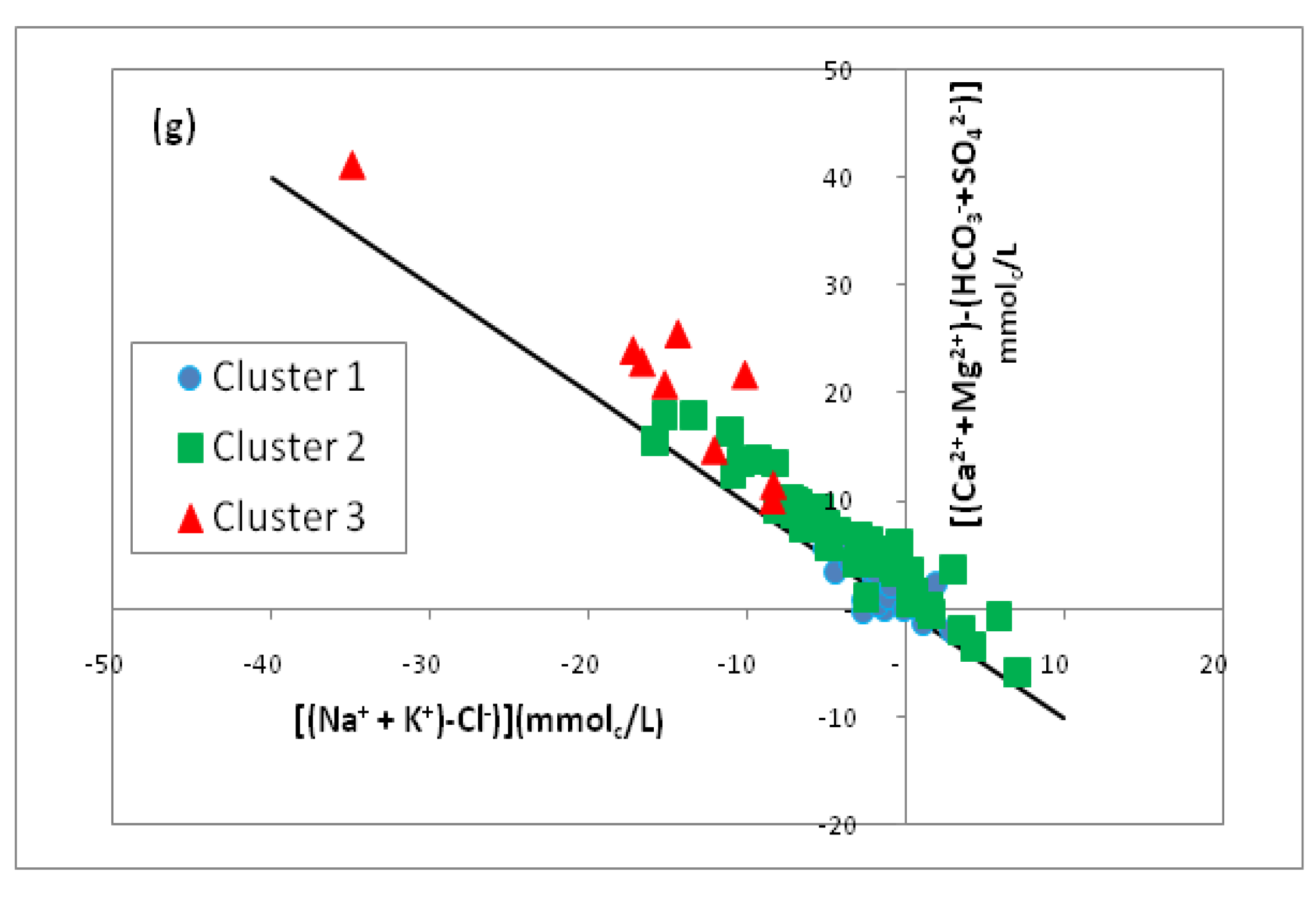
3.3.2. Ion Exchange Process
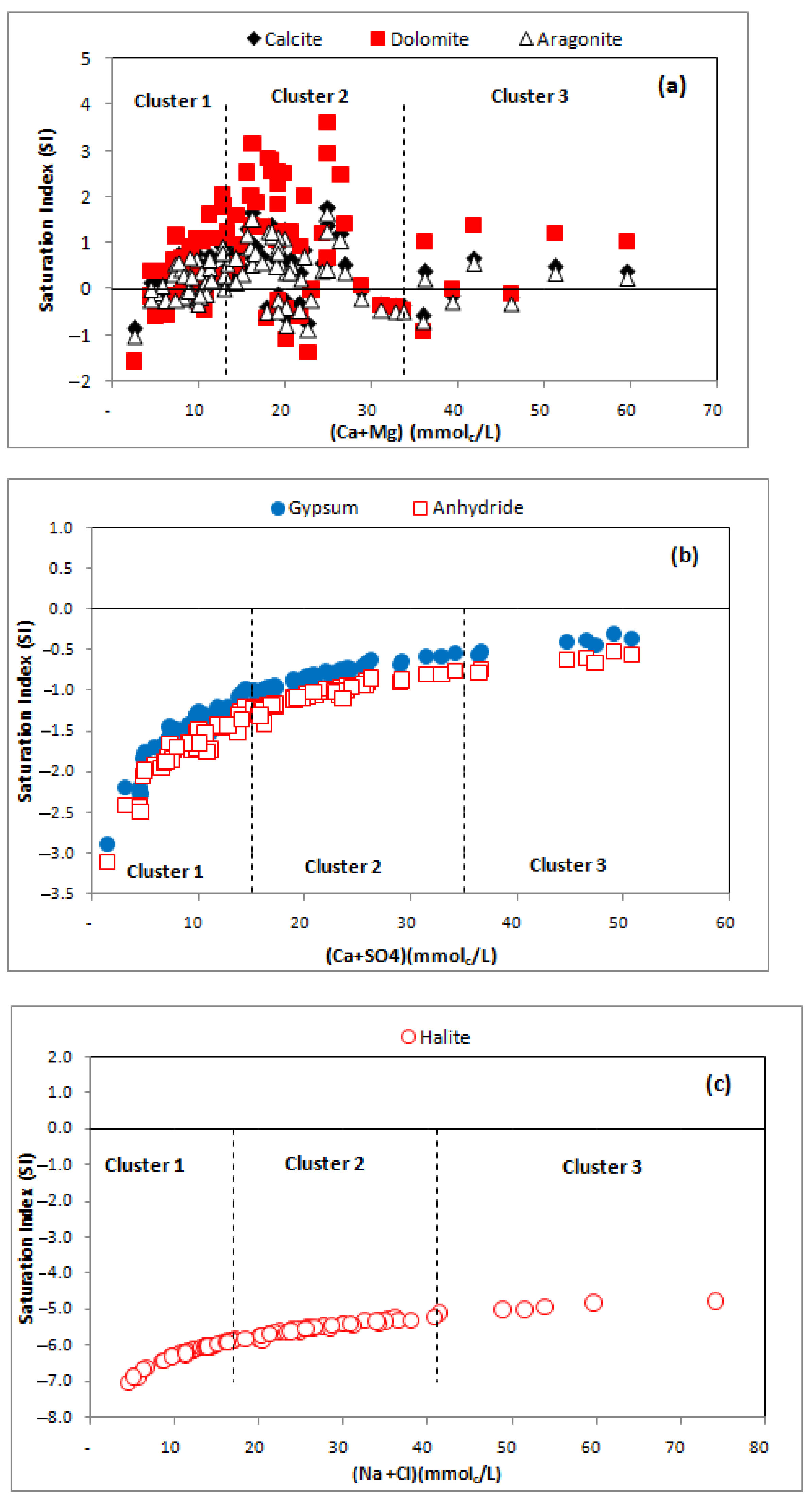
3.4. Geochemical Modelling
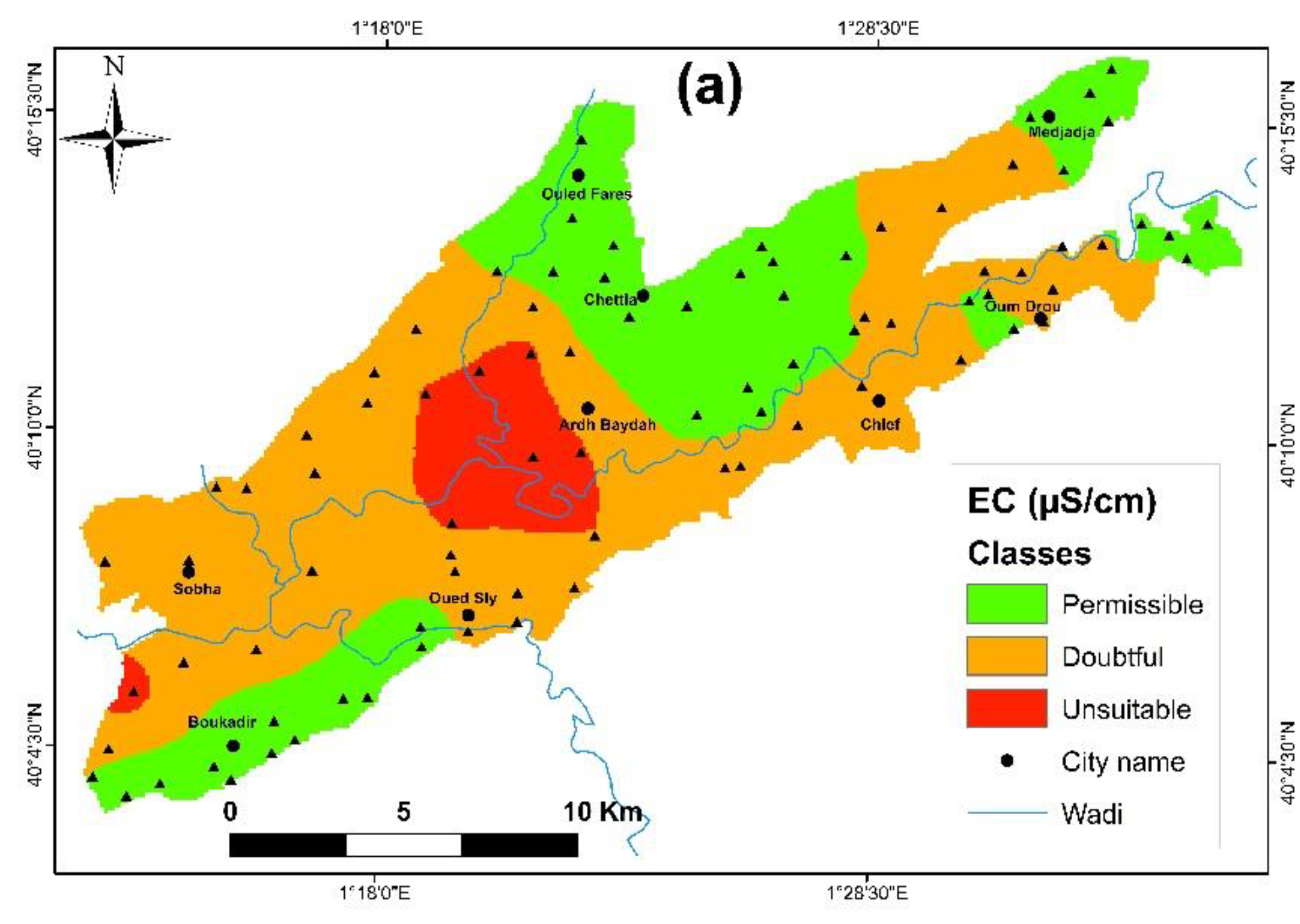
3.5. Assessment of Groundwater Irrigation Parameters
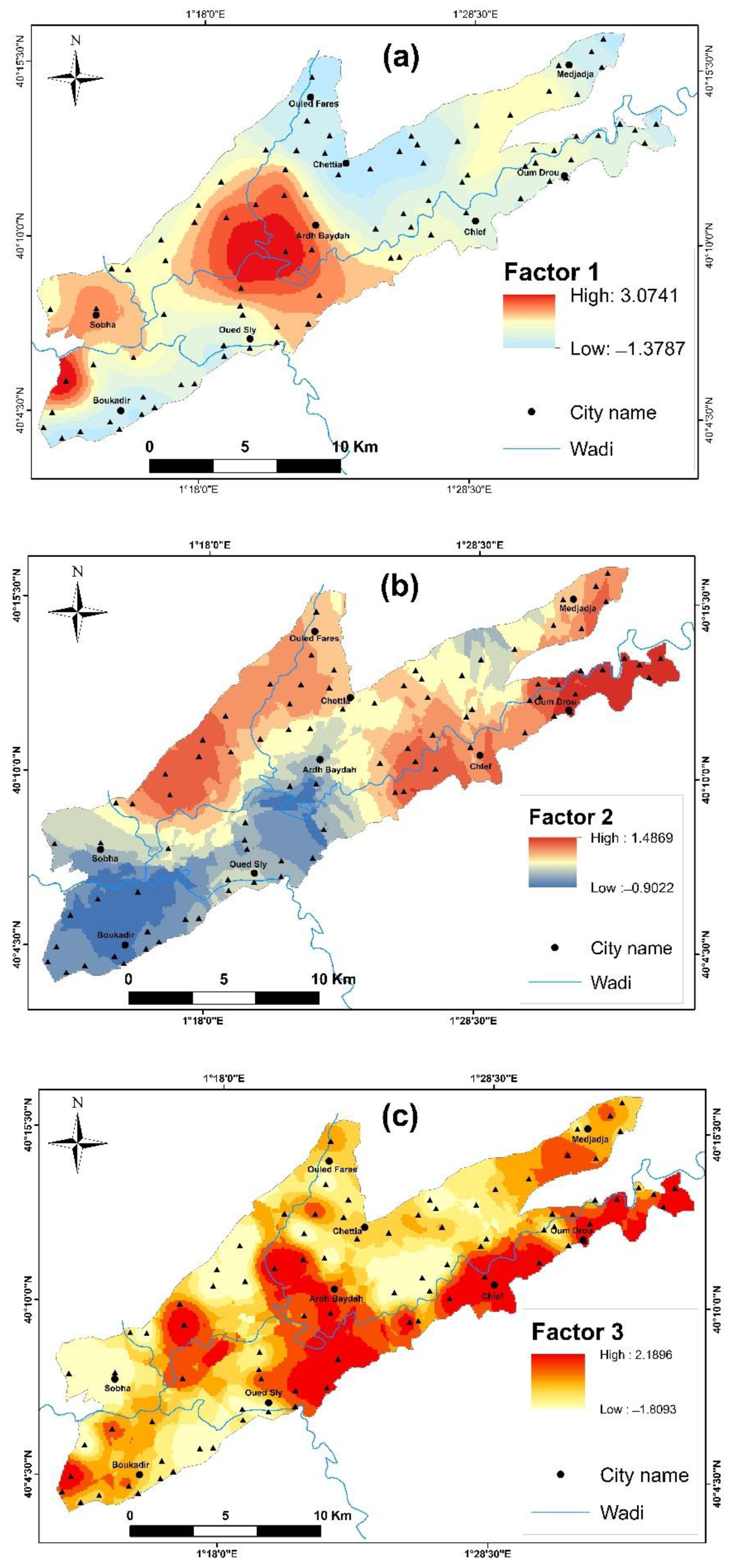
3.6. Geostatistical Modelling
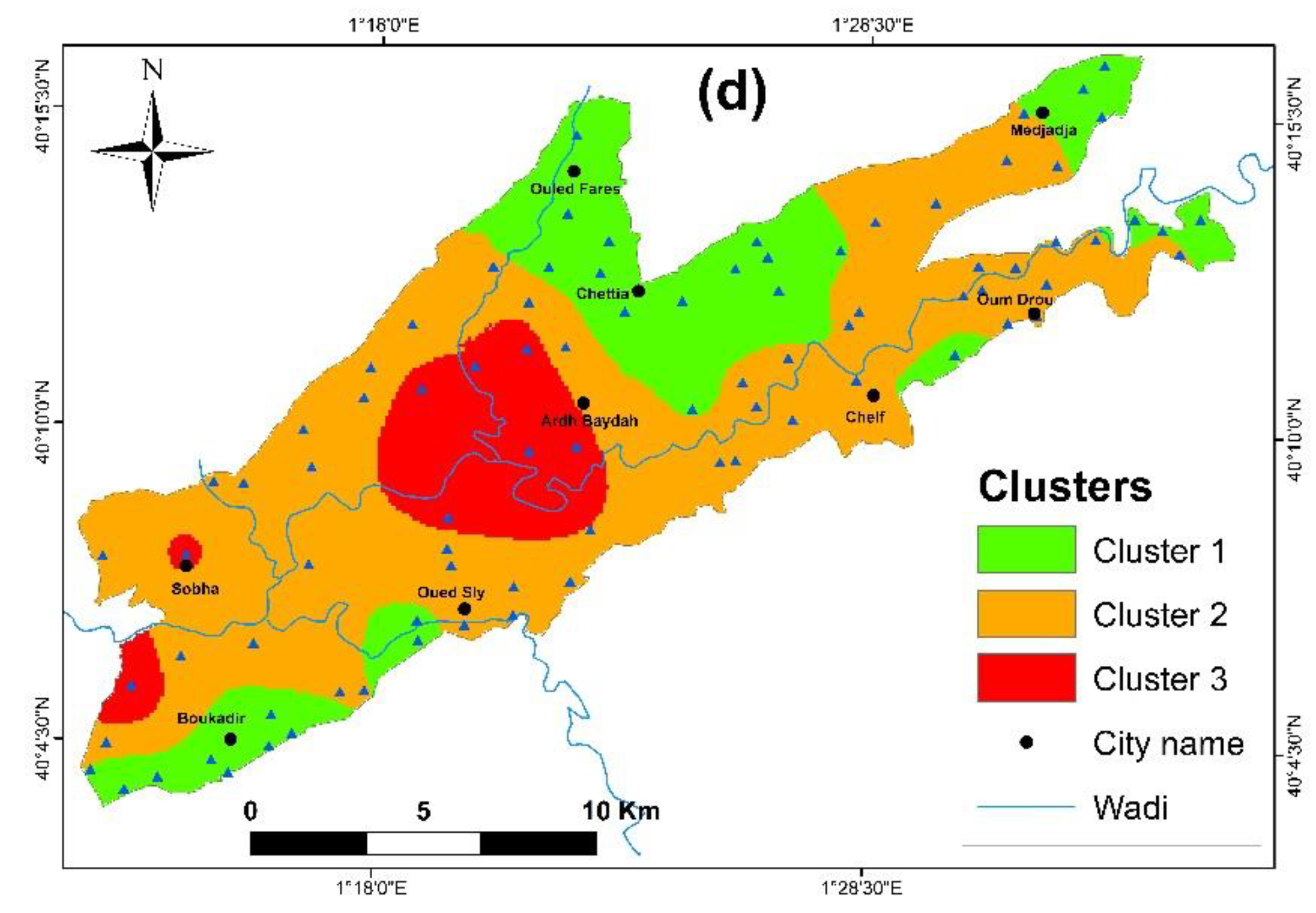
Combination of Factor Analysis and Geostatistical Modeling
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Shah, T. Groundwater Governance and Irrigated Agriculture; Paper No. 19; Global Water Partnership (GWP): Stockholm, Sweden, 2014; p. 67. [Google Scholar]
- Kuper, M.; Fayssen, N.; Hammani, A.; Hartani, T.; Marlet, S.; Hamamouche, M.F.; Ameur, F. Liberation or Anarchy? The Janus Nature of Groundwater Use on North Africa’s New Irrigation Frontiers. In Integrated Groundwater Management: Concepts, Approaches and Challenges; Jakeman, A.J., Barreteau, O., Hunt, R.J., Rinaudo, J.D., Ross, A., Eds.; Springer: Dordrecht, The Netherlands, 2016; pp. 583–615. [Google Scholar]
- Goyal, S.K.; Chaudhary, B.S.; Singh, O.; Sethi, G.K.; Thakur, P.K. GIS based spatial distribution mapping and suitability evaluation of groundwater quality for domestic and agricultural purpose in Kaithal district, Haryana state, India. Environ. Earth Sci. 2010, 61, 1587–1597. [Google Scholar] [CrossRef]
- Jangam, C.M.; Sanam, S.R.; Chaturvedi, M.K.; Padmakar, C.; Pujari, P.R.; Labhasetwar, P.K. Impact assessment of on-site sanitation system on groundwater quality in alluvial settings: A case study from Lucknow city in North India. Environ. Monit. Assess. 2015, 187, 614. [Google Scholar] [CrossRef] [PubMed]
- Alexakis, D.E. Meta-Evaluation of Water Quality Indices. Application into Groundwater Resources. Water 2020, 12, 1890. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhou, B.; Dong, F.; Liu, Z.; Ostovari, Y. Spatial Variability of Groundwater Quality for Freshwater Production in a Semi-Arid Area. Water 2021, 13, 3024. [Google Scholar] [CrossRef]
- Vasanthavigar, M.; Srinivasamoorthy, K.; Vijayaragavan, K.; Rajiv Ganthi, R.; Chidambaram, S.; Anandhan, P.; Manivannan, R.; Vasudevan, S. Application of water quality index for groundwater quality assessment: Thirumanimuttar sub-basin, Tamilnadu, India. Environ. Monit. Assess. 2010, 171, 595–609. [Google Scholar] [CrossRef] [PubMed]
- Belkhiri, L.; Boudoukha, A.; Mouni, L.; Baouz, T. Multivariate Statistical Characterization of Groundwater Quality in Ain Azel Plain, Algeria. Afr. J. Environ. Sci. Technol. 2010, 4, 526–534. [Google Scholar]
- Chebbah, M.; Allia, Z. Geochemistry and hydrogeochemical process of groundwater in the Souf valley of Low Septentrional Sahara, Algeria. Afr. J. Environ. Sci. Technol. 2015, 9, 261–273. [Google Scholar] [CrossRef]
- Bouderbala, A.; Remini, B.; Saaed Hamoudi, A.; Antonio Pulido-Bosch, A. Application of Multivariate Statistical Techniques for Characterization of Groundwater Quality in the Coastal Aquifer of Nador, Tipaza (Algeria). Acta Geophys. 2016, 64, 670–693. [Google Scholar] [CrossRef] [Green Version]
- Bouderbala, A.; Gharbi, B.Y. Hydrogeochemical characterization and groundwater quality assessment in the intensive agricultural zone of the Upper Cheliff plain, Algeria. Environ. Earth Sci. 2017, 76, 744. [Google Scholar] [CrossRef]
- Slimani, R.; Guendouz, A.; Trolard, F.; Moulla, A.S.; Hamdi-Aïssa, B.; Bourrié, G. Identification of dominant hydrogeochemical processes for groundwaters in the Algerian Sahara supported by inverse modeling of chemical and isotopic data. Hydrol. Earth Syst. Sci. 2017, 21, 1669–1691. [Google Scholar] [CrossRef] [Green Version]
- Bouteraa, O.; Mebarki, A.; Bouaicha, F.; Nouaceur, Z.; Laignel, B. Groundwater quality assessment using multivariate analysis, geostatistical modeling, and water quality index (WQI): A case of study in the Boumerzoug-El Khroub valley of Northeast Algeria. Acta Geochim. 2019, 38, 796–814. [Google Scholar] [CrossRef]
- Bouaicha, F.; Dib, H.; Bouteraa, O.; Manchar, N.; Boufaa, K.; Chabour, N.; Demdoum, A. Geochemical assessment, mixing behavior and environmental impact of thermal waters in the Guelma geothermal system, Algeria. Acta Geochim. 2019, 38, 683–702. [Google Scholar] [CrossRef]
- Bouteldjaoui, F.; Bessenasse, M.; Kettab, A.; Scheytt, T. Combining geology, hydrogeology and groundwater flow for the assessment of groundwater in the Zahrez Basin, Algeria. Arab. J. Geosci. 2019, 12, 804. [Google Scholar] [CrossRef]
- Kouadra, R.; Demdoum, A.; Chabour, N. The use of hydrogeochemical analyses and multivariate statistics for the characterization of thermal springs in the Constantine area, Northeastern Algeria. Acta Geochim. 2019, 38, 292–306. [Google Scholar] [CrossRef]
- Kouadra, R.; Demdoum, A. Hydrogeochemical characteristics of groundwater and quality assessment for the purposes of drinking and irrigation in Bougaa area, Northeastern Algeria. Acta Geochim. 2020, 39, 642–654. [Google Scholar] [CrossRef]
- Medjani, F.; Djidel, M.; Labar, S.; Bouchagoura, L.; Rezzag Bara, C. Groundwater physico-chemical properties and water quality changes in shallow aquifers in arid saline wetlands, Ouargla, Algeria. Appl. Water Sci. 2021, 11, 82. [Google Scholar] [CrossRef]
- Barkat, A.; Bouaicha, F.; Bouteraa, O.; Mester, T.; Ata, B.; Balla, D.; Rahal, Z.; Szabó, G. Assessment of Complex Terminal Groundwater Aquifer for Different Use of Oued Souf Valley (Algeria) Using Multivariate Statistical Methods, Geostatistical Modeling, and Water Quality Index. Water 2021, 13, 1609. [Google Scholar] [CrossRef]
- Francisco, S.M.; Jiménez-Espinosa, R.; Pulido-Bosch, A. Mapping groundwater quality variables using PCA and geostatistics: A case study of Bajo Andarax, southeastern Spain. Hydrol. Sci. J. 2001, 46, 227–242. [Google Scholar]
- Hao, Z.; Duoxi, Y.; Haifeng, L.; Ningning, Z.; Liang, X. Application of principal component analysis and Bayes discrimination approach in water source identification. Coal. Geol. Explor. 2017, 45, 87–93. [Google Scholar]
- Singh, K.P.; Malik, A.; Mohan, D.; Sinha, S. Multivariate statistical techniques for the evaluation of spatial and temporal variationsin water quality of Gomti River (India)—A case study. Water Res. 2004, 38, 3980–3992. [Google Scholar] [CrossRef]
- Singh, C.K.; Kumar, A.; Shashtri, S.; Kumar, A.; Kumar, P.; Mallick, J. Multivariate statistical analysis and geochemical modeling for geochemical assessment of groundwater of Delhi, India. J. Geochem. Explor. 2017, 17, 59–71. [Google Scholar]
- Mohamed, I.; Othman, F.; Ibrahim, A.I.N.; Alaa-Eldin, M.E.; Yunus, R.M. Assessment of water quality parameters using multivariate analysis for Klang River basin, Malaysia. Environ. Monit. Assess. 2015, 187, 4182. [Google Scholar] [CrossRef]
- Alberto, W.D.; Del Pilar, D.M.; Valeria, A.M.; Fabiana, P.S.; Cecilia, H.A.; De Los Angeles, B.M. Pattern recognition techniques for theevaluation of spatial and temporal variations in water quality. A case study: Suquıa River Basin (Cordoba-Argentina). Water Res. 2001, 35, 2881–2894. [Google Scholar] [CrossRef]
- Selvakumar, S.; Chandrasekar, N.; Srinivas, Y.; Selvam, S.; Kaliraj, S.; Magesh, N.S.; Venkatramanan, S. Hydrogeochemical processes controlling the groundwater salinity in the coastal aquifers of Southern Tamil Nadu, India. Mar. Pollut. Bull. 2022, 174, 113264. [Google Scholar] [CrossRef]
- Chen, K.; Liu, Q.; Peng, W.; Liu, X. Source apportionment and natural background levels of major ions in shallow groundwater using multivariate statistical method: A case study in Huaibei Plain, China. J. Environ. Manag. 2022, 301, 113806. [Google Scholar] [CrossRef]
- Azzellino, A.; Colombo, L.; Lombi, S.; Marchesi, V.; Piana, A.; Andrea, M.; Alberti, L. Groundwater diffuse pollution in functional urban areas: The need to define anthropogenic diffuse pollution background levels. Sci. Total Environ. 2019, 656, 1207–1222. [Google Scholar] [CrossRef]
- Pereira, H.G.; Renca, S.; Sataiva, J. A case study on geochemical anomaly identification through principal component analysis supplementary projection. Appl. Geochem. 2003, 18, 37–44. [Google Scholar] [CrossRef] [Green Version]
- Love, D.; Hallbauer, D.; Amos, A.; Hranova, R. Factor analysis as a tool in groundwater quality management: Two Southern Africancase studies. Phys. Chem. Earth 2004, 29, 1135–1143. [Google Scholar]
- Meng, S.X.; Maynard, J.B. Use of statistical analysis to formulate conceptual models of geochemical behavior: Water chemical data from the Botucatu aquifer in Sao Paulo state. Braz. J. Hydrol. 2001, 250, 78–97. [Google Scholar] [CrossRef]
- Chen, L.; Feng, Q. Geostatistical analysis of temporal and spatial variations in groundwater levels and quality in the Minqin oasis, Northwest China. Environ. Earth Sci. 2013, 70, 1367–1378. [Google Scholar] [CrossRef]
- Venkatramanan, S.; Chung, S.Y.; Kim, T.H.; Kim, B.W.; Selvam, S. Geostatistical techniques to evaluate groundwater contamination and its sources in Miryang City, Korea. Environ. Earth Sci. 2016, 75, 994. [Google Scholar] [CrossRef]
- Shadrin, D.; Nikitin, A.; Tregubova, P.; Terekhova, V.; Jana, R.; Matveev, S.; Pukalchik, M. An Automated Approach to Groundwater Quality Monitoring—Geospatial Mapping Based on Combined Application of Gaussian Process Regression and Bayesian Information Criterion. Water 2021, 13, 400. [Google Scholar] [CrossRef]
- El Baba, M.; Kayastha, P.; Huysmans, M.; De Smedt, F. Evaluation of the Groundwater Quality Using the Water Quality Index and Geostatistical Analysis in the Dier al-Balah Governorate, Gaza Strip, Palestine. Water 2020, 12, 262. [Google Scholar] [CrossRef] [Green Version]
- Ben Moussa, A.; Chandoul, S.; Mzali, H.; Bel Haj Salem, S.; Elmejri, H.; Zouari, K.; Hafiane, A.; Mrabet, H. Hydrogeochemistry and evaluation of groundwater suitability for irrigation purpose in the Mornag region, northeastern Tunisia. Environ. Dev. Sustain. 2021, 23, 2698–2718. [Google Scholar] [CrossRef]
- Douaoui, A.E.K.; Hervé, N.; Walter, C.H. Detecting salinity hazards with in a semiarid context by means of combining soil and remote sensing data. Geoderma 2006, 134, 217–230. [Google Scholar] [CrossRef]
- Bradaï, A.; Douaoui, A.E.K.; Bettahar, N.; Yahiaoui, I. Improving the prediction accuracy of groundwater salinity mapping using indicator kriging method. J. Irrig. Drain. Eng. ASCE 2016, 142, 04016023. [Google Scholar] [CrossRef]
- Ayers, R.S.; Westcot, D.W. Food, Water Quality for Agriculture, Irrigation and Drainage; Agriculture Organization of the United Nations (FAO): Rome, Italy, 1994; ISBN 92-5-102263-1. [Google Scholar]
- Kim, K.O.; Yun, S.T.; Choi, B.Y.; Chae, G.T.; Joo, Y.; Kim, K.; Kim, H.S. Hydrochemical and multivariate statistical interpretations of spatial controls ofnitrate concentrations in a shallow alluvial aquifer around oxbow lakes (Osongarea, central Korea). J. Contam. Hydrol. 2009, 107, 114–127. [Google Scholar] [CrossRef] [PubMed]
- Jiang, J.; Wu, Y.; Groves, C.; Yuan, D.; Kambesis, P. Natural and anthropogenic factors affecting the groundwater quality in the Nandong karst undergroundriver system in Yunan, China. J. Contam. Hydrol. 2010, 109, 49–61. [Google Scholar] [CrossRef] [PubMed]
- Yidana, S.M.; Yidana, A. Assessing groundwater quality using water quality index and multivariate statistical analysis–the Voltaian Basin, Ghana. J. Environ. Earth Sci. 2010, 59, 1461–1473. [Google Scholar] [CrossRef]
- Yidana, S.M.; Banoeng-Yakubo, B.; Akabzaa, T.M. Analysis of groundwater quality using multivariate and spatial analyses in the Keta basin, Ghana. J. Afr. Earth Sci. 2010, 58, 220–234. [Google Scholar] [CrossRef]
- Kaur, L.; Rishi, M.S.; Sharma, S.; Sharma, B.; Lata, R.; Singh, G. Hydrogeochemical characterization of groundwater in alluvial plains of river Yamuna in northern India: An insight of controlling processes. J. King Saud Univ.-Sci. 2019, 31, 1245–1253. [Google Scholar] [CrossRef]
- Office National d’Irrigation et de Drainage Centre (ONIDC). Annuel Rapport (R1); ONIDC: Alger, Algéri, 2018. [Google Scholar]
- Belmiloud, N.; Bettahar, N. Modeling the Evolution of Nitrate Pollution of Groundwater in the Plain of Western Middle Cheliff. Am. J. Environ. Sci. 2016, 12, 16–26. [Google Scholar] [CrossRef] [Green Version]
- Bradaï, A.; Douaoui, A.E.K.; Hartani, T. Some problems of irrigation water management in Lower-Cheliff plain (Algeria). J. Environ. Sci. Eng. 2012, 1, 271–278. [Google Scholar] [CrossRef]
- Amichi, H.; Bouarfa, S.; Kuper, M.; Ducourtieu, O.; Imache, A.; Fusiller, J.L.; Bazin, G.; Hartani, T.; Chehat, F. How does unequal access to groundwater contribute to marginalization of small farmers? The case of public lands in Algeria. Irrig. Drain. 2012, 61 (Suppl. 1), 34–44. [Google Scholar] [CrossRef]
- Perrodon, A. Étude Géologique des Bassins Néogènes Sublittoraux de L’Algérie Nord Occidentale. Ph.D. Thesis, Universitéd’Alger, El Djazair, Algeria, 1957. [Google Scholar]
- SCET AGRI. Bilan des ressources en sol. In Étude du Réaménagement et de L’Extension du Périmètre du Moyen Cheliff; Rap A1.2.1. Pub. Ministère de L’Hydraulique: Alger, Algerie, 1984. [Google Scholar]
- SCET AGRI. Hydrologie-Hydrogéologie et bilan des ressources. In Étude du Réaménagement et de L’Extension du Périmètre du Moyen Chéliff; Rap A1.1.2. Pub. Ministère de L’Hydraulique: Alger, Algerie, 1984. [Google Scholar]
- ABH-CZ. Cadastre Hydraulique, Mission II; Agence de Bassin Hydrographique Cheliff-Zahrez: Chlef, Algerie, 2012. [Google Scholar]
- American Public Health Association (APHA). Standard Methods for the Examination of Water and Wastewater; APHA: Washington DC, USA, 2005. [Google Scholar]
- Domenico, P.A.; Schwartz, F.W. Physical and Chemical Hydrogeology; Wiley: New York, NY, USA, 1990; pp. 410–420. [Google Scholar]
- Khanoranga; Khalid, S. An assessment of groundwater quality for irrigation and drinking purposes around brick kilns in three districts of Balochistan province, Pakistan, through water quality index and multivariate statistical approaches. J. Geochem. Explor. 2018, 197, 14–26. [Google Scholar] [CrossRef]
- SPSS Software, version 20.0; IBM SPSS Statistics for Windows; IBM Corp: Armonk, NY, USA, 2011.
- Güler, C.; Thyne, G.D.; McCray, J.E.; Turner, K.A. Evaluation of graphical and multivariate statistical methods for classification of water chemistry data. Hydrogeol. J. 2002, 10, 455–474. [Google Scholar] [CrossRef]
- Helena, B.; Pardo, R.; Vega, M.; Barrado, E.; Fernandez, J.M.; Fernandez, L. Temporal evolution of groundwater composition in an alluvial aquifer (Pissuerga River, Spain) by principal component analysis. Water Res. 2000, 34, 807–816. [Google Scholar] [CrossRef]
- Singh, P.; Mishra, P.K. Geochemical assessment of groundwater quality for its suitability for drinking and irrigation purpose in rural areas of Sant Ravidas Nagar (Bhadohi), Uttar Pradesh. Geol. Ecol. Landsc 2018, 2, 127–136. [Google Scholar]
- Kaiser, H.F. The application of electronic computers to factor analysis. Educ. Psychol. Measur. 1960, 20, 141–151. [Google Scholar] [CrossRef]
- Liu, C.W.; Lin, K.H.; Kuo, Y.M. Application of factor analysis in the assessment of groundwater quality in a blackfoot disease area in Taiwan. Sci. Total Environ. 2003, 313, 77–89. [Google Scholar] [CrossRef]
- Parkhurst, D.L.; Apelo, C.A.J. User’s Guide to PHREEQC (Version 2)—A Computer Program for Speciation, Batch-Reaction, One Dimensional Transport, and Inverse Geochemical Calculations. United States Geological Survey. In Water Resources Investigations; Report 99-4259; USGS Publications: Washington, DC, USA, 1999. [Google Scholar]
- Matheron, G. Les Variables Régionalisées et Leur Estimation. Une Application de la Théorie des Fonctions Aléatoires Aux Sciences dela Nature; Masson et CIE: Masson, Paris, 1965. [Google Scholar]
- Webster, R.; Oliver, M.A. Geostatistics for Environmental Scientist; John Wiley and Sons: Chichester, UK, 2001; p. 149. [Google Scholar]
- Delhomme, J.P. Kriging in the Hydrosciences. Adv. Water Resour. 1978, 1, 251–266. [Google Scholar] [CrossRef]
- Bodrud-Doza, M.D.; Towfiqul Islam, A.R.M.; Ahmed, F.; Das, S.; Saha, N.; Safiur Rahman, M. Characterization of groundwater quality using water evaluation indices, multivariate statistics and geostatistics in central Bangladesh. Water Sci. 2016, 30, 19–40. [Google Scholar] [CrossRef] [Green Version]
- Piper, A.M. A graphic procedure in the geochemical interpretation of water-analyses. Trans. Am. Geophys. Union 1944, 25, 914–928. [Google Scholar] [CrossRef]
- Wilcox, L.V. Classification and Use of Irrigation Waters; US Department of Agriculture: Washington, DC, USA, 1955; p. 969.
- Chadha, D.K. A proposed new diagram for geochemical classification of natural waters and interpretation of chemical data. Hydrogeol. J. 1999, 7, 431–439. [Google Scholar] [CrossRef]
- Thilagavathi, R.; Chidambaram, S.; Prasanna, M.V.; Thivya, C.; Singaraja, C. A study on groundwater geochemistry and water quality in layered aquifers system of Pondicherry region, southeast India. Appl. Water Sci. 2012, 2, 253–269. [Google Scholar] [CrossRef] [Green Version]
- Subramani, T.; Rajmohan, N.; Elango, L. Groundwater geochemistry and identification of hydrogeochemical processes in a hard rock region, Southern India. Environ. Monit. Assess. 2010, 162, 123–137. [Google Scholar] [CrossRef] [PubMed]
- Sami, K. Recharge mechanisms and geochemical processes in a semi-arid sedimentary basin, Eastern Cape, South Africa. J Hydrol. 1992, 139, 27–48. [Google Scholar] [CrossRef]
- Krishnaraj, S.; Murugesan, V.; Vijayaraghavan, K.; Sabarathinam, C.; Paluchamy, A.; Ramachandran, M. Use of hydrochemistry and stable isotopes as tools for groundwater evolution and contamination investigations. Geosciences 2011, 1, 16–25. [Google Scholar] [CrossRef]
- Hounslow, A.W. Water Quality Data: Analysis and Interpretation; CRC Lewis Publishers: New York, NY, USA, 1995. [Google Scholar]
- May, A.L.; Loucks, M.D. Solute and isotopic geochemistry and groundwater flow in the Central Wasatch range, Utah. J. Hydrol. 1995, 172, 31–59. [Google Scholar] [CrossRef]
- Tziritis, E.; Skordas, K.; Kelepertsis, A. The use of hydrogeochemical analyses and multivariate statistics for the characterization of groundwater resources in a complex aquifer system. A case study in Amyros River basin, Thessaly, central Greece. Environ. Earth Sci. 2016, 75, 339. [Google Scholar] [CrossRef]
- Kumar, P.S.; Jegathambal, P.; James, E.J. Multivariate and geostatistical analysis of groundwater quality in Palar river basin. Int. J. Geol. 2011, 4, 108–119. [Google Scholar]
- Li, P.; Zhang, Y.; Yang, N.; Jing, L.; Yu, P. Major ion chemistry and quality assessment of groundwater in and around a mountainous tourist town of China. Expos. Health 2016, 8, 239–252. [Google Scholar] [CrossRef]
- Fisher, R.S.; Mulican, W.F.I. Hydrochemical evaluation of sodium-sulphate and sodium-chloride groundwater beneath the northern Chihuahuan desert, trans-Pecos, Texas USA. Hydrogeol. J. 1997, 10, 455–474. [Google Scholar]
- Sheikhy Narany, T.; Ramli, M.F.; Aris, A.Z.; Sulaiman, W.N.A.; Fakharian, K. Spatiotemporal variation of groundwater quality using integrated multivariate statistical and geostatistical approaches in Amol-Babol Plain, Iran. Environ. Monit. Assess. 2014, 186, 5797–5815. [Google Scholar] [CrossRef] [PubMed]
- Clark, I.D. Groundwater Geochemistry and Isotopes; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Rajmohan, N.; Elango, L. Identification and evolution of hydrogeochemical processes in the groundwater environment in an area of the Palar and Cheyyar River Basins, southern India. Environ. Geol. 2004, 46, 47–61. [Google Scholar] [CrossRef]
- Appelo, C.A.; Postma, D. Geochemistry, Groundwater and Pollution; Balkema: Rotterdam, The Netherlands, 1993. [Google Scholar]
- Güler, C.; Thyne, G.D. Hydrologic and geologic factors controlling surface and groundwater chemistry in Indian wells-Owens valley area, southeastern California, USA. J. Hydrol. 2004, 285, 177–198. [Google Scholar] [CrossRef]
- Tarki, M.; Dassi, L.; Hamed, Y.; Jedoui, Y. Geochemical and isotopic composition of groundwater in the Complex Terminal aquifer in southwestern Tunisia, with emphasis on the mixing by vertical leakage. Environ. Earth Sci. 2010, 64, 85–95. [Google Scholar] [CrossRef]
- Tijani, M.N. Hydrochemical assessment of groundwater in Moro area, Kwara State, Nigeria. Environ. Geol. 1994, 24, 194–202. [Google Scholar] [CrossRef]
- Richards, L.A. Diagnosis and Improvement of Saline and Alkaline Soils. Soil Sci. 1954, 64, 432. [Google Scholar] [CrossRef]
- Collins, R.; Jenkins, A. The Impact of Agricultural Land Use on Stream Chemistry in the Middle Hills of the Himalayas, Nepal. J. Hydrol. 1996, 185, 71–86. [Google Scholar] [CrossRef]
- Arslan, H. Spatial and temporal mapping of groundwater salinity using ordinary kriging and indicator kriging: The case of Bafra Plain, Turkey. Agric. Water Manag. 2012, 113, 57–63. [Google Scholar] [CrossRef]
- Ohmer, M.; Liesch, T.; Goeppert, N.; Goldscheider, N. On the optimal selection of interpolation methods for groundwater contouring: An example of propagation of uncertainty regarding inter-aquifer exchange. Adv. Water Resour. 2017, 109, 121–132. [Google Scholar] [CrossRef]
- Marlet, S.; Job, J.O. Processus et gestion de la salinite’ des sols. In Traité D’Irrigation, 2nd ed.; Tiercelin, J.R., Vidal, A., Eds.; Tec & Doc., Lavoisier: Paris, France, 2006. [Google Scholar]









| Variables | Units | Cluster 1 (31 Samples) | Cluster 2 (47 Samples) | Cluster 3 (9 Samples) | Ayers and Westcot (1994) [39] | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Min | Max | Mean | SD | Min | Max | Mean | SD | Min. | Max. | Mean | SD | |||
| Ca | mg/L | 25 | 198 | 109.6 | 38.9 | 73 | 292 | 196.4 | 49.9 | 186 | 500 | 366.2 | 32.8 | 400 |
| Mg | 4.74 | 89.5 | 38.6 | 21.1 | 40 | 241 | 111.6 | 45.9 | 67 | 415 | 263.4 | 33.1 | 60 | |
| Na | 31.6 | 190 | 104.9 | 36.1 | 110 | 480 | 242.2 | 85.9 | 220 | 590 | 381.0 | 40.8 | 919 | |
| K | 0.5 | 4.6 | 2.7 | 1.0 | 0 | 13 | 2.5 | 2.4 | 0 | 5 | 1.9 | 0.6 | 12 | |
| Cl | 72 | 361 | 214.9 | 76.8 | 222.3 | 919.5 | 494.8 | 174.2 | 750 | 937.5 | 1129.8 | 113.7 | 1063 | |
| SO4 | 13 | 361 | 119.6 | 79.3 | 117.3 | 957 | 479.7 | 196.2 | 580 | 400 | 1077.8 | 97.6 | 960 | |
| HCO3 | 137 | 427 | 275.2 | 68.1 | 70 | 683.2 | 312.5 | 142.5 | 93 | 336 | 221.3 | 28.4 | 630 | |
| NO3 | 13.1 | 150 | 64.9 | 31.5 | 6 | 63.2 | 25.1 | 12.7 | 0 | 5 | 2.1 | 1.69 | 10 | |
| EC | µS/cm | 802 | 1826 | 1358.7 | 282.9 | 1926 | 3658 | 2725.9 | 495.8 | 4550 | 8230 | 5843.3 | 1100.9 | 3000 |
| pH | - | 7.05 | 7.85 | 7.36 | 0.20 | 6.80 | 8.31 | 7.5 | 0.4 | 6.8 | 7.51 | 7.20 | 0.22 | 8.5 |
| Variables | Component Data Values | ||
|---|---|---|---|
| First Component | Second Component | Third Component | |
| EC | 0.955 | 0.006 | 0.093 |
| Cl | 0.911 | −0.178 | 0.148 |
| Ca | 0.877 | −0.023 | 0.212 |
| SO4 | 0.867 | −0.154 | 0.254 |
| Mg | 0.863 | −0.205 | 0.290 |
| Na | 0.796 | 0.154 | −0.055 |
| pH | −0.060 | 0.983 | −0.041 |
| HCO3 | −0.071 | 0.957 | −0.195 |
| K | −0.032 | 0.282 | −0.837 |
| NO3 | 0.394 | 0.049 | 0.769 |
| Initial Eigenvalues of variances in % | 48.087 | 20.861 | 15.578 |
| Cumulative of variance % | 48.087 | 68.948 | 84.526 |
| Anhydrite | Calcite | Dolomite | Gypsum | Halite | |
|---|---|---|---|---|---|
| Cluster 1 | |||||
| Min | −3.11 | −1.02 | − 0.87 | −1.57 | −2.89 |
| Max | −1.21 | 0.91 | 1.05 | 2.05 | −0.99 |
| Mean | −1.84 | 0.08 | 0.22 | 0.29 | −1.62 |
| SD | 0.39 | 0.39 | 0.39 | 0.70 | 0.39 |
| Cluster 2 | |||||
| Min | −1.76 | −0.89 | −0.75 | −1.37 | −1.54 |
| Max | −0.77 | 1.63 | 1.77 | 3.6 | −0.55 |
| Mean | −1.14 | 0.39 | 0.53 | 1.15 | −0.92 |
| SD | 0.23 | 0.64 | 0.64 | 1.23 | 0.23 |
| Cluster 3 | |||||
| Min | −1.10 | −0.72 | −0.58 | −0.92 | −0.88 |
| Max | −0.53 | 0.54 | 0.68 | 1.42 | −0.31 |
| Mean | −0.71 | 0.08 | 0.23 | 0.63 | −0.50 |
| SD | 0.17 | 0.42 | 0.43 | 0.80 | 0.17 |
| Parameters | Range | Class | Number of Samples | Percent |
|---|---|---|---|---|
| EC (µS/cm) (Wilox 1955) [68] | C1 < 250 | Excellent | 0 | 0 |
| 250 < C2 < 750 | Good | 0 | 0 | |
| 750 < C3 < 2250 | permissible | 41 | 47.13 | |
| 2250 < C4 < 5000 | Doubtful | 39 | 44.83 | |
| C5 > 5000 | Unsuitable | 7 | 8.04 | |
| % Na (Wilox 1955) [68] | 0–20 | Excellent | 5 | 5.75 |
| 20–40 | Good | 63 | 72.41 | |
| 40–60 | Permissible | 15 | 17.24 | |
| 60–80 | Doubtful | 4 | 4.6 | |
| >80 | Unsuitable | 0 | 0 | |
| SAR (Richards 1954) [87] | S1 < 10 | Excellent | 87 | 100 |
| 10 < S2 < 18 | good | 0 | 0 | |
| 18 < S3 < 26 | Doubtful | 0 | 0 | |
| S4 > 26 | unsuitable | 0 | 0 |
| Variogram Parameters | Prediction Precision | |||||||
|---|---|---|---|---|---|---|---|---|
| Parameters | Transformation | Model | Nugget (C0) | Partial Sill (C) | Spatial Dependence | Mean | Root-Mean- Square Standardized Error | |
| EC | Log | Exponential | 0.0154 | 0.2927 | 4.99 | Strong | 0.125 | 0.9441 |
| %Na | Log | Rational Quadratic | 0.0499 | 0.0471 | 51.44 | Moderate | −0.178 | 1.0283 |
| SAR | Log | Spherical | 0.0783 | 0.1506 | 34.21 | Moderate | −0.009 | 1.0440 |
| Factor 1 | Original Data | Spherical | 0.0968 | 0.9916 | 8.89 | Strong | 0.0132 | 1.1242 |
| Factor 2 | Original Data | Spherical | 0.8051 | 0.2252 | 78.14 | Weak | −0.0073 | 0.9972 |
| Factor 3 | Original Data | Spherical | 0.1388 | 0.8247 | 14.40 | Strong | −0.0362 | 1.0304 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bradai, A.; Yahiaoui, I.; Douaoui, A.; Abdennour, M.A.; Gulakhmadov, A.; Chen, X. Combined Modeling of Multivariate Analysis and Geostatistics in Assessing Groundwater Irrigation Sustenance in the Middle Cheliff Plain (North Africa). Water 2022, 14, 924. https://doi.org/10.3390/w14060924
Bradai A, Yahiaoui I, Douaoui A, Abdennour MA, Gulakhmadov A, Chen X. Combined Modeling of Multivariate Analysis and Geostatistics in Assessing Groundwater Irrigation Sustenance in the Middle Cheliff Plain (North Africa). Water. 2022; 14(6):924. https://doi.org/10.3390/w14060924
Chicago/Turabian StyleBradai, Abdelhamid, Ibrahim Yahiaoui, Abdelkader Douaoui, Mohamed Amine Abdennour, Aminjon Gulakhmadov, and Xi Chen. 2022. "Combined Modeling of Multivariate Analysis and Geostatistics in Assessing Groundwater Irrigation Sustenance in the Middle Cheliff Plain (North Africa)" Water 14, no. 6: 924. https://doi.org/10.3390/w14060924








