Blending Irrigation Water Sources with Different Salinities and the Economic Damage of Salinity: The Case of Israel
Abstract
:1. Introduction
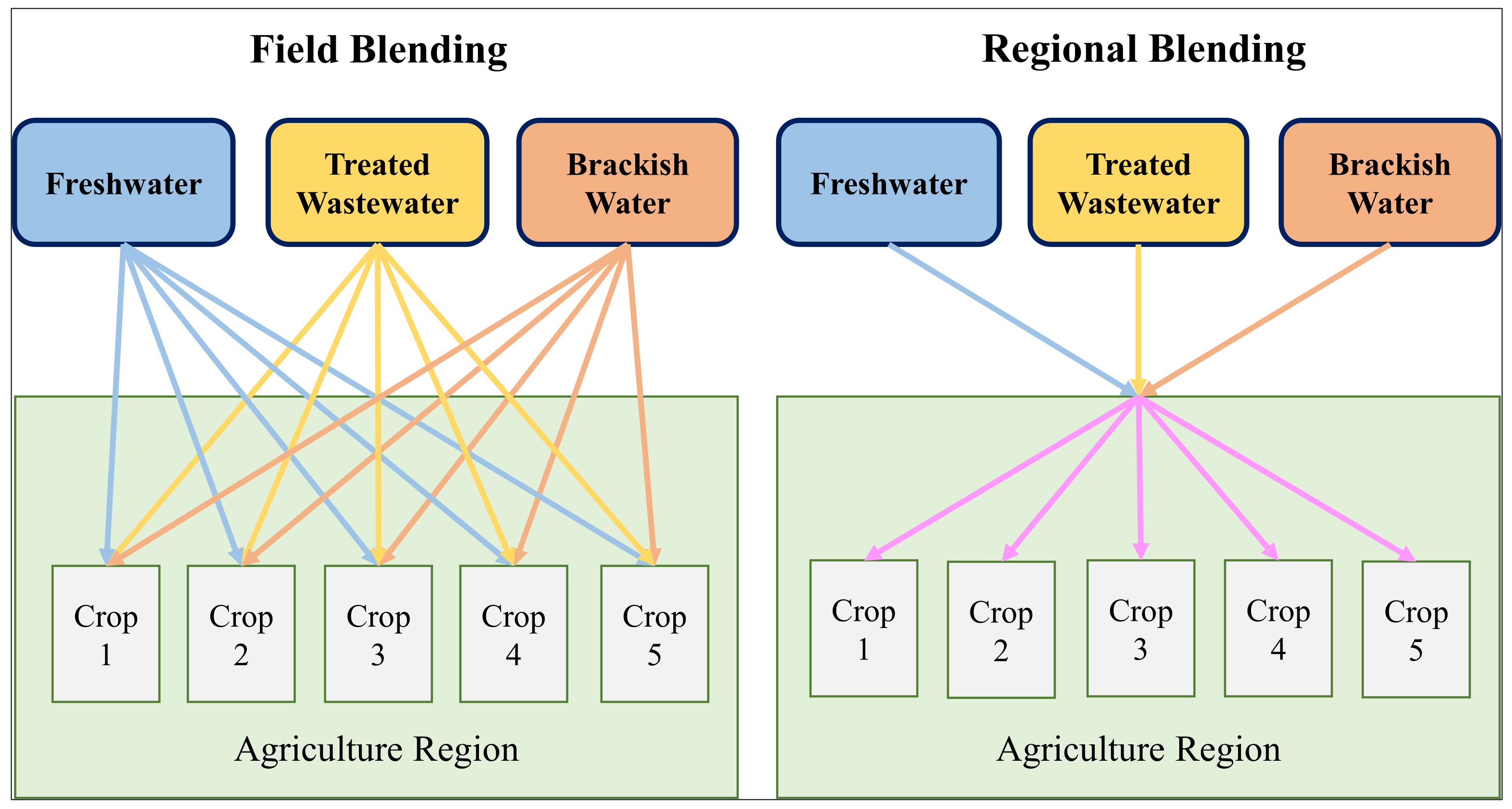
2. Methods
3. Results
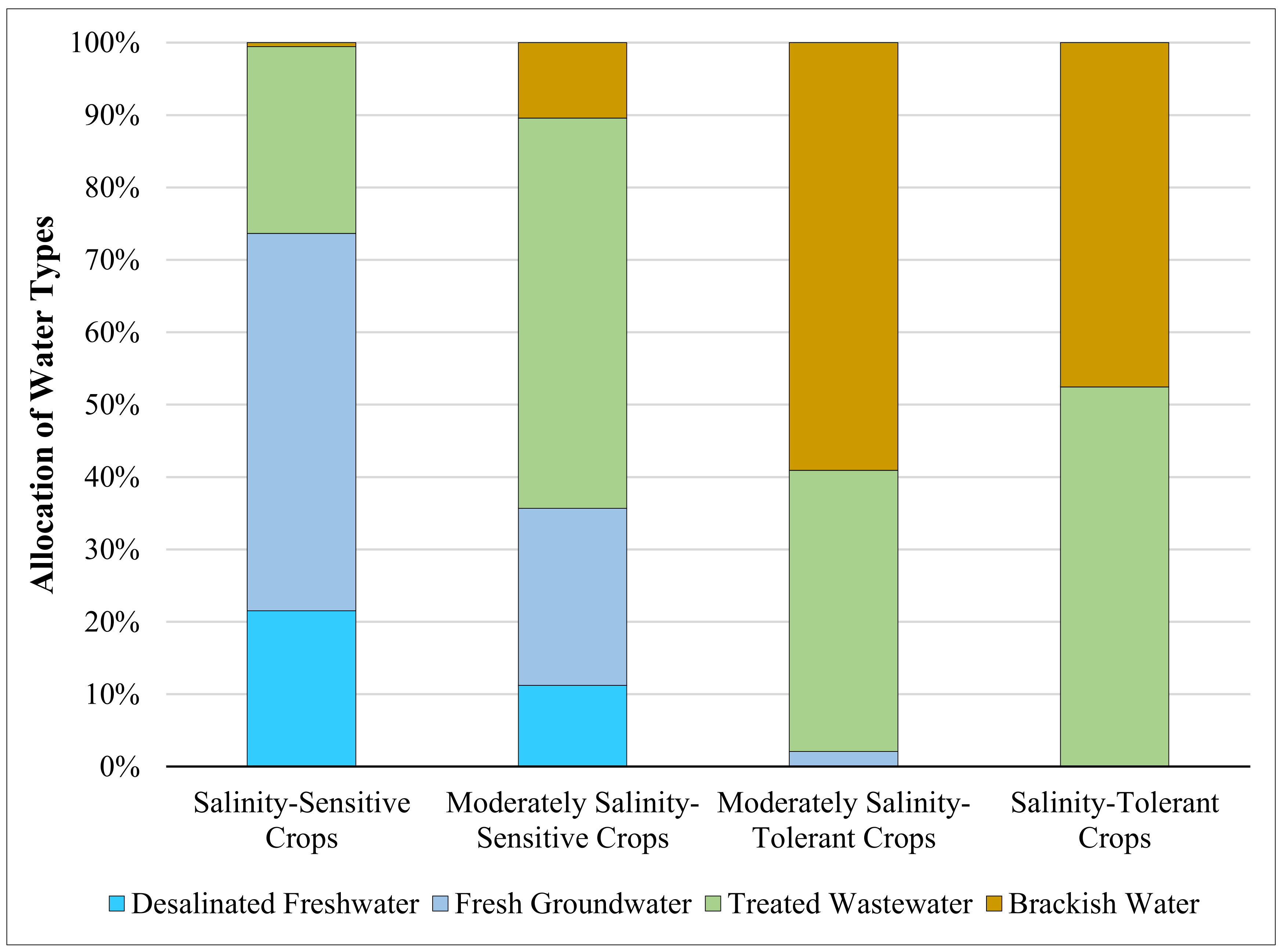
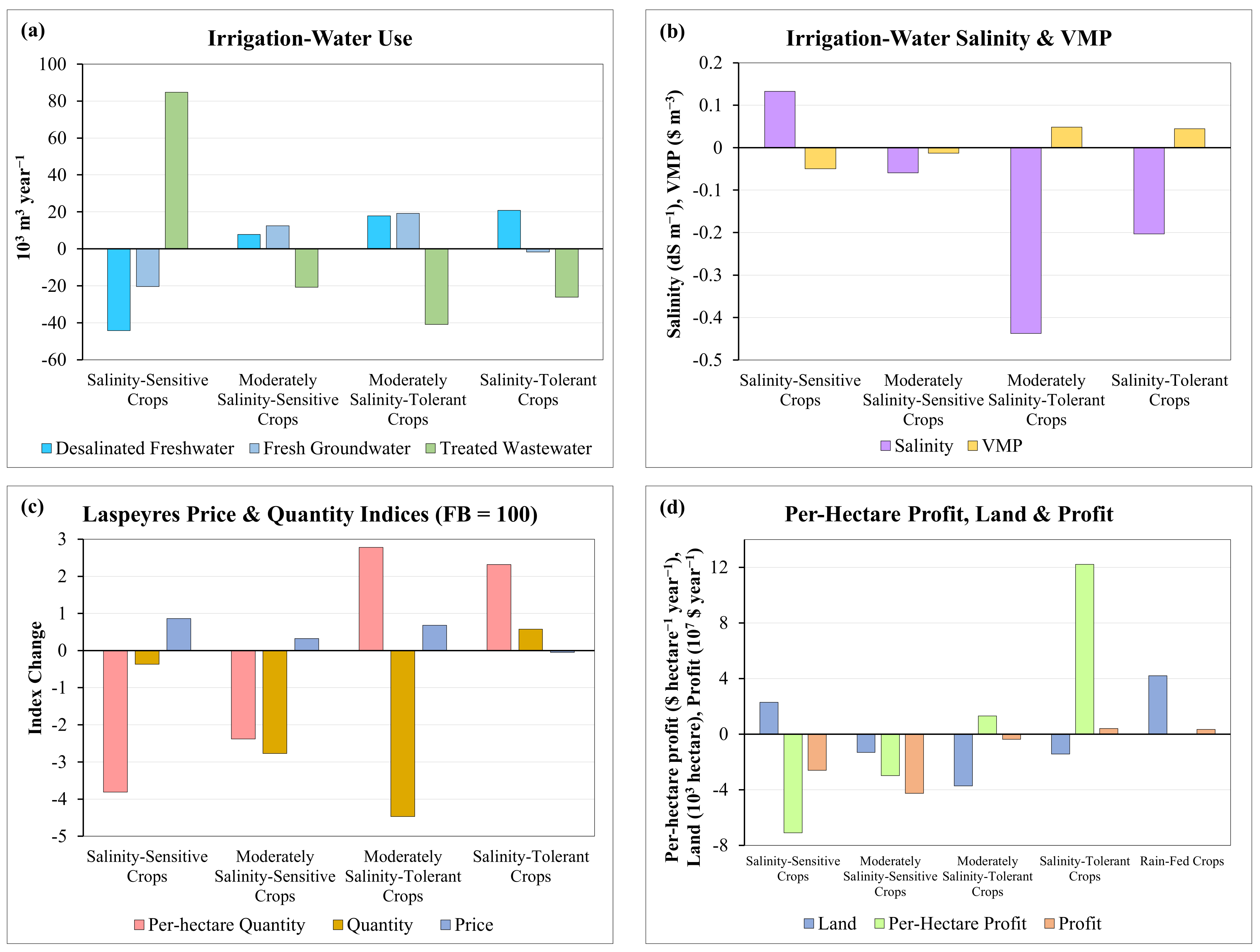
3.1. Water Supply
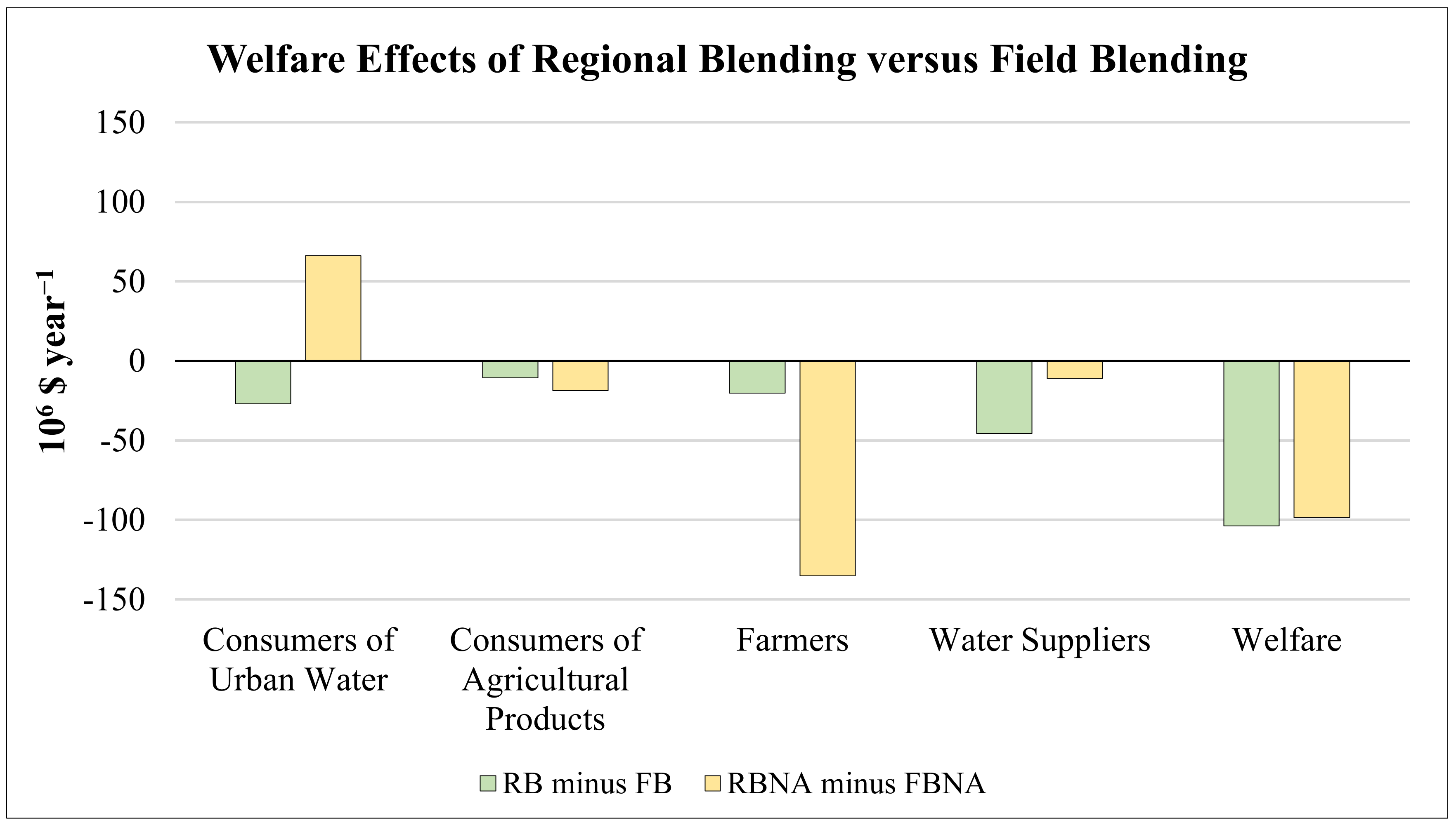
3.2. Welfare
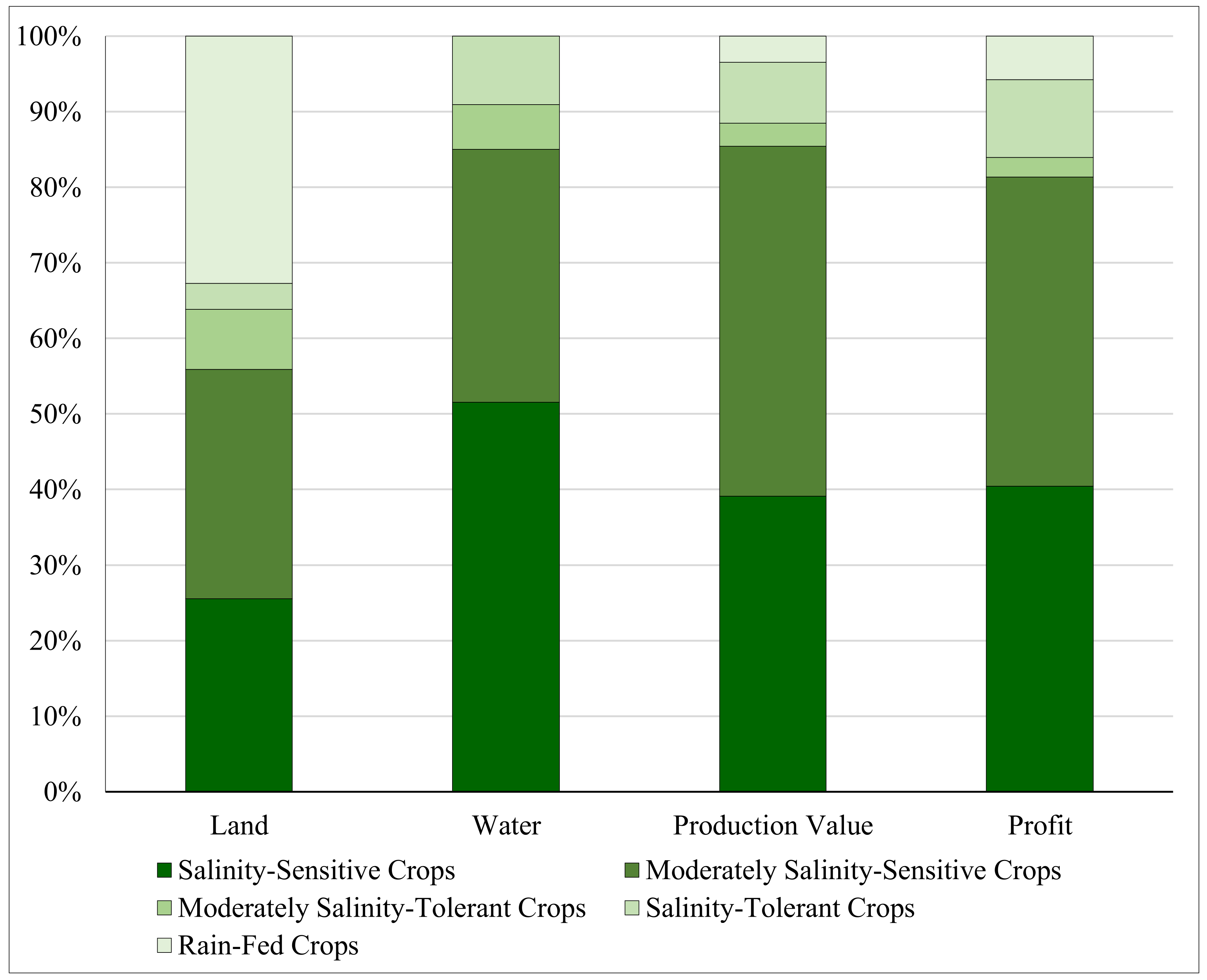
3.3. Land and Water Management
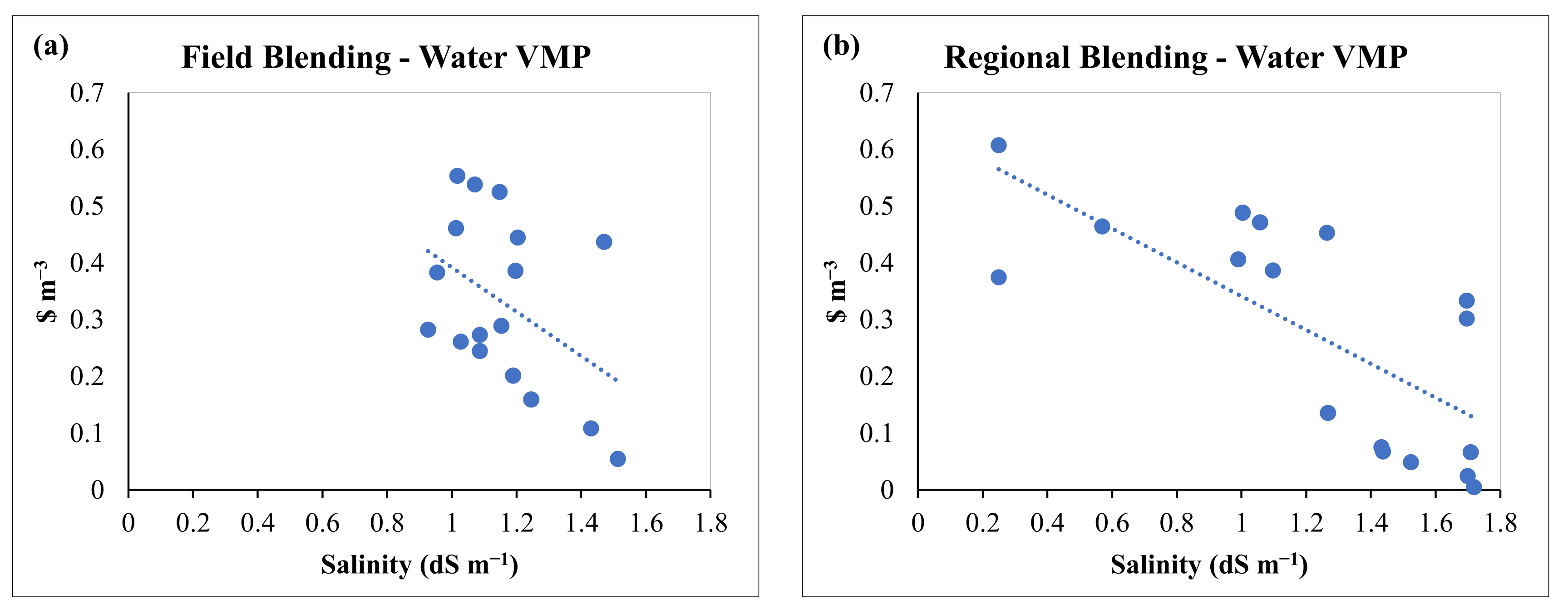
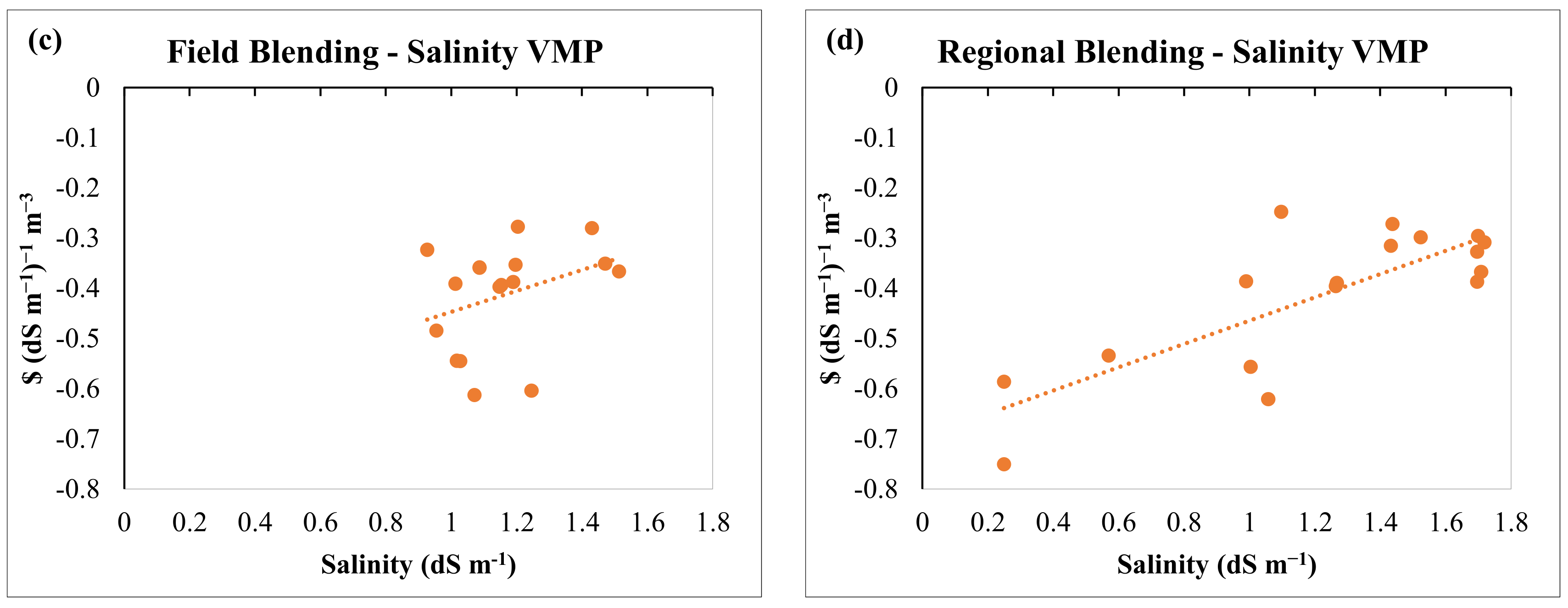
3.4. Salinity Damage
4. Conclusions
5. Discussion
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| EC | Electrical Conductivity |
| FB | Field Blending |
| FBNA | Field Blending No Adaptation |
| MYWAS | Multi Year Water Allocation System |
| PMP | Positive Mathematical Programming |
| RB | Regional Blending |
| RBNA | Regional Blending No Adaptation |
| TWW | Treated Wastewater |
| VALUE | Vegetative Agricultural Land Use Economic |
| VMP | Value of Marginal Product |
Appendix A. Preliminary Calibration Stage
References
- Hillel, D. Salinity Management for Sustainable Irrigation: Integrating Science, Environment, and Economics; World Bank Publications: Washington, DC, USA, 2000. [Google Scholar]
- Water and Climate Change—The United Nations World Water Development Report; The United Nations: New York, NY, USA, 2020; Available online: https://www.unwater.org/publications/world-water-development-report-2020/ (accessed on 6 November 2021).
- Qadir, M.; Quillérou, E.; Nangia, V.; Murtaza, G.; Singh, M.; Thomas, R.J.; Drechsel, P.; Noble, A.D. Economics of salt-induced land degradation and restoration. Nat. Resour. Forum 2014, 38, 282–295. [Google Scholar] [CrossRef]
- Zaman, M.; Shahid, S.A.; Heng, L. Soil salinity: Historical perspectives and a world overview of the problem. In Guideline for Salinity Assessment, Mitigation and Adaptation Using Nuclear and Related Techniques; Springer: Cham, Switzerland, 2018; pp. 43–53. [Google Scholar]
- Vergine, P.; Salerno, C.; Libutti, A.; Beneduce, L.; Gatta, G.; Berardi, G.; Pollice, A. Closing the water cycle in the agro-industrial sector by reusing treated wastewater for irrigation. J. Cleaner Prod. 2017, 164, 587–596. [Google Scholar] [CrossRef]
- Dai, A.; Zhao, T.; Chen, J. Climate change and drought: A precipitation and evaporation perspective. Curr. Clim. Change Rep. 2018, 4, 301–312. [Google Scholar] [CrossRef]
- Rodell, M.; Famiglietti, J.S.; Wiese, D.N.; Reager, J.T.; Beaudoing, H.K.; Landerer, F.W.; Lo, M.H. Emerging trends in global freshwater availability. Nature 2018, 557, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Russo, D.; Laufer, A.; Bar-Tal, A. Improving water uptake by trees planted on a clayey soil and irrigated with low-quality water by various management means: A numerical study. Agric. Water Manag. 2020, 229, 105891. [Google Scholar] [CrossRef]
- Hopmans, J.W.; Qureshi, A.S.; Kisekka, I.; Munns, R.; Grattan, S.R.; Rengasamy, P.; Ben-Gal, A.; Assouline, S.; Javaux, M.; Minhas, P.S.; et al. Critical knowledge gaps and research priorities in global soil salinity. Adv. Agron. 2021, 169, 1–191. [Google Scholar]
- Darre, N.C.; Toor, G.S. Desalination of water: A review. Curr. Pollut. Rep. 2018, 4, 104–111. [Google Scholar] [CrossRef]
- Jones, E.; Qadir, M.; van Vliet, M.T.; Smakhtin, V.; Kang, S.M. The state of desalination and brine production: A global outlook. Sci. Tot. Environ. 2019, 657, 1343–1356. [Google Scholar] [CrossRef]
- Singh, A. Conjunctive use of water resources for sustainable irrigated agriculture. J. Hydrol. 2014, 519, 1688–1697. [Google Scholar] [CrossRef]
- Gupta, S.K.; Singh, R.B.; Verma, A.K.; Chauhan, C.P.S. Conjunctive use of fresh and saline waters: Comparison of sequential, switching and blending modes. J. Soil Salin. Water Qual. 2015, 7, 79–89. [Google Scholar]
- Peragón, J.M.; Pérez-Latorre, F.J.; Delgado, A.; Tóth, T. Best management irrigation practices assessed by a GIS-based decision tool for reducing salinization risks in olive orchards. Agric. Water Manag. 2018, 202, 33–41. [Google Scholar] [CrossRef]
- Li, J.; Gao, Y.; Zhang, X.; Tian, P.; Li, J.; Tian, Y. Comprehensive comparison of different saline water irrigation strategies for tomato production: Soil properties, plant growth, fruit yield and fruit quality. Agric. Water Manag. 2019, 213, 521–533. [Google Scholar] [CrossRef]
- Parkinson, H.L.; Maletic, J.T.; Wagner, J.P.; Sachs, M.S. Desalting saline ground water for irrigation: A case study, Buckeye Area, Arizona. Water Resour. Res. 1970, 6, 1496–1500. [Google Scholar] [CrossRef]
- Knapp, K.C.; Dinar, A. Reuse of agricultural drainage waters: An economic analysis. J. Am. Water Resour. Assoc. 1984, 20, 521–525. [Google Scholar] [CrossRef]
- Dinar, A.; Letey, J.; Vaux, H.J., Jr. Optimal ratios of saline and nonsaline irrigation waters for crop production. Soil Sci. Soc. Am. J. 1986, 50, 440–443. [Google Scholar] [CrossRef]
- Kan, I.; Schwabe, K.A.; Knapp, K.C. Microeconomics of irrigation with saline water. J. Agric. Resour. Econ. 2002, 27, 16–39. [Google Scholar]
- Kan, I. Yield quality and irrigation with saline water under environmental limitations: The case of processing tomatoes in California. Agric. Econ. 2008, 38, 57–66. [Google Scholar] [CrossRef]
- Feinerman, E.; Yaron, D. Economics of irrigation water mixing within a farm framework. Water Resour. Res. 1983, 19, 337–345. [Google Scholar] [CrossRef] [Green Version]
- Kan, I.; Rapaport-Rom, M. Regional blending of fresh and saline irrigation water: Is it efficient? Water Resour. Res. 2012, 48, W07517. [Google Scholar] [CrossRef]
- Fisher, F.M.; Huber-Lee, A.T. Liquid Assets: An Economic Approach for Water Management and Conflict Resolution in the Middle East and Beyond; RFF Press: Washington, DC, USA, 2005. [Google Scholar]
- Booker, J.F.; Howitt, R.E.; Michelsen, A.M.; Young, R.A. Economics and the modeling of water resource and policies. Nat. Resour. Model. 2012, 25, 168–218. [Google Scholar] [CrossRef]
- Fisher, F.M.; Huber-Lee, A.T. The value of water: Optimizing models for sustainable management, infrastructure planning, and conflict resolution. Desalin. Water Treat. 2011, 31, 1–23. [Google Scholar] [CrossRef]
- Harou, J.J.; Pulido-Velazquez, M.; Rosenberg, D.E.; Medellín-Azuara, J.; Lund, J.R.; Howitt, R.E. Hydro-economic models: Concepts, design, applications, and future prospects. J. Hydrol. 2009, 375, 627–643. [Google Scholar] [CrossRef] [Green Version]
- Housh, M.; Ostfeld, A.; Shamir, U. Optimal multiyear management of a water supply system under uncertainty: Robust counterpart approach. Water Resour. Res. 2011, 47, W10515. [Google Scholar] [CrossRef]
- Lavee, D.; Ritov, M.; Becker, N. Is desalination the most sustainable alternative for water-shortage mitigation in Israel? Int. J. Sustain. Econ. 2011, 3, 410–424. [Google Scholar] [CrossRef]
- Reznik, A.; Feinerman, E.; Finkelshtain, I.; Kan, I.; Fisher, F.; Huber-Lee, A.; Joyce, B. The cost of covering costs: A nationwide model for water pricing. Water Econ. Pol. 2016, 2, 1650024. [Google Scholar] [CrossRef]
- Reznik, A.; Feinerman, E.; Finkelshtain, I.; Fisher, F.; Huber-Lee, A.; Joyce, B.; Kan, I. Economic implications of agricultural reuse of treated wastewater in Israel: A statewide long-term perspective. Ecol. Econ. 2017, 135, 222–233. [Google Scholar] [CrossRef] [Green Version]
- Saglam, Y. Welfare Implications of Water Shortages: Higher Prices of Desalination. Available at SSRN: https://ssrn.com/abstract=2271865 (accessed on 23 November 2021).
- Tanaka, S.K.; Zhu, T.J.; Lund, J.R.; Howitt, R.E.; Jenkins, M.W.; Pulido, M.A.; Tauber, M.; Ritzema, R.S.; Ferreira, I.C. Climate warming and water management adaptation for California. Clim. Change 2006, 76, 361–387. [Google Scholar] [CrossRef]
- Howitt, R.E.; MacEwan, D.; Medellín-Azuara, J.; Lund, J.R. Economic Modeling of Agriculture and Water in California Using the Statewide Agricultural Production Model—Report for the California Department of Water Resources; University of California: Davis, CA, USA, 2010. [Google Scholar]
- Welle, P.D.; Medellín-Azuara, J.; Viers, J.H.; Mauter, M.S. Economic and policy drivers of agricultural water desalination in California’s central valley. Agric. Water Manag. 2017, 194, 192–203. [Google Scholar] [CrossRef]
- Slater, Y.; Finkelshtain, I.; Reznik, A.; Kan, I. Large-scale desalination and the external impact on irrigation—Water salinity: Economic analysis for the case of Israel. Water Resour. Res. 2020, 56, e2019WR025657. [Google Scholar] [CrossRef]
- Kislev, Y. The Water Economy of Israel—Policy Paper No. 2011.15; Taub Center for Social Policy Studies in Israel: Jerusalem, Israel, 2011; Available online: http://taubcenter.org.il/wp-content/files_mf/thewatereconomyofisrael.pdf (accessed on 23 November 2021).
- Howitt, R.E. Positive mathematical programming. Am. J. Agric. Econ. 1995, 77, 329–342. [Google Scholar] [CrossRef]
- Maas, E.V.; Hoffman, G.J. Crop salt tolerance—Current assessment. J. Irrig. Drain. Div. Am. Soc. Civil Eng. 1977, 103, 115–134. [Google Scholar] [CrossRef]
- Assouline, S.; Russo, D.; Silber, A.; Or, D. Balancing water scarcity and quality for sustainable irrigated agriculture. Water Resour. Res. 2015, 51, 3419–3436. [Google Scholar] [CrossRef]
- Malchi, T.; Maor, Y.; Tadmor, G.; Shenker, M.; Chefetz, B. Irrigation of root vegetables with treated wastewater: Evaluating uptake of pharmaceuticals and the associated human health risks. Environ. Sci. Technol. 2014, 48, 9325–9333. [Google Scholar] [CrossRef] [PubMed]
- Christou, A.; Agüera, A.; Bayona, J.M.; Cytryn, E.; Fotopoulos, V.; Lambropoulou, D.; Manaia, C.M.; Michael, C.; Revitt, M.; Schröder, P.; et al. The potential implications of reclaimed wastewater reuse for irrigation on the agricultural environment: The knowns and unknowns of the fate of antibiotics and antibiotic resistant bacteria and resistance genes—A review. Water Res. 2017, 123, 448–467. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Miarov, O.; Tal, A.; Avisar, D. A critical evaluation of comparative regulatory strategies for monitoring pharmaceuticals in recycled wastewater. J. Environ. Manag. 2020, 254, 109794. [Google Scholar] [CrossRef] [PubMed]
- Ogunmokun, F.A.; Wallach, R. Remediating the adverse effects of treated wastewater irrigation by repeated on-surface surfactant application. Water Resour. Res. 2021, 57, e2020WR029429. [Google Scholar] [CrossRef]
- Grandclément, C.; Seyssiecq, I.; Piram, A.; Wong-Wah-Chung, P.; Vanot, G.; Tiliacos, N.; Roche, N.; Doumenq, P. From the conventional biological wastewater treatment to hybrid processes, the evaluation of organic micropollutant removal: A review. Water Res. 2017, 111, 297–317. [Google Scholar] [CrossRef] [Green Version]
- Feinerman, E.; Tsur, Y. Perennial crops under stochastic water supply. Agric. Econ. 2014, 45, 757–766. [Google Scholar] [CrossRef]
- Ofori, S.; Puškáčová, A.; Růžičková, I.; Wanner, J. Treated wastewater reuse for irrigation: Pros and cons. Sci. Tot. Environ. 2021, 760, 144026. [Google Scholar] [CrossRef]

Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Slater, Y.; Reznik, A.; Finkelshtain, I.; Kan, I. Blending Irrigation Water Sources with Different Salinities and the Economic Damage of Salinity: The Case of Israel. Water 2022, 14, 917. https://doi.org/10.3390/w14060917
Slater Y, Reznik A, Finkelshtain I, Kan I. Blending Irrigation Water Sources with Different Salinities and the Economic Damage of Salinity: The Case of Israel. Water. 2022; 14(6):917. https://doi.org/10.3390/w14060917
Chicago/Turabian StyleSlater, Yehuda, Ami Reznik, Israel Finkelshtain, and Iddo Kan. 2022. "Blending Irrigation Water Sources with Different Salinities and the Economic Damage of Salinity: The Case of Israel" Water 14, no. 6: 917. https://doi.org/10.3390/w14060917





