Hydrodynamic Characteristics at Intersection Areas of Ship and Bridge Pier with Skew Bridge
Abstract
:1. Introduction
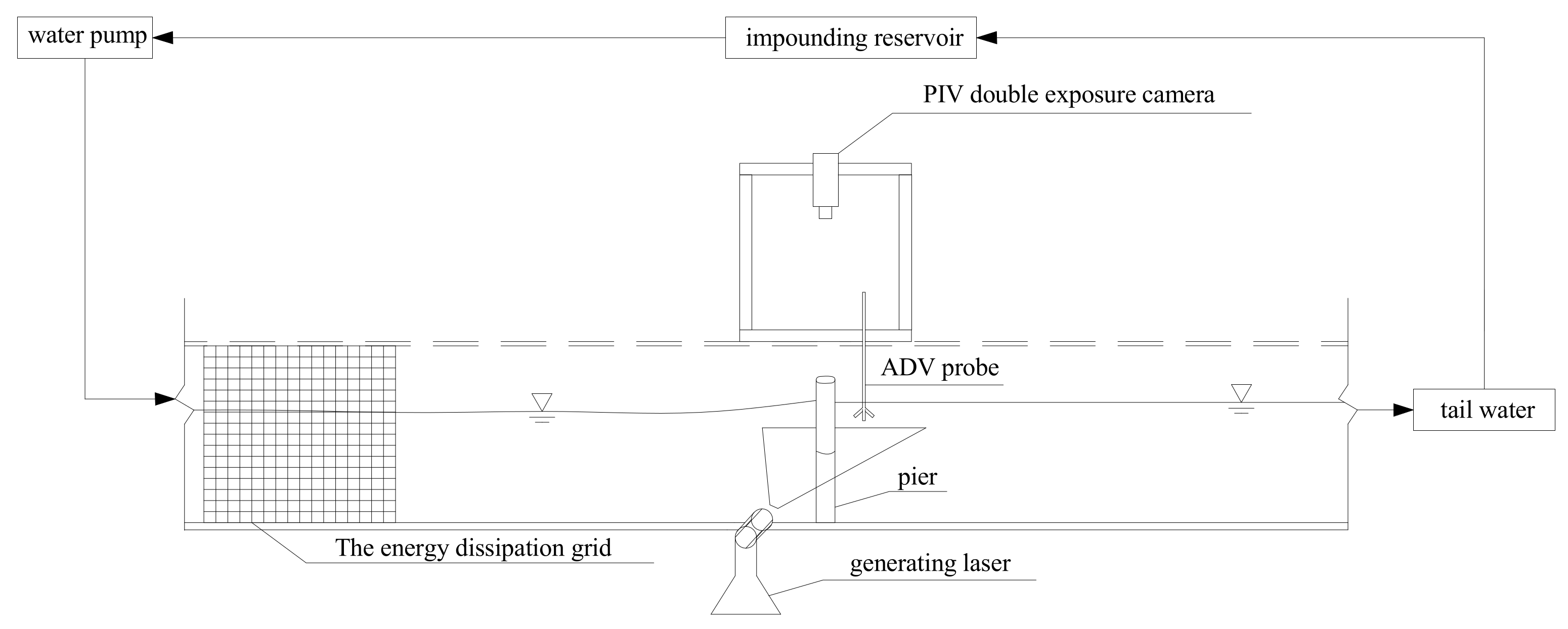
2. Model Test
2.1. Model Test of Flow around a Round-Ended Pier
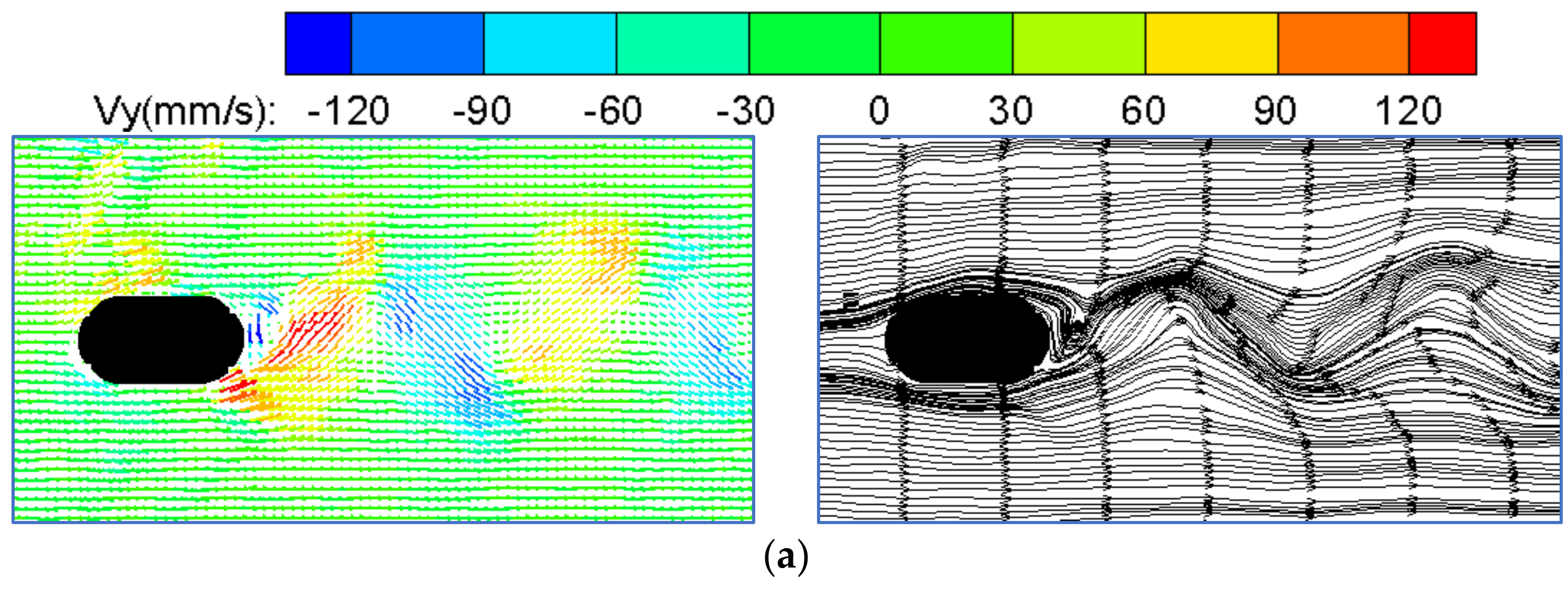
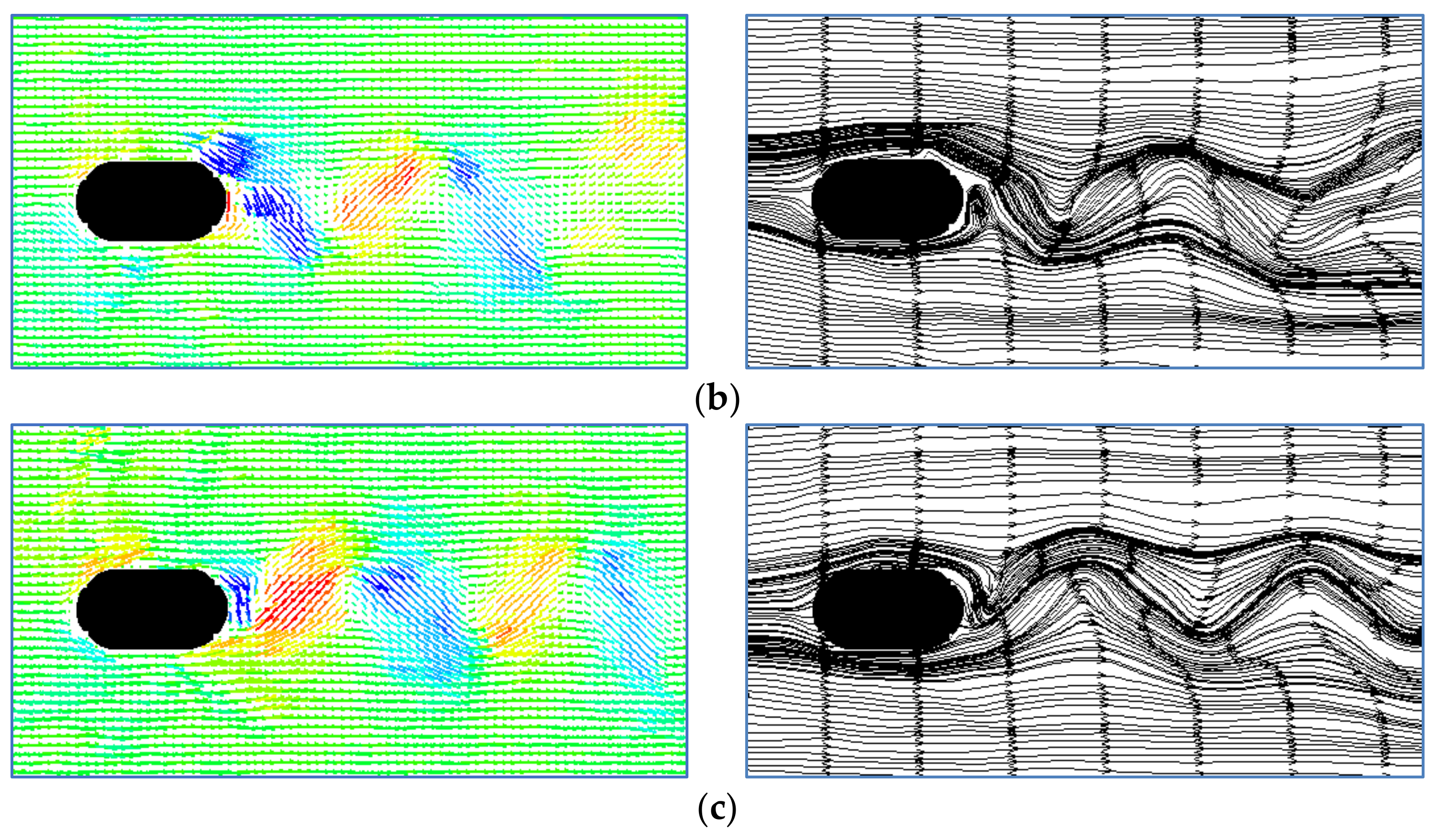
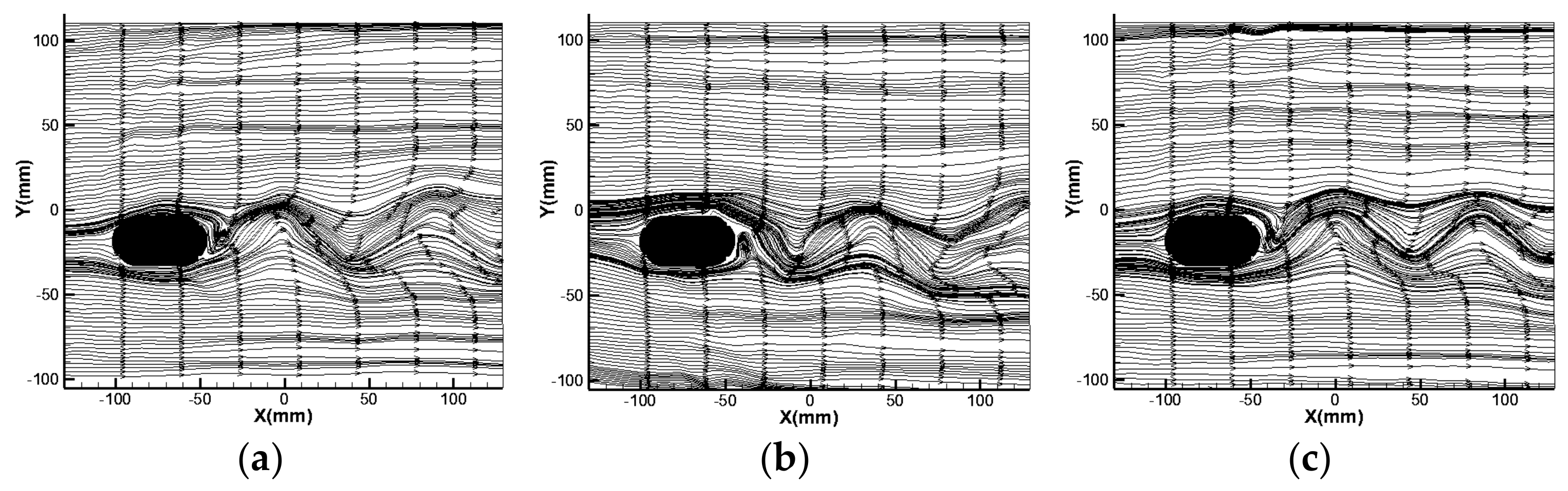
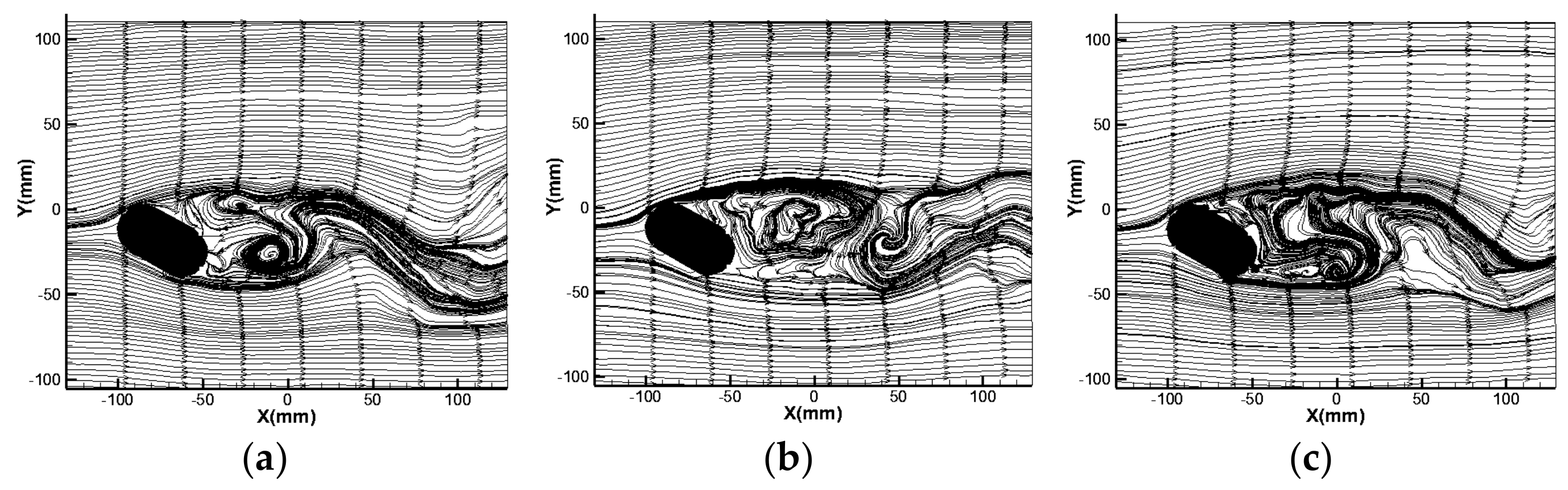
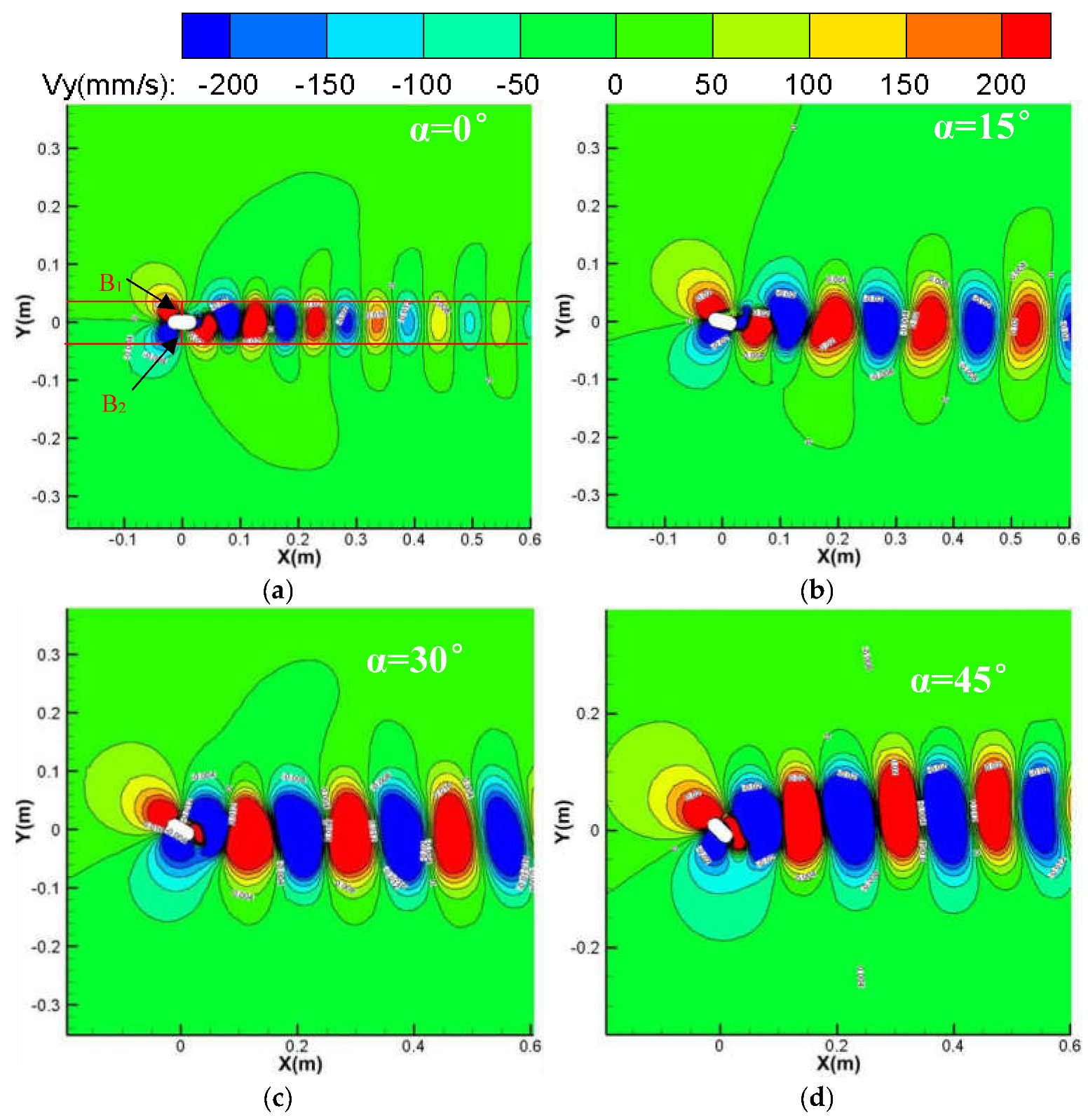
2.1.1. Flow Patterns and Fields around a Pier on a Fixed Bed
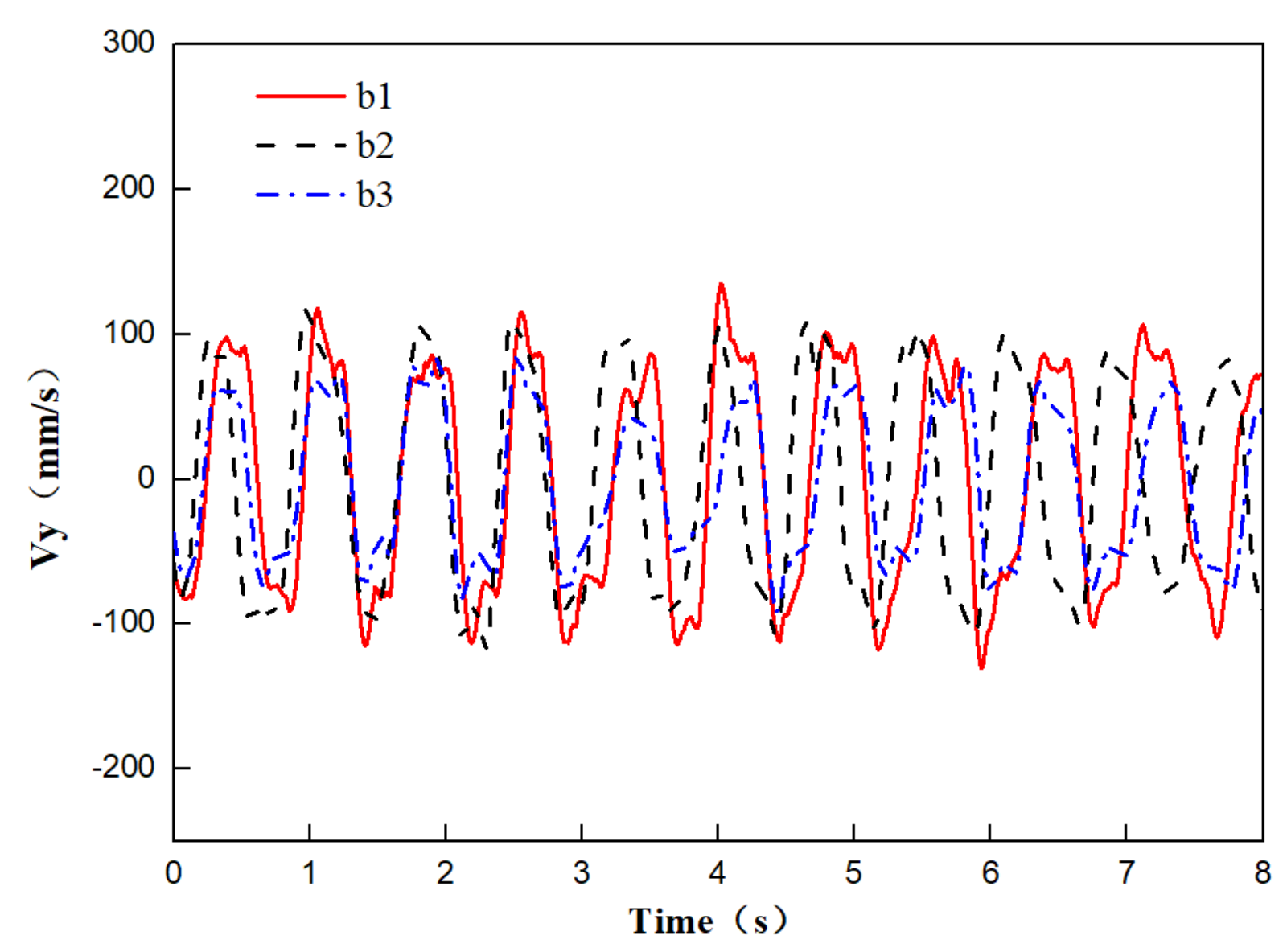
2.1.2. Analysis of Test Results
- Analysis of the flow around a pier when the flow angle of attack is 0°
- Effect of flow angle of attack on the flow pattern around the round-ended pier
2.2. Physical Model Test of Ship–Bridge Intersection
2.2.1. Test Model and Equipment
2.2.2. Analysis of the Test Results
3. Numerical Modeling
3.1. Establishment of a Geometric Model and the Arrangement of Simulation Groups
3.1.1. Analysis of Test Results
3.1.2. Numerical Simulation
3.2. Governing Equation
3.2.1. Flow Governing Equation
3.2.2. Flow Governing Equation
3.3. Meshing Methods and Application of Self-Compiled UDFs
3.3.1. Grid Division and Dynamic Grid Method
3.3.2. Self-Compiling UDF Process
4. Verification and Analysis of Numerical Simulation Results
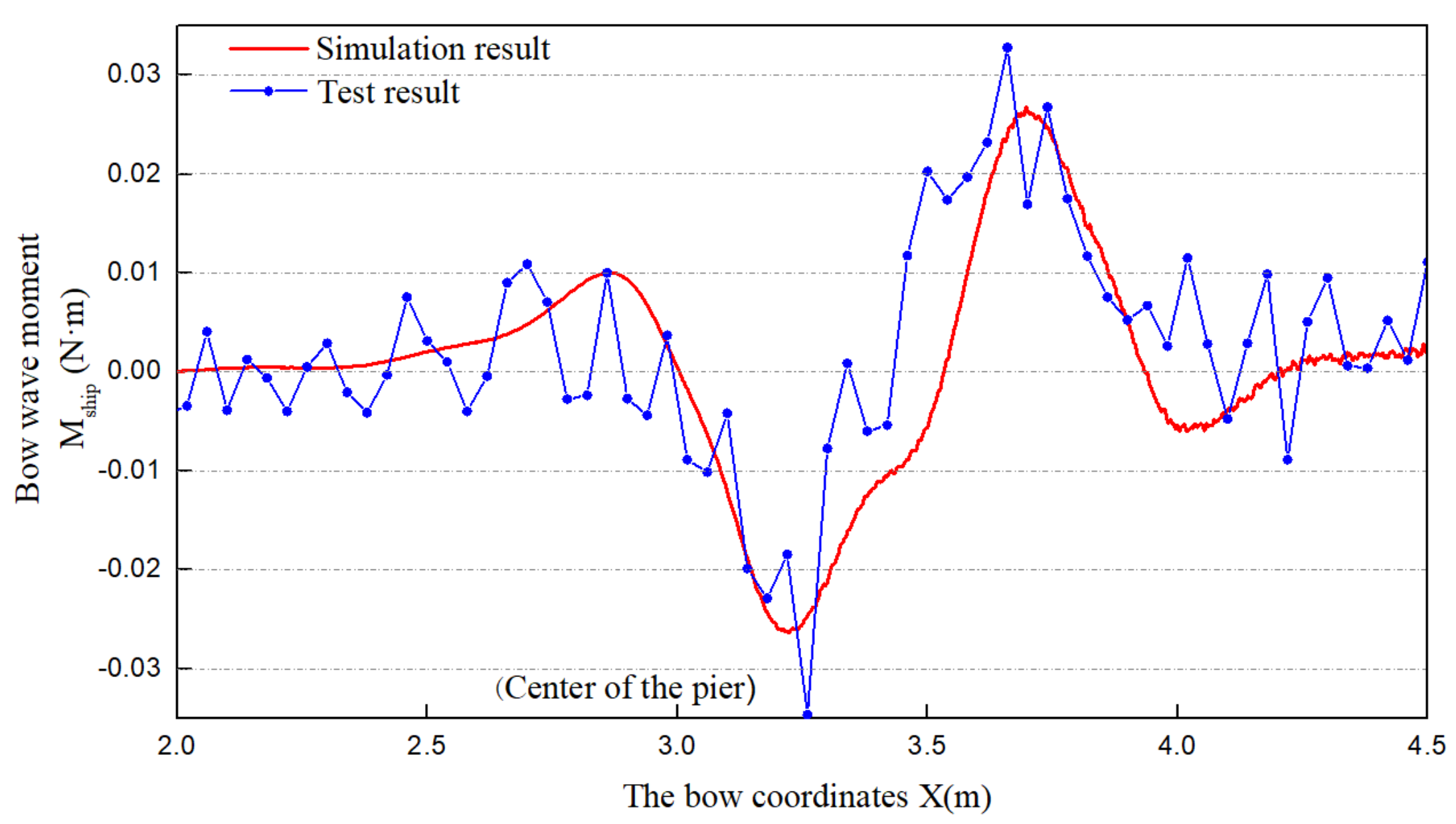
4.1. Verification of Numerical Simulation Results
4.1.1. Verification of Flow Field and Vorticity Field around Flow
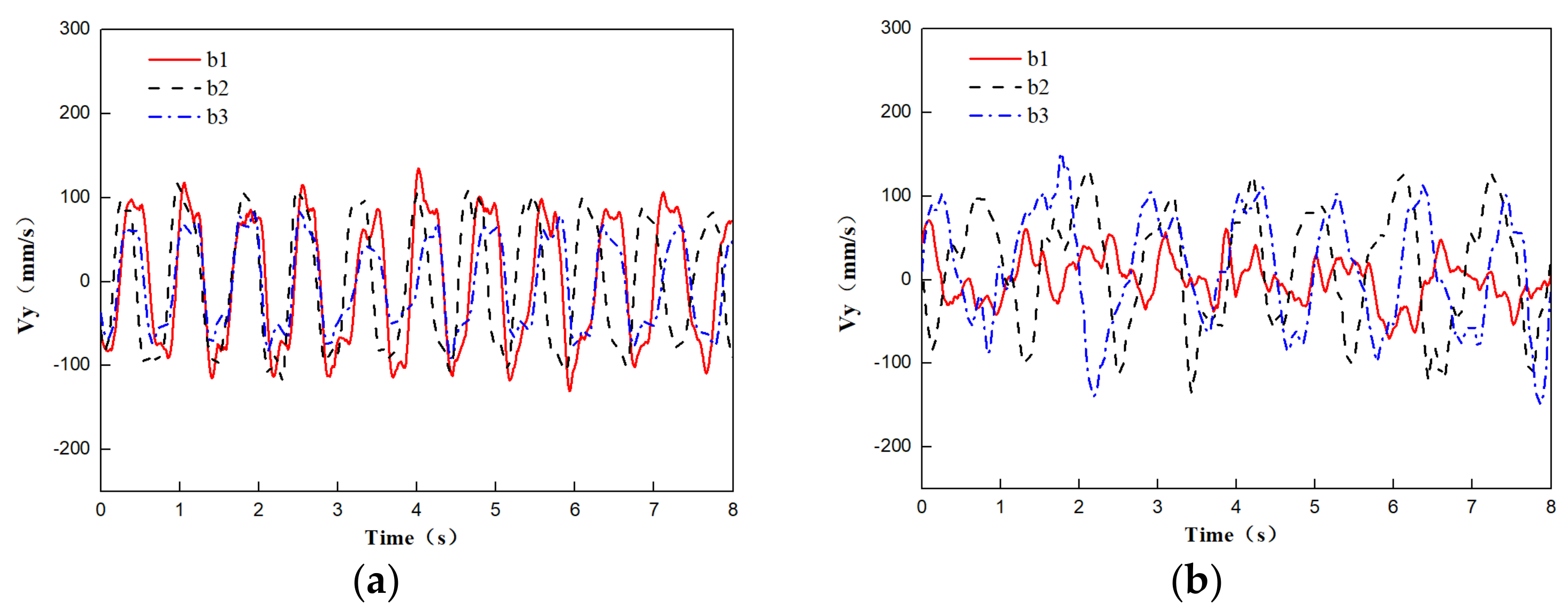
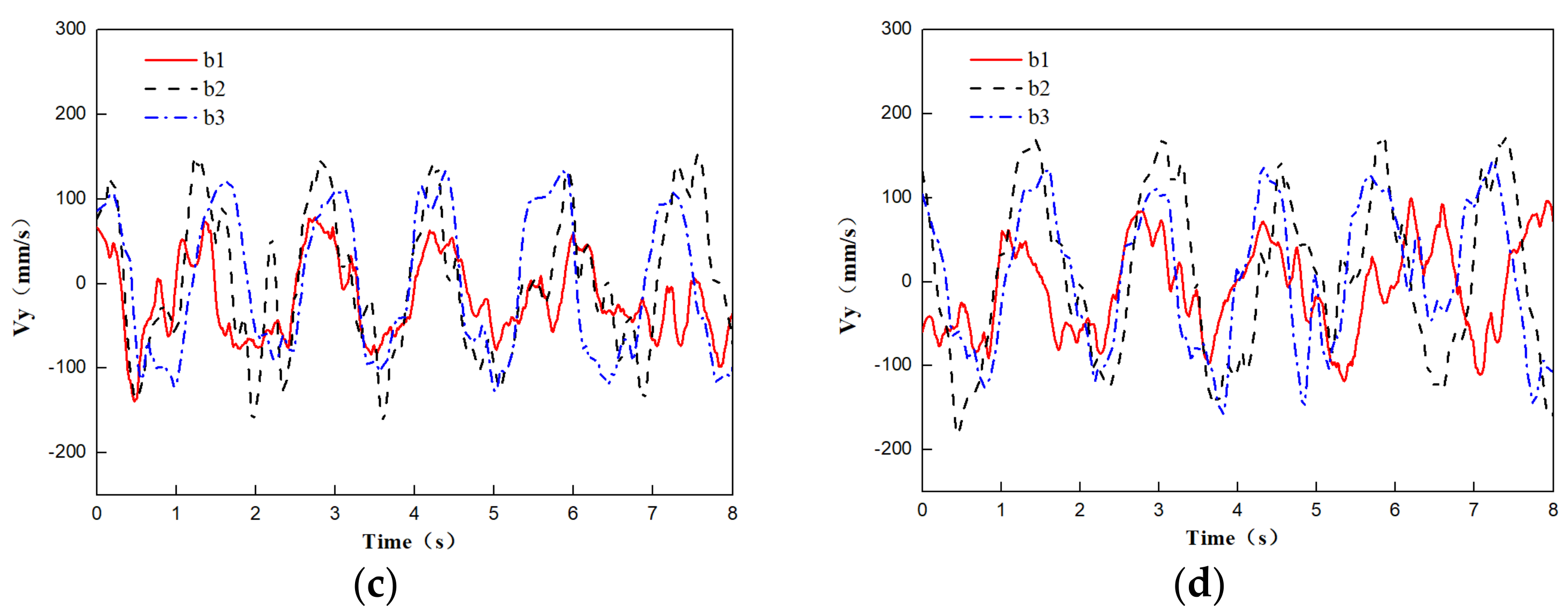
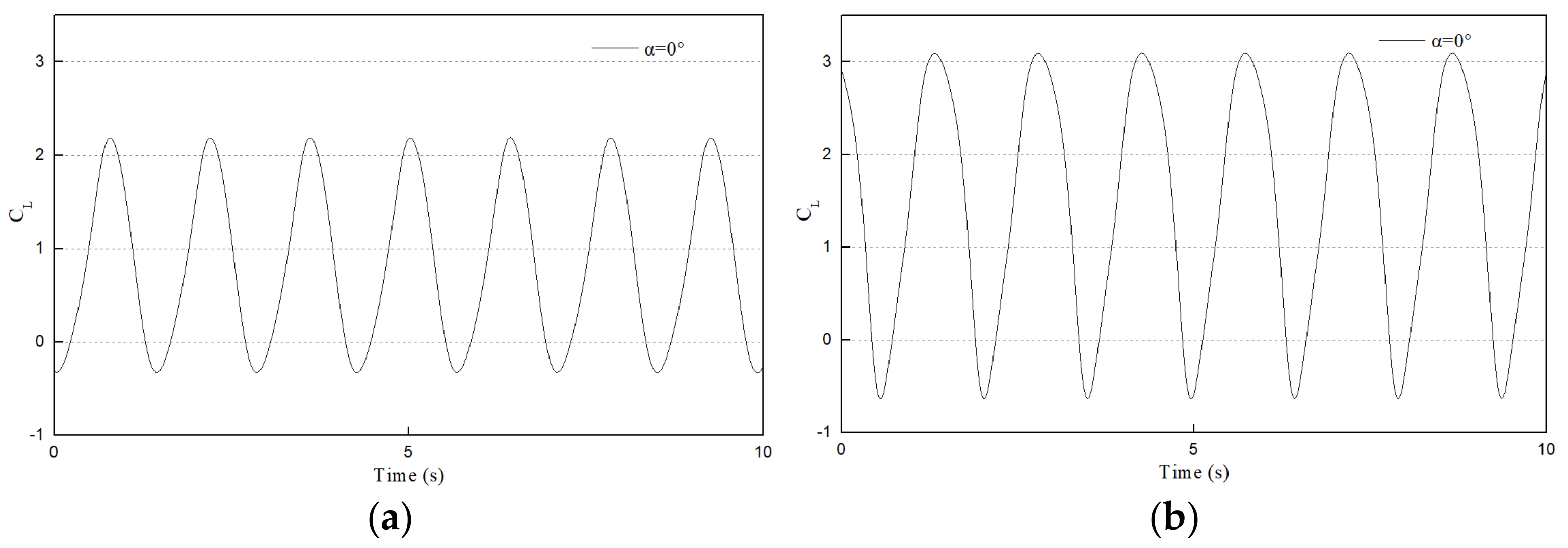
4.1.2. Verification of Trailing Vortex Shedding Frequency and Transverse Velocity behind a Round-Ended Pier
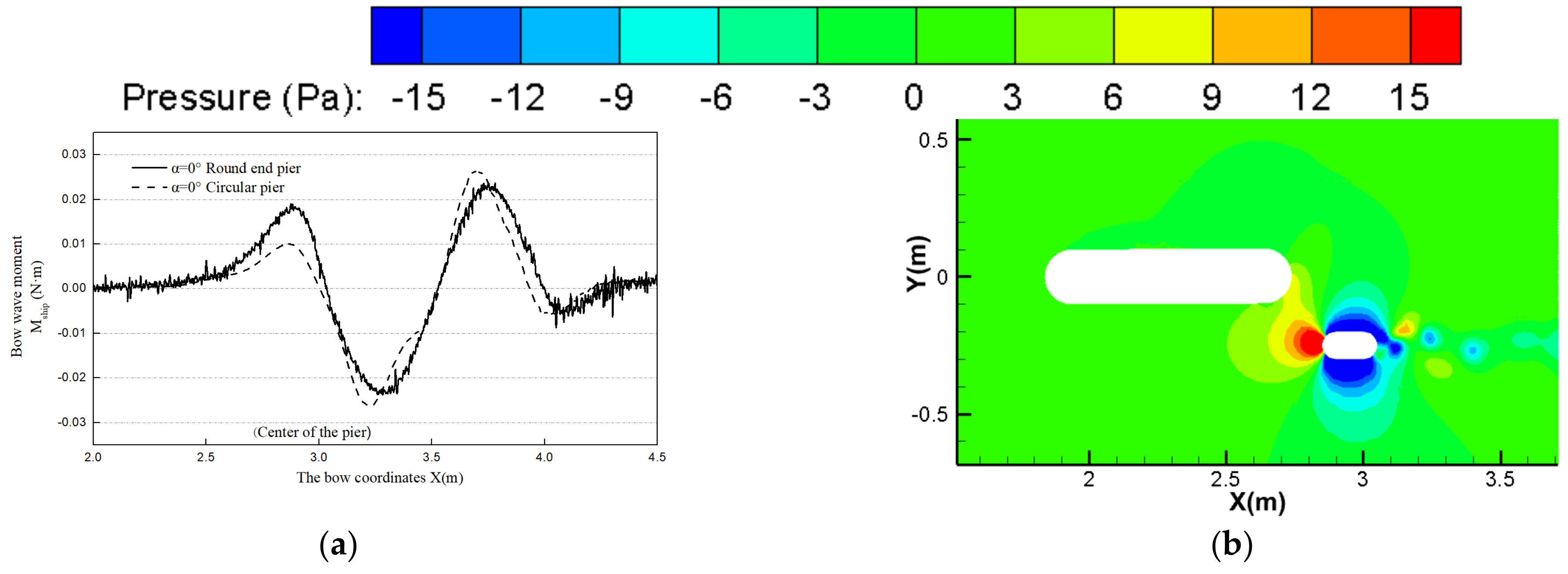
4.1.3. Numerical Verification of Bow Roll Moment and Its Evolution Law
4.2. Verification of Numerical Simulation Results
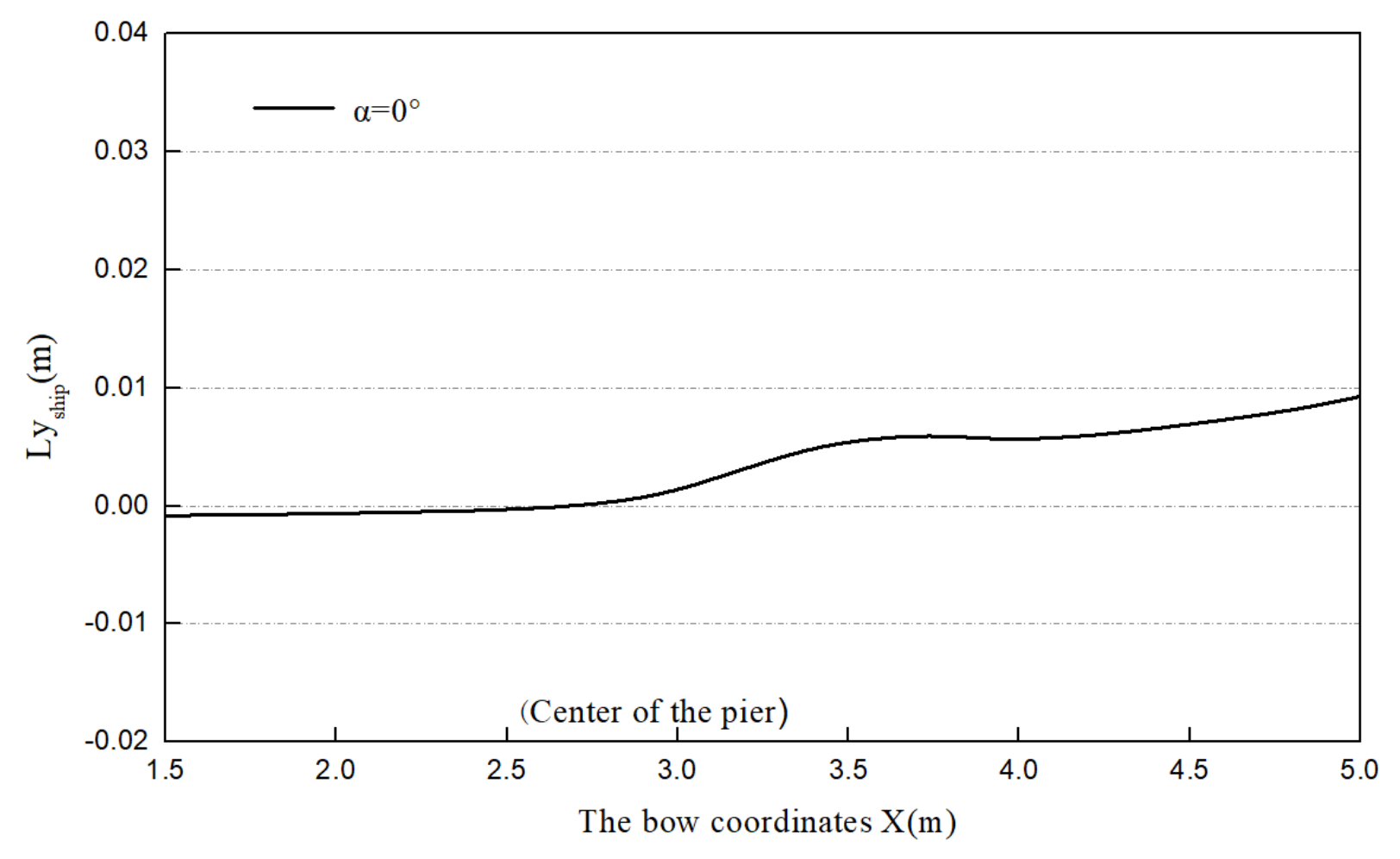
4.3. Influence of Flow around a Round-Ended Pier with α = 0° on Moving Ship
4.4. Analysis of the Influence of Flow around a Circular-Ended Pier on Moving Ship
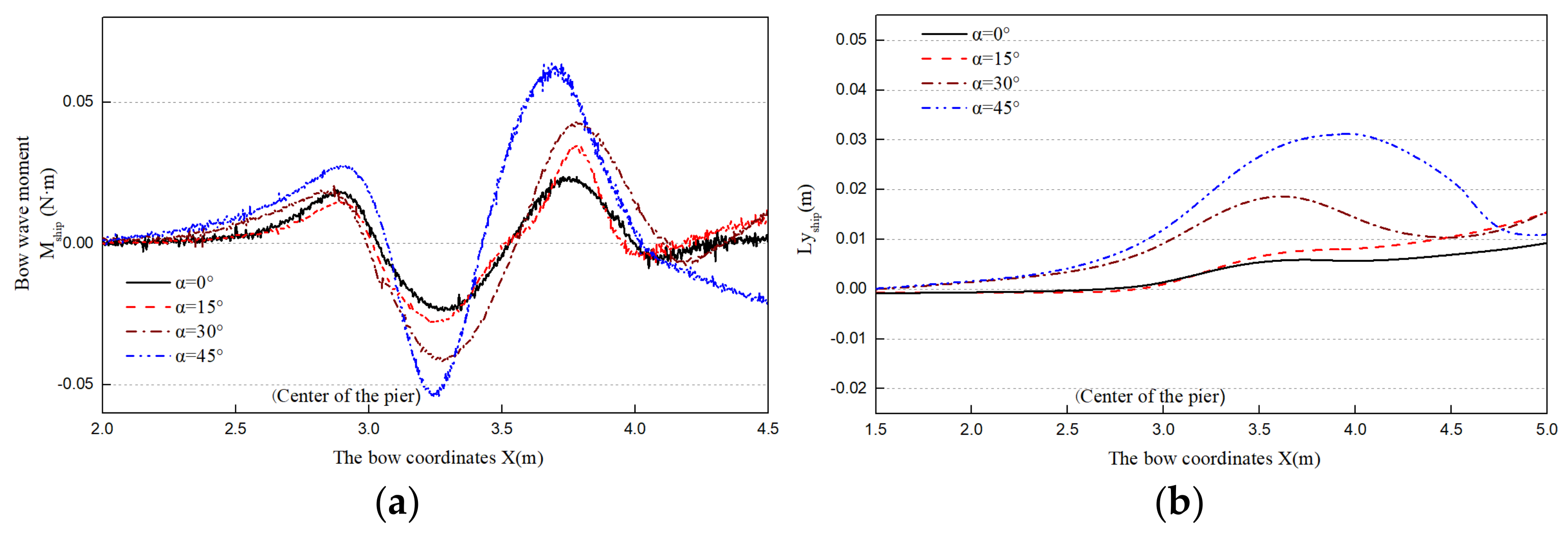
4.5. Influence of Flow Angle of Attack on Ships Sailing on Both Sides of a Round-Ended Pier
4.5.1. Influence of Flow Angle of Attack on Ships Sailing on the Upstream Side of a Round-Ended Pier
4.5.2. Influence of Flow Angle of Attack on Ships Sailing on the Back Side of a Round-Ended Pier
4.5.3. Influence of Transverse Distance between the Ship and Pier on a Ship Sailing in a Skew Bridge Area
5. Discussion
6. Conclusions
- (1)
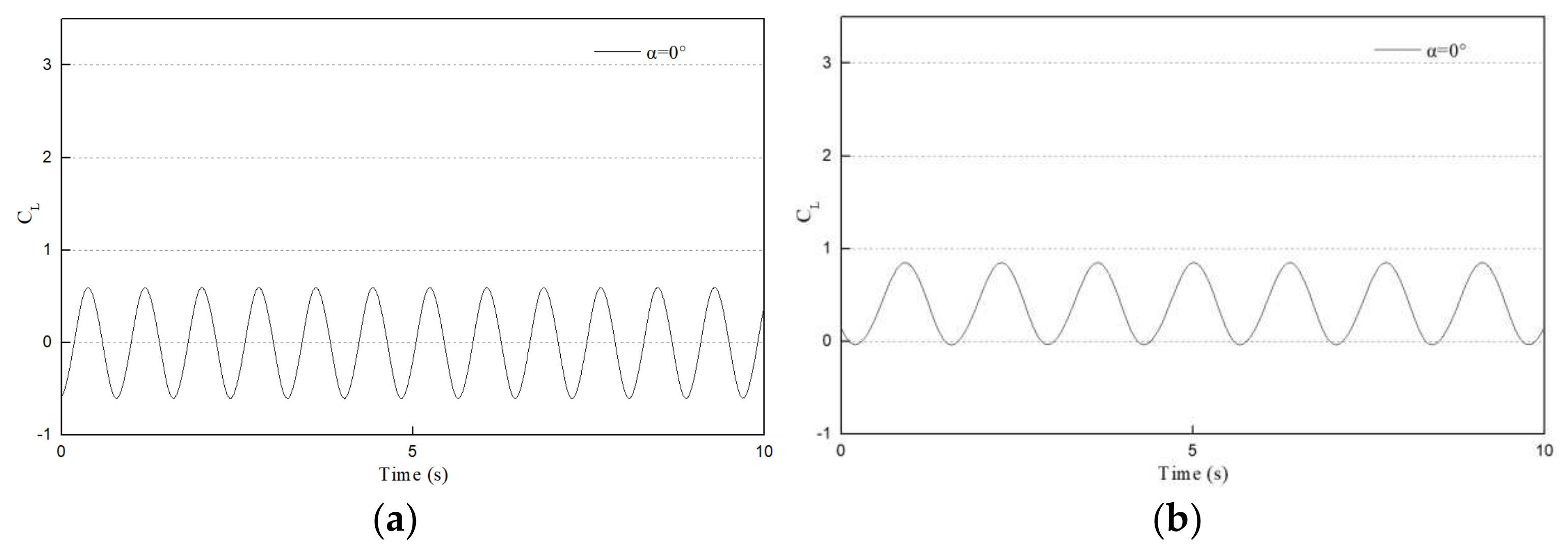
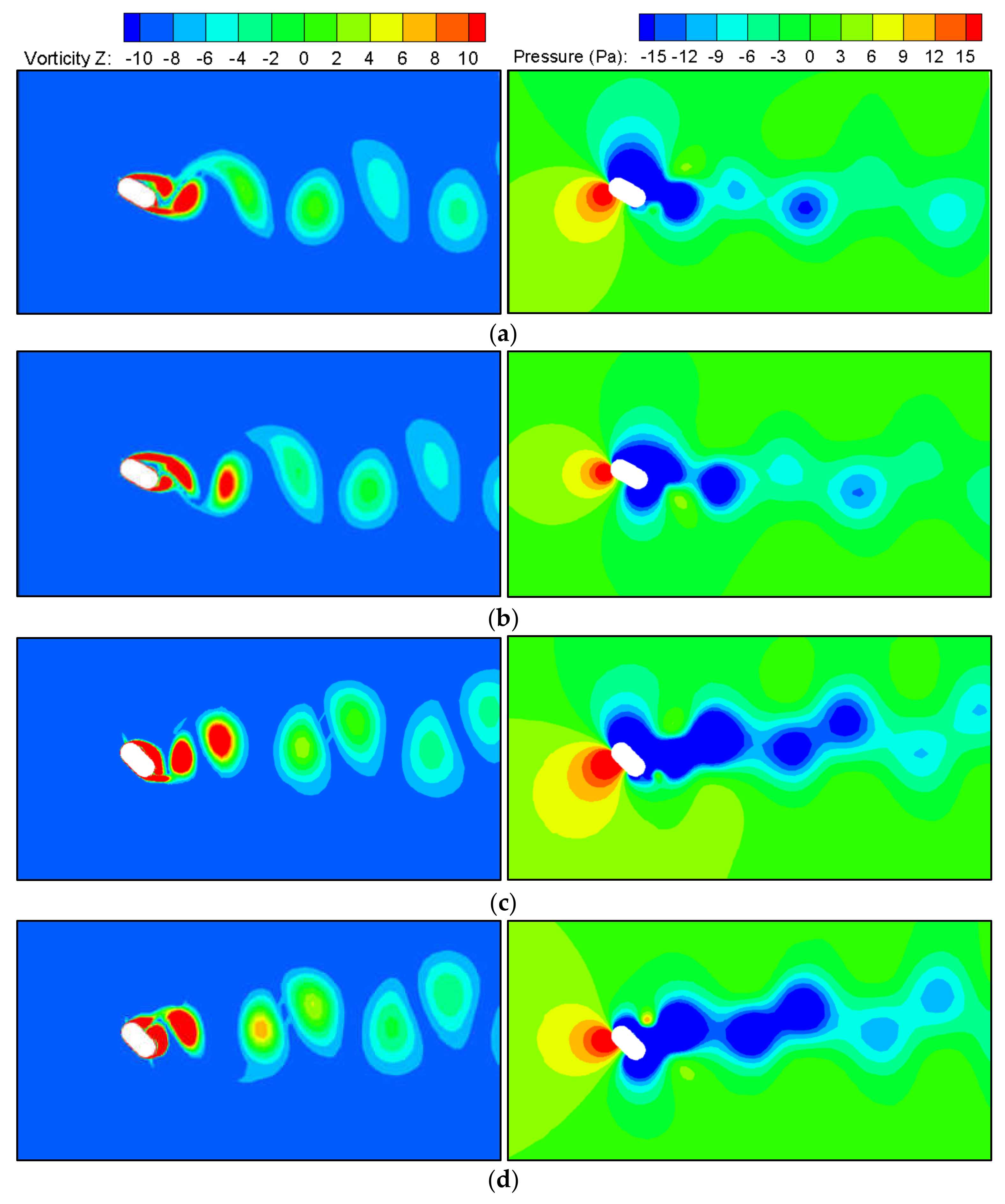
- The PIV flume test and numerical model test were conducted to study the influence of the flow angle of attack on the flow field and pressure field around a round-ended pier without vessel. The results showed that the fluctuation period of the downstream transverse velocity of the round-ended pier is consistent with the trailing vortex shedding period of the flow around the pier. This period is prolonged with the increase in the flow angle of attack of the pier, but the trailing vortex shedding period tends to be stable at α ≥ 15°. The trailing vortex shedding periods of α = 0°, 15°, 30°, and 45° are 0.8, 1.4, 1.5, and 1.6 s, respectively. Due to the water-blocking effect of the round-ended pier, a positive water pressure area is generated in front of the pier, and this area swings back and forth to the left and right banks when the flow angle of attack α ≥ 30°. A negative water pressure area is generated downstream of the boundary layer separation point of the flow around both sides of the pier, and the pressure area is different on both sides of the pier with the increase in the flow angle of attack. The negative water pressure area of the trailing vortex on the back flow side of the pier is larger than that on the upstream side, and the negative water pressure area generated by the shedding vortex system shifts to the back flow side of the pier with the increase in α.
- (2)
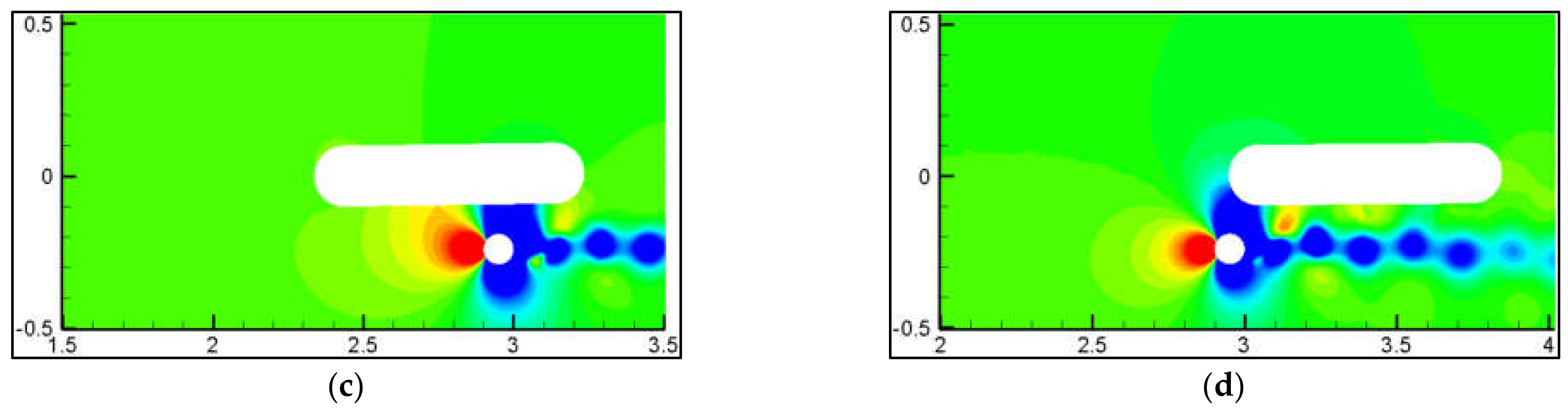
- The accuracy of the numerical simulation results of the ship–bridge intersection was verified based on the ship–bridge intersection model test. The process of the ship drifting through the bridge pier in the channel with a flow rate of 0.283 m/s was deduced by numerical simulation, when the ship–bridge transverse spacing was 1b. The results showed that the ship will be affected by three continuous fluctuation peaks of the bow roll moment, and the ship will experience a change in the bow roll moment direction, from ‘positive’ to ‘negative’ and then from ‘negative’ to ‘positive’. Moreover, the center of gravity position trajectory presents a ‘straw hat’ shape, and the ship will then maintain its attitude, to leave the bridge area.
- (3)
- Through a numerical simulation, the process of a ship passing both sides of the pier with different flow angles of attack at a speed of 0.566 m/s and ship–bridge spacing of 1b was deduced, and the change laws of the bow roll moment and the position of the center of gravity were analyzed. The results showed that the first positive peak value and the second positive peak value of the bow roll moment decrease with the increase in α when the transverse spacing between the ship and pier is constant, and the ship’s attitude is stable. When the ship moves from the back flow side of the bridge pier, although the increase in α has little influence on the overall positive peak value of the bow roll moment, the changes in the negative peak value and second positive peak value are significant, the ship’s navigation attitude is unstable, and the ship has a risk of colliding with the bridge pier and sweeping.
- (4)
- The width of the area that has a significant influence on navigable ships, judged by the hydrodynamic action of the ship on the skew bridge area, is the same as the result judged from the transverse velocity. For the ship class referred to in this study, it is reasonable to take the range of the transverse velocity limit of 0.3 m/s in the bridge area as the area having a significant influence on navigable ships. Combined with the analysis of the impact of the flow angle of attack, this study provides a reference for the width of channel design in skew bridge areas.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Salaheldin, T.M.; Imran, J.; Chaudhry, M.H. Numerical modeling of three-dimensional flow field around circular piers. J. Hydraul. Eng. 2004, 130, 91–100. [Google Scholar] [CrossRef]
- Vijayasree, B.A.; Eldho, T.I.; Mazumder, B.S. Turbulence statistics of flow causing scour around circular and oblong piers. J. Hydraul. Res. 2020, 58, 673–686. [Google Scholar] [CrossRef]
- Melville, B.W. Local Scour at Bridge Sites. Ph.D. Thesis, University of Auckland, Auckland, New Zealand, 1975. [Google Scholar]
- Kumar, A.; Kothyari, U.; Ranga, R.; Kittur, G. Flow structure and scour around circular compound bridge piers—A review. J. Hydro-Environ. Res. 2012, 6, 251–265. [Google Scholar] [CrossRef]
- Beheshti, A.A.; Ataie-Ashtiani, B. Scour Hole Influence on Turbulent Flow Field around Complex Bridge Piers. Flow Turbul. Combust. 2016, 97, 451–474. [Google Scholar] [CrossRef]
- Ulrich, J.; Michael, M. Flow around a scoured bridge pier: A stereoscopic PIV analysis. Exp. Fluids 2020, 61, 251–265. [Google Scholar] [CrossRef]
- Chang, W.Y.; Constantinescu, G.; Lien, H.C.; Tsai, W.F.; Lai, J.S.; Loh, C.H. Flow Structure around Bridge Piers of Varying Geometrical Complexity. J. Hydraul. Eng. 2013, 139, 812–826. [Google Scholar] [CrossRef]
- Aly, A.M.; Dougherty, E. Bridge pier geometry effects on local scour potential: A comparative study. Ocean Eng. 2021, 234, 109326. [Google Scholar] [CrossRef]
- Link, O.; Henríquez, S.; Ettmer, B. Physical scale modelling of scour around bridge piers. J. Hydraul. Res. 2019, 57, 227–237. [Google Scholar] [CrossRef]
- Al-Saffar, M. The Influence of Dimensional and Dimensionless Parameters on the Dynamics of the Horseshoe Vortex Upstream of a Circular Cylinder. Ph.D. Thesis, University of Sheffield, Sheffield, UK, 2016. [Google Scholar]
- Chakrabarti, S.K.; McBride, M. Model tests on current forces on a large bridge pier near an existing pier. J. Shore Mech. Arct. Eng. 2005, 127, 212–219. [Google Scholar] [CrossRef]
- Daichin; Lee, S.J. Flow structure of the wake behind an elliptic cylinder close to a free surface. KSME Int. J. 2001, 15, 1784–1793. [Google Scholar] [CrossRef]
- Gautam, P.; Eldho, T.I.; Mazumder, B.S.; Behera, M.R. Experimental study of flow and turbulence characteristics around simple and complex piers using PIV. Exp. Therm. Fluid Sci. 2019, 100, 193–206. [Google Scholar] [CrossRef]
- Carnacina, L.; Leonardi, N.; Pagliara, S. Characteristics of Flow Structure around Cylindrical Bridge Piers in Pressure-Flow Conditions. Water 2019, 11, 2240. [Google Scholar] [CrossRef] [Green Version]
- Paul, I.; Prakash, K.A.; Vengadesan, S. Numerical analysis of laminar fluid flow characteristics past an elliptic cylinder. Int. J. Numer. Methods Heat Fluid Flow 2014, 24, 1570–1594. [Google Scholar] [CrossRef]
- Shi, X.; Alam, M.; Bai, H. Wakes of elliptical cylinders at low Reynolds number. Int. J. Heat Fluid Flow 2020, 82, 108553. [Google Scholar] [CrossRef]
- Zhang, C.; Zou, Z.; Wang, H.M. Numerical prediction of the unsteady hydrodynamic interaction between a ship and a bridge pier. Chin. J. Hydrodyn. 2012, 27, 359–364. (In Chinese) [Google Scholar]
- Tuck, E.O.; Newman, J.N. Hydrodynamic interactions between ships. In Proceedings of the Symposium on Naval Hydrodynamics, Pap and Discuss, Cambridge, UK, 24–28 June 1977. [Google Scholar]
- Liu, X.P.; Qian, D.Y.; Fang, S.S.; Zhang, Y. Study on the width of turbulent area around pier with ship impact. Appl. Mech. Mater. 2012, 137, 186–191. [Google Scholar] [CrossRef]
- Wang, H.Z.; Zou, Z.J. Numerical prediction of hydrodynamic forces on a ship passing through a lock with different configurations. J. Hydrodyn. 2014, 26, 1–9. [Google Scholar] [CrossRef]
- Li, L.; Yuan, Z.M.; Ji, C.; Li, M.X.; Gao, Y. Investigation on the unsteady hydrodynamic loads of ship passing by bridge piers by a 3-D boundary element method. Eng. Anal. Bound. Elem. 2018, 94, 122–133. [Google Scholar] [CrossRef] [Green Version]
- Geng, Y.F.; Guo, H.Q.; Ke, X. The flow characteristics around bridge piers under the impact of a ship. J. Hydrodyn. 2020, 32, 1165–1177. [Google Scholar] [CrossRef]
- GB50139-2014. Navigation Standards for Inland Rivers; Planning Publishing Press: Beijing, China, 2014. [Google Scholar]
- TB10002-2017. Code for Design of Railway Bridges and Culverts; Railway Publishing House: Beijing, China, 2017. [Google Scholar]








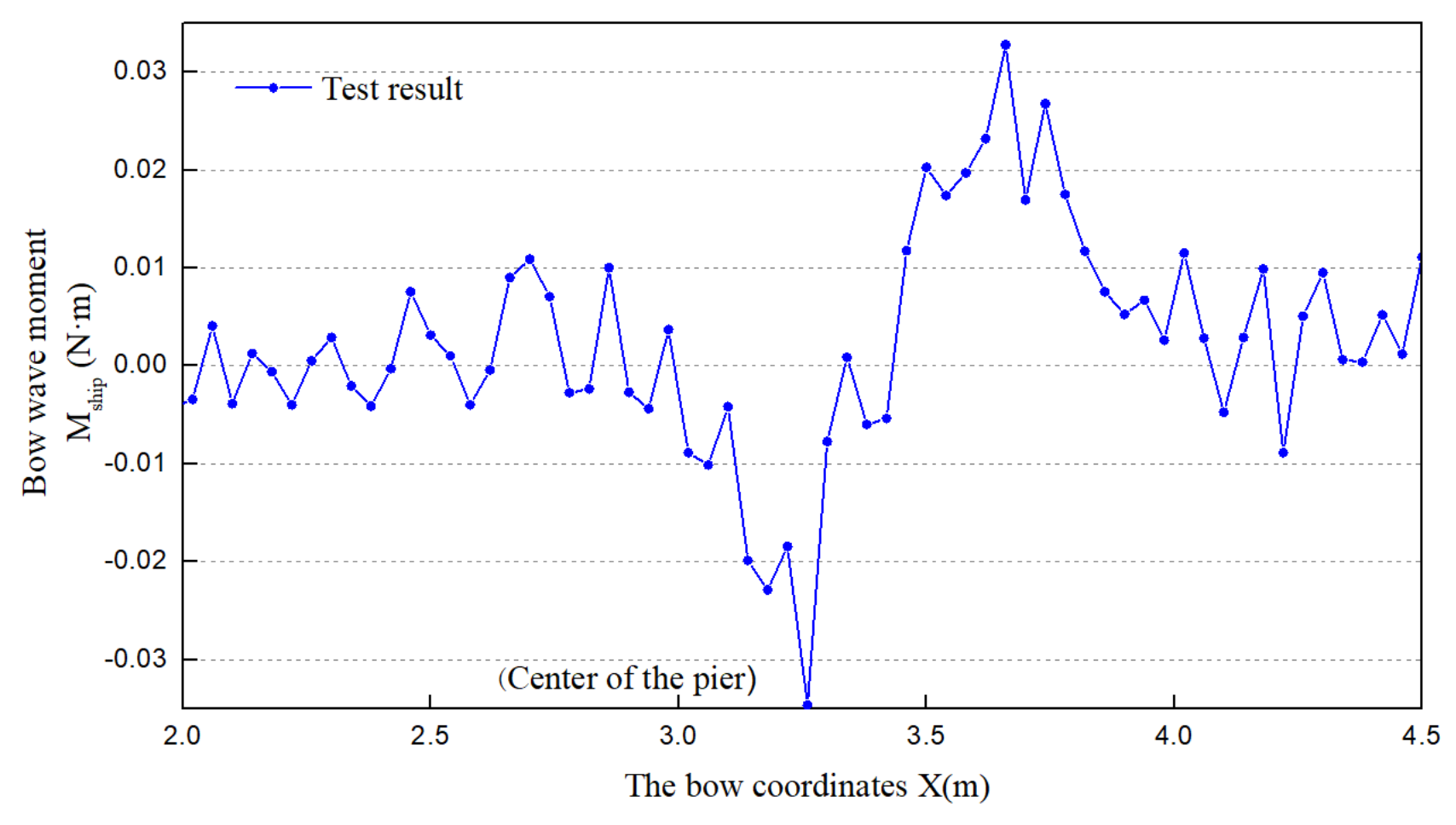
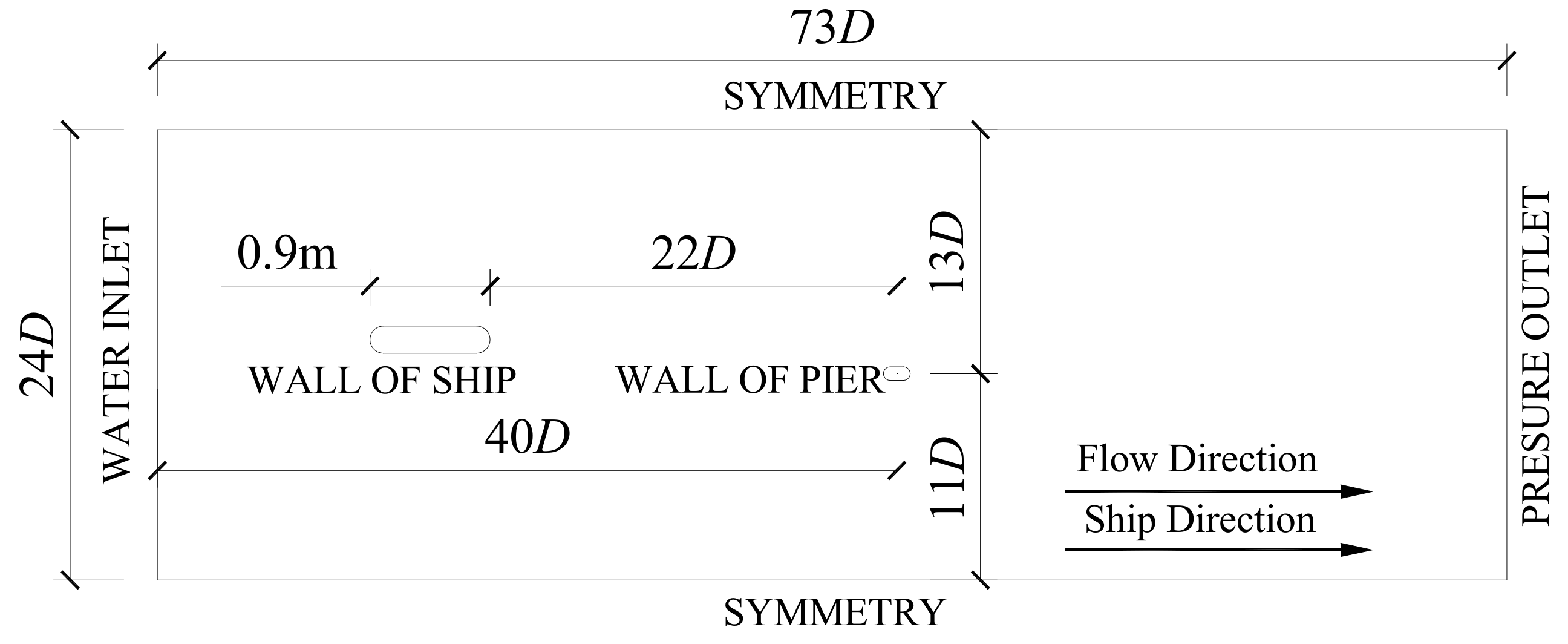
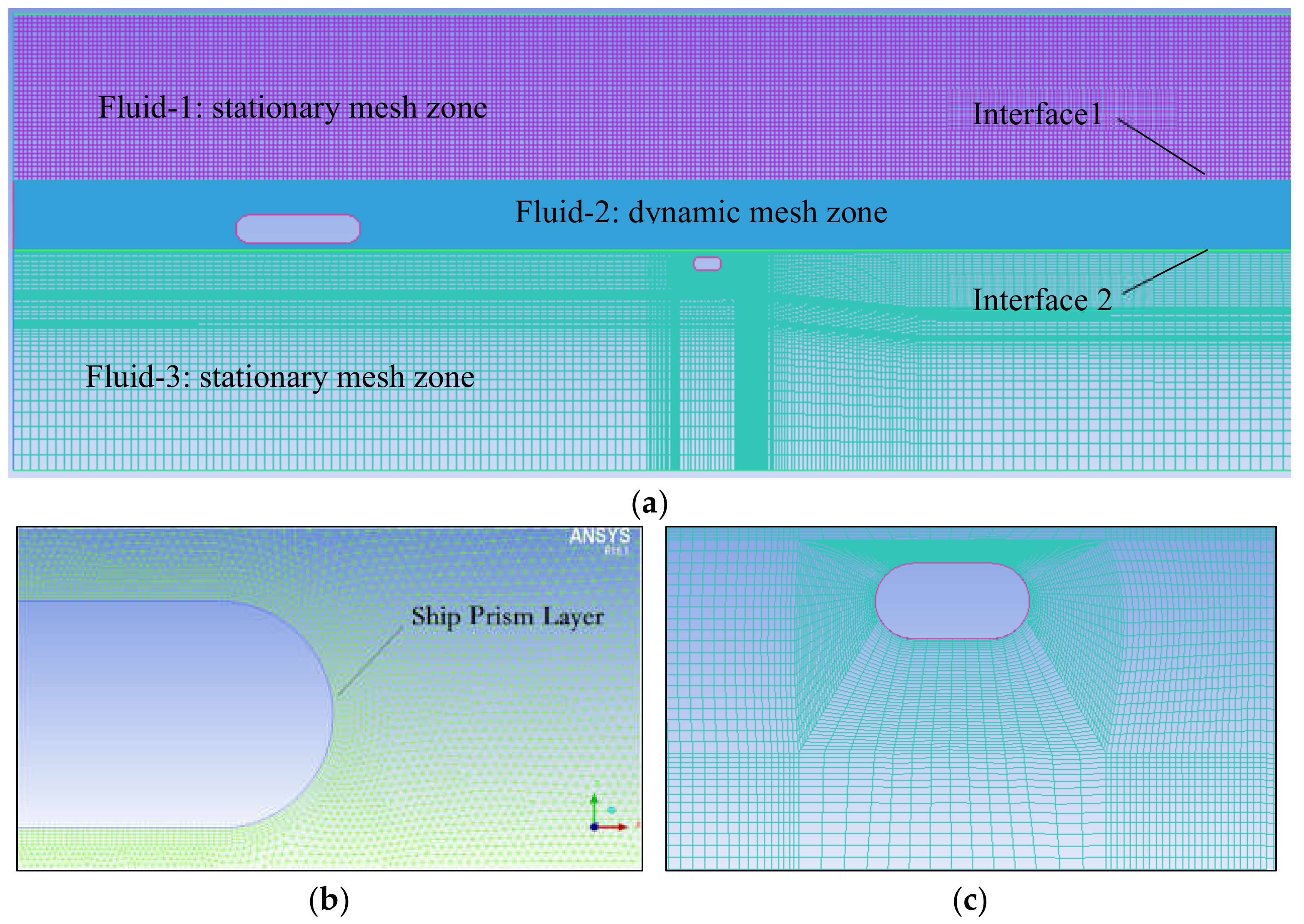


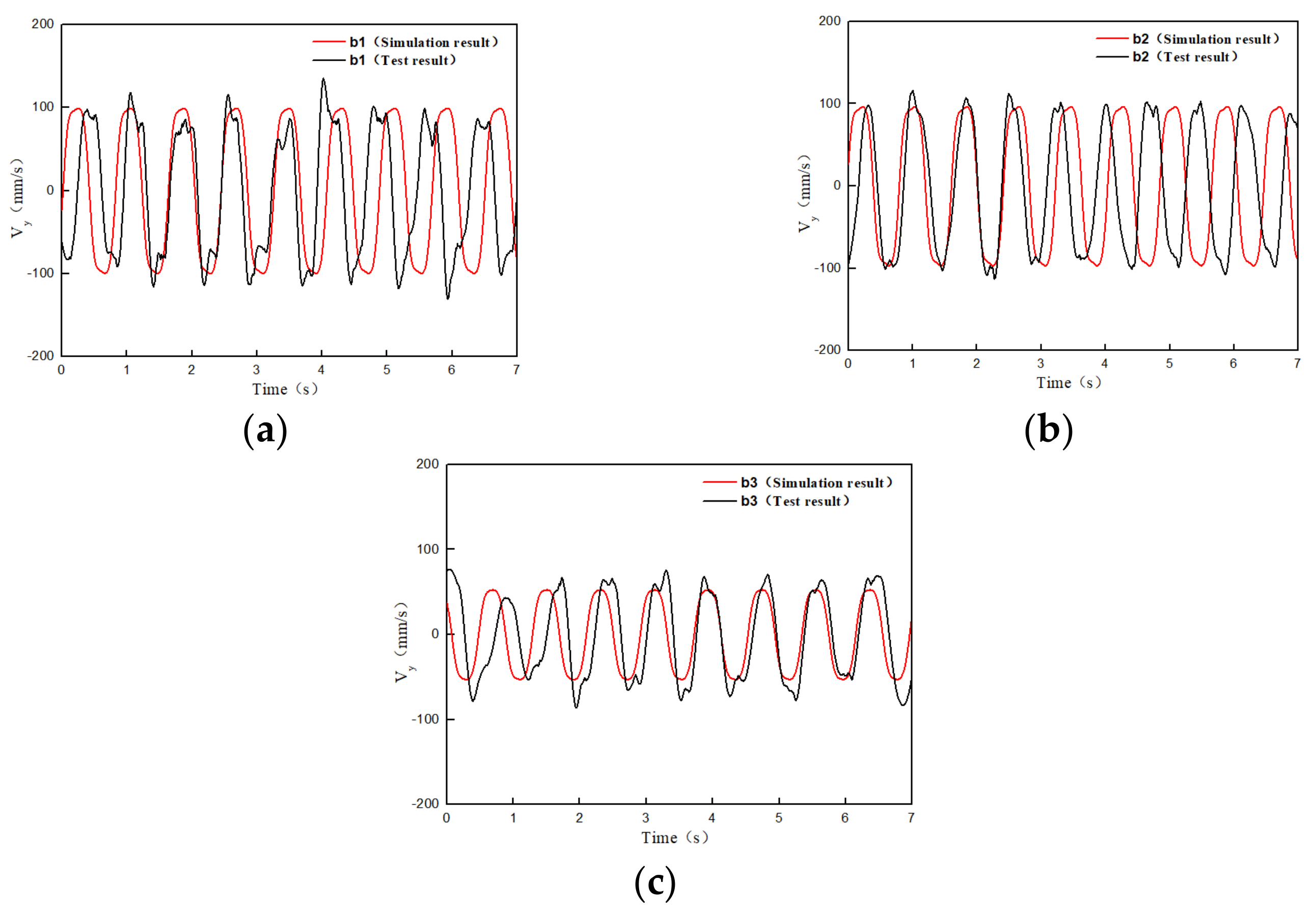









| V = 0.141 m/s | Flow Angle of Attack of Round-Ended Pier (α) | |||
|---|---|---|---|---|
| 0° | 15° | 30° | 45° | |
| PIV/ADV | √ | √ | √ | √ |
| Set Time Category | Pier Section Shape | Driving Area | Transverse Spacing between a Ship and Pier | Flow Angle of Attack of the Pier α |
|---|---|---|---|---|
| Validation group | Circular shape (diameter = 1 m) | / | 1b | / |
| Different flow angles of attack | Rounded shape | (1) The backflow side of the pier (2) The upstream side of the pier | 1b | 0° 15° 30° 45° |
| Distance between different ships and piers | Rounded shape | The backflow side of the pier | 1b, 1.2b, 1.5b, 2b 1b, 1.5b, 2b, 2.5b, 3b 1b, 2b, 3b, 4b | 15° 30° 45° |
| Parameter | Flow Angle of Attack (α°) | First Positive Peak (N·m) | The Incremental (N·m) | Negative Peak (N·m) | The Incremental (N·m) | Second Positive Peak (N·m) | The Incremental (N·m) |
|---|---|---|---|---|---|---|---|
| Bow roll moment | 0 | 0.0189 | / | −0.0238 | / | 0.0236 | / |
| 15 | 0.0319 | 0.0130 | −0.0271 | −0.0033 | 0.0317 | 0.0081 | |
| 30 | 0.0364 | 0.0045 | −0.0371 | −0.0100 | 0.0358 | 0.0041 | |
| 45 | 0.0422 | 0.0058 | −0.0495 | −0.0124 | 0.0530 | 0.0172 |
| Parameter | Flow Angle of Attack (α°) | First Positive Peak (N·m) | The Incremental (N·m) | Negative Peak (N·m) | The Incremental (N·m) | Second Positive peak (N·m) | The Incremental (N·m) |
|---|---|---|---|---|---|---|---|
| Bow roll moment | 0 | 0.0189 | / | −0.0238 | / | 0.0236 | / |
| 15 | 0.0180 | −0.0009 | −0.0287 | −0.0049 | 0.0353 | 0.0117 | |
| 30 | 0.0190 | 0.0040 | −0.0411 | −0.0124 | 0.0398 | 0.0045 | |
| 45 | 0.0277 | 0.0087 | −0.0539 | −0.0128 | 0.0625 | 0.0227 |
| Flow Angle of Attack (α°) | Transverse Spacing between Ship and Pier | First Positive Peak (N·m) | The Incremental (N·m) | Negative Peak (N·m) | The Incremental (N·m) | Second Positive Peak (N·m) | The Incremental (N·m) |
|---|---|---|---|---|---|---|---|
| 15 | 1.0b | 0.0150 | / | −0.0287 | / | 0.0353 | / |
| 1.2b | 0.0123 | −0.0027 | −0.0271 | 0.0016 | 0.0302 | −0.0051 | |
| 1.5b | 0.0081 | −0.0042 | −0.0257 | 0.0014 | 0.0240 | −0.0062 | |
| 2.0b | 0.0069 | −0.0012 | −0.0254 | 0.0003 | 0.0231 | −0.0009 | |
| 30 | 1.0b | 0.0190 | / | −0.0411 | / | 0.0398 | / |
| 1.5b | 0.0129 | −0.0061 | −0.0377 | 0.0034 | 0.0396 | −0.0002 | |
| 2.0b | 0.0104 | −0.0025 | −0.0262 | 0.0115 | 0.0383 | −0.0013 | |
| 2.5b | 0.0082 | −0.0010 | −0.0222 | 0.0040 | 0.0282 | −0.0101 | |
| 3.0b | 0.0079 | −0.0003 | −0.0216 | 0.0006 | 0.0253 | −0.0029 | |
| 45 | 1.0b | 0.0277 | / | −0.0539 | / | 0.0625 | / |
| 2.0b | 0.0133 | −0.0144 | −0.0291 | 0.0248 | 0.0383 | −0.0242 | |
| 3.0b | 0.0076 | −0.0057 | −0.0199 | 0.0092 | 0.0244 | −0.0139 | |
| 4.0b | 0.0069 | −0.0007 | −0.0188 | 0.0011 | 0.0242 | −0.0002 |
| Flow Angle of Attack (α) | 0° | 15° | 30° | 45° |
|---|---|---|---|---|
| Ship on the backflow side of the pier (B1) | 1b | 1.5b | 1.9b | 3b |
| Ship on the upstream side of the pier (B2) | 1b | 1.4b | 2.2b | 2b |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, A.; Zhang, G.; Liu, X.; Yu, Y.; Zhang, X.; Ma, H.; Zhang, J. Hydrodynamic Characteristics at Intersection Areas of Ship and Bridge Pier with Skew Bridge. Water 2022, 14, 904. https://doi.org/10.3390/w14060904
Li A, Zhang G, Liu X, Yu Y, Zhang X, Ma H, Zhang J. Hydrodynamic Characteristics at Intersection Areas of Ship and Bridge Pier with Skew Bridge. Water. 2022; 14(6):904. https://doi.org/10.3390/w14060904
Chicago/Turabian StyleLi, Anbin, Genguang Zhang, Xiaoping Liu, Yuanhao Yu, Ximin Zhang, Huigang Ma, and Jiaqiang Zhang. 2022. "Hydrodynamic Characteristics at Intersection Areas of Ship and Bridge Pier with Skew Bridge" Water 14, no. 6: 904. https://doi.org/10.3390/w14060904






