Dynamic Modeling of Crop–Soil Systems to Design Monitoring and Automatic Irrigation Processes: A Review with Worked Examples
Abstract
:1. Introduction
2. Dynamic Crop–Soil Model Components
2.1. Crop and Growth Models
| Model | Inputs | Driving Variable | Output Variables | References | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Environmental | Manipulated | ||||||||||||
| Radiation | Temperatures (max, min) | Rainfall Precipitation | Reference Evapotranspiration | Wind | Humidity | Irrigation Moisture | Fertilization | Other | Yield | Other | |||
| APEX | √ | √ | √ | √ | √ | √ | √ | • Soil preparation | Cumulative | √ | • Carbon and nitrogen transformations | [25] | |
| • Pesticide | temperature | • Costs | |||||||||||
| • Crop rotation | |||||||||||||
| • Tillage | |||||||||||||
| APSIM | √ | √ | √ | √ | √ | √ | • Vapor pressure | Thermal time | √ | • Dry matter | [26] | ||
| accumulation | |||||||||||||
| AquaCrop | √ | √ | √ | √ | • CO2 concentration | Water content | √ | • Irrigation | [27] | ||||
| • Soil fertility level | and fluxes | • Water losses | |||||||||||
| • Weed management | • Soil water | ||||||||||||
| CropSyst | √ | √ | √ | • Soil profile | Thermal time | √ | • Above-ground root biomass accumulation | [28] | |||||
| • Management of scheduled events | accumulation | ||||||||||||
| • Fertilization | |||||||||||||
| • Residue fate | |||||||||||||
| DAISY | √ | √ | √ | √ | √ | √ | √ | √ | • Soil properties | Air temperature | • Water balance | [29] | |
| • Sowing/planting | • Heat balance | ||||||||||||
| • Soil tillage | • Solute balance | ||||||||||||
| • Harvest | • Pesticide fate | ||||||||||||
| DNDC | √ | √ | √ | √ | √ | √ | √ | • Redox potential Eh | Air temperature | √ | • Gas emissions | [30,31] | |
| • Oxygen concentration | • N leaching | ||||||||||||
| • Climate file | • Weather | ||||||||||||
| • Soil profile | • Soil carbon sequestration | ||||||||||||
| • Tillage | |||||||||||||
| DSSAT | √ | √ | √ | √ | √ | √ | √ | • CO2 concentration | Thermal time | √ | • Weather | [32] | |
| • Soil profile | accumulation | • Soil profile | |||||||||||
| • Crop profile | • Fertilization | ||||||||||||
| • Management profile | • Irrigation | ||||||||||||
| EPIC | √ | √ | √ | √ | √ | √ | √ | • Soil profile | Solar | √ | • Productivity | [33] | |
| • Soil erosion | radiation | • Waste management | |||||||||||
| • Pesticide | • Plant competition | ||||||||||||
| • Homogeneous soil assumption | • Pesticide fate | ||||||||||||
| • Crop rotation | • Furrow diking | ||||||||||||
| • Tillage | |||||||||||||
| SALUS | √ | √ | √ | √ | √ | • Tillage | Solar | √ | • Development stages | [34] | |||
| • Residue fate | radiation | • Fertilization | |||||||||||
| • Pesticide | • N leaching | ||||||||||||
| • Soil erosion | • Irrigation | ||||||||||||
| STICS | √ | √ | √ | √ | √ | √ | √ | √ | Cropping | Plant carbon | √ | • Nitrate leaching | [35] |
| schema | accumulation [36] | • Drainage | |||||||||||
| SWAP | √ | √ | √ | √ | √ | √ | • Crop rotation | Thermal time | • Dry weight (stems/leaves) | [37] | |||
| • Solute transport | • Water management | ||||||||||||
| WOFOST | √ | √ | √ | √ | √ | √ | √ | √ | • CO2 concentration | Thermal time | √ | • Biomass | [38] |
| • Vapor pressure | • Water use | ||||||||||||
| • Management profile | |||||||||||||
| Model | Water Balance | Nutrient Balance | Evapotranspiration | Growth-Core Main State Variable | Biomass or Yield Formation | Stresses |
|---|---|---|---|---|---|---|
| APEX | Probabilistic distribution |
|
| Potential increase in biomass Monteith 1977 |
| |
| APSIM |
| Nitrogen uptake rate |
|
| Potential biomass accumulation |
|
| AquaCrop | Soil water balance | Salt balance by transfer of solutes |
|
| Cumulative crop transpiration limited by biomass water productivity |
|
| CropSyst |
| N Transformations N absorption rate Chemical budget (salinity, pesticide) |
|
| Tanner and Sinclair (1983), daily biomass accumulation Monteith (1977) at low vapor pressure deficit |
|
| DAISY |
| Nitrogen dynamics |
| • Beer’s law | Accumulation of dry matter and nitrogen |
|
| DNDC | • Algebraic equation |
| Water-use efficiency limited by VPD [39] |
| Daily cumulative temperature conditioned by N demand uptake Water demand uptake | •Water |
| DSSAT | Mass-balance (Differential equations by soil layer) |
|
|
| Growing degree-days (GDD) |
|
| EPIC |
| Leaching equations Sediment transport Mineralization |
|
| Conversion of Intercepted light to biomass |
|
| SALUS | • Mass balance |
| • Penman (1948) (modified by Shuttleworth 2007) |
| Carbon assimilation |
|
| STICS | • Mass balance equation | Functional ratio equation |
|
| Plant carbon accumulation [40] |
|
| SWAP |
| Nitrogen cycle |
| • LAI | Daily net assimilation depending on the intercepted light |
|
| WOFOST | • Mass balance by soil layer | SWAMP model for solute transport | • Penman (1948) |
| Daily net assimilation depending on the intercepted light |
|
2.1.1. First Level
2.1.2. Second Level
2.1.3. Third Level
2.2. Compartmental Approach
2.3. State-Space Representation and Variable Definition
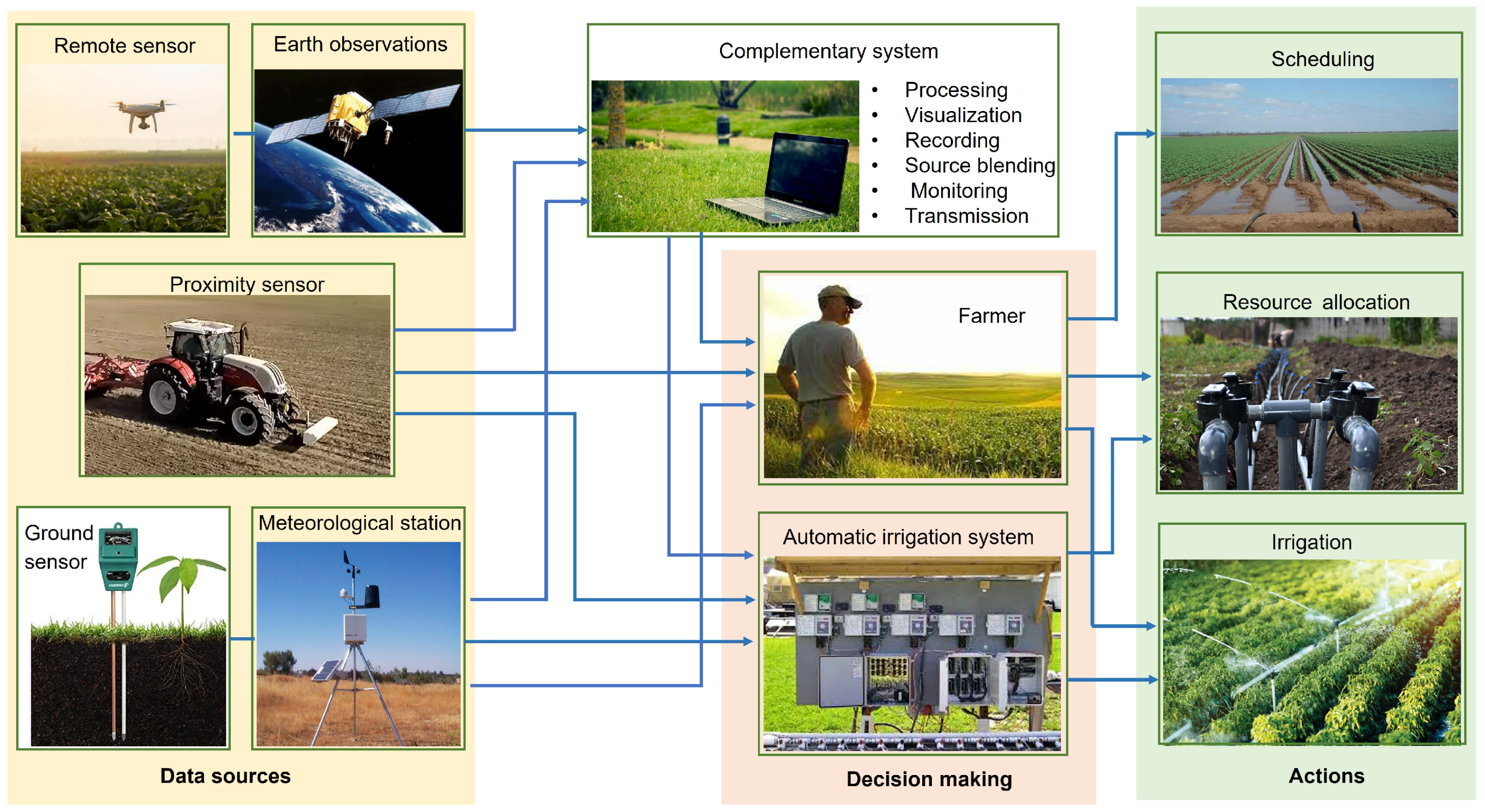
3. Sensors and Instrumentation
4. Model Identification
- data collection;
- definition of the model objectives (simulation or control) and of the model structure;
- identifiability study;
- parameter estimation;
- evaluation of parameter uncertainties and of confidence intervals in the model prediction;
- model validation and cross-validation.
4.1. Identifiability
4.2. Parameter Estimation
4.3. Model Validation and Uncertainty Analysis
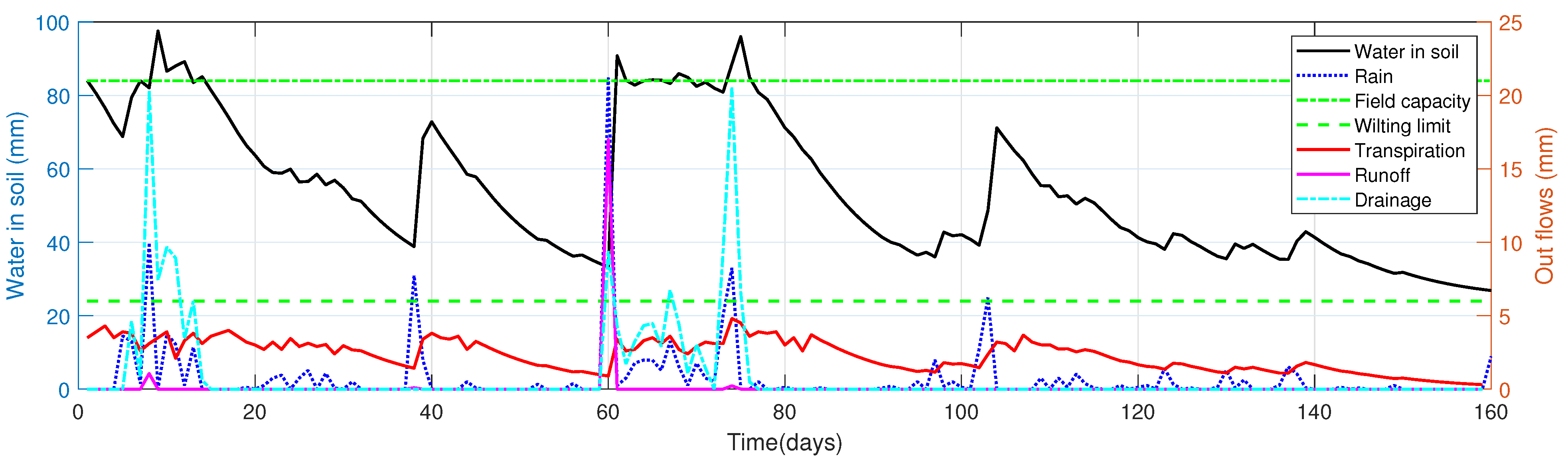
4.4. Illustrative Example: Water Balance in Soil
5. State Estimation and Software Sensors
5.1. Observability
Observability Analysis of a Plant-Growth Model
5.2. Software Sensors in Agriculture
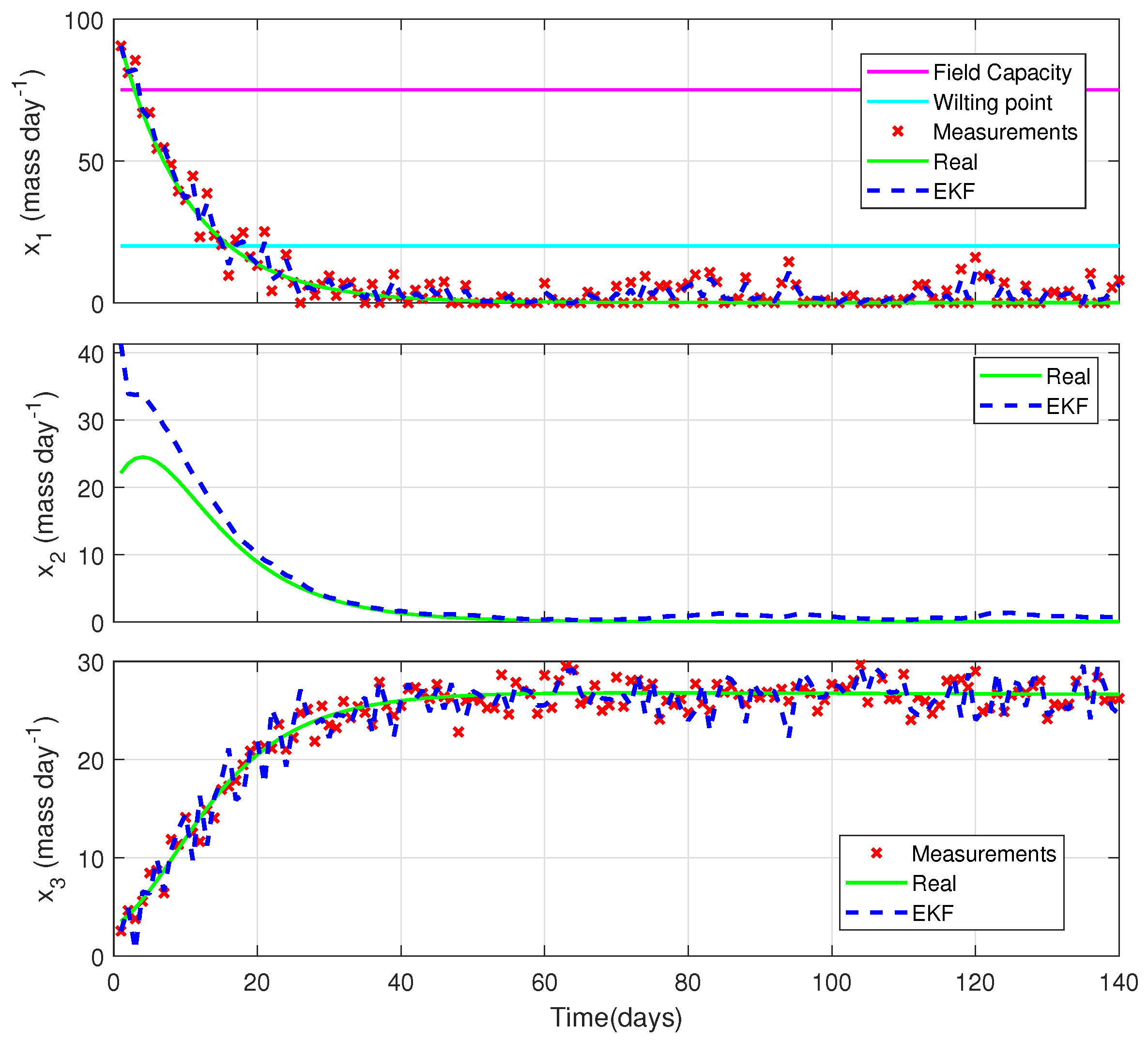
5.3. Illustrative Example: State Estimation with a Generic Crop Model
- The water absorption rate of the plant is less than or equal to the rate of loss of water from the pond, i.e., ;
- The dry matter accumulation rate of the plant is approximately equal to the rate of decrease in the water inside the plant that goes toward photosynthesis, i.e., ;
- The rate of water loss through transpiration is larger than the rate of water loss through evaporation, i.e., ;
- The degradation rate of the plant is larger than the rate of water loss through evaporation, i.e., ;
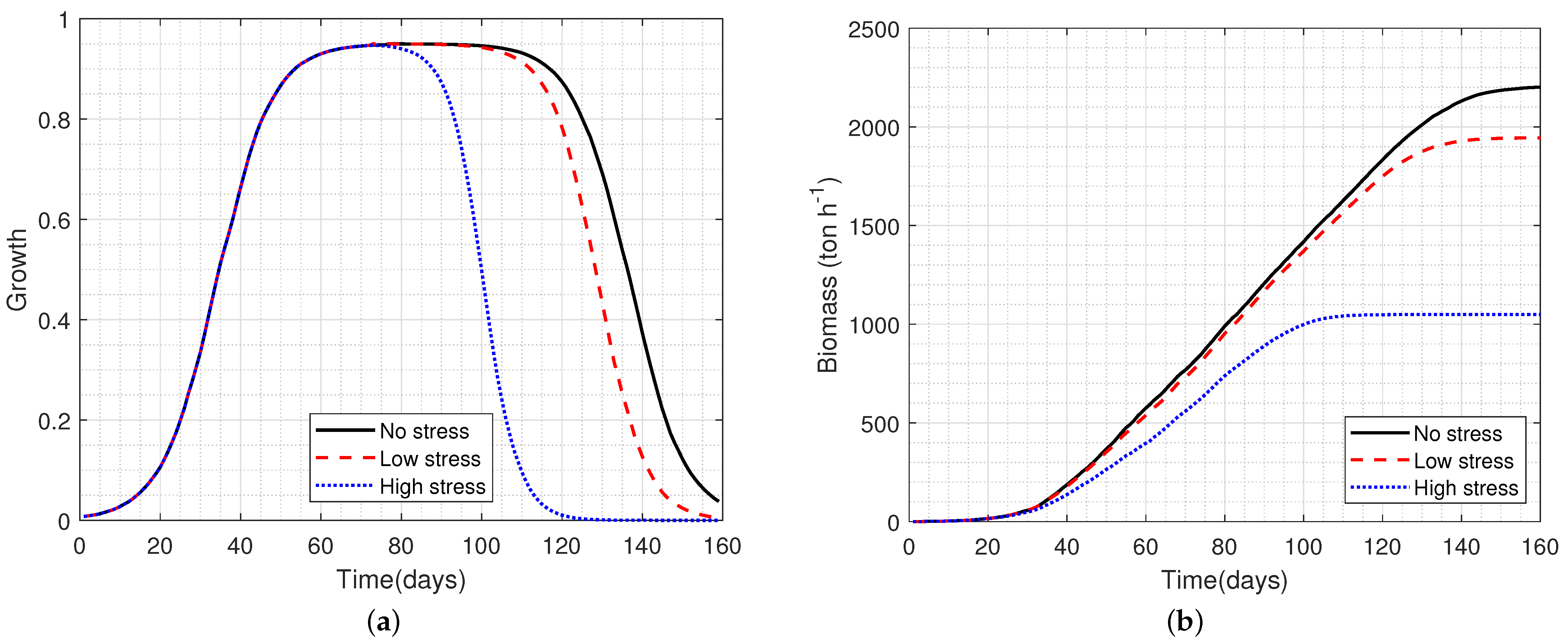
- The crop is wheat on a short life cycle of 140 days under no stress conditions. Therefore, water and nutrients are readily available and do not limit growth;
- There is neither damage from pests and diseases nor any competition from weeds growing in the field;
- and can be measured by existing technology, i.e., by RS based on images, and the measurements are collected daily.
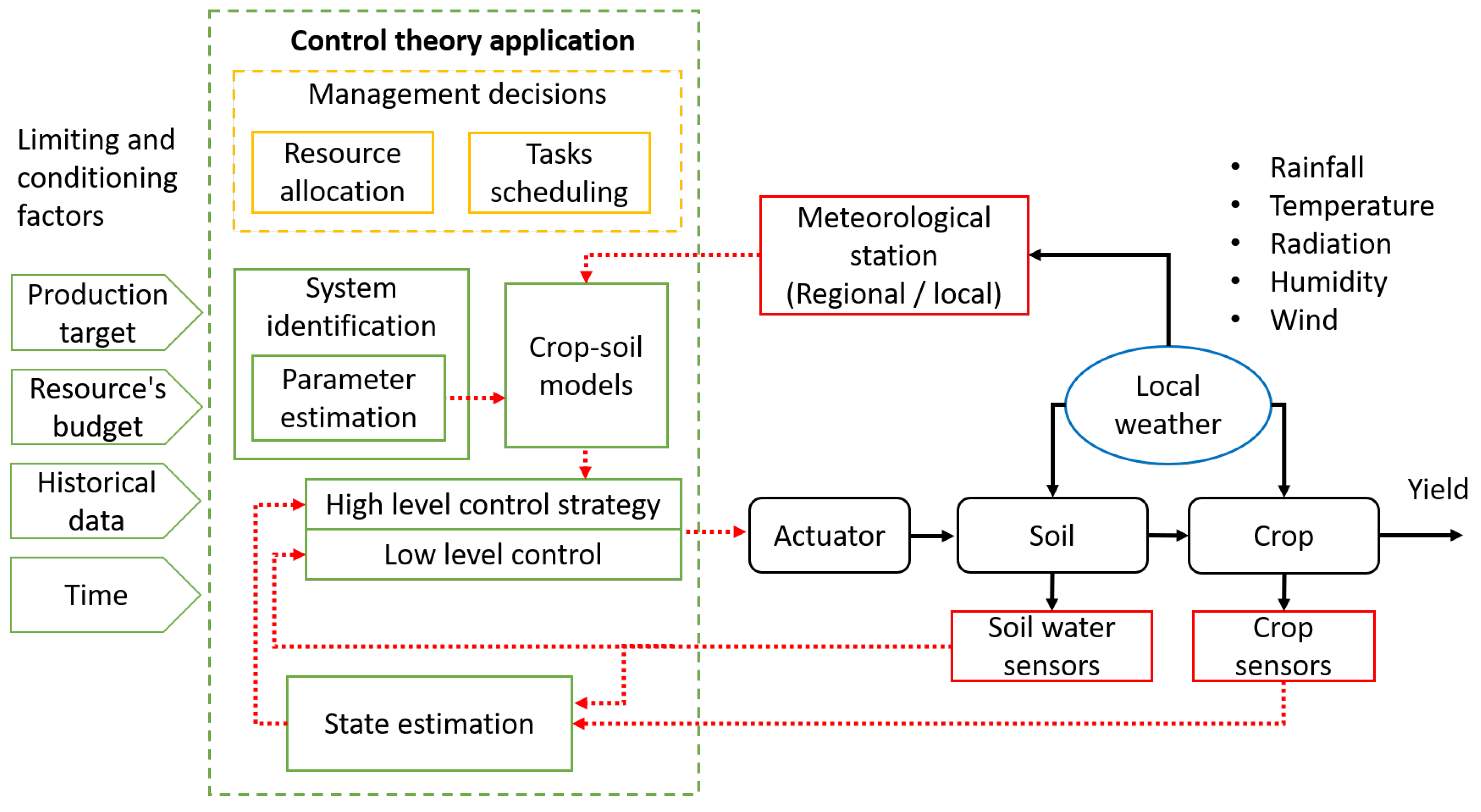
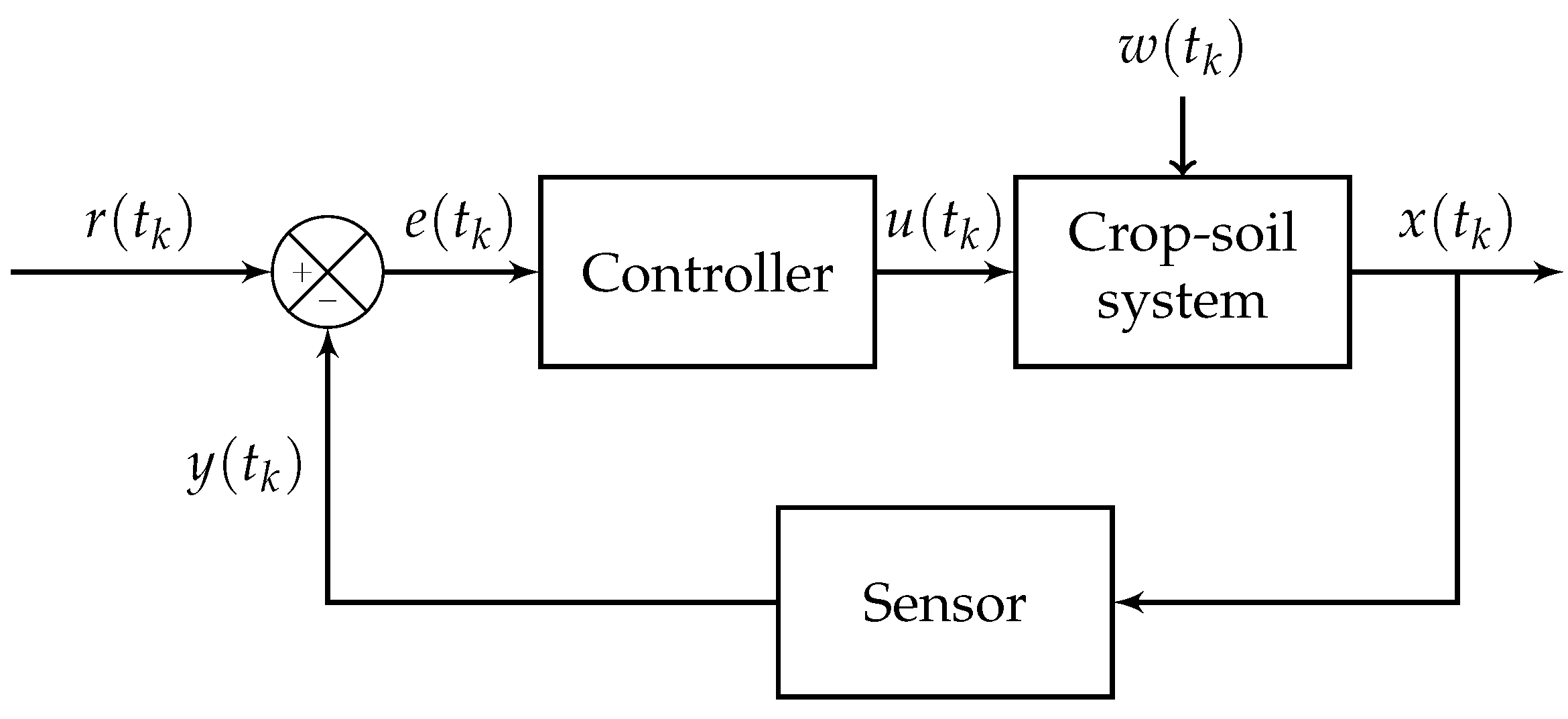
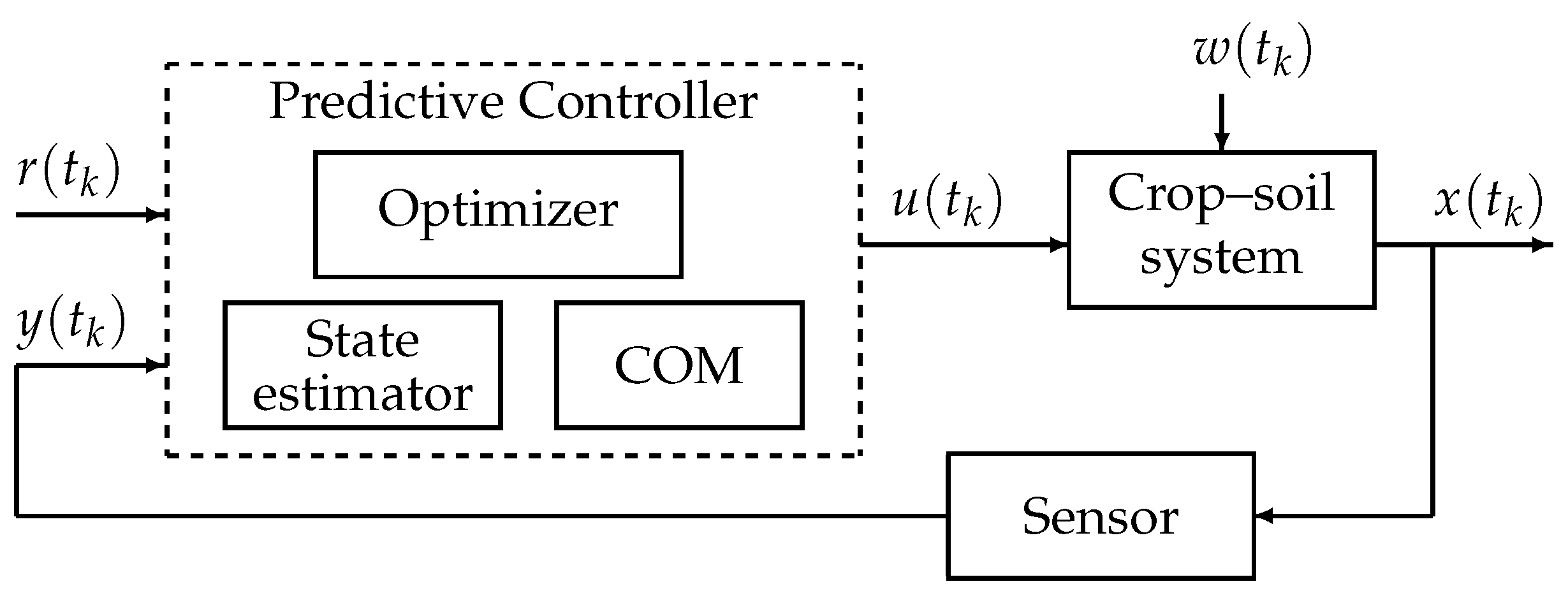
6. Irrigation Control
6.1. Control Paradigms
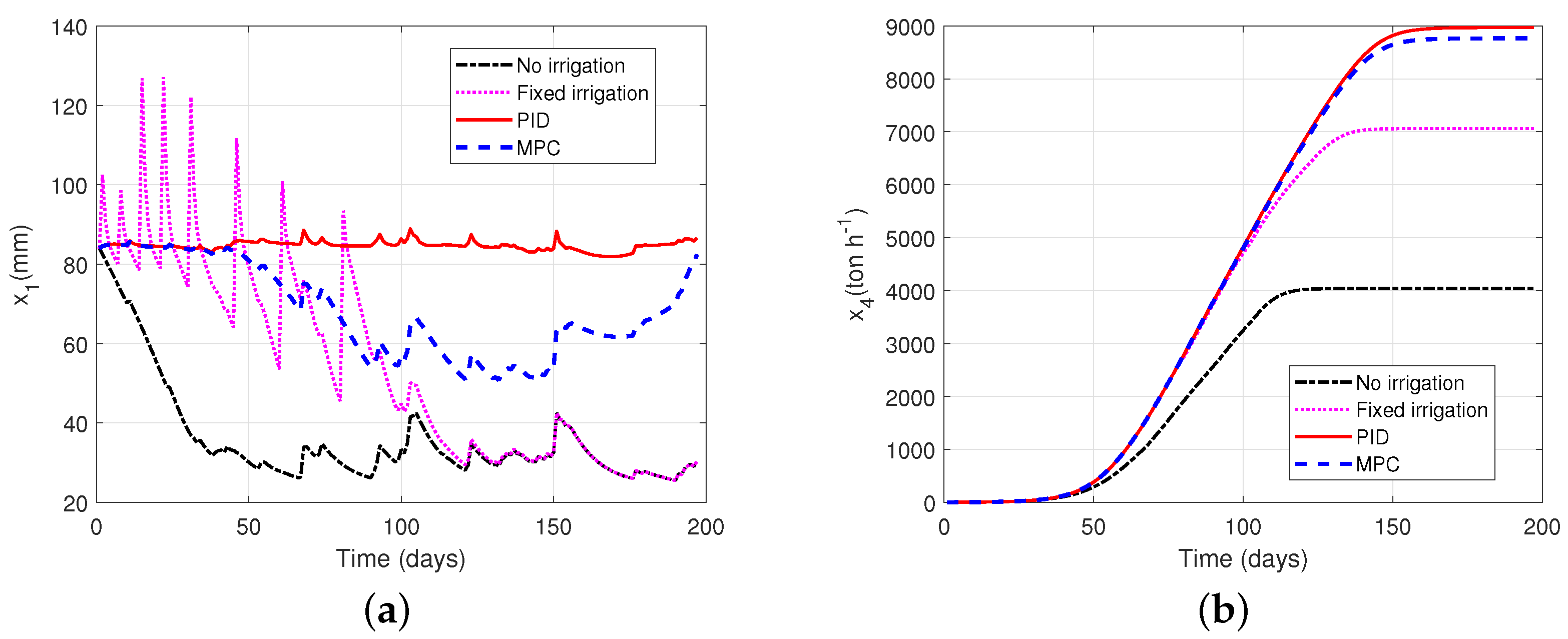
6.2. Illustrative Example: PID and Model Predictive Control
7. Spatial Heterogeneity
8. Conclusions and Perspectives
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Campanhola, C.; Pandey, S. Sustainable Food and Agriculture: An Integrated Approach; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Velasco-Muñoz, J.F.; Aznar-Sánchez, J.A.; Belmonte-Ureña, L.J.; Román-Sánchez, I.M. Sustainable water use in agriculture: A review of worldwide research. Sustainability 2018, 10, 1084. [Google Scholar] [CrossRef] [Green Version]
- Lamnabhi-Lagarrigue, F.; Annaswamy, A.; Engell, S.; Isaksson, A.; Khargonekar, P.; Murray, R.M.; Nijmeijer, H.; Samad, T.; Tilbury, D.; Van den Hof, P. Systems & Control for the future of humanity, research agenda: Current and future roles, impact and grand challenges. Annu. Rev. Control 2017, 43, 1–64. [Google Scholar]
- Nouri, H.; Stokvis, B.; Galindo, A.; Blatchford, M.; Hoekstra, A.Y. Water scarcity alleviation through water footprint reduction in agriculture: The effect of soil mulching and drip irrigation. Sci. Total Environ. 2019, 653, 241–252. [Google Scholar] [CrossRef] [PubMed]
- Ashofteh, P.S.; Bozorg-Haddad, O.; Loáiciga, H.A. Development of adaptive strategies for irrigation water demand management under climate change. J. Irrig. Drain. Eng. 2017, 143, 04016077. [Google Scholar] [CrossRef]
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Toward a new generation of agricultural system data, models, and knowledge products: State of agricultural systems science. Agric. Syst. 2017, 155, 269–288. [Google Scholar] [CrossRef]
- Jones, J.W.; Antle, J.M.; Basso, B.; Boote, K.J.; Conant, R.T.; Foster, I.; Godfray, H.C.J.; Herrero, M.; Howitt, R.E.; Janssen, S.; et al. Brief history of agricultural systems modeling. Agric. Syst. 2017, 155, 240–254. [Google Scholar] [CrossRef] [PubMed]
- Jin, X.; Kumar, L.; Li, Z.; Feng, H.; Xu, X.; Yang, G.; Wang, J. A review of data assimilation of remote sensing and crop models. Eur. J. Agron. 2018, 92, 141–152. [Google Scholar] [CrossRef]
- Siad, S.M.; Iacobellis, V.; Zdruli, P.; Gioia, A.; Stavi, I.; Hoogenboom, G. A review of coupled hydrologic and crop growth models. Agric. Water Manag. 2019, 224, 105746. [Google Scholar] [CrossRef]
- Zhou, H.; Zhao, W. Modeling soil water balance and irrigation strategies in a flood-irrigated wheat-maize rotation system. A case in dry climate, China. Agric. Water Manag. 2019, 221, 286–302. [Google Scholar] [CrossRef]
- Huang, J.; Gómez-Dans, J.L.; Huang, H.; Ma, H.; Wu, Q.; Lewis, P.E.; Liang, S.; Chen, Z.; Xue, J.H.; Wu, Y.; et al. Assimilation of remote sensing into crop growth models: Current status and perspectives. Agric. For. Meteorol. 2019, 276–277, 107609. [Google Scholar] [CrossRef]
- Karthikeyan, L.; Chawla, I.; Mishra, A.K. A review of remote sensing applications in agriculture for food security: Crop growth and yield, irrigation, and crop losses. J. Hydrol. 2020, 586, 124905. [Google Scholar] [CrossRef]
- Liakos, K.G.; Busato, P.; Moshou, D.; Pearson, S.; Bochtis, D. Machine learning in agriculture: A review. Sensors 2018, 18, 2674. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lytos, A.; Lagkas, T.; Sarigiannidis, P.; Zervakis, M.; Livanos, G. Towards smart farming: Systems, frameworks and exploitation of multiple sources. Comput. Netw. 2020, 172, 107147. [Google Scholar] [CrossRef]
- Cobbenhagen, A.; Antunes, D.; van de Molengraft, M.; Heemels, W. Opportunities for control engineering in arable precision agriculture. Annu. Rev. Control. 2021, 51, 47–55. [Google Scholar] [CrossRef]
- Romero, R.; Muriel, J.; García, I.; de la Peña, D.M. Research on automatic irrigation control: State of the art and recent results. Agric. Water Manag. 2012, 114, 59–66. [Google Scholar] [CrossRef]
- McCarthy, A.C.; Hancock, N.H.; Raine, S.R. Advanced process control of irrigation: The current state and an analysis to aid future development. Irrig. Sci. 2013, 31, 183–192. [Google Scholar] [CrossRef]
- Conde, G.; Quijano, N.; Ocampo-Martinez, C. Modeling and control in open-channel irrigation systems: A review. Annu. Rev. Control. 2021, 51, 163–171. [Google Scholar] [CrossRef]
- Di Paola, A.; Valentini, R.; Santini, M. An overview of available crop growth and yield models for studies and assessments in agriculture. J. Sci. Food Agric. 2016, 96, 709–714. [Google Scholar] [CrossRef]
- Rossiter, D. Biophysical models in land evaluation. In Encyclopedia of Land Use, Land cCover and Soil Sciences: Land Evaluation; EOLSS Publishers/UNESCO: Oxford, UK, 2009; Volume 2, pp. 181–195. [Google Scholar]
- Keating, B.A.; Thorburn, P.J. Modelling crops and cropping systems—Evolving purpose, practice and prospects. Eur. J. Agron. 2018, 100, 163–176. [Google Scholar] [CrossRef]
- Walters, J.P.; Archer, D.W.; Sassenrath, G.F.; Hendrickson, J.R.; Hanson, J.D.; Halloran, J.M.; Vadas, P.; Alarcon, V.J. Exploring agricultural production systems and their fundamental components with system dynamics modelling. Ecol. Model. 2016, 333, 51–65. [Google Scholar] [CrossRef] [Green Version]
- Bruinsma, J. World Agriculture: Towards 2015/2030: An FAO Perspective; Routledge: London, UK, 2017. [Google Scholar]
- Yu, L.; Gao, X.; Zhao, X. Global synthesis of the impact of droughts on crops’ water-use efficiency (WUE): Towards both high WUE and productivity. Agric. Syst. 2020, 177, 102723. [Google Scholar] [CrossRef]
- Williams, J.R.; Izaurralde, R.; Singh, V.; Frevert, D. The APEX model. In Watershed Models; CRC Press: Boca Raton, FL, USA, 2006; pp. 437–482. [Google Scholar]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef] [Green Version]
- Steduto, P.; Hsiao, T.C.; Raes, D.; Fereres, E. AquaCrop—The FAO Crop Model to Simulate Yield Response to Water: I. Concepts and Underlying Principles. Agron. J. 2009, 101, 426–437. [Google Scholar] [CrossRef] [Green Version]
- Stöckle, C.O.; Donatelli, M.; Nelson, R. CropSyst, a cropping systems simulation model. Eur. J. Agron. 2003, 18, 289–307. [Google Scholar] [CrossRef]
- Abrahamsen, P.; Hansen, S. Daisy: An open soil-crop-atmosphere system model. Environ. Model. Softw. 2000, 15, 313–330. [Google Scholar] [CrossRef]
- Li, C.; Frolking, S.; Crocker, G.J.; Grace, P.R.; Klír, J.; Körchens, M.; Poulton, P.R. Simulating trends in soil organic carbon in long-term experiments using the DNDC model. Geoderma 1997, 81, 45–60. [Google Scholar] [CrossRef]
- Gilhespy, S.L.; Anthony, S.; Cardenas, L.; Chadwick, D.; del Prado, A.; Li, C.; Misselbrook, T.; Rees, R.M.; Salas, W.; Sanz-Cobena, A.; et al. First 20 years of DNDC (DeNitrification DeComposition): Model evolution. Ecol. Model. 2014, 292, 51–62. [Google Scholar] [CrossRef] [Green Version]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Williams, J.; Jones, C.; Kiniry, J.; Spanel, D.A. The EPIC crop growth model. Trans. ASAE 1989, 32, 497–0511. [Google Scholar] [CrossRef]
- Basso, B.; Ritchie, J.T. Simulating Crop Growth and Biogeochemical Fluxes in Response to Land Management Using the SALUS Model; Oxford University Press: Oxford, UK, 2015; Volume 2015. [Google Scholar]
- Brisson, N.; Mary, B.; Ripoche, D.; Jeuffroy, M.H.; Ruget, F.; Nicoullaud, B.; Gate, P.; Devienne-Barret, F.; Antonioletti, R.; Durr, C.; et al. STICS: A generic model for the simulation of crops and their water and nitrogen balances. I. Theory and parameterization applied to wheat and corn. Agronomie 1998, 18, 311–346. [Google Scholar] [CrossRef]
- de Wit, C.T. Transpiration and Crop Yields; Technical Report; Wageningen University: Wageningen, The Netherlands, 1958. [Google Scholar]
- Kroes, J.; Van Dam, J.; Bartholomeus, R.; Groenendijk, P.; Heinen, M.; Hendriks, R.; Mulder, H.; Supit, I.; Van Walsum, P. SWAP Version 4; Technical Report; Wageningen Environmental Research: Wageningen, The Netherlands, 2017. [Google Scholar]
- Van Diepen, C.v.; Wolf, J.; Van Keulen, H.; Rappoldt, C. WOFOST: A simulation model of crop production. Soil Use Manag. 1989, 5, 16–24. [Google Scholar] [CrossRef]
- Aber, J.D.; Federer, C.A. A generalized, lumped-parameter model of photosynthesis, evapotranspiration and net primary production in temperate and boreal forest ecosystems. Oecologia 1992, 92, 463–474. [Google Scholar] [CrossRef] [PubMed]
- De Wit, C. Potential Photosynthesis Crop Surfaces. Neth. J. Agric. Sci. 1959, 7, 141–149. [Google Scholar]
- Jiang, T.; Dou, Z.; Liu, J.; Gao, Y.; Malone, R.W.; Chen, S.; Feng, H.; Yu, Q.; Xue, G.; He, J. Simulating the Influences of Soil Water Stress on Leaf Expansion and Senescence of Winter Wheat. Agric. For. Meteorol. 2020, 291, 108061. [Google Scholar] [CrossRef]
- Woli, P.; Jones, J.W.; Ingram, K.T.; Fraisse, C.W. Agricultural Reference Index for Drought (ARID). Agron. J. 2012, 104, 287–300. [Google Scholar] [CrossRef]
- Zhao, C.; Liu, B.; Xiao, L.; Hoogenboom, G.; Boote, K.J.; Kassie, B.T.; Pavan, W.; Shelia, V.; Kim, K.S.; Hernandez-Ochoa, I.M.; et al. A SIMPLE crop model. Eur. J. Agron. 2019, 104, 97–106. [Google Scholar] [CrossRef]
- Holzworth, D.P.; Huth, N.I.; deVoil, P.G.; Zurcher, E.J.; Herrmann, N.I.; McLean, G.; Chenu, K.; van Oosterom, E.J.; Snow, V.; Murphy, C.; et al. APSIM—Evolution towards a new generation of agricultural systems simulation. Environ. Model. Softw. 2014, 62, 327–350. [Google Scholar] [CrossRef]
- Wang, E.; Martre, P.; Zhao, Z.; Ewert, F.; Maiorano, A.; Rötter, R.P.; Kimball, B.A.; Ottman, M.J.; Wall, G.W.; White, J.W.; et al. The uncertainty of crop yield projections is reduced by improved temperature response functions. Nat. Plants 2017, 3, 17102. [Google Scholar] [CrossRef] [Green Version]
- Donatelli, M.; Magarey, R.D.; Bregaglio, S.; Willocquet, L.; Whish, J.P.; Savary, S. Modelling the impacts of pests and diseases on agricultural systems. Agric. Syst. 2017, 155, 213–224. [Google Scholar] [CrossRef]
- Ritchie, J. A user-orientated model of the soil water balance in wheat. In Wheat Growth and Modelling; Springer: Berlin/Heidelberg, Germany, 1985; pp. 293–305. [Google Scholar]
- Cameron, K.; Di, H.J.; Moir, J. Nitrogen losses from the soil/plant system: A review. Ann. Appl. Biol. 2013, 162, 145–173. [Google Scholar] [CrossRef]
- Shibu, M.; Leffelaar, P.; Van Keulen, H.; Aggarwal, P. LINTUL3, a simulation model for nitrogen-limited situations: Application to rice. Eur. J. Agron. 2010, 32, 255–271. [Google Scholar] [CrossRef]
- Thornley, J.H.; France, J. Mathematical Models in Agriculture: Quantitative Methods for the Plant, Animal and Ecological Sciences; Cabi: Wallingford, UK, 2007. [Google Scholar]
- Zhang, S.; Tao, F.; Zhang, Z. Uncertainty from model structure is larger than that from model parameters in simulating rice phenology in China. Eur. J. Agron. 2017, 87, 30–39. [Google Scholar] [CrossRef] [Green Version]
- Wallach, D.; Thorburn, P.J. Estimating uncertainty in crop model predictions: Current situation and future prospects. Eur. J. Agron. 2017, 88, A1–A7. [Google Scholar] [CrossRef]
- Sowe, S.K.; Simmon, E.; Zettsu, K.; de Vaulx, F.; Bojanova, I. Cyber-Physical-Human Systems: Putting People in the Loop. IT Prof. 2016, 18, 10–13. [Google Scholar] [CrossRef] [Green Version]
- Mittelbach, H.; Lehner, I.; Seneviratne, S.I. Comparison of four soil moisture sensor types under field conditions in Switzerland. J. Hydrol. 2012, 430, 39–49. [Google Scholar] [CrossRef]
- Kashyap, B.; Kumar, R. Sensing Methodologies in Agriculture for Soil Moisture and Nutrient Monitoring. IEEE Access 2021, 9, 14095–14121. [Google Scholar] [CrossRef]
- Zare, E.; Arshad, M.; Zhao, D.; Nachimuthu, G.; Triantafilis, J. Two-dimensional time-lapse imaging of soil wetting and drying cycle using EM38 data across a flood irrigation cotton field. Agric. Water Manag. 2020, 241, 106383. [Google Scholar] [CrossRef]
- Zare, E.; Wang, J.; Zhao, D.; Arshad, M.; Triantafilis, J. Scope to map available water content using proximal sensed electromagnetic induction and gamma-ray spectrometry data. Agric. Water Manag. 2021, 247, 106705. [Google Scholar] [CrossRef]
- Qu, Y.; Zhu, Y.; Han, W.; Wang, J.; Ma, M. Crop leaf area index observations with a wireless sensor network and its potential for validating remote sensing products. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 7, 431–444. [Google Scholar] [CrossRef]
- Viña, A.; Gitelson, A.A.; Nguy-Robertson, A.L.; Peng, Y. Comparison of different vegetation indices for the remote assessment of green leaf area index of crops. Remote Sens. Environ. 2011, 115, 3468–3478. [Google Scholar] [CrossRef]
- Li, X.; Liu, Q.; Yang, R.; Zhang, H.; Zhang, J.; Cai, E. The design and implementation of the leaf area index sensor. Sensors 2015, 15, 6250–6269. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Neale, C.M.U.; Geli, H.M.E.; Kustas, W.P.; Alfieri, J.G.; Gowda, P.H.; Evett, S.R.; Prueger, J.H.; Hipps, L.E.; Dulaney, W.P.; Chávez, J.L.; et al. Soil water content estimation using a remote sensing based hybrid evapotranspiration modeling approach. Adv. Water Resour. 2012, 50, 152–161. [Google Scholar] [CrossRef]
- Dalezios, N.R.; Dercas, N.; Spyropoulos, N.V.; Psomiadis, E. Remotely sensed methodologies for crop water availability and requirements in precision farming of vulnerable agriculture. Water Resour. Manag. 2019, 33, 1499–1519. [Google Scholar] [CrossRef]
- Campos, I.; González-Gómez, L.; Villodre, J.; González-Piqueras, J.; Suyker, A.E.; Calera, A. Remote sensing-based crop biomass with water or light-driven crop growth models in wheat commercial fields. Field Crop. Res. 2018, 216, 175–188. [Google Scholar] [CrossRef]
- Meng, B.; Ge, J.; Liang, T.; Yang, S.; Gao, J.; Feng, Q.; Cui, X.; Huang, X.; Xie, H. Evaluation of remote sensing inversion error for the above-ground biomass of alpine meadow grassland based on multi-source satellite data. Remote Sens. 2017, 9, 372. [Google Scholar] [CrossRef] [Green Version]
- Kumar, L.; Mutanga, O. Remote sensing of above-ground biomass. Remote Sens. 2017, 9, 935. [Google Scholar] [CrossRef] [Green Version]
- Lu, D.; Chen, Q.; Wang, G.; Liu, L.; Li, G.; Moran, E. A survey of remote sensing-based aboveground biomass estimation methods in forest ecosystems. Int. J. Digit. Earth 2016, 9, 63–105. [Google Scholar] [CrossRef]
- Khanal, S.; Fulton, J.; Shearer, S. An overview of current and potential applications of thermal remote sensing in precision agriculture. Comput. Electron. Agric. 2017, 139, 22–32. [Google Scholar] [CrossRef]
- Lu, L.; Kuenzer, C.; Wang, C.; Guo, H.; Li, Q. Evaluation of three MODIS-derived vegetation index time series for dryland vegetation dynamics monitoring. Remote Sens. 2015, 7, 7597–7614. [Google Scholar] [CrossRef] [Green Version]
- Shen, L.; He, Y.; Guo, X. Suitability of the normalized difference vegetation index and the adjusted transformed soil-adjusted vegetation index for spatially characterizing loggerhead shrike habitats in North American mixed prairie. J. Appl. Remote Sens. 2013, 7, 073574. [Google Scholar] [CrossRef]
- Ren, H.; Zhou, G.; Zhang, F. Using negative soil adjustment factor in soil-adjusted vegetation index (SAVI) for aboveground living biomass estimation in arid grasslands. Remote Sens. Environ. 2018, 209, 439–445. [Google Scholar] [CrossRef]
- Chao, Z.; Liu, N.; Zhang, P.; Ying, T.; Song, K. Estimation methods developing with remote sensing information for energy crop biomass: A comparative review. Biomass Bioenergy 2019, 122, 414–425. [Google Scholar] [CrossRef]
- Amaral, L.R.; Molin, J.P.; Portz, G.; Finazzi, F.B.; Cortinove, L. Comparison of crop canopy reflectance sensors used to identify sugarcane biomass and nitrogen status. Precis. Agric. 2015, 16, 15–28. [Google Scholar] [CrossRef]
- Krienke, B.; Ferguson, R.B.; Schlemmer, M.; Holland, K.; Marx, D.; Eskridge, K. Using an unmanned aerial vehicle to evaluate nitrogen variability and height effect with an active crop canopy sensor. Precis. Agric. 2017, 18, 900–915. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Loew, A.; Zhang, S.; Wang, J.; Niesel, J. Spatial downscaling of satellite soil moisture data using a vegetation temperature condition index. IEEE Trans. Geosci. Remote Sens. 2015, 54, 558–566. [Google Scholar] [CrossRef]
- Caldwell, T.G.; Bongiovanni, T.; Cosh, M.H.; Halley, C.; Young, M.H. Field and laboratory evaluation of the CS655 soil water content sensor. Vadose Zone J. 2018, 17, 1–16. [Google Scholar] [CrossRef] [Green Version]
- Bittelli, M. Measuring soil water content: A review. HortTechnology 2011, 21, 293–300. [Google Scholar] [CrossRef]
- Zhao, Y.; Tong, R.j.; Chen, M.Q.; Xia, F. Relative humidity sensor based on hollow core fiber filled with GQDs-PVA. Sens. Actuators B Chem. 2019, 284, 96–102. [Google Scholar] [CrossRef]
- Che, Y.; Ma, S.; Xing, F.; Li, S.; Dai, Y. An improvement of the retrieval of temperature and relative humidity profiles from a combination of active and passive remote sensing. Meteorol. Atmos. Phys. 2019, 131, 681–695. [Google Scholar] [CrossRef]
- Yao, X.; Yao, X.; Jia, W.; Tian, Y.; Ni, J.; Cao, W.; Zhu, Y. Comparison and intercalibration of vegetation indices from different sensors for monitoring above-ground plant nitrogen uptake in winter wheat. Sensors 2013, 13, 3109–3130. [Google Scholar] [CrossRef]
- Yang, B.; Wang, M.; Sha, Z.; Wang, B.; Chen, J.; Yao, X.; Cheng, T.; Cao, W.; Zhu, Y. Evaluation of aboveground nitrogen content of winter wheat using digital imagery of unmanned aerial vehicles. Sensors 2019, 19, 4416. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- SU, S.L.; Singh, D.; Baghini, M.S. A critical review of soil moisture measurement. Measurement 2014, 54, 92–105. [Google Scholar] [CrossRef]
- Fritz, S.; See, L.; Bayas, J.C.L.; Waldner, F.; Jacques, D.; Becker-Reshef, I.; Whitcraft, A.; Baruth, B.; Bonifacio, R.; Crutchfield, J.; et al. A comparison of global agricultural monitoring systems and current gaps. Agric. Syst. 2019, 168, 258–272. [Google Scholar] [CrossRef]
- Chauhan, S.; Darvishzadeh, R.; Boschetti, M.; Pepe, M.; Nelson, A. Remote sensing-based crop lodging assessment: Current status and perspectives. ISPRS J. Photogramm. Remote Sens. 2019, 151, 124–140. [Google Scholar] [CrossRef] [Green Version]
- Li, X.; McCarty, G.W. Application of topographic analyses for mapping spatial patterns of soil properties. In Geospatial Analyses of Earth Observation (EO) Data; IntechOpen: London, UK, 2019. [Google Scholar] [CrossRef] [Green Version]
- Sreeja, B.; Manoj Kumar, S.; Sherubha, P.; Sasirekha, S. Crop monitoring using wireless sensor networks. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]
- Thakur, D.; Kumar, Y.; Kumar, A.; Singh, P.K. Applicability of wireless sensor networks in precision agriculture: A review. Wirel. Pers. Commun. 2019, 107, 471–512. [Google Scholar] [CrossRef]
- Cui, X.; Guo, X.; Wang, Y.; Wang, X.; Zhu, W.; Shi, J.; Lin, C.; Gao, X. Application of remote sensing to water environmental processes under a changing climate. J. Hydrol. 2019, 574, 892–902. [Google Scholar] [CrossRef]
- Liu, C.A.; Chen, Z.X.; Yun, S.H.A.O.; Chen, J.S.; Hasi, T.; PAN, H.Z. Research advances of SAR remote sensing for agriculture applications: A review. J. Integr. Agric. 2019, 18, 506–525. [Google Scholar] [CrossRef] [Green Version]
- Babaeian, E.; Sadeghi, M.; Jones, S.B.; Montzka, C.; Vereecken, H.; Tuller, M. Ground, proximal, and satellite remote sensing of soil moisture. Rev. Geophys. 2019, 57, 530–616. [Google Scholar] [CrossRef] [Green Version]
- Tenzin, S.; Siyang, S.; Pobkrut, T.; Kerdcharoen, T. Low cost weather station for climate-smart agriculture. In Proceedings of the 2017 9th international conference on knowledge and smart technology (KST), Chonburi, Thailand, 1–4 February 2017; pp. 172–177. [Google Scholar]
- Walter, E.; Pronzato, L. Identification of Parametric Models from Experimental Data; Springer: Berlin/Heidelberg, Germany, 1997. [Google Scholar]
- Keesman, K.J. System Identification: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011. [Google Scholar]
- Wieland, F.G.; Hauber, A.L.; Rosenblatt, M.; Tönsing, C.; Timmer, J. On structural and practical identifiability. Curr. Opin. Syst. Biol. 2021, 25, 60–69. [Google Scholar] [CrossRef]
- Bellu, G.; Saccomani, M.P.; Audoly, S.; D’Angiò, L. DAISY: A new software tool to test global identifiability of biological and physiological systems. Comput. Methods Programs Biomed. 2007, 88, 52–61. [Google Scholar] [CrossRef] [Green Version]
- Chis, O.; Banga, J.R.; Balsa-Canto, E. GenSSI: A software toolbox for structural identifiability analysis of biological models. Bioinformatics 2011, 27, 2610–2611. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Ovchinnikov, A.; Pogudin, G.; Yap, C. SIAN: Software for structural identifiability analysis of ODE models. Bioinformatics 2019, 35, 2873–2874. [Google Scholar] [CrossRef]
- Villaverde, A.F. Observability and structural identifiability of nonlinear biological systems. Complexity 2019, 2019. [Google Scholar] [CrossRef] [Green Version]
- Monod, H.; Naud, C.; Makowski, D. Uncertainty and sensitivity analysis for crop models. In Working with Dynamic Crop Models: Evaluation, Analysis, Parameterization, and Applications; Elsevier: Amsterdam, The Netherlands, 2006; Volume 4, pp. 55–100. [Google Scholar]
- Lamboni, M.; Makowski, D.; Lehuger, S.; Gabrielle, B.; Monod, H. Multivariate global sensitivity analysis for dynamic crop models. Field Crop. Res. 2009, 113, 312–320. [Google Scholar] [CrossRef]
- Sarrazin, F.; Pianosi, F.; Wagener, T. Global Sensitivity Analysis of environmental models: Convergence and validation. Environ. Model. Softw. 2016, 79, 135–152. [Google Scholar] [CrossRef] [Green Version]
- Gunarathna, M.; Sakai, K.; Nakandakari, T.; Momii, K.; Kumari, M. Sensitivity Analysis of Plant-and Cultivar-Specific Parameters of APSIM-Sugar Model: Variation between Climates and Management Conditions. Agronomy 2019, 9, 242. [Google Scholar] [CrossRef] [Green Version]
- Lauvernet, C.; Hascoet, L.; Le Dimet, F.X.; Baret, F. Using Automatic Differentiation to study the sensitivity of a crop model. In Recent Advances in Algorithmic Differentiation; Springer: Berlin/Heidelberg, Germany, 2012; pp. 59–69. [Google Scholar]
- Brisson, N.; Gary, C.; Justes, E.; Roche, R.; Mary, B.; Ripoche, D.; Zimmer, D.; Sierra, J.; Bertuzzi, P.; Burger, P.; et al. An overview of the crop model STICS. Eur. J. Agron. 2003, 18, 309–332. [Google Scholar] [CrossRef]
- Vanuytrecht, E.; Raes, D.; Steduto, P.; Hsiao, T.C.; Fereres, E.; Heng, L.K.; Vila, M.G.; Moreno, P.M. AquaCrop: FAO’s crop water productivity and yield response model. Environ. Model. Softw. 2014, 62, 351–360. [Google Scholar] [CrossRef]
- Tittonell, P.; Corbeels, M.; Van Wijk, M.T.; Giller, K.E. FIELD—A summary simulation model of the soil–crop system to analyse long-term resource interactions and use efficiencies at farm scale. Eur. J. Agron. 2010, 32, 10–21. [Google Scholar] [CrossRef]
- Tremblay, M.; Wallach, D. Comparison of parameter estimation methods for crop models. Agronomie 2004, 24, 351–365. [Google Scholar] [CrossRef] [Green Version]
- Wallach, D.; Buis, S.; Lecharpentier, P.; Bourges, J.; Clastre, P.; Launay, M.; Bergez, J.E.; Guerif, M.; Soudais, J.; Justes, E. A package of parameter estimation methods and implementation for the STICS crop-soil model. Environ. Model. Softw. 2011, 26, 386–394. [Google Scholar] [CrossRef]
- Dumont, B.; Leemans, V.; Mansouri, M.; Bodson, B.; Destain, J.P.; Destain, M.F. Parameter identification of the STICS crop model, using an accelerated formal MCMC approach. Environ. Model. Softw. 2014, 52, 121–135. [Google Scholar] [CrossRef] [Green Version]
- Wallach, D.; Nissanka, S.P.; Karunaratne, A.S.; Weerakoon, W.; Thorburn, P.J.; Boote, K.J.; Jones, J.W. Accounting for both parameter and model structure uncertainty in crop model predictions of phenology: A case study on rice. Eur. J. Agron. 2017, 88, 53–62. [Google Scholar] [CrossRef]
- Vrugt, J.A.; Ter Braak, C.J. DREAM (D): An adaptive Markov Chain Monte Carlo simulation algorithm to solve discrete, noncontinuous, and combinatorial posterior parameter estimation problems. Hydrol. Earth Syst. Sci. 2011, 15, 3701–3713. [Google Scholar] [CrossRef] [Green Version]
- Martí, R.; Resende, M.G.; Ribeiro, C.C. Multi-start methods for combinatorial optimization. Eur. J. Oper. Res. 2013, 226, 1–8. [Google Scholar] [CrossRef]
- Floudas, C.A.; Gounaris, C.E. A review of recent advances in global optimization. J. Glob. Optim. 2009, 45, 3–38. [Google Scholar] [CrossRef]
- Wallach, D.; Makowski, D.; Jones, J.W.; Brun, F. Working with Dynamic Crop Models: Methods, Tools and Examples for Agriculture and Environment; Academic Press: Cambridge, MA, USA, 2018. [Google Scholar]
- Yan, L.; Jin, J.; Wu, P. Impact of parameter uncertainty and water stress parameterization on wheat growth simulations using CERES-Wheat with GLUE. Agric. Syst. 2020, 181, 102823. [Google Scholar] [CrossRef]
- Li, Z.; He, J.; Xu, X.; Jin, X.; Huang, W.; Clark, B.; Yang, G.; Li, Z. Estimating genetic parameters of DSSAT-CERES model with the GLUE method for winter wheat (Triticum aestivum L.) production. Comput. Electron. Agric. 2018, 154, 213–221. [Google Scholar] [CrossRef] [Green Version]
- Jones, J.W.; He, J.; Boote, K.J.; Wilkens, P.; Porter, C.; Hu, Z. Estimating DSSAT cropping system cultivar-specific parameters using Bayesian techniques. Methods Introd. Syst. Model. Into Agric. Res. 2011, 2, 365–393. [Google Scholar]
- Seidel, S.J.; Palosuo, T.; Thorburn, P.; Wallach, D. Towards improved calibration of crop models—Where are we now and where should we go? Eur. J. Agron. 2018, 94, 25–35. [Google Scholar] [CrossRef]
- Zhang, T.; Su, J.; Liu, C.; Chen, W.H. Bayesian calibration of AquaCrop model for winter wheat by assimilating UAV multi-spectral images. Comput. Electron. Agric. 2019, 167, 105052. [Google Scholar] [CrossRef]
- Tennøe, S.; Halnes, G.; Einevoll, G.T. Uncertainpy: A python toolbox for uncertainty quantification and sensitivity analysis in computational neuroscience. Front. Neuroinform. 2018, 12, 49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herman, J.; Usher, W. SALib: An open-source Python library for sensitivity analysis. J. Open Source Softw. 2017, 2, 97. [Google Scholar] [CrossRef]
- Woli, P.; Jones, J.W.; Ingram, K.T. Assessing the Agricultural Reference Index for Drought (ARID) Using Uncertainty and Sensitivity Analyses. Agron. J. 2013, 105, 150–160. [Google Scholar] [CrossRef]
- Huang, D.; Wang, J.; Khayatnezhad, M. Estimation of actual evapotranspiration using soil moisture balance and remote sensing. Iran. J. Sci. Technol. Trans. Civ. Eng. 2021, 45, 2779–2786. [Google Scholar] [CrossRef]
- Lopez-Jimenez, J.; Quijano, N.; Vande Wouwer, A. An Agent-Based Crop Model Framework for Heterogeneous Soils. Agronomy 2021, 11, 85. [Google Scholar] [CrossRef]
- Bogaerts, P.; Vande Wouwer, A. Software sensors for bioprocesses. ISA Trans. 2003, 42, 547–558. [Google Scholar] [CrossRef]
- Goffaux, G.; Vande Wouwer, A. Bioprocess state estimation: Some classical and less classical approaches. In Control and Observer Design for Nonlinear Finite and Infinite Dimensional Systems; Springer: Berlin/Heidelberg, Germany, 2005; pp. 111–128. [Google Scholar]
- Villaverde, A.F.; Tsiantis, N.; Banga, J.R. Full observability and estimation of unknown inputs, states and parameters of nonlinear biological models. J. R. Soc. Interface 2019, 16, 20190043. [Google Scholar] [CrossRef] [Green Version]
- Zeitz, M. Observability canonical (phase-variable) form for non-linear time-variable systems. Int. J. Syst. Sci. 1984, 15, 949–958. [Google Scholar] [CrossRef]
- Gauthier, J.P.; Kupka, I.A. Observability and observers for nonlinear systems. SIAM J. Control. Optim. 1994, 32, 975–994. [Google Scholar] [CrossRef]
- Moreno, J.A.; Rocha-Cózatl, E.; Wouwer, A.V. A dynamical interpretation of strong observability and detectability concepts for nonlinear systems with unknown inputs: Application to biochemical processes. Bioprocess Biosyst. Eng. 2014, 37, 37–49. [Google Scholar] [CrossRef] [PubMed]
- Díaz-González, V.; Rojas-Palma, A.; Carrasco-Benavides, M. How Does Irrigation Affect Crop Growth? A Mathematical Modeling Approach. Mathematics 2022, 10, 151. [Google Scholar] [CrossRef]
- Bannister, R. A review of operational methods of variational and ensemble-variational data assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 607–633. [Google Scholar] [CrossRef] [Green Version]
- Dorigo, W.A.; Zurita-Milla, R.; de Wit, A.J.; Brazile, J.; Singh, R.; Schaepman, M.E. A review on reflective remote sensing and data assimilation techniques for enhanced agroecosystem modeling. Int. J. Appl. Earth Obs. Geoinf. 2007, 9, 165–193. [Google Scholar] [CrossRef]
- Sedano, F.; Kempeneers, P.; Hurtt, G. A Kalman filter-based method to generate continuous time series of medium-resolution NDVI images. Remote Sens. 2014, 6, 12381–12408. [Google Scholar] [CrossRef] [Green Version]
- Lü, H.; Yu, Z.; Zhu, Y.; Drake, S.; Hao, Z.; Sudicky, E.A. Dual state-parameter estimation of root zone soil moisture by optimal parameter estimation and extended Kalman filter data assimilation. Adv. Water Resour. 2011, 34, 395–406. [Google Scholar] [CrossRef]
- Agyeman, B.T.; Bo, S.; Sahoo, S.R.; Yin, X.; Liu, J.; Shah, S.L. Soil moisture map construction by sequential data assimilation using an extended Kalman filter. J. Hydrol. 2021, 598, 126425. [Google Scholar] [CrossRef]
- Mansouri, M.; Dumont, B.; Destain, M.F. Modeling and prediction of nonlinear environmental system using Bayesian methods. Comput. Electron. Agric. 2013, 92, 16–31. [Google Scholar] [CrossRef] [Green Version]
- Rui, L.; Li, C.j.; Dong, Y.y.; Feng, L.; Wang, J.h.; Yang, X.d.; Pan, Y.c. Assimilation of remote sensing and crop model for LAI estimation based on ensemble Kaiman Filter. Agric. Sci. China 2011, 10, 1595–1602. [Google Scholar]
- Zhao, Y.; Chen, S.; Shen, S. Assimilating remote sensing information with crop model using Ensemble Kalman Filter for improving LAI monitoring and yield estimation. Ecol. Model. 2013, 270, 30–42. [Google Scholar] [CrossRef]
- Huang, J.; Sedano, F.; Huang, Y.; Ma, H.; Li, X.; Liang, S.; Tian, L.; Zhang, X.; Fan, J.; Wu, W. Assimilating a synthetic Kalman filter leaf area index series into the WOFOST model to improve regional winter wheat yield estimation. Agric. For. Meteorol. 2016, 216, 188–202. [Google Scholar] [CrossRef]
- Nagarajan, K.; Judge, J.; Graham, W.D.; Monsivais-Huertero, A. Particle filter-based assimilation algorithms for improved estimation of root-zone soil moisture under dynamic vegetation conditions. Adv. Water Resour. 2011, 34, 433–447. [Google Scholar] [CrossRef]
- Fang, H.; Liang, S.; Hoogenboom, G.; Teasdale, J.; Cavigelli, M. Corn-yield estimation through assimilation of remotely sensed data into the CSM-CERES-Maize model. Int. J. Remote Sens. 2008, 29, 3011–3032. [Google Scholar] [CrossRef]
- Yildirak, K.; Kalaylıoglu, Z.; Mermer, A. Bayesian estimation of crop yield function: Drought based wheat prediction model for tigem farms. Environ. Ecol. Stat. 2015, 22, 693–704. [Google Scholar] [CrossRef]
- Nychka, D.; Anderson, J.L. Data assimilation. In Handbook of Spatial Statistics; CRC Press: Boca Raton, FL, USA, 2010; pp. 477–492. [Google Scholar]
- Chen, Y.; Cournède, P.H. Data assimilation to reduce uncertainty of crop model prediction with convolution particle filtering. Ecol. Model. 2014, 290, 165–177. [Google Scholar] [CrossRef] [Green Version]
- Visioli, A. Practical PID Control; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Goodchild, M.; Kühn, K.; Jenkins, M.; Burek, K.; Button, A. A method for precision closed-loop irrigation using a modified PID control algorithm. Sens. Transducers 2015, 188, 61. [Google Scholar]
- Goodchild, M.S.; Jenkins, M.D.; Whalley, W.R.; Watts, C.W. A novel dielectric tensiometer enabling precision PID-based irrigation control of polytunnel-grown strawberries in coir. Biosyst. Eng. 2018, 165, 70–76. [Google Scholar] [CrossRef]
- Lozoya, C.; Mendoza, C.; Aguilar, A.; Román, A.; Castelló, R. Sensor-based model driven control strategy for precision irrigation. J. Sens. 2016, 2016, 9784071. [Google Scholar] [CrossRef] [Green Version]
- Lozoya, C.; Mendoza, C.; Mejía, L.; Quintana, J.; Mendoza, G.; Bustillos, M.; Arras, O.; Solís, L. Model predictive control for closed-loop irrigation. Ifac Proc. Vol. 2014, 47, 4429–4434. [Google Scholar] [CrossRef] [Green Version]
- Balbis, L. Economic Model Predictive Control for Irrigation Systems. In Proceedings of the 2019 8th International Conference on Modeling Simulation and Applied Optimization (ICMSAO), Manama, Bahrain, 5–17 April 2019; pp. 1–4. [Google Scholar]
- Delgoda, D.; Malano, H.; Saleem, S.K.; Halgamuge, M.N. Irrigation control based on model predictive control (MPC): Formulation of theory and validation using weather forecast data and AQUACROP model. Environ. Model. Softw. 2016, 78, 40–53. [Google Scholar] [CrossRef]
- Shang, C.; Chen, W.H.; Stroock, A.D.; You, F. Robust model predictive control of irrigation systems with active uncertainty learning and data analytics. IEEE Trans. Control. Syst. Technol. 2019, 28, 1493–1504. [Google Scholar] [CrossRef] [Green Version]
- Winkler, D.A.; Carreira-Perpiñán, M.Á.; Cerpa, A.E. Plug-and-play irrigation control at scale. In Proceedings of the 2018 17th ACM/IEEE International Conference on Information Processing in Sensor Networks (IPSN), Porto, Portugal, 11–13 April 2018; pp. 1–12. [Google Scholar]
- Liu, Z.; Xu, Q. An automatic irrigation control system for soilless culture of lettuce. Water 2018, 10, 1692. [Google Scholar] [CrossRef] [Green Version]
- Chrouta, J.; Chakchouk, W.; Zaafouri, A.; Jemli, M. Modeling and control of an irrigation station process using heterogeneous cuckoo search algorithm and fuzzy logic controller. IEEE Trans. Ind. Appl. 2018, 55, 976–990. [Google Scholar] [CrossRef]
- Mendes, W.R.; Araújo, F.M.U.; Dutta, R.; Heeren, D.M. Fuzzy control system for variable rate irrigation using remote sensing. Expert Syst. Appl. 2019, 124, 13–24. [Google Scholar] [CrossRef]
- Marinescu, T.; Arghira, N.; Hossu, D.; Fagarasan, I.; Stamatescu, I.; Stamatescu, G.; Calofir, V.; Iliescu, S. Advanced control strategies for irrigation systems. In Proceedings of the 2017 9th IEEE International Conference on Intelligent Data Acquisition and Advanced Computing Systems: Technology and Applications (IDAACS), Bucharest, Romania, 21–23 September 2017; Volume 2, pp. 843–848. [Google Scholar]
- Lopez-Jimenez, J.; Quijano, N.; Vande Wouwer, A. Towards agent-based modeling of crop irrigation. In Proceedings of the 11th International Conference on Simulation and Modelling in the Food and Bio-Industry (FOODSIM), Ghent, Belgium, 6–10 September 2020; pp. 185–189. [Google Scholar]
- Thieu, N.; Fredlund, D.; Hung, V. General partial differential equation solvers for saturated-unsaturated seepage. In Unsaturated Soils for Asia; CRC Press: Boca Raton, FL, USA, 2020; pp. 201–206. [Google Scholar]
- Rai, P.K.; Tripathi, S. Gaussian process for estimating parameters of partial differential equations and its application to the Richards equation. Stoch. Environ. Res. Risk Assess. 2019, 33, 1629–1649. [Google Scholar] [CrossRef]
- Mewes, B.; Schumann, A.H. IPA (v1): A framework for agent-based modelling of soil water movement. Geosci. Model Dev. 2018, 11, 2175–2187. [Google Scholar] [CrossRef] [Green Version]
- Whitman, J.E.; Maske, H.; Kingravi, H.A.; Chowdhary, G. Evolving Gaussian Processes and Kernel Observers for Learning and Control in Spatiotemporally Varying Domains: With Applications in Agriculture, Weather Monitoring, and Fluid Dynamics. IEEE Control Syst. Mag. 2021, 41, 30–69. [Google Scholar] [CrossRef]
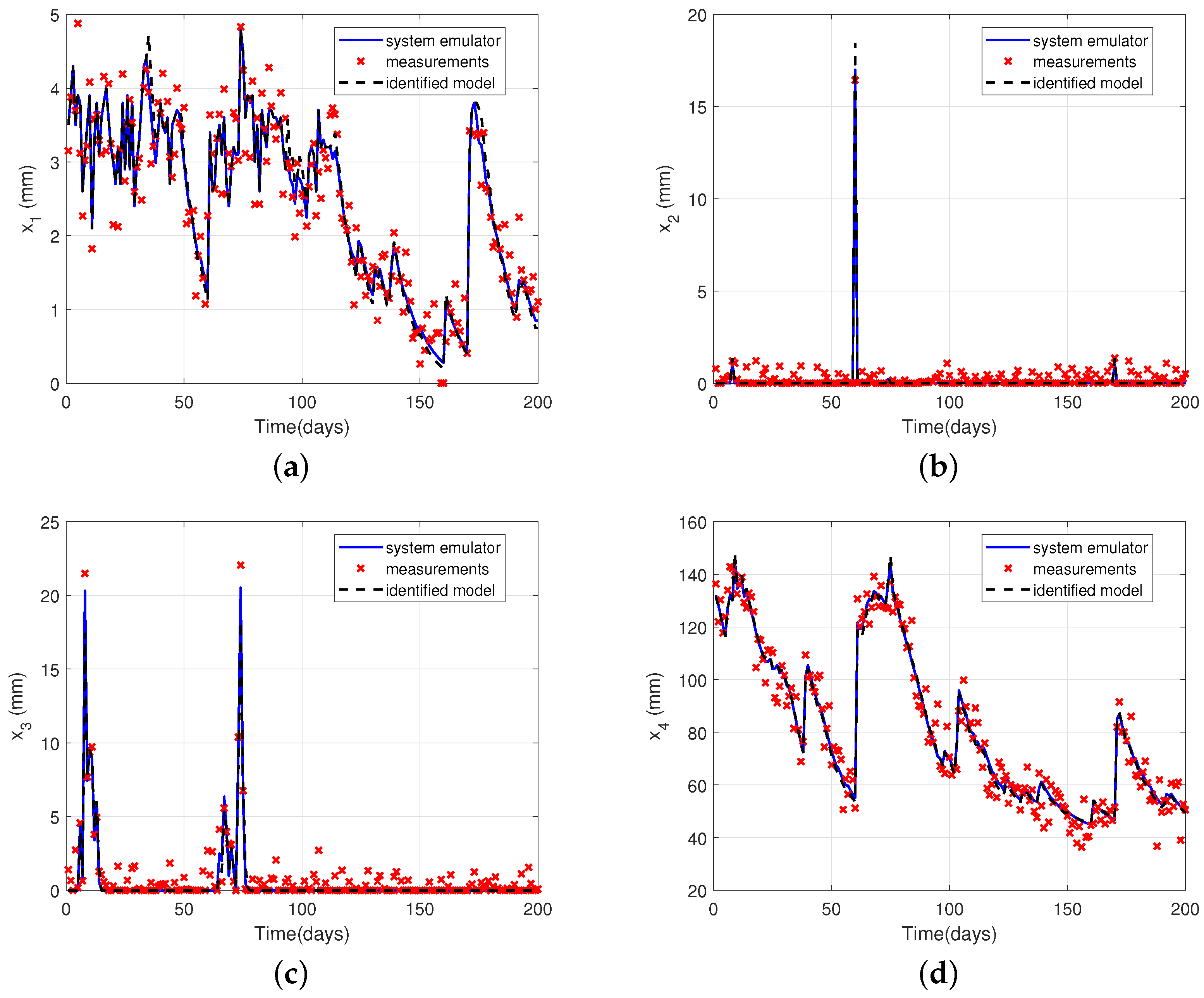
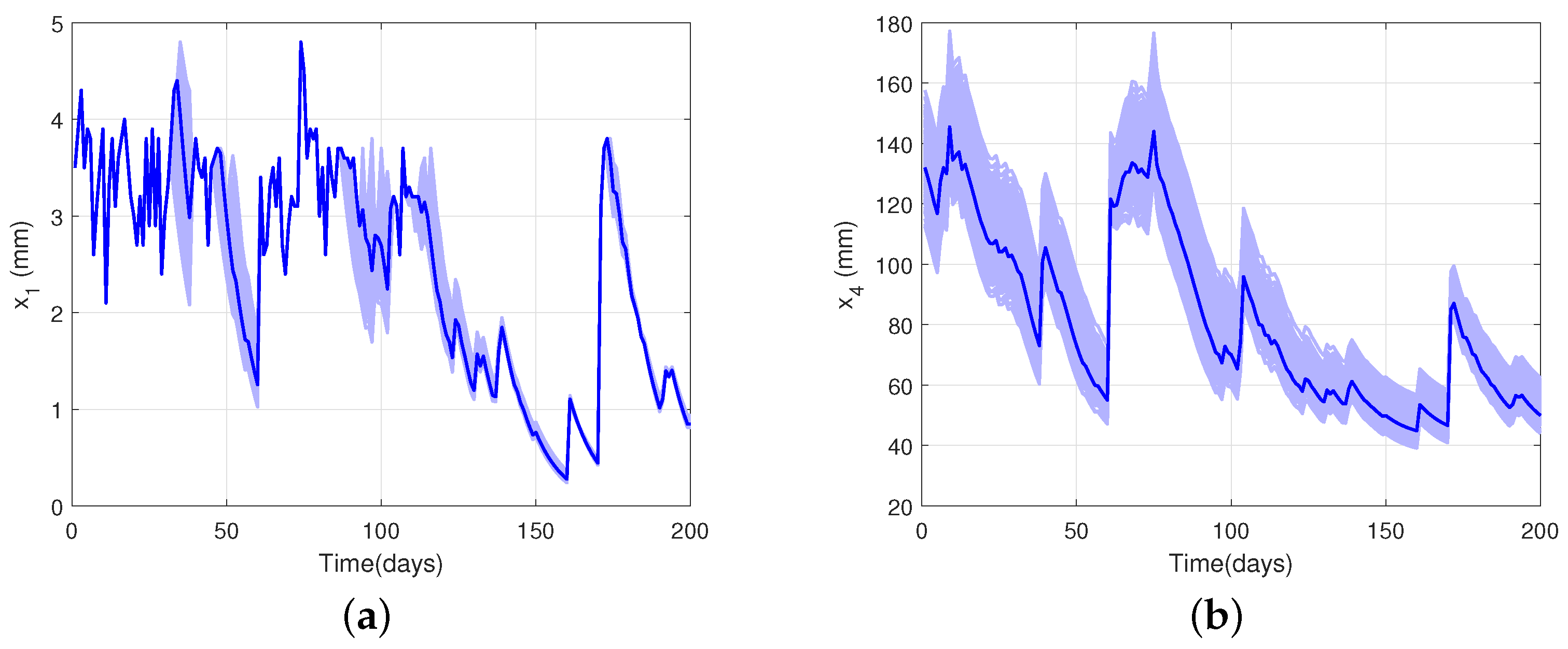

| Shape | Equation | Uses | Reference |
|---|---|---|---|
| Linear | Water drought | [41] | |
| Water-logging | [42] | ||
| Soil salinity | [27] | ||
| CO concentration | [43,44] | ||
| Air temperature | [45] | ||
| Convex | Soil fertility | [31] | |
| Water drought | [27] | ||
| Logistic | Air temperature | [19,27] | |
| Pests and diseases | [46] |
| Variable | Description | Type | Reference |
|---|---|---|---|
| SM | Soil moisture | D, R, P | [54,55,56,57] |
| LAI | Leaf area index | R, P | [58,59,60] |
| ET | Evapotranspiration | D, R | [61,62] |
| PAR | Photosynthetically active radiation | R | [8,63] |
| AGB | Aboveground biomass | D, R | [64,65,66] |
| DVS | Developmental state | D | [11,67] |
| NDVI | Normalized vegetation index | R | [63,64,67] |
| EVI | Enhanced vegetation index | R | [67,68] |
| TSAVI | Transformed soil-adjusted vegetation index | R | [69,70] |
| VI | Vegetation index | R | [63,71] |
| LNA | Leaf nitrogen accumulation | D, P | [12,72] |
| CC | Canopy cover | R | [72,73] |
| CNA | Canopy nitrogen accumulation | R | [12,72] |
| VTCI | Vegetation temperature condition index | R | [11,74] |
| SWC | Soil water content | D, P | [55,75,76] |
| RH | Relative humidity | D, R, P | [77,78] |
| AGN | Aboveground nitrogen accumulation | D, R | [79,80] |
| Parameter | Description | Unit | Nominal Value | Identified Value | Confidence Lb | Interval Ub | Deviation |
|---|---|---|---|---|---|---|---|
| Water uptake coefficient | - | 0.096 | 0.0869 | 0.0792 | 0.0947 | 8.9% | |
| Drainage coefficient | - | 0.55 | 0.6545 | 0.5825 | 0.7265 | 11.0% | |
| Runoff curve number | - | 65 | 64.9794 | 62.8535 | 67.1053 | 3.3% | |
| Available water capacity | - | 0.24 | 0.1990 | 0.1791 | 0.2189 | 10.0% | |
| Root zone depth | mm | 600 | 464.9227 | 422.1499 | 507.6956 | 9.2% | |
| Wilting point | - | 0.075 | 0.0865 | 0.0792 | 0.0938 | 8.4% |
| Name | Description | Unit | Value |
|---|---|---|---|
| Irrigation | |||
| Water in soil for plant water consumption | |||
| Water inside the plant available for its growth | |||
| Biomass (amount of dry matter) | |||
| Inner rate of decrease in the pond water | 0.00001 | ||
| Intrinsic rate of water that goes to the plant | 2.0 | ||
| Limiting factor constant of | 20.0 | ||
| Intrinsic rate of increase in the water inside the plant | 1.0 | ||
| Rate of decrease in water inside the plant | 0.1 | ||
| Intrinsic rate of water decrease by photosynthesis | 0.01 | ||
| Limiting factor constant of | 0.1 | ||
| Intrinsic growth rate per unit of water inside the plant | 0.01 | ||
| Plant degradation rate | 0.0001 |
| Method | Main Equations | Basic Description | Estimated Variables | Model | References |
|---|---|---|---|---|---|
| KF | The Kalman filter is an optimal estimator for linear systems with Gaussian observations. It provides the expectation of the state and the covariance of the estimation error. It proceeds in two steps: prediction and correction. It exists in several forms: discrete time, continuous time and continuous (prediction)–discrete (correction) time. | NDVI | [133] | ||
| EKF | The extended Kalman filter is based on a model that is linearized along the state estimate trajectory. It requires the on-line computation of the Jacobian matrices. It is no longer an optimal estimator and may diverge. The EKF provides a practical and popular solution for nonlinear systems with Gaussian observations. | SM | [134] | ||
| SW | [135] | ||||
| UKF | The unscented Kalman filter propagates a few sampling points, called sigma points, through the nonlinear model and computes the weighted sample’s mean and covariance. The UKF does not require model linearization and provides more accurate and precise estimates in the case of nonlinear systems under Gaussian noise. | LAI, SM | STICS | [136] | |
| EnKF | The ensemble Kalman filter is a Monte Carlo filter, which is suitable for systems with a large number of variables. It is well suited for systems described by partial differential equations and their discretization by finite difference or element techniques. It assumes Gaussian observations. | LAI | CERES-Wheat | [137] | |
| LAI, SM | WOFOST | [138,139] | |||
| LAI, SM, VTCI | DSSAT | [11] | |||
| Method | Main Equations | Basic Description | Estimated Variables | Model | References |
|---|---|---|---|---|---|
| PF | In the particle filter, a large number of particles are propagated through the nonlinear model, and the posterior distribution is reconstructed. A PF is suitable for nonlinear systems with non-Gaussian observations. It is computationally expensive, but it is amenable to parallel computation. | AGB, LAI | STICS | [11] | |
| LAI | DSSAT LSP-DSSAT | [11] | |||
| RZSM | LSP-DSSAT | [140] | |||
| VF | The variational filter aims at approximating the posterior distribution with a parametric density of an assumed form. The primary mechanism of the VF is to minimize the Kullback–Leiber divergence between the assumed posterior distribution and the hypothetically true posterior. This approximation approach lends itself to an optimization problem. | LAI, HUR1, HUR2 | mini-STICS | [136] | |
| 3DVAR | Variational assimilation is the iterative minimization of a cost function . This solution represents the a posteriori maximum likelihood estimate of the true state given the background (previous forecast) and observations. The use of adjoint operations (based on the chain rule for partial differentiation) allows the calculation of the gradient of the cost function. | LAI | CERES-Maize | [141] | |
| 4DVAR | 4DVAR adds an extra time point in the cost function. 4DVAR is actually a direct generalization of 3DVAR for handling observations that are distributed in time. | LAI | WOFOST | [11] | |
| LAI, NDVI | DSSAT | [11] | |||
| HBM | Hierarchical Bayesian modeling is based on the theoretical foundation of conditional probability distribution. The problem is decomposed into layers. Each layer is connected by the conditional probability, and the solution of a complex joint probability problem is converted into the solution of a series of simpler problems. | NDVI | [142] | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lopez-Jimenez, J.; Vande Wouwer, A.; Quijano, N. Dynamic Modeling of Crop–Soil Systems to Design Monitoring and Automatic Irrigation Processes: A Review with Worked Examples. Water 2022, 14, 889. https://doi.org/10.3390/w14060889
Lopez-Jimenez J, Vande Wouwer A, Quijano N. Dynamic Modeling of Crop–Soil Systems to Design Monitoring and Automatic Irrigation Processes: A Review with Worked Examples. Water. 2022; 14(6):889. https://doi.org/10.3390/w14060889
Chicago/Turabian StyleLopez-Jimenez, Jorge, Alain Vande Wouwer, and Nicanor Quijano. 2022. "Dynamic Modeling of Crop–Soil Systems to Design Monitoring and Automatic Irrigation Processes: A Review with Worked Examples" Water 14, no. 6: 889. https://doi.org/10.3390/w14060889








