Precipitation Variability and Drought Assessment Using the SPI: Application to Long-Term Series in the Strait of Gibraltar Area
Abstract
:1. Introduction
2. Case Study: Climate and Context
3. Materials and Methods
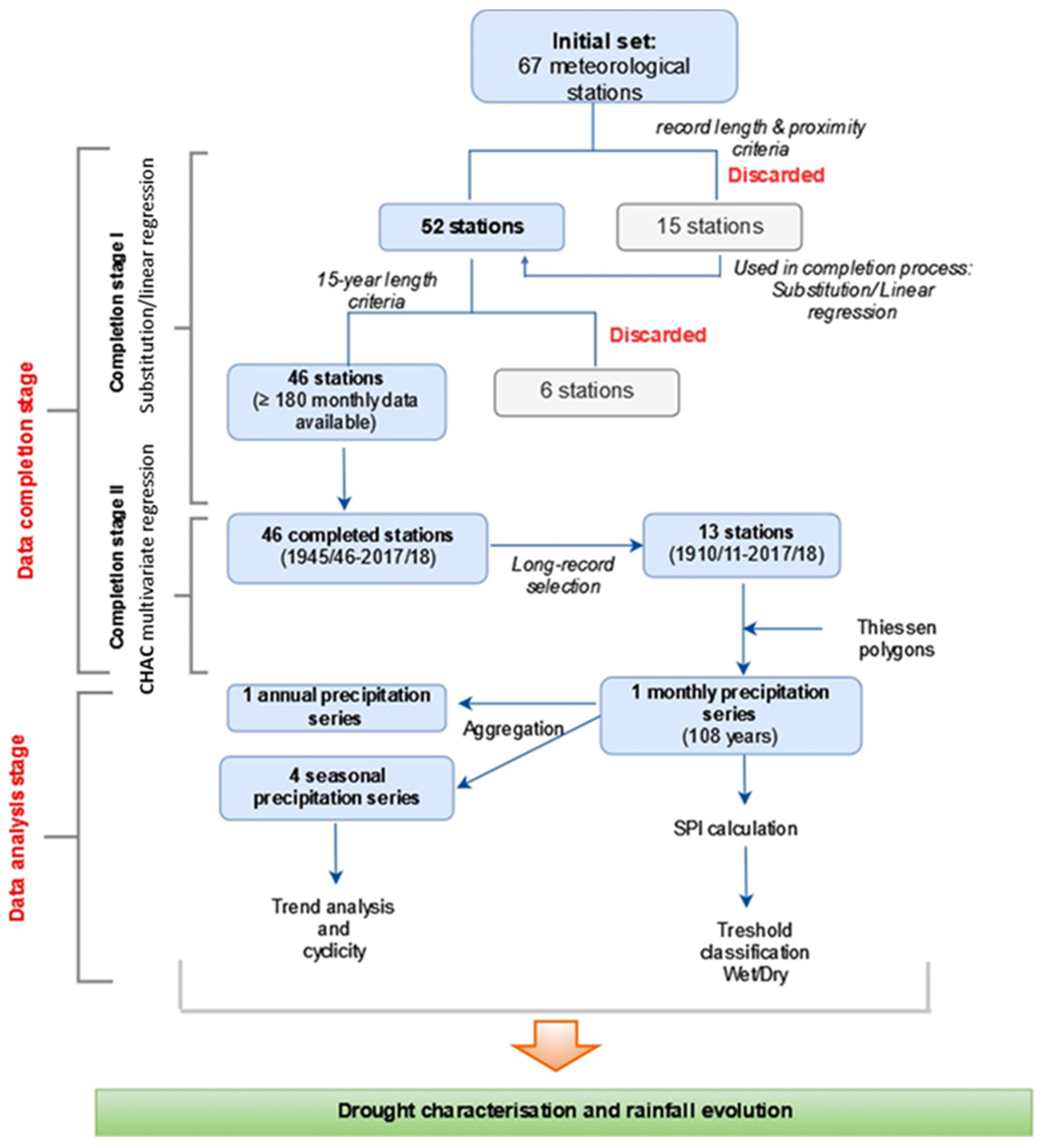
3.1. Precipitation Data
3.2. Methodology
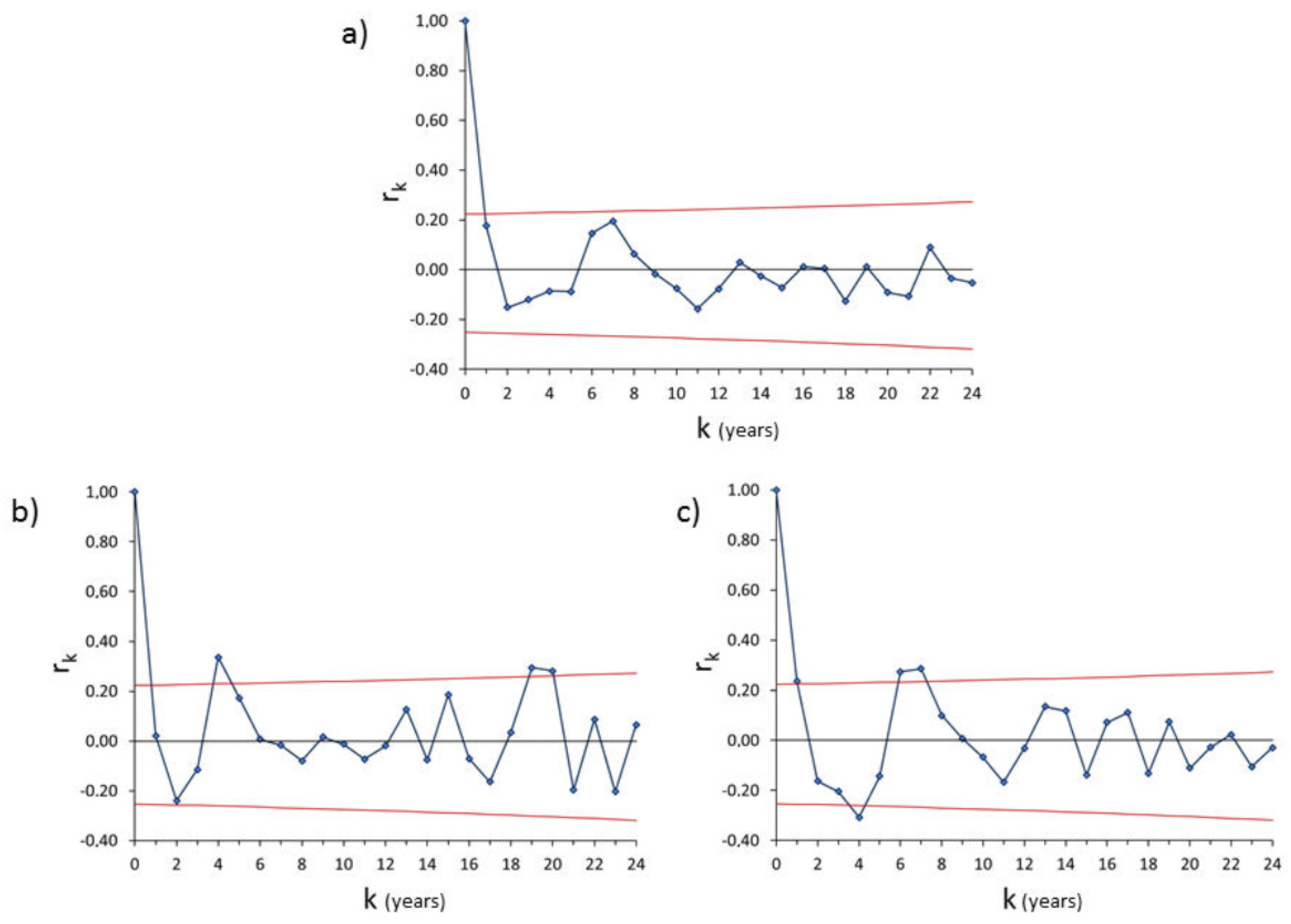
3.2.1. Processing of Hydrological Series and Statistical Analysis
3.2.2. Integration within McKee’s Standardized Precipitation Index (SPI)
4. Results: Precipitation Series Analysis and SPI Evolution
5. Discussion
6. Conclusions
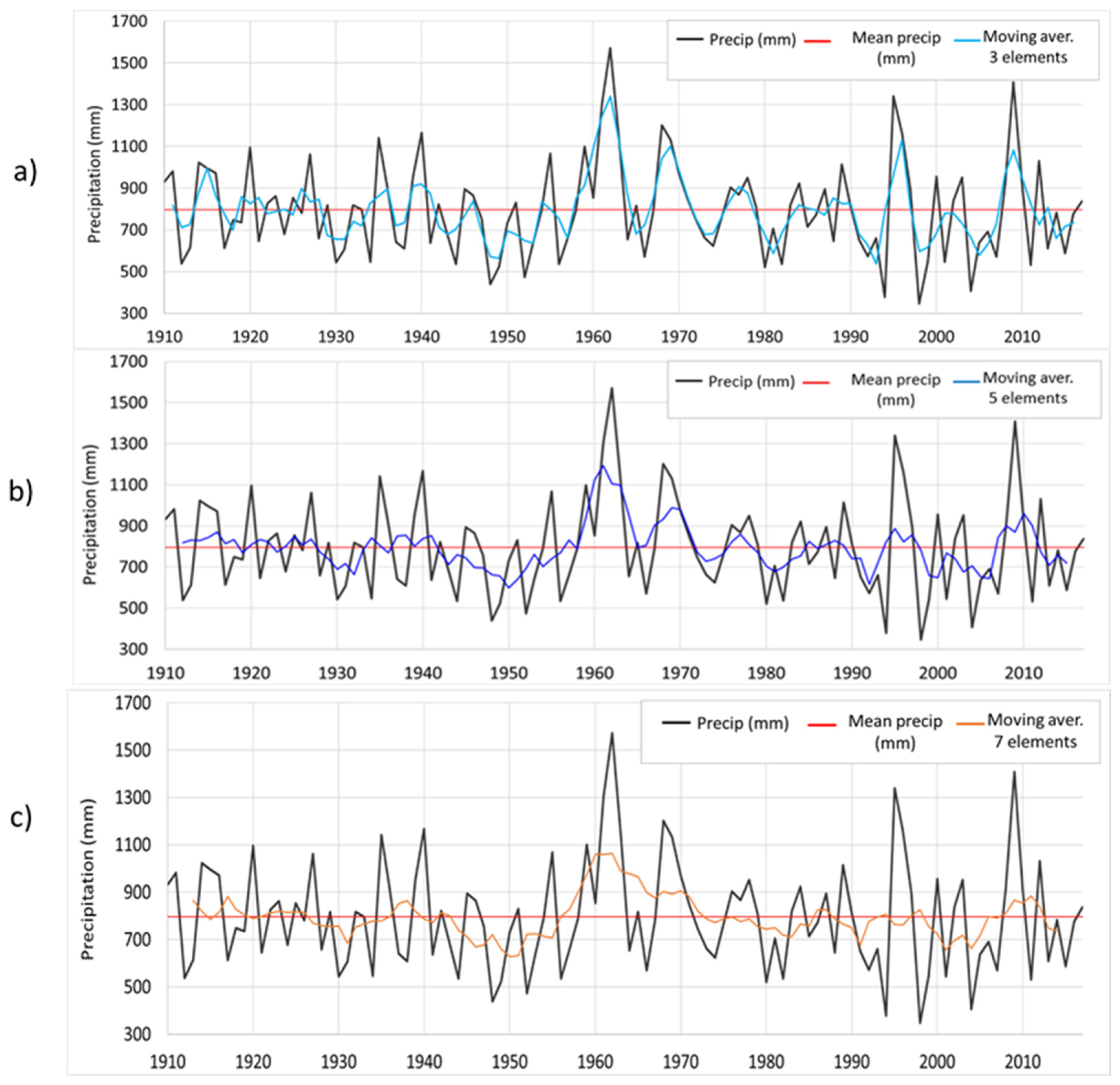
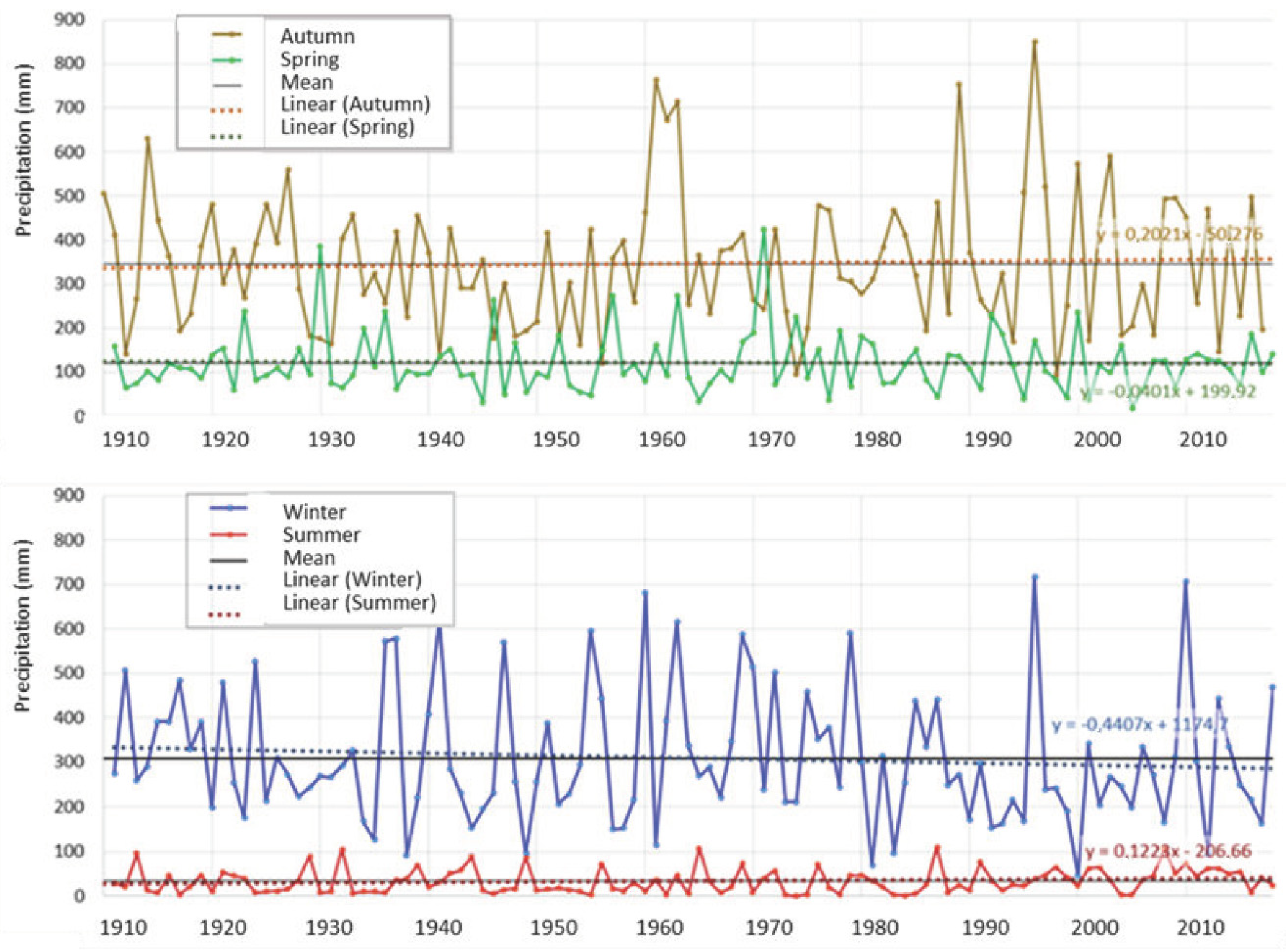
- The distribution of monthly mean precipitation shows a marked seasonality, in line with the typical patterns of Mediterranean climates. Rainfall concentrates between the end of the autumn and winter months (October to March), with average precipitation exceeding 85 mm/month and a maximum of 140 mm/month in December. Conversely, in summer months, mean monthly rainfall is less than 20 mm/month. Seasonal analysis throughout the study period evidenced a slight shift in winter rainfall towards autumn and summer months, which could lead to a reduction in effective rainfall.
- The interannual variation of precipitation for the whole basin ranges between the 365 mm recorded in the dry year 1998/99 and the 1606 mm in the wet year 1962/63, with a coefficient of variation of 28.2%. The analysis of average precipitation indicated that the period 1940–1950 was very dry, with an average rainfall close to 720 mm/year (11% below the basin’s average). On the contrary, the decade 1960–70 was very humid, with rainfall close to 1000 mm/year (23% higher than the average). In addition, a clear change in the precipitation pattern that affects the cyclicity, frequency and intensity of dry and wet episodes was detected. In this regard, precipitation displays greater irregularity since the 1960s, with droughts and wet periods of greater intensity and frequency.
- Although the 108-year series does not display a clear downward trend and precipitation remains relatively stable, a slight decrease in the order of 15 mm/100 years was detected. This figure has to be interpreted cautiously given its susceptibility to the extreme values of the period considered. In any case, no significant trend towards a decrease in precipitation was detected, contrary to the predictive models of climate change, particularized to the study area.
- The SPI enabled identifying 26 events of drought during the 108-year period analyzed, of which 12 were severe (SPI < −1.5) and 6 extreme (SPI < −2.0), with return periods of 9 and 18 years, respectively. The distribution of droughts was uneven over the 108-year period. Of the six extreme droughts detected, four took place in the second half of the study period. Likewise, in the case of wet episodes, of the four extremely wet periods, and three took place in the second half of the series.
- The study area is very likely to undergo longer and more severe drought episodes in the future; thus, having detailed information on precipitation series and drought duration, magnitude, frequency and return periods is crucial to devise early warning systems and for better water management and impact mitigation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- World Meteorological Organization (WMO). Report on Drought and Countries Affected by Drought During 1974–1985; WMO: Geneva, Switzerland, 1986; Volume 118, p. 22. [Google Scholar]
- IPCC. The Intergovernmental Panel on Climate Change. Glossary. Available online: https://www.ipcc.ch/sr15/chapter/glossary/ (accessed on 10 August 2021).
- Wilhite, D.A.; Svoboda, M.D.; Hayes, M.J. Understanding the complex impacts of drought: A key to enhancing drought mitigation and preparedness. Water Resour. Manag. 2007, 21, 763–774. [Google Scholar] [CrossRef] [Green Version]
- Wilhite, D.A.; Glantz, M.H. Understanding the drought phenomenon: The role of definitions. Water Int. 1985, 10, 111–120. [Google Scholar] [CrossRef] [Green Version]
- Heim, R. A Review of Twentieth- Century Drought Indices Used in the United States. Am. Meteorol. Soc. 2002, 83, 1149–1166. [Google Scholar] [CrossRef] [Green Version]
- Dai, A.; Trenberth, K.E.; Karl, T.R. Global variations in droughts and wet spells: 1900–1995. Geophys. Res. Lett. 1998, 25, 3367–3370. [Google Scholar] [CrossRef] [Green Version]
- Strzepek, K.; Yohe, G.; Neumann, J.; Bohelert, B. Characterizing changes in drought risk for the United States from climate change. Environ. Res. Lett. 2010, 5, 044012. Available online: https://iopscience.iop.org/article/10.1088/1748-9326/5/4/044012/meta (accessed on 10 February 2022). [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The relation of drought frequency and duration to time scales. In Proceedings of the Eighth Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; Department of Atmospheric Science Colorado State University: Fort Collins, CO, USA, 1993; Volume 17, pp. 179–184. [Google Scholar]
- Palmer, W.C. Meteorological Drought; US Department of Commerce, Weather Bureau: Washington, DC, USA, 1965; pp. 1–65.
- Tsakiris, G.; Vangelis, H. Towards a Drought Watch System based on spatial SPI. Water Resour. Manag. 2004, 18, 1–12. [Google Scholar] [CrossRef]
- Weghorst, K. The Reclamation Drought Index. Guidelines and Practical Applications; Bureau of Reclamation: Denver, CO, USA, 1996; p. 6.
- Byun, H.R.; Wilhite, D.A. Objective quantification of drought severity and duration. J. Clim. 1999, 12, 2747–2756. [Google Scholar] [CrossRef]
- Tsakiris, G.; Pangalou, D.; Vangelis, H. Regional drought assessment based on the Reconnaissance Drought Index (RDI). Water Resour. Manag. 2007, 21, 821–833. [Google Scholar] [CrossRef]
- Keyantash, J.; Dracup, J.A. The Quantification of Drought: An Evaluation of Drought Indices. Bull. Am. Meteorol. Soc. 2002, 83, 1167–1180. [Google Scholar] [CrossRef]
- Hayes, M. Drought Indices. In Van Nostrand′s Scientific Encyclopedia; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Morid, S.; Smakhtin, V.; Bagherzadeh, K. Drought forecasting using artificial neural networks and time series of drought indices. Int. J. Climatol. 2007, 27, 2103–2111. [Google Scholar] [CrossRef]
- Borji, M.; Malekian, A.; Salajegheh, A.; Ghadimi, M. Multi-time-scale analysis of hydrological drought forecasting using support vector regression (SVR) and artificial neural networks (ANN). Arab. J. Geosci. 2016, 9, 725. [Google Scholar] [CrossRef]
- Tian, Y.; Xu, Y.P.; Wang, G. Agricultural drought prediction using climate indices based on Support Vector Regression in Xiangjiang River basin. Sci. Total Environ. 2018, 622–623, 710–720. [Google Scholar] [CrossRef] [PubMed]
- Belayneh, A.; Adamowski, J.; Khalil, B.; Ozga-Zielinski, B. Long-term SPI drought forecasting in the Awash River Basin in Ethiopia using wavelet neural networks and wavelet support vector regression models. J. Hydrol. 2014, 508, 418–429. [Google Scholar] [CrossRef]
- Khan, M.M.H.; Muhammad, N.S.; El-Shafie, A. Wavelet based hybrid ANN-ARIMA models for meteorological drought forecasting. J. Hydrol. 2020, 590, 125380. [Google Scholar] [CrossRef]
- Hoerling, M.; Eischeid, J.; Perlwitz, J.; Quan, X.; Zhang, T.; Pegion, P. On the increased frequency of Mediterranean drought. J. Clim. 2012, 25, 2146–2161. [Google Scholar] [CrossRef] [Green Version]
- Dubrovský, M.; Hayes, M.; Duce, P.; Trnka, M.; Svoboda, M.; Zara, P. Multi-GCM projections of future drought and climate variability indicators for the Mediterranean region. Reg. Environ. Chang. 2014, 14, 1907–1919. [Google Scholar] [CrossRef]
- Sousa, P.M.; Trigo, R.M.; Aizpurua, P.; Nieto, R.; Gimeno, L.; García-Herrera, R. Trends and extremes of drought indices throughout the 20th century in the Mediterranean. Nat. Hazards Earth Syst. Sci. 2011, 11, 33–51. [Google Scholar] [CrossRef] [Green Version]
- Di Lena, B.; Vergni, L.; Antenucci, F.; Todisco, F.; Mannocchi, F. Analysis of drought in the region of Abruzzo (Central Italy) by the Standardized Precipitation Index. Theor. Appl. Climatol. 2014, 115, 41–52. [Google Scholar] [CrossRef]
- Hertig, E.; Tramblay, Y. Regional downscaling of Mediterranean droughts under past and future climatic conditions. Glob. Planet. Chang. 2017, 151, 36–48. [Google Scholar] [CrossRef]
- Caloiero, T.; Veltri, S.; Caloiero, P.; Frustaci, F. Drought analysis in Europe and in the Mediterranean basin using the standardized precipitation index. Water 2018, 10, 1043. [Google Scholar] [CrossRef] [Green Version]
- Vogel, J.; Paton, E.; Aich, V.; Bronstert, A. Increasing compound warm spells and droughts in the Mediterranean Basin. Weather Clim. Extrem. 2021, 32, 100312. [Google Scholar] [CrossRef]
- Parracho, A.C.; Melo-Gonçalves, P.; Rocha, A. Regionalisation of precipitation for the Iberian Peninsula and climate change. Phys. Chem. Earth Parts A/B/C 2016, 94, 146–154. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Differences in spatial patterns of drought on different time scales: An analysis of the Iberian Peninsula. Water Resour. Manag. 2006, 20, 37–60. [Google Scholar] [CrossRef]
- Lorenzo-Lacruz, J.; Vicente-Serrano, J.M.; Gonzalez-Hidalgo, J.C.; López-Moreno, J.I.; Cortesi, N. Hydrological drought response to meteorological drought in the Iberian Peninsula. Clim. Res. 2013, 58, 117–131. [Google Scholar] [CrossRef] [Green Version]
- Merino, A.; López, L.; Hermida, L.; Sánchez, J.L.; García-Ortega, E.; Gascón, E.; Fernández-González, S. Identification of drought phases in a 110-year record from Western Mediterranean basin: Trends, anomalies and periodicity analysis for Iberian Peninsula. Glob. Planet. Chang. 2015, 133, 96–108. [Google Scholar] [CrossRef]
- Coll, J.R.; Aguilar, E.; Ashcroft, L. Drought variability and change across the Iberian Peninsula. Theoretical and Applied Climatology. Theor. Appl. Climatol. 2017, 130, 901–916. [Google Scholar] [CrossRef] [Green Version]
- Páscoa, P.; Gouveia, C.M.; Russo, A.; Trigo, R.M. Drought trends in the Iberian Peninsula over the last 112 years. Adv. Meteorol. 2017, 2017, 4653126. [Google Scholar] [CrossRef] [Green Version]
- García-Valdecasas, M.O.; Gámiz-Fortis, S.; Romero-Jiménez, E.; Rosa-Canóvas, J.J.; Yeste, P.; Castro-Díez, Y.; Esteban-Parra, M.J. Projected changes in the Iberian Peninsula drought characteristics. Sci. Total Environ. 2021, 757, 143702. [Google Scholar] [CrossRef]
- Vicente-Serrano, S.M. Spatial and temporal analysis of droughts in the Iberian Peninsula (1910–2000). Hydrol. Sci. J. 2006, 51, 83–97. [Google Scholar] [CrossRef]
- Peña-Gallardo, M.; Gámiz-Fortis, S.R.; Castro-Díez, Y.; Esteban-Parra, M.J. Análisis comparativo de índices de sequía en Andalucía para el periodo 1901–2012. Cuad. Investig. Geogr. 2016, 42, 67–88. [Google Scholar] [CrossRef] [Green Version]
- Ayuso, J.; Ayuso-Ruiz, P.; García-Marín, A.; Estévez, J.; Taguas, E. Local Analysis of the Characteristics and Frequency of Extreme Droughts in Málaga Using the SPI (Standardized Precipitation Index). In Project Management and Engineering. Lecture Notes in Management and Industrial Engineering; Ayuso Muñoz, J., Yagüe Blanco, J., Capuz-Rizo, S., Eds.; Springer: Cham, Switzerland, 2015; pp. 167–179. [Google Scholar] [CrossRef]
- Pulido-Calvo, I.; Gutiérrez-Estrada, J.C.; Sanz-Fernández, V. Drought and ecological flows in the lower Guadiana river basin (Southwest Iberian Peninsula). Water 2020, 12, 677. [Google Scholar] [CrossRef] [Green Version]
- Kottek, M.; Grieser, J.; Beck, C.; Rudolf, B.; Rubel, F. World map of the Köppen-Geiger climate classification updated. Meteorol. Z. 2006, 15, 259–263. [Google Scholar] [CrossRef]
- Zazo, S.; Molina, J.L.; Ruiz-Ortiz, V.; Vélez-Nicolás, M.; García-López, S. Modeling River Runo ff Temporal Behavior through a through a Hybrid Causal–Hydrological (HCH). Method. Water 2020, 12, 3137. [Google Scholar] [CrossRef]
- Ruiz-Ortiz, V.; García-López, S.; Solera, A.; Paredes Arquiola, J. Contribution of decision support systems to water management improvement in basins with high evaporation in Mediterranean climates. Hydrol. Res. 2019, 50, 1020–1036. [Google Scholar] [CrossRef]
- Ruiz-Ortiz, V.; García-López, S.; Vélez-Nicolás, M.; Sánchez-Bellón, A.; Contreras de Villar, A.; Contreras, F. Learning from hydrological and hydrogeological problems in civil engineering. Study of reservoirs in Andalusia, Spain. Eng. Geol. 2021, 282, 105916. [Google Scholar] [CrossRef]
- Vélez-Nicolás, M.; García-López, S.; Ruiz-Ortiz, V.; Sanchez-Bellón, A. Towards a sustainable and adaptive groundwater management: Lessons from the Benalup Aquifer (Southern Spain). Sustainability 2020, 12, 5215. [Google Scholar] [CrossRef]
- Acuña, J.; Felipe, O.; Ordoñez, J.; Arboleda, F. Análisis regional de frecuencia de precipitación anual para la determinación de mapas de sequías. Rev. Peru. Geo-Atmos. 2011, 3, 104–115. [Google Scholar]
- Núñez, J.H.; Verbist, K.; Wallis, J.R.; Schaefer, M.G.; Morales, L.; Cornelis, W.M. Regional frequency analysis for mapping drought events in north-central Chile. J. Hydrol. 2011, 405, 352–366. [Google Scholar] [CrossRef] [Green Version]
- CEDEX (Centro de Estudios y Experimentación de Obras Públicas). CHAC: Cálculo Hidrometeorológico de Aportaciones y Crecidas. Manual CHAC; CEDEX: Madrid, Spain, 2013; 76p, Available online: http://ceh-flumen64.cedex.es/chac/ (accessed on 23 January 2022).
- National Drought Mitigation Center. SPI Program. Available online: https://drought.unl.edu/monitoring/SPI/SPIProgram.aspx (accessed on 27 March 2021).
- European Drought Observatory, European Commission. SPI: Standardized Precipitation Index; EDO: Munchen, Germany, 2020; p. 6. Available online: https://edo.jrc.ec.europa.eu/documents/factsheets/factsheet_spi.pdf (accessed on 17 September 2021).
- Chervenkov, H.; Tsonevsky, I.; Slavov, K. Presentation of Four Centennial-long Global Gridded Datasets of the Standardized Precipitation Index. Int. J. Environ. Agric. Res. 2015, 2, 93–105. [Google Scholar]
- Rahmat, S.N.; Jayasuriya, N.; Bhuiyan, M. Assessing droughts using meteorological drought indices in Victoria, Australia. Hydrol. Res. 2015, 46, 463–476. [Google Scholar] [CrossRef]
- Hayes, M.; Svoboda, M.; Wall, N.; Wildhalm, M. The lincoln declaration on drought indices: Universal meteorological drought index recommended. Bull. Am. Meteorol. Soc. 2011, 92, 485–488. [Google Scholar] [CrossRef] [Green Version]
- García-Barrón, L.; Aguilar, M.; Sousa, A. Evolution of annual rainfall irregularity in the southwest of the Iberian Peninsula. Theor. Appl. Climatol. 2011, 103, 13–26. [Google Scholar] [CrossRef]
- Romero, R.; Guijarro, J.A.; Ramis, C.; Alonso, S. A 30-year (1964–1993) daily rainfall data base for the Spanish Mediterranean regions: First exploratory study. Int. J. Climatol. 1998, 18, 541–560. [Google Scholar] [CrossRef]
- Bladé, I.; Castro-Díez, Y.; Gutiérrez, J.M.; Herrera, S.; López-Moreno, J.I.; Vicente-Serrano, S. Tendencias atmosféricas en la Península Ibérica durante el periodo instrumental en el contexto de la variabilidad natural. In Clima en España: Pasado, Presente y Futuro; Pérez, F.F., Boscolo, R., Eds.; Ministerio de Ciencia e Innovación, Ministerio de Medio Ambiente y Medio Rural y Marino: Madrid, Spain, 2010; pp. 25–42. Available online: http://www.clivar.es/?q=es (accessed on 11 June 2021).
- Río, S.; Herrero, L.; Fraile, R.; Penas, A. Spatial distribution of recent rainfall trends in Spain (1961–2006). Int. J. Climatol. 2011, 31, 656–667. [Google Scholar] [CrossRef]
- Paredes, D.; Trigo, R.M.; García-Herrera, H.; Trigo, I.F. Understanding precipitation changes in Iberia in early spring: Weather typing and storm-tracking approaches. J. Hydrometeorol. 2006, 7, 101–113. [Google Scholar] [CrossRef] [Green Version]
- García, J.A.; Gallego, M.C.; Serrano, A.; Vaquero, J.M. Trends in block-seasonal extreme rainfall over the Iberian Peninsula in the second half of the twentieth century. J. Clim. 2007, 20, 113–130. [Google Scholar] [CrossRef]
- López-Bustins, J.A.; Sánchez-Lorenzo, A.; Azorín-Molina, C.; Ordóñez-López, A. Tendencias de la Precipitación Invernal en la Fachada Oriental de la Península Ibérica. In Cambio Climático Regional y sus Impactos; Sigró Rodríguez, J., Brunet India, M., Anfrons, E.A., Eds.; Asociación Española de Climatología: Tarragona, Spain, 2008; pp. 161–171. Available online: http://hdl.handle.net/20.500.11765/8562 (accessed on 22 October 2021).
- Hidalgo-Muñoz, J.M.; Argüeso, D.; Gámiz-Fortis, S.R.; Esteban-Parra, M.J.Y.; Castro-Díez, Y. Variability of the extreme rainfall events in the South of the Iberian Peninsula. Geophys. Res. Abstr. 2009, 11, 7771–7772. [Google Scholar]
- Hidalgo-Muñoz, J.M.; Argueso, D.; Gamiz-Fortis, S.R.; Esteban-Parra, M.J.; Castro-Diez, Y. Trends of extreme precipitation and associated synoptic patterns over the southern Iberian Peninsula. J. Hydrol. 2011, 409, 497–511. [Google Scholar] [CrossRef]
- Halifa-Marín, A.; Lorente-Plazas, R.; Pravia-Sarabia, E.; Montávez, J.P.; Jiménez-Guerrero, P. Atlantic and Mediterranean influence promoting an abrupt change in winter precipitation over the southern Iberian Peninsula. Atmos. Res. 2021, 253, 105485. [Google Scholar] [CrossRef]
- Trigo, R.M.; Pozo-Vázquez, M.; Osborn, T.; Castro-Díez, Y.; Gámiz-Fortis, S.; Esteban-Parra, M.J. North Atlantic oscillation influence on precipitation, river flow and water resources in the Iberian Peninsula. Int. J. Climatol. 2004, 24, 925–944. [Google Scholar] [CrossRef]
- Rodríguez-Puebla, C.; Nieto, S. Trends of precipitation over the Iberian Peninsula and the North Atlantic Oscillation under climate change conditions. Int. J. Climatol. 2010, 30, 1807–1815. [Google Scholar] [CrossRef]
- Bonaccorso, B.; Peres, D.; Cancelliere, A.; Rossi, G. Large Scale Probabilistic Drought Characterization Over Europe. Water Resour. Manag. 2013, 27, 1675–1692. [Google Scholar] [CrossRef]
- Spinoni, J.; Naumann, G.; Vogt, J.; Barbosa, P. The biggest drought events in Europe from 1950 to 2012. J. Hydrol. Reg. Stud. 2015, 3, 509–524. [Google Scholar] [CrossRef]
- Madueño, J.M.M. El Cambio Climático en Andalucía: Escenarios Actuales y Futuros del Clima. 2008. Available online: https://www.juntadeandalucia.es/medioambiente/portal/articulos (accessed on 13 June 2021).
- Junta de Andalucía, Consejería de Medio Ambiente. Plan Andaluz de Acción por el Clima. Programa de Adaptación. 2011. Available online: https://www.juntadeandalucia.es/medioambiente/portal/landing-page-planificacion/-/asset_publisher/Jw7AHImcvbx0/content/programa-de-adaptaci-c3-b3n-plan-andaluz-de-acci-c3-b3n-por-el-clima-2007-2012-/20151 (accessed on 27 June 2021).
- Junta de Andalucía, Consejería de Medio Ambiente y Ordenación del Territorio. El Clima de Andalucía en el Siglo XXI. Escenarios Locales de Cambio Climático de Andalucía. Actualización al 4° Informe del IPCC. Available online: https://www.juntadeandalucia.es/medioambiente/portal/landing-page-publicacion/-/asset_publisher/FytOUWH22K7t/content/el-clima-de-andaluc-c3-ada-en-el-siglo-xxi.-escenarios-locales-de-cambio-clim-c3-a1tico-de-andaluc-c3-ada.-actualizaci-c3-b3n-al-4-c2-ba-informe-del-2/20151 (accessed on 20 June 2021).
- Gebrehiwot, T.; van der Veen, A.; Maathuis, B. Spatial and temporal assessment of drought in the Northern highlands of Ethiopia. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 309–321. [Google Scholar] [CrossRef]
- Cheval, S. The Standardized Precipitation Index—An overview. Rom. J. Meteorol. 2015, 12, 17–64. [Google Scholar]
- Vicente-Serrano, S.M.; Begería, S.; Lorenzo-Lacruz, J.; Camarero, J.J.; López-Moreno, J.I.; Azorin-Molina, C.; Revuelto, J.; Morán-Tejeda, E.; Sanchez-Lorenzo, A. Performance of drought indices for ecological, agricultural and hydrological applications. Earth Interact. 2012, 16, 1–27. [Google Scholar] [CrossRef] [Green Version]
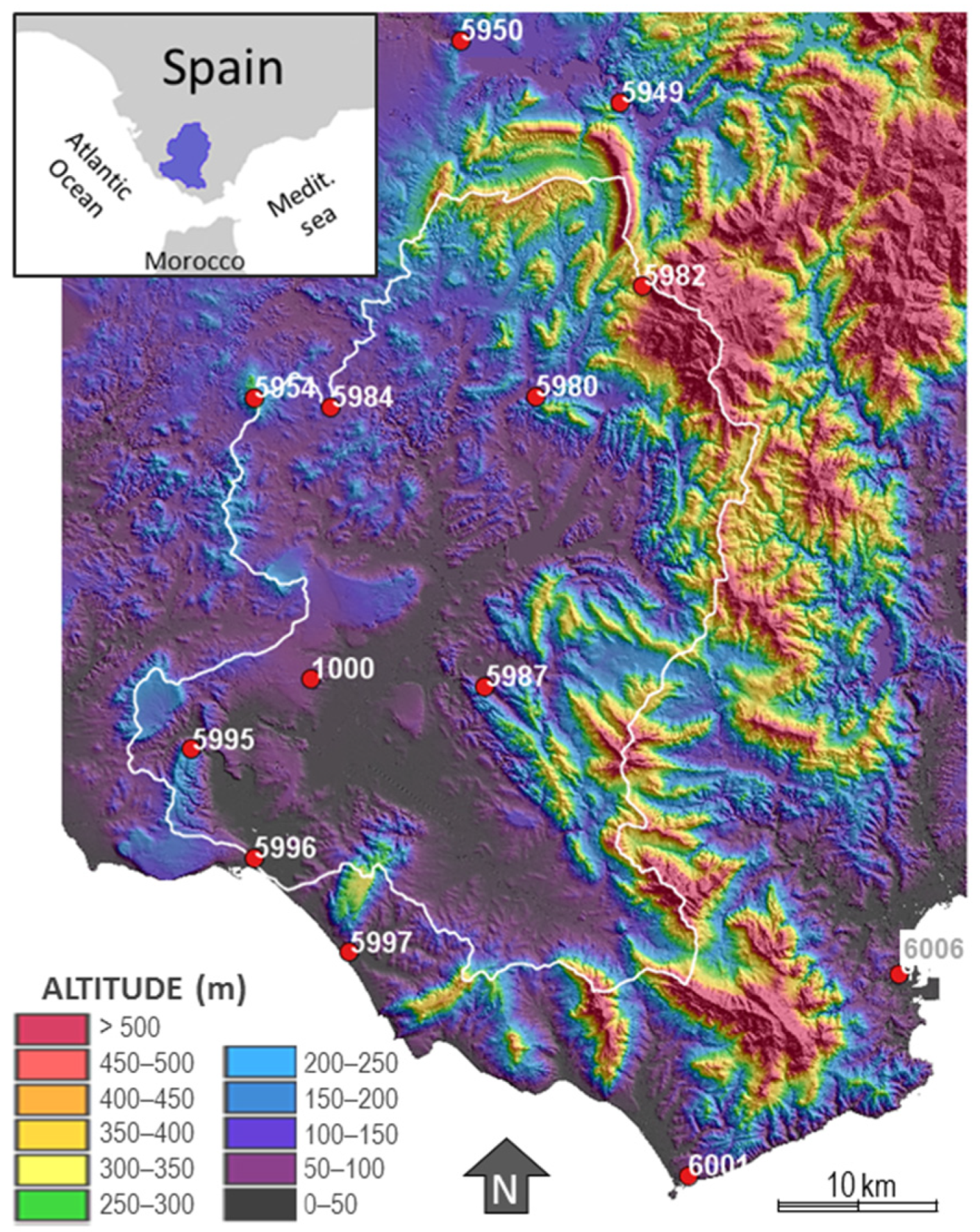
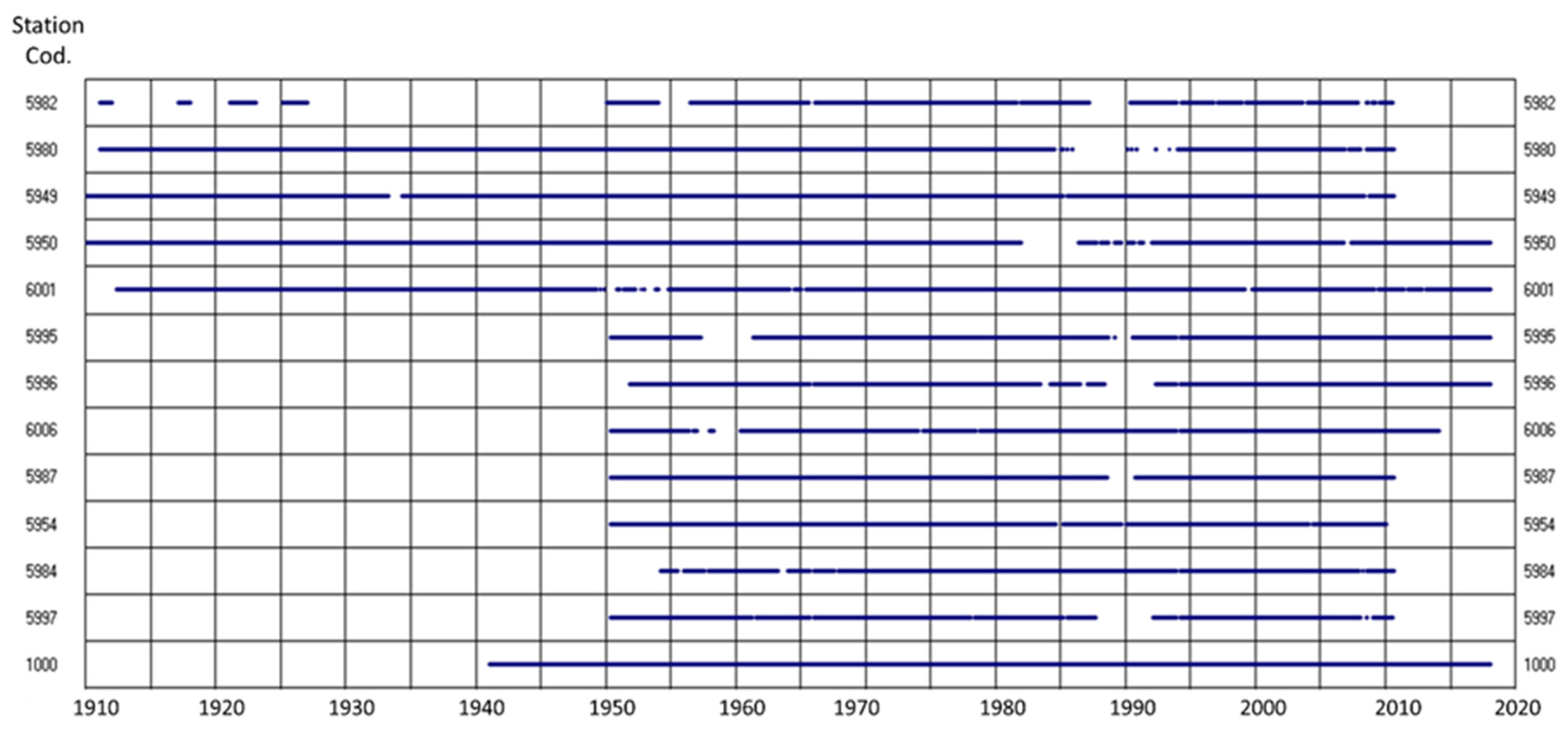



| Code | X-UTM (m) | Y-UTM (m) | Altitude (m) | Registration Start | Registration End | Nº Months with Available Data before CHAC | % Completed Using CHAC |
|---|---|---|---|---|---|---|---|
| 5980 | 255,885 | 4,038,918 | 149 | 1911 | 2011 | 1080 | 16.7 |
| 5982 | 262,834 | 4,046,066 | 428 | 1911 | 2011 | 695 | 46.4 |
| 6006 | 279,442 | 4,001,645 | 27 | 1951 | 2014 | 709 | 45.3 |
| 5996 | 237,680 | 4,009,124 | 7 | 1952 | 2018 | 720 | 44.4 |
| 5997 | 243,864 | 4,003,017 | 7 | 1951 | 2011 | 620 | 52.1 |
| 5949 | 261,395 | 4,057,889 | 127 | 1910 | 2011 | 1181 | 8.9 |
| 5954 | 237,691 | 4,038,835 | 277 | 1951 | 2010 | 686 | 47.1 |
| 5984 | 242,657 | 4,038,223 | 94 | 1954 | 2011 | 633 | 51.1 |
| 5987 | 252,610 | 4,020,194 | 23 | 1951 | 2011 | 692 | 46.6 |
| 5950 | 251,069 | 4,061,885 | 135 | 1909 | 2011 | 1202 | 7.2 |
| 6001 | 265,784 | 3,988,615 | 37 | 1866 | 2018 | 1175 | 9.3 |
| 5995 | 233,629 | 4,016,127 | 187 | 1951 | 2011 | 640 | 50.6 |
| 1000 | 241,394 | 4,020,710 | 46 | 1941 | 2018 | 924 | 28.7 |
| SPI Values | Characterization |
|---|---|
| >2.0 | Extremely wet |
| 1.5 to 1.99 | Very wet |
| 1.0 to 1.49 | Moderately wet |
| −0.99 to +0.99 | Normal |
| −1.0 to −1.49 | Moderately dry |
| −1.5 to −1.99 | Severely dry |
| <−2.0 | Extremely dry |
| Severe Drought | Extreme Drought | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Onset | End * | Duration (Months) | Extreme SPI Value | SPI Sum | Mean SPI | Onset | End * | Duration (Months) | Extreme SPI Value | SPI Sum | Mean SPI |
| February 1913 | November 1914 | 21 | −2.1 | −15.88 | −0.76 | February 1913 | November 1914 | 21 | −2.1 | −15.88 | −0.76 |
| November 1938 | December 1939 | 13 | −1.82 | −13.63 | −1.05 | ||||||
| February 1949 | November 1951 | 33 | −2.52 | −40.11 | −1.22 | April 1949 | November 1951 | 31 | −2.52 | −36.6 | −1.18 |
| June 1953 | February 1955 | 20 | −1.6 | −19.66 | −0.98 | ||||||
| March 1957 | December 1957 | 9 | −1.51 | −8.55 | −0.95 | ||||||
| November 1958 | October 1959 | 11 | −1.77 | −4.82 | −0.44 | ||||||
| October 1981 | February 1982 | 4 | −3.01 | −5.93 | −1.48 | November 1981 | February 1982 | 3 | −3.01 | −4.31 | −1.44 |
| January 1995 | January 1996 | 12 | −2.53 | −22.69 | −1.89 | May 1996 | January 1996 | 8 | −2.53 | −15.86 | −1.98 |
| December 1998 | December 2000 | 24 | −2.5 | −40.72 | −1.7 | February 1999 | December 2000 | 22 | −2.5 | −37.06 | −1.68 |
| January 2002 | December 2002 | 11 | −1.96 | −14.2 | −1.29 | ||||||
| April 2005 | November 2008 | 43 | −2.3 | −45.02 | −1.05 | May 2005 | November 2008 | 42 | −2.3 | −43.45 | −1.03 |
| December 2017 | March 2018 | 3 | −1.55 | −3.75 | −1.25 | ||||||
| Very Wet Periods | Extremely Wet Periods | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Onset | End | Duration (Months) | Extreme SPI Value | SPI Sum | Mean SPI | Onset | End | Duration (Months) | Extreme SPI Value | SPI Sum | Mean SPI |
| February 1912 | February 1912 | 1 | 1.62 | 1.62 | - | ||||||
| October 1921 | October 1921 | 1 | 1.52 | 1.52 | - | ||||||
| November 1936 | January 1937 | 2 | 1.56 | 3.07 | 1.54 | ||||||
| April 1941 | May 1941 | 2 | 1.52 | 3.02 | 1.51 | ||||||
| October 1960 | December 1960 | 3 | 1.79 | 5.16 | 1.72 | ||||||
| March 1962 | August 1964 | 29 | 3.11 | 63.05 | 1.71 | March 1962 | March 1964 | 17 | 3.11 | 42.48 | 2.5 |
| September 1969 | August 1970 | 9 | 2.68 | 16.4 | 1.72 | January 1970 | January 1970 | 1 | 2.68 | 2.68 | - |
| March 1972 | March 1972 | 1 | 1.6 | 1.6 | - | ||||||
| January 1977 | February 1977 | 2 | 1.68 | 3.24 | 1.62 | ||||||
| October 1979 | November 1979 | 2 | 1.65 | 3.16 | 1.58 | ||||||
| December 1989 | January 1990 | 2 | 1.65 | 3.27 | 1.64 | ||||||
| January 1996 | November 1997 | 23 | 3.47 | 48.07 | 1.75 | April 1996 | February 1997 | 11 | 3.47 | 27.04 | 2.46 |
| February 2010 | January 2011 | 12 | 2.59 | 25.42 | 1.78 | April 2010 | December 2010 | 9 | 2.59 | 20.08 | 2.23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vélez-Nicolás, M.; García-López, S.; Ruiz-Ortiz, V.; Zazo, S.; Molina, J.L. Precipitation Variability and Drought Assessment Using the SPI: Application to Long-Term Series in the Strait of Gibraltar Area. Water 2022, 14, 884. https://doi.org/10.3390/w14060884
Vélez-Nicolás M, García-López S, Ruiz-Ortiz V, Zazo S, Molina JL. Precipitation Variability and Drought Assessment Using the SPI: Application to Long-Term Series in the Strait of Gibraltar Area. Water. 2022; 14(6):884. https://doi.org/10.3390/w14060884
Chicago/Turabian StyleVélez-Nicolás, Mercedes, Santiago García-López, Verónica Ruiz-Ortiz, Santiago Zazo, and José Luis Molina. 2022. "Precipitation Variability and Drought Assessment Using the SPI: Application to Long-Term Series in the Strait of Gibraltar Area" Water 14, no. 6: 884. https://doi.org/10.3390/w14060884









