Spatial Non-Stationarity-Based Landslide Susceptibility Assessment Using PCAMGWR Model
Abstract
:1. Introduction
2. Study Area and Dataset
2.1. Overview of the Study Area
2.2. Dataset Preparation
3. Materials and Methods
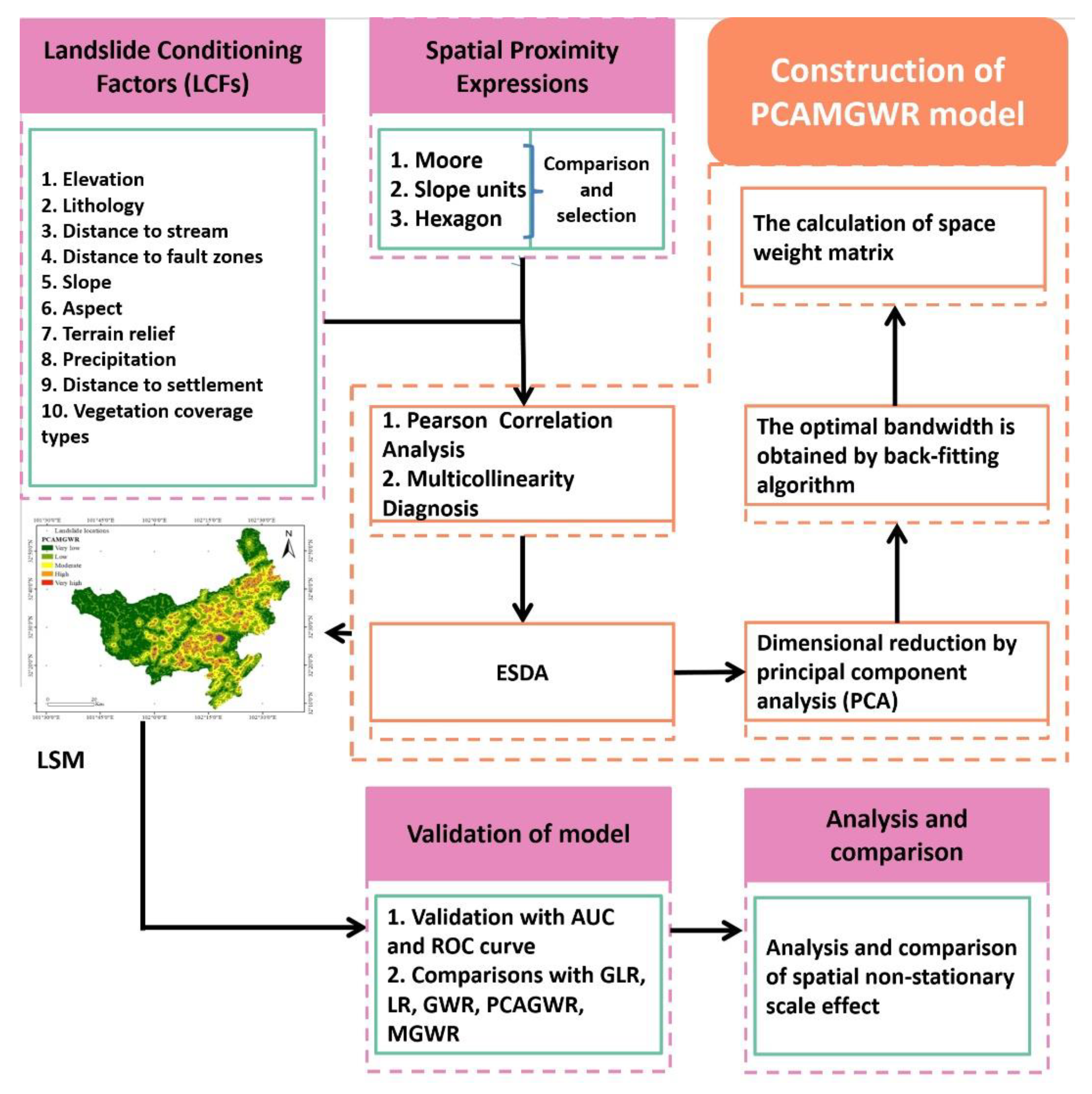
3.1. Flowchart
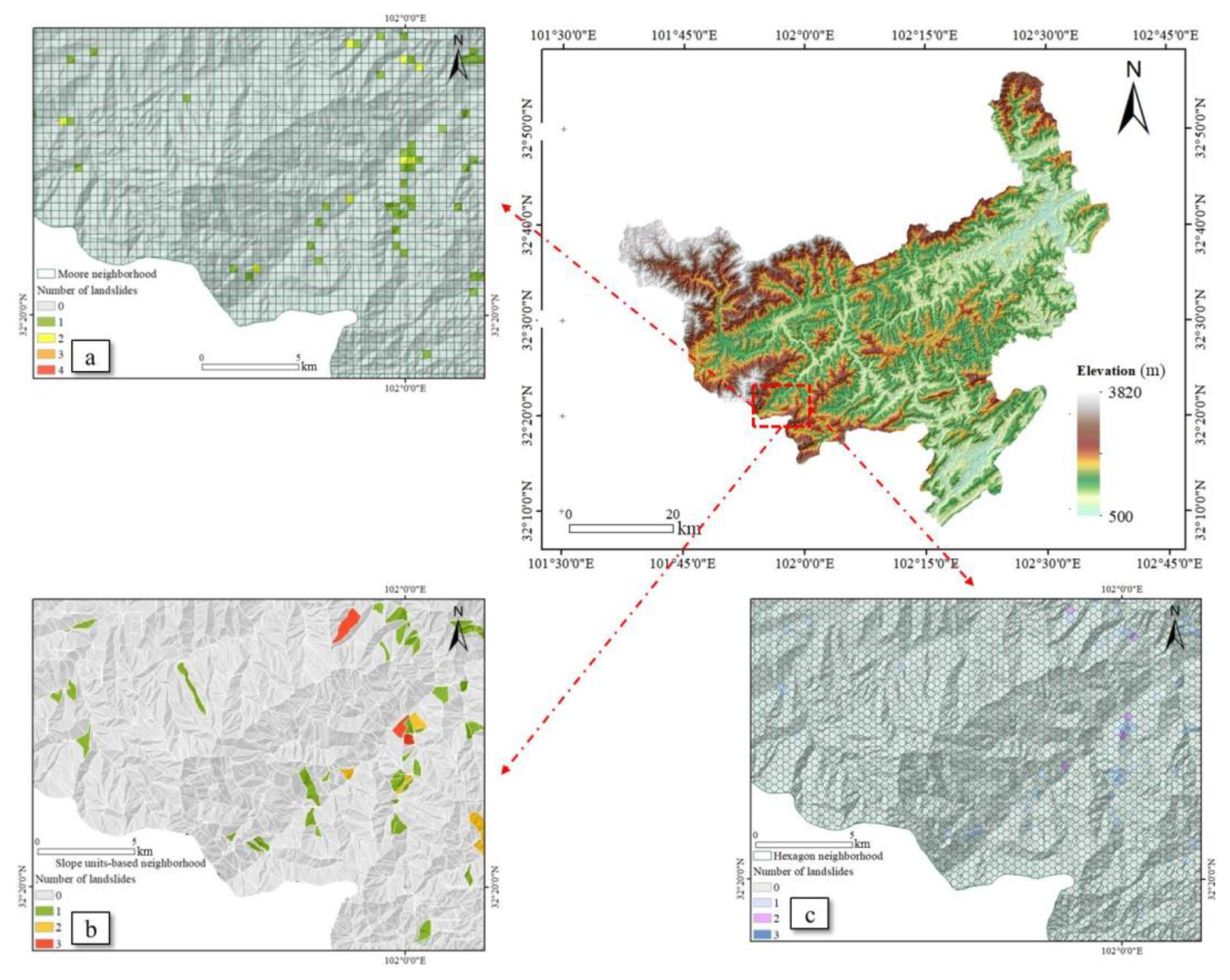
- Three spatial neighborhood expressions were constructed in GIS—Moore neighborhoods, slope-unit-based neighborhoods, and hexagonal neighborhoods. The segmentation metric function proposed by Espindola [46] was then used for the prime spatial proximity expression and the extracted LCF was used as the input of the PCAMGWR model.
- Based on the geoenvironmental condition of the study area, LCFs were selected, and thematic layers of LCFs were prepared. Then, the LCFs were analyzed using Pearson correlation analysis and multicollinearity test.
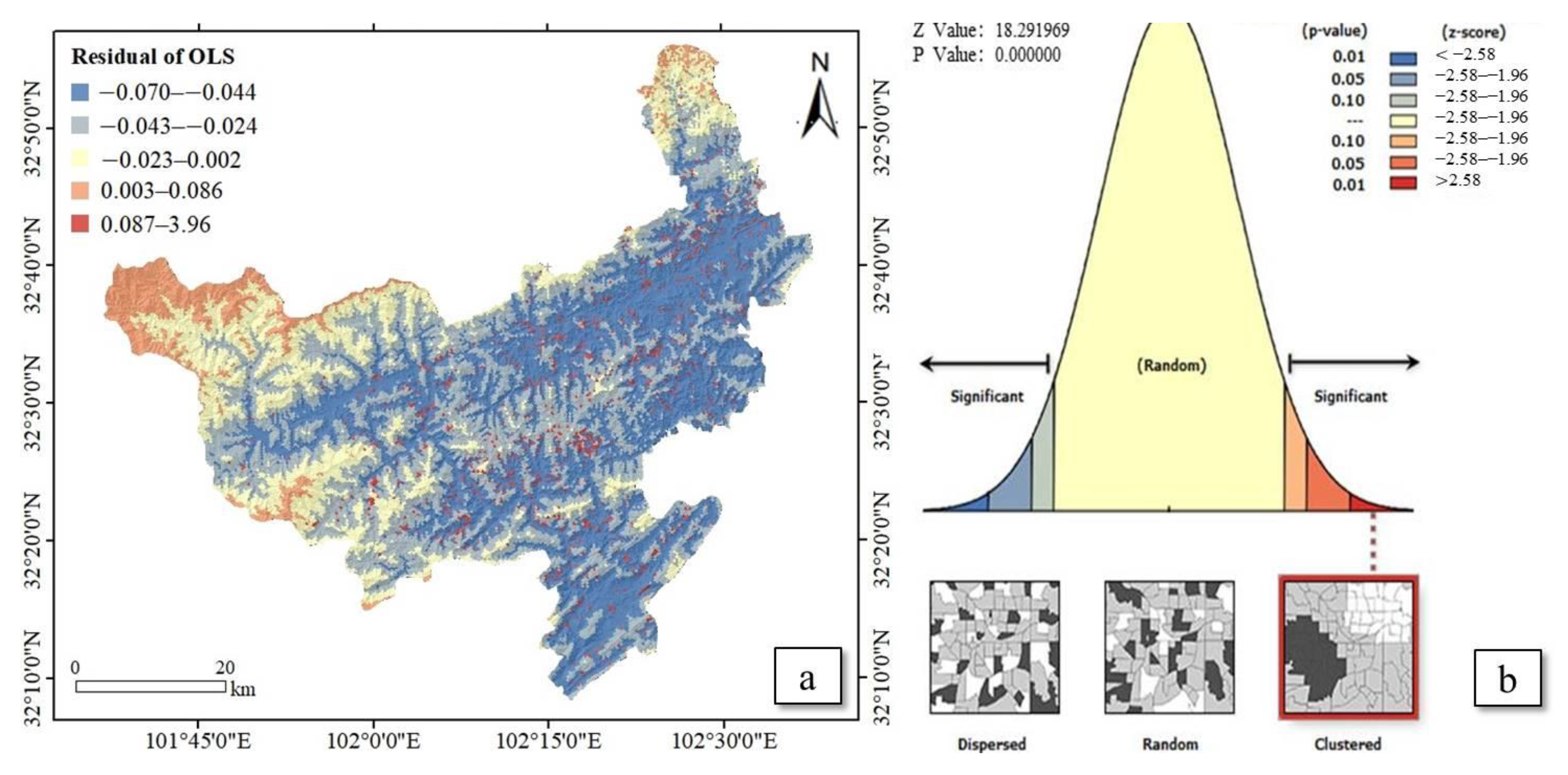
- ESDA was used to investigate the validity of global regression, and the residual obtained by Ordinary Least Squares (OLS) was analyzed based on Moran’s I autocorrelation.
- PCAMGWR model was established for exploring the influence of spatial non-stationarity and factor correlation on LSM.
- The accuracy of the proposed model was verified using statistical measures, and the spatial non-stationarity scale effect was analyzed and compared.
3.2. Expression of Spatial Proximity Selection Method
3.3. Factor Analysis
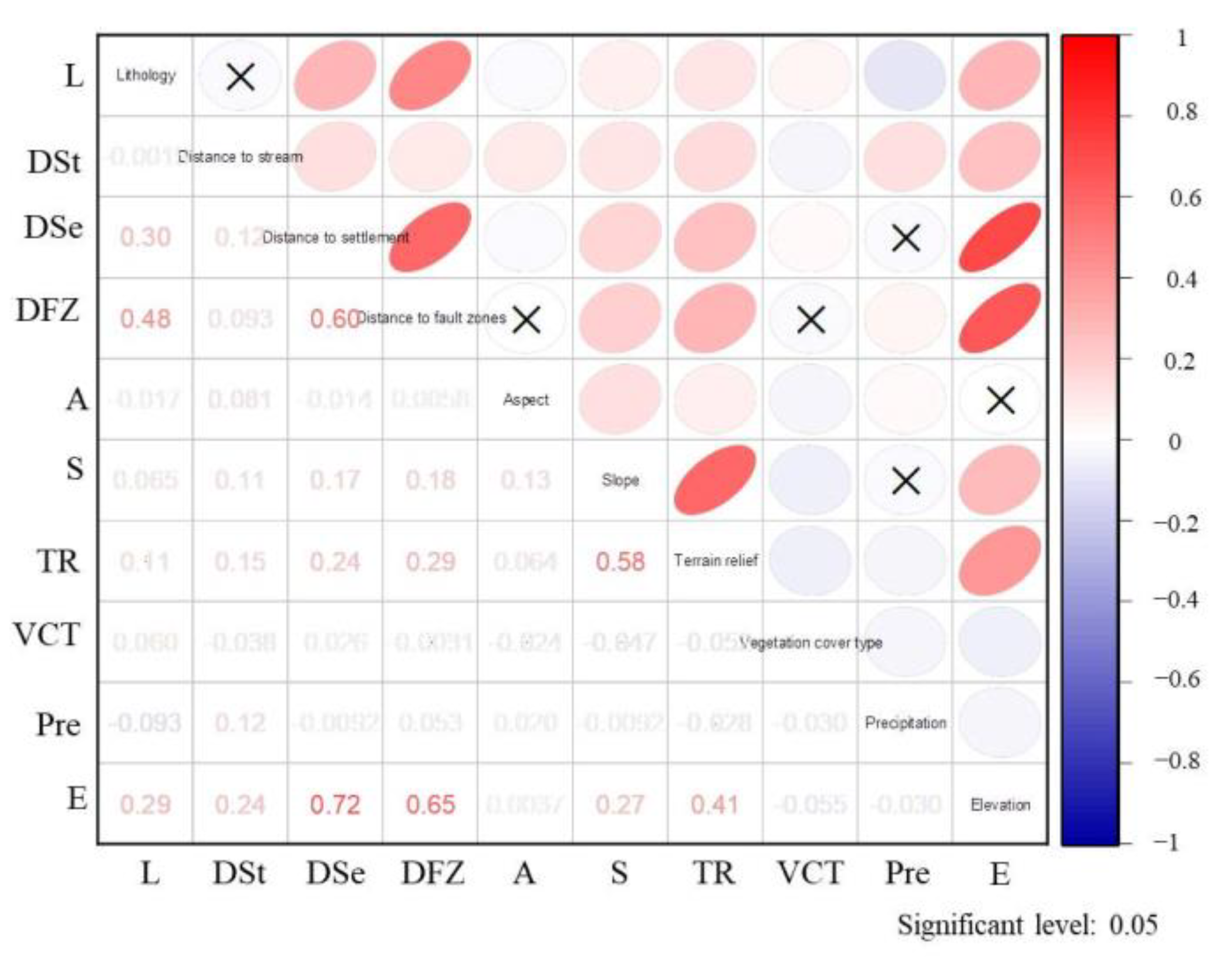
3.3.1. Correlation Analysis
3.3.2. Multicollinearity Test
3.4. ESDA
3.5. Validation Method
4. PCAMGWR Modeling
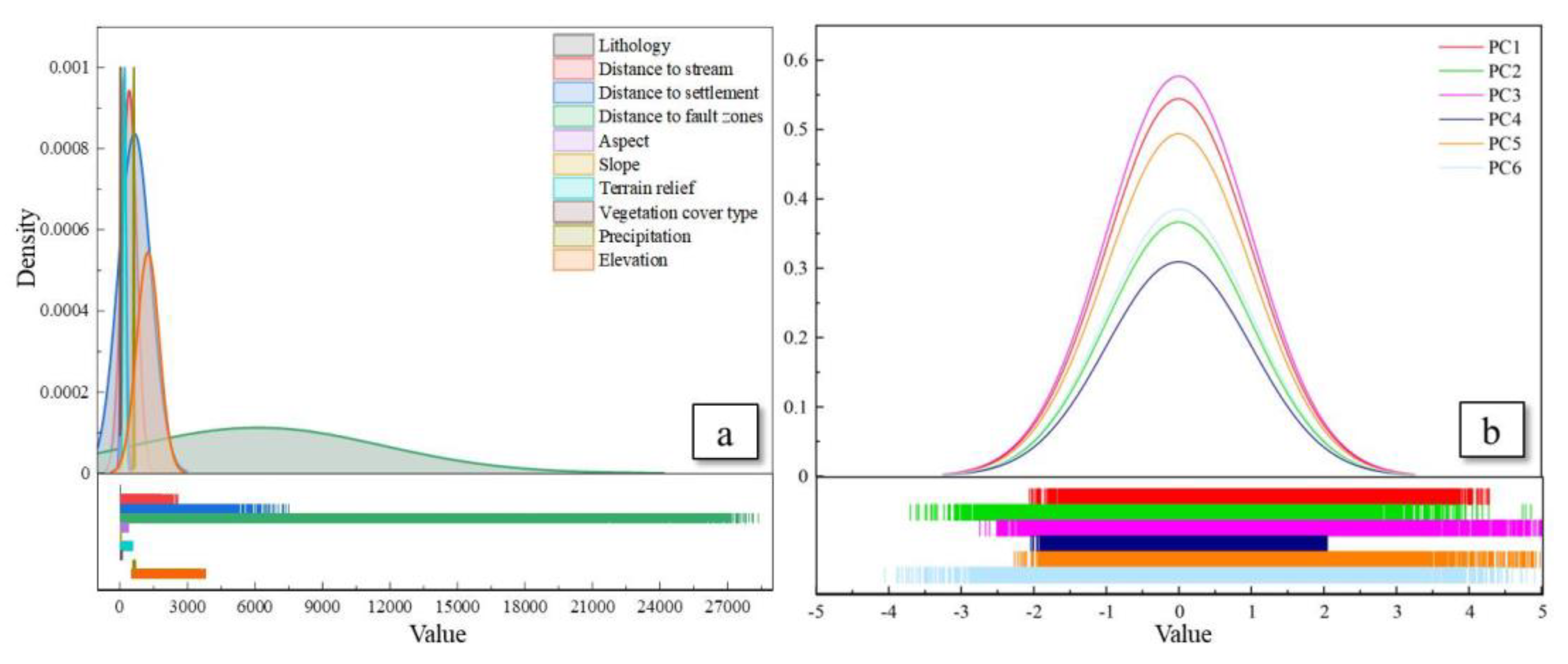
4.1. Principal Component Analysis (PCA)
4.2. MGWR
5. Results
5.1. Expression of Spatial Proximity
5.2. Correlation Analysis and Multicollinearity Test
5.3. ESDA
5.4. LSMs Based on PCAMGWR Model
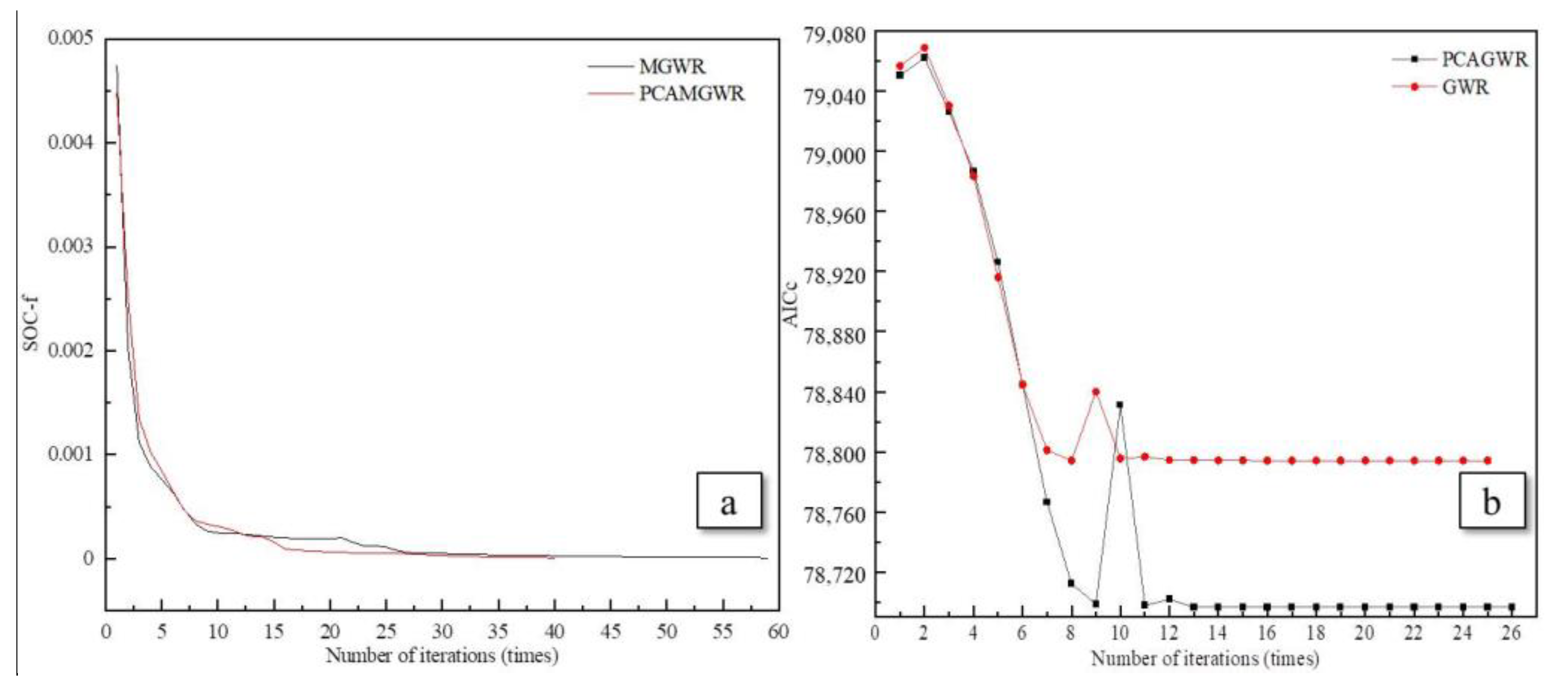
5.5. Analysis and Comparison of Spatial Non-Stationarity Scale Effect
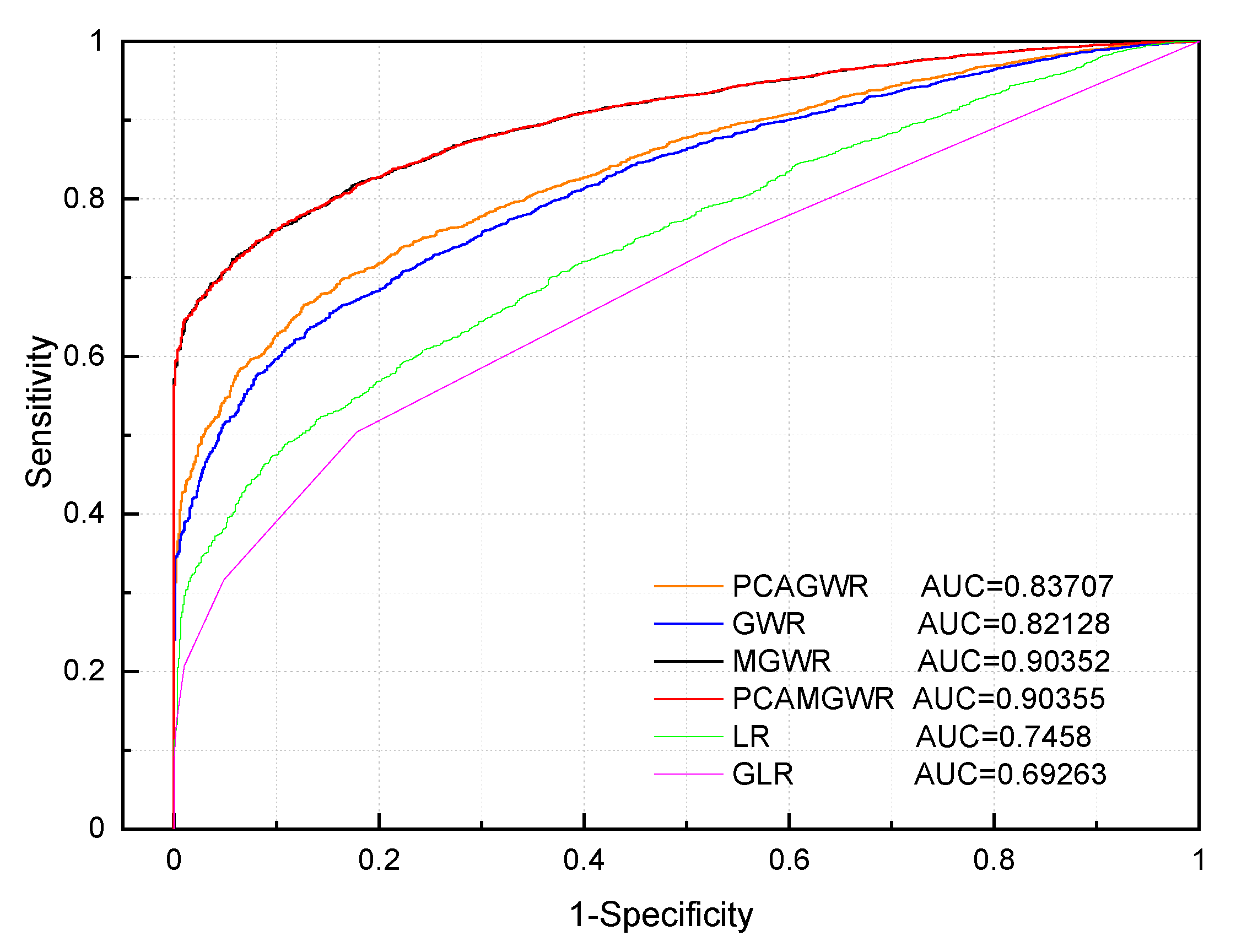
5.6. Validation and Accuracy Assessment
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Froude, M.J.; Petley, D.N. Global fatal landslide occurrence from 2004 to 2016. Nat. Hazards Earth Syst. Sci. 2018, 18, 2161–2181. [Google Scholar] [CrossRef] [Green Version]
- Haque, U.; da Silva, P.F.; Devoli, G.; Pilz, J.; Zhao, B.; Khaloua, A.; Wilopo, W.; Andersen, P.; Lu, P.; Lee, J.; et al. The human cost of global warming: Deadly landslides and their triggers (1995–2014). Sci. Total Environ. 2019, 682, 673–684. [Google Scholar] [CrossRef] [PubMed]
- Available online: http://www.mnr.gov.cn/ (accessed on 1 June 2021).
- Guzzetti, F.; Reichenbach, P.; Cardinali, M.; Galli, M.; Ardizzone, F. Probabilistic landslide hazard assessment at the basin scale. Geomorphology 2005, 72, 272–299. [Google Scholar] [CrossRef]
- Corominas, J.; Esgleas, J.; Baeza, C. Risk mapping in the Pyrenees area: A case study. Hydrol. Mt. Reg. II Artificial Reserv. Water Slopes 1990, 194, 425–428. [Google Scholar]
- Zhu, A.X.; Wang, R.; Qiao, J.; Chen, Y.; Cai, Q.; Zhou, C. Mapping landslide susceptibility in the Three Gorges area, China using GIS, expert knowledge and fuzzy logic. In Proceedings of the International Conference of GIS Remote Sensing in Hydrology, Water Resources and Environment, Sandouping, China, 16–19 September 2004; pp. 385–391. [Google Scholar]
- Sarkar, S.; Kanungo, D.P.; Patra, A.K.; Kumar, P. GiS based spatial data analysis for landslide susceptibility mapping. J. Mt. Sci. 2008, 5, 52–62. [Google Scholar] [CrossRef]
- Magliulo, P.; Di Lisio, A.; Russo, F. Comparison of GIS-based methodologies for the landslide susceptibility assessment. Geoinformatica 2009, 13, 253–265. [Google Scholar] [CrossRef]
- Feizizadeh, B.; Blaschke, T.; Ieee. Comparing Gis-Multicriteria Decision Analysis for Landslide Susceptibility Mapping for the Urmia Lake Basin, Iran. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Munich, Germany, 22–27 July 2012; pp. 5390–5393. [Google Scholar]
- Panchal, S.; Shrivastava, A.K. Application of analytic hierarchy process in landslide susceptibility mapping at regional scale in GIS environment. J. Stat. Manag. Syst. 2020, 23, 199–206. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H.; Marui, H.; Kanno, T. Landslides in Sado Island of Japan: Part II. GIS-based susceptibility mapping with comparisons of results from two methods and verifications. Eng. Geol. 2005, 81, 432–445. [Google Scholar] [CrossRef]
- Wang, W.D.; Xie, C.M.; Du, X.G. Landslides susceptibility mapping based on geographical information system, GuiZhou, south-west China. Environ. Geol. 2009, 58, 33–43. [Google Scholar] [CrossRef]
- Chalkias, C.; Kalogirou, S.; Ferentinou, M. Landslide susceptibility, Peloponnese Peninsula in South Greece. J. Maps 2014, 10, 211–222. [Google Scholar] [CrossRef]
- Thiebes, B.; Bell, R.; Glade, T. Deterministic Landslide Susceptibility Analyis-A Case Study in the Swabian Alb. In Proceedings of the Conference -Geomorphology for the Future, Obergurgl, Austria, 2–7 September 2007; pp. 177–184. [Google Scholar]
- Ferentinou, M.; Chalkias, C. Mapping Mass Movement Susceptibility across Greece with GIS, ANN and Statistical Methods; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zezere, J.L.; Pereira, S.; Melo, R.; Oliveira, S.C.; Garcia, R.A.C. Mapping landslide susceptibility using data-driven methods. Sci. Total Environ. 2017, 589, 250–267. [Google Scholar] [CrossRef] [PubMed]
- Chauhan, S.; Sharma, M.; Arora, M.K.; Gupta, N.K. Landslide Susceptibility Zonation through ratings derived from Artificial Neural Network. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 340–350. [Google Scholar] [CrossRef]
- Bai, S.B.; Wang, J.; Thiebes, B.; Cheng, C.; Chang, Z.Y. Susceptibility assessments of the Wenchuan earthquake-triggered landslides in Longnan using logistic regression. Environ. Earth Sci. 2014, 71, 731–743. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Sahin, E.K.; Colkesen, I. Landslide susceptibility mapping using GIS-based multi-criteria decision analysis, support vector machines, and logistic regression. Landslides 2014, 11, 425–439. [Google Scholar] [CrossRef]
- Dagdelenler, G.; Nefeslioglu, H.A.; Gokceoglu, C. Modification of seed cell sampling strategy for landslide susceptibility mapping: An application from the Eastern part of the Gallipoli Peninsula (Canakkale, Turkey). Bull. Eng. Geol. Environ. 2016, 75, 575–590. [Google Scholar] [CrossRef]
- Chalkias, C.; Polykretis, C.; Karymbalis, E.; Soldati, M.; Ghinoi, A.; Ferentinou, M. Exploring spatial non-stationarity in the relationships between landslide susceptibility and conditioning factors: A local modeling approach using geographically weighted regression. Bull. Eng. Geol. Environ. 2020, 79, 2799–2814. [Google Scholar] [CrossRef]
- Brenning, A. Spatial prediction models for landslide hazards: Review, comparison and evaluation. Nat. Hazards Earth Syst. Sci. 2005, 5, 853–862. [Google Scholar] [CrossRef]
- O’Sullivan, D. Geographically weighted regression: The analysis of spatially varying relationships. Geogr. Anal. 2003, 35, 272–275. [Google Scholar] [CrossRef]
- Li, J.; Wang, W.; Han, Z.; Li, Y.; Chen, G. Exploring the Impact of Multitemporal DEM Data on the Susceptibility Mapping of Landslides. Appl. Sci. 2020, 10, 2518. [Google Scholar] [CrossRef] [Green Version]
- Leyk, S.; Norlund, P.U.; Nuckols, J.R. Robust assessment of spatial non-stationarity in model associations related to pediatric mortality due to diarrheal disease in Brazil. Spat. Spatio-Temporal Epidemiol. 2012, 3, 95–105. [Google Scholar] [CrossRef] [Green Version]
- Tu, J. Spatially varying relationships between land use and water quality across an urbanization gradient explored by geographically weighted regression. Appl. Geogr. 2011, 31, 376–392. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, J.; Xu, S.; Zhao, Y. An Extended Semi-Supervised Regression Approach with Co-Training and Geographical Weighted Regression: A Case Study of Housing Prices in Beijing. Isprs Int. J. Geo-Inf. 2016, 5, 4. [Google Scholar] [CrossRef] [Green Version]
- Monjaras-Vega, N.A.; Briones-Herrera, C.I.; Vega-Nieva, D.J.; Calleros-Flores, E.; Corral-Rivas, J.J.; Lopez-Serrano, P.M.; Pompa-Garcia, M.; Rodriguez-Trejo, D.A.; Carrillo-Parra, A.; Gonzalez-Caban, A.; et al. Predicting forest fire kernel density at multiple scales with geographically weighted regression in Mexico. Sci. Total Environ. 2020, 718, 137313. [Google Scholar] [CrossRef] [PubMed]
- Liu, K.; Qiao, Y.; Shi, T.; Zhou, Q. Study on coupling coordination and spatiotemporal heterogeneity between economic development and ecological environment of cities along the Yellow River Basin. Environ. Sci. Pollut. Res. 2021, 28, 6898–6912. [Google Scholar] [CrossRef]
- Erener, A.; Düzgün, H.S.B. Improvement of statistical landslide susceptibility mapping by using spatial and global regression methods in the case of More and Romsdal (Norway). Landslides 2010, 7, 55–68. [Google Scholar] [CrossRef]
- Sabokbar, H.F.; Roodposhti, M.S.; Tazik, E. Landslide susceptibility mapping using geographically-weighted principal component analysis. Geomorphology 2014, 226, 15–24. [Google Scholar] [CrossRef]
- Xianyu, Y. Study on the Landslide Susceptibility Evaluation Method Based on Multi-Source Data and Multi-Scale Analysis. Ph.D. Thesis, China University of Geosciences, Wuhan, China, 2016. [Google Scholar]
- Feuillet, T.; Coquin, J.; Mercier, D.; Cossart, E.; Decaulne, A.; Jónsson, H.P.; Sæmundsson, þ. Focusing on the spatial non-stationarity of landslide predisposing factors in northern Iceland: Do paraglacial factors vary over space? Prog. Phys. Geogr. 2014, 38, 354–377. [Google Scholar] [CrossRef]
- Fotheringham, A.S.; Brunsdon, C.F.; Charlton, M.E. Geographically Weighted Regression: The Analysis of Spatially Varying Relationships; John Wiley and Sons: Chichester, UK, 2002. [Google Scholar]
- Wang, Y.; Fang, Z.; Wang, M.; Peng, L.; Hong, H. Comparative study of landslide susceptibility mapping with different recurrent neural networks. Comput. Geosci. 2020, 138, 104445. [Google Scholar] [CrossRef]
- Jun, C.; Yinghao, Z. Spatial Adjancency Query Based on Voronoi Diagram. Geomat. Inf. Sci. Wuhan Univ. 1998, 23, 4. [Google Scholar]
- Jinting, Z.; Rui, Z. Study on the influence factors of housing price in the urban area of Bohai RingMegalopolis. based on geographically weighted regression. Territ. Nat. Resour. Study 2019, 828, 87–93. [Google Scholar] [CrossRef]
- Carr, D.B.; Olsen, A.R.; White, D. Hexagon Mosaic Maps for Display of Univariate and Bivariate Geographical Data. Am. Cartogr. 1994, 19, 228–236. [Google Scholar] [CrossRef]
- Birch, C.P.D.; Oom, S.P.; Beecham, J.A. Rectangular and hexagonal grids used for observation, experiment and simulation in ecology. Ecol. Model. 2007, 206, 347–359. [Google Scholar] [CrossRef]
- Han, Z.; Li, Y.; Du, Y.; Wang, W.; Chen, G. Noncontact detection of earthquake-induced landslides by an enhanced image binarization method incorporating with Monte-Carlo simulation. Geomat. Nat. Hazards Risk 2019, 10, 219–241. [Google Scholar] [CrossRef]
- Kamp, U.; Growley, B.J.; Khattak, G.A.; Owen, L.A. GIS-based landslide susceptibility mapping for the 2005 Kashmir earthquake region. Geomorphology 2008, 101, 631–642. [Google Scholar] [CrossRef]
- Ayalew, L.; Yamagishi, H. The application of GIS-based logistic regression for landslide susceptibility mapping in the Kakuda-Yahiko Mountains, Central Japan. Geomorphology 2005, 65, 15–31. [Google Scholar] [CrossRef]
- Li, Y.; Chen, G.; Tang, C.; Zhou, G.; Zheng, L. Rainfall and earthquake-induced landslide susceptibility assessment using GIS and Artificial Neural Network. Nat. Hazards Earth Syst. Sci. 2012, 12, 2719–2729. [Google Scholar] [CrossRef]
- Demir, G.; Aytekin, M.; Akgun, A.; Ikizler, S.B.; Tatar, O. A comparison of landslide susceptibility mapping of the eastern part of the North Anatolian Fault Zone (Turkey) by likelihood-frequency ratio and analytic hierarchy process methods. Nat. Hazards 2013, 65, 1481–1506. [Google Scholar] [CrossRef]
- Reichenbach, P.; Rossi, M.; Malamud, B.D.; Mihir, M.; Guzzetti, F. A review of statistically-based landslide susceptibility models. Earth-Sci. Rev. 2018, 180, 60–91. [Google Scholar] [CrossRef]
- Espindola, G.M.; Camara, G.; Reis, I.A.; Bins, L.S.; Monteiro, A.M. Parameter selection for region-growing image segmentation algorithms using spatial autocorrelation. Int. J. Remote Sens. 2006, 27, 3035–3040. [Google Scholar] [CrossRef]
- Zhao, B.; Ge, Y.; Chen, H. Landslide susceptibility assessment for a transmission line in Gansu Province, China by using a hybrid approach of fractal theory, information value, and random forest models. Environ. Earth Sci. 2021, 80, 441. [Google Scholar] [CrossRef]
- Rogers, G.S. A course in theoretical statistics. Technometrics 1969, 11, 840–841. [Google Scholar] [CrossRef]
- Arabameri, A.; Pradhan, B.; Rezaei, K.; Sohrabi, M.; Kalantari, Z. GIS-based landslide susceptibility mapping using numerical risk factor bivariate model and its ensemble with linear multivariate regression and boosted regression tree algorithms. J. Mt. Sci. 2019, 16, 595–618. [Google Scholar] [CrossRef]
- Cama, M.; Lombardo, L.; Conoscenti, C.; Rotigliano, E. Improving transferability strategies for debris flow susceptibility assessment: Application to the Saponara and Itala catchments (Messina, Italy). Geomorphology 2017, 288, 52–65. [Google Scholar] [CrossRef]
- Ukoumunne, O.C.; Gulliford, M.C.; Chinn, S. A note on the use of the variance inflation factor for determining sample size in cluster randomized trials. J. R. Stat. Soc. Ser. D (Stat.) 2002, 51, 479–484. [Google Scholar] [CrossRef]
- Hu, X.; Hong, W.; Qiu, R.; Hong, T.; Chen, C.; Wu, C. Geographic variations of ecosystem service intensity in Fuzhou City, China. Sci. Total Environ. 2015, 512, 215–226. [Google Scholar] [CrossRef]
- Wulder, M.; Boots, B. Local spatial autocorrelation characteristics of remotely sensed imagery assessed with the Getis statistic. Int. J. Remote Sens. 1998, 19, 2223–2231. [Google Scholar] [CrossRef]
- Li, H.; Chen, Y.; Deng, S.; Chen, M.; Fang, T.; Tan, H. Eigenvector Spatial Filtering-Based Logistic Regression for Landslide Susceptibility Assessment. ISPRS Int. J. Geo-Inf. 2019, 8, 332. [Google Scholar] [CrossRef] [Green Version]
- Goetz, J.N.; Guthrie, R.H.; Brenning, A. Integrating physical and empirical landslide susceptibility models using generalized additive models. Geomorphology 2011, 129, 376–386. [Google Scholar] [CrossRef]
- Akgun, A.; Turk, N. Mapping erosion susceptibility by a multivariate statistical method: A case study from the Ayvalik region, NW Turkey. Comput. Geosci. 2011, 37, 1515–1524. [Google Scholar] [CrossRef]
- Abdul-Wahab, S.A.; Bakheit, C.S.; Al-Alawi, S.M. Principal component and multiple regression analysis in modelling of ground-level ozone and factors affecting its concentrations. Environ. Model. Softw. 2005, 20, 1263–1271. [Google Scholar] [CrossRef]
- Demsar, U.; Harris, P.; Brunsdon, C.; Fotheringham, A.S.; McLoone, S. Principal Component Analysis on Spatial Data: An Overview. Ann. Assoc. Am. Geogr. 2013, 103, 106–128. [Google Scholar] [CrossRef]
- Harris, P.; Brunsdon, C.; Charlton, M. Geographically weighted principal components analysis. Int. J. Geogr. Inf. Sci. 2011, 25, 1717–1736. [Google Scholar] [CrossRef]
- Brunsdon, C.; Fotheringham, A.S.; Charlton, M.E. Geographically Weighted Regression: A Method for Exploring Spatial Nonstationarity. Geogr. Anal. 2010, 28, 281–298. [Google Scholar] [CrossRef]
- Wh Ee Ler, D.; Tiefelsdorf, M. Multicollinearity and correlation among local regression coefficients in geographically weighted regression. J. Geogr. Syst. 2005, 7, 161–187. [Google Scholar] [CrossRef]
- Farber, S.; Paez, A. A systematic investigation of cross-validation in GWR model estimation: Empirical analysis and Monte Carlo simulations. J. Geogr. Syst. 2007, 9, 371–396. [Google Scholar] [CrossRef]
- Paez, A.; Farber, S.; Wheeler, D. A simulation-based study of geographically weighted regression as a method for investigating spatially varying relationships. Environ. Plan. A Econ. Space 2011, 43, 2992–3010. [Google Scholar] [CrossRef]
- Wolf, L.J.; Oshan, T.M.; Fotheringham, A.S. Single and Multiscale Models of Process Spatial Heterogeneity. Geogr. Anal. 2018, 50, 223–246. [Google Scholar] [CrossRef] [Green Version]
- Fotheringham, A.S.; Yang, W.; Kang, W. Multiscale Geographically Weighted Regression (MGWR). Ann. Am. Assoc. Geogr. 2017, 107, 1247–1265. [Google Scholar] [CrossRef]
- Yu, H.; Fotheringham, A.S.; Li, Z.; Oshan, T.; Wolf, L.J. On the measurement of bias in geographically weighted regression models. Spat. Stat. 2020, 38, 100453. [Google Scholar] [CrossRef]
- Hastie, T.J.; Tibshirani, R.J. Generalized Additive Models Chapman and Hall; Lifetime Data Analysis; Routledge: Oxfordshire, UK, 1990. [Google Scholar]
- Evans, D. Spatial analyses of crime. Geography 2001, 86, 211–223. [Google Scholar]
- Pareta, K.; Kumar, J.; Pareta, U. Landslide Hazard Zonation using Quantitative Methods in GIS. Int. J. Geospatial. Eng. Technol. 2012, 1, 1–9. [Google Scholar]
- Xing, X.; Wu, C.; Li, J.; Li, X.; Zhang, L.; He, R. Susceptibility assessment for rainfall-induced landslides using a revised logistic regression method. Nat. Hazards 2021, 106, 97–117. [Google Scholar] [CrossRef]
- Suhua, Z.; Wei, W.; Guangqi, C.; Baochen, L.; Ligang, F. A Combined Weight of Evidence and Logistic Regression Method for Susceptibility Mapping of Earthquake-induced Landslides: A Case Study of the April 20, 2013 Lushan Earthquake, China. Acta Geol. Sin. Engl. Ed. 2016, 90, 511–524. [Google Scholar] [CrossRef]
- Huang, Y.; Zhao, L. Review on landslide susceptibility mapping using support vector machines. CATENA 2018, 165, 520–529. [Google Scholar] [CrossRef]
- Li, Y.; Liu, X.; Han, Z.; Dou, J. Spatial Proximity-Based Geographically Weighted Regression Model for Landslide Susceptibility Assessment: A Case Study of Qingchuan Area, China. Applied Sciences 2020, 10, 1107. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Pradhan, B.; Sameen, M.I.; Chen, W.; Xu, C. Spatial prediction of rotational landslide using geographically weighted regression, logistic regression, and support vector machine models in Xing Guo area (China). Geomat. Nat. Hazards Risk 2017, 8, 1997–2022. [Google Scholar] [CrossRef] [Green Version]
- Gao, Y.; Huang, J.; Li, S.; Li, S. Spatial pattern of non-stationarity and scale-dependent relationships between NDVI and climatic factors—A case study in Qinghai-Tibet Plateau, China. Ecol. Indic. 2012, 20, 170–176. [Google Scholar] [CrossRef]
- Yu, H.; Fotheringham, A.S.; Li, Z.; Oshan, T.; Kang, W.; Wolf, L.J. Inference in Multiscale Geographically Weighted Regression. Geogr. Anal. 2020, 52, 87–106. [Google Scholar] [CrossRef]






| LCFs | VIF | TOL |
|---|---|---|
| Lithology | 1.328 | 0.753 |
| Distance to stream | 1.109 | 0.901 |
| Distance to settlement | 2.255 | 0.443 |
| Distance to fault zones | 2.195 | 0.456 |
| Aspect | 1.025 | 0.975 |
| Slope | 1.540 | 0.650 |
| Terrain relief | 1.719 | 0.582 |
| Vegetation cover type | 1.019 | 0.981 |
| Precipitation | 1.052 | 0.950 |
| Elevation | 2.861 | 0.350 |
| LCFs | PC1 | PC2 | PC3 | PC4 | PC5 | PC6 |
|---|---|---|---|---|---|---|
| Lithology | 0.500 | −0.448 | −0.160 | 0.109 | −0.211 | 0.176 |
| Distance to stream | 0.272 | 0.322 | 0.542 | 0.156 | 0.071 | −0.621 |
| Distance to settlement | 0.782 | −0.267 | 0.120 | −0.018 | −0.012 | −0.065 |
| Distance to fault zones | 0.803 | −0.291 | 0.097 | 0.003 | −0.084 | 0.163 |
| Aspect | 0.058 | 0.396 | 0.031 | 0.509 | −0.740 | 0.088 |
| Slope | 0.483 | 0.630 | −0.337 | 0.027 | 0.182 | 0.171 |
| Terrain relief | 0.604 | 0.528 | −0.286 | −0.042 | 0.227 | 0.075 |
| Vegetation cover type | −0.034 | −0.277 | −0.190 | 0.819 | 0.450 | −0.058 |
| Precipitation | −0.012 | 0.164 | 0.740 | 0.109 | 0.232 | 0.592 |
| Elevation | 0.865 | −0.086 | 0.112 | −0.084 | 0.000 | −0.147 |
| Model | AIC | AICc | BIC | AUC |
|---|---|---|---|---|
| PCAMGWR | 78,228.039 | 78,291.042 | 85,829.127 | 0.89773 |
| MGWR | 78,232.004 | 78,295.213 | 85,845.297 | 0.89771 |
| PCAGWR | 78,682.364 | 78,696.459 | 82,307.355 | 0.83198 |
| GWR | 78,785.304 | 78,794.218 | 81,672.072 | 0.81701 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Huang, S.; Li, J.; Huang, J.; Wang, W. Spatial Non-Stationarity-Based Landslide Susceptibility Assessment Using PCAMGWR Model. Water 2022, 14, 881. https://doi.org/10.3390/w14060881
Li Y, Huang S, Li J, Huang J, Wang W. Spatial Non-Stationarity-Based Landslide Susceptibility Assessment Using PCAMGWR Model. Water. 2022; 14(6):881. https://doi.org/10.3390/w14060881
Chicago/Turabian StyleLi, Yange, Shuangfei Huang, Jiaying Li, Jianling Huang, and Weidong Wang. 2022. "Spatial Non-Stationarity-Based Landslide Susceptibility Assessment Using PCAMGWR Model" Water 14, no. 6: 881. https://doi.org/10.3390/w14060881





