Predicting Daily Suspended Sediment Load Using Machine Learning and NARX Hydro-Climatic Inputs in Semi-Arid Environment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area Description
2.2. Datasets
2.2.1. Concentration of Suspended Solid Measurements
2.2.2. Rainfall and Runoff Measurements
2.3. Methodology
2.3.1. Machine Learning Models
Random Forest
AdaBoost
Support Vector Machine (SVM)
Artificial Neural Network (ANN)
k-Nearest Neighbor (k-NN)
2.3.2. NARX Input Method
2.3.3. Model Evaluation Metrics
- If GA = 1, model is perfect;
- If 0.75 ≤ GA < 1 or 1 < GA ≤ 1.35, the model is excellent;
- If 1.35 < GA ≤ 2 or 0.5 ≤ GA < 0.75, the model is good;
- If GA > 2 or GA < 0.5, the model is poor and considered unsuitable for simulation purposes.
3. Results
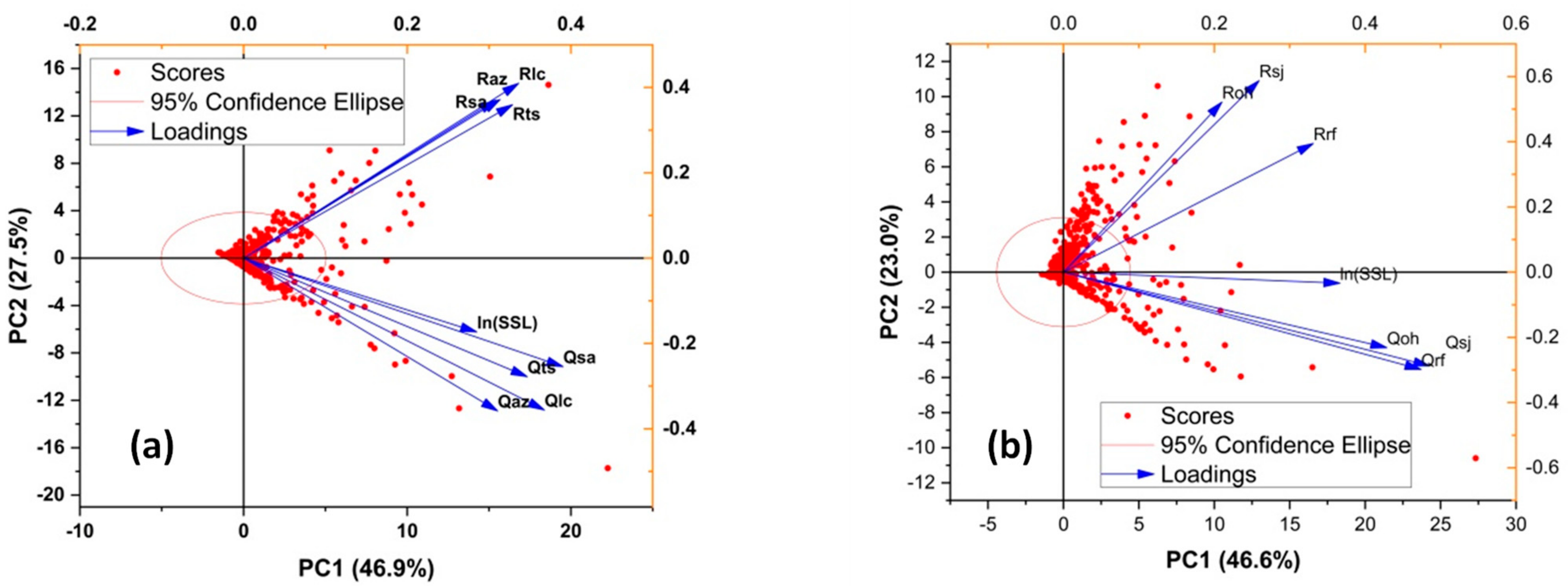
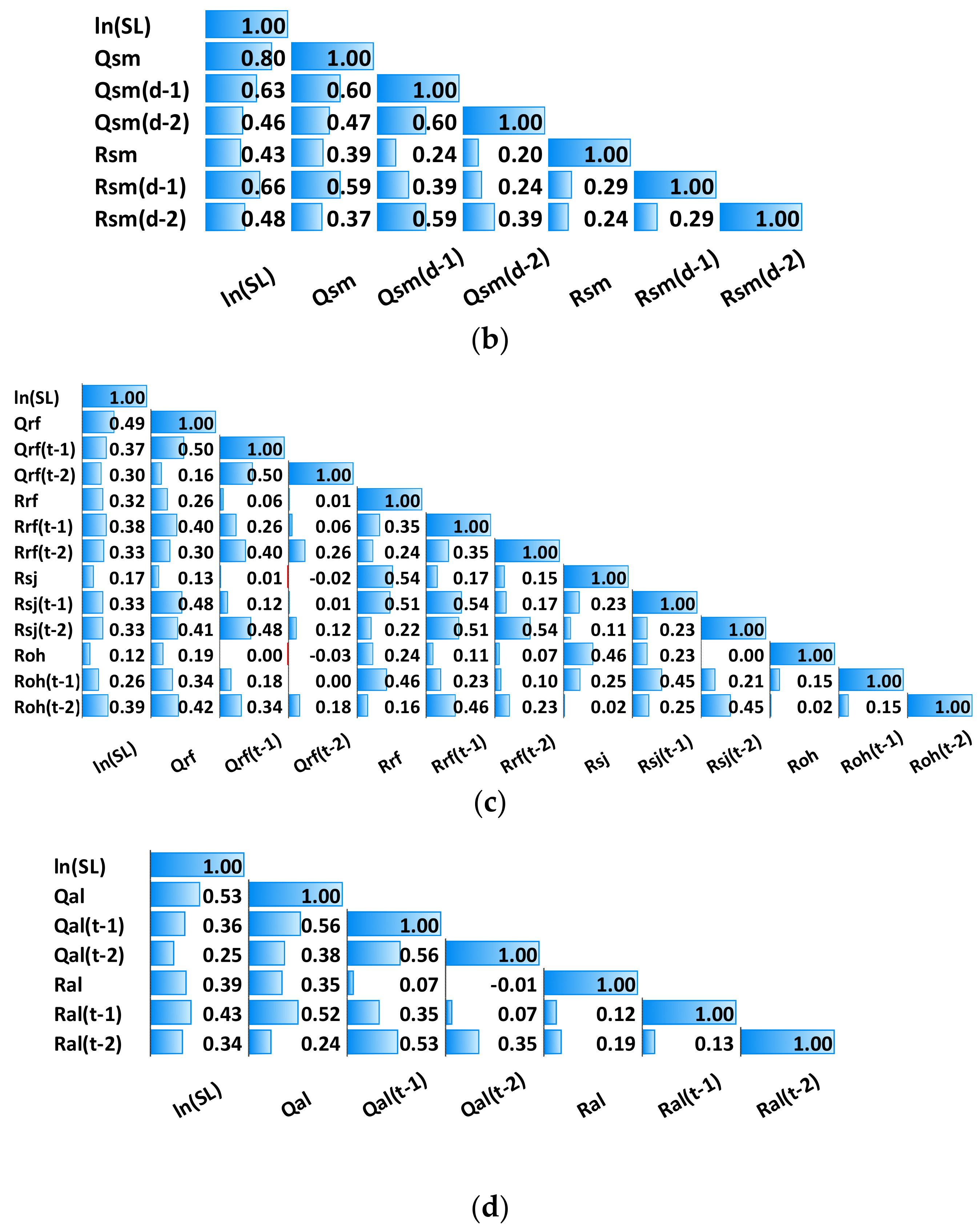
3.1. Exploratory Data Analysis (EDA)
3.2. Training Process of the Machine Learning Models
3.3. Validation of the ML Models
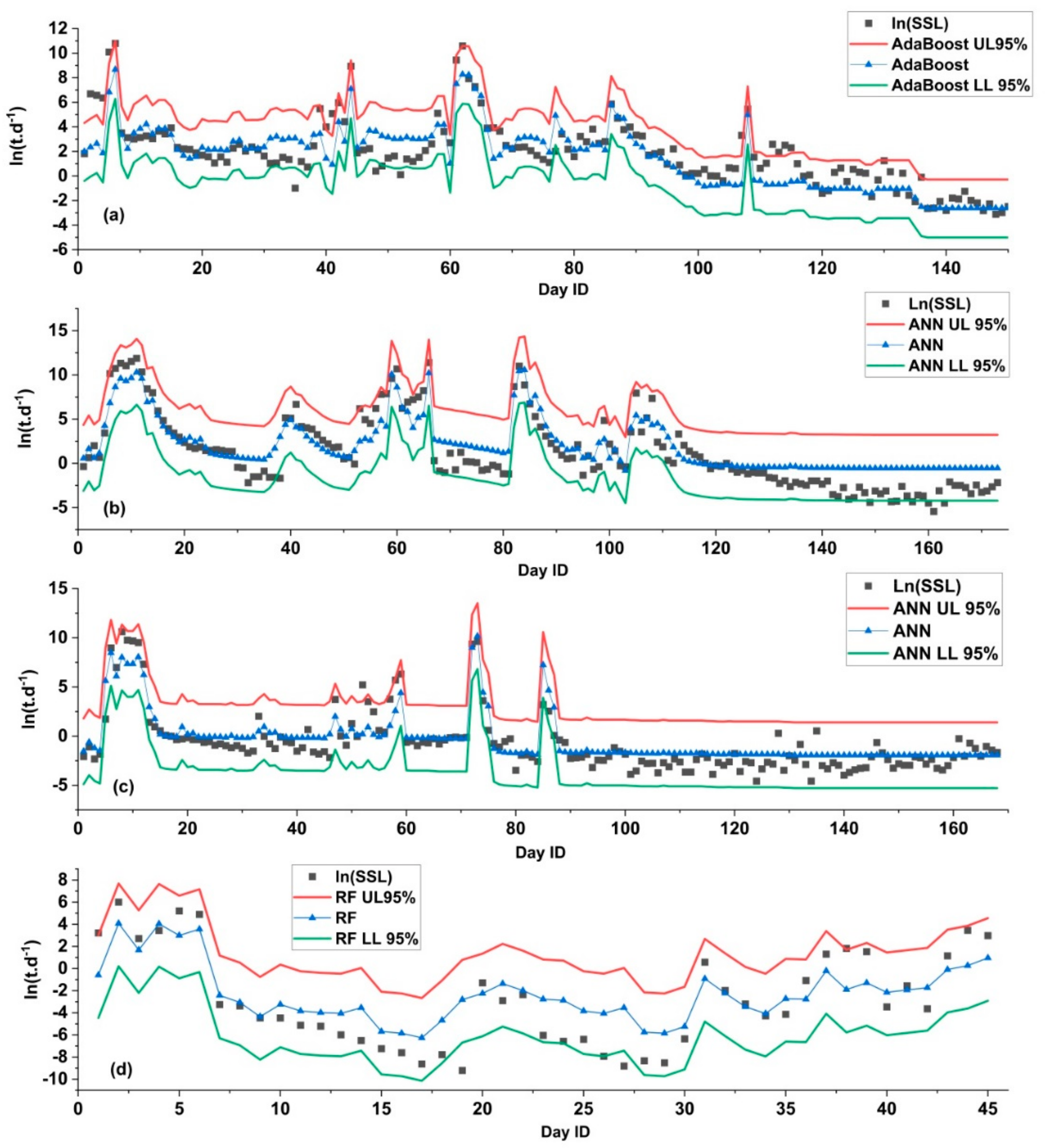
3.4. Generalization Ability and Uncertainties
4. Discussion
5. Conclusions
- Empowering machine learning by adopting the NARX hydro-climatic input variable method is valuable in the prediction of the daily suspended sediment load;
- The artificial neural network is accurate in simulating the SSL in two basins out of four, followed by AdaBoost and random forest models;
- The generalization ability metric demonstrated the stability of the applied models in predicting the SSL.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gibson, S.; Floyd, I.; Sánchez, A.; Heath, R. Comparing single-phase, non-Newtonian approaches with experimental results: Validating flume-scale mud and debris flow in HEC-RAS. Earth Surf. Process. Landf. 2021, 46, 540–553. [Google Scholar] [CrossRef]
- Pähtz, T.; Clark, A.H.; Valyrakis, M.; Durán, O. The Physics of Sediment Transport Initiation, Cessation, and Entrainment Across Aeolian and Fluvial Environments. Rev. Geophys. 2020, 58, e2019RG000679. [Google Scholar] [CrossRef]
- Van Kessel, T.; Blom, C. Rheology of cohesive sediments: Comparison between a natural and an artificial mud. J. Hydraul. Res. 1998, 36, 591–612. [Google Scholar] [CrossRef]
- Wang, H.; Zentar, R.; Wang, D. Rheological Characterization of Fine-Grained Sediments under Steady and Dynamic Condi-tions. Int. J. Geomech. 2022, 22, 4021260. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, W.; Han, S.; Sun, G. Influences of retrogressive erosion of reservoir on sedimentation of its downstream river channel—A case study on Sanmenxia Reservoir and the Lower Yellow River. Int. J. Sediment Res. 2017, 32, 373–383. [Google Scholar] [CrossRef]
- Česonienė, L.; Šileikienė, D.; Dapkienė, M. Relationship between the Water Quality Elements of Water Bodies and the Hydrometric Parameters: Case Study in Lithuania. Water 2020, 12, 500. [Google Scholar] [CrossRef] [Green Version]
- Ustaoglu, F.; Tepe, B. Water quality and sediment contamination assessment of Pazarsuyu Stream, Turkey using multivariate statistical methods and pollution indicators. Int. Soil Water Conserv. Res. 2019, 7, 47–56. [Google Scholar] [CrossRef]
- Wischmeier, W.H.; Smith, D.D. Predicting Rainfall-Erosion Losses from Cropland East of the Rocky Mountains: Guide for Selection of Practices for Soil and Water Conservation; US Department of Agriculture: Washington, DC, USA, 1965. [Google Scholar]
- Williams, J.R.; Berndt, H.D. Sediment Yield Prediction Based on Watershed Hydrology. Trans. ASAE 1977, 20, 1100–1104. [Google Scholar] [CrossRef]
- Renard, K.G.; Foster, G.R.; Weesies, G.A.; Porter, J.P. RUSLE: Revised universal soil loss equation. J. Soil Water Conserv. 1991, 46, 30–33. [Google Scholar]
- Sadeghi, S.; Gholami, L.; Darvishan, A.K.; Saeidi, P. A review of the application of the MUSLE model worldwide. Hydrol. Sci. J. 2014, 59, 365–375. [Google Scholar] [CrossRef] [Green Version]
- Bouguerra, H.; Bouanani, A.; Khanchoul, K.; Derdous, O.; Tachi, S.E. Mapping erosion prone areas in the Bouhamdane watershed (Algeria) using the Revised Universal Soil Loss Equation through GIS. J. Water Land Dev. 2017, 32, 13–23. [Google Scholar] [CrossRef]
- Bouguerra, S.; Jebari, S.; Tarhouni, J. An analysis of sediment production and control in Rmel river basin using InVEST sediment retention model. J. New Sci. 2019, 66, 4170–4181. [Google Scholar]
- El Bilali, A.; Taleb, A.; Brouziyne, Y. Comparing four machine learning model performances in forecasting the alluvial aquifer level in a semi-arid region. J. Afr. Earth Sci. 2021, 181, 104244. [Google Scholar] [CrossRef]
- El Bilali, A.; Taleb, A. Prediction of irrigation water quality parameters using machine learning models in a semi-arid environment. J. Saudi Soc. Agric. Sci. 2020, 19, 439–451. [Google Scholar] [CrossRef]
- el Bilali, A.; Abdeslam, T.; Mazigh, N.; Moukhliss, M. Prediction of chemical water quality used for drinking purposes based on artificial neural networks. Moroc. J. Chem. 2020, 3, 665–672. [Google Scholar]
- Chen, C.; He, W.; Zhou, H.; Xue, Y.; Zhu, M. A comparative study among machine learning and numerical models for simulating groundwater dynamics in the Heihe River Basin, northwestern China. Sci. Rep. 2020, 10, 3904. [Google Scholar] [CrossRef] [Green Version]
- Mohanty, S.; Jha, M.K.; Raul, S.K.; Panda, R.K.; Sudheer, K.P. Using Artificial Neural Network Approach for Simultaneous Forecasting of Weekly Groundwater Levels at Multiple Sites. Water Resour. Manag. 2015, 29, 5521–5532. [Google Scholar] [CrossRef]
- Khozani, Z.S.; Bonakdari, H.; Zaji, A.H. Estimating shear stress in a rectangular channel with rough boundaries using an optimized SVM method. Neural Comput. Appl. 2018, 30, 2555–2567. [Google Scholar] [CrossRef]
- Khozani, Z.S.; Safari, M.J.S.; Mehr, A.D.; Mohtar, W.H.M.W. An ensemble genetic programming approach to develop incipient sediment motion models in rectangular channels. J. Hydrol. 2020, 584, 124753. [Google Scholar] [CrossRef]
- Al Dahoul, N.; Essam, Y.; Kumar, P.; Ahmed, A.N.; Sherif, M.; Sefelnasr, A.; Elshafie, A. Suspended sediment load prediction using long short-term memory neural network. Sci. Rep. 2021, 11, 7826. [Google Scholar] [CrossRef]
- Nourani, V.; Gokcekus, H.; Gelete, G. Estimation of Suspended Sediment Load Using Artificial Intelligence-Based Ensemble Model. Complex 2021, 2021, 6633760. [Google Scholar] [CrossRef]
- Ampomah, R.; Hosseiny, H.; Zhang, L.; Smith, V.; Sample-Lord, K. A Regression-Based Prediction Model of Suspended Sediment Yield in the Cuyahoga River in Ohio Using Historical Satellite Images and Precipitation Data. Water 2020, 12, 881. [Google Scholar] [CrossRef] [Green Version]
- El Bilali, A.; Taleb, A.; Nafii, A.; Alabjah, B.; Mazigh, N. Prediction of sodium adsorption ratio and chloride concentration in a coastal aquifer under seawater intrusion using machine learning models. Environ. Technol. Innov. 2021, 23, 101641. [Google Scholar] [CrossRef]
- Alabjah, B.; Amraoui, F.; Chibout, M.M.; Slimani, M. Assessment of saltwater contamination extent in the coastal aquifers of Chaouia (Morocco) using the electric recognition. J. Hydrol. 2018, 566, 363–376. [Google Scholar] [CrossRef]
- El Bilali, A.; Taghi, Y.; Briouel, O.; Taleb, A.; Brouziyne, Y. A framework based on high-resolution imagery datasets and MCS for forecasting evaporation loss from small reservoirs in groundwater-based agriculture. Agric. Water Manag. 2021, 262, 107434. [Google Scholar] [CrossRef]
- Mazigh, N.; Taleb, A.; El Bilali, A.; Ballah, A. The Effect of Erosion Control Practices on the Vulnerability of Soil Degradation in Oued EL Malleh Catchment using the USLE Model Integrated into GIS, Morocco. Trends Sci. 2022, 19, 2059. [Google Scholar] [CrossRef]
- Ezzaouini, M.A.; Mahé, G.; Kacimi, I.; Zerouali, A. Comparison of the MUSLE Model and two years of Solid Transport Measurement, in the Bouregreg Basin, and Impact on the sedimentation in the Sidi Mohamed Ben Abdellah Reservoir, Morocco. Water 2020, 12, 1882. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Aggarwal, C.C. Data Mining; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: New York, NY, USA, 2006. [Google Scholar]
- Bonaccorso, G. Machine Learning Algorithms: Popular Algorithms for Data Science and Machine Learning; Packt Publishing Ltd.: Birmingham, UK, 2018. [Google Scholar]
- Freund, Y.; Schapire, R.E. A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef] [Green Version]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction; Springer Science & Business Media: New York, NY, USA, 2009. [Google Scholar]
- Kubat, M. An Introduction to Machine Learning; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Liaw, A.; Wiener, M. Classification and regression by randomForest. R News 2002, 2, 18–22. [Google Scholar]
- Oshiro, T.M.; Perez, P.S.; Baranauskas, J.A. How Many Trees in a Random Forest? In International Workshop on Machine Learning and Data Mining in Pattern Recognition; Springer: Berlin/Heidelberg, Germany, 2012; pp. 154–168. [Google Scholar] [CrossRef]
- Schapire, R.E. A brief introduction to boosting. Int. Jt. Conf. Artif. Intell. 1999, 2, 1401–1406. [Google Scholar]
- Freund, Y.; Schapire, R.E. Experiments with a New Boosting Algorithm. In Proceedings of the ICML ’96 13th International Conference on Machine Learning, Bari, Italy, 3–6 July 1996; pp. 148–156. [Google Scholar]
- EL Bilali, A.; Taleb, A.; Bahlaoui, M.A.; Brouziyne, Y. An integrated approach based on Gaussian noises-based data augmentation method and Ada, Boost model to predict faecal coliforms in rivers with small dataset. J. Hydrol. 2021, 599, 126510. [Google Scholar] [CrossRef]
- Vapnik, V.N. The Nature of Statistical Learning Theory, 2nd ed.; Springer: New York, NY, USA, 2000. [Google Scholar]
- Ghosh, S. SVM-PGSL coupled approach for statistical downscaling to predict rainfall from GCM output. J. Geophys. Res. Earth Surf. 2010, 115, D22. [Google Scholar] [CrossRef] [Green Version]
- Dawson, C.; Wilby, R. An artificial neural network approach to rainfall-runoff modelling. Hydrol. Sci. J. 1998, 43, 47–66. [Google Scholar] [CrossRef]
- Schalkoff, R.J. Artificial Neural Networks; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Yoon, H.; Jun, S.-C.; Hyun, Y.; Bae, G.-O.; Lee, K.-K. A comparative study of artificial neural networks and support vector machines for predicting groundwater levels in a coastal aquifer. J. Hydrol. 2011, 396, 128–138. [Google Scholar] [CrossRef]
- El Bilali, A.; Moukhliss, M.; Taleb, A.; Nafii, A.; Alabjah, B.; Brouziyne, Y.; Mazigh, N.; Teznine, K.; Mhamed, M. Predicting daily pore water pressure in embankment dam: Empowering Machine Learning-based modeling. Environ. Sci. Pollut. Res. 2022. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Wang, L.; Long, F.; Liao, W.; Liu, H. Prediction of anaerobic digestion performance and identification of critical operational parameters using machine learning algorithms. Bioresour. Technol. 2020, 298, 122495. [Google Scholar] [CrossRef]
- Adnan, R.M.; Liang, Z.; El-Shafie, A.; Zounemat-Kermani, M.; Kisi, O. Prediction of Suspended Sediment Load Using Data-Driven Models. Water 2019, 11, 2060. [Google Scholar] [CrossRef] [Green Version]
- Tadesse, A.; Dai, W. Prediction of sedimentation in reservoirs by combining catchment based model and stream based model with limited data. Int. J. Sediment Res. 2019, 34, 27–37. [Google Scholar] [CrossRef]
- Kondolf, G.M.; Gao, Y.; Annandale, G.W.; Morris, G.L.; Jiang, E.; Zhang, J.; Cao, Y.; Carling, P.; Fu, K.; Guo, Q.; et al. Sustainable sediment management in reservoirs and regulated rivers: Experiences from five continents. Earths Future 2014, 2, 256–280. [Google Scholar] [CrossRef]



| Name of Hydrological Station | River | Basin Area (km2) | N°IRE ABHBC Code | Period of Observation Considered | Number of CSS Sample | Mean Period (g/L) | Max Period (g/L) | Min Period (g/L) | Standard Deviation |
|---|---|---|---|---|---|---|---|---|---|
| Aguibat Ziar | Bouregreg | 3681 | 3118/13 | 1 September 2016 to 31 August 2021 | 1253 | 0.83 | 32.72 | 0.00 | 1.08 |
| Ras Fathia | Grou | 3485 | 989/20 | 1634 | 1.20 | 86.9 | 0.00 | 1.70 | |
| S.M. Cherif | Mechraa | 656 | 2673/20 | 1662 | 0.63 | 16.89 | 0.00 | 0.76 | |
| Ain Loudah | Korifla | 699 | 2674/21 | 470 | 1.05 | 24.7 | 0.00 | 1.47 |
| Name of Sub-Basin | Rainfall Station | N°IRE Code | Mean (mm) | Max (mm) | Min (mm) | Standard Deviation |
|---|---|---|---|---|---|---|
| Bouregreg basin at Aguibat Ziar | Aguibat Ziar | 3118/13 | 1.3 | 122.5 | 0.0 | 2.23 |
| Lalla Chafia | 0.9 | 42.9 | 0.0 | 1.64 | ||
| Sidi Amar | 1.1 | 50.0 | 0.0 | 1.94 | ||
| Tslat | 1.3 | 60.0 | 0.0 | 2.11 | ||
| Grou at Ras Fathia | Ras Fathia | 989/20 | 1.0 | 41.2 | 0.0 | 1.81 |
| Sidi Jabeur | 0.8 | 44.5 | 0.0 | 1.50 | ||
| Ouljat Haboub | 0.8 | 39.8 | 0.0 | 1.38 | ||
| Korefla basin at Ain Loudah | Ain Loudah | 2674/21 | 0.9 | 59.6 | 0.0 | 1.57 |
| Korefla basin at S.M. Cherif | S.M. Cherif | 2673/20 | 0.9 | 54.7 | 0.0 | 1.56 |
| Name of Sub-Basin | Rainfall Station | N°IRE Code | Mean (m3/s) | Max (m3/s) | Min (m3/s) | Standard Deviation |
|---|---|---|---|---|---|---|
| Bouregreg basin at Aguibat Ziar | Aguibat Ziar | 3118/13 | 4.16 | 199.04 | 0.00 | 5.64 |
| Lalla Chafia | 3.06 | 196.70 | 0.00 | 4.85 | ||
| Sidi Amar | 0.48 | 24.04 | 0.00 | 0.61 | ||
| Tslat | 0.81 | 23.50 | 0.00 | 1.04 | ||
| Grou at Ras Fathia | Ras Fathia | 989/20 | 4.58 | 349.21 | 0.00 | 6.59 |
| Sidi Jabeur | 3.74 | 326.54 | 0.00 | 5.29 | ||
| Ouljat Haboub | 3.52 | 262.37 | 0.00 | 5.43 | ||
| Korefla basin at Ain Loudah | Ain Loudah | 2674/21 | 0.52 | 48.83 | 0.00 | 0.88 |
| Korefla basin at S.M. Cherif | S.M. Cherif | 2673/20 | 0.42 | 38.58 | 0.00 | 0.62 |
| Model | Parameters/Functions/Algorithm |
|---|---|
| RF | 50 Trees |
| AdaBoost | Loss function: exponential |
| learning rate: 0.5 | |
| Estimator number: 250 | |
| SVR | C = 350 |
| Kernel function: RBF (γ = 1.3) | |
| -function loss, | |
| k-NN | k = 5 |
| Distance function: Euclidian | |
| ANN | 3 layers |
| 12 neurons in hidden layer | |
| Algorithm: Levenberg | |
| Function activation: Sigmoid | |
| Identity in output layer | |
| Epoch number: 1000 | |
| Learning rate: 0.01 | |
| Momentum coefficient: 0.85 |
| Models | r | RMSE | NSE | |
|---|---|---|---|---|
| ML | Musle_Calibrated | |||
| Aguibat Ziar | ||||
| Random Forest | 0.92 | 1.18 | 0.84 | |
| AdaBoost | 0.92 | 1.20 | 0.84 | |
| SVM | 0.76 | 1.95 | 0.57 | 0.46 |
| kNN | 0.88 | 1.49 | 0.75 | |
| Neural Network | 0.79 | 1.83 | 0.62 | |
| Ras Fathia | ||||
| Random Forest | 0.89 | 1.50 | 0.80 | |
| AdaBoost | 0.89 | 1.54 | 0.78 | |
| SVM | 0.78 | 2.08 | 0.61 | 0.02 |
| kNN | 0.85 | 1.83 | 0.70 | |
| Neural Network | 0.82 | 1.90 | 0.67 | |
| SM Cherif | ||||
| Random Forest | 0.79 | 1.62 | 0.62 | |
| AdaBoost | 0.76 | 1.74 | 0.56 | |
| SVM | 0.73 | 1.79 | 0.54 | 0.47 |
| kNN | 0.68 | 2.01 | 0.41 | |
| Neural Network | 0.76 | 1.70 | 0.58 | |
| Ain Loudah | ||||
| Random Forest | 0.87 | 1.91 | 0.76 | |
| AdaBoost | 0.84 | 2.13 | 0.70 | |
| SVM | 0.81 | 2.26 | 0.66 | 0.30 |
| kNN | 0.83 | 2.26 | 0.66 | |
| Neural Network | 0.84 | 2.12 | 0.70 | |
| Models | r | RMSEln (t·d−1) | NSE |
|---|---|---|---|
| Aguibat Ziar | |||
| RF | 0.84 | 1.52 | 0.68 |
| AdaBoost | 0.84 | 1.51 | 0.68 |
| SVM | 0.79 | 1.68 | 0.61 |
| kNN | 0.78 | 1.81 | 0.55 |
| ANN | 0.80 | 1.61 | 0.64 |
| Ras Fathia | |||
| RF | 0.90 | 2.27 | 0.70 |
| AdaBoost | 0.88 | 2.38 | 0.67 |
| SVM | 0.90 | 2.35 | 0.68 |
| kNN | 0.82 | 2.56 | 0.62 |
| ANN | 0.92 | 1.99 | 0.77 |
| SM Cherif | |||
| RF | 0.86 | 1.53 | 0.74 |
| AdaBoost | 0.84 | 1.66 | 0.69 |
| SVM | 0.85 | 1.69 | 0.69 |
| kNN | 0.82 | 1.75 | 0.66 |
| ANN | 0.91 | 1.34 | 0.80 |
| Ain Loudah | |||
| RF | 0.90 | 2.60 | 0.64 |
| AdaBoost | 0.84 | 2.76 | 0.61 |
| SVM | 0.84 | 2.96 | 0.55 |
| kNN | 0.78 | 3.19 | 0.47 |
| ANN | 0.86 | 2.72 | 0.61 |
| Basin | RF | AdaBoost | SVM | kNN | ANN | |
|---|---|---|---|---|---|---|
| GA | 1.29 | 1.26 | 0.86 | 1.21 | 0.88 | |
| Aguibat Ziar | LL 95% | −2.88 | −2.93 | −3.71 | −3.88 | −3.50 |
| UL 95% | 2.73 | 2.80 | 3.78 | 2.87 | 3.71 | |
| GA | 1.52 | 1.54 | 1.13 | 1.40 | 1.04 | |
| Ras Fathia | LL 95% | −3.02 | −3.05 | −4.11 | −3.92 | −3.68 |
| UL 95% | 2.85 | 3.00 | 4.03 | 3.02 | 3.78 | |
| GA | 0.94 | 0.96 | 0.94 | 0.87 | 0.79 | |
| SM Cherif | LL 95% | −3.22 | −3.20 | −3.55 | −4.35 | −3.35 |
| UL 95% | 3.14 | 3.57 | 3.45 | 3.26 | 3.33 | |
| GA | 1.36 | 1.30 | 1.31 | 1.41 | 1.28 | |
| Ain Loudah | LL 95% | −3.88 | −4.26 | −4.47 | −4.89 | −4.18 |
| UL 95% | 3.59 | 4.08 | 4.41 | 3.65 | 4.16 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezzaouini, M.A.; Mahé, G.; Kacimi, I.; El Bilali, A.; Zerouali, A.; Nafii, A. Predicting Daily Suspended Sediment Load Using Machine Learning and NARX Hydro-Climatic Inputs in Semi-Arid Environment. Water 2022, 14, 862. https://doi.org/10.3390/w14060862
Ezzaouini MA, Mahé G, Kacimi I, El Bilali A, Zerouali A, Nafii A. Predicting Daily Suspended Sediment Load Using Machine Learning and NARX Hydro-Climatic Inputs in Semi-Arid Environment. Water. 2022; 14(6):862. https://doi.org/10.3390/w14060862
Chicago/Turabian StyleEzzaouini, Mohamed Abdellah, Gil Mahé, Ilias Kacimi, Ali El Bilali, Abdelaziz Zerouali, and Ayoub Nafii. 2022. "Predicting Daily Suspended Sediment Load Using Machine Learning and NARX Hydro-Climatic Inputs in Semi-Arid Environment" Water 14, no. 6: 862. https://doi.org/10.3390/w14060862







