Study on the SBA-15 Silica and ETS-10 Titanosilicate as Efficient Adsorbents for Cu(II) Removal from Aqueous Solution
Abstract
:1. Introduction
2. Materials and Methods
Sorption Experiments
3. Results and Discussion
3.1. pH Effect on the Adsorption Process
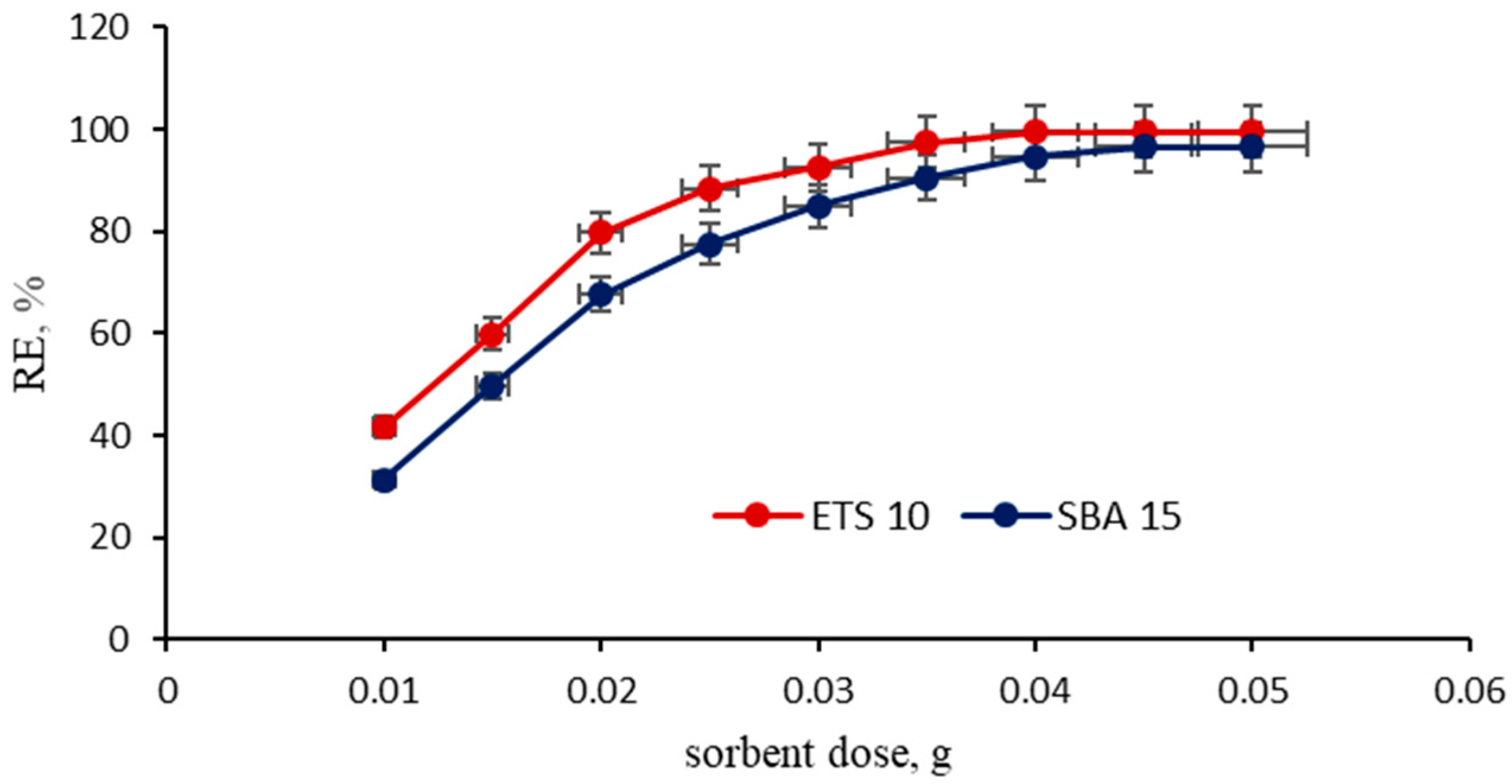
3.2. Effect of Adsorbent Dosage
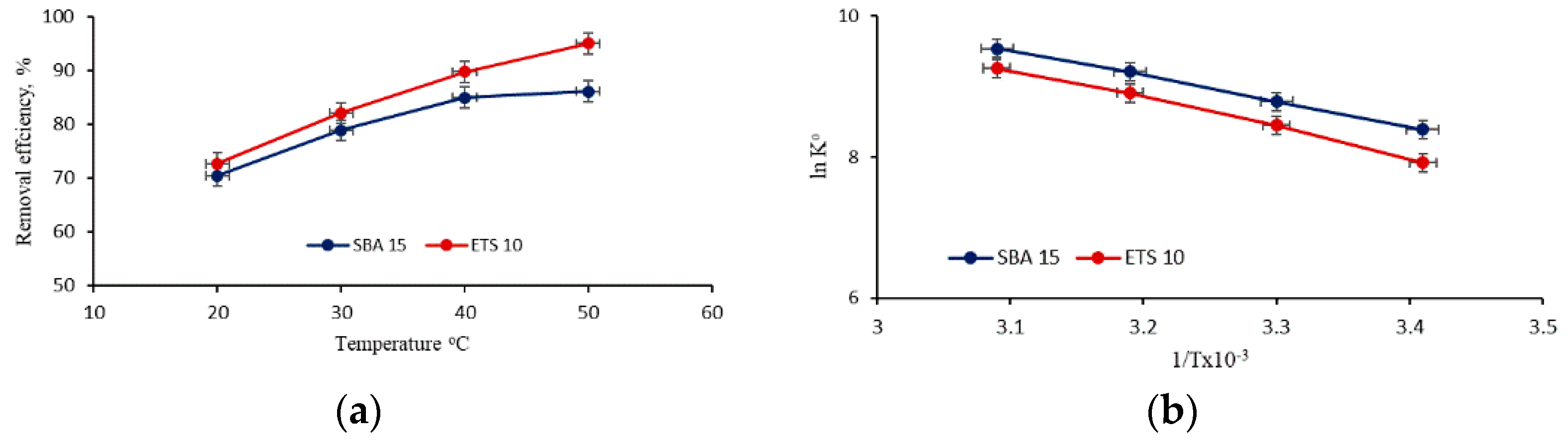
3.3. Equilibrium Isotherm, Kinetics and Thermodynamic Studies
3.3.1. Adsorption Equilibrium Isotherm
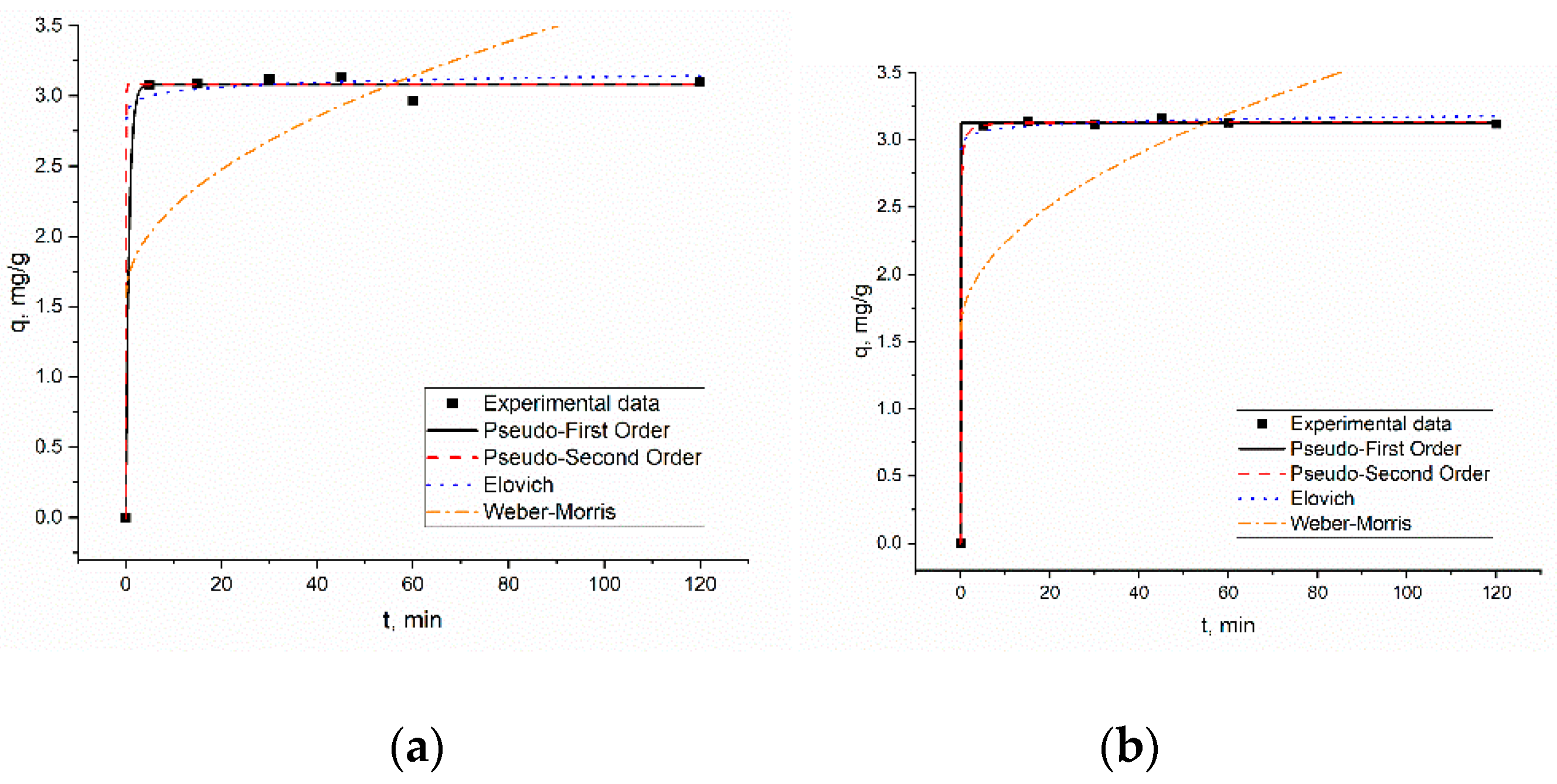
3.3.2. Adsorption Kinetics
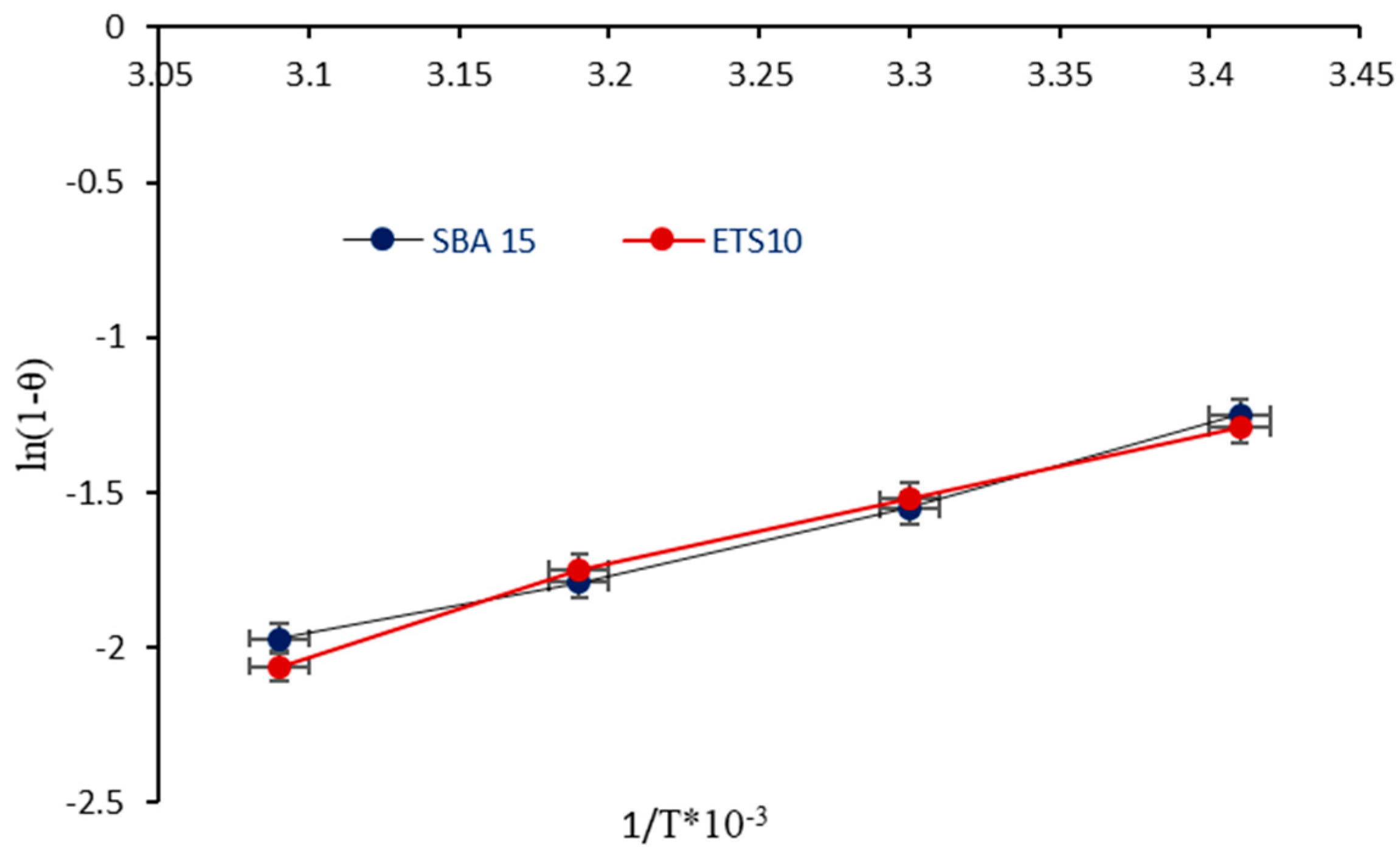
3.3.3. Thermodynamic Parameters
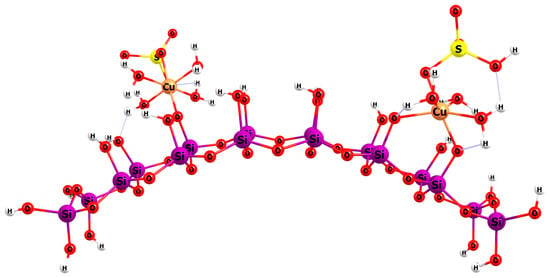
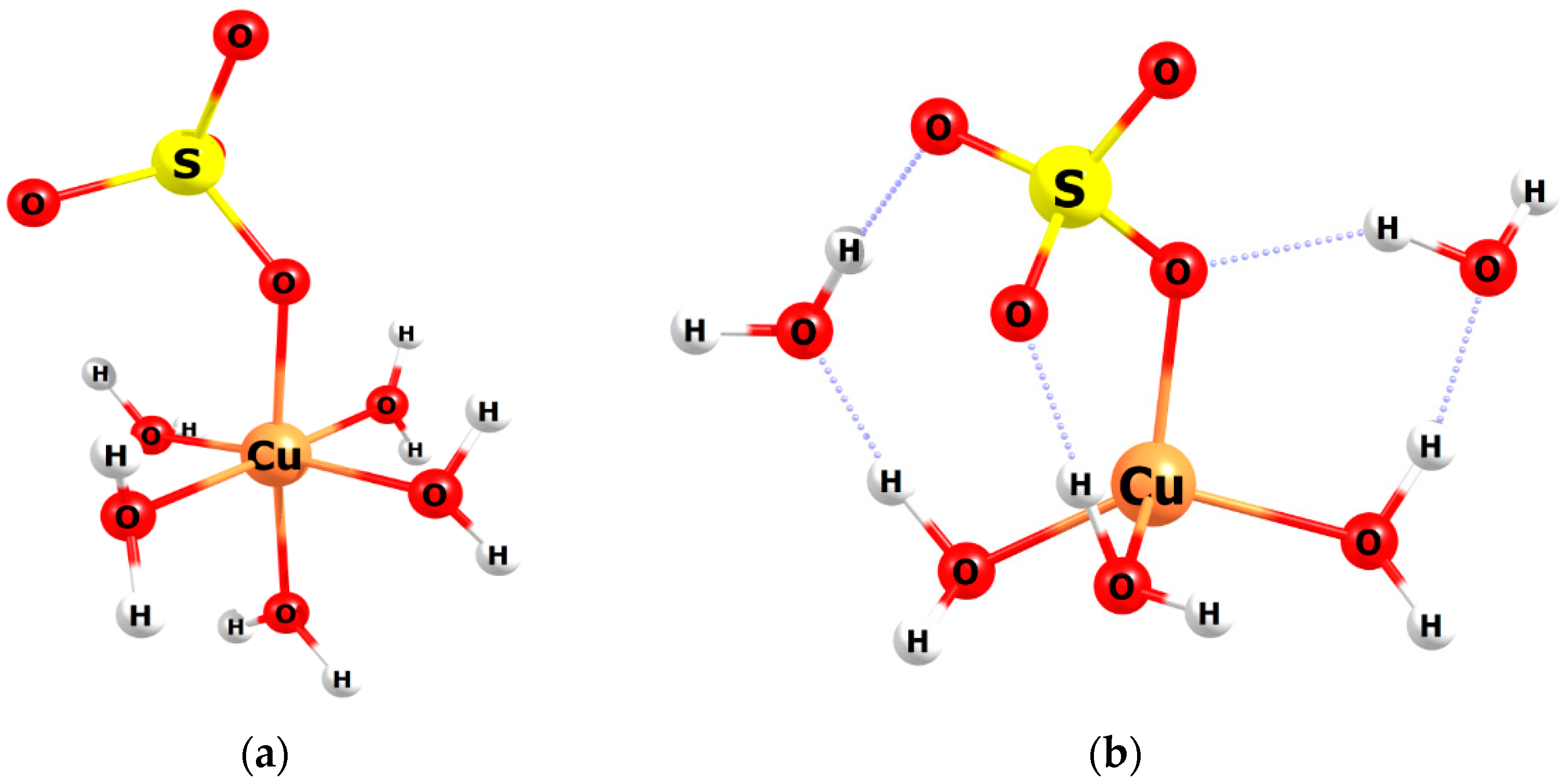
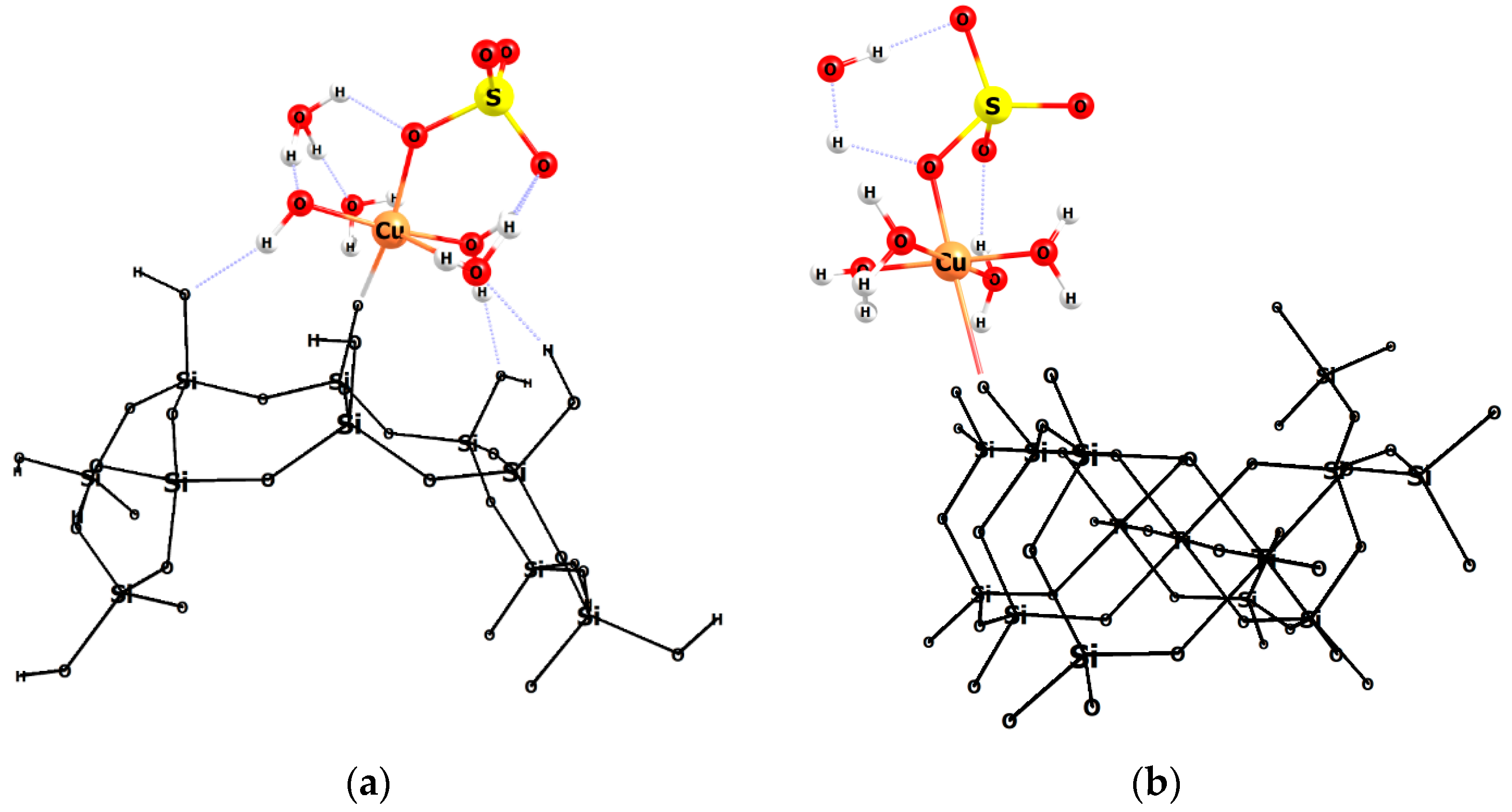
3.4. Modelling of the Interactions
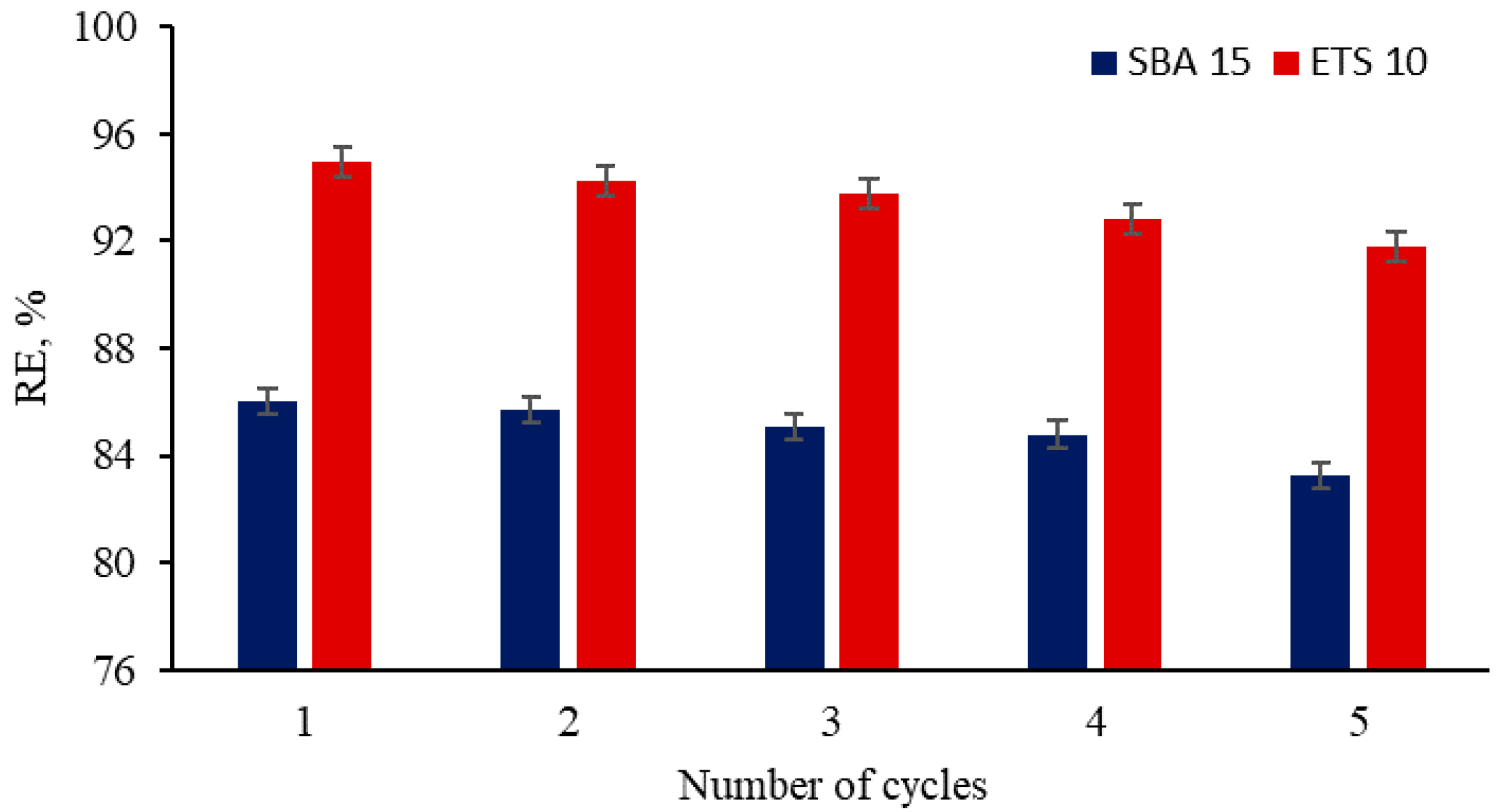
4. Regeneration and Reusability of Sorbents
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Anastopoulos, I.; Massas, I.; Ehaliotis, C. Use of residues and by-products of the olive-oil production chain for the removal of pollutants from environmental media: A review of batch biosorption approaches. J. Environ. Sci. Health Part A Toxic/Hazard. Subst. Environ. Eng. 2015, 50, 677–718. [Google Scholar] [CrossRef] [PubMed]
- González, A.G.; Pokrovsky, S.O.; Santana-Casiano, J.M.; González-Dávila, M. Bioadsorption of heavy metals. In Prospects and Challenges in Algal Biotechnology; Tripathi, B., Kumar, D., Eds.; Springer: Singapore, 2017; pp. 233–255. [Google Scholar] [CrossRef]
- Peng, Q.; Liu, Y.; Zeng, G.; Xu, W.; Yang, C.; Zhang, J. Biosorption of copper(II) by immobilizing Saccharomyces cerevisiae on the surface of chitosan-coated magnetic nanoparticles from aqueous solution. J. Hazard. Mater. 2010, 177, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Ofomaja, A.E.; Naidoo, E.B.; Modise, S.J. Biosorption of copper(II) and lead(II) onto potassium hydroxide treated pine cone powder. J. Environ. Manag. 2010, 91, 1674. [Google Scholar] [CrossRef] [PubMed]
- Moyo, M.; Chirinda, A.; Nharingo, T. Removal of copper from aqueous solution using chemically treated potato (Solanum tuberosum) leaf powder. Clean Soil Air Water 2016, 44, 488–495. [Google Scholar] [CrossRef]
- Ekere, N.R.; Agwogie, A.B.; Ihedioha, J.N. Studies of biosorption of Pb2+, Cd2+ and Cu2+ from aqueous solutions using Adansonia digitata root powders. Int. J. Phytoremediat. 2016, 18, 116–125. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, Y.; Shi, H.; Peng, Y.; Fan, X.; Li, C. The molecular mechanisms of copper metabolism and its roles in human diseases. Pflügers Arch. Eur. J. Physiol. 2020, 472, 1415–1429. [Google Scholar] [CrossRef]
- Montazeri, A.; Akhlaghi, M.; Barahimi, A.R.; Jahanbazi Jahan Abad, A.; Jabbari, R. The Role of Metals in Neurodegenerative Diseases of the Central Nervous System. Shefaye Khatam. 2020, 8, 130–146. [Google Scholar] [CrossRef]
- Mathys, Z.; White, A. Copper and Alzheimer’s Disease. Adv. Neurobiol. 2017, 18, 199–216. [Google Scholar] [CrossRef]
- Lundström, M.; Liipo, J.; Taskinen, P.; Aromaa, J. Copper precipitation during leaching of various copper sulfide concentrates with cupric chloride in acidic solutions. Hydrometallurgy 2016, 166, 136–142. [Google Scholar] [CrossRef]
- Labidi, A.; Salaberria, A.M.; Fernandes, S.C.M.; Labidi, J.; Abderrabba, M. Adsorption of copper on chitin-based materials: Kinetic and thermodynamic studies. J. Taiwan Inst. Chem. Eng. 2016, 65, 140–148. [Google Scholar] [CrossRef]
- Mushtaq, M.; Bhatti, H.N.; Iqbal, M.; Noreen, S. Eriobotrya japonica seed biocomposite efficiency for copper adsorption: Isotherms, kinetics, thermodynamic and desorption studies. J. Environ. Manag. 2016, 176, 21–33. [Google Scholar] [CrossRef]
- Abdelfattah, I.; Ismail, A.A.; Sayed, F.A.; Almedolab, A.; Aboelghait, K.M. Biosorption of heavy metals ions in real industrial wastewater using peanut husk as efficient and cost effective adsorbent. Environ. Nanotechnol. Monit. Manag. 2016, 6, 176–183. [Google Scholar] [CrossRef]
- Duan, H.; Wang, S.; Yang, X.; Yuan, X.; Zhang, Q.; Huang, Z.; Guo, H. Simultaneous separation of copper from nickel in ammoniacal solutions using supported liquid membrane containing synergistic mixture of M5640 and TRPO. Chem. Eng. Res. Des. 2017, 117, 460–471. [Google Scholar] [CrossRef]
- Ntagia, E.; Rodenas, P.; Ter Heijne, A.; Buisman, C.J.N.; Sleutels, T.H.J.A. Hydrogen as electron donor for copper removal in bioelectrochemical systems. Int. J. Hydrog. Energy 2016, 41, 5758–5764. [Google Scholar] [CrossRef] [Green Version]
- Ntimbani, R.N.; Simate, G.S.; Ndlovu, S. Removal of copper ions from dilute synthetic solution using staple ion exchange fibres: Dynamic studies. J. Environ. Chem. Eng. 2016, 4, 3143–3150. [Google Scholar] [CrossRef]
- Lambert, A.; Drogui, P.; Daghrir, R.; Zaviska, F.; Benzaazoua, M. Removal of copper in leachate from mining residues using electrochemical technology. J. Environ. Manag. 2014, 133, 78–85. [Google Scholar] [CrossRef]
- Ahluwalia, S.S.; Goyal, D. Removal of heavy metals by waste tea-leaves from aqueous solution. Eng. Life Sci. 2005, 5, 158–162. [Google Scholar] [CrossRef]
- Awual, M.R.; Hasan, M.M.; Khaleque, M.A.; Sheikh, M.C. Treatment of copper(II) containing wastewater by a newly developed ligand based facial conjugate materials. Chem. Eng. J. 2016, 288, 368–376. [Google Scholar] [CrossRef]
- Holub, M.; Balintova, M.; Kovacova, Z. Evaluation of Zeolite Adsorption Properties for Cu(II) Removal from Acidic Aqueous Solutions in Fixed-Bed Column System. Proceedings 2018, 2, 1293. [Google Scholar] [CrossRef]
- Xiao, F.; Cheng, J.; Cao, W.; Yang, C.; Chen, J.; Luo, Z. Removal of heavy metals from aqueous solution using chitosan—Combined magnetic biochars. J. Colloid. Interface. Sci. 2019, 540, 579–584. [Google Scholar] [CrossRef]
- Hussain, S.T.; Khaleefa Ali, S.A. Removal of heavy metal by ion exchange using bentonite clay. J. Ecol. Eng. 2021, 22, 104–111. [Google Scholar] [CrossRef]
- Ali, I.; Burakov, A.E.; Melezhik, A.V.; Babkin, A.V.; Burakova, I.V.; Neskomornaya, M.E.A.; Galunin, E.V.; Tkachev, A.G.; Kuznetsov, D.V. Removal of Copper(II) and Zinc(II) Ions in Water on a Newly Synthesized Polyhydroquinone/Graphene Nanocomposite Material: Kinetics, Thermodynamics and Mechanism. ChemistrySelect 2019, 4, 12708–12718. [Google Scholar] [CrossRef]
- Wang, Z.; Xu, W.; Jie, F.; Zhao, Z.; Zhou, K.; Liu, H. The selective adsorption performance and mechanism of multiwall magnetic carbon nanotubes for heavy metals in wastewater. Sci. Rep. 2021, 11, 16878. [Google Scholar] [CrossRef] [PubMed]
- De Luca, P.; Bernaudo, I.; Elliani, R.; Tagarelli, A.; Nagy, J.; Macario, A. Industrial Waste Treatment by ETS-10 Ion Exchanger Material. Materials 2018, 11, 2316. [Google Scholar] [CrossRef] [Green Version]
- Lv, L.; Su, F.; Zhao, X.S. Microporous titanosilicate ETS-10 for the removal of divalent heavy metals. Stud. Surf. Sci. Catal. 2005, 156, 933–940. [Google Scholar] [CrossRef]
- De Luca, P.; Poulsen, T.G.; Salituro, A.; Tedeschi, A.; Vuono, D.; Kònya, Z.; Madaràsz, D.; Nagy, J.B. Evaluation and comparison of the ammonia adsorption capacity of titanosilicates ETS-4 and ETS-10 and aluminotitanosilicates ETAS-4 and ETAS-10. J. Therm. Anal. Calorim. 2015, 122, 1257–1267. [Google Scholar] [CrossRef]
- De Luca, P.; Chiodo, A.; Nagy, J.B. Activated ceramic materials with deposition of photocatalytic titano-silicate micro-crystals. Sustain. Chem. 2011, 154, 155–165. [Google Scholar] [CrossRef] [Green Version]
- Awual, M.R.; Rahman, I.M.M.; Yaita, T.; Khaleque, M.A.; Ferdows, M. pH dependent Cu(II) and Pd(II) ions detection and removal from aqueous media by an efficient mesoporous adsorbent. Chem. Eng. J. 2014, 236, 100–109. [Google Scholar] [CrossRef]
- Zinicovscaia, I.; Yushin, N.; Humelnicu, D.; Grozdov, D.; Ignat, M.; Demcak, S.; Humelnicu, I. Sorption of Ce(III) by silica SBA-15 and titanosilicate ETS-10 from aqueous solution. Water 2021, 13, 3263. [Google Scholar] [CrossRef]
- Langmuir, I. The adsorption of gases on plane surfaces of glass, mica and platinum. J. Am. Chem. Soc. 1918, 143, 1361–1403. [Google Scholar] [CrossRef] [Green Version]
- Freundlich, H.M.F. Over the adsorption in solution. J. Phys. Chem. 1906, 57, 385–471. [Google Scholar]
- Temkin, M. Adsorption equilibrium and the kinetics of processes on non-homogeneous surfaces and in the interaction between adsorbed molecules. Zh. Fiz. Chim. 1941, 15, 296–332. [Google Scholar]
- Hall, K.R.; Eagleton, L.C.; Acrivos, A.; Vermeulen, T. Pore- and Solid-Diffusion Kinetics in Fixed-Bed Adsorption under Constant-Pattern Conditions. Ind. Eng. Chem. 1966, 5, 212–223. [Google Scholar] [CrossRef]
- Ho, Y.S.; Huang, C.T.; Huang, H.W. Equilibrium sorption isotherm for metal ions on tree fern. Process Biochem. 2002, 37, 1421–1430. [Google Scholar] [CrossRef]
- Keskinkan, O.; Göksu, M.Z.L.; Yüceer, A.; Basıbüyük, M.; Forster, C.F. Heavy metal adsorption characteristics of a submerged aquatic plant (Myriophylum spicatum). Process Biochem. 2003, 39, 179–183. [Google Scholar] [CrossRef]
- Özer, A.; Özer, D.; Özer, A. The adsorption of copper(II) ions on to dehydrated wheat bran (DWB):determination of the equilibrium and thermodynamic parameters. Process Biochem. 2004, 39, 2183–2191. [Google Scholar] [CrossRef]
- Liu, X.; Chen, Z.-Q.; Han, B.; Su, C.-L.; Han, Q.; Chen, W.-Z. Biosorption of copper ions from aqueous solution using rape straw powders: Optimization, equilibrium and kinetic studies. Ecotoxicol. Environ. Saf. 2018, 150, 251–259. [Google Scholar] [CrossRef]
- Witek-Krowiak, A. Analysis of temperature-dependent biosorption of Cu2+ ions on sunflower hulls: Kinetics, equilibrium and mechanism of the process. Chem. Eng. J. 2012, 192, 13–20. [Google Scholar] [CrossRef]
- Dinu, M.V.; Dinu, I.A.; Lazar, M.M.; Dragan, E.S. Chitosan-based ion-imprinted cryo-composites with excellent selectivity for copper ions. Carbohydr. Polym. 2018, 186, 140–149. [Google Scholar] [CrossRef]
- Reddy, K.H.D.; Seshaiaha, K.; Reddy, A.V.R.; Lee, S.M. Optimization of Cd(II), Cu(II) and Ni(II) biosorption by chemically modified Moringa oleifera leaves powder. Carbohydr. Polym. 2012, 88, 1077–1086. [Google Scholar] [CrossRef]
- Putra, W.P.; Kamari, A.; Yusoff, S.N.M.; Fauziah Ishak, C.; Mohamed, A.; Hashim, N.; Md Isa, I. Biosorption of Cu(II), Pb(II) and Zn(II) Ions from Aqueous Solutions Using Selected Waste Materials: Adsorption and Characterisation Studies. J. Encapsulation Adsorpt. Sci. 2014, 4, 25–35. [Google Scholar] [CrossRef] [Green Version]
- Bazargan-Lari, R.; Zafarani, H.R.; Bahrololoom, M.E.; Nemati, A. Removal of Cu(II) ions from aqueous solutions by low-cost natural hydroxyapatite/chitosan composite: Equilibrium, kinetic and thermodynamic studies. J. Taiwan Inst. Chem. Eng. 2014, 45, 1642–1648. [Google Scholar] [CrossRef]
- Laus, R.; Costa, T.G.; Szpoganicz, B.; Favere, V.T. Adsorption and desorption of Cu(II), Cd(II) and Pb(II) ions using chitosan crosslinked with epichlorohydrin-triphosphate as the adsorbent. J. Hazard. Mater. 2010, 183, 233–241. [Google Scholar] [CrossRef]
- Langergren, S. About the theory of so-called adsorption of soluble substance. Kung. Sven. Veten Hand. 1898, 24, 1–39. [Google Scholar]
- Ho, Y.S.; Mckay, G. Pseudo-second order model for sorption processes. Process Biochem. 1999, 34, 451–465. [Google Scholar] [CrossRef]
- Weber, W.J.; Morris, J.C. Kinetics of adsorption on carbon from solution. ASCE Sanit. Eng. Div. J. 1963, 89, 31–39. [Google Scholar] [CrossRef]
- Juang, R.S.; Chen, M.L. Application of the Elovich equation to the kinetics of metal sorption with solvent-impregnated resins. Ind. Eng. Chem. Res. 1997, 36, 813–820. [Google Scholar] [CrossRef]
- Guo, Z.; Liu, X.; Huang, H. Kinetics and thermodynamics of reserpine adsorption onto strong acidic cationic exchange fiber. PLoS ONE 2015, 10, e0138619. [Google Scholar] [CrossRef] [Green Version]
- Kumar, A.; Rout, S.; Ghosh, M.; Singhal, R.K.; Ravi, P.M. Thermodynamic parameters of U (VI) sorption onto soils in aquatic systems. SpringerPlus 2013, 2, 530. [Google Scholar] [CrossRef] [Green Version]
- Lütke, S.F.; Igansi, A.V.; Pegoraro, L.; Dotto, G.L.; Pinto, L.L.A.; Cadaval, T.R.S. Preparation of activated carbon from black wattle bark waste and its application for phenol adsorption. J. Environ. Chem. Eng. 2019, 7, 103396. [Google Scholar] [CrossRef]
- Sundaram, C.S.; Viswanathan, N.; Meenakshi, S. Defluoridation chemistry of synthetic hydroxyapatite at nano scale: Equilibrium and kinetic studies. J. Hazard. Mater. 2008, 155, 206–215. [Google Scholar] [CrossRef] [PubMed]

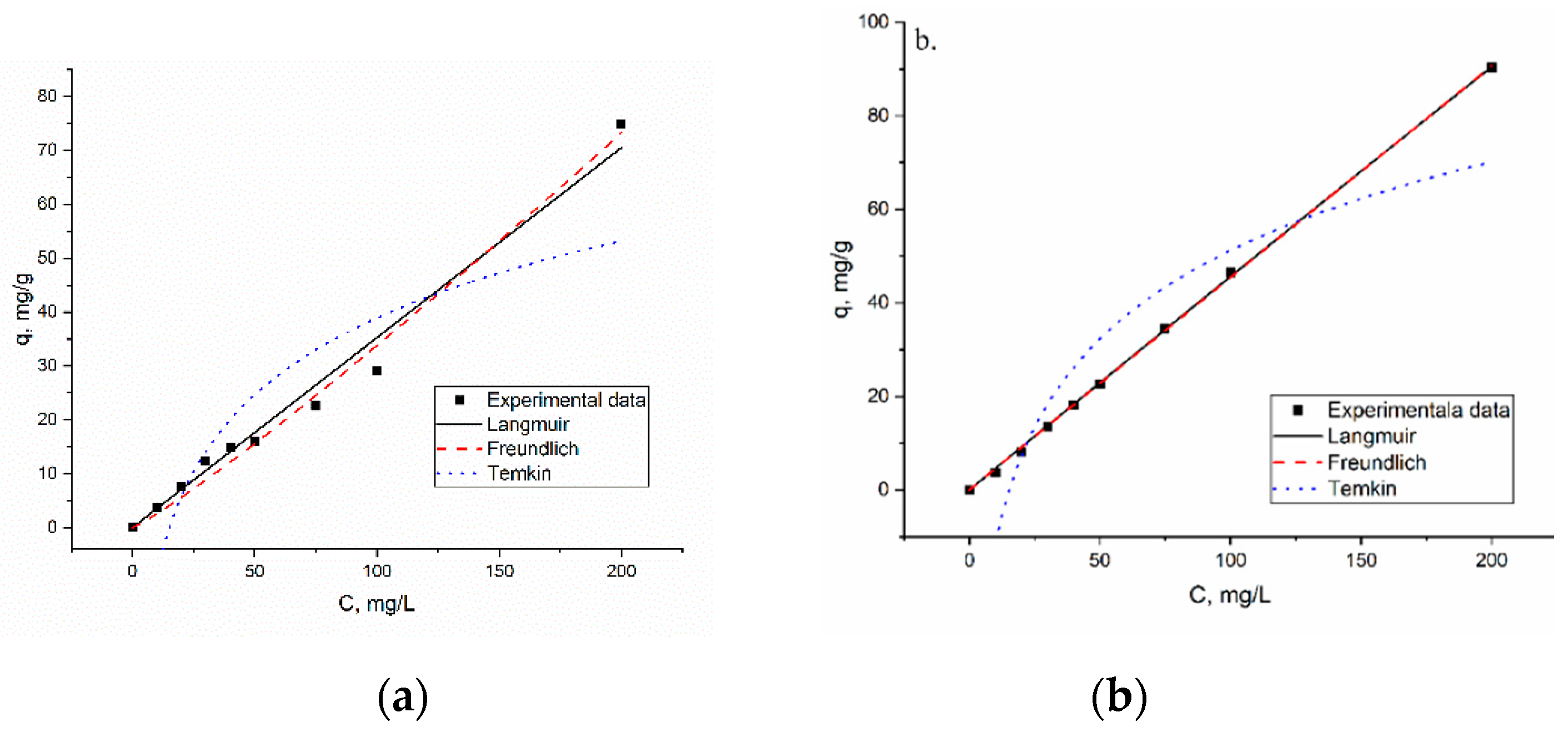
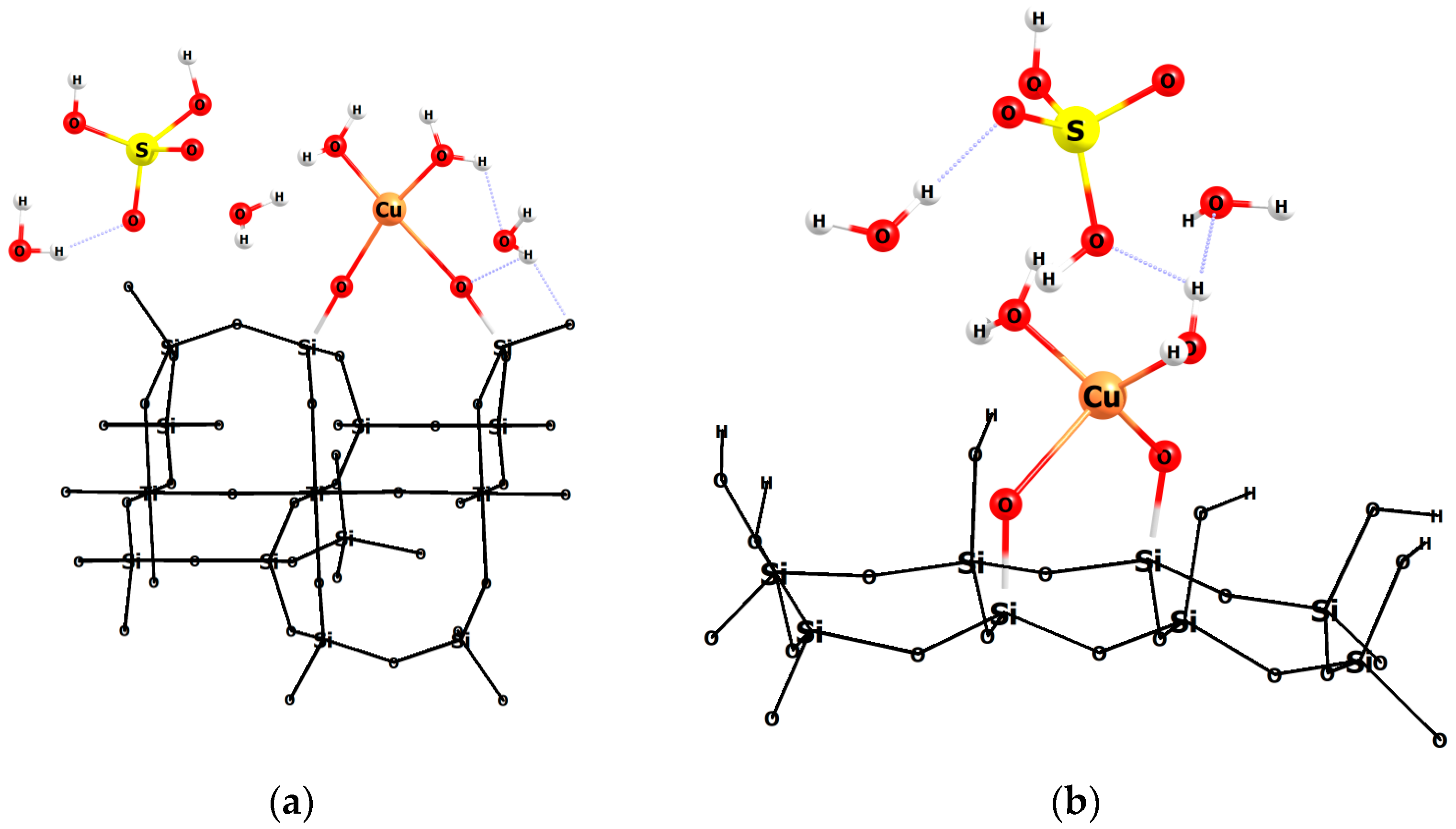
| Model | Parameters | Silica SBA-15 | Titanosilicate ETS-10 |
|---|---|---|---|
| Langmuir | qm, mg/g | 52.71 | 172.53 |
| KL, L/mg | 2.04 | 8.73 | |
| RL | 0.002–0.046 | 0.0005–0.011 | |
| R2 | 0.984 | 0.999 | |
| Freundlich | KF, mg/g | 0.197 | 0.460 |
| 1/n | 0.95 | 0.86 | |
| R2 | 0.977 | 0.985 | |
| Temkin | aT, L/g | 0.066 | 0.65 |
| bT, kJ/mol | 0.0118 | 0.089 | |
| R2 | 0.735 | 0.833 |
| Adsorbent | Conditions | q, mg/g | Reference |
|---|---|---|---|
| Mesoporous silica SBA-15 | pH = 5, t = 23 °C | 52.71 | Present study |
| Titanosilicate ETS-10 | pH = 5, t = 23 °C | 172.53 | Present study |
| Rape straw powders | pH = 4.77, t = 20 °C | 34.29 | [38] |
| Sunflower hulls | pH = 5, t = 20 °C | 49.74 | [39] |
| Chitosan based ion-imprinted cryo-composites | pH = 4.5 | 260 | [40] |
| Chemical modified Moringa oleifera leaves powder | pH = 6, t = 50 °C | 167.9 | [41] |
| Coconut tree sawdust | pH = 6 | 3.89 | [42] |
| Eggshell | pH = 6 | 34.48 | [43] |
| Sugarcane bagasse | pH = 6 | 3.65 | [42] |
| N-HAP/Chitosan | pH = 7.5, t = 25 °C | 113.66 | [43] |
| Chitosan crosslinked with epichlorohydrin-triphosphate | pH = 6, t = 25 °C | 130.38 | [44] |
| Parameter | Silica SBA-15 | Titanosilicate ETS-10 | |
|---|---|---|---|
| qexp, mg/g | 3.13 | 3.16 | |
| PFO | qe,cal, mg/g | 3.08 | 3.13 |
| k1, min−1 | 1.463 | 194.67 | |
| R2 | 0.997 | 0.999 | |
| PSO | qe, cal, mg/g | 3.081 | 3.135 |
| k2, g/mg·min | 2.87·1044 | 7.321 | |
| R2 | 0.997 | 0.999 | |
| Elovich | α, mg/g·min | 6.29·1026 | 7.08·1034 |
| β, g/min | 22.133 | 27.81 | |
| R2 | 0.994 | 0.998 | |
| Weber–Morris | kdiff | 0.204 | 0.208 |
| Ci | 1.565 | 1.577 | |
| R2 | 0.284 | 0.295 |
| Sorbent | ΔH0, kJ/mol | ΔS0, kJ/mol∙K | ΔG0, kJ/mol | |||
|---|---|---|---|---|---|---|
| 293 | 303 | 313 | 323 | |||
| SBA-15 | 30.09 | 0.172 | −20.31 | −22.03 | −23.75 | −25.47 |
| ETS-10 | 34.86 | 0.185 | −19.35 | −21.19 | −23.05 | −24.89 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Humelnicu, D.; Zinicovscaia, I.; Humelnicu, I.; Ignat, M.; Yushin, N.; Grozdov, D. Study on the SBA-15 Silica and ETS-10 Titanosilicate as Efficient Adsorbents for Cu(II) Removal from Aqueous Solution. Water 2022, 14, 857. https://doi.org/10.3390/w14060857
Humelnicu D, Zinicovscaia I, Humelnicu I, Ignat M, Yushin N, Grozdov D. Study on the SBA-15 Silica and ETS-10 Titanosilicate as Efficient Adsorbents for Cu(II) Removal from Aqueous Solution. Water. 2022; 14(6):857. https://doi.org/10.3390/w14060857
Chicago/Turabian StyleHumelnicu, Doina, Inga Zinicovscaia, Ionel Humelnicu, Maria Ignat, Nikita Yushin, and Dmitrii Grozdov. 2022. "Study on the SBA-15 Silica and ETS-10 Titanosilicate as Efficient Adsorbents for Cu(II) Removal from Aqueous Solution" Water 14, no. 6: 857. https://doi.org/10.3390/w14060857
APA StyleHumelnicu, D., Zinicovscaia, I., Humelnicu, I., Ignat, M., Yushin, N., & Grozdov, D. (2022). Study on the SBA-15 Silica and ETS-10 Titanosilicate as Efficient Adsorbents for Cu(II) Removal from Aqueous Solution. Water, 14(6), 857. https://doi.org/10.3390/w14060857