Study on the Effect of Water Flux in Osmotic Microbial Fuel Cells on Membrane Water Content and Resistance
Abstract
:1. Introduction
2. Materials and Methods
2.1. OsMFC Setup and Operation
2.2. Analytical Methods
3. Results and Discussion
3.1. Water Transport
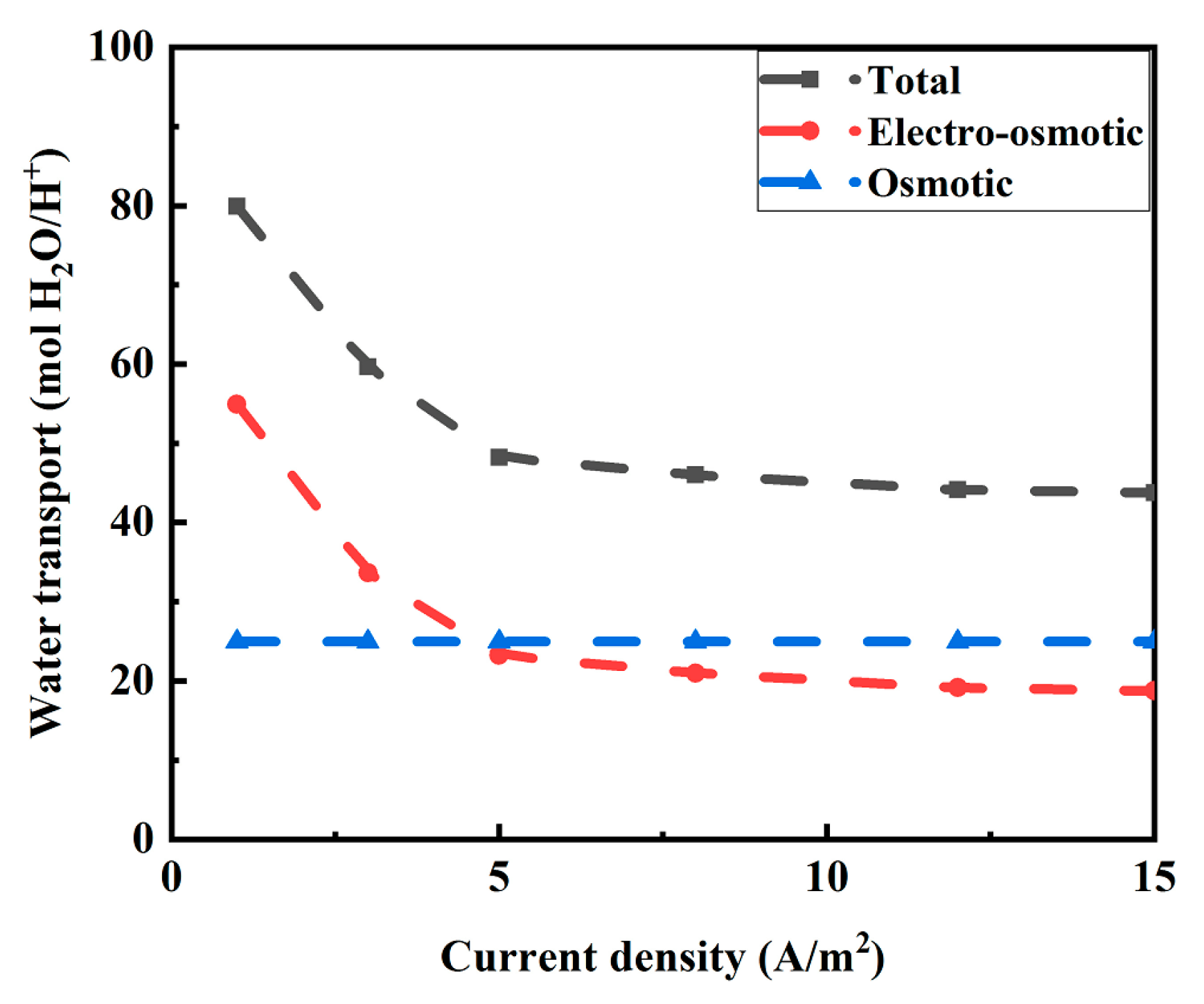
3.1.1. Osmotic and Electro-Osmotic Water Transport in OsMFCs
3.1.2. Measured Osmotic Water Transport
3.1.3. Measured Electro-Osmotic Transport
3.1.4. Higher Water Transport at Lower Current Density
3.2. Water Content
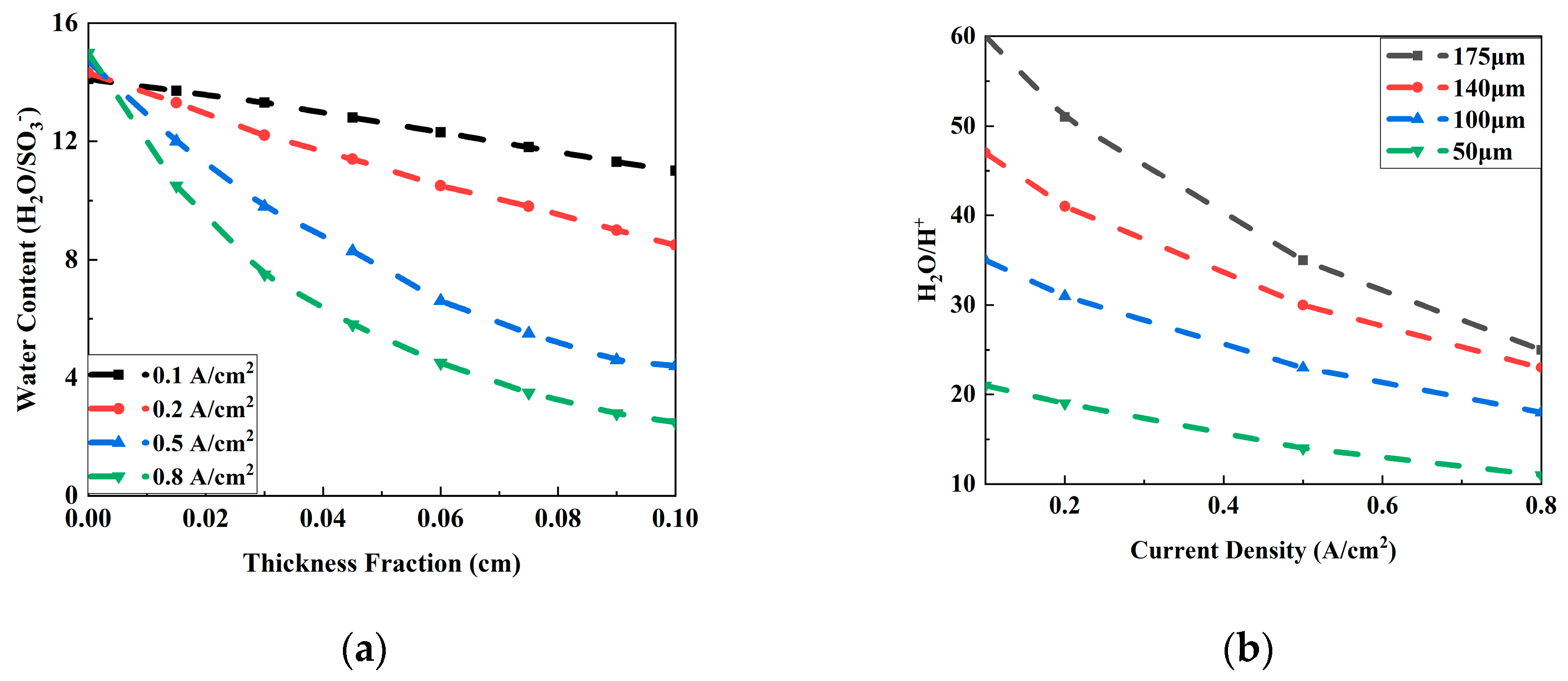
3.2.1. The Effect of Current Density on Water Content
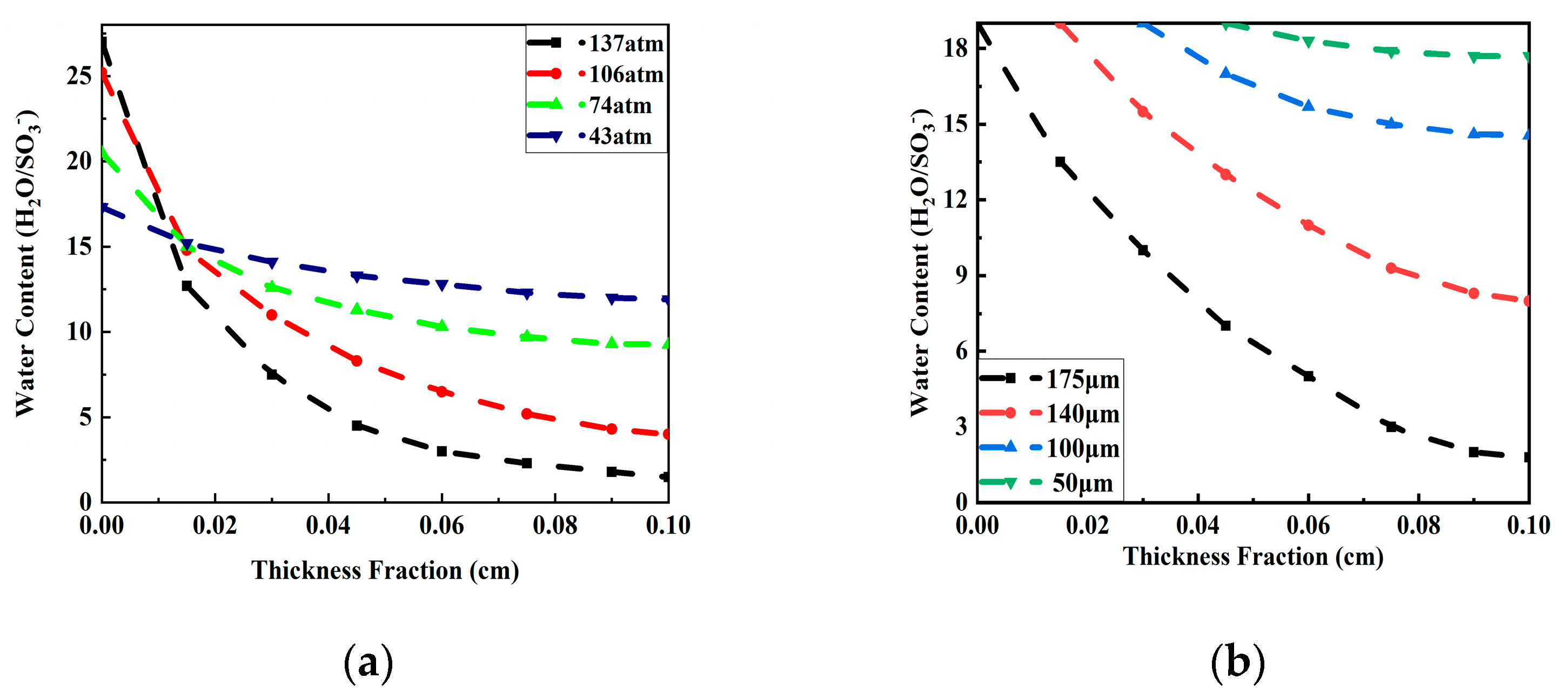
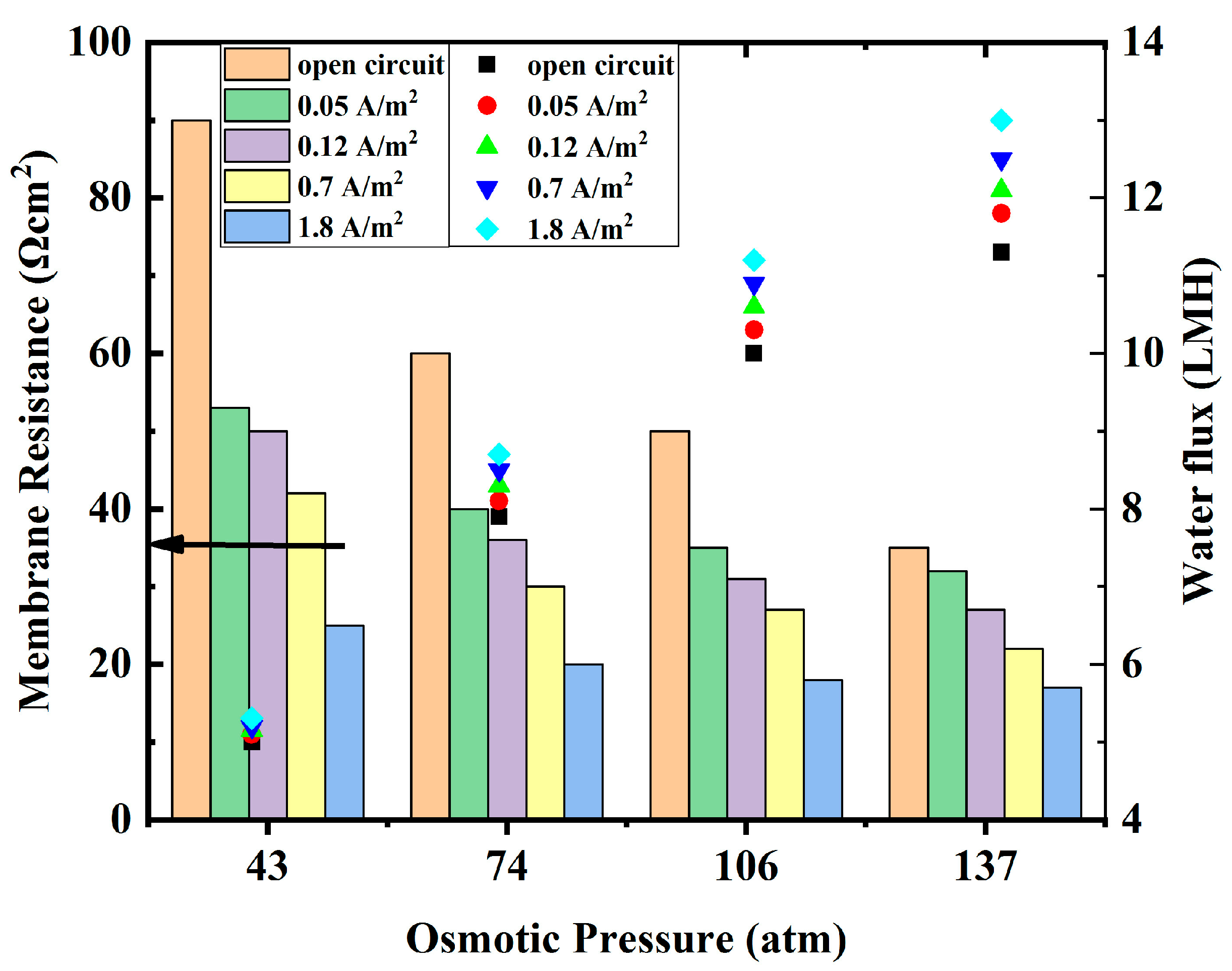
3.2.2. The Effect of Osmotic Pressure on Water Content
3.2.3. Water Content of Different Membrane Thicknesses
3.3. Membrane Resistance
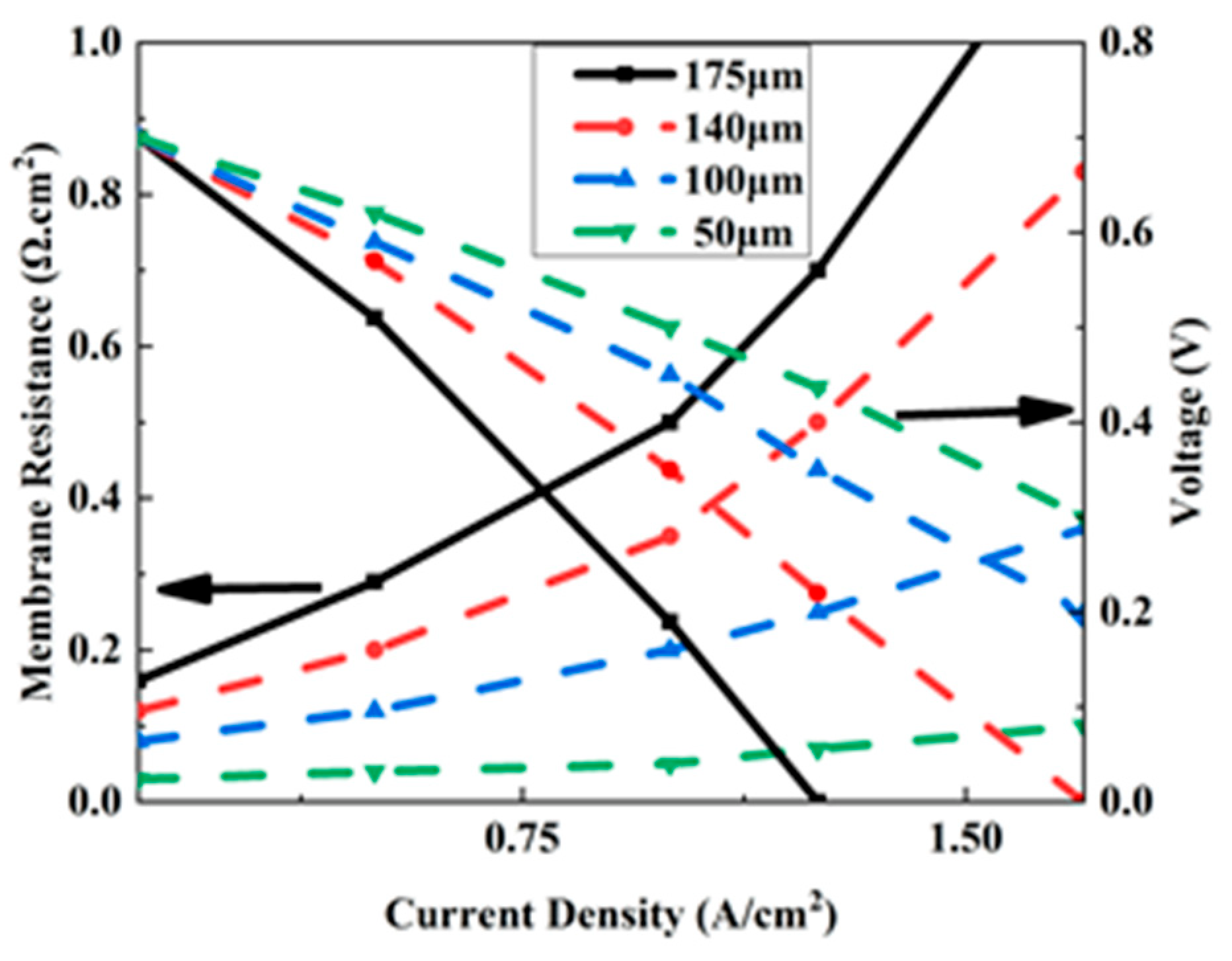
3.3.1. Effect of Membrane Thickness on Membrane Resistance and Voltage
3.3.2. The Effect of Current and Osmotic Pressure on Membrane Resistance and Water Flux
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chen, L.; Gu, Y.S.; Cao, C.Q.; Zhang, J.; Ng, J.E.; Tang, C.Y. Performance of a submerged anaerobic membrane bioreactor with forward osmosis membrane for low-strength wastewater treatment. Water Res. 2014, 50, 114–123. [Google Scholar] [CrossRef]
- Zhang, Y.X.; He, W.H.; Ren, L.J.; Stager, J.; Evans, P.J.; Logan, B.E. COD removal characteristics in air-cathode microbial fuel cells. Bioresour. Technol. 2015, 176, 23–31. [Google Scholar] [CrossRef]
- Cath, T.Y.; Childress, A.E.; Elimelech, M. Forward osmosis: Principles, applications, and recent developments. J. Membr. Sci. 2006, 281, 70–87. [Google Scholar] [CrossRef]
- Ge, Z.; Ping, Q.; Xiao, L.; He, Z. Reducing effluent discharge and recovering bioenergy in an osmotic microbial fuel cell treating domestic wastewater. Desalination 2013, 312, 52–59. [Google Scholar] [CrossRef]
- Logan, B.E.; Hamelers, B.; Rozendal, R.; Schröder, U.; Keller, J.; Freguia, S.; Aelterman, P.; Verstraete, W.; Rabaey, K. Microbial fuel cells: Methodology and technology. Environ. Sci. Technol. 2006, 40, 5181–5192. [Google Scholar] [CrossRef] [PubMed]
- Werner, C.M.; Logan, B.E.; Saikaly, P.E.; Amy, G.L. Wastewater treatment, energy recovery and desalination using a forward osmosis membrane in an air-cathode microbial osmotic fuel cell. J. Membr. Sci. 2013, 428, 116–122. [Google Scholar] [CrossRef]
- Zhang, F.; Brastad, K.S.; He, Z. Integrating forward osmosis into microbial fuel cells for wastewater treatment, water extraction and bioelectricity generation. Environ. Sci. Technol. 2011, 45, 6690–6696. [Google Scholar] [CrossRef]
- Eikerling, M.; Kharkats, Y.I.; Kornyshev, A.A.; Volkovich, Y.M. Phenomenological theory of electro-osmotic effect and water management in polymer electrolyte proton-conducting membranes. J. Electrochem. Soc. 1988, 145, 2648. [Google Scholar] [CrossRef]
- Lutchmiah, K.; Verliefde, A.R.D.; Roest, K.; Rietveld, L.C.; Cornelissen, E.R. Forward osmosis for application in wastewater treatment: A review. Water Res. 2014, 58, 179–197. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottsfeld, S. Polymer electrolyte fuel cells model. J. Electrochem. Soc. 1991, 138, 2334. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Wilson, M.S.; Gottesfled, S. Characterization of polymer electrolyte fuel cells using ac impedance spectroscopy. J. Electrochem. Soc. 1996, 143, 587–599. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Seawater desalination using renewable energy sources. Prog. Energy Combust. Sci. 2005, 31, 242–281. [Google Scholar] [CrossRef]
- Gierke, T.D.; Munn, G.E.; Wilson, F.C. The morphology in nafion perfluorinated membrane products, as determined by wide and small angle x-ray studies. J. Polym. Sci. Pol. Phys. 1981, 19, 1687–1704. [Google Scholar] [CrossRef]
- Lu, Y.; Jia, J.; Miao, H.; Ruan, W.; Wang, X. Performance improvement and biofouling mitigation in osmotic microbial fuel cells via in situ formation of silver nanoparticles on forward osmosis membrane. Membranes 2020, 10, 122. [Google Scholar] [CrossRef]
- Kang, M.S.; Choi, Y.J.; Choi, I.J.; Yoon, T.H.; Moon, S.H. Electrochemical characterization of sulfonated poly(aryleneetherulfone)(S-PES) cation exchange membranes. J. Membr. Sci. 2003, 216, 39–53. [Google Scholar] [CrossRef]
- Berezina, N.P.; Kononenko, N.A.; Dyomina, O.A.; Gnusin, N.P. Characterization of ion-exchange membrane materials: Properties vs. structure. Adv. Colloid Interface Sci. 2008, 139, 3–28. [Google Scholar] [CrossRef]
- Długołęcki, P.; Ogonowski, P.; Metz, S.J.; Saakes, M.; Nijmeijer, K.; Wessling, M. On the resistances of membrane, diffusion boundary layer and double layer in ion exchange membrane transport. J. Membr. Sci. 2010, 349, 69–379. [Google Scholar] [CrossRef]
- Wang, K.Y.; Ong, R.C.; Chung, T.S. Double-skinned forward osmosis membranes for reducing internal concentration polarization within the porous sublayer. Ind. Eng. Chem. Res. 2010, 49, 4824–4831. [Google Scholar] [CrossRef]
- Mohamed Berber, R.; Ismail, M.S.; Pourkashanian, M. Mohamed Barakat Zakaria Hegazy. Promising Membrane for Polymer Electrolyte Fuel Cells Shows Remarkable Proton Conduction over Wide Temperature and Humidity Ranges. ACS Appl. Polym. Mater. 2021, 3, 4275–4286. [Google Scholar] [CrossRef]
- Long, C.; Zhao, T.; Tian, L.; Liu, Q.; Wang, F.H.; Wang, Z.H.; Zhu, H. Highly Stable and Conductive Multicationic Poly(biphenyl indole) with Extender Side Chains for Anion Exchange Membrane Fuel Cells. ACS Appl. Energy Mater. 2021, 4, 6154–6165. [Google Scholar] [CrossRef]
- Pham, T.A.; Nam, L.V.; Choi, E.; Lee, M.S.; Jun, T.S.; Jang, S.; Kim, S.M. Mechanically Stable Thinned Membrane for a High-Performance Polymer Electrolyte Membrane Fuel Cell via a Plasma-Etching and Annealing Process. Energy Fuels 2021, 35, 11525–11532. [Google Scholar] [CrossRef]
- Bellows, R.J.; Lin, M.Y.; Arif, M.; Thompson, A.K.; Jacobson, D. Neutron Imaging Technique for In Situ Measurement of water transport gradients within Nafion in Polymer Electrolyte Fuel Cells. J. Electrochem. Soc. 2000, 146, 1099. [Google Scholar] [CrossRef]
- Al-Mamun, A.; Baawain, M.S.; Dhar, B.R.; Kim, I.S. Improved recovery of bioenergy and osmotic water in an osmotic microbial fuel cell using micro-diffuser assisted marine aerobic biofilm on cathode. Biochem. Eng. J. 2017, 128, 235–242. [Google Scholar] [CrossRef]
- Oda, Y.; Yawataya, T. On the electro-osmotic water transport through cation exchange resin membranes. Bull. Chem. Soc. Jpn. 1955, 28, 263–269. [Google Scholar] [CrossRef] [Green Version]
- Tombalakian, A.S.; Barton, H.J.; Graydon, W.F. Electroösmotic water transport across ion-exchange membranes. J. Phys. Chem. A 1962, 66, 1006–1009. [Google Scholar] [CrossRef]
- Lakshminarayaniah, N. Transport Phenomena in Artificial Membranes. Chem Rev. 1965, 65, 491–565. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Fu, B.; Xi, J.; Hu, H.; Liang, P.; Huang, X.; Zhang, X. Remediation of simulated malodorous surface water by columnar air-cathode microbial fuel cells. Sci. Total Environ. 2019, 687, 287–296. [Google Scholar] [CrossRef]
- Qin, M.; Ping, Q.; Lu, Y.; Abu-Reesh, I.M.; He, Z. Understanding electricity generation in osmotic microbial fuel cells through integrated experimental investigation and mathematical modeling. Bioresour. Technol. 2015, 195, 194–201. [Google Scholar] [CrossRef]
- Zabolotsky, V.I.; Nikonenko, V.V. Effect of structural membrane inhomogeneity on transport properties. J. Membr. Sci. 1993, 79, 181–198. [Google Scholar] [CrossRef]
- Yaroslavtsev, A.B. Perfluorinated ion-exchange membranes. Poly. Sci. Ser. A 2013, 55, 674–698. [Google Scholar] [CrossRef]
- Veerman, J.; de Jong, R.M.; Saakes, M.; Metz, S.J.; Harmsen, G.J. Reverse electrodialysis: Comparison of six commercial membrane pairs on the thermodynamic efficiency and power density. J. Membr. Sci. 2009, 343, 7–15. [Google Scholar] [CrossRef]
- Spiegler, K.S. Transport processes in ionic membranes. Trans. Faraday Soc. 1958, 54, 1408–1428. [Google Scholar] [CrossRef]


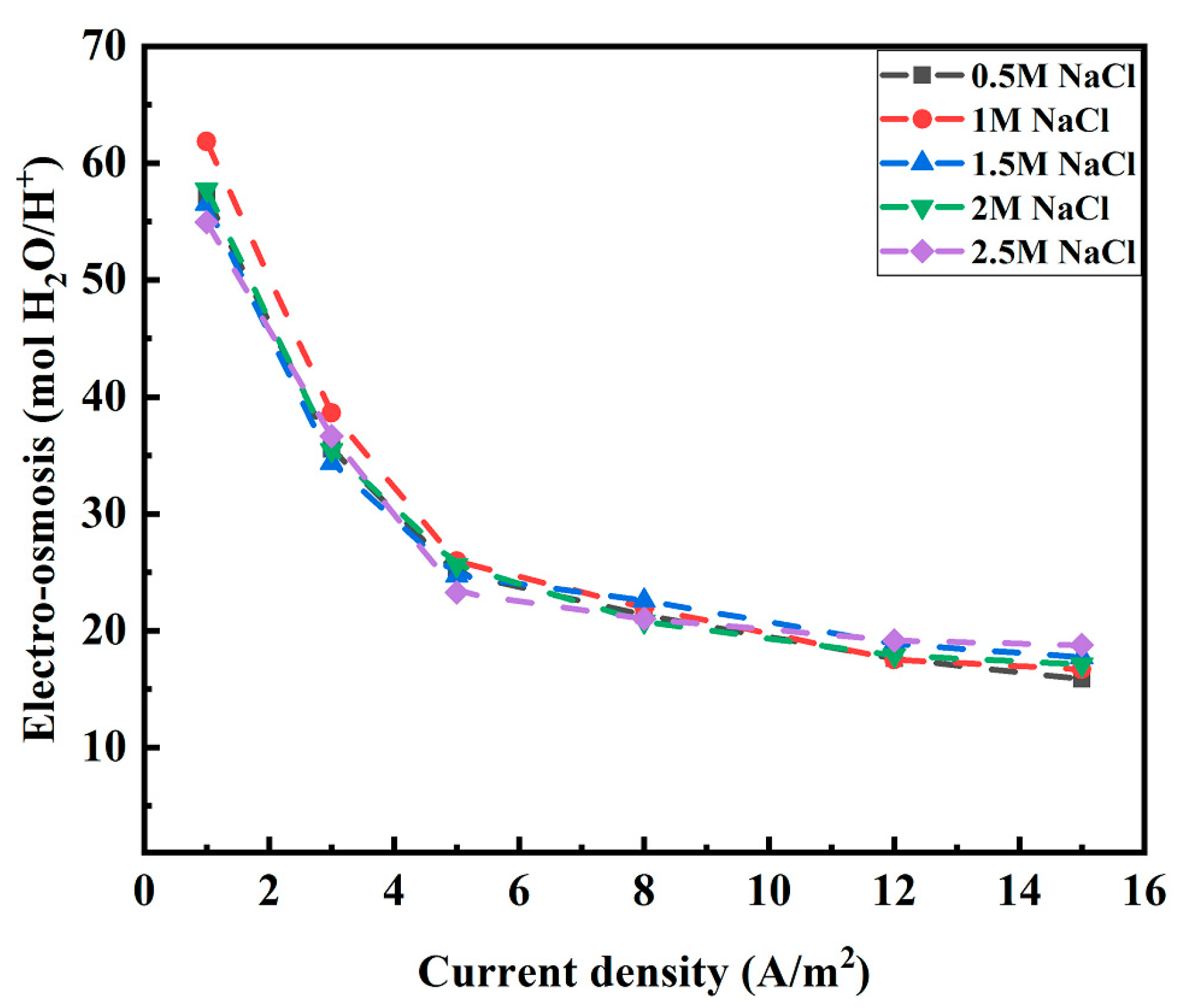
| Current Density A/m2 | Moles of Water Transported per Mole of Protons Delivered | ||||
|---|---|---|---|---|---|
| 0.5 M | 1 M | 1.5 M | 2 M | 2.5 M | |
| 1 | 57.12 | 61.86 | 56.52 | 57.76 | 54.95 |
| 3 | 35.52 | 38.63 | 34.37 | 35.45 | 36.64 |
| 5 | 24.92 | 25.93 | 24.73 | 25.62 | 23.25 |
| 8 | 21.32 | 21.97 | 22.57 | 20.76 | 21.00 |
| 12 | 17.60 | 17.52 | 18.87 | 17.86 | 19.15 |
| 15 | 15.83 | 16.68 | 17.72 | 17.11 | 18.75 |
| Moles of water transported per Faraday of current passed | |||||
| 1 | 235.80 | 218.80 | 216.80 | 213.00 | 231.20 |
| 3 | 127.93 | 133.60 | 101.80 | 110.73 | 127.10 |
| 5 | 75.72 | 71.58 | 66.39 | 69.07 | 72.07 |
| 8 | 63.78 | 62.39 | 57.85 | 87.99 | 58.02 |
| 12 | 53.13 | 56.04 | 45.39 | 50.85 | 50.71 |
| 15 | 47.96 | 46.30 | 43.30 | 47.62 | 46.75 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Song, Y.; Duan, L. Study on the Effect of Water Flux in Osmotic Microbial Fuel Cells on Membrane Water Content and Resistance. Water 2022, 14, 848. https://doi.org/10.3390/w14060848
Zhao Y, Song Y, Duan L. Study on the Effect of Water Flux in Osmotic Microbial Fuel Cells on Membrane Water Content and Resistance. Water. 2022; 14(6):848. https://doi.org/10.3390/w14060848
Chicago/Turabian StyleZhao, Yang, Yonghui Song, and Liang Duan. 2022. "Study on the Effect of Water Flux in Osmotic Microbial Fuel Cells on Membrane Water Content and Resistance" Water 14, no. 6: 848. https://doi.org/10.3390/w14060848
APA StyleZhao, Y., Song, Y., & Duan, L. (2022). Study on the Effect of Water Flux in Osmotic Microbial Fuel Cells on Membrane Water Content and Resistance. Water, 14(6), 848. https://doi.org/10.3390/w14060848







