Modelling Intense Combined Load Transport in Open Channel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Combined-Load Model
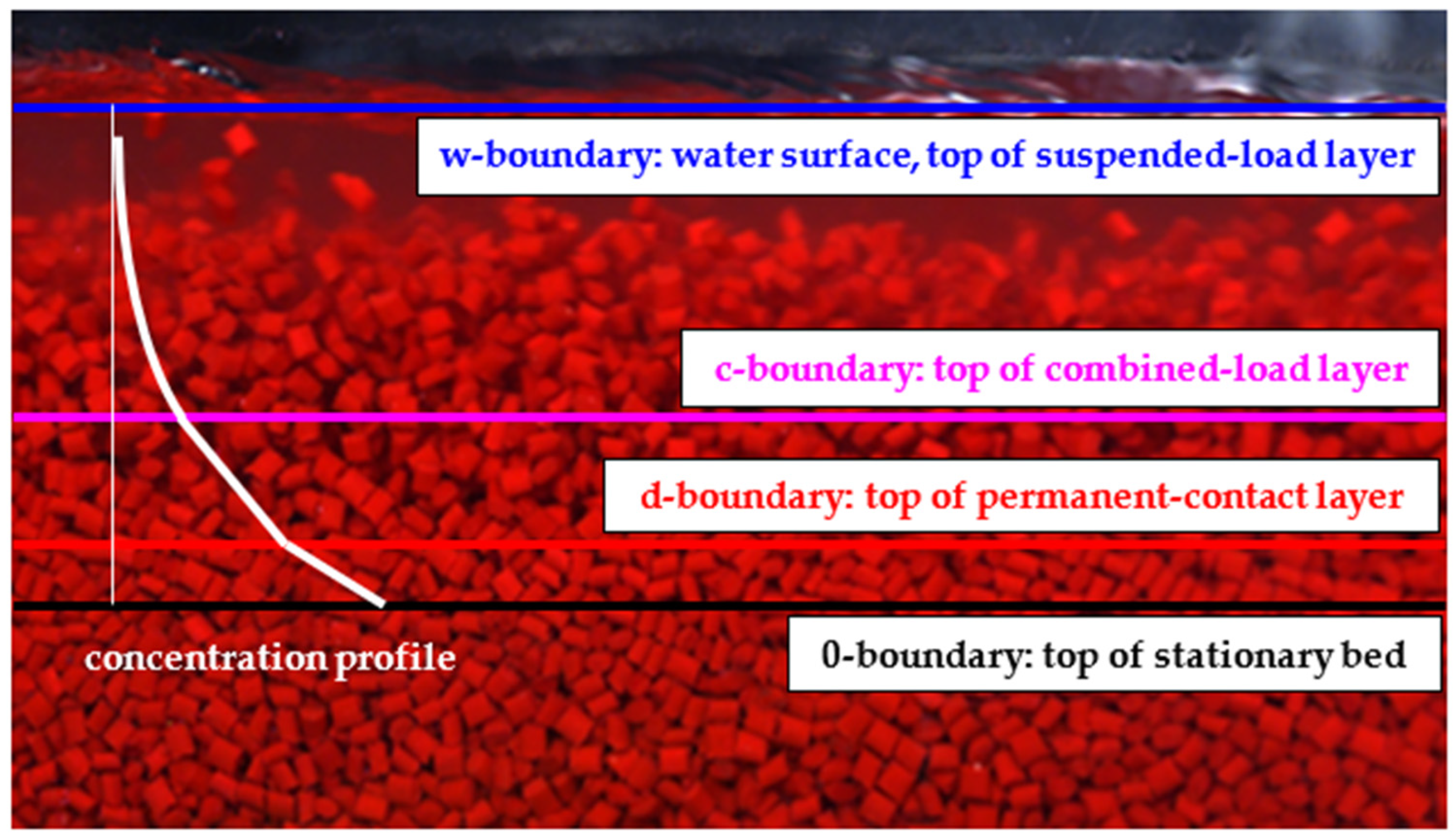
2.1.1. Modelled Conditions
- The stationary bed (granular deposit with the plane surface expressed as the 0-boundary);
- the permanent-contact (dense sliding) layer (its top is the d-boundary);
- the combined-load (collision and turbulent suspension) layer (its top is the c-boundary);
- the suspended-load (turbulent suspension) layer (its top is the water surface, the w-boundary).
2.1.2. Model Assumptions
2.1.3. Model Principles and Applied Theoretical Concepts
2.1.4. Model Features
- Inputs: Solid/liquid properties: d, ρs, w, ρf, μf
- Flow: H, ω
- Constants: c0, cd, ε, β0, κ, Cbd, Cini, Cη
- Major outputs: Positions of interfaces between layers: yd, yc
- Distributions of velocity and solids concentration in layers: u(y), c(y)
2.1.5. Model Equations and Computational Procedure
2.2. Experimental Work
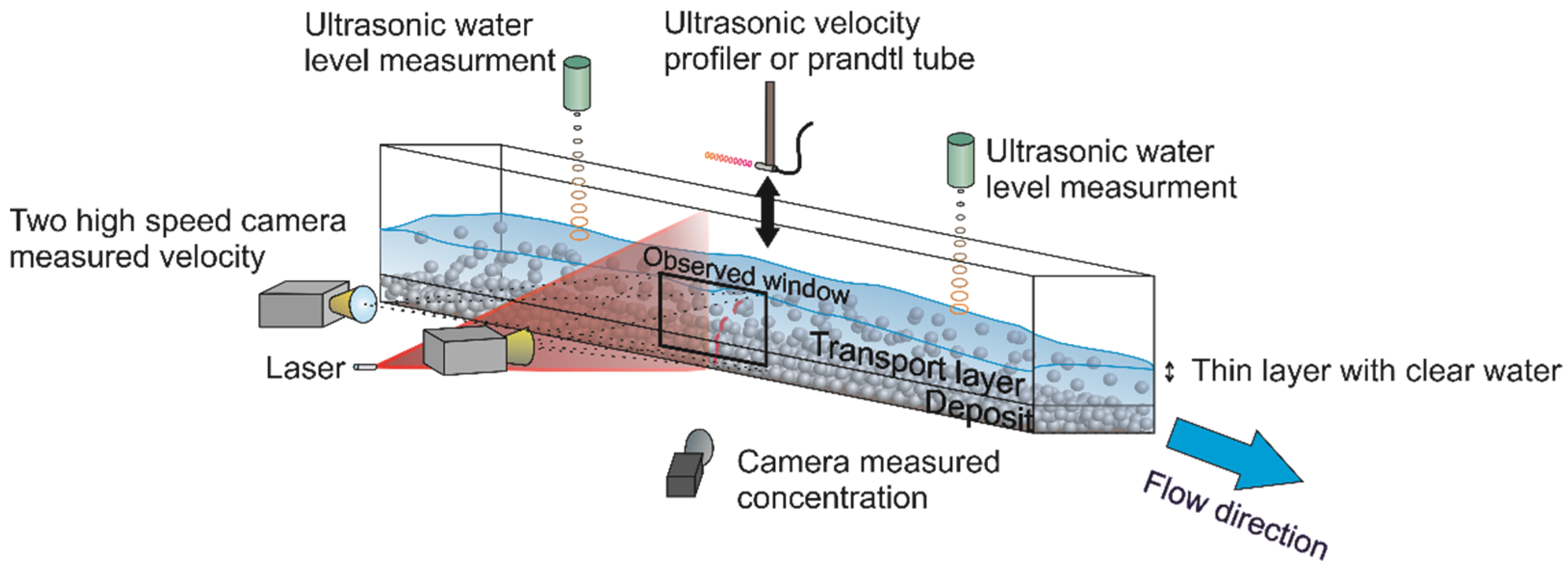
2.2.1. Experimental Set-Up
2.2.2. Measuring Techniques
2.2.3. Tested Solids
2.2.4. Experimental Flow Conditions
2.2.5. Experimental Data Set
3. Results
3.1. Experimental Results
3.1.1. Concentration Profiles
3.1.2. Velocity Profiles
3.2. Model Predictions
3.2.1. Concentration Profiles
3.2.2. Velocity Profiles
4. Discussion
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ACVP | Acoustic Concentration and Velocity Profiler |
| DPT | Differential Pressure Transmitter |
| ERT | Electrical Resistivity Tomography |
| UVP | Ultrasonic Velocity Profiler |
Appendix A
References
- Cao, Z.; Pender, G.; Meng, J. Explicit formulation of the Shields diagram for incipient motion of sediment. J. Hydraul. Eng. 2006, 132, 1097–1684. [Google Scholar] [CrossRef]
- Garcia, M.M. Sedimentation Engineering; American Society of Civil Engineers: Reston, VA, USA, 2008. [Google Scholar]
- Capart, H.; Fraccarollo, L. Transport layer structure in intense bed-load. Geophys. Res. Lett. 2011, 38, L20402. [Google Scholar] [CrossRef]
- Revil-Baudard, T.; Chauchat, J.; Hurther, D.; Barraud, P.-A. Investigation of sheet-flow processes based on novel acoustic high-resolution velocity and concentration measurements. J. Fluid Mech. 2015, 767, 1–30. [Google Scholar] [CrossRef] [Green Version]
- Pugh, F.J.; Wilson, K.C. Velocity and concentration distributions in sheet flow above plane beds. J. Hydraul. Eng. 1999, 125, 117–125. [Google Scholar] [CrossRef]
- Matoušek, V. Concentration profiles and solids transport above stationary deposit in enclosed conduit. J. Hydraul. Eng. ASCE 2009, 135, 1101–1106. [Google Scholar] [CrossRef]
- Gillies, R.G.; Shook, C.A. Concentration distributions of sand slurries in horizontal pipe flow. Part. Sci. Technol. 1994, 12, 45–69. [Google Scholar] [CrossRef]
- Sumer, B.M.; Kozakiewitz, A.; Fredsøe, J.; Deigaard, R. Velocity and concentration profiles in sheet-flow layer of movable bed. J. Hydraul. Eng. 1996, 122, 549–558. [Google Scholar] [CrossRef]
- Matoušek, V.; Krupička, J.; Picek, T. Validation of transport and friction formulae for upper plane bed by experiments in rectangular pipes. J. Hydrol. Hydromech. 2013, 61, 120–125. [Google Scholar] [CrossRef] [Green Version]
- Capart, H.; Young, D.L.; Zech, Y. Voronoi imaging methods for the measurement of granular flows. Exp. Fluids 2002, 32, 121–135. [Google Scholar] [CrossRef]
- Spinewine, B.; Capart, H.; Larcher, M.; Zech, Y. Three-dimensional Voronoi imaging methods for the measurement of near-wall particulate flows. Exp. Fluids 2003, 34, 227–241. [Google Scholar] [CrossRef]
- Spinewine, B.; Capart, H.; Fraccarollo, L.; Larcher, M. Laser stripe measurements of near-wall solid fraction in channel flows of liquid-granular mixtures. Exp. Fluids 2011, 50, 1507–1525. [Google Scholar] [CrossRef]
- Armanini, A.; Capart, H.; Fraccarollo, L.; Larcher, M. Rheological stratification in experimental free-surface flows of granular-liquid mixtures. J. Fluid Mech. 2005, 532, 269–319. [Google Scholar] [CrossRef] [Green Version]
- Larcher, M.; Fraccarollo, L.; Armanini, A.; Capart, H. Set of measurement data from flume experiments on steady uniform debris flows. J. Hydraul. Res. 2007, 45, 59–71. [Google Scholar] [CrossRef]
- Spinewine, B.; Capart, H. Intense bed-load due to a sudden dam-break. J. Fluid Mech. 2013, 731, 579–614. [Google Scholar] [CrossRef]
- Cheng, Z.; Hsu, T.-J.; Calantoni, J. Sedfoam: A multi-dimensional Eulerian two-phase model for sediment transport and its application to momentary bed failure. Coast. Eng. 2017, 119, 32–50. [Google Scholar] [CrossRef] [Green Version]
- Gonzalez-Ondina, J.M.; Fraccarollo, L.; Liu, P.L.F. Two-level, two-phase model for intense, turbulent sediment transport. J. Fluid Mech. 2018, 839, 198–238. [Google Scholar] [CrossRef] [Green Version]
- Berzi, D. Analytical solution of collisional sheet flows. ASCE J. Hydraul. Eng. 2011, 137, 1200–1207. [Google Scholar] [CrossRef]
- Berzi, D.; Fraccarollo, L. Inclined, collisional sediment transport. Phys. Fluids 2013, 25, 106601. [Google Scholar] [CrossRef] [Green Version]
- McTigue, D.F. Mixture theory for suspended sediment transport. J. Hydraul. Div. ASCE 1981, 107, 659–673. [Google Scholar] [CrossRef]
- Wilson, K.C.; Pugh, F.J. Dispersive-force modelling of turbulent suspension in heterogeneous slurry flow. Can. J. Chem. Eng. 1988, 66, 721–727. [Google Scholar] [CrossRef]
- Berzi, D. Transport formula for collisional sheet flows with turbulent suspension. J. Hydraul. Eng. 2013, 139, 359–363. [Google Scholar] [CrossRef]
- Berzi, D.; Fraccarollo, L. Intense sediment transport: Collisional to turbulent suspension. Phys. Fluids 2016, 28, 023302. [Google Scholar] [CrossRef] [Green Version]
- Matoušek, V.; Bareš, V.; Krupička, J.; Picek, T.; Zrostlík, Š. Experimental investigation of internal structure of open-channel flow with intense transport of sediment. J. Hydrol. Hydromech. 2015, 63, 318–326. [Google Scholar] [CrossRef] [Green Version]
- Matoušek, V.; Zrostlík, Š. Laboratory testing of granular kinetic theory for intense bed load transport. J. Hydrol. Hydromech. 2018, 66, 330–336. [Google Scholar] [CrossRef]
- Matoušek, V.; Zrostlík, Š.; Fraccarollo, L.; Prati, A.; Larcher, M. Internal structure of intense collisional bed load transport. Earth Surf. Process. Landf. 2019, 44, 2285–2296. [Google Scholar] [CrossRef]
- Matoušek, V.; Zrostlík, Š. Collisional transport model for intense bed load. J. Hydrol. Hydromech. 2020, 68, 60–69. [Google Scholar] [CrossRef] [Green Version]
- Matoušek, V.; Zrostlík, Š. Combined load in open channel: Modelling of transport layer at high bed shear. In Proceedings of the River Flow 2020, Delft, The Netherlands, 7–10 July 2020; Uijttewaal, W., Franca, M.J., Valero, D., Chavarrias, V., Arbós, C.Y., Schielen, R., Crosato, A., Eds.; Taylor & Francis Group: London, UK, 2020; pp. 308–315. [Google Scholar]
- Berzi, D.; Fraccarollo, L. Turbulence locality and granularlike fluid shear viscosity in collisional suspensions. Phys. Rev. Lett. 2015, 115, 194501. [Google Scholar] [CrossRef] [Green Version]
- Berzi, D.; Larcan, E. Flow resistance of inertial debris flows. J. Hydraul. Eng. 2013, 139, 187–194. [Google Scholar] [CrossRef]
- Garzó, V.; Dufty, J.W. Dense fluid transport for inelastic hard spheres. Phys. Rev. E 1999, 59, 5895. [Google Scholar] [CrossRef] [Green Version]
- Torquato, S. Nearest-neighbor statistics for packings of hard spheres and disks. Phys. Rev. E 1995, 51, 3170–3182. [Google Scholar] [CrossRef]
- Bareš, V.; Zrostlík, Š.; Picek, T.; Krupička, J.; Matoušek, V. On local velocity measurement in gravity-driven flows with intense bedload of coarse lightweight particles. Flow Meas. Instrum. 2016, 51, 68–78. [Google Scholar] [CrossRef]
- Krupička, J.; Picek, T.; Zrostlík, Š. Reduction of uncertainties in laser stripe measurement of solid particles concentration. Acta Polytech. 2018, 58, 171–178. [Google Scholar] [CrossRef]



| SUN25 | |
|---|---|
| d [mm] | 2.8 |
| S [-] | 1.28 |
| w [mm/s] | 76.5 |
| w [-] | 0.987 |
| R [-] | 217 |
| Test 1 | Test 2 | Test 3 | Test 4 | Test 5 | |
|---|---|---|---|---|---|
| ω [-] | 0.0257 | 0.0142 | 0.0154 | 0.0098 | 0.0070 |
| H [-] | 20.4 | 25.5 | 20.0 | 25.1 | 22.7 |
| Re [-] | 4.0 × 104 | 6.1 × 104 | 4.1 × 104 | 5.1 × 104 | 4.0 × 104 |
| θ0,flow [-] | 1.88 | 1.30 | 1.10 | 0.88 | 0.57 |
| u*0,flow/w [-] | 1.57 | 1.31 | 1.20 | 1.08 | 0.86 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matoušek, V. Modelling Intense Combined Load Transport in Open Channel. Water 2022, 14, 572. https://doi.org/10.3390/w14040572
Matoušek V. Modelling Intense Combined Load Transport in Open Channel. Water. 2022; 14(4):572. https://doi.org/10.3390/w14040572
Chicago/Turabian StyleMatoušek, Václav. 2022. "Modelling Intense Combined Load Transport in Open Channel" Water 14, no. 4: 572. https://doi.org/10.3390/w14040572






