Calibration of Adjustment Coefficient of the Viscous Boundary in Particle Discrete Element Method Based on Water Cycle Algorithm
Abstract
:1. Introduction
2. Construction of Viscous Boundary in the PDEM
2.1. Basic Principles of the Viscous Boundary
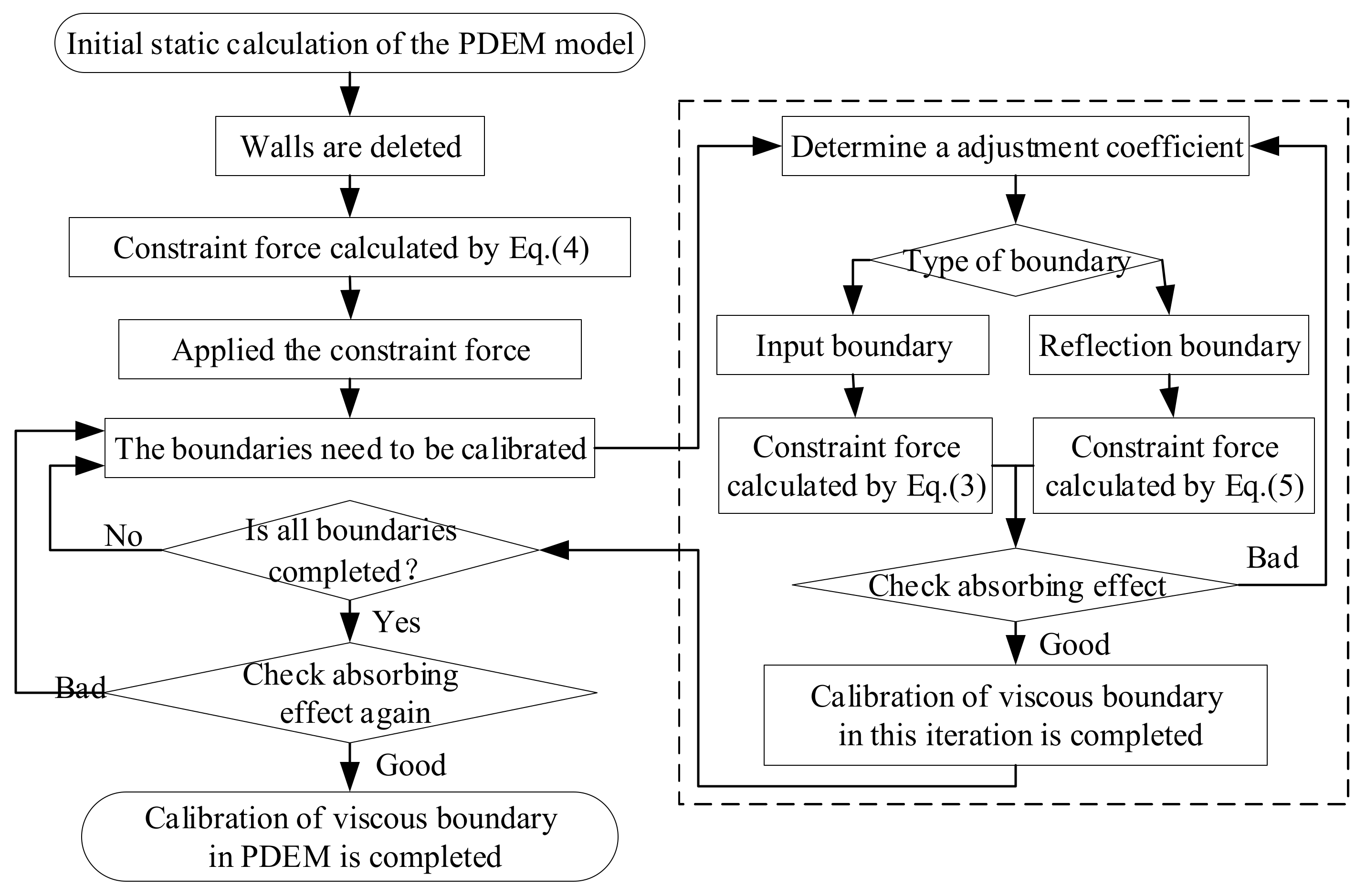
2.2. Application of Viscous Boundary in the PDEM
2.3. Verification of the Viscous Boundary in the PDEM
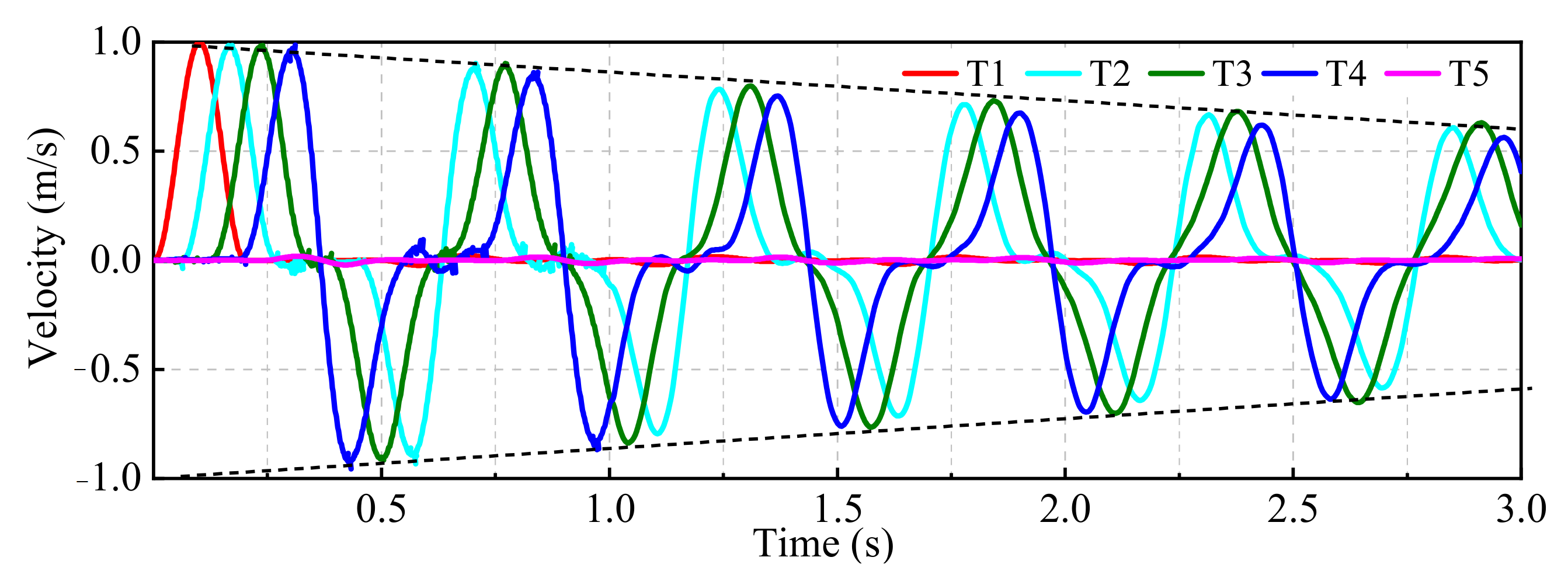
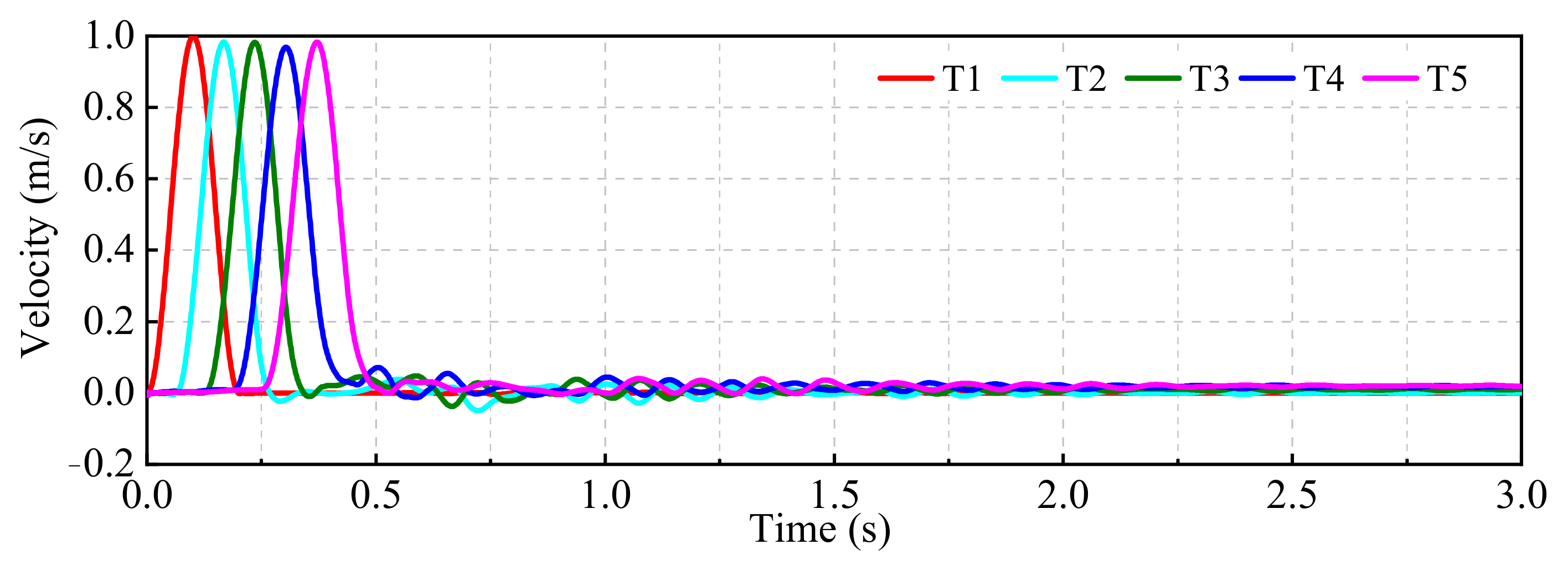
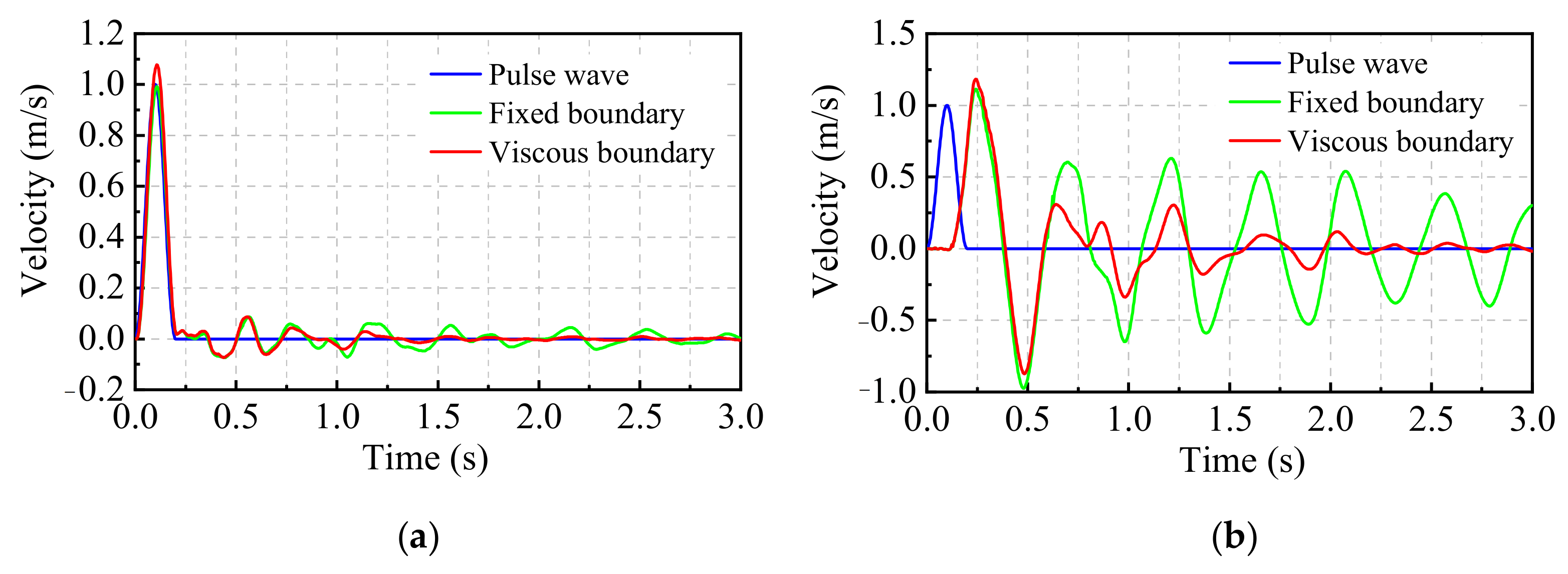
2.3.1. Dynamic Response Analysis of the Fixed Boundary
2.3.2. Dynamic Response Analysis of the Viscous Boundary
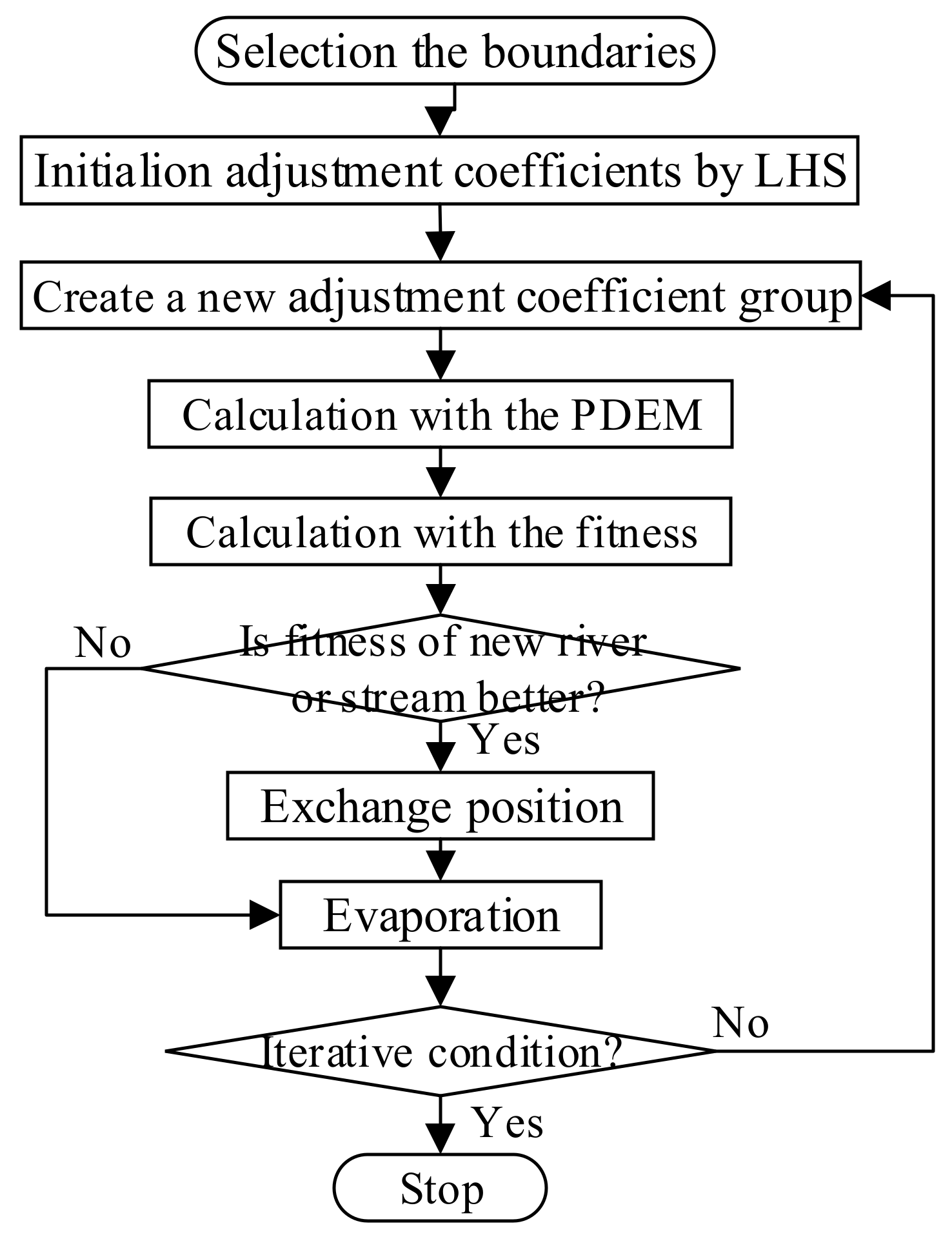
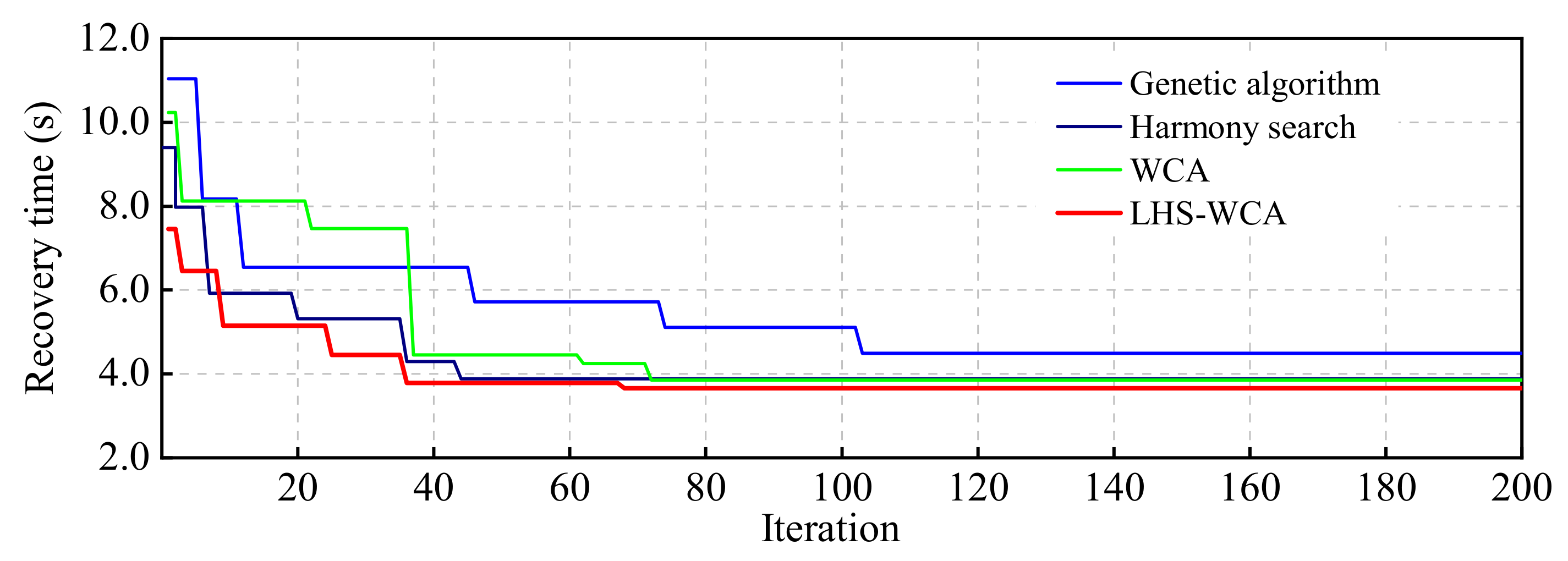
3. Establishment of LHS-WCA Algorithm
3.1. Basic Principles of the WCA
3.2. LHS-WCA Algorithm
4. Calibration Model of Adjustment Coefficients of the Viscous Boundary
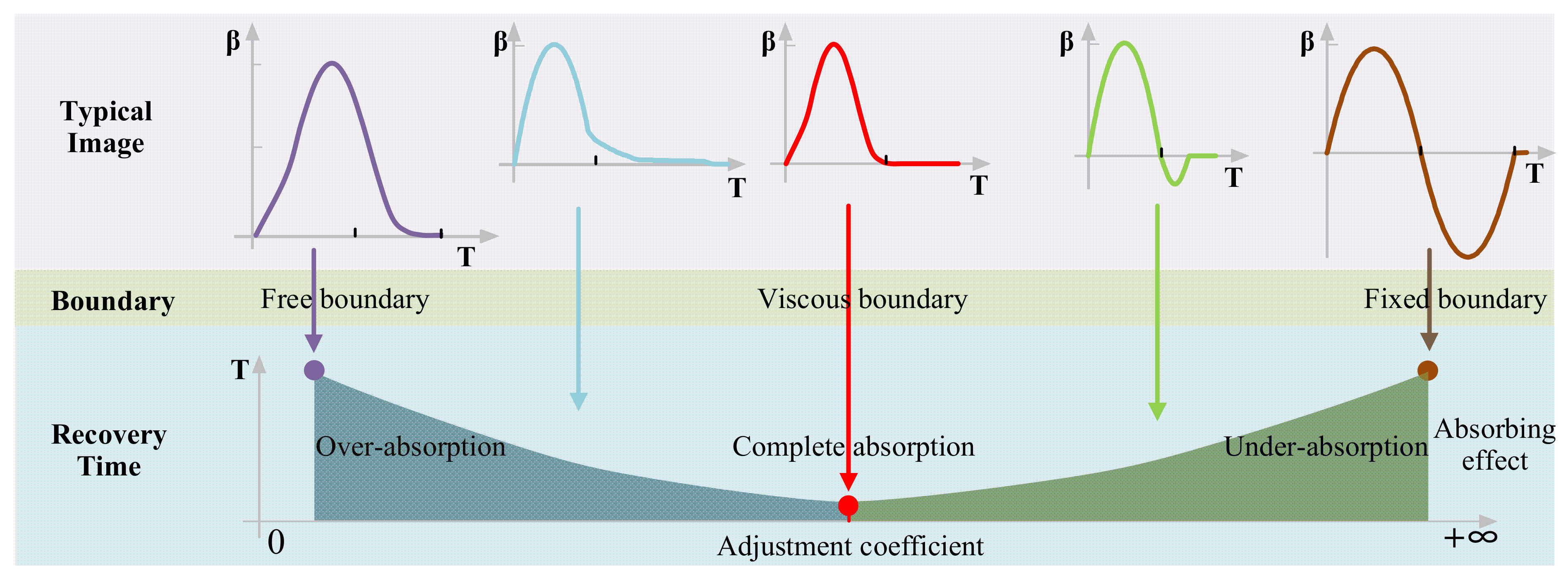
4.1. The proposition of Calibration Problem
4.2. Well-Posedness of the Calibration Problem
4.3. Feasibility and Construction of the Calibration Model
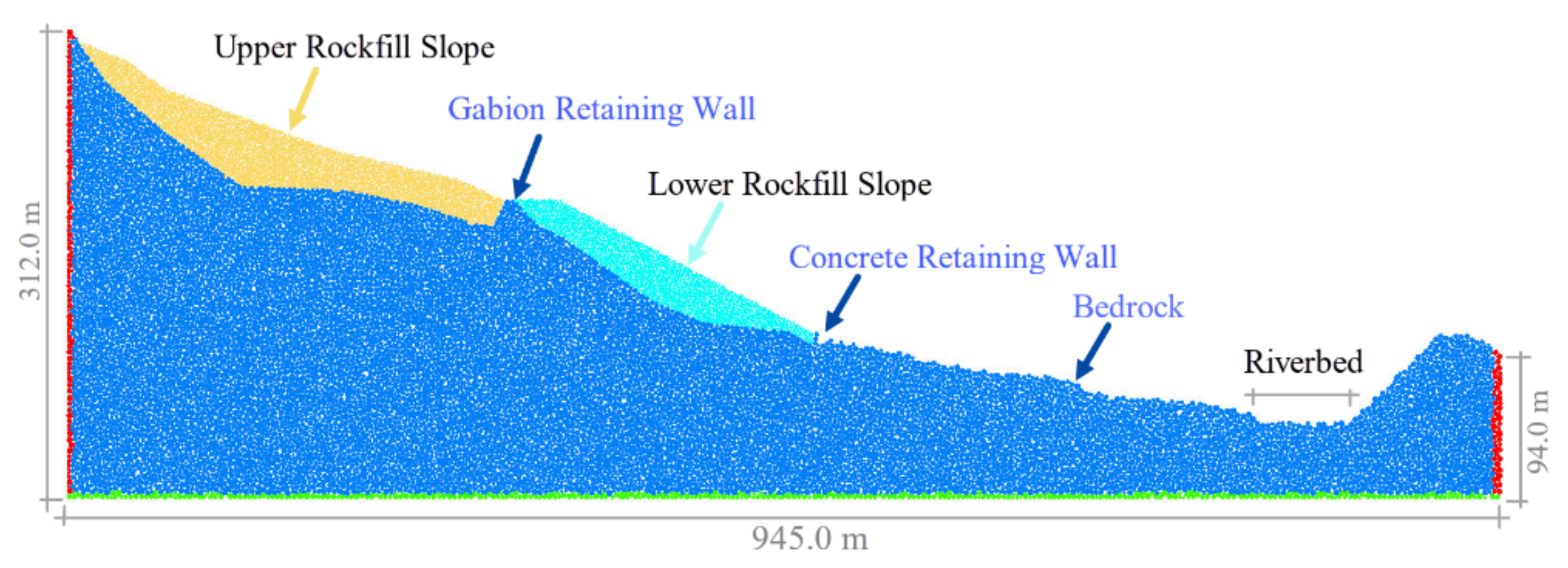
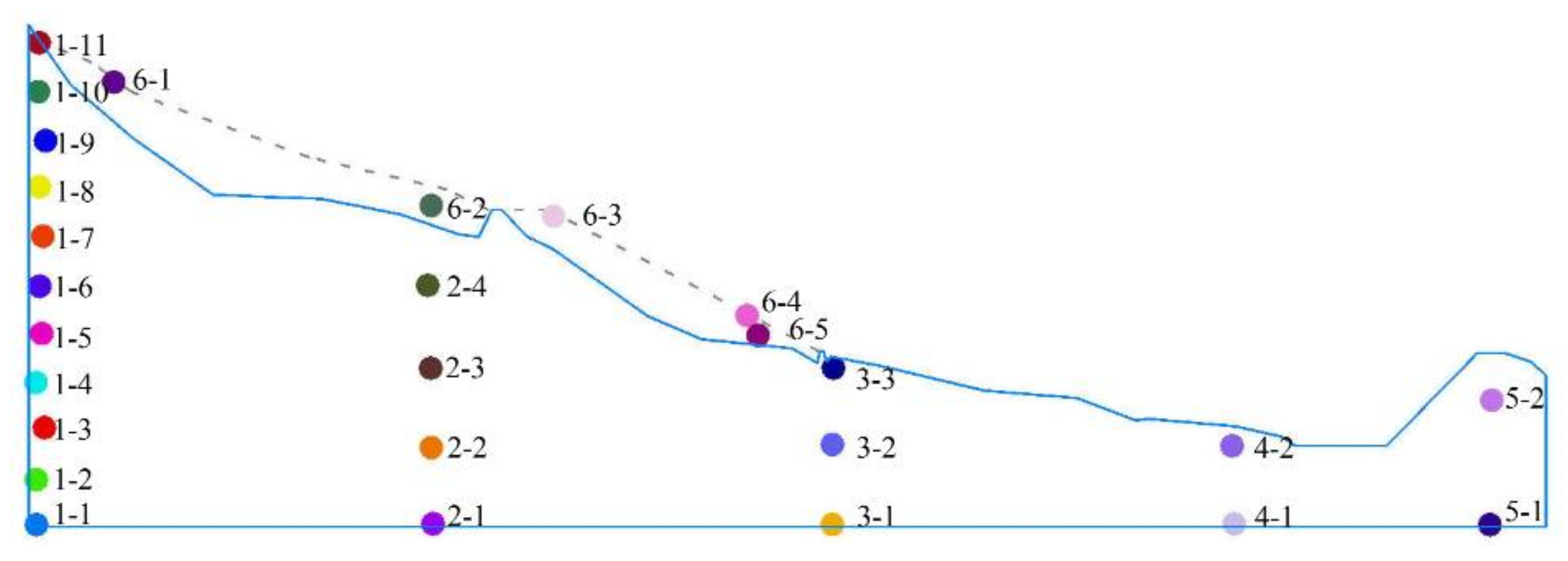
5. Case Study
5.1. Calibration of Microscopic Parameters of the Rockfill
5.2. Calibration of Adjustment Coefficients of the Viscous Boundary and Its Effect Analysis
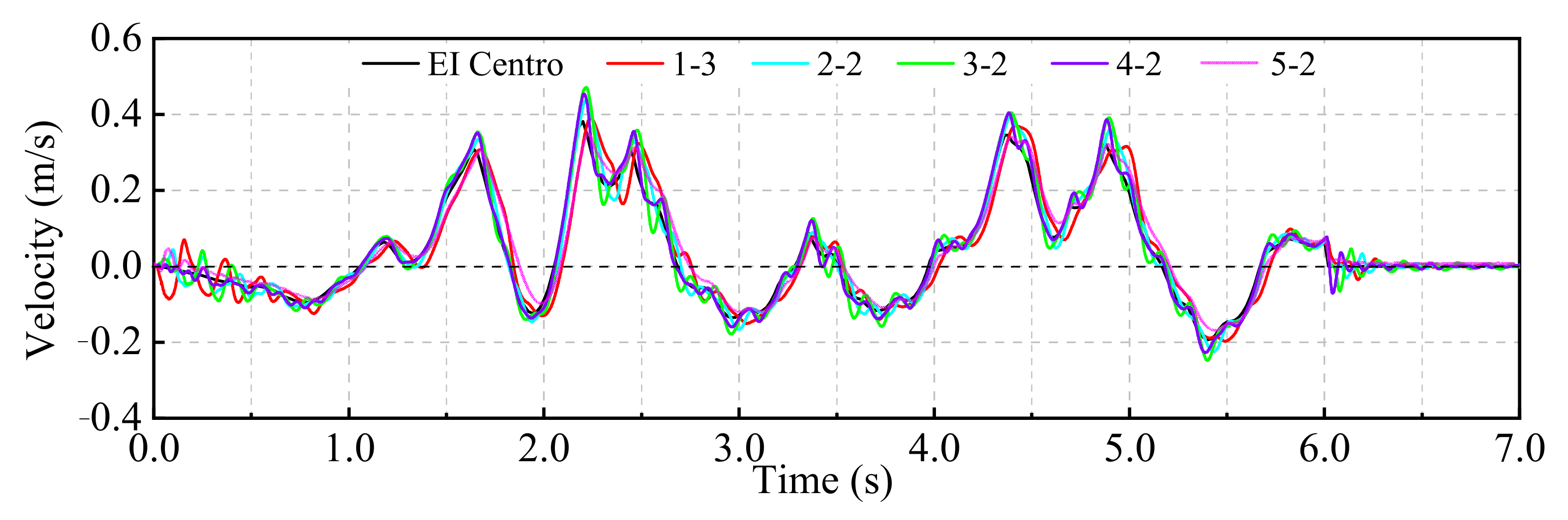
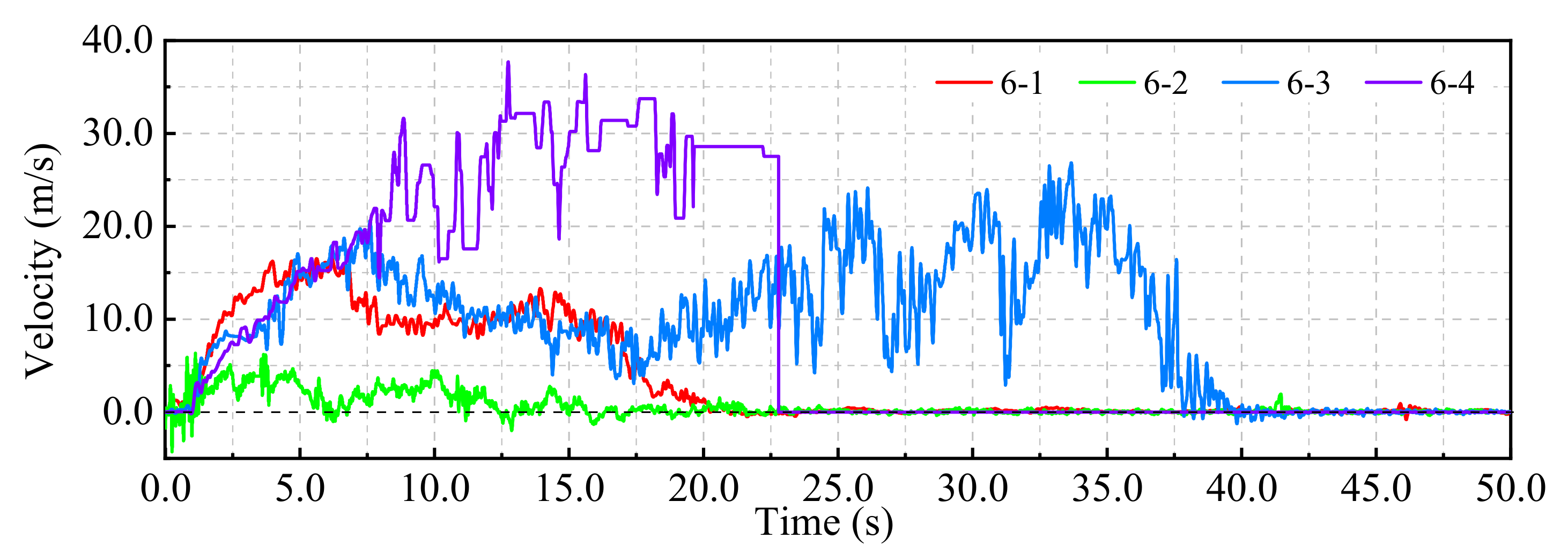
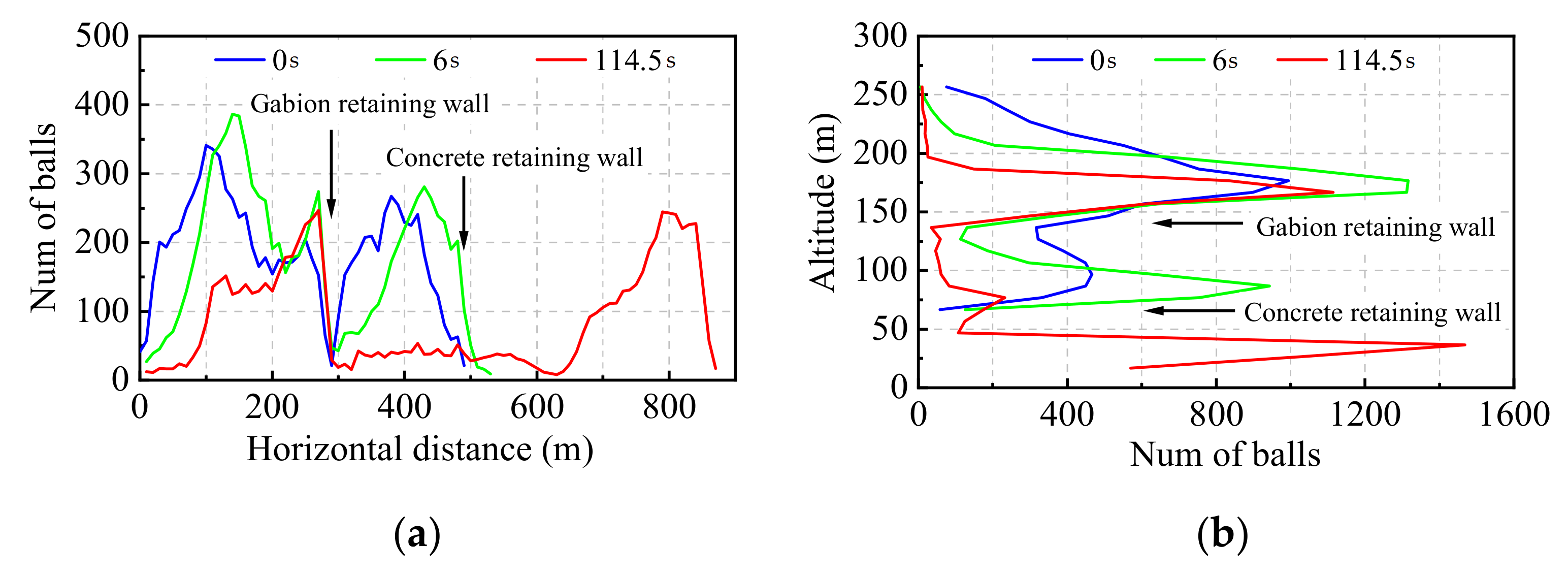
5.3. Time History Analysis of the Rockfill Slope
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Cundall, P.A.; Strack, O.D. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Liu, Q.; Sun, L.; Tang, X. Investigate the influence of the in-situ stress conditions on the grout penetration process in fractured rocks using the combined finite-discrete element method. Eng. Anal. Bound. Elem. 2019, 106, 86–101. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, C.; Yang, C.; Ma, C.; Pan, Z. Effect of fine-grained dipping interlayers on mechanical behavior of tailings using discrete element method. Eng. Anal. Bound. Elem. 2019, 104, 288–299. [Google Scholar] [CrossRef]
- Zhou, W.; Ma, G.; Liu, J.Y.; Chang, X.L.; Li, S.L.; Xu, K. Review of macro- and mesoscopic analysis on rockfill materials in high dams. Sci. Sin. Technol. 2018, 48, 1068–1080. (In Chinese) [Google Scholar] [CrossRef]
- Maranha, D.N.E. Advances in Rockfill Structures; Springer: New York, NY, USA, 1991; pp. 11–23. [Google Scholar] [CrossRef]
- Zhang, R.; Sun, Y.; Song, E. Simulation of dynamic compaction and analysis of its efficiency with the material point method. Comput. Geotech. 2019, 116, 103218.1–103218.19. [Google Scholar] [CrossRef]
- Shahzadi, G.; Soulaïmani, A. Deep Neural Network and Polynomial Chaos Expansion-Based Surrogate Models for Sensitivity and Uncertainty Propagation: An Application to a Rockfill Dam. Water 2021, 13, 1830. [Google Scholar] [CrossRef]
- Xiao, Q. Simulating the hydraulic heave phenomenon with multiphase fluid flows using cfd-dem. Water 2020, 12, 1077. [Google Scholar] [CrossRef] [Green Version]
- Tang, C.L.; Hu, J.C.; Lin, M.L.; Yuan, R.M.; Cheng, C.C. The mechanism of the 1941 Tsaoling landslide, Taiwan: Insight from a 2D discrete element simulation. Environ. Earth Sci. 2013, 70, 1005–1019. [Google Scholar] [CrossRef] [Green Version]
- Zhou, J.W.; Cui, P.; Fang, H. Dynamic process analysis for the formation of Yangjiagou landslide-dammed lake triggered by the Wenchuan earthquake, China. Landslides 2013, 10, 331–342. [Google Scholar] [CrossRef]
- Chen, X.; Wang, H. Slope failure of noncohesive media modelled with the combined finite–discrete element method. Appl. Sci. 2019, 9, 579. [Google Scholar] [CrossRef] [Green Version]
- Mendes, N.; Zanotti, S.; Lemos, J.V. Seismic Performance of Historical Buildings Based on Discrete Element Method: An Adobe Church. J. Earthq. Eng. 2018, 24, 1270–1289. [Google Scholar] [CrossRef]
- Zhu, C.; Huang, Y.; Sun, J. Solid-like and liquid-like granular flows on inclined surfaces under vibration—Implications for earthquake-induced landslides. Comput. Geotech. 2020, 123, 103598. [Google Scholar] [CrossRef]
- Zheng, Y.; Wang, R.; Chen, C.; Sun, C.; Zhang, W. Dynamic analysis of anti-dip bedding rock slopes reinforced by pre-stressed cables using discrete element method. Eng. Anal. Bound. Elem. 2021, 130, 79–93. [Google Scholar] [CrossRef]
- Zhang, J.W.; Zhang, M.X.; Li, M.C.; Min, Q.L.; Shi, B.W.; Song, L.G. Nonlinear dynamic response of a CC-RCC combined dam structure under oblique incidence of near-fault ground motions. Appl. Sci. 2020, 10, 885. [Google Scholar] [CrossRef] [Green Version]
- Karabulut, M.; Kartal, M.E. Seismic analysis of Roller Compacted Concrete (RCC) dams considering effect of viscous boundary conditions. Comput. Concr. 2020, 25, 255–266. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, Y.; Peng, G. Effect of water pressure on mechanical behavior of concrete under dynamic compression state. Constr. Build. Mater. 2016, 125, 501–509. [Google Scholar] [CrossRef]
- Bao, H.; Hatzor, Y.H.; Xin, H. A new viscous boundary condition in the two-dimensional discontinuous deformation analysis method for wave propagation problems. Rock Mech. Rock Eng. 2012, 45, 919–928. [Google Scholar] [CrossRef]
- Cui, F.P.; Xiong, C.; Wu, Q.; Xu, Q.; Li, N.; Wu, N.A.; Cui, L. Dynamic response of the Daguangbao landslide triggered by the Wenchuan earthquake with a composite hypocenter. Geomat. Nat. Hazards Risk 2021, 12, 2170–2193. [Google Scholar] [CrossRef]
- Gu, J.; Zhao, Z.Y. Considerations of the discontinuous deformation analysis on wave propagation problems. Int. J. Numer. Anal. Met. 2009, 33, 1449–1465. [Google Scholar] [CrossRef]
- Yang, C.W.; Zhang, J.J.; Zhang, M. A prediction model for horizontal run-out distance of landslides triggered by Wenchuan earthquake. Earthq. Eng. Eng. Vib. 2013, 12, 201–208. [Google Scholar] [CrossRef]
- Yang, C.W.; Feng, N.; Zhang, J.J.; Bi, J.W.; Zhang, J. Research on time-frequency analysis method of seismic stability of covering-layer type slope subjected to complex wave. Environ. Earth Sci. 2015, 74, 5295–5306. [Google Scholar] [CrossRef]
- Shi, C.; Zhang, Q.; Wang, S.N. Numerical Simulation Technology and Application with Particle Flow Code (PFC5.0); China Architecture and Building Press: Beijing, China, 2018; pp. 11–23. [Google Scholar]
- Zhou, X.; Sheng, Q.; Cui, Z. Dynamic boundary setting for discrete element method considering the seismic problems of rock masses. Granul. Matter 2019, 21, 66. [Google Scholar] [CrossRef]
- Zhou, X.T.; Sheng, Q.; Leng, X.L.; Fu, X.D.; Cui, Z. Viscous artificial boundary for seismic dynamic time-history analysis with granular discrete element method and its application. Chin. J. Rock Mech. Eng. 2017, 4, 154–165. (In Chinese) [Google Scholar] [CrossRef]
- Zhou, X.T.; Wei, P.F.; Fu, X.D.; Li, L.H.; Xue, X.H. Dynamic Process and Mechanism of the Catastrophic Taihongcun Landslide Triggered by the 2008 Wenchuan Earthquake Based on Field Investigations and Discrete Element Method Simulations. Front. Earth Sci. 2021, 9, 710031. [Google Scholar] [CrossRef]
- Wang, J.; Chi, S.; Shao, X.; Zhou, X. Determination of the mechanical parameters of the microstructure of rockfill materials in triaxial compression DEM simulation. Comput. Geotech. 2021, 137, 104265. [Google Scholar] [CrossRef]
- Zhang, P.T.; Sun, X.J.; Zhou, X.J.; Zhang, Y.X. Experimental simulation and a Rapid reliable calibration method of rockfill microscopic parameters by considering flexible boundary. Powder Technol. 2021, 396, 279–290. [Google Scholar] [CrossRef]
- Eskandar, H.; Sadollah, A.; Bahreininejad, A.; Hamdi, M. Water cycle algorithm—A novel metaheuristic optimization method for solving constrained engineering optimization problems. Comput. Struct. 2012, 110–111, 151–166. [Google Scholar] [CrossRef]
- Shields, M.D.; Zhang, J.X. The generalization of Latin hypercube sampling. Reliab. Eng. Syst. Safe. 2016, 148, 96–108. [Google Scholar] [CrossRef] [Green Version]
- Yang, Z.P.; Lai, Y.L.; Liu, S.L.; Tian, X.; Hu, Y.X.; Ren, S.P. Dynamic stability and failure mode of slopes with overlying weak rock mass under frequent micro-seismic actions. Chin. J. Geotech. Eng. 2019, 41, 131–140. (In Chinese) [Google Scholar] [CrossRef]
- Qiao, S.; Zhou, Y.; Zhou, Y.; Wang, R. A simple water cycle algorithm with percolation operator for clustering analysis. Soft Comput. 2016, 23, 4081–4095. [Google Scholar] [CrossRef]
- Mahdavi-Nasab, N.; Abouei Ardakan, M.; Mohammadi, M. Water cycle algorithm for solving the reliability-redundancy allocation problem with a choice of redundancy strategies. Commun. Stat. Theory Methods 2019, 49, 2728–2748. [Google Scholar] [CrossRef]
- Ghosh, P.K.; Sadhu, P.K.; Basak, R.; Sanyal, A. Energy efficient design of three phase induction motor by water cycle algorithm—sciencedirect. Ain Shams Eng. J. 2020, 11, 1139–1147. [Google Scholar] [CrossRef]
- Hadjaissa, A.; Ameur, K.; Boutoubat, M. AWCA-based optimization of a fuzzy sliding-mode controller for stand-alone hybrid renewable power system. Soft Comput. 2019, 3, 7831–7842. [Google Scholar] [CrossRef]
- Mahdavi, S.H.; Rofooei, F.R.; Sadollah, A.; Xu, C. A wavelet-based scheme for impact identification of framed structures using combined genetic and water cycle algorithms. J. Sound Vib. 2019, 443, 25–46. [Google Scholar] [CrossRef]
- Xu, Y.; Mei, Y. A modified water cycle algorithm for long-term multi-reservoir optimization. Appl. Soft Comput. 2018, 71, 317–332. [Google Scholar] [CrossRef]
- Heidari, A.A.; Ali Abbaspour, R.; Rezaee Jordehi, A. An efficient chaotic water cycle algorithm for optimization tasks. Neural Comput. Appl. 2017, 28, 57–85. [Google Scholar] [CrossRef]
- Osaba, E.; Del Ser, J.; Sadollah, A.; Bilbao, M.N.; Camacho, D. A discrete water cycle algorithm for solving the symmetric and asymmetric traveling salesman problem. Appl. Soft Comput. 2018, 71, 277–290. [Google Scholar] [CrossRef]
- Nasir, M.; Sadollah, A.; Choi, Y.H.; Kim, J.H. A comprehensive review on water cycle algorithm and its applications. Neural Comput. Appl. 2020, 32, 17433–17488. [Google Scholar] [CrossRef]
- Sayyaadi, H.; Sadollah, A.; Yadav, A.; Yadav, N. Stability and iterative convergence of water cycle algorithm for computationally expensive and combinatorial internet shopping optimisation problems. J. Exp. Theor. Artif. Intell. 2019, 31, 701–721. [Google Scholar] [CrossRef]
- Kleijnen, J. Kriging metamodeling in simulation: A review. Eur. J. Oper. Res. 2009, 192, 707–716. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.P.; Li, B. 3D viscoelastic artificial boundary unified in static and dynamic state. Sci. China Ser. E Eng. Mater. Sci. 2005, 9, 72–86. (In Chinese) [Google Scholar] [CrossRef]
- Ma, C.H.; Jie, Y.; Zenz, G.; Staudacher, E.J.; Cheng, L. Calibration of the microparameters of the discrete element method using a relevance vector machine and its application to rockfill materials. Adv. Eng. Softw. 2020, 147, 102833. [Google Scholar] [CrossRef]
- Liu, Y.F. Damic Response of Slope Based on Particle Flow Theory. Master’s Thesis, Southwest Jiaotong University, Chengdu, China, 2016. (In Chinese). [Google Scholar]





| Dimension | Type of Wave | Range | Recommendation [43] |
|---|---|---|---|
| 2D | Transverse wave | 0.35–0.65 | 1/2 |
| longitudinal wave | 0.8–1.2 | 2/2 | |
| 3D | Transverse wave | 0.5–1.0 | 2/3 |
| longitudinal wave | 1.0–2.0 | 4/3 |
| Longitudinal Wave | S-Wave | ||||
|---|---|---|---|---|---|
| Adjustment coefficients | Boundary | Range | Calibration results | Range | Calibration results |
| Left (reflection) | [0.5, 2.0] | 0.97 | [0.2, 1.5] | 0.65 | |
| Right (reflection) | [0.5, 2.0] | 0.96 | [0.2, 1.5] | 0.68 | |
| Bottom (input) | [0.5, 2.0] | 1.02 | [0.2, 1.5] | 0.61 | |
| Simulated wave velocity (m/s) | 3512 | 1853 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, C.; Gao, Z.; Yang, J.; Cheng, L.; Zhao, T. Calibration of Adjustment Coefficient of the Viscous Boundary in Particle Discrete Element Method Based on Water Cycle Algorithm. Water 2022, 14, 439. https://doi.org/10.3390/w14030439
Ma C, Gao Z, Yang J, Cheng L, Zhao T. Calibration of Adjustment Coefficient of the Viscous Boundary in Particle Discrete Element Method Based on Water Cycle Algorithm. Water. 2022; 14(3):439. https://doi.org/10.3390/w14030439
Chicago/Turabian StyleMa, Chunhui, Zhiyue Gao, Jie Yang, Lin Cheng, and Tianhao Zhao. 2022. "Calibration of Adjustment Coefficient of the Viscous Boundary in Particle Discrete Element Method Based on Water Cycle Algorithm" Water 14, no. 3: 439. https://doi.org/10.3390/w14030439
APA StyleMa, C., Gao, Z., Yang, J., Cheng, L., & Zhao, T. (2022). Calibration of Adjustment Coefficient of the Viscous Boundary in Particle Discrete Element Method Based on Water Cycle Algorithm. Water, 14(3), 439. https://doi.org/10.3390/w14030439









