Groundwater Vulnerability Analysis of Tirnavos Basin, Central Greece: An Application of RIVA Method
Abstract
:1. Introduction
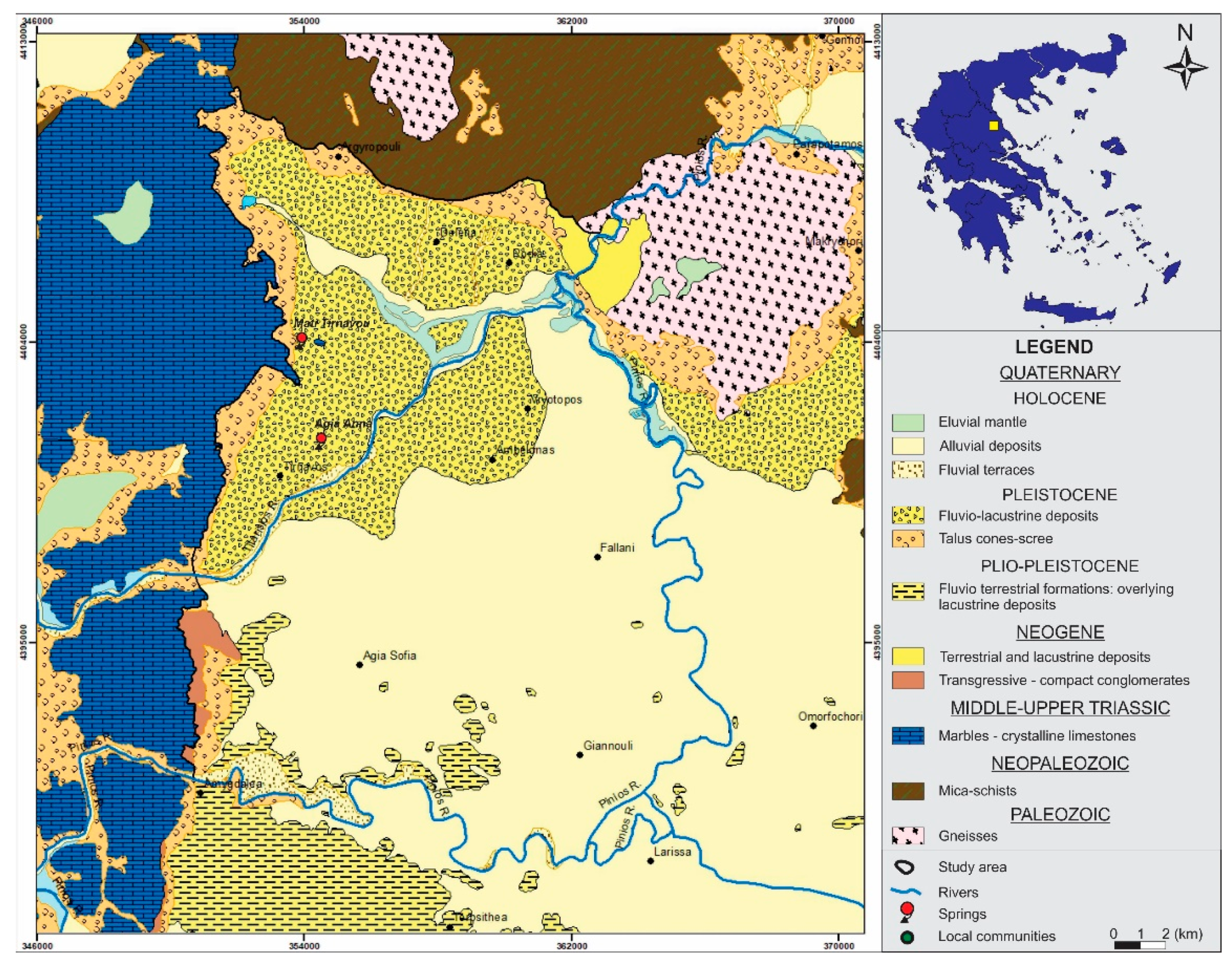
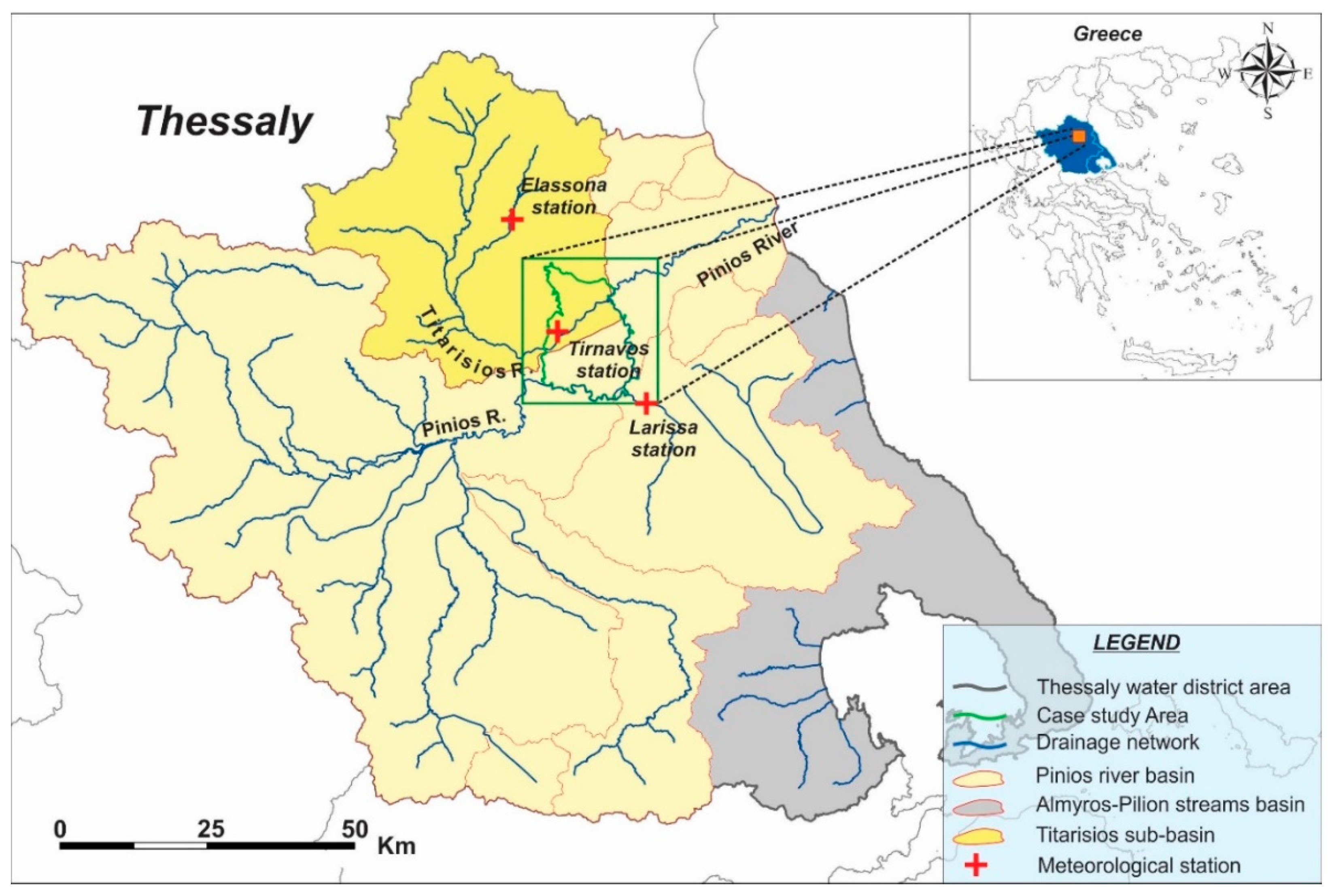
2. Case Study Area
3. Materials and Methods
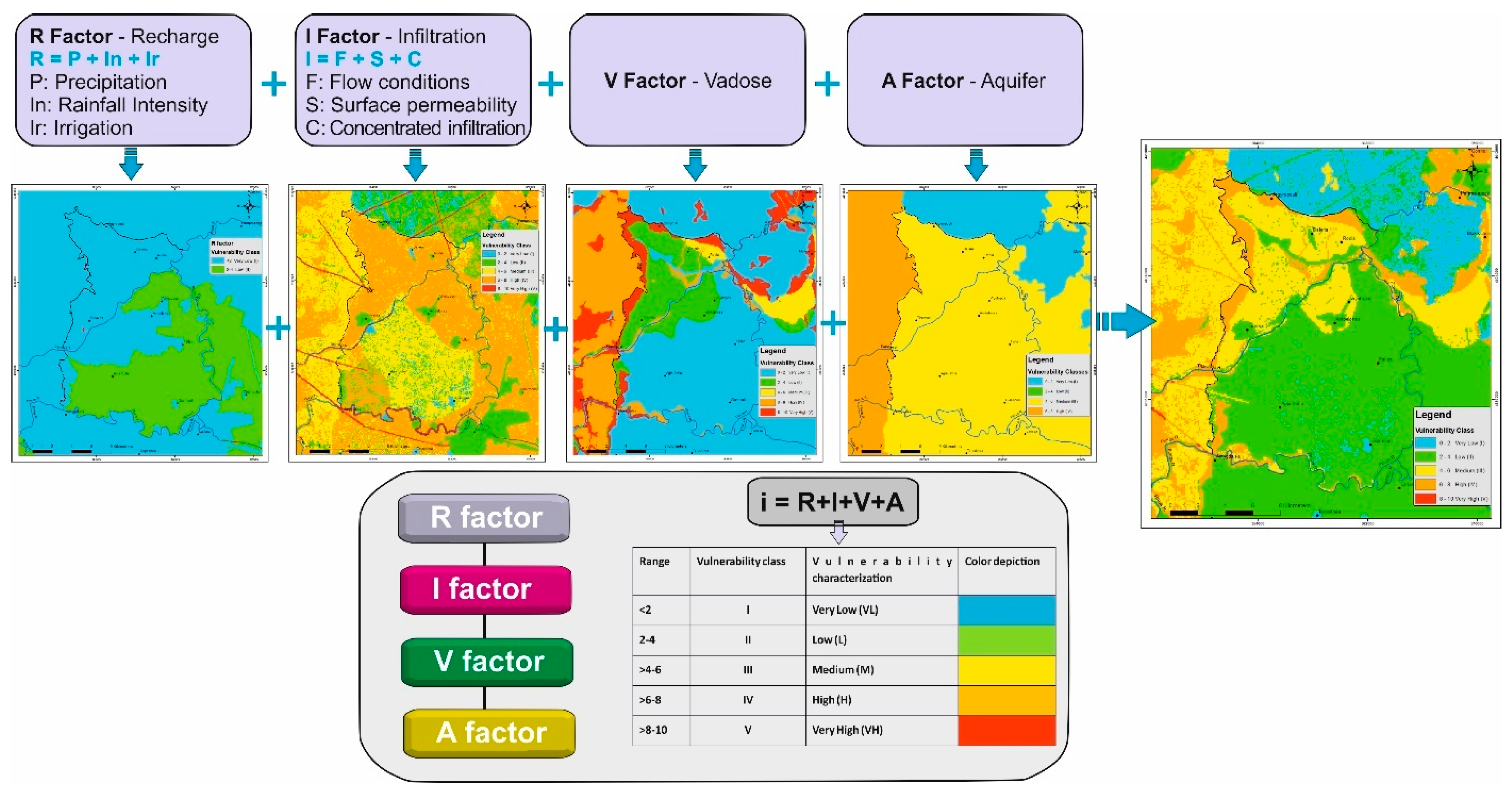
4. Results
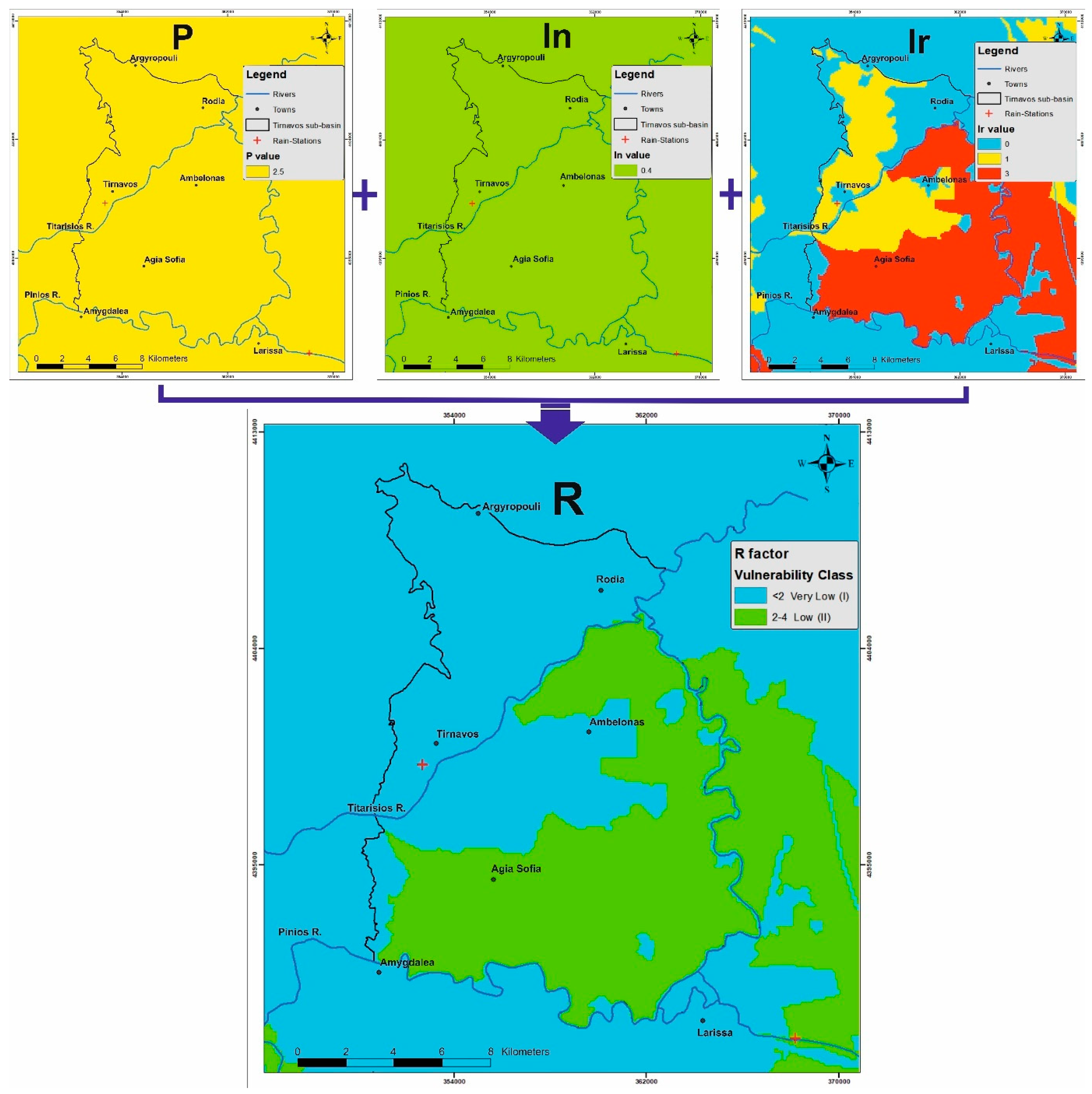
4.1. R Factor Description
- R = recharge factor
- P = precipitation sub-factor
- In = rainfall intensity sub-factor
- Ir = irrigation recharge sub-factor
4.1.1. P Sub-Factor Calculation
4.1.2. In Sub-Factor Calculation
- In = intensity value of rainfall
- ΣΡ = total precipitation at a given period (mm)
- Σd = total number of rainfall days in the same period (days)
4.1.3. Ir Sub-Factor Calculation
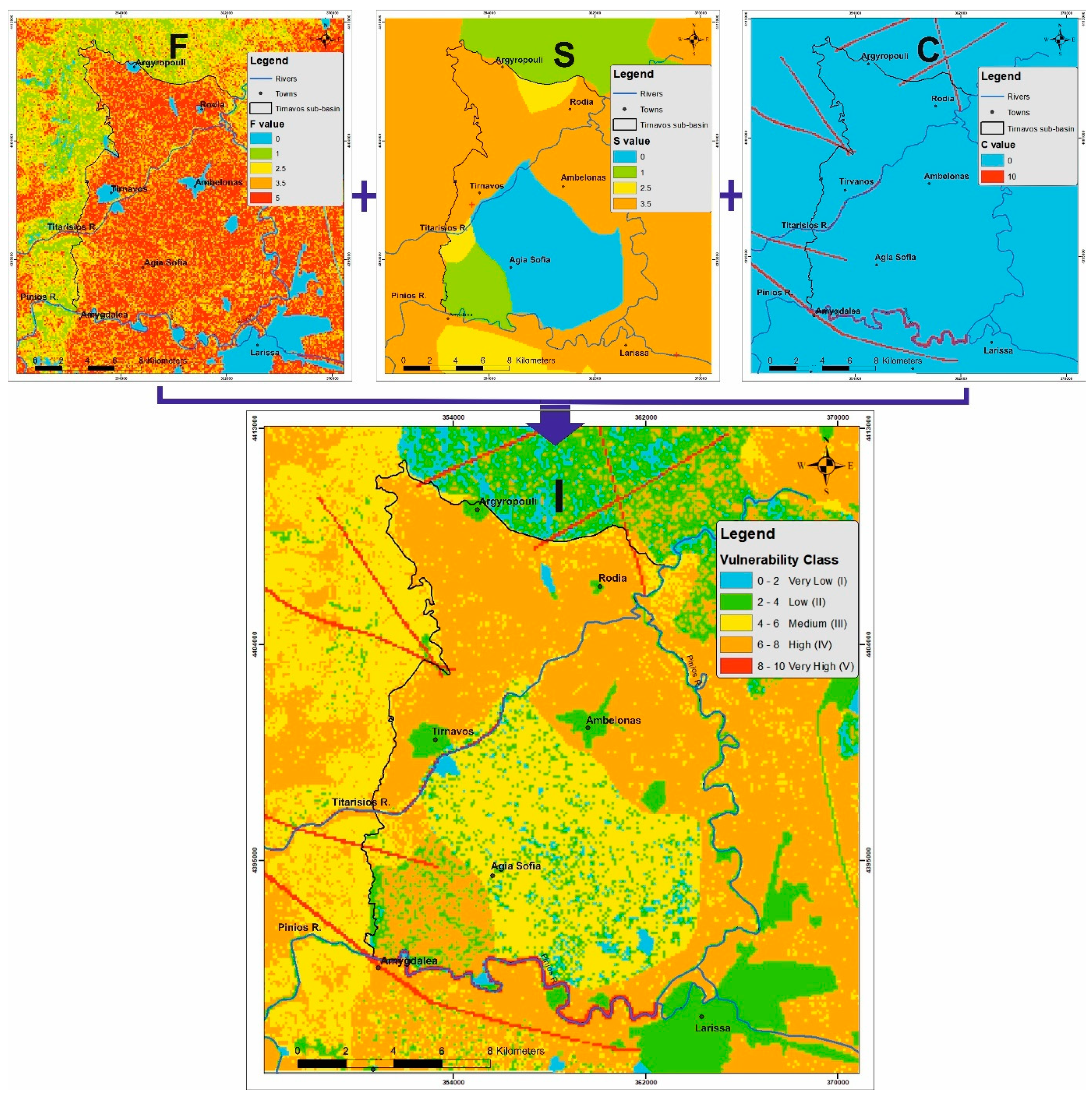
4.2. I Factor Description
- I = infiltration factor
- F = flow conditions sub-factor
- S = permeability of the surface medium
- C = concentrated infiltration sub-factor
4.2.1. F Sub-Factor Calculation
4.2.2. S Sub-Factor Calculation
4.2.3. C Sub-Factor Calculation
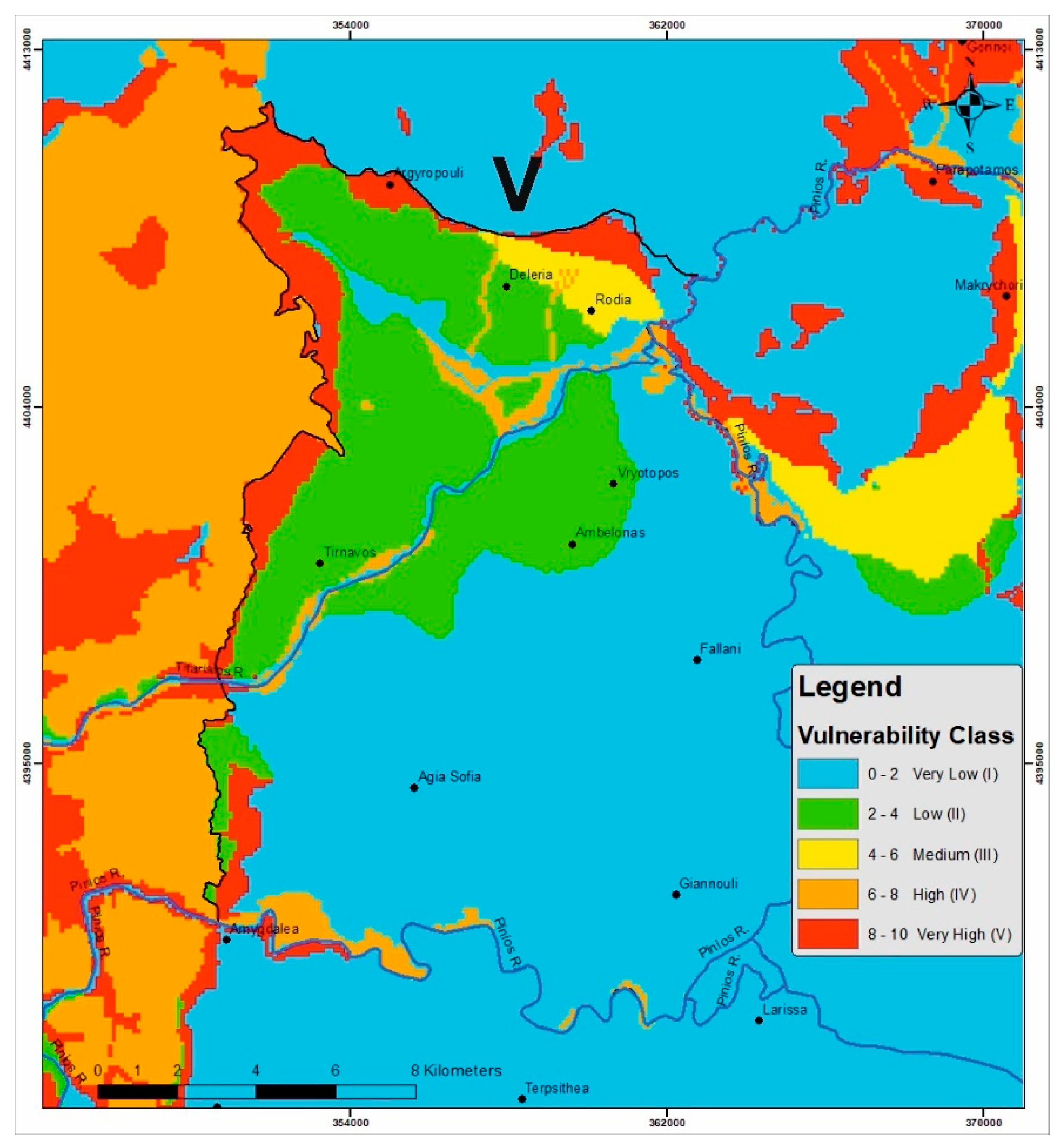
4.3. V Factor Description
- Initially, each geological formation of the vadose zone of the study area is classified according to its dominant lithological type, prior to any secondary effects (e.g., karstification), and is attributed a “reference layer (ly) value” based on its permeability range, as shown in Table S9 in the supplementary documents.
- The “ly” values are multiplied by the fracturing or karstification factor (f), corresponding to an internal modification of the initial value “ly” due to secondary effects that impact permeability. The “f” factor derives from assessing the fracturing/karstification degree of the considered geological formation (only for the lithified) based on the values of Table S10 in the supplementary documents.
- The derived product is multiplied by the total thickness of the formation in meters to provide the final value of the protective cover (pc), which corresponds to a class of V factor, shown in Table S11 (Supplementary document). If the vadose zone consists of more than one layer in the vertical dimension, each formation is calculated individually as described, and then, all are summed up to calculate the final “pc” value.
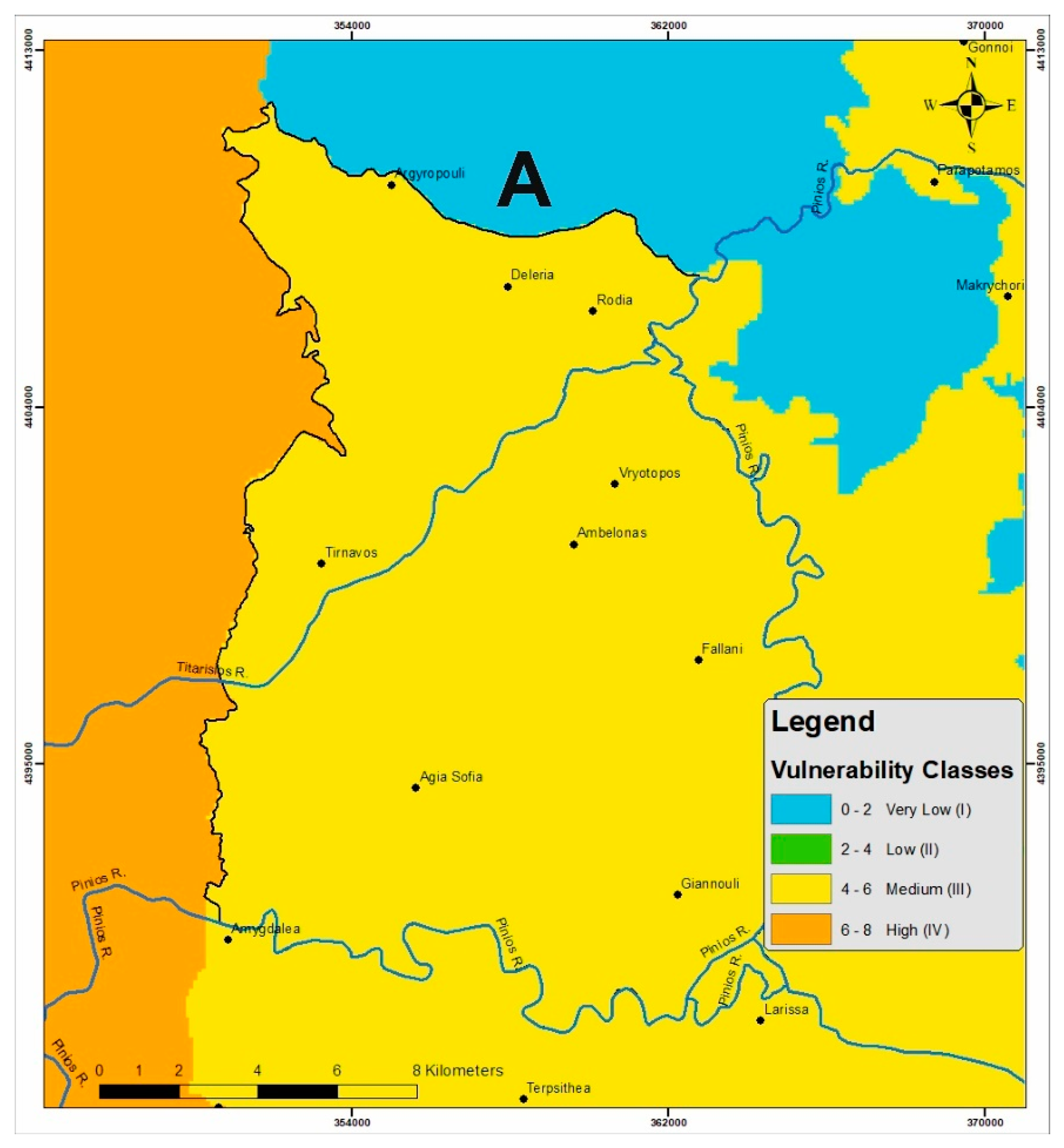
4.4. A Factor Description
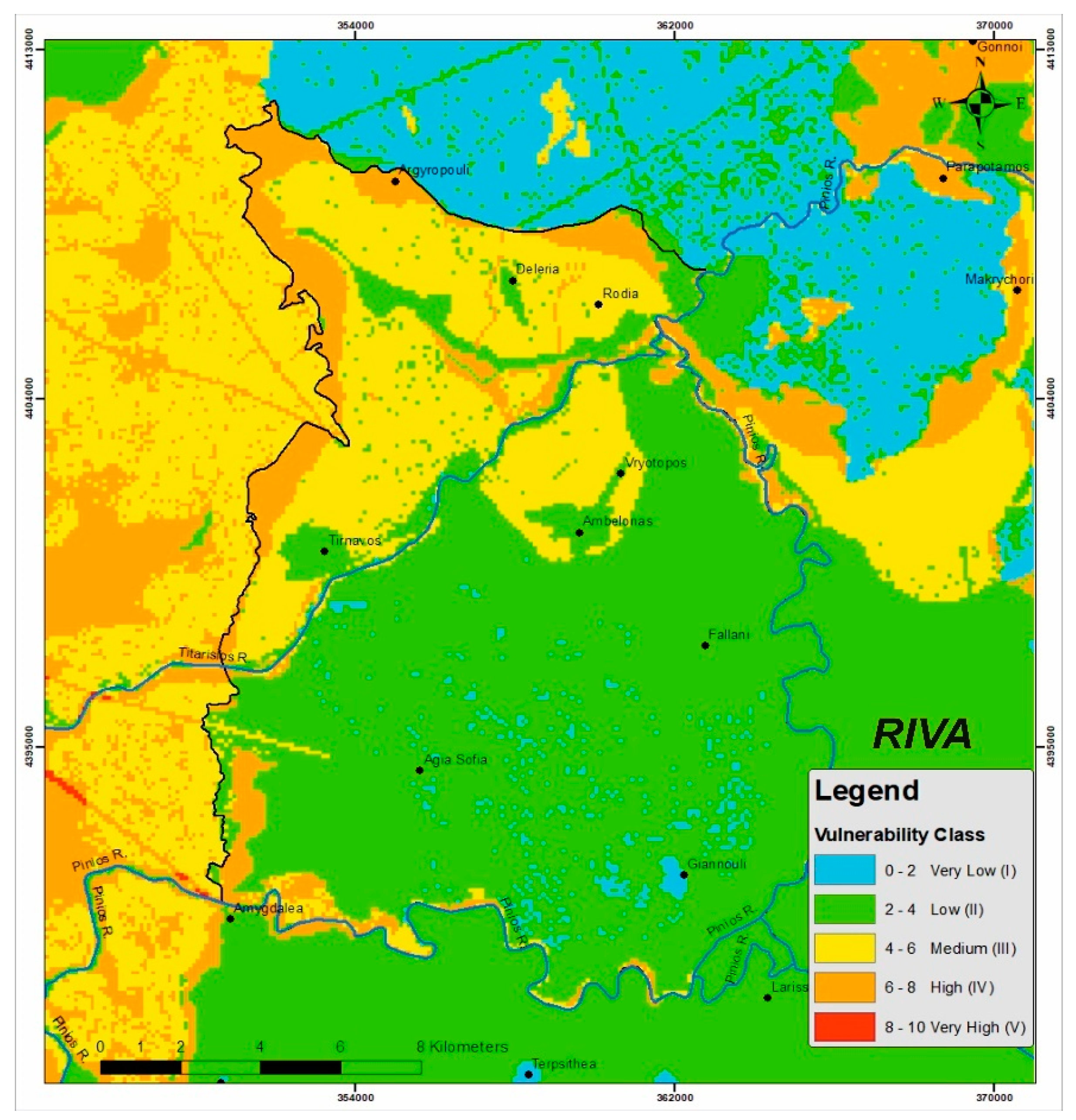
4.5. Compilation of Results
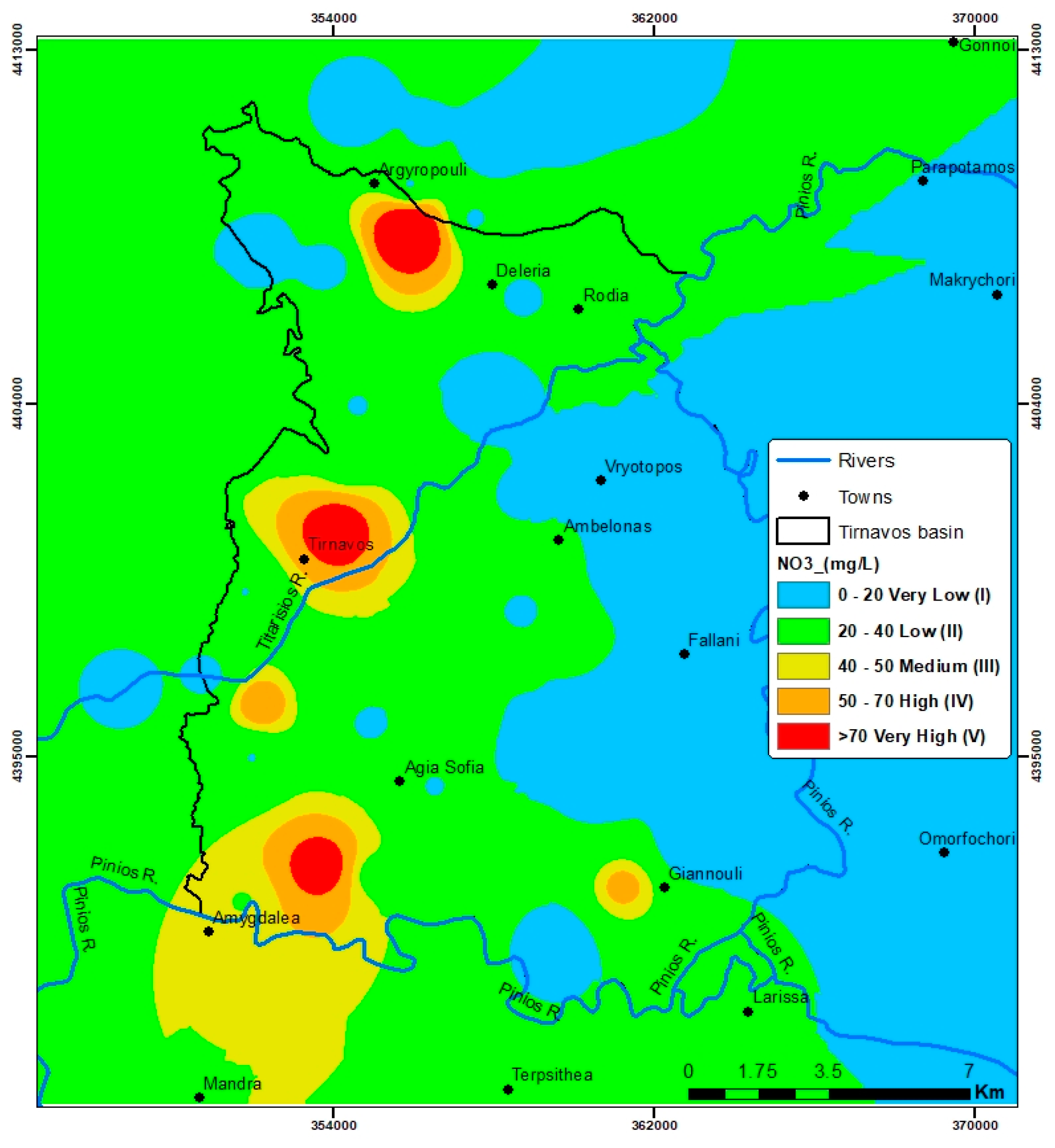
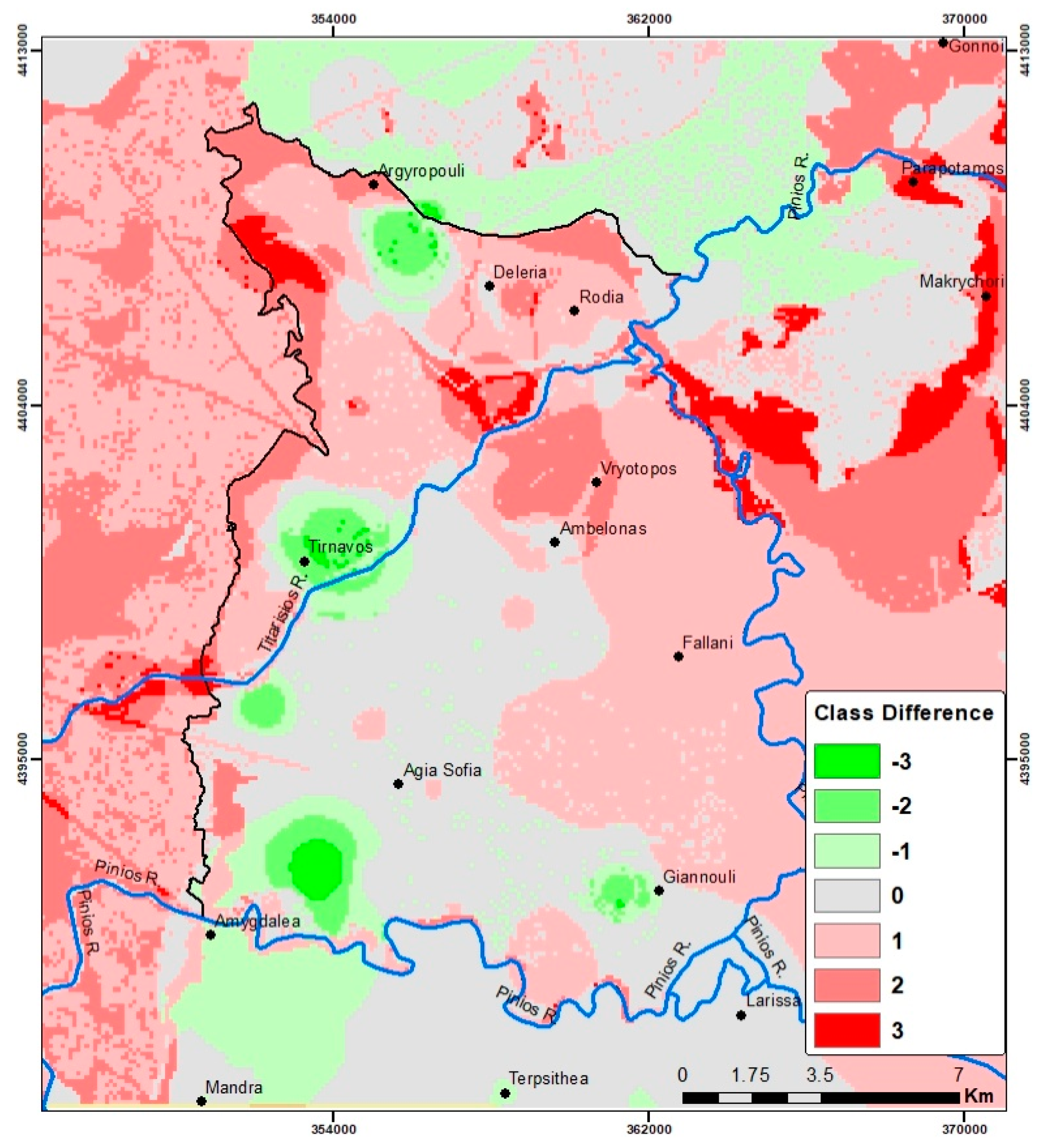
4.6. Validation
5. Discussion
- Insight to the factors used
- Challenges and problems
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Younger, P.L. Groundwater in the Environment: An Introduction; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar]
- Wachniew, P.; Zurek, A.J.; Stumpp, C.; Gemitzi, A.; Gargini, A.; Filippini, M.; Rozanski, K.; Meeks, J.; Kværner, J.; Witczak, S. Toward operational methods for the assessment of intrinsic groundwater vulnerability: A review. Crit. Rev. Environ. Sci. Technol. 2016, 46, 827–884. [Google Scholar] [CrossRef]
- Nageswara, R.K.; Narendra, K. Mapping and evaluation of urban sprawling in the Mehadrigedda watershed in Visakhapatnam metropolitan region using remote sensing and GIS. Curr. Sci. 2006, 91, 1552–1557. [Google Scholar]
- Lindström, R. Groundwater Vulnerability Assessment Using Process-Based Models. Ph.D. Thesis, KTH, Stockholm, Sweden, 2005. [Google Scholar]
- Milnes, E. Process-based groundwater salinisation risk assessment methodology: Application to the Akrotiri aquifer (Southern Cyprus). J. Hydrol. 2011, 399, 29–47. [Google Scholar] [CrossRef] [Green Version]
- Popescu, I.C.; Brouyère, S.; Dassargues, A. The APSÛ method for process-based groundwater vulnerability assessment. Hydrogeol. J. 2019, 27, 2563–2579. [Google Scholar] [CrossRef]
- Masetti, M.; Sterlacchini, S.; Ballabio, C.; Sorichetta, A.; Poli, S. Influence of threshold value in the use of statistical methods for groundwater vulnerability assessment. Sci. Total Environ. 2009, 407, 3836–3846. [Google Scholar] [CrossRef]
- Sorichetta, A.; Masetti, M.; Ballabio, C.; Sterlacchini, S.; Beretta, G.P. Reliability of groundwater vulnerability maps obtained through statistical methods. J. Environ. Manag. 2011, 92, 1215–1224. [Google Scholar] [CrossRef]
- Li, X.; Philp, J.; Cremades, R.; Roberts, A.; He, L.; Li, L.; Yu, Q. Agricultural vulnerability over the Chinese Loess Plateau in response to climate change: Exposure, sensitivity, and adaptive capacity. Ambio 2016, 45, 350–360. [Google Scholar] [CrossRef] [Green Version]
- Gogu, R.C.; Dassargues, A. Current trends and future challenges in groundwater vulnerability assessment using overlay and index methods. Environ. Geol. 2000, 39, 549–559. [Google Scholar] [CrossRef]
- Antonakos, A.K.; Lambrakis, N.J. Development and testing of three hybrid methods for the assessment of aquifer vulnerability to nitrates, based on the drastic model, an example from NE Korinthia, Greece. J. Hydrol. 2007, 333, 288–304. [Google Scholar] [CrossRef]
- Pacheco, F.A.L.; Pires, L.M.G.R.; Santos, R.M.B.; Fernandes, L.S. Factor weighting in DRASTIC modeling. Sci. Total Environ. 2015, 505, 474–486. [Google Scholar] [CrossRef]
- Boufekane, A.; Saighi, O. Application of groundwater vulnerability overlay and index methods to the Jijel plain area (Algeria). Groundwater 2018, 56, 143–156. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shirazi, S.M.; Imran, H.M.; Akib, S. GIS-based DRASTIC method for groundwater vulnerability assessment: A review. J. Risk Res. 2012, 15, 991–1011. [Google Scholar] [CrossRef]
- Focazio, M.J. Assessing Ground-Water Vulnerability to Contamination: Providing Scientifically Defensible Information for Decision Makers; US Government Printing Office: Washington, DC, USA, 1984; Volume 1224. [Google Scholar]
- Brindha, K.; Elango, L. Cross comparison of five popular groundwater pollution vulnerability index approaches. J. Hydrol. 2015, 524, 597–613. [Google Scholar] [CrossRef]
- Aller, L.; Bennett, T.; Lehr, J.; Petty, R.J.; Hackett, G. DRASTIC: A Standardized System for Evaluating Ground Water Pollution Potential Using Hydrogeologic Settings; US Environmental Protection Agency: Washington, DC, USA, 1987; Volume 455. [Google Scholar]
- Foster, S.S.D. Fundamental Concepts in Aquifer Vulnerability, Pollution Risk and Protection Strategy; Netherlands Organization for Applied Scientific Research: The Hague, The Netherlands, 1987; Volume 38, pp. 69–86. [Google Scholar]
- Stempvoort, D.V.; Ewert, L.; Wassenaar, L. Aquifer vulnerability index: A GIS-compatible method for groundwater vulnerability mapping. Can. Water Resour. J. 1993, 18, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Navulur, K.C.S. Groundwater Vulnerability Evaluation to Nitrate Pollution on a Regional Scale Using GIS. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 1996. [Google Scholar]
- Doerfliger, N.; Jeannin, P.Y.; Zwahlen, F. Water vulnerability assessment in karst environments: A new method of defining protection areas using a multi-attribute approach and GIS tools (EPIK method). Environ. Geol. 1999, 39, 165–176. [Google Scholar] [CrossRef] [Green Version]
- Lappas, I.; Kallioras, A.; Pliakas, F.; Rondogianni, T. Groundwater vulnerability assessment to seawater intrusion through GIS-based Galdit method. Case study: Atalanti coastal aquifer, central Greece. Bull. Geol. Soc. Greece 2016, 50, 798–807. [Google Scholar] [CrossRef] [Green Version]
- Petelet-Giraud, E.; Dörfliger, N.; Crochet, P. RISKE: Méthode d’évaluation multicritère de la cartographie de la vulnérabilité des aquifères karstiques. Application aux systèmes des Fontanilles et Cent-Fonts (Hérault, Sud de la France). Hydrogéologie (Orléans) 2000, 4, 71–88. [Google Scholar]
- Allouche, N.; Maanan, M.; Gontara, M.; Rollo, N.; Jmal, I.; Bouri, S. A global risk approach to assessing groundwater vulnerability. Environ. Model. Softw. 2017, 88, 168–182. [Google Scholar] [CrossRef]
- Vrba, J.; Zaporozec, A. Guidebook on Mapping Groundwater Vulnerability; Heise: Niedersachsen, Germany, 1994. [Google Scholar]
- Tziritis, E.; Pisinaras, V.; Panagopoulos, A.; Arampatzis, G. RIVA: A new proposed method for assessing intrinsic groundwater vulnerability. Environ. Sci. Pollut. Res. 2020, 28, 7043–7067. [Google Scholar] [CrossRef]
- Zwahlen, F. Vulnerability and Risk Mapping for the Protection of Carbonate (Karst) Aquifers; Office for Official Publications of the European Communities: Luxembourg, 2003; Available online: https://www.cost.eu/publications/vulnerability-and-risk-mapping-for-the-protection-of-carbonate-karst-aquifers-final-report/(PDF) (accessed on 18 January 2022).
- Vrouhakis, I.; Panagopoulos, A.; Stamatis, G. Current Quality and Quantity Status of Tirnavos sub-Basin Water System—Central Greece. In Proceedings of the 11th International Hydrogeological Congress of the Greece, Athens, Greece, 4–6 October 2017. [Google Scholar]
- European Environment Agency. CORINE Land Cover, Methodology and Nomenclature. Available online: https://www.eea.europa.eu/publications/COR0-landcover (accessed on 18 January 2022).
- Plastiras, V. Geological Map of Greece, Larissa Sheet; Institute of Geology and Mineral Exploitation: Athens, Greece, 1982. [Google Scholar]
- Miggiros, G. Geological Map of Greece, Gonnoi Sheet; Institute of Geology and Mineral Exploitation: Athens, Greece, 1980. [Google Scholar]
- Alexandridis, T.; Panagopoulos, A.; Galanis, G.; Alexiou, I.; Cherif, I.; Chemin, Y.; Stavrinos, E.; Bilas, G.; Zalidis, G. Combining remotely sensed surface energy fluxes and GIS analysis of groundwater parameters for irrigation assessment. Irrig. Sci. 2014, 32, 127–140. [Google Scholar] [CrossRef]
- Panagopoulos, A. A Methodology for Groundwater Resources Management of a Typical Alluvial Aquifer System in Greece. Ph.D. Thesis, School of Earth Sciences, Faculty of Science, University of Birmingham, Birmingham, UK, 1995. [Google Scholar]
- Vrouhakis, I.; Tziritis, E.; Panagopoulos, A.; Kulls, C.; Stamatis, G. The Use of Environmental Stable Isotopes at the Tirnavos Alluvial Basin (Central Greece). In Proceedings of the 15th International Congress of the Geological Society of Greece, Athens, Greece, 22–24 May 2019. [Google Scholar]
- Demitrack, A. The Late Quaternary Geologic History of the Larissa Plain, Thessaly, Greece: Tectonic, Climatic, and Human Impact on the Landscape. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1986; p. 117, (Unpublished). [Google Scholar]
- Vrouhakis, I.; Pisinaras, V.; Panagopoulos, A.; Stamatis, G. Multivariate Statistical Analyses of Groundwater Hydrochemical Data of Tirnavos Sub-basin (Central Greece). In Proceedings of the 16th International Conference on Environmental Science and Technology, Rhodes, Greece, 4–7 September 2019. [Google Scholar]
- Hellenic National Meteorological Service (HNMS), Digital Data, 1989–2018. Available online: http://emy.gr/emy/en (accessed on 18 January 2022).
- National Centers for Environmental Informations (NCEI), Digital Data, 1989–2018. Available online: https://www.ncei.noaa.gov/ (accessed on 18 January 2022).
- Greek Payment Authority of Common Agricultural Policy Aid Schemes (OPEKEPE), Digital Data. 2015. Available online: https://www.opekepe.gr/en/contact-us-en (accessed on 18 January 2022).
- Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) Global Digital Elevation Model Version 3 (GDEM 003), Digital Data. Available online: https://asterweb.jpl.nasa.gov/gdem.asp (accessed on 18 January 2022).
- Toulios, M.; Katsilouli, E.; Georgiou, T.; Argyropoulos, G.; Dimogiannis, D. Soil Study of Tirnavos Area; National Agricultural Research Foundation, Soil Mapping and Classification Institute: Larissa, Greece, 1997. [Google Scholar]
- Caputo, R.; Helly, B.; Pavlides, S.; Papadopoulos, G. Palaeoseismological investigation of the Tyrnavos fault (Thessaly, central Greece). Tectonophysics 2004, 394, 1–20. [Google Scholar] [CrossRef]
- Karakostas, V.; Papazachos, C.; Papadimitriou, E.; Foumelis, M.; Kiratzi, A.; Pikridas, C.; Kostoglou, A.; Kkallas, C.; Chatzis, N.; Bitharis, S.; et al. The March 2021 Tyrnavos, central Greece, doublet (Μw6. 3 and Mw6. 0): Aftershock relocation, faulting details, coseismic slip and deformation. Bull. Geol. Soc. Greece 2021, 58, 131–178. [Google Scholar] [CrossRef]
- Grenoble, S. Study for the Development of Groundwater in the Thessaly Plain; Technical Report for Groundwater in the Thessaly Plain; Land Reclamation Services of Greece: Thessaly, Greece, 1974. [Google Scholar]
- Antonaropoulos, P.; Vainalis, D. Hydrogeological Study of Artificial Recharge of the Karstic System of Titarisios—Pinios Rivers of Tirnavos Area; Technical Report for Pinios Rivers of Tirnavos Area; Land Reclamation Services of Greece: Larissa, Greece, 2010. [Google Scholar]
- Constantinides, D. Hydrodynamique d’un Systeme Aquifere Heterogene. Ph.D. Thesis, Universite de Grenoble, Saint-Martin-d’Hères, France, 1978. [Google Scholar]
- Davis, S.N.; Turk, L.J. Best well depth in crystalline rocks. Johns. Drillers J. 1969, 41, 1–5. [Google Scholar]
- Freeze, R.A.; Cherry, J.A. Groundwater; Prentice-Hall: Englewood Cliffs, NJ, USA, 1979; 604p. [Google Scholar]
- Voudouris, K. Hydrogeology of the Environment. In Groundwater and Environment; Tziolas Publications: Thessaloniki, Greece, 2009; Volume 460. [Google Scholar]
- Neuner, M.; Smith, L.; Blowes, D.W.; Sego, D.C.; Smith, L.J.; Fretz, N.; Gupton, M. The Diavik waste rock project: Water flow through mine waste rock in a permafrost terrain. Appl. Geochem. 2013, 36, 222–233. [Google Scholar] [CrossRef]
- Owor, M.; Taylor, R.G.; Tindimugaya, C.; Mwesigwa, D. Rainfall intensity and groundwater recharge: Empirical evidence from the Upper Nile Basin. Environ. Res. Lett. 2019, 4, 035009. [Google Scholar] [CrossRef]
- Mileham, L.; Taylor, R.G.; Todd, M.; Tindimugaya, C.; Thompson, J. The impact of climate change on groundwater recharge and runoff in a humid, equatorial catchment: Sensitivity of projections to rainfall intensity. Hydrol. Sci. J. 2009, 54, 727–738. [Google Scholar] [CrossRef] [Green Version]
- Guzzetti, F.; Peruccacci, S.; Rossi, M.; Stark, C.P. The rainfall intensity–duration control of shallow landslides and debris flows: An update. Landslides 2008, 5, 3–17. [Google Scholar] [CrossRef]
- Pavlis, M.; Cummins, E. Assessing the vulnerability of groundwater to pollution in Ireland based on the COST-620 Pan-European approach. J. Environ. Manag. 2014, 133, 162–173. [Google Scholar] [CrossRef]
- Koutsi, R.; Stournaras, G. Groundwater Vulnerability Assessment in the Loussi Polje area, N Peloponessus: The PRESK Method. In Advances in the Research of Aquatic Environment; Springer: Berlin/Heidelberg, Germany, 2014; pp. 335–342. [Google Scholar] [CrossRef]
- Kallioras, A.; Pliakas, F.; Skias, S.; Gkiougkis, I. Groundwater Vulnerability Assessment at S.W. Rhodope Aquifer System in N.E. Greece. In Advances in the Research of Aquatic Environment; Springer: Berlin/Heidelberg, Germany, 2011; pp. 351–358. [Google Scholar] [CrossRef]
- Lohani, S.; Baffaut, C.; Thompson, A.L.; Aryal, N.; Bingner, R.L.; Bjorneberg, D.L.; Bosch, D.D.; Bryant, R.B.; Buda, A.; Dabney, S.M.; et al. Performance of the Soil Vulnerability Index with respect to slope, digital elevation model resolution, and hydrologic soil group. J. Soil Water Conserv. 2020, 75, 12–27. [Google Scholar] [CrossRef] [Green Version]
- Descroix, L.; Viramontes, D.; Vauclin, M.; Barrios, J.G.; Esteves, M. Influence of soil surface features and vegetation on runoff and erosion in the Western Sierra Madre (Durango, Northwest Mexico). Catena 2001, 43, 115–135. [Google Scholar] [CrossRef]
- El Kateb, H.; Zhang, H.; Zhang, P.; Mosandl, R. Soil erosion and surface runoff on different vegetation covers and slope gradients: A field experiment in Southern Shaanxi Province, China. Catena 2013, 105, 1–10. [Google Scholar] [CrossRef]
- United States Department of Agriculture. Soil Taxonomy a Basic System of Soil Classification for Making and Interpreting Soil Surveys, 2nd ed.; Agriculture Handbook; United States Department of Agriculture: Washington, DC, USA, 1999; p. 436. [Google Scholar]
- Lewis, M.A.; Cheney, C.S.; O Dochartaigh, B.E. Guide to Permeability Indices (CR/06/160N); British Geological Survey: Nottingham, UK, 2006; p. 29, (Unpublished). [Google Scholar]
- Panagopoulos, G.P.; Antonakos, A.K.; Lambrakis, N.J. Optimization of the DRASTIC method for groundwater vulnerability assessment via the use of simple statistical methods and GIS. Hydrogeol. J. 2006, 14, 894–911. [Google Scholar] [CrossRef]
- Ravbar, N.; Goldscheider, N. Proposed methodology of vulnerability and contamination risk mapping for the protection of karst aquifers in Slovenia. Acta Carsologica 2007, 36, 3. [Google Scholar] [CrossRef] [Green Version]
- Bear, J. Dynamics of Fluids in Porous Media; Courier Corporation: Chelmsford, MA, USA, 1988. [Google Scholar]
- Ghazavi, R.; Ebrahimi, Z. Assessing groundwater vulnerability to contamination in an arid environment using DRASTIC and GOD models. Int. J. Environ. Sci. Technol. 2015, 12, 2909–2918. [Google Scholar] [CrossRef] [Green Version]
- Zghibi, A.; Merzougui, A.; Chenini, I.; Ergaieg, K.; Zouhri, L.; Tarhouni, J. Groundwater vulnerability analysis of Tunisian coastal aquifer: An application of DRASTIC index method in GIS environment. Groundw. Sustain. Dev. 2016, 2, 169–181. [Google Scholar] [CrossRef]
- EU Commission. Council Directive 91/676/EEC of 12 December 1991 concerning the protection of waters against pollution caused by nitrates from agricultural sources. Off. J. Eur. Community 1991, L375, 1–8. [Google Scholar]
- Chao, W.A.N.G.; Pei-Fang, W.A.N.G. Migration of infiltrated NH4 and NO3 in a soil and groundwater system simulated by a soil tank. Pedosphere 2008, 18, 628–637. [Google Scholar] [CrossRef]
- Tziritis, E.; Lombardo, L. Estimation of intrinsic aquifer vulnerability with index-overlay and statistical methods: The case of eastern Kopaida, central Greece. Appl. Water Sci. 2017, 7, 2215–2229. [Google Scholar] [CrossRef] [Green Version]
- Vías, J.M.; Andreo, B.; Perles, M.J.; Carrasco, F.; Vadillo, I.; Jiménez, P. Proposed method for groundwater vulnerability mapping in carbonate (karstic) aquifers: The COP method. Hydrogeol. J. 2006, 14, 912–925. [Google Scholar] [CrossRef]
- Haidu, I.; Nistor, M.M. Groundwater vulnerability assessment in the Grand Est region, France. Quat. Int. 2020, 547, 86–100. [Google Scholar] [CrossRef]
- Qiang, W.; Bo, L.; Yulong, C. Vulnerability assessment of groundwater inrush from underlying aquifers based on variable weight model and its application. Water Resour. Manag. 2016, 30, 3331–3345. [Google Scholar] [CrossRef]
- Meerkhan, H.; Teixeira, J.; Espinha Marques, J.; Afonso, M.J.; Chaminé, H.I. Delineating groundwater vulnerability and protection zone mapping in fractured rock masses: Focus on the DISCO index. Water 2016, 8, 462. [Google Scholar] [CrossRef] [Green Version]
- Thomas, R.; Duraisamy, V. Hydrogeological delineation of groundwater vulnerability to droughts in semi-arid areas of western Ahmednagar district. Egypt. J. Remote Sens. Space Sci. 2018, 21, 121–137. [Google Scholar] [CrossRef]
- Kumari, R.; Datta, P.S.; Rao, M.S.; Mukherjee, S.; Azad, C. Anthropogenic perturbations induced groundwater vulnerability to pollution in the industrial Faridabad District, Haryana, India. Environ. Earth Sci. 2018, 77, 187. [Google Scholar] [CrossRef]
- Karyotis, T.; Panagopoulos, A.; Pateras, D.; Panoras, A.; Danalatos, N.; Angelakis, C.; Kosmas, C. The Greek Action Plan for the mitigation of nitrates in water resources of the vulnerable district of Thessaly. J. Mediterr. Ecol. 2002, 3, 77–83. [Google Scholar]
- EU Commission. Directive 2000/60/EC of the European Parliament and of the Council of 23 October 2000 establishing a framework for Community action in the field of water policy. Off. J. Eur. Communities 2000, L327, 1–72. [Google Scholar]
- EU Commission. CAP Reform—A Long-Term Perspective for Sustainable Agriculture. 2003. Available online: https://ec.europa.eu/commission/presscorner/detail/en/IP_03_99 (accessed on 18 January 2022).
- Koukidou, Ι.; Panagopoulos, A. Application of FEFLOW for the simulation of groundwater flow at the Tirnavos (central Greece) alluvial basin aquifer system. Bull. Geol. Soc. Greece 2010, 43, 1747–1757. [Google Scholar] [CrossRef] [Green Version]
- Tziatzios, G.; Sidiropoulos, P.; Vasiliades, L.; Tzabiras, J.; Papaioannou, G.; Mylopoulos, N.; Loukas, A. Effects of climate change on groundwater nitrate modelling. In Proceedings of the International Conference on Protection and Restoration of the Environment XIV, Thessaloniki, Greece, 3–6 July 2018. [Google Scholar]
- Lyra, A.; Loukas, A.; Sidiropoulos, P.; Tziatzios, G.; Mylopoulos, N. An integrated modeling system for the evaluation of water resources in coastal agricultural watersheds: Application in Almyros Basin, Thessaly, Greece. Water 2021, 13, 268. [Google Scholar] [CrossRef]
- Panagopoulos, A.; Domakinis, C.; Arampatzis, G.; Charoulis, A.; Vrouhakis, I.; Panoras, A. Seasonal Variations of Aquifer Intrinsic Vulnerability in an Intensively Cultivated Vulnerable Basin of Greece. In Innovative Strategies and Policies for Soil Conservation; Fullen, Μ., Famodimu, J., Karyotis, T., Noulas, C., Panagopoulos, A., Rubio, J., Gabriels, D., Eds.; Catena Verlag: Reiskirchen, Germany, 2015. [Google Scholar]
- Luoma, S.; Okkonen, J.; Korkka-Niemi, K. Comparison of the AVI, modified SINTACS and GALDIT vulnerability methods under future climate-change scenarios for a shallow low-lying coastal aquifer in southern Finland. Hydrogeol. J. 2017, 25, 203–222. [Google Scholar] [CrossRef] [Green Version]
- Panagopoulos, A.; Arampatzis, G.; Tziritis, E.; Pisinaras, V.; Herrmann, F.; Kunkel, R.; Wendland, F. Assessment of climate change impact in the hydrological regime of River Pinios basin, central Greece. Desalination Water Treat. 2016, 57, 2256–2267. [Google Scholar] [CrossRef]
- Tziritis, E.; Pisinaras, V.; Kunkel, R.; Panagopoulos, A.; Arampatzis, G.; Wendland, F. Assessing the Potential Effects of Climate Change in the Hydrologic Budget of a Large Mediterranean Basin: The Case of River Pinios Basin, Central Greece. In Proceedings of the International Conference Adapt to Climate, Nicosia, Cyprus, 27–28 May 2014; pp. 1–13. [Google Scholar]
- Kotsopoulos, S.; Nastos, P.; Ghionis, G.; Lazogiannis, K.; Poulos, S.; Alexiou, I.; Panagopoulos, A.; Farsirotou, E.; Alamanis, N. Evaporation and Evapotranspiration Estimates under Present and Future Climate Conditions. In Proceedings of the 12th International Conference, Protection & Restoration of the Environment—PRE12, Skiathos Island, Greece, 29 June–4 July 2014; pp. 91–97. [Google Scholar]

| Factor | Sub-Factor | Material | Source |
|---|---|---|---|
| R | P | Rainfall data series | [37,38] |
| In | Rainfall data series | [37,38] | |
| Ir | Spatial data of irrigated fields | [39] | |
| Dominant irrigation methods | Local Land Reclamations Organizations (Tirnavou, Agia Sofia, Ambelona) personal communication | ||
| I | F | Digital Elevation Model | [40] |
| Land use | [39] | ||
| S | Soil map | [41] | |
| Degree of karstification | [28,32] | ||
| Geological map | [30,31] | ||
| C | Main fault zones | [42,43] | |
| Hydraulic interactions | [28,32] | ||
| V | - | Piezometric data (alluvial) | [28,34,36] |
| Bottom of confining aquifer | [44] | ||
| Piezometric data (karst) | [45] | ||
| Metamorphic formations weathered mantle | [28] | ||
| A | - | Hydraulic conductivity (Alluvial aquifer) | [33,44] |
| Hydraulic conductivity (Marbles, Gneisses, Schists) | [46,47,48,49] |
| Modelled-Monitored Class | Percentage |
|---|---|
| −3 | 0.33 |
| −2 | 1.61 |
| −1 | 11.27 |
| 0 | 29.14 |
| 1 | 41.11 |
| 2 | 13.82 |
| 3 | 2.72 |
| 100.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vrouhakis, I.; Tziritis, E.; Stamatis, G.; Panagopoulos, A. Groundwater Vulnerability Analysis of Tirnavos Basin, Central Greece: An Application of RIVA Method. Water 2022, 14, 534. https://doi.org/10.3390/w14040534
Vrouhakis I, Tziritis E, Stamatis G, Panagopoulos A. Groundwater Vulnerability Analysis of Tirnavos Basin, Central Greece: An Application of RIVA Method. Water. 2022; 14(4):534. https://doi.org/10.3390/w14040534
Chicago/Turabian StyleVrouhakis, Ioannis, Evangelos Tziritis, Georgios Stamatis, and Andreas Panagopoulos. 2022. "Groundwater Vulnerability Analysis of Tirnavos Basin, Central Greece: An Application of RIVA Method" Water 14, no. 4: 534. https://doi.org/10.3390/w14040534
APA StyleVrouhakis, I., Tziritis, E., Stamatis, G., & Panagopoulos, A. (2022). Groundwater Vulnerability Analysis of Tirnavos Basin, Central Greece: An Application of RIVA Method. Water, 14(4), 534. https://doi.org/10.3390/w14040534