Mitigation of Hydroelastic Responses in a Very Large Floating Structure by a Connected Vertical Porous Flexible Barrier
Abstract
:1. Introduction
2. Hydroelastic Response on a Single-Layer Fluid
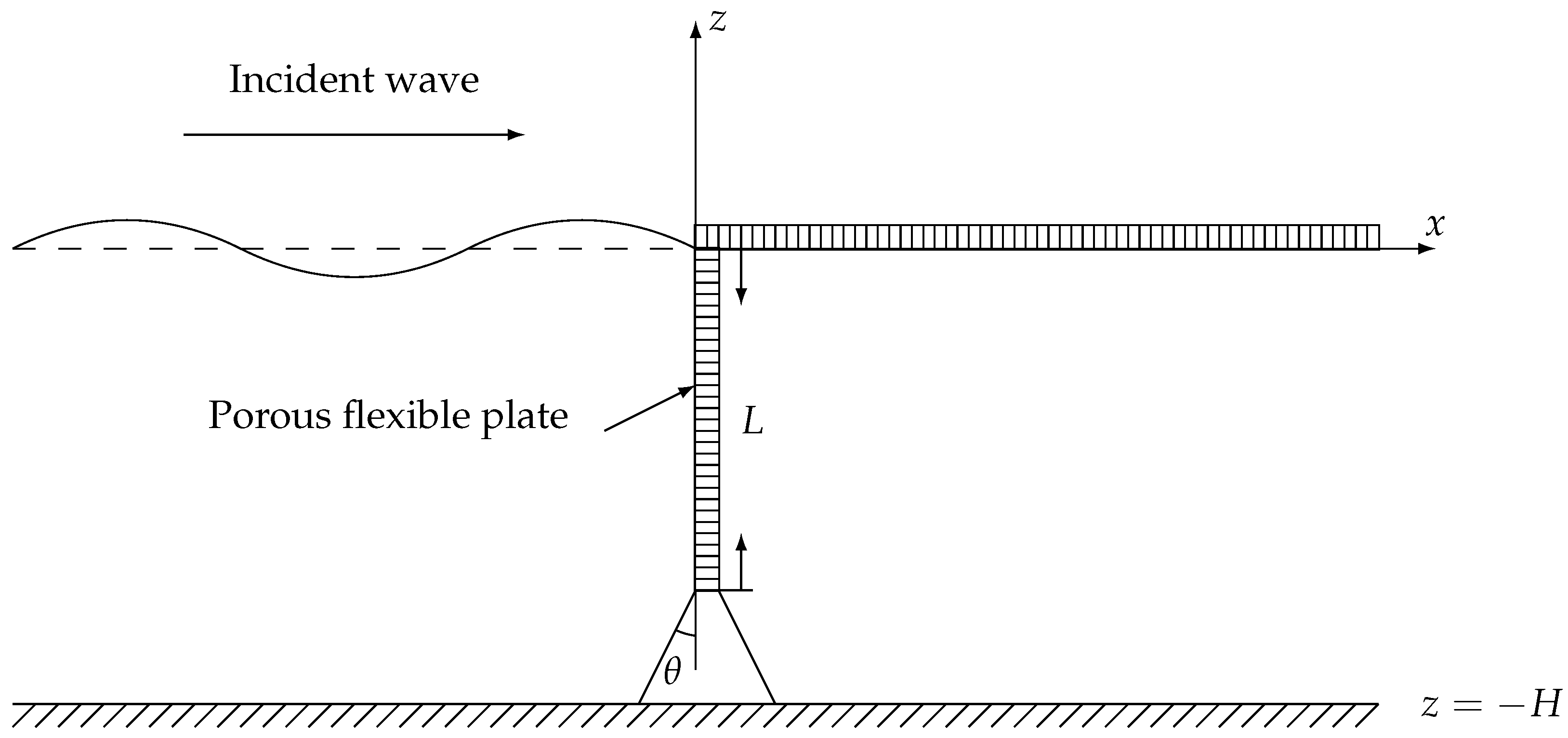
2.1. Wave Interaction with a Semi-Infinite Floating Plate
2.1.1. Mathematical Formulation
2.1.2. Method of Solution
2.2. Wave Interaction with a Finite Elastic Plate
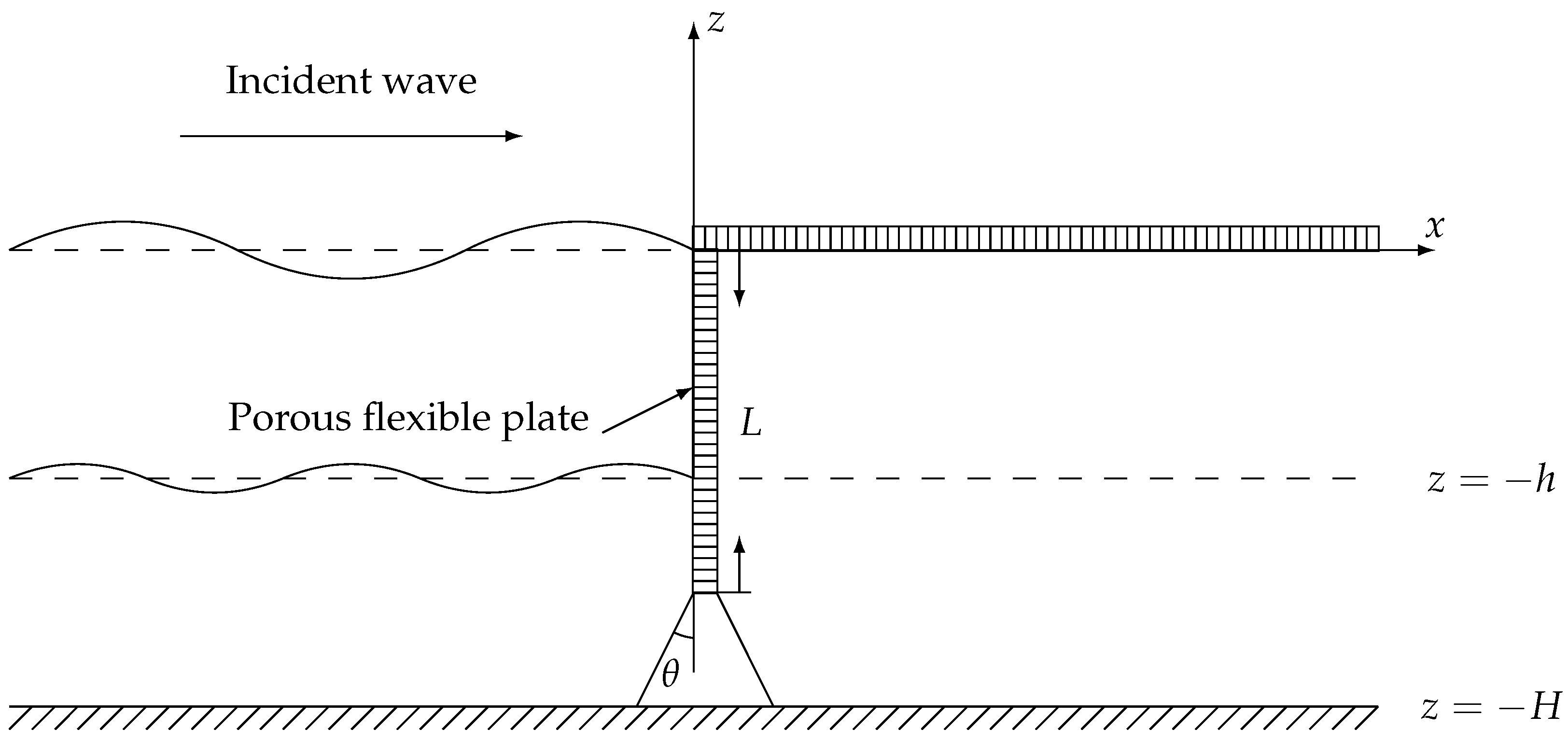
3. Wave Interaction on a Two-Layer Fluid
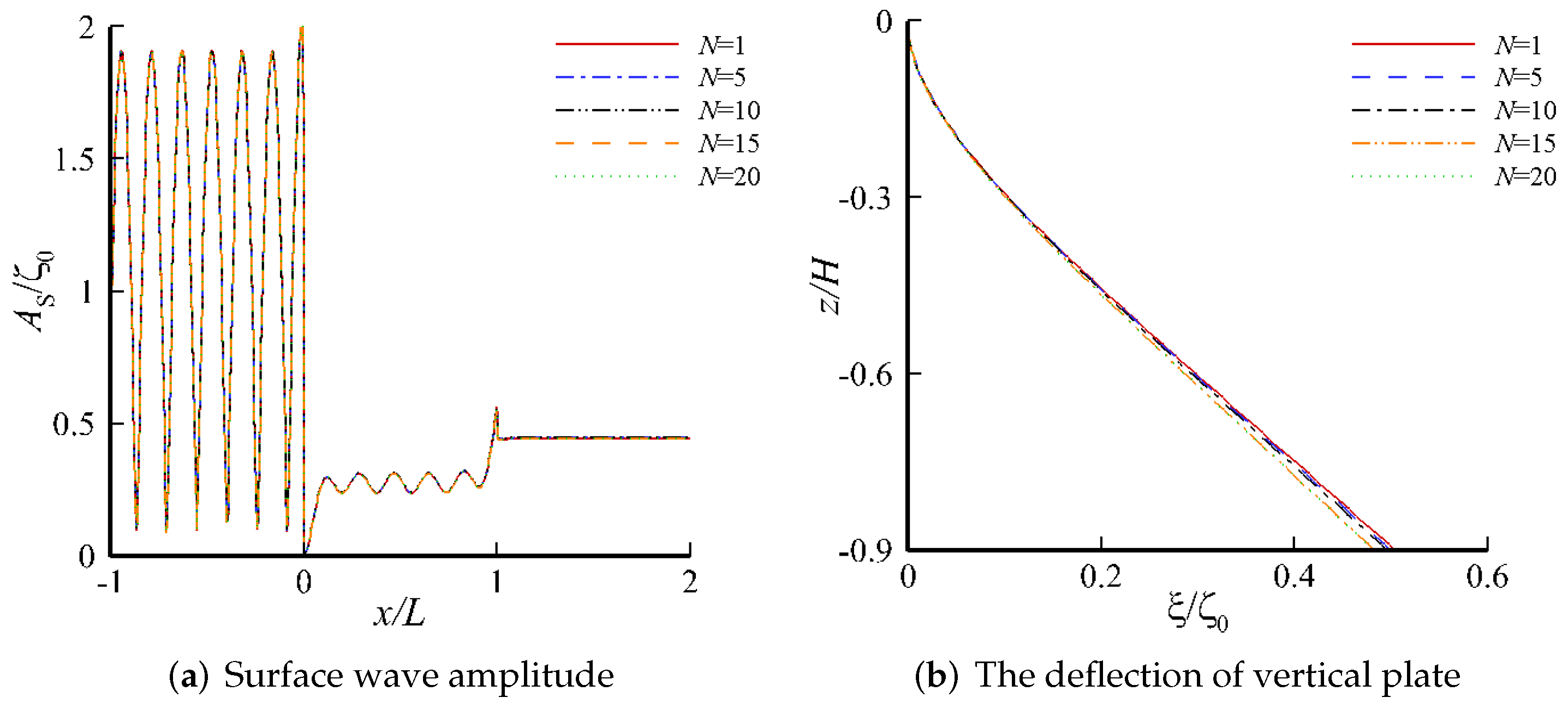
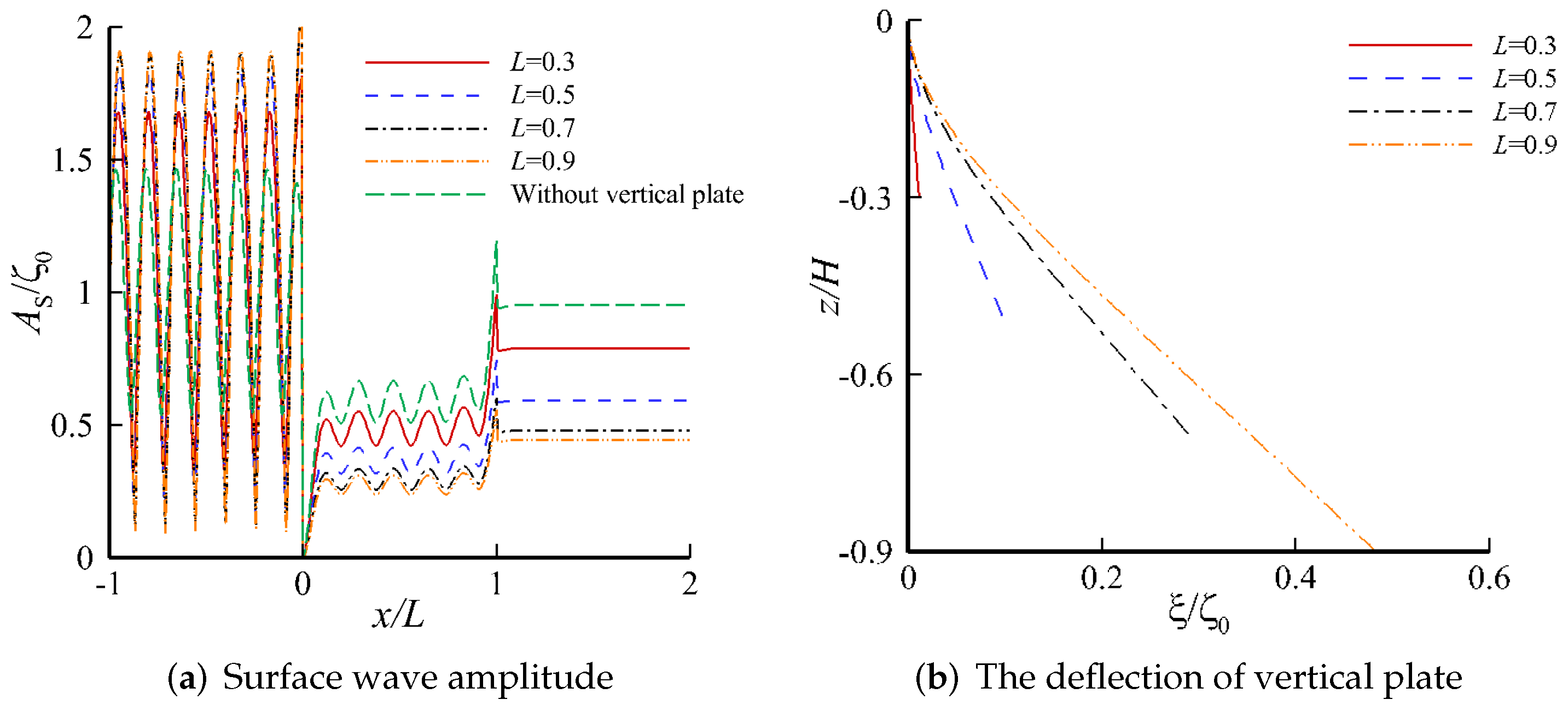
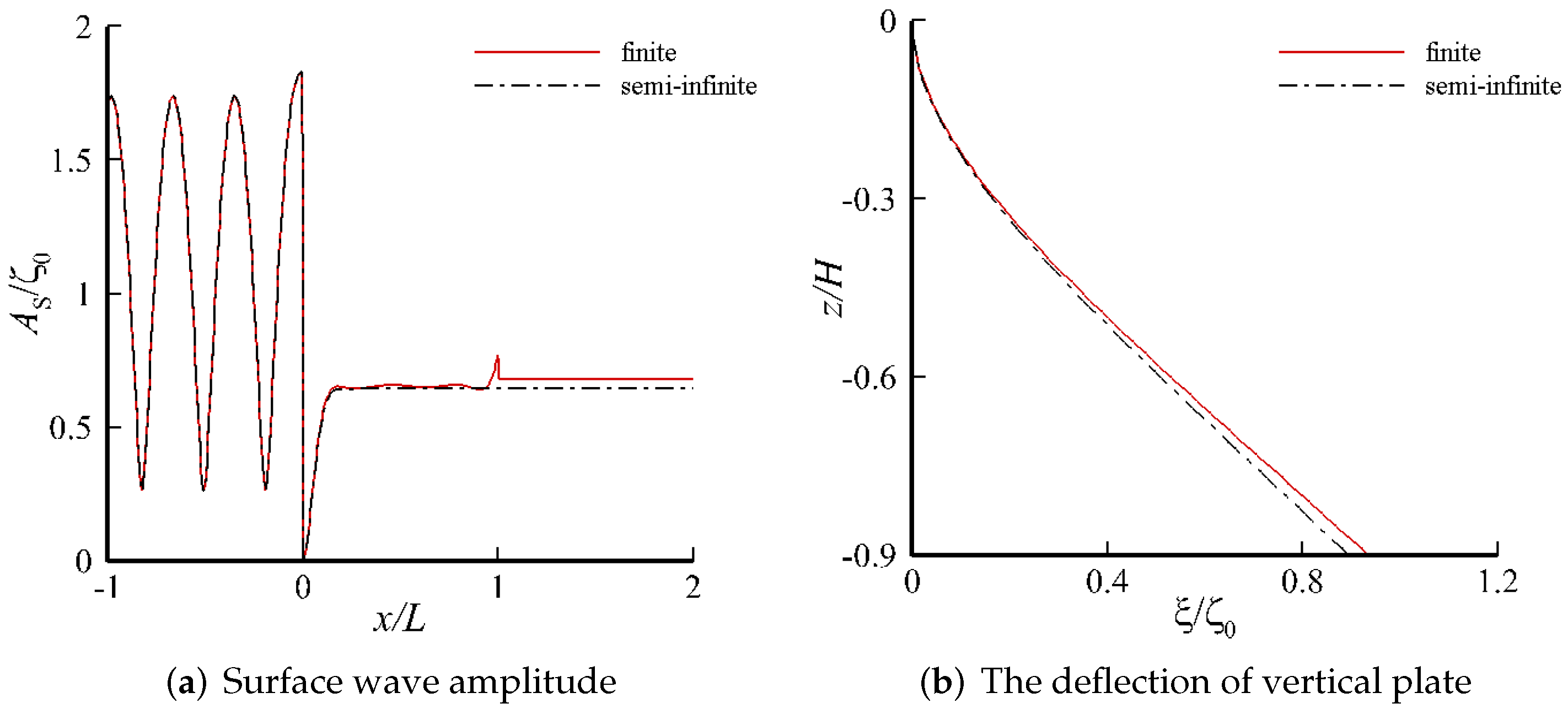
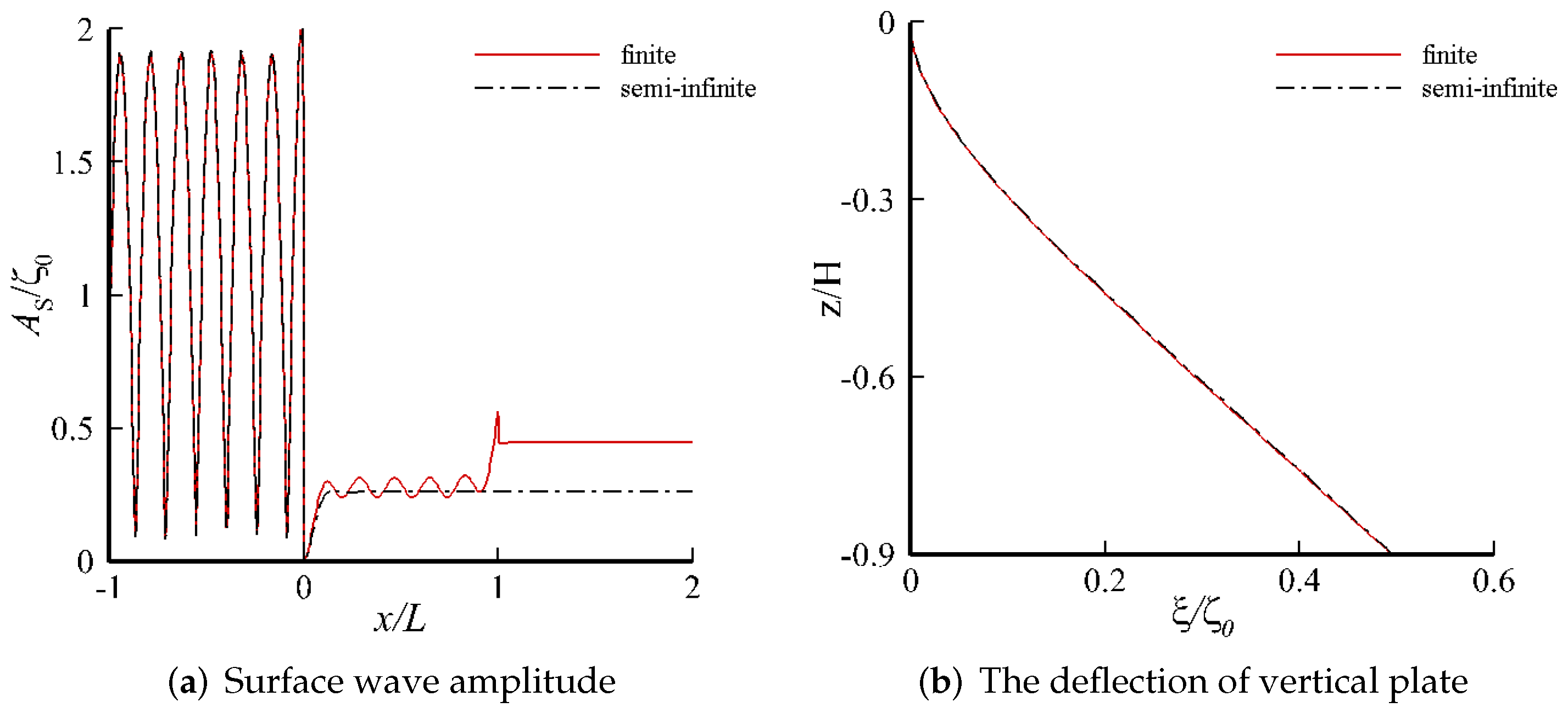
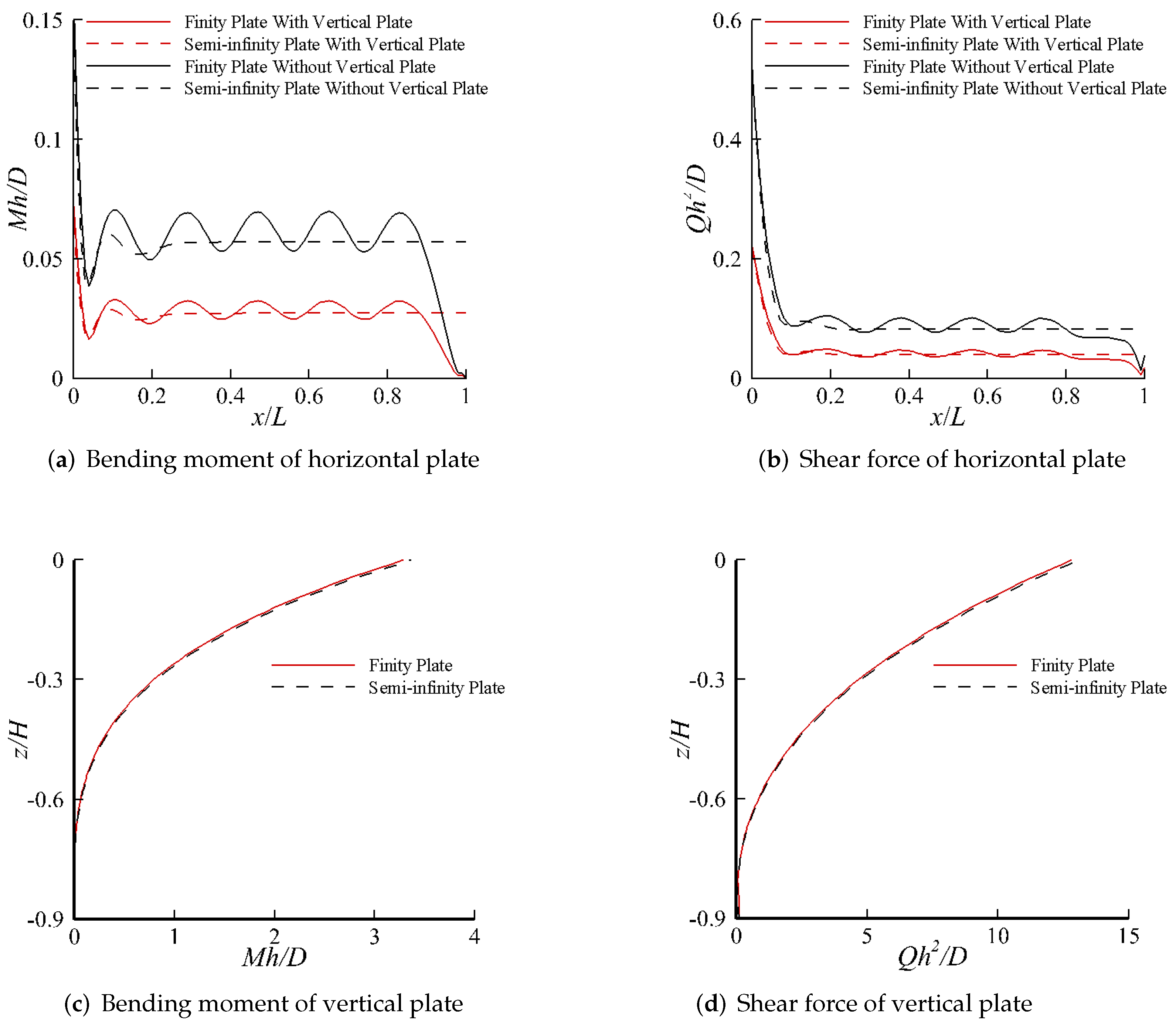
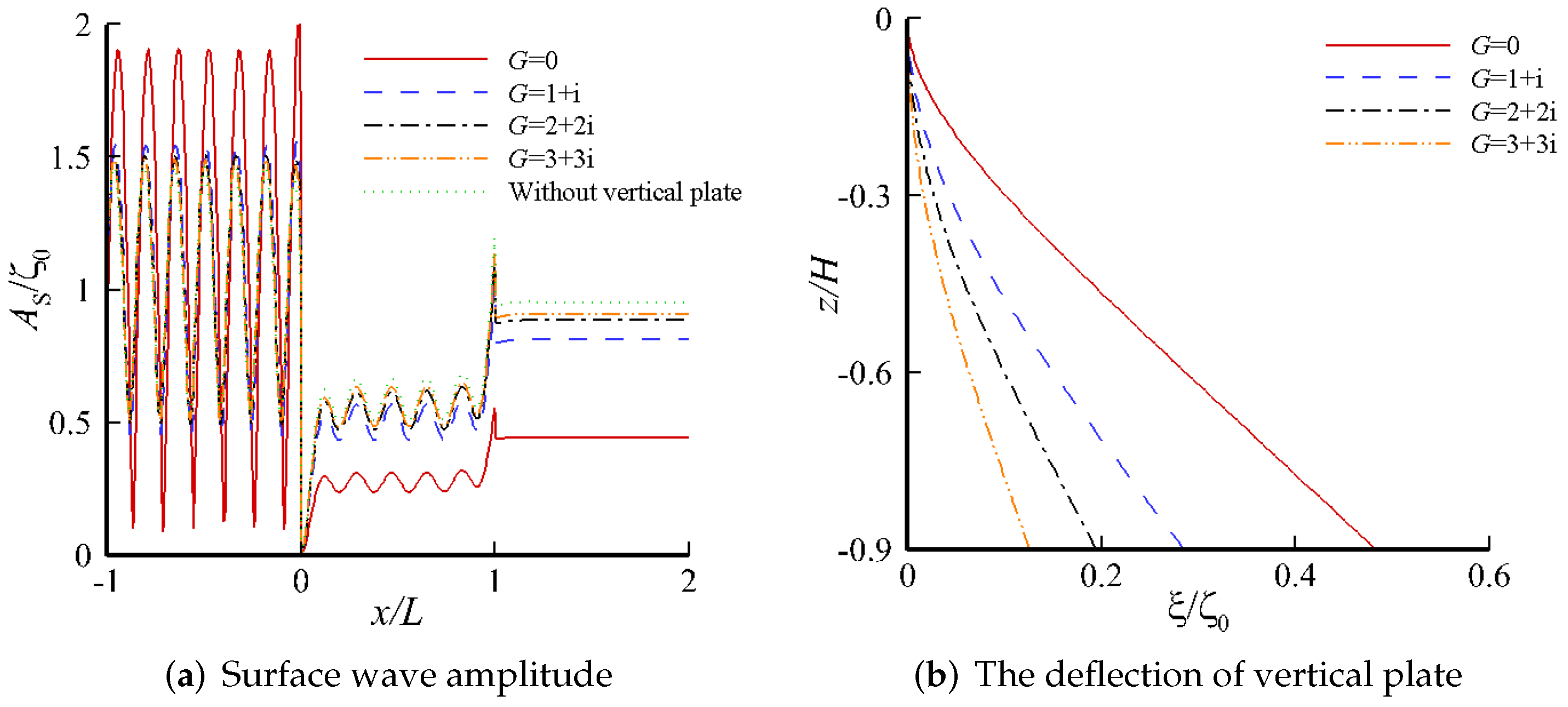
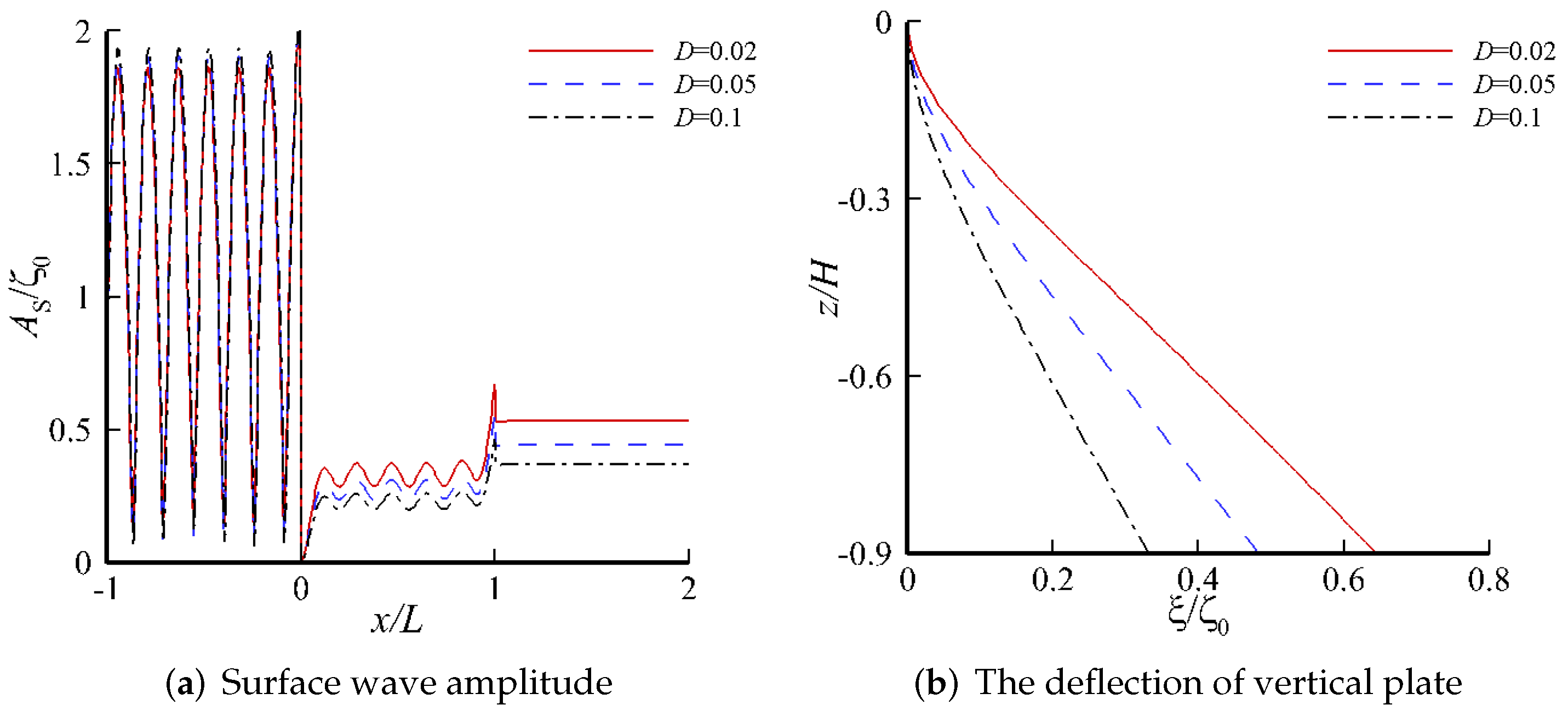
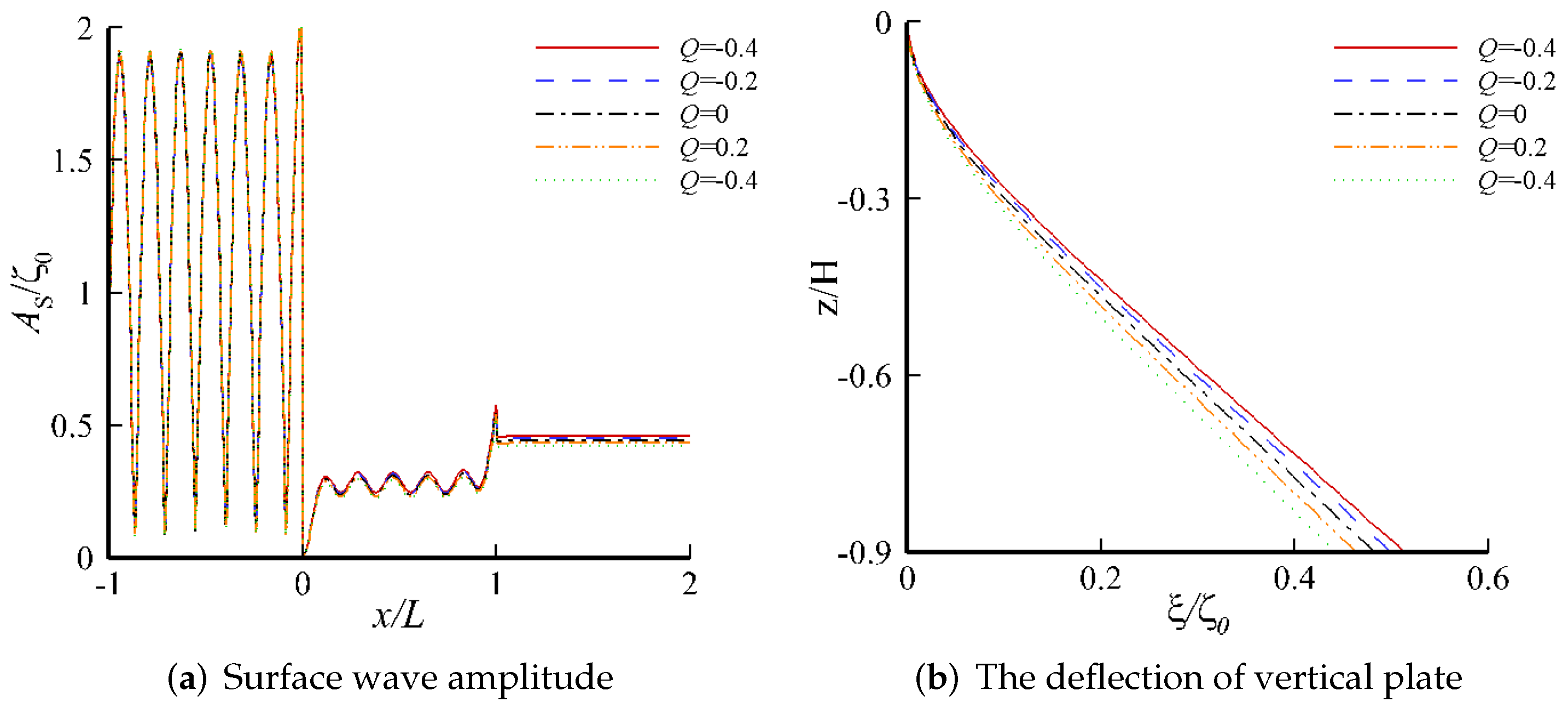
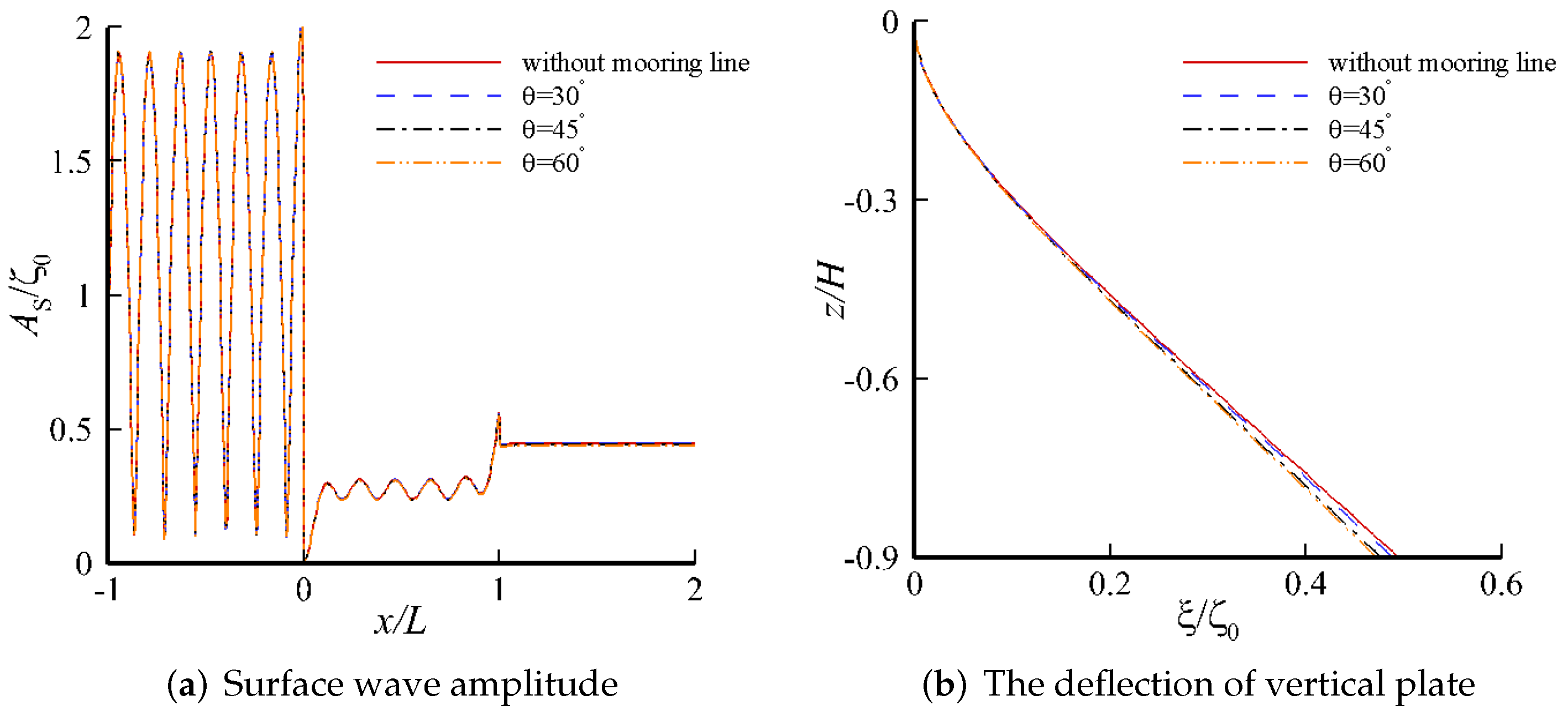
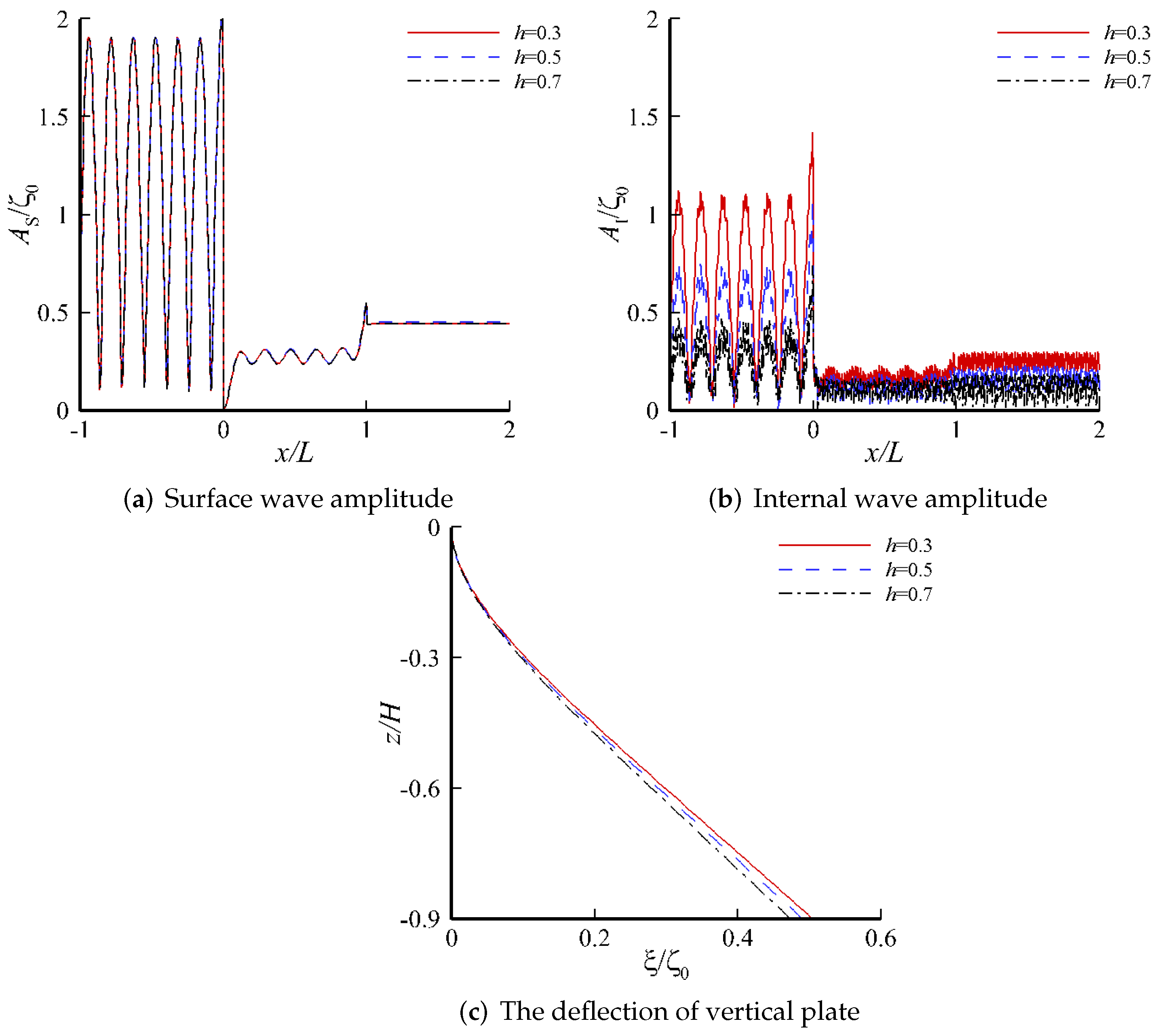
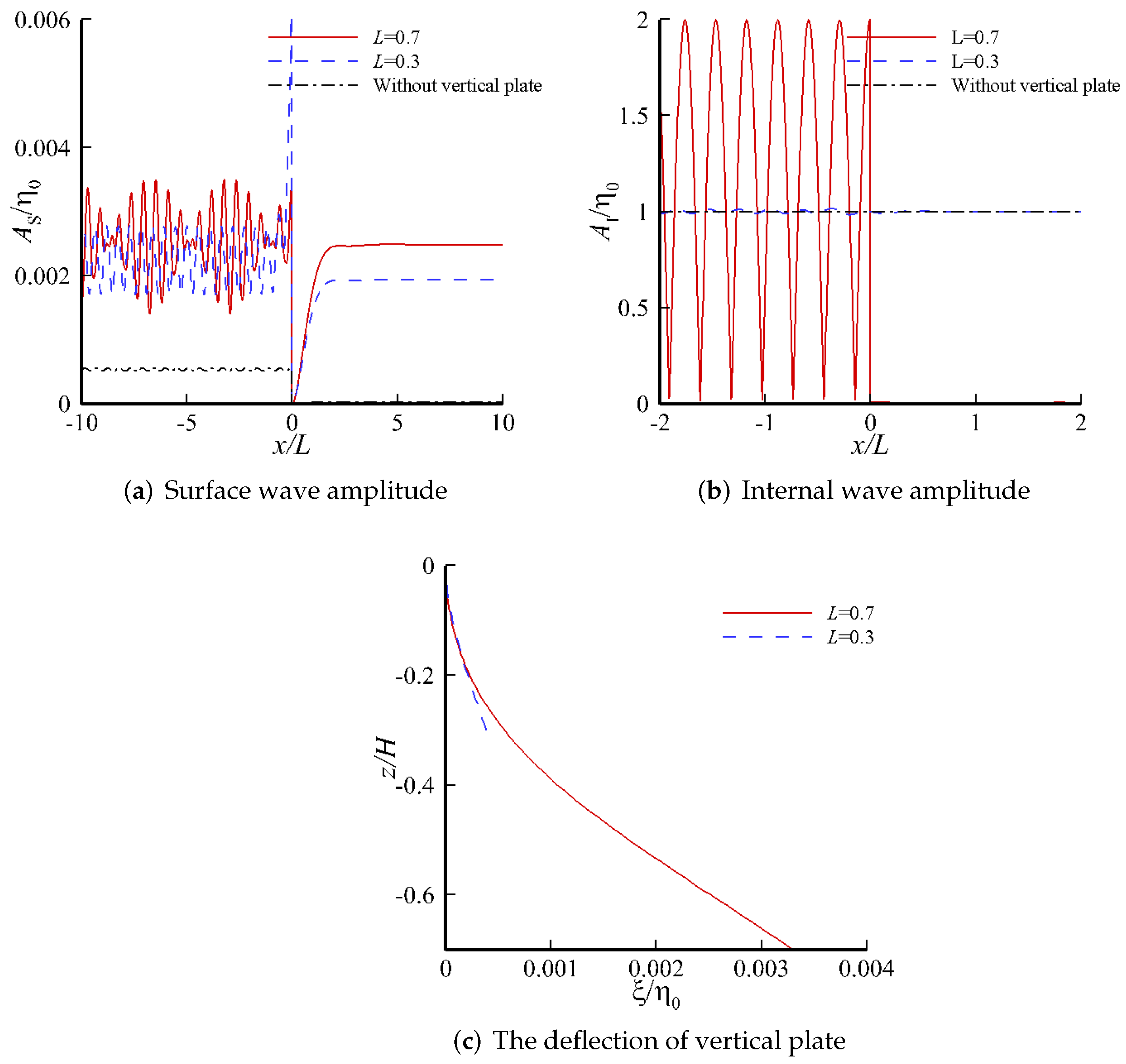
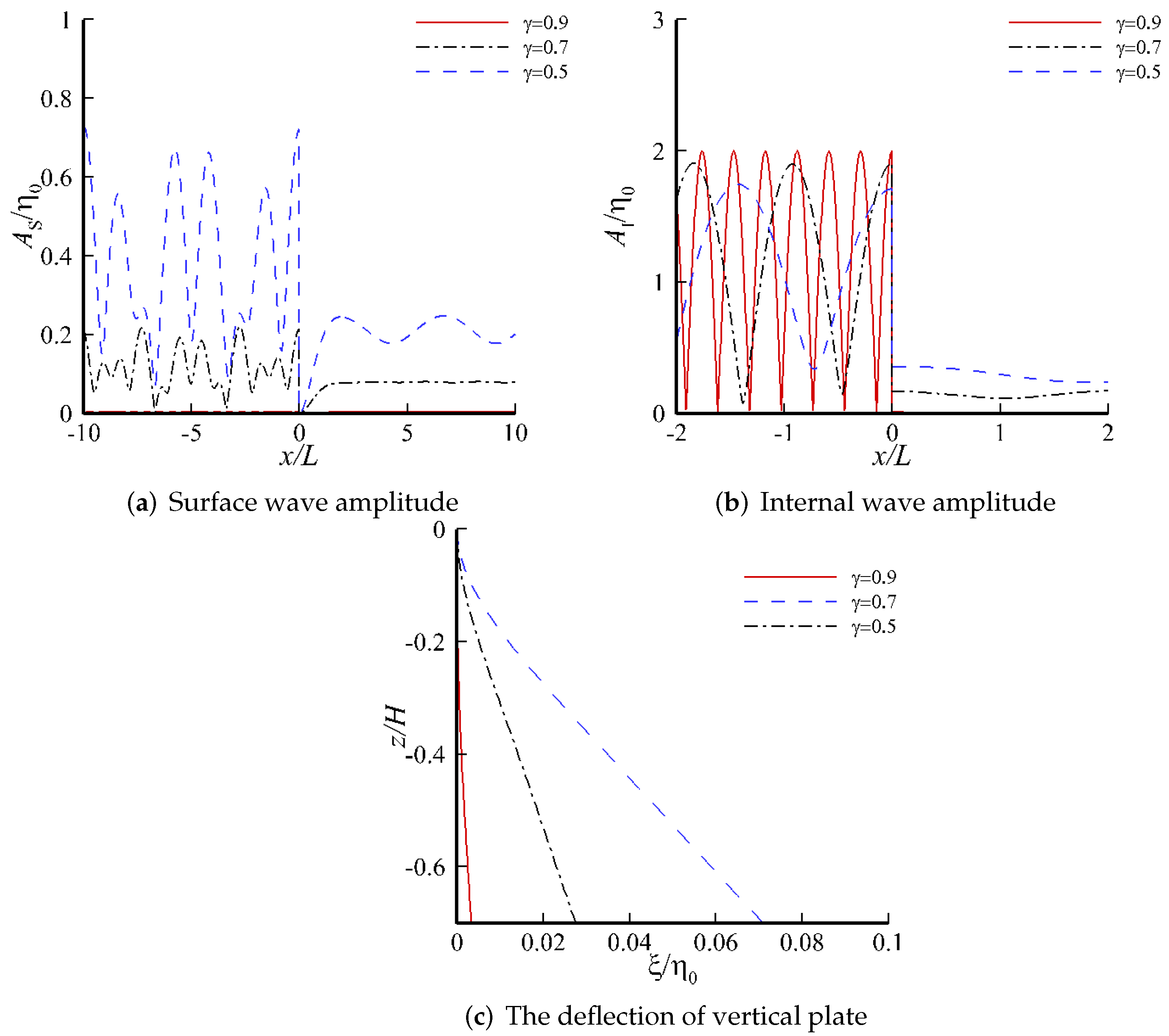
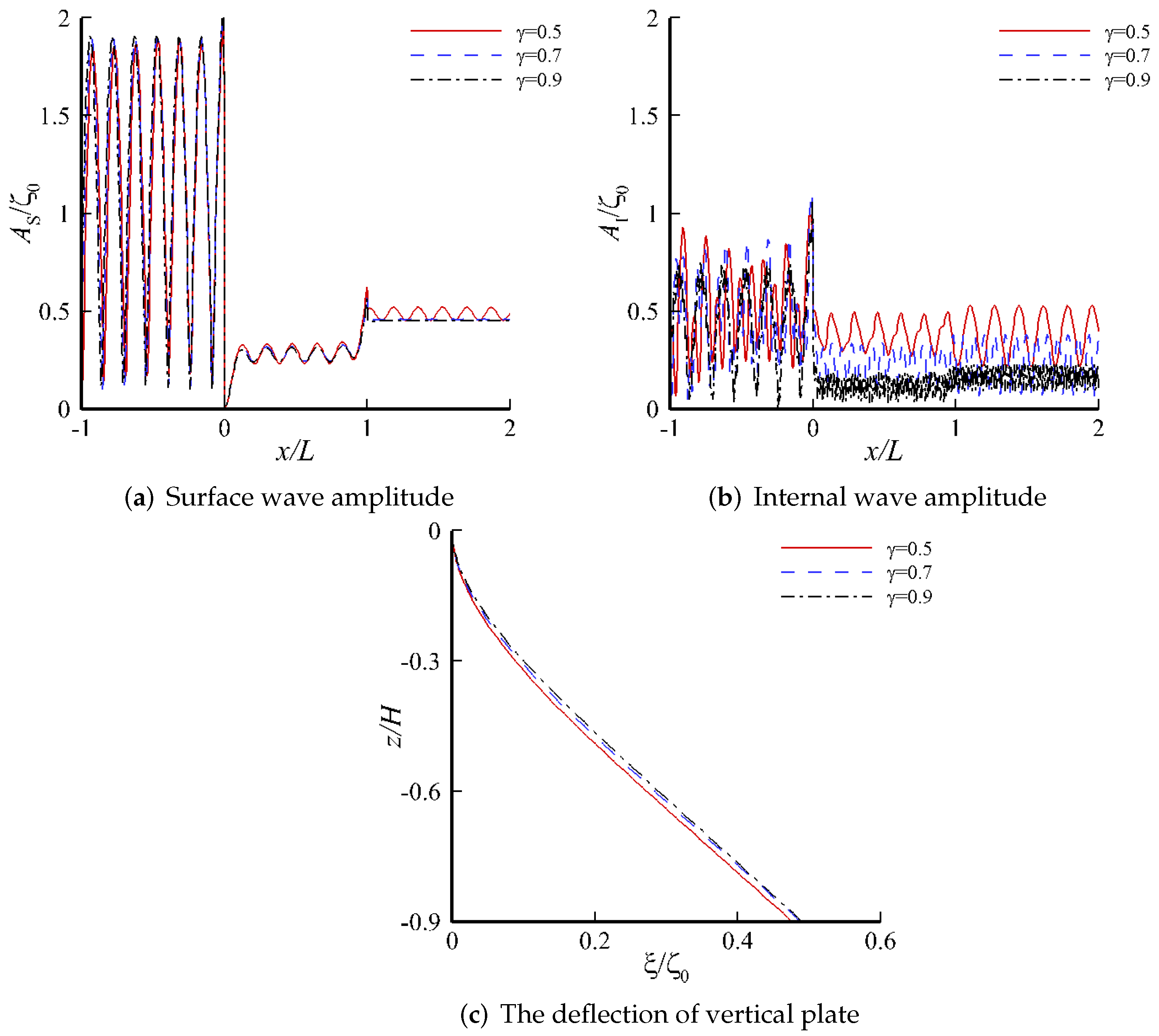
4. Results and Discussion
4.1. Rate of Energy Flux
4.2. Response on a Single-Layer Fluid
4.3. Response on the Two-Layer Fluid
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Derivation Process of the Unknown Coefficients for a Finite Plate Model in a Single-Layer Fluid
Appendix B. Derivation Process of the Unknown Coefficients in the Two-Layer Fluid
References
- Watanabe, E.; Utsunomiya, T.; Wang, C.M. Hydroelastic analysis of pontoon-type VLFS: A literature survey. Eng. Struct. 2004, 26, 245–256. [Google Scholar] [CrossRef]
- Andrianov, A.I. Hydroelastic Analysis of Very Large Floating Structures. Ph.D. Thesis, Delft University of Technology, Delft, The Netherlands, 2005. [Google Scholar]
- Wang, C.M.; Tay, Z.Y. Very large floating structures: Applications, research and development. Procedia Eng. 2011, 14, 62–72. [Google Scholar] [CrossRef] [Green Version]
- Lamas-Pardo, M.; Iglesias, G.; Carral, L. A review of Very large floating structures (VLFS) for coastal and offshore uses. Ocean Eng. 2015, 109, 677–690. [Google Scholar] [CrossRef]
- Wang, C.M.; Tay, Z.Y.; Takagi, K.; Utsunomiya, T. Literature review of methods for mitigating hydroelastic response of VLFS under wave action. Appl. Mech. Rev. 2010, 63, 030802. [Google Scholar] [CrossRef]
- Takagi, K.; Shimada, K.; Ikebuchi, T. An anti-motion device for a very large floating structure. Mar. Struct. 2000, 13, 421–436. [Google Scholar] [CrossRef]
- Masanobu, S.; Kato, S.; Maeda, K.; Namba, Y. Response of the mega-float equipped with novel wave energy absorber. In Proceedings of the ASME 2003 22nd International Conference on Offshore Mechanics and Arctic Engineering, Cancun, Mexico, 8–13 June 2003; American Society of Mechanical Engineers Digital Collection: New York, NY, USA, 2003; pp. 727–734. [Google Scholar]
- Lee, S.M.; Takaki, M.; Iwano, M. Estimation of the radiation forces on submerged-plate oscillating near a free surface by composite grid method. In Proceedings of the Transactions of the West-Japan Society of Naval Architects the 105th West-Japna Society of Naval Architects Meeting (Joint Autumn Meeting of Three Societies of Naval Architects in Japan); The Japan Society of Naval Architects and Ocean Engineers: Tokyo, Japan, 2003; pp. 113–122. Available online: https://www.jstage.jst.go.jp/article/wjsna/105/0/105_0_7/_article/-char/ja/ (accessed on 24 November 2021).
- Pham, D.C.; Wang, C.M.; Utsunomiya, T. Hydroelastic analysis of pontoon-type circular VLFS with an attached submerged plate. Appl. Ocean. Res. 2008, 30, 287–296. [Google Scholar] [CrossRef]
- Cheng, Y.; Ji, C.; Zhai, G.; Oleg, G. Dual inclined perforated anti-motion plates for mitigating hydroelastic response of a VLFS under wave action. Ocean Eng. 2016, 121, 572–591. [Google Scholar] [CrossRef]
- Nguyen, H.; Wang, C.; Flocard, F.; Pedroso, D. Extracting energy while reducing hydroelastic responses of VLFS using a modular raft wec-type attachment. Appl. Ocean. Res. 2019, 84, 302–316. [Google Scholar] [CrossRef]
- Nguyen, H.; Wang, C.; Luong, V. Two-mode WEC-type attachment for wave energy extraction and reduction of hydroelastic response of pontoon-type VLFS. Ocean Eng. 2020, 197, 106875. [Google Scholar] [CrossRef]
- Feng, M.W.; Sun, Z.C.; Liang, S.X.; Liu, B.J. Hydroelastic response of VLFS with an attached submerged horizontal solid/porous plate under wave action. China Ocean Eng. 2020, 34, 451–462. [Google Scholar] [CrossRef]
- Ohmatsu, S. Overview: Research on wave loading and responses of VLFS. Mar. Struct. 2005, 18, 149–168. [Google Scholar] [CrossRef]
- Squire, V.A. Synergies between VLFS hydroelasticity and sea ice research. Int. J. Offshore Polar Eng. 2008, 18, 241–253. [Google Scholar]
- Fox, C.; Squire, V.A. On the oblique reflexion and transmission of ocean waves at shore fast sea ice. Philos. Trans. R. Soc. Phys. Eng. Sci. 1994, 347, 185–218. [Google Scholar]
- Sahoo, T.; Yip, T.L.; Chwang, A.T. Scattering of surface waves by a semi-infinite floating elastic plate. Phys. Fluids 2001, 13, 3215–3222. [Google Scholar] [CrossRef] [Green Version]
- Xu, F.; Lu, D.Q. An optimization of eigenfunction expansion method for the interaction of water waves with an elastic plate. J. Hydrodyn. 2009, 21, 526–530. [Google Scholar] [CrossRef]
- Xu, F.; Lu, D.Q. Wave scattering by a thin elastic plate floating on a two-layer fluid. Int. J. Eng. Sci. 2010, 48, 809–819. [Google Scholar] [CrossRef]
- Meng, Q.R.; Lu, D.Q. Hydroelastic interaction between water waves and thin elastic plate floating on three-layer fluid. Appl. Math. Mech. - Engl. Ed. 2017, 38, 567–584. [Google Scholar] [CrossRef]
- Yu, X.; Chwang, A.T. Wave-induced oscillation in harbor with porous breakwaters. J. Waterw. Port Coast. Ocean. Eng. 1994, 120, 125–144. [Google Scholar] [CrossRef]
- Yip, T.L.; Sahoo, T.; Chwang, A.T. Trapping of surface waves by porous and flexible structures. Wave Motion 2002, 35, 41–54. [Google Scholar] [CrossRef]
- Kumar, P.S.; Sahoo, T. Wave interaction with a flexible porous breakwater in a two-layer fluid. J. Eng. Mech. 2006, 132, 1007–1014. [Google Scholar] [CrossRef]
- Mandal, S.; Behera, H.; Sahoo, T. Oblique wave interaction with porous, flexible barriers in a two-layer fluid. J. Eng. Math. 2016, 100, 1–31. [Google Scholar] [CrossRef]
- Singla, S.; Martha, S.C.; Sahoo, T. Mitigation of structural responses of a very large floating structure in the presence of vertical porous barrier. Ocean Eng. 2018, 165, 505–527. [Google Scholar] [CrossRef]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pu, J.; Lu, D.-Q. Mitigation of Hydroelastic Responses in a Very Large Floating Structure by a Connected Vertical Porous Flexible Barrier. Water 2022, 14, 294. https://doi.org/10.3390/w14030294
Pu J, Lu D-Q. Mitigation of Hydroelastic Responses in a Very Large Floating Structure by a Connected Vertical Porous Flexible Barrier. Water. 2022; 14(3):294. https://doi.org/10.3390/w14030294
Chicago/Turabian StylePu, Jun, and Dong-Qiang Lu. 2022. "Mitigation of Hydroelastic Responses in a Very Large Floating Structure by a Connected Vertical Porous Flexible Barrier" Water 14, no. 3: 294. https://doi.org/10.3390/w14030294
APA StylePu, J., & Lu, D.-Q. (2022). Mitigation of Hydroelastic Responses in a Very Large Floating Structure by a Connected Vertical Porous Flexible Barrier. Water, 14(3), 294. https://doi.org/10.3390/w14030294




