Long-Term Temporal Flood Predictions Made Using Convolutional Neural Networks
Abstract
:1. Introduction
2. Study Area and Data Description
2.1. Study Area
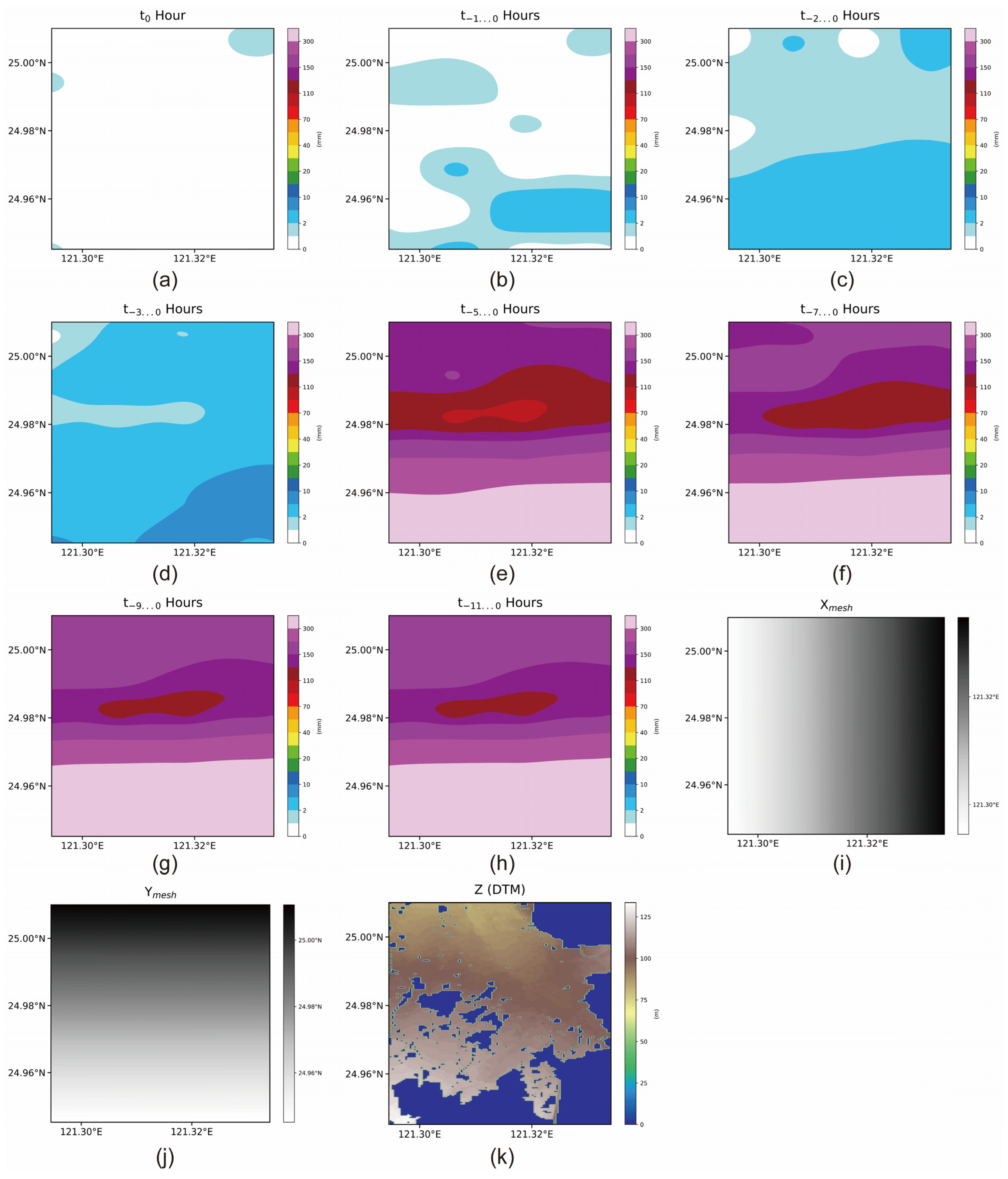
2.2. Rainfall Data
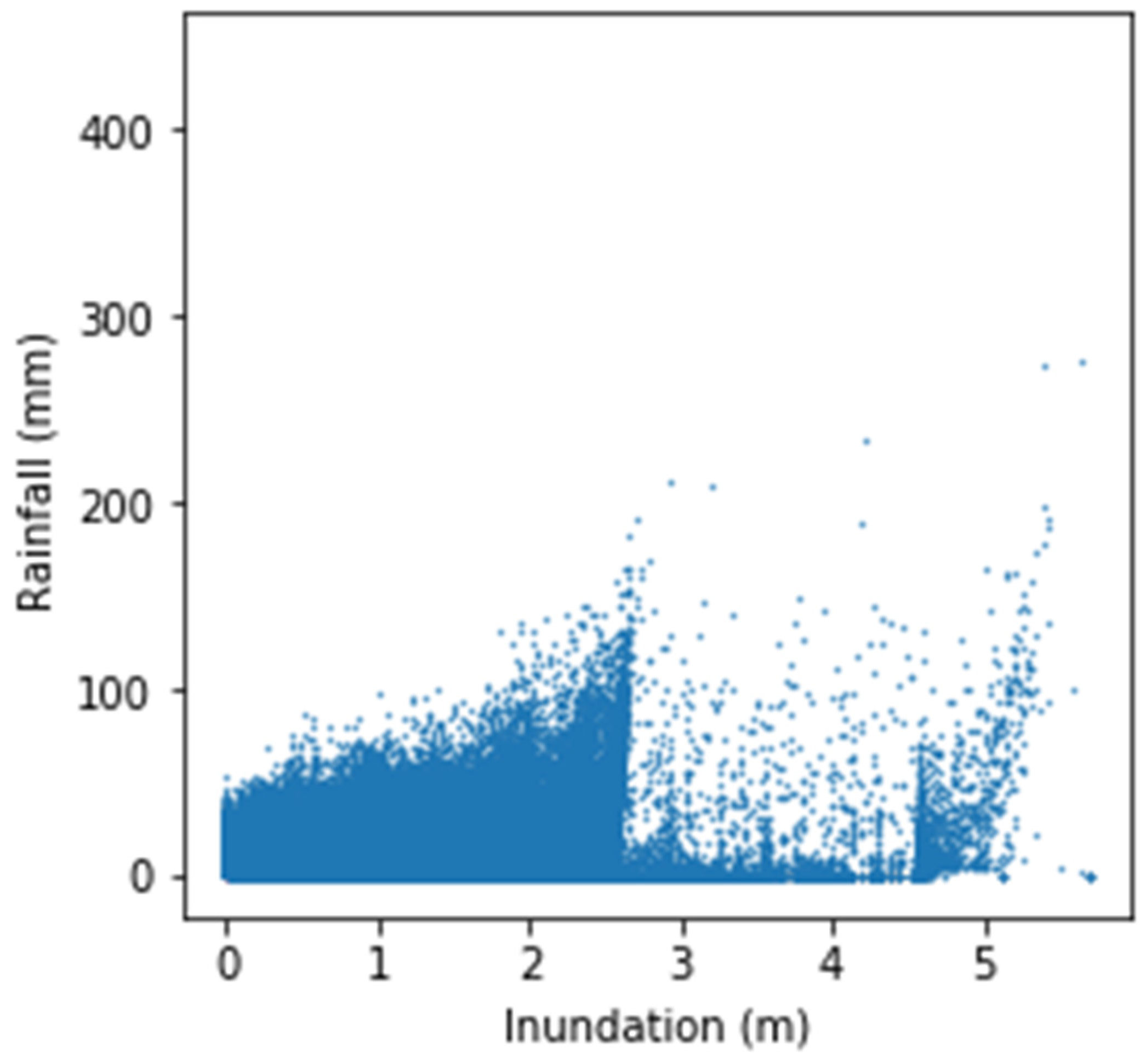
2.3. Flooding Data
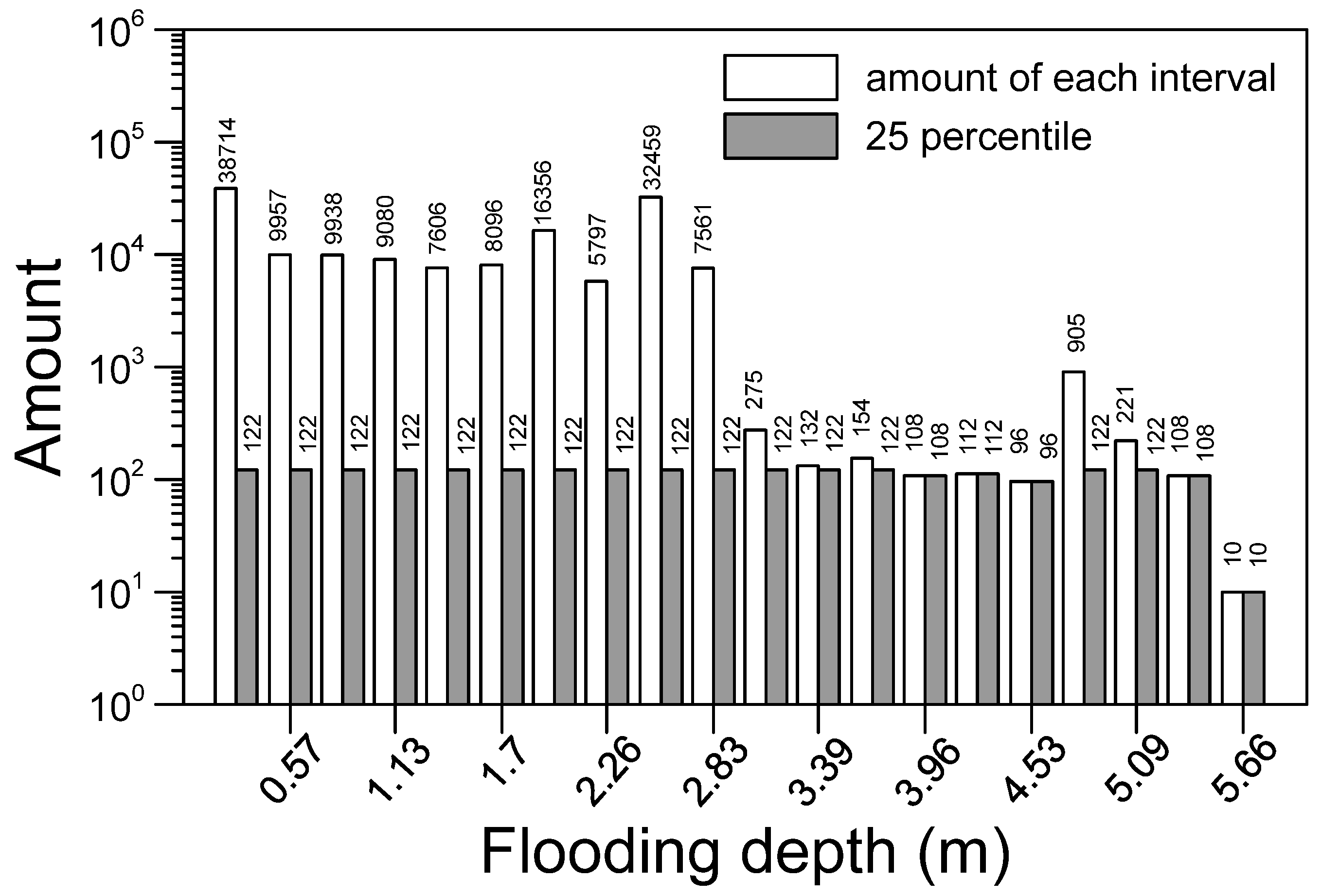
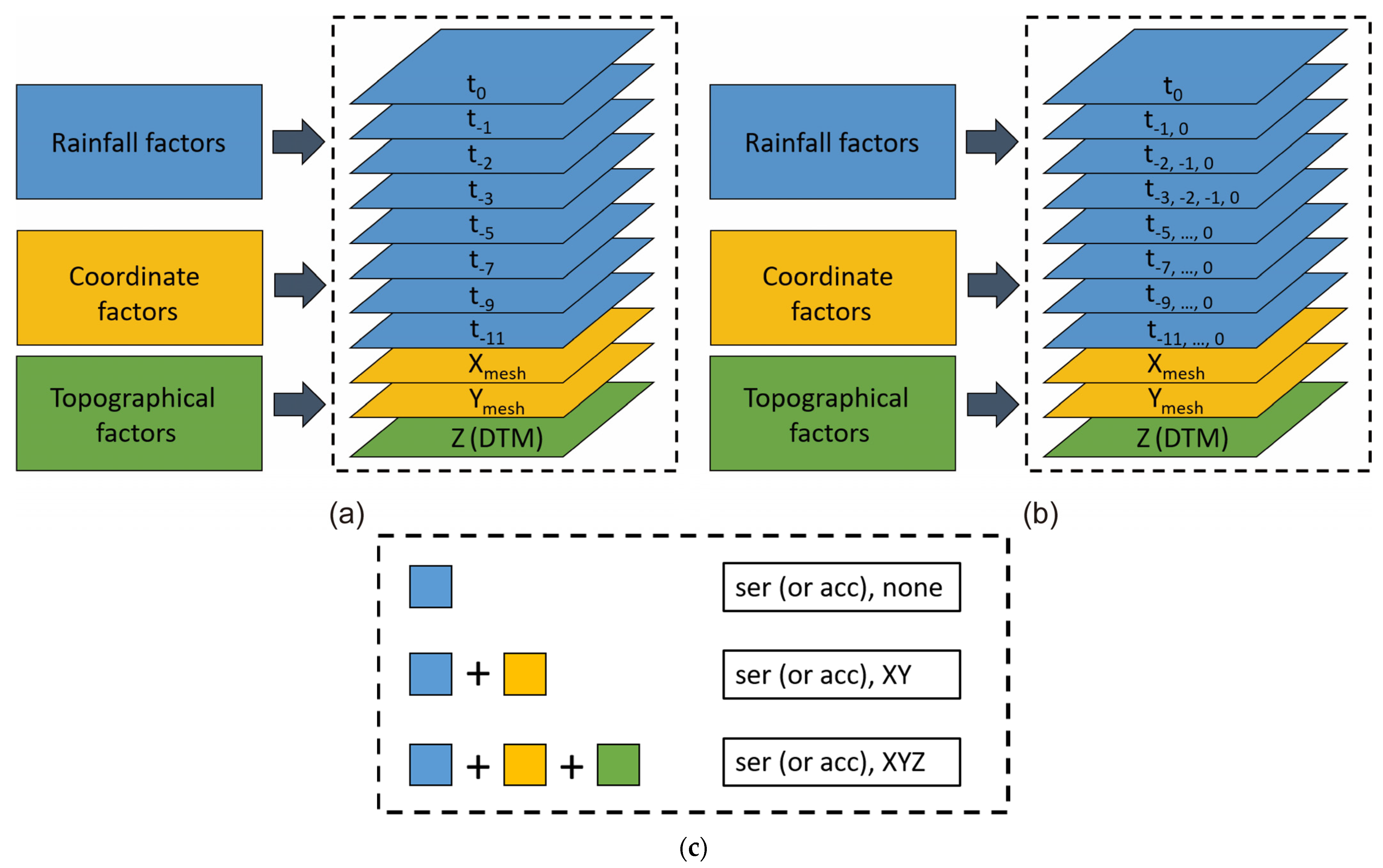
2.4. Strategy of Data Selection from the Database
3. Methods
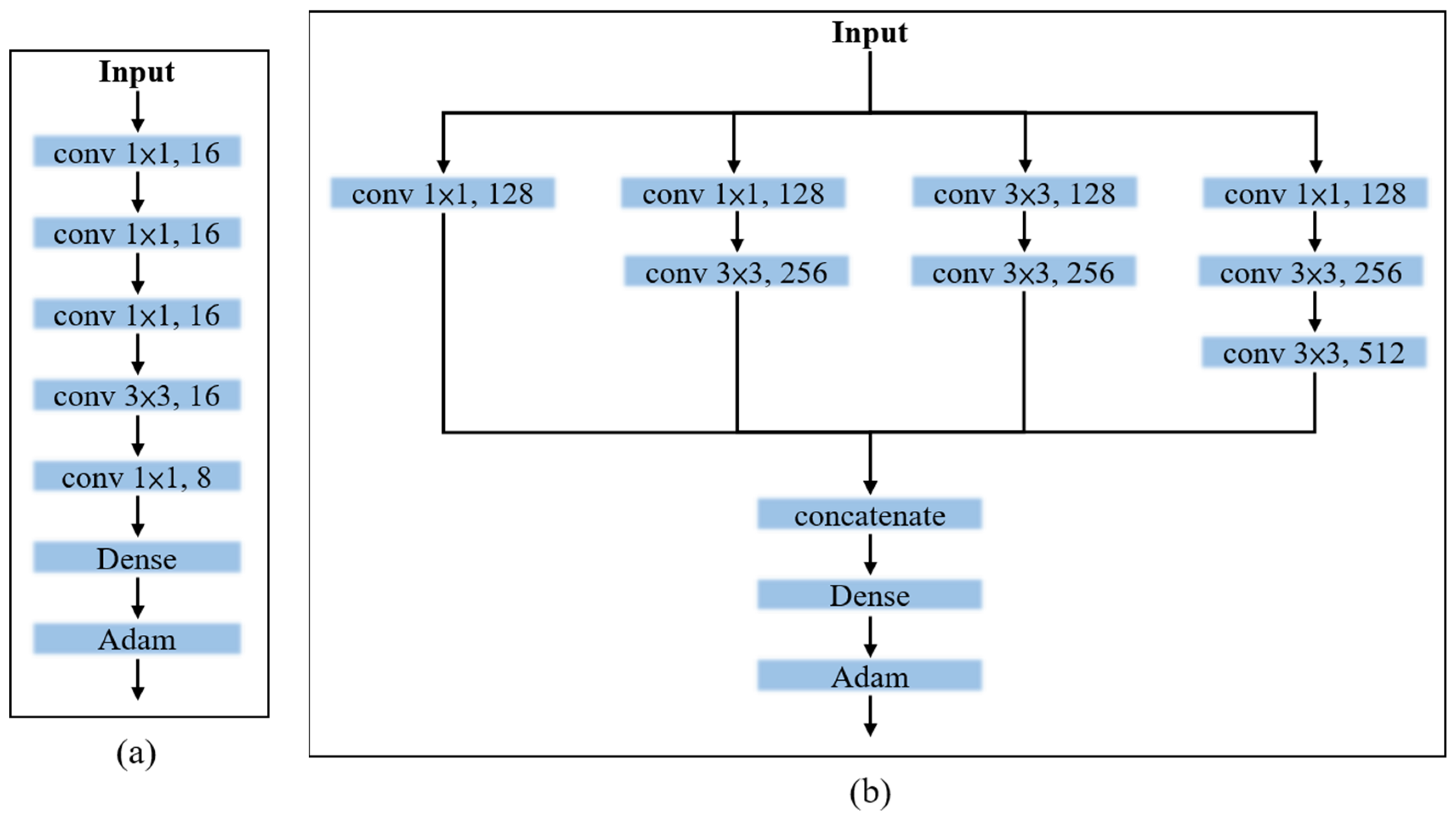
3.1. Convolutional Neural Networks
3.2. Data Combination for Training
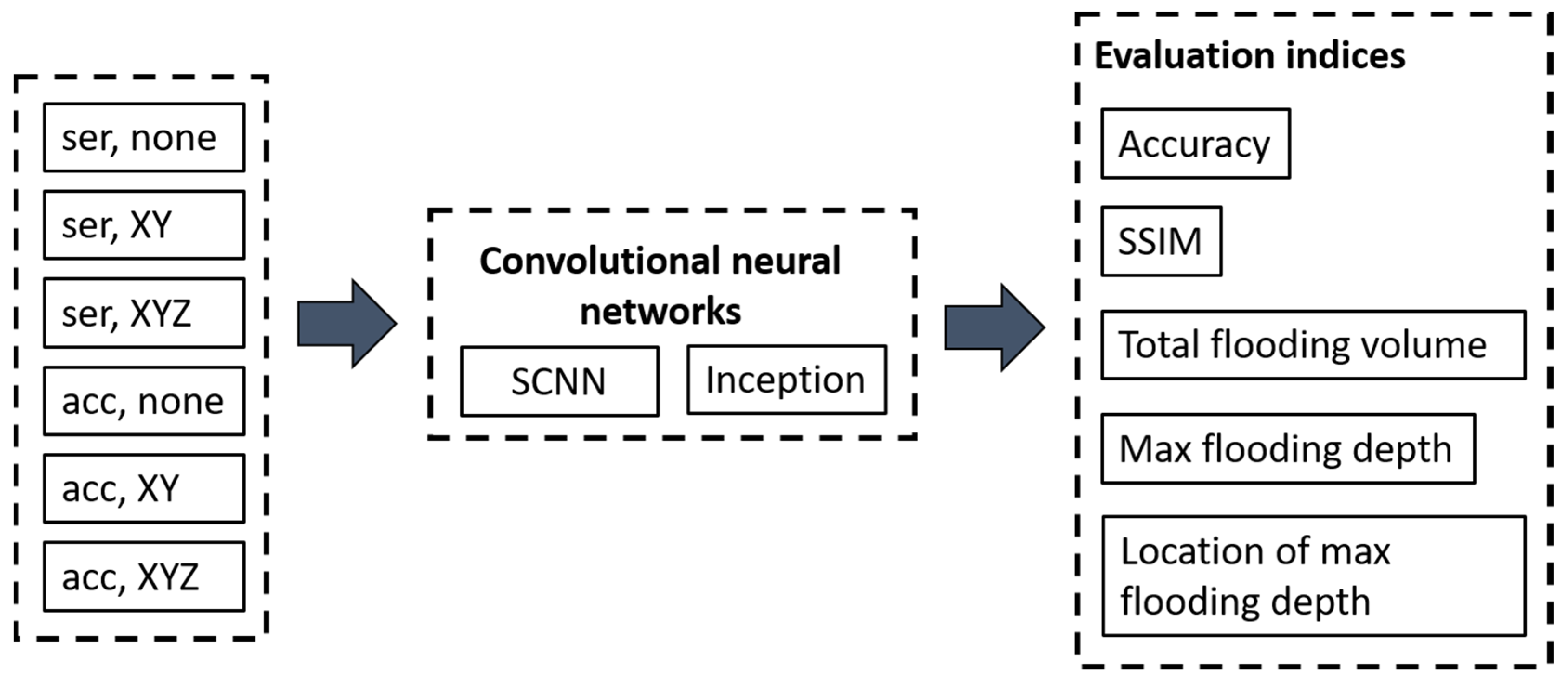
3.3. Evaluation Methods
3.3.1. SSIM
3.3.2. Comparisons of Differences in Location for the Maximum Flooding Depth, Maximum Flooding Depth, and Total Flooding Volume
4. Result Analysis
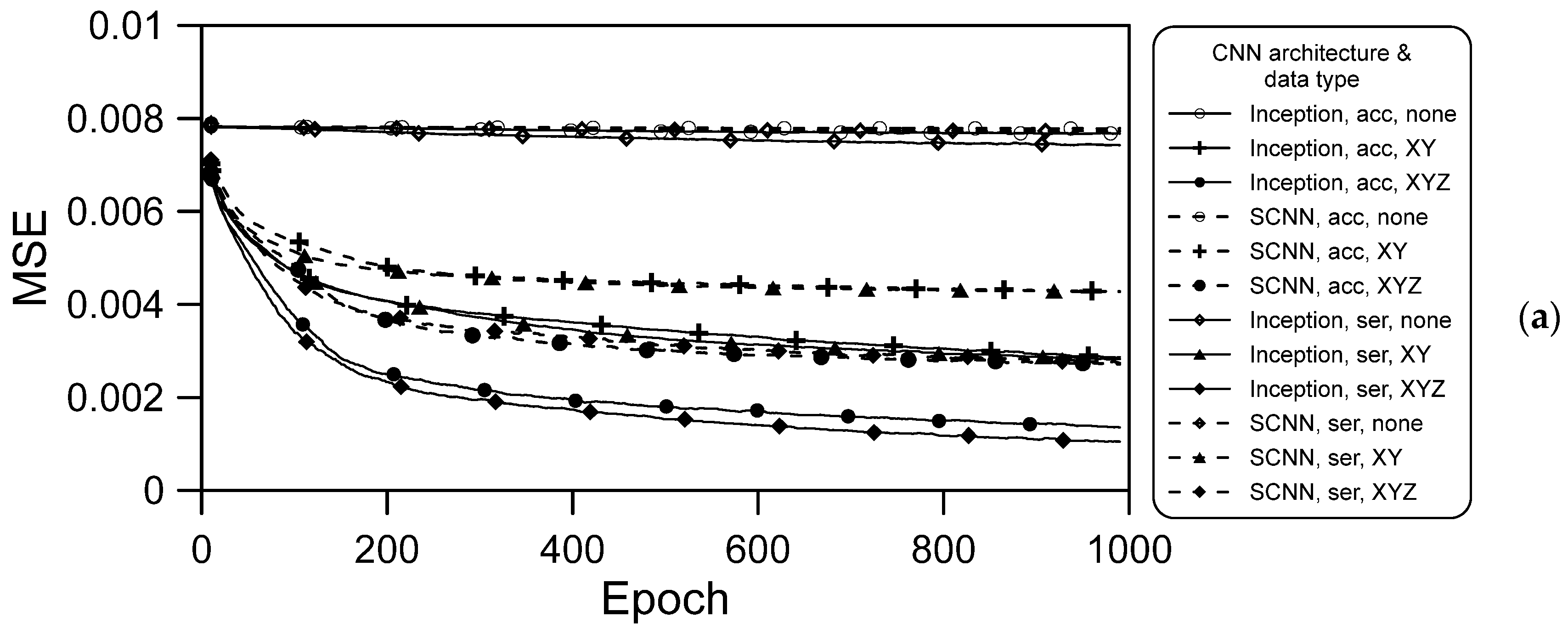
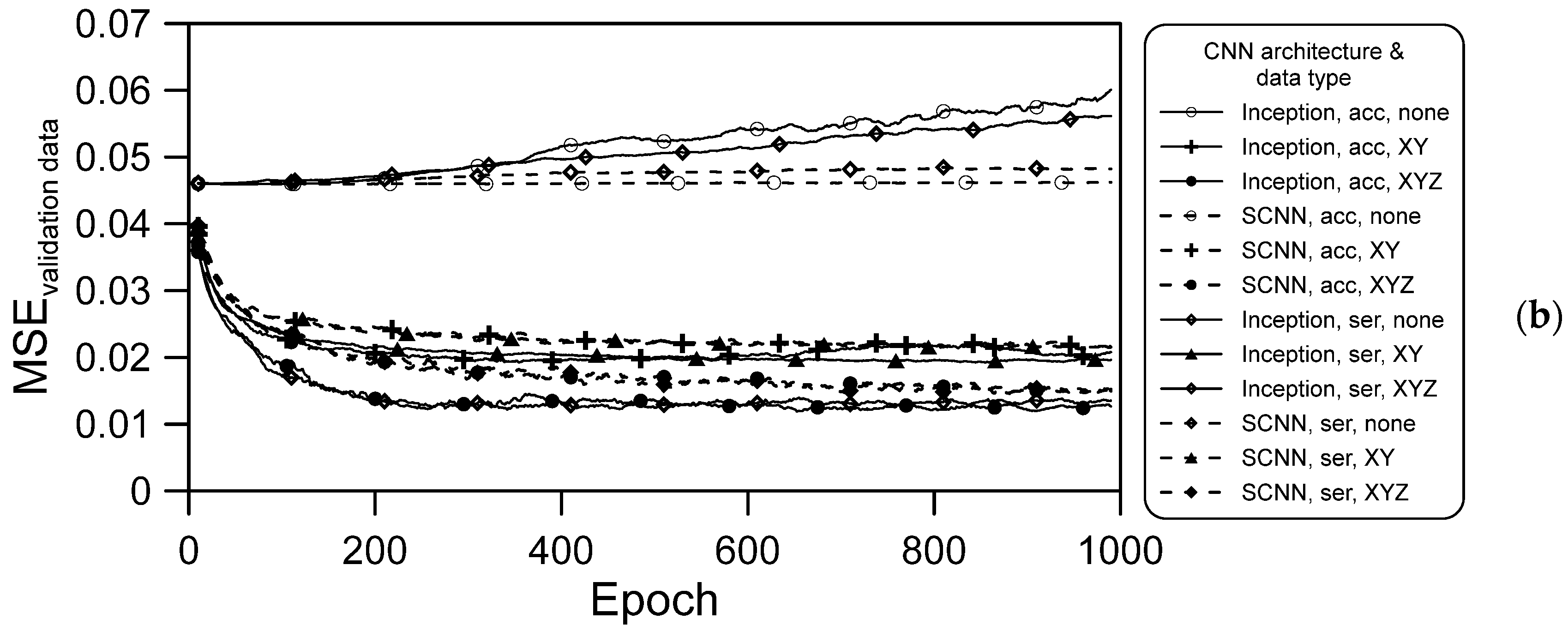
Model Comparison
- The training data not containing spatial information resulted in no convergence during the training process (Figure 9a), and the result obtained with the validation data was also divergent, as illustrated in Figure 9b. However, when spatial information was included, regardless of whether it was XY coordinates orYZ coordinates (including terrain elevation), convergence was gradually achieved in the training process;
- For both deep learning architectures and for both series hourly and accumulated rainfall data, the convergence obtained when XYZ spatial information was included was better than that achieved when XY spatial information only was included. Thus, elevation information is vital in CNN models used for flooding prediction;
- When the same data were used for training both architectures, convergence in the training was much better when using the Inception architecture than when using the SCNN architecture. We attribute this to the Inception architecture parameters being more numerous, which meant that more information was learned after separate training and merging of various training branches;
- For a given deep learning architecture and type of spatial information, the convergence achieved using the series hourly rainfall data was slightly better than that achieved using the accumulated rainfall data. For the training data, the effects of CNN architecture and spatial information type are stronger than that of rainfall data type.
5. Discussion
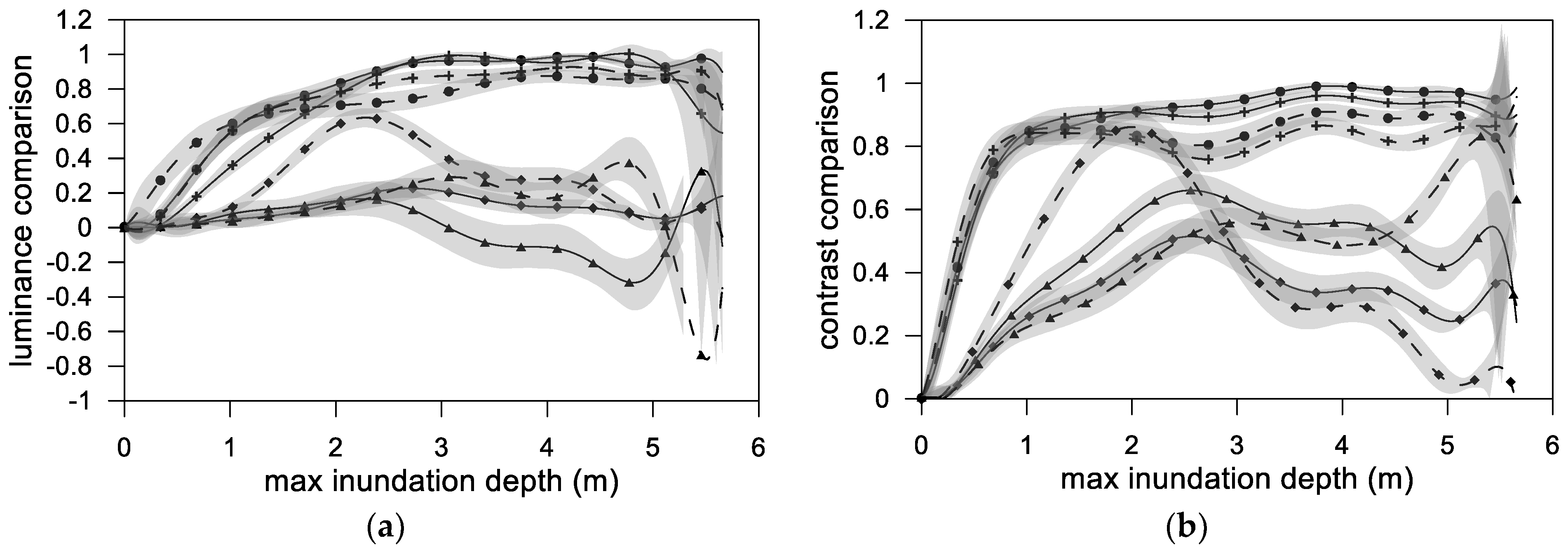
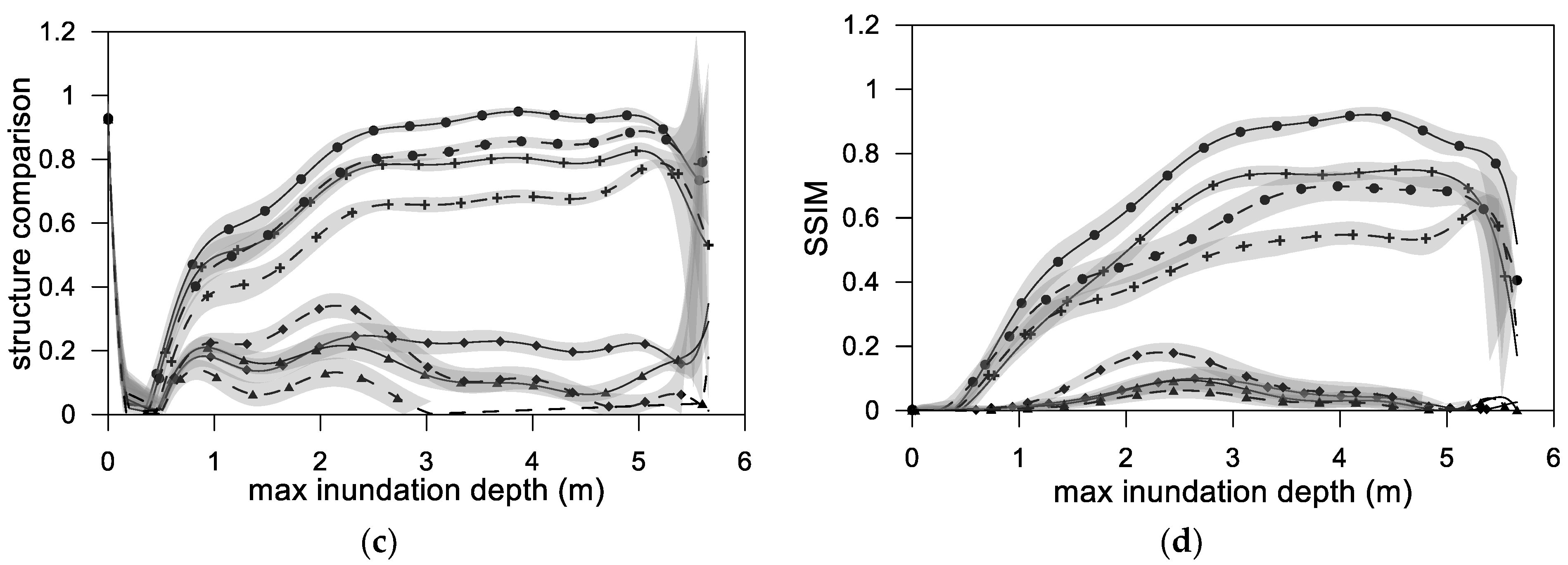
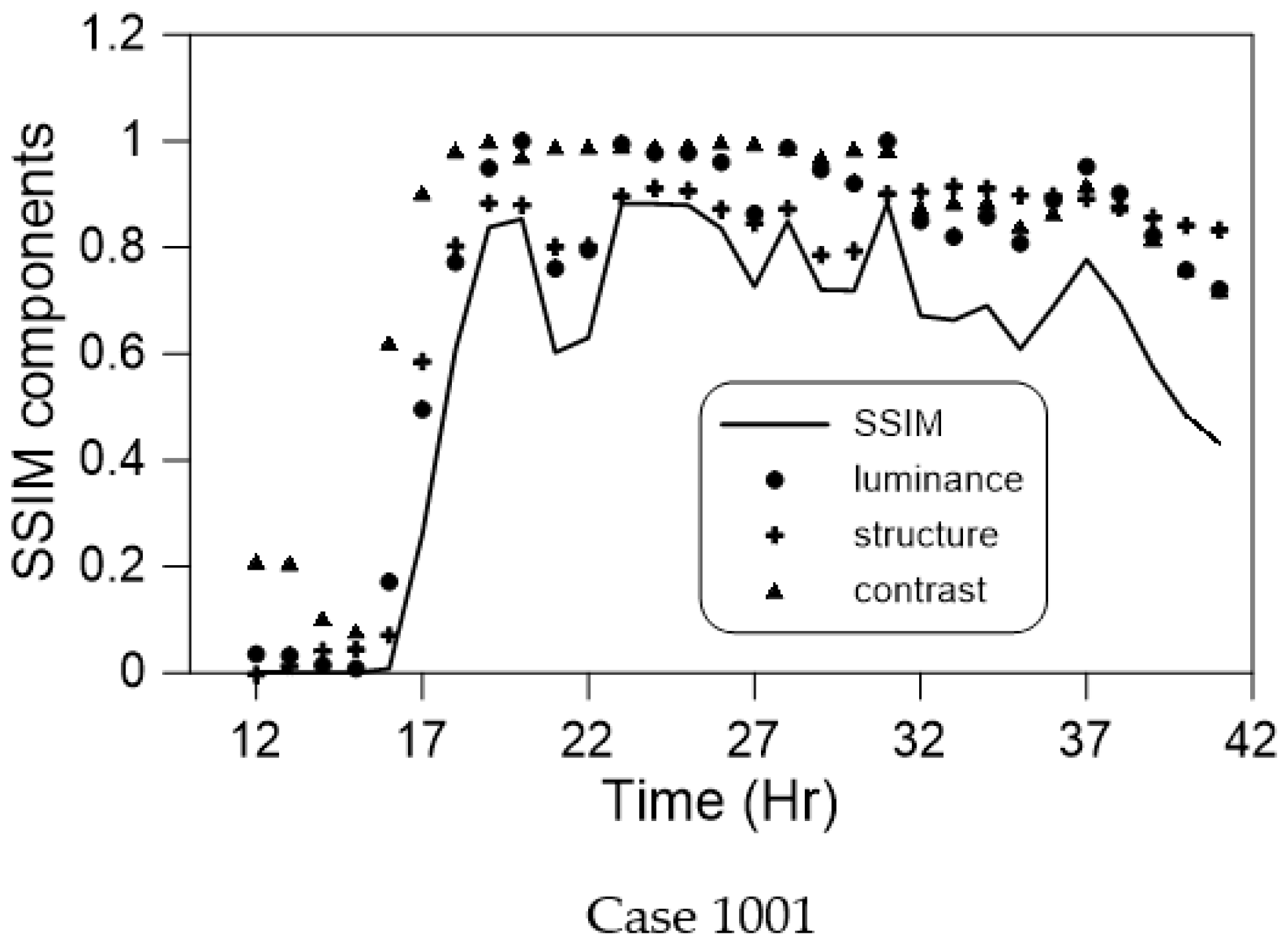
5.1. Similarity
- For both the SCNN and Inception architectures, when the accumulated rainfall data were used, the luminance, contrast, structure, and final synthesis (SSIM) results were more favorable than those obtained when the hourly time-series rainfall data were employed;
- The similarity at a small flooding depth was not ideal because in the initial stage of flooding, few grids were flooded. The few numbers of flooded grids severely affected the similarity results. A possible way to improve this is to increase the amount of training data with a small flooding depth;
- When using the hourly time-series rainfall data as the training data, the similarity at various maximum flooding depths fluctuated and was nonuniform, regardless of whether the spatial information contained terrain elevation. Thus, neither architecture could stably learn the time-series rainfall data;
- Regardless of the deep learning architecture that was employed and whether hourly time-series or accumulated rainfall were used, the use of spatial information, including terrain elevation, led to much more favorable results than the nonuse of this information;
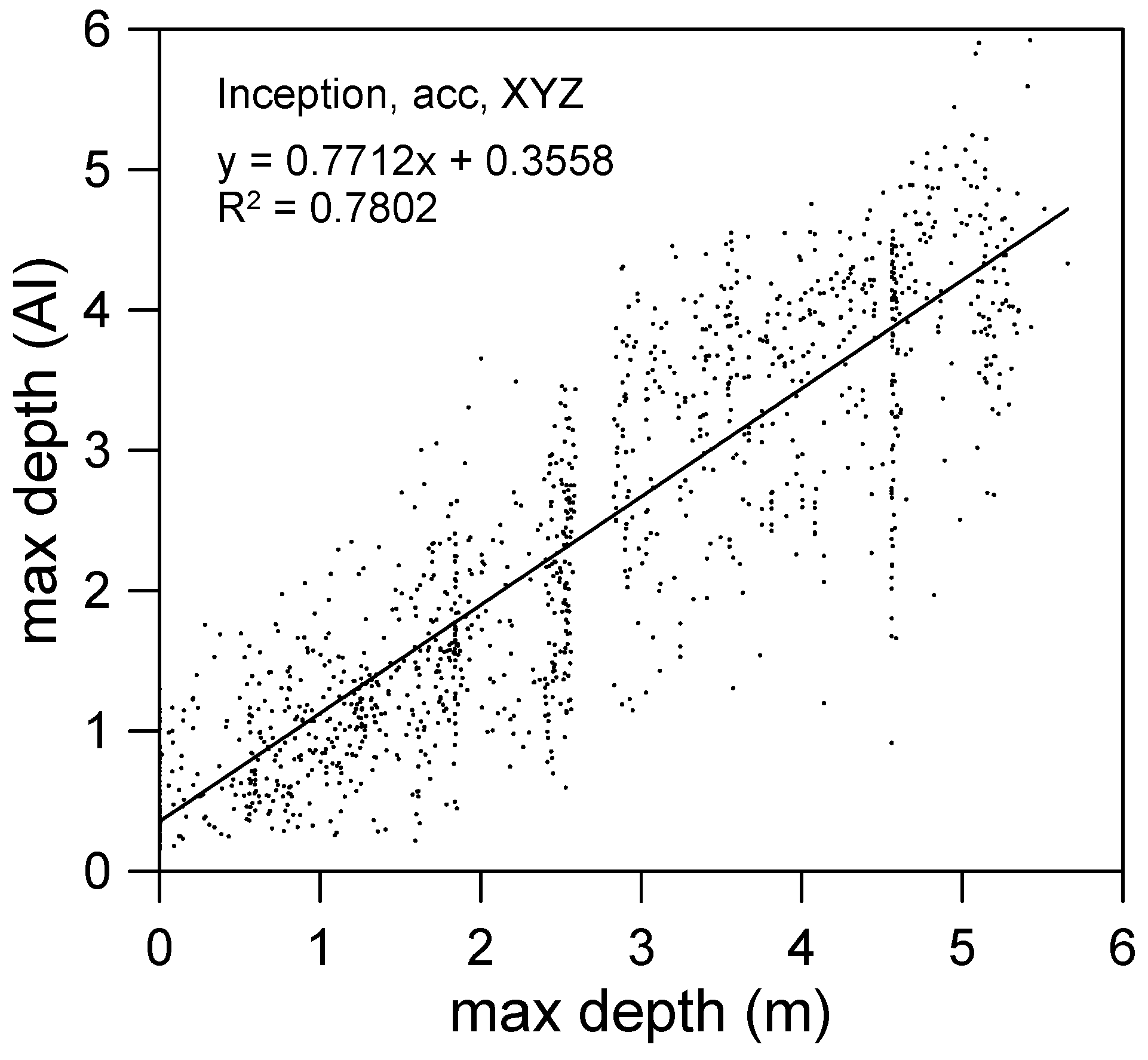
- A divergence was discovered near the maximum flooding depth. This was because when high-order polynomial regression is used, oscillation occurs at the edge of the interval; this is called the Runge phenomenon [34]. The phenomenon occurs when using polynomial interpolation with high-degree polynomials over a set of equally spaced interpolation points.
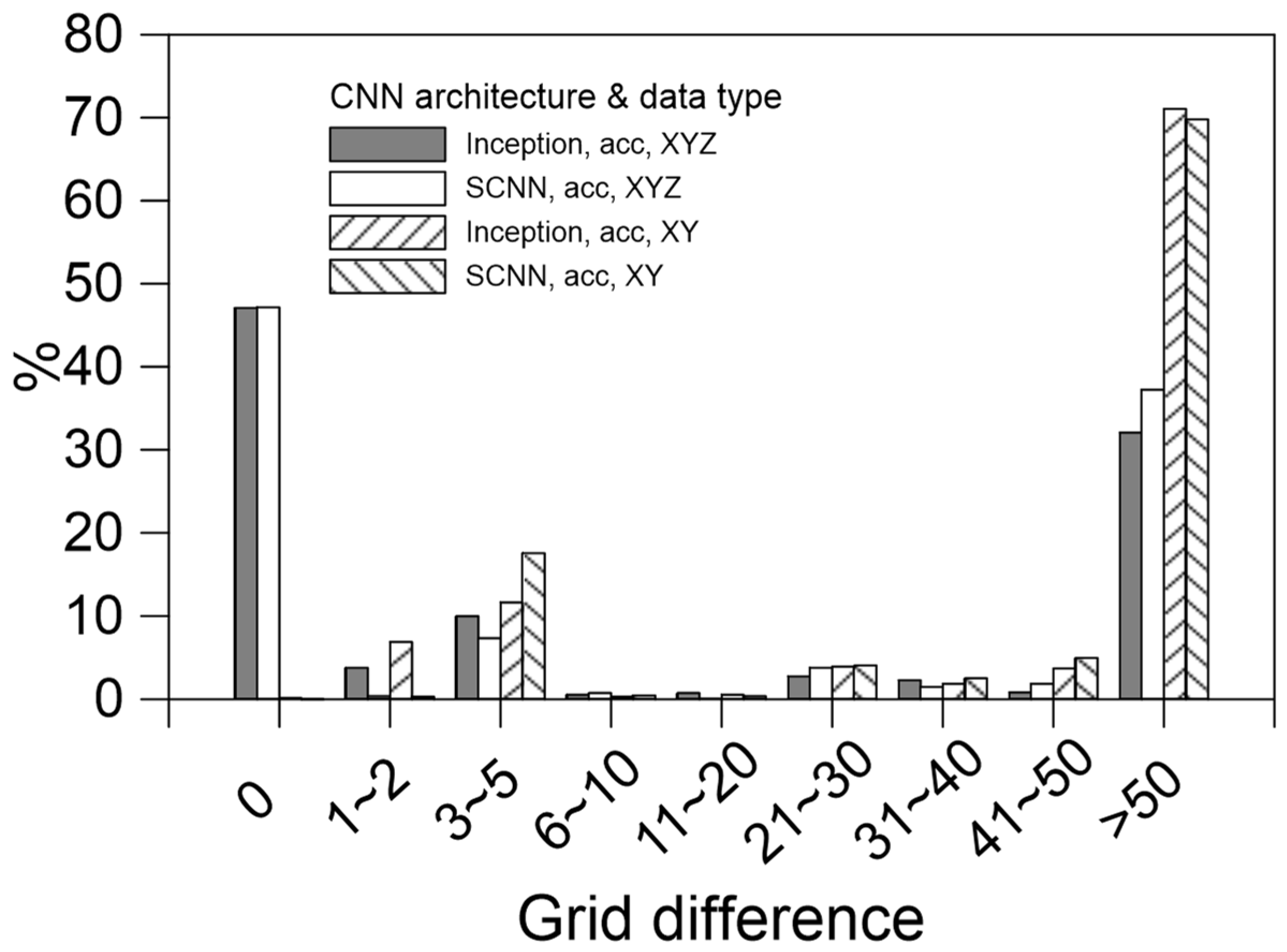
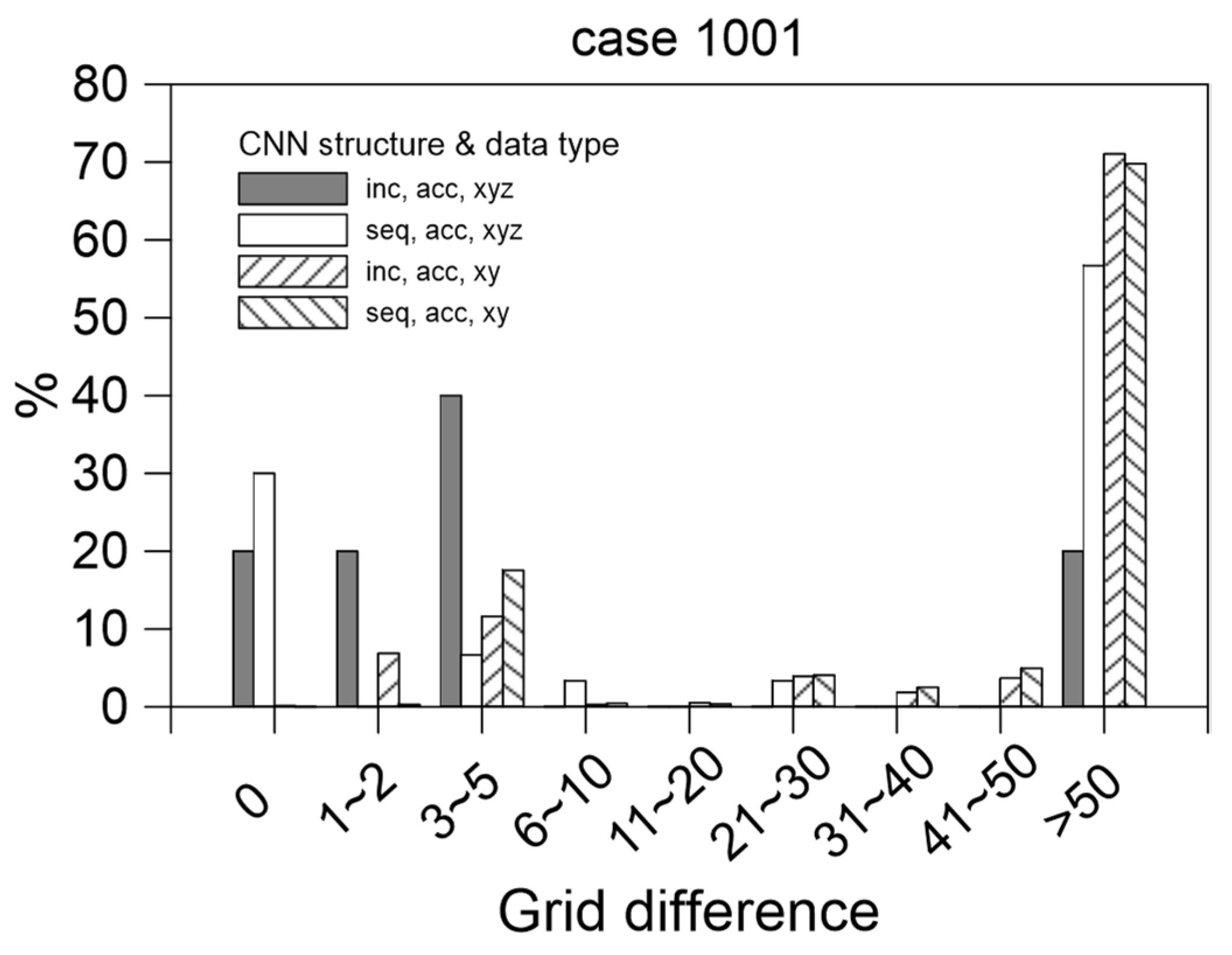
5.2. Comparison of Locations at Which Maximum Flooding Occurred
- The result obtained using the training data containing spatial information XYZ was far more accurate than that obtained using the training data containing only spatial information XY;
- The maximum position was found to be correct approximately 47% of the time. The grid position was within five grids of the actual position approximately 60% of the time; this percentage was much higher than 1/(360 × 201) = 1.38 × 10−5, indicating that the model could learn the flooding position and did not simply guess the location randomly.
5.3. Maximum Flooding Depth Prediction
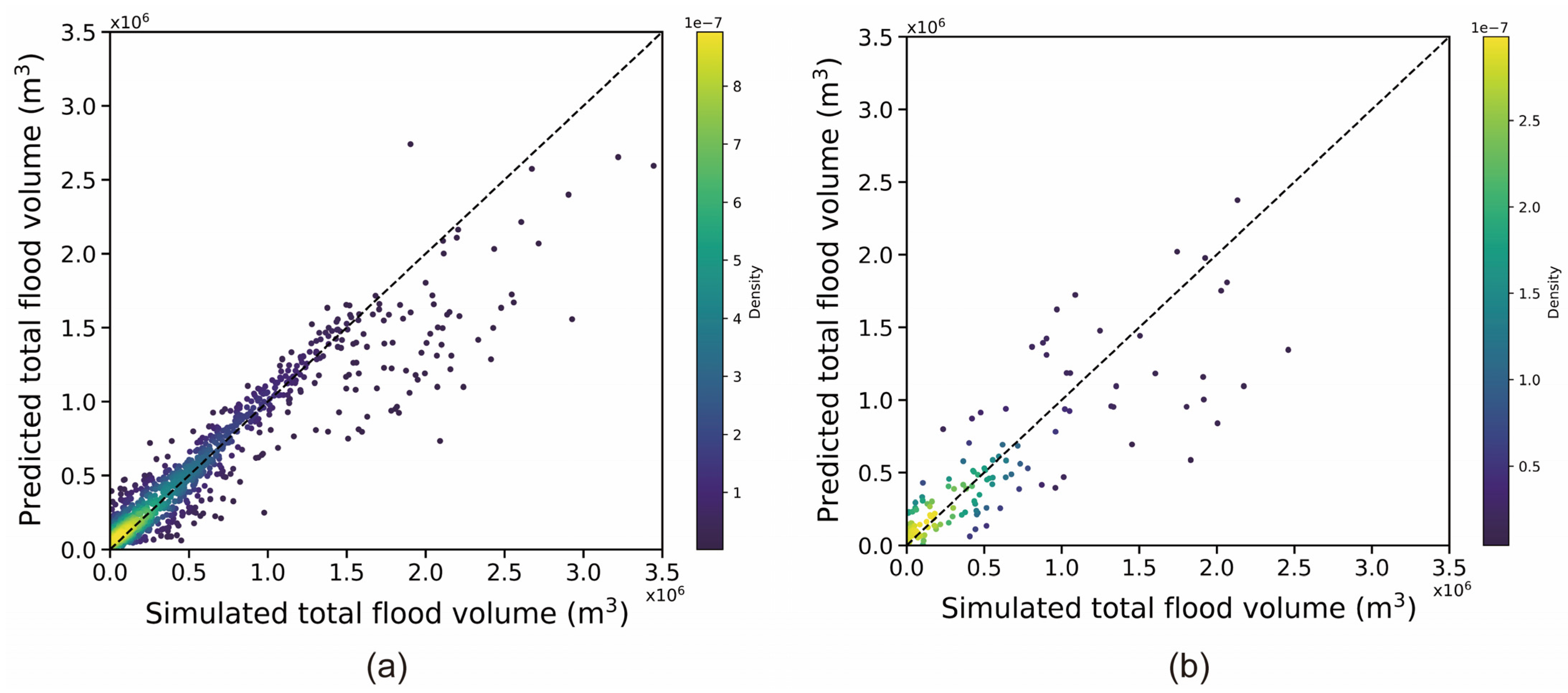
5.4. Total Flooding Volume
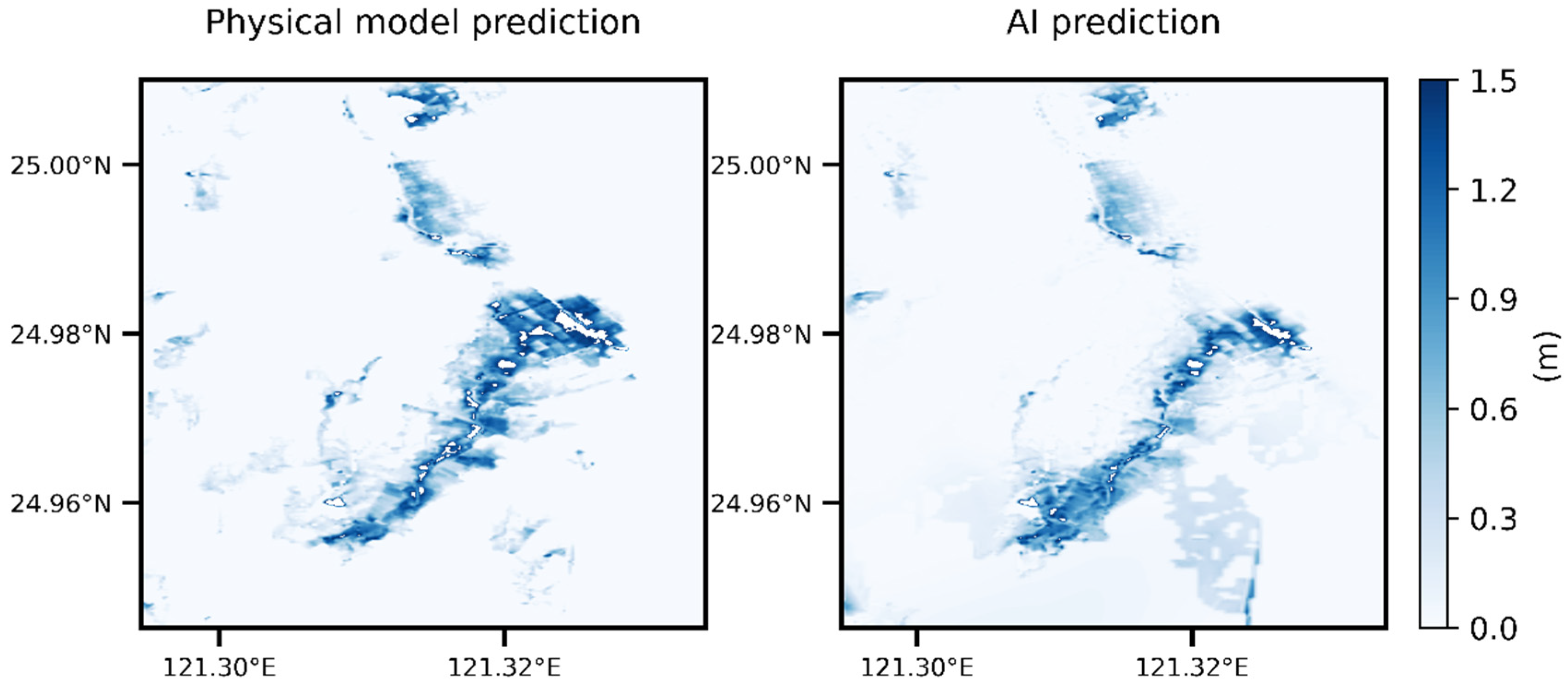
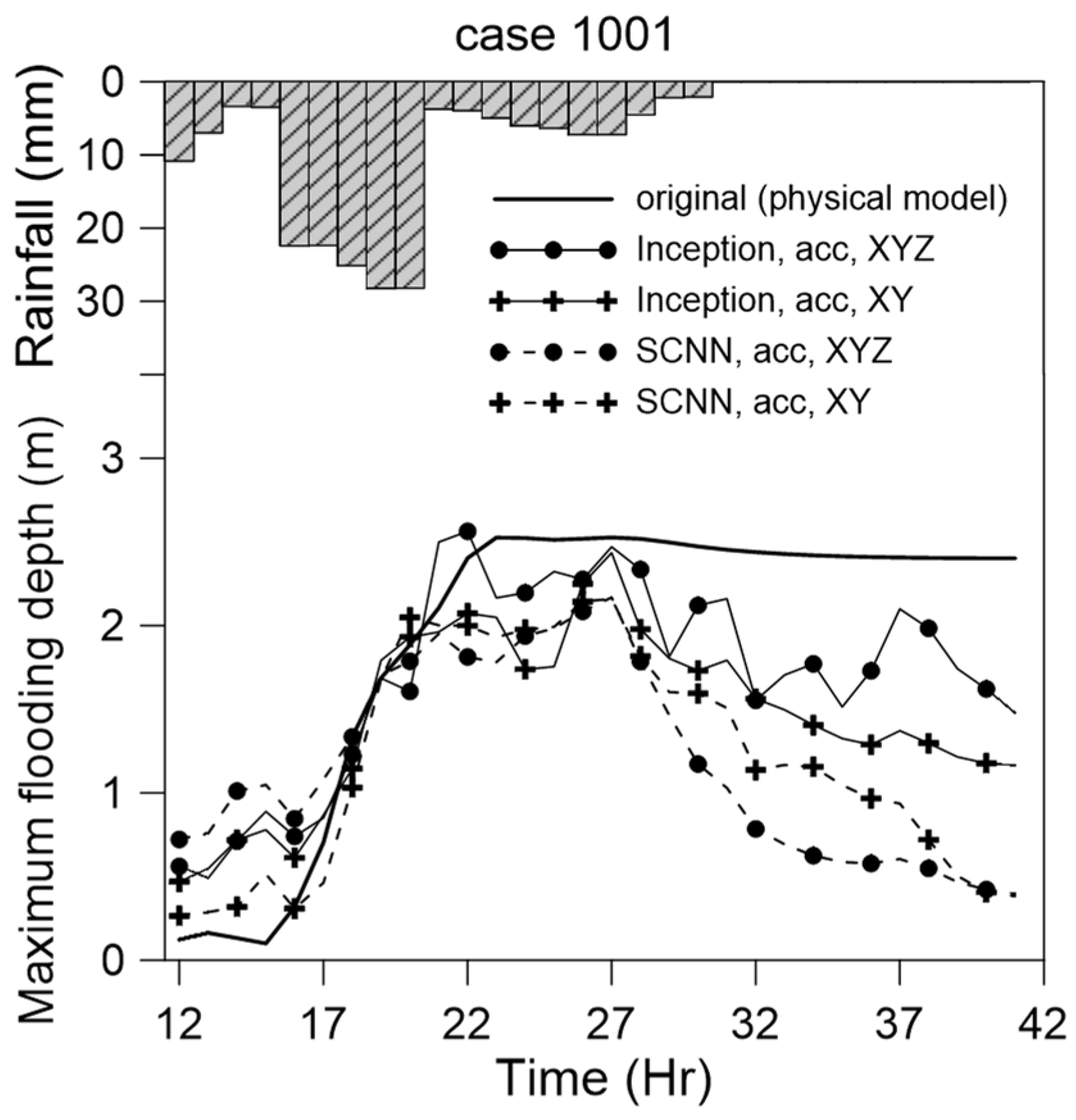
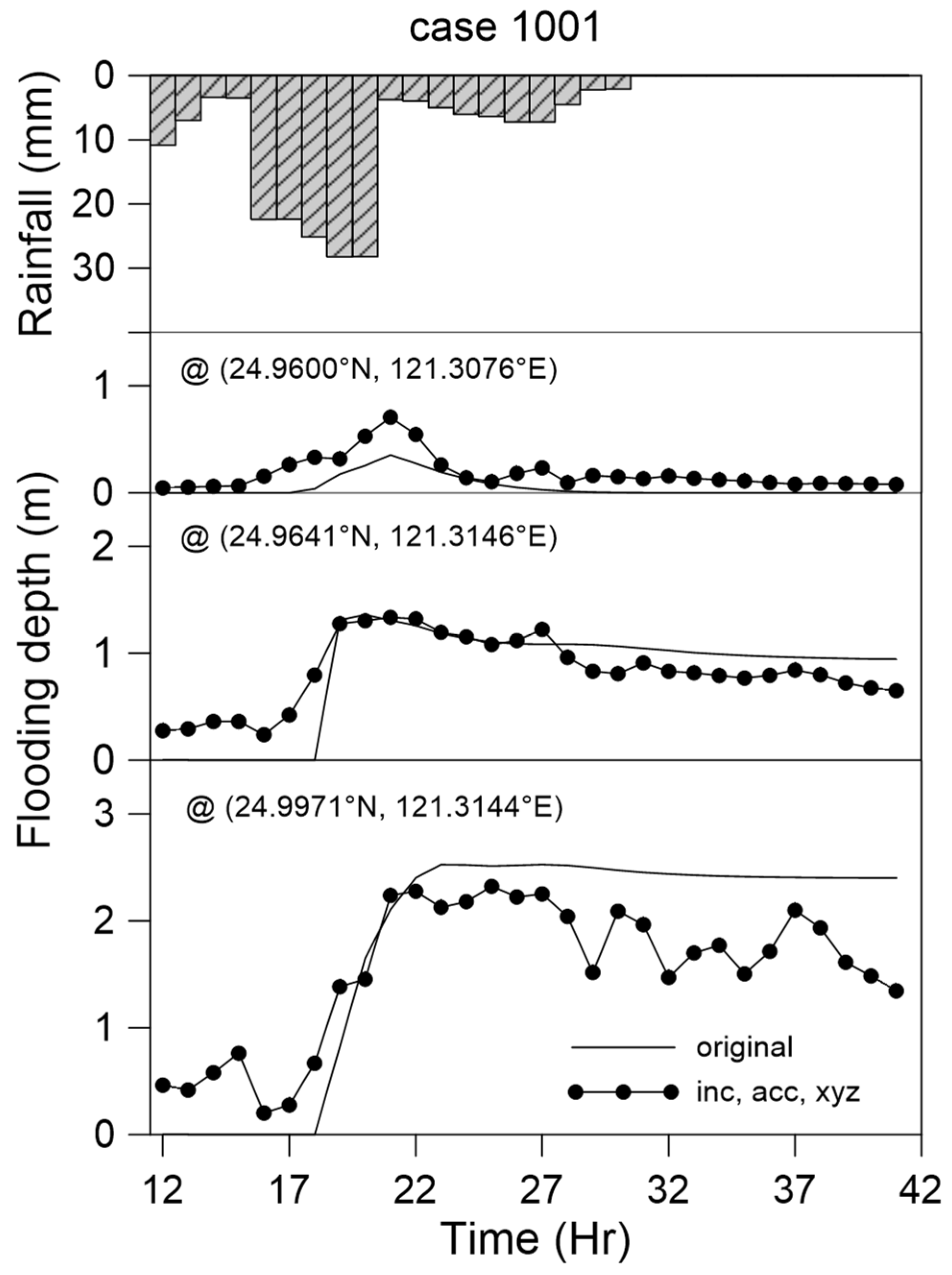
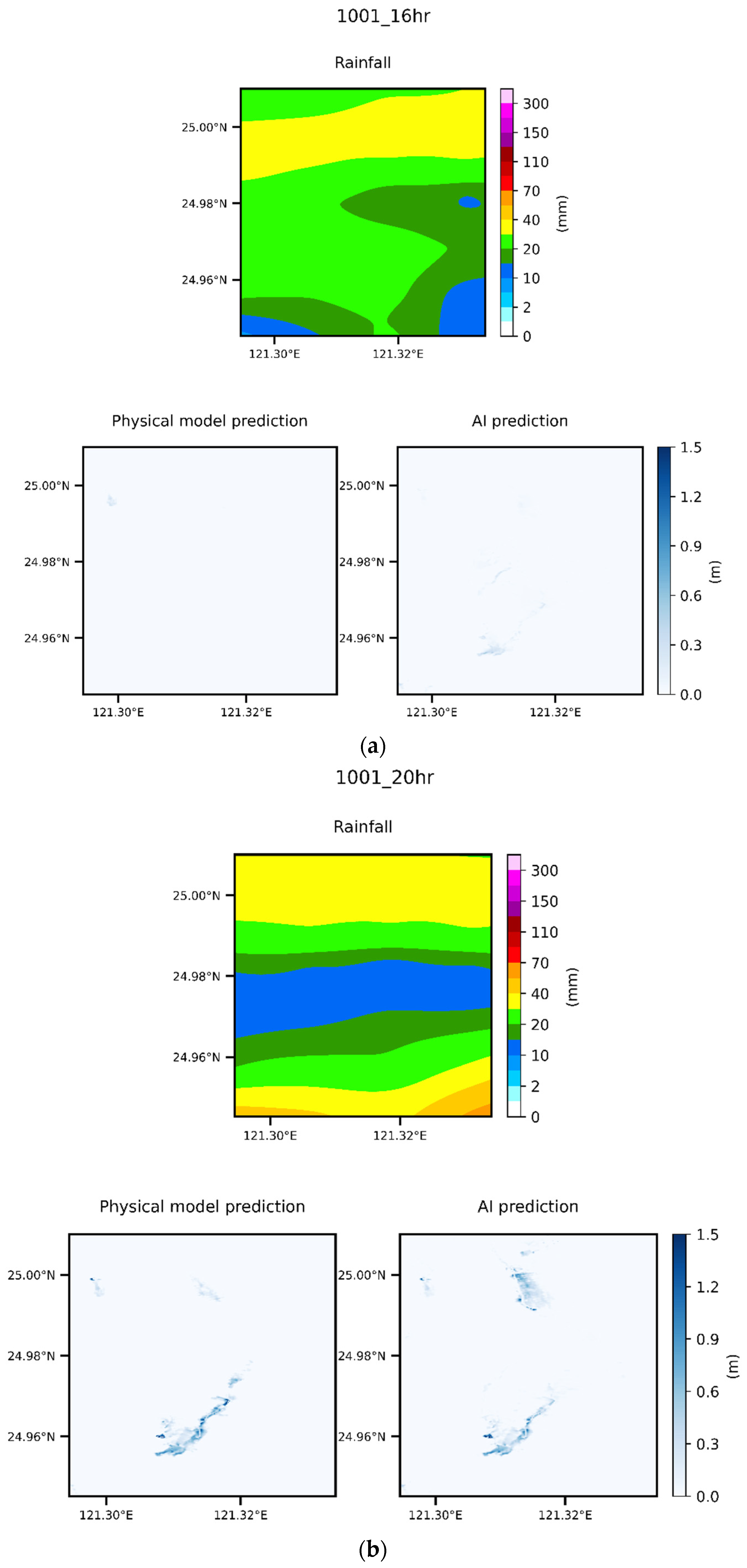
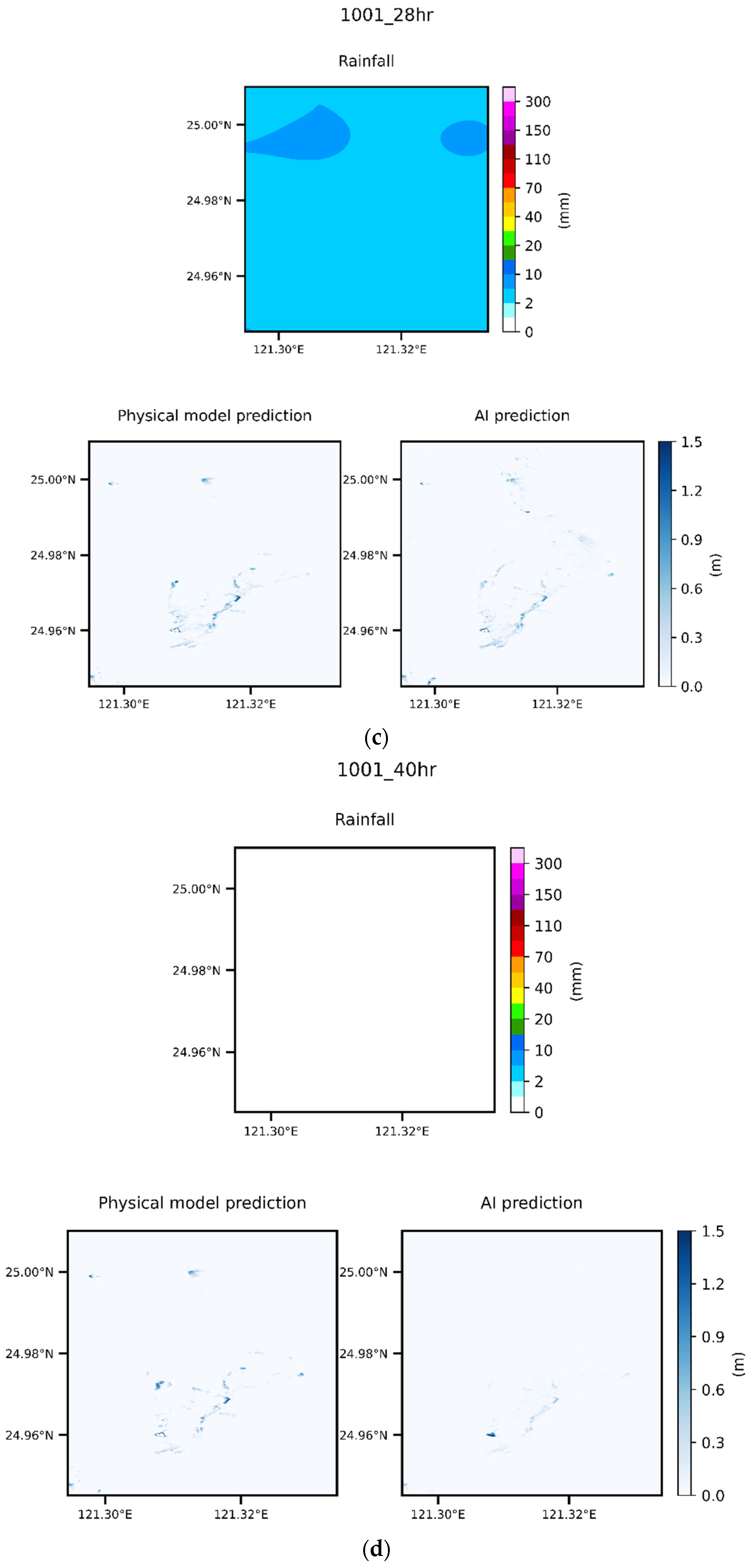
5.5. Case Comparison
6. Conclusions
- This study used the SCNN architecture, which has few parameters, and the Inception architecture, which has numerous parameters, to make flooding predictions when training with the same data. The results revealed that the Inception architecture achieved excellent results;
- Using multiple and randomization methods, this study employed 21 actual rainfall events to produce 6000 rainfall events of various durations. The physical model we constructed could simulate a flooding situation under extreme rainfall. A total of 218,850 sets of rainfall data were generated from the data of 6000 events. We divided the maximum flooding depth of all data into 20 groups and calculated the amount of data in each group. Only 0.653% of all the data were taken out for training, and this achieved favorable results;
- When spatial information was not included in the training dataset, convergence could not be achieved with either CNN architecture. Inclusion of XYZ information in the training data resulted in optimal results;
- More accurate training results were obtained when using accumulated rainfall data than when using hourly time-series rainfall data;
- This study used the SSIM to compare the flooding results predicted by the AI and physical models. When the water level was low because there were few deep-water grid samples, the similarity was low, and some other errors that occurred were due to the Runge effect. In all the other findings, excellent graphical similarity was discovered. The results obtained using deep learning to predict the flooding range and depth were very similar to the original data. Therefore, the method proposed in this paper obtained favorable results when used to predict flooding caused by heavy rain;
- Because of the sampling of the training data, the overall predicted water depth slightly shifted. In the future, the accuracy for low water levels can be improved by increasing the amount of the low water level or early rainfall data through data resampling.
- The deep learning models proposed in this study were trained with rainfall data and corresponding flooding depth data but without real-time data, which could be used to modify the prediction results. Therefore, the forecasted rainfall data can be input into our models to obtain long-term flooding forecasts, which would aid in disaster prevention and response, and provide responders with more time to prepare.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Karamuz, E.; Romanowicz, R.J.; Doroszkiewicz, J. The use of unmanned aerial vehicles in flood hazard assessment. J. Flood Risk Manag. 2020, 13, e12622. [Google Scholar] [CrossRef]
- Lee, I.; Kang, J.; Seo, G. Applicability Analysis of Ultra-Light UAV for Flooding Site Survey in South Korea. ISPRS Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 30, 185–189. [Google Scholar] [CrossRef] [Green Version]
- Schumann, G.J.P.; Muhlhausen, J.; Andreadis, K. The Value of a UAV-Acquired DEM for Flood Inundation Mapping and Modeling. EGU Gen. Assem. Conf. Abstr. 2016, 18, EPSC2016–EPSC10158. [Google Scholar]
- Salmoral, G.; Rivas-Casado, M.; Muthusamy, M.; Butler, D.; Menon, P.P.; Leinster, P. Guidelines for the use of unmanned aerial systems in flood emergency response. Water 2020, 12, 521. [Google Scholar] [CrossRef] [Green Version]
- Teng, J.; Jakeman, A.J.; Vaze, J.; Croke, B.F.W.; Dutta, D.; Kim, S. Flood inundation modelling: A review of methods, recent advances and uncertainty analysis. Environ. Model. Softw. 2017, 90, 201–216. [Google Scholar] [CrossRef]
- Fernández-Pato, J.; Caviedes-Voullième, D.; García-Navarro, P. Rainfall/runoff simulation with 2D full shallow water equations: Sensitivity analysis and calibration of infiltration parameters. J. Hydrol. 2016, 536, 496–513. [Google Scholar] [CrossRef]
- Kim, B.; Sanders, B.F.; Famiglietti, J.S.; Guinot, V. Urban flood modeling with porous shallow-water equations: A case study of model errors in the presence of anisotropic porosity. J. Hydrol. 2015, 523, 680–692. [Google Scholar] [CrossRef] [Green Version]
- Cea, L.; Garrido, M.; Puertas, J. Experimental validation of two-dimensional depth-averaged models for forecasting rainfall–runoff from precipitation data in urban areas. J. Hydrol. 2010, 382, 88–102. [Google Scholar] [CrossRef]
- Costabile, P.; Macchione, F. Enhancing river model set-up for 2-D dynamic flood modelling. Environ. Model. Softw. 2015, 67, 89–107. [Google Scholar] [CrossRef]
- Leandro, J.; Chen Albert, S.; Djordjević, S.; Savić Dragan, A. Comparison of 1D/1D and 1D/2D coupled (Sewer/Surface) hydraulic models for urban flood simulation. J. Hydraul. Eng. 2009, 135, 495–504. [Google Scholar] [CrossRef]
- Guidolin, M.; Chen, A.S.; Ghimire, B.; Keedwell, E.C.; Djordjević, S.; Savić, D.A. A weighted cellular automata 2D inundation model for rapid flood analysis. Environ. Model. Softw. 2016, 84, 378–394. [Google Scholar] [CrossRef]
- Lohani, A.K.; Goel, N.; Bhatia, K. Improving real time flood forecasting using fuzzy inference system. J. Hydrol. 2014, 509, 25–41. [Google Scholar] [CrossRef]
- Rezaeianzadeh, M.; Tabari, H.; Yazdi, A.A.; Isik, S.; Kalin, L. Flood flow forecasting using ANN, ANFIS and regression models. Neural Comput. Appl. 2014, 25, 25–37. [Google Scholar] [CrossRef]
- Elsafi, S.H. Artificial Neural Networks (ANNs) for flood forecasting at Dongola Station in the River Nile, Sudan. Alex. Eng. J. 2014, 53, 655–662. [Google Scholar] [CrossRef]
- Choubin, B.; Moradi, E.; Golshan, M.; Adamowski, J.; Sajedi-Hosseini, F.; Mosavi, A. An ensemble prediction of flood susceptibility using multivariate discriminant analysis, classification and regression trees, and support vector machines. Sci. Total Environ. 2019, 651, 2087–2096. [Google Scholar] [CrossRef]
- Khosravi, K.; Pham, B.T.; Chapi, K.; Shirzadi, A.; Shahabi, H.; Revhaug, I.; Prakash, I.; Bui, D.T. A comparative assessment of decision trees algorithms for flash flood susceptibility modeling at Haraz watershed, northern Iran. Sci. Total Environ. 2018, 627, 744–755. [Google Scholar] [CrossRef]
- Tehrany, M.S.; Pradhan, B.; Mansor, S.; Ahmad, N. Flood susceptibility assessment using GIS-based support vector machine model with different kernel types. Catena 2015, 125, 91–101. [Google Scholar] [CrossRef]
- Zhao, G.; Pang, B.; Xu, Z.; Peng, D.; Zuo, D. Urban flood susceptibility assessment based on convolutional neural networks. J. Hydrol. 2020, 590, 125235. [Google Scholar] [CrossRef]
- Jamali, B.; Bach, P.M.; Cunningham, L.; Deletic, A. A cellular automata fast flood evaluation (CA-ffé) model. Water Resour. Res. 2019, 55, 4936–4953. [Google Scholar] [CrossRef] [Green Version]
- Guo, Z.; Leitão, J.P.; Simões, N.E.; Moosavi, V. Data-driven flood emulation: Speeding up urban flood predictions by deep convolutional neural networks. J. Flood Risk Manag. 2021, 14, e12684. [Google Scholar] [CrossRef]
- Berkhahn, S.; Fuchs, L.; Neuweiler, I. An ensemble neural network model for real-time prediction of urban floods. J. Hydrol. 2019, 575, 743–754. [Google Scholar] [CrossRef]
- Chang, L.C.; Shen, H.Y.; Chang, F.J. Regional flood inundation nowcast using hybrid SOM and dynamic neural networks. J. Hydrol. 2014, 519, 476–489. [Google Scholar] [CrossRef]
- Wu, S.J.; Tung, Y.K.; Yang, J.C. Stochastic generation of hourly rainstorm events. Stoch. Environ. Res. Risk Assess. 2006, 21, 195–212. [Google Scholar] [CrossRef]
- Wu, S.J.; Hsu, C.T.; Chang, C.H. Stochastic modelling of gridded short-term rainstorms. Hydrol. Res. 2021, 52, 876–904. [Google Scholar] [CrossRef]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Conference on Operating Systems Design and Implementation, Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- Aghdam, H.; Heravi, E. Guide to Convolutional Neural Networks: A Practical Application to Traffic-Sign Detection and Classification; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar] [CrossRef]
- Szegedy, C.; Vanhoucke, V.; Ioffe, S.; Shlens, J.; Wojna, Z. Rethinking the Inception Architecture for Computer Vision. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 2818–2826. [Google Scholar] [CrossRef] [Green Version]
- Min, L.; Qiang, C.; Shuicheng, Y. Network in network. arXiv 2014, arXiv:1312.4400. [Google Scholar] [CrossRef]
- Scherer, D.; Müller, A.; Behnke, S. Evaluation of pooling operations in convolutional architectures for object recognition. In Artificial Neural Networks–ICANN 2010-Lecture Notes in Computer Science; Diamantaras, K., Duch, W., Iliadis, L.S., Eds.; ICANN, Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Kingma, D.; Ba, J. Adam: A Method for Stochastic Optimization. International Conference on Learning Representations. arXiv 2014, arXiv:1412.6980v9 2014. [Google Scholar] [CrossRef]
- LeCun, Y.; Jackel, L.D.; Bottou, L.; Cortes, C.; Denker, J.S.; Drucker, H.; Guyon, I.; Muller, U.A.; Sackinger, E.; Simard, P.; et al. Learning algorithms for classification: A comparison on handwritten digit recognition. Neural Netw. Stat. Mech. Perspective 1995, 261, 2. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Gutierrez-Osuna, R. Lecture notes in Kernel Density Estimation for CSCE 666: Pattern Analysis at Texas A&M University. 2020. Available online: https://pdf4pro.com/view/l7-kernel-density-estimation-texas-a-amp-m-university-5b8da8.html (accessed on 17 December 2022).
- Runge, C. Über empirische Funktionen und die Interpolation zwischen äquidistanten Ordinaten. Z. Fur. Math. Phys. 1901, 46, 224–243. [Google Scholar]


| Event | Start Time | End Time | Duration (h) | Areal Average Rainfall (mm) |
|---|---|---|---|---|
| 1 | 17/07/2005 10:00 | 18/07/2005 18:00 | 33 | 36.4 |
| 2 | 04/08/2005 09:00 | 06/08/2005 00:00 | 40 | 65.8 |
| 3 | 31/08/2005 07:00 | 01/09/2005 08:00 | 26 | 55.2 |
| 4 | 01/10/2005 23:00 | 02/10/2005 18:00 | 20 | 30.3 |
| 5 | 26/07/2008 22:00 | 28/07/2008 22:00 | 49 | 66.8 |
| 6 | 12/09/2008 02:00 | 09/15/2008 00:00 | 71 | 235.9 |
| 7 | 21/10/2010 00:00 | 10/22/2010 13:00 | 38 | 224.7 |
| 8 | 11/06/2012 21:00 | 12/06/2012 23:00 | 27 | 294.2 |
| 9 | 14/06/2012 11:00 | 15/06/2012 06:00 | 20 | 42.0 |
| 10 | 26/08/2012 09:00 | 27/08/2012 08:00 | 24 | 31.5 |
| 11 | 11/05/2013 01:00 | 13/05/2013 01:00 | 49 | 90.3 |
| 12 | 12/07/2013 16:00 | 13/07/2013 14:00 | 23 | 26.7 |
| 13 | 04/10/2013 14:00 | 06/10/2013 23:00 | 58 | 2.3 |
| 14 | 20/05/2014 20:00 | 22/05/2014 00:00 | 29 | 96.9 |
| 15 | 22/07/2014 21:00 | 24/07/2014 03:00 | 31 | 36.1 |
| 16 | 21/09/2014 16:00 | 22/09/2014 12:00 | 21 | 25.2 |
| 17 | 07/08/2015 08:00 | 08/08/2015 13:00 | 30 | 125.5 |
| 18 | 27/09/2015 14:00 | 29/09/2015 05:00 | 40 | 99.7 |
| 19 | 26/09/2016 10:00 | 28/09/2016 04:00 | 43 | 49.4 |
| 20 | 02/06/2017 10:00 | 04/06/2017 04:00 | 39 | 288.6 |
| 21 | 12/09/2017 22:00 | 14/09/2017 12:00 | 39 | 9.1 |
| Group | Statistical Properties of Rainfall | Number of Events | |
|---|---|---|---|
| 1 | Mean | 1000 | |
| Standard deviation | |||
| 2 | Mean | 1000 | |
| Standard deviation | |||
| 3 | Mean | 1000 | |
| Standard deviation | |||
| 4 | Mean | 3000 | |
| Standard deviation | |||
| Model | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Architecture | SCNN | Inception | ||||||||||
| Rainfall type | Series hourly (ser) | Accumulated (acc) | Series hourly (ser) | Accumulated (acc) | ||||||||
| Space type | None | XY | XYZ | None | XY | XYZ | None | XY | XYZ | None | XY | XYZ |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.-W.; Lin, G.-F.; Hsu, C.-T.; Wu, S.-J.; Tfwala, S.S. Long-Term Temporal Flood Predictions Made Using Convolutional Neural Networks. Water 2022, 14, 4134. https://doi.org/10.3390/w14244134
Wang H-W, Lin G-F, Hsu C-T, Wu S-J, Tfwala SS. Long-Term Temporal Flood Predictions Made Using Convolutional Neural Networks. Water. 2022; 14(24):4134. https://doi.org/10.3390/w14244134
Chicago/Turabian StyleWang, Hau-Wei, Gwo-Fong Lin, Chih-Tsung Hsu, Shiang-Jen Wu, and Samkele Sikhulile Tfwala. 2022. "Long-Term Temporal Flood Predictions Made Using Convolutional Neural Networks" Water 14, no. 24: 4134. https://doi.org/10.3390/w14244134





