Modeling Hydrological Regimes of Floodplain Wetlands Using Remote Sensing and Field Survey Data
Abstract
1. Introduction
2. Materials and Methods
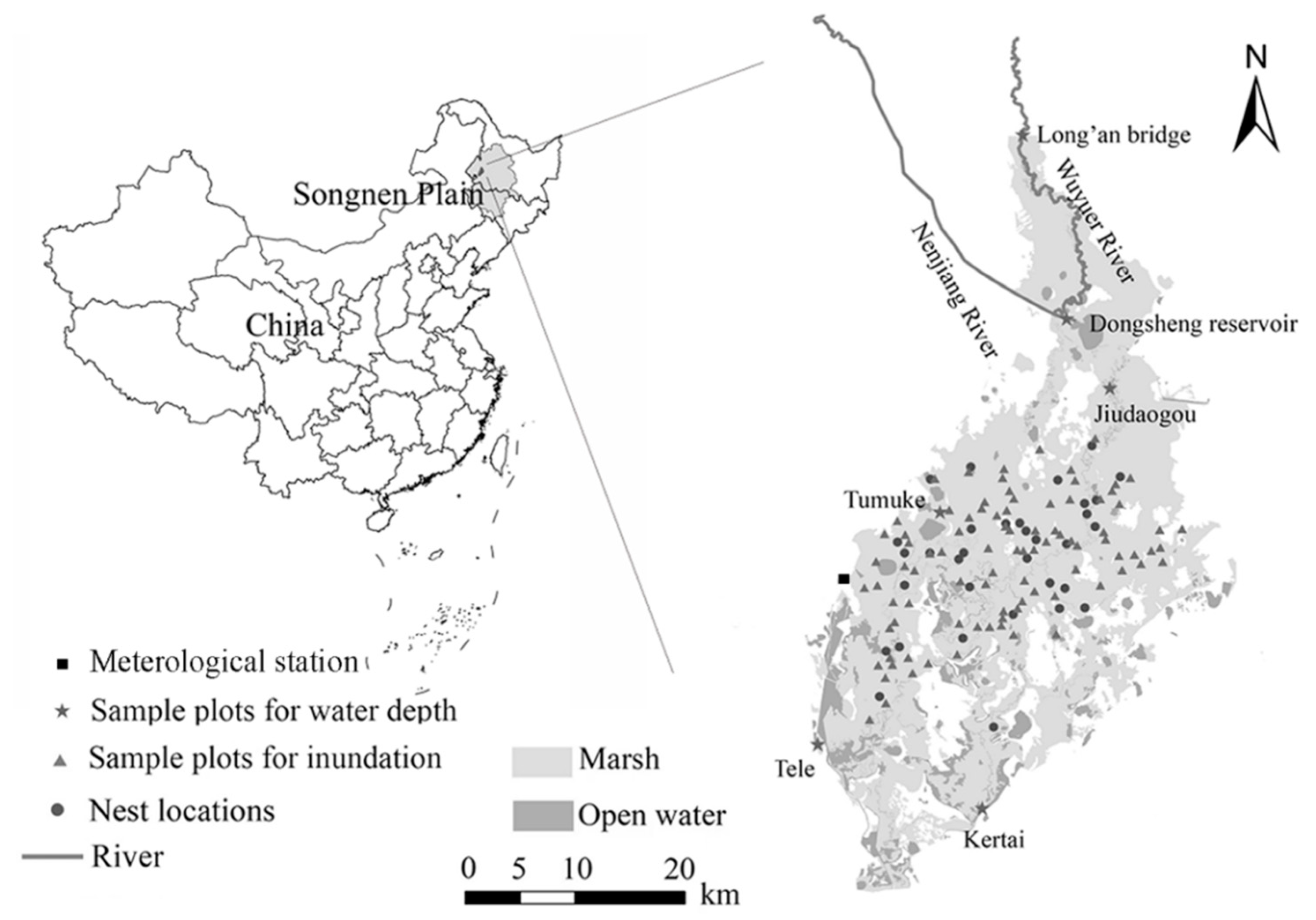
2.1. Study Area
2.2. Data
2.3. Model Description
2.4. Model Parameters
2.5. Model Calibration and Evaluation
3. Results
3.1. Simulation of Water Levels
3.2. Simulation of Inundation Extent
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bian, H.F.; Yan, T.T.; Zhang, Z.X.; He, C.G.; Sheng, L.X. Mapping deciduous broad-leaved forested swamps using ALOS/Palsar data. Chin. Geogra. Sci. 2016, 26, 352–365. [Google Scholar] [CrossRef]
- Mitsch, W.J.; Gosselink, J.G. The value of wetlands: Importance of scale and landscape setting. Ecol. Econ. 2000, 35, 25–33. [Google Scholar] [CrossRef]
- Webb, J.A.; Wallis, E.M.; Stewardson, M.J. A systematic review of published evidence linking wetland plants to water regime components. Aqua. Bot. 2012, 103, 1–14. [Google Scholar] [CrossRef]
- Na, X.D.; Zang, S.Y.; Zhang, N.N.; Cui, J. Impact of land use and land cover dynamics on Zhalong wetland reserve ecosystem, Heilongjiang Province, China. Int. J. Environ. Sci. Technol. 2015, 12, 445–454. [Google Scholar] [CrossRef]
- Schulte, M.L.; McLaughlin, D.L.; Wurster, F.C.; Balentine, K.; Speiran, G.K.; Aust, W.M.; Stewart, R.D.; Varner, J.M.; Jones, C.N. Linking ecosystem function and hydrologic regime to inform restoration of a forested peatland. J. Environ. Manag. 2019, 233, 342–351. [Google Scholar] [CrossRef]
- Na, X.D.; Zang, S.Y.; Wu, C.S.; Li, W.L. Mapping forested wetlands in the Great Zhan River Basin through integrating optical, radar, and topographical data classification techniques. Environ. Monit. Assess. 2015, 187, 696. [Google Scholar] [CrossRef] [PubMed]
- Huang, C.; Chen, Y.; Wu, J.P. Mapping spatio-temporal flood inundation dynamics at large river basin scale using time-series flow data and MODIS imagery. Int. J. Appl. Earth Obs. 2014, 26, 350–362. [Google Scholar] [CrossRef]
- Xie, C.; Xu, J.; Shao, Y.; Cui, B.S.; Goel, K.; Zhang, Y.J.; Yuan, M.H. Long term detection of water depth changes of coastal wetlands in the Yellow River Delta based on distributed scatterer interferometry. Remote Sens. Environ. 2015, 164, 238–253. [Google Scholar] [CrossRef][Green Version]
- Yin, J.; Zhao, Q.; Yu, D.P.; Lin, N.; Kubanek, J.L.; Ma, G.Y.; Liu, M.; Pepeg, A. Long-term flood-hazard modeling for coastal areas using InSAR measurements and a hydrodynamic model: The case study of Lingang New City, Shanghai. J. Hydrol. 2019, 571, 593–604. [Google Scholar] [CrossRef]
- Arega, F. Hydrodynamic modeling and characterizing of Lagrangian flows in the West Scott Creek wetlands system, South Carolina. J. Hydro-Environ. Res. 2013, 7, 50–60. [Google Scholar] [CrossRef]
- Felder, G.; Zischg, A.; Weingartner, R. The effect of coupling hydrologic and hydrodynamic models on probable maximum flood estimation. J. Hydrol. 2017, 550, 157–165. [Google Scholar] [CrossRef]
- Milzow, C.; Burg, V.; Kinzelbach, W. Estimating future ecoregion distributions within the Okavango Delta Wetlands based on hydrological simulations and future climate and development scenarios. J. Hydrol. 2010, 381, 89–100. [Google Scholar] [CrossRef]
- Wen, L.; Macdonald, R.; Morrison, T.; Hameed, T.; Saintilan, N.; Ling, J. From hydrodynamic to hydrological modelling: Investigating long-term hydrological regimes of key wetlands in the Macquarie Marshes, a semi-arid lowland floodplain in Australia. J. Hydrol. 2013, 500, 45–61. [Google Scholar] [CrossRef]
- Fleischmann, A.; Siqueira, V.; Paris, A.; Collischonn, W.; Paiva, R.; Pontes, P.; Crétaux, J.F.; Bergé-Nguyen, M.; Biancamaria, S.; Gosset, M.; et al. Modelling hydrologic and hydrodynamic processes in basins with large semi-arid wetlands. J. Hydrol. 2018, 561, 943–959. [Google Scholar] [CrossRef]
- Wester, S.J.; Grimson, R.; Minotti, P.G.; Booij, M.J.; Brugnach, M. Hydrodynamic modelling of a tidal delta wetland using an enhanced quasi-2D model. J. Hydrol. 2018, 559, 315–326. [Google Scholar] [CrossRef]
- Yeo, I.Y.; Lang, M.W.; Lee, S.; McCarty, G.W.; Sadeghi, A.M.; Yetemen, O.; Huang, C.Q. Mapping landscape-level hydrological connectivity of headwater wetlands to downstream waters: A geospatial modeling approach-Part 1. Sci. Total Environ. 2019, 653, 1546–1556. [Google Scholar] [CrossRef]
- Logah, F.Y.; Amisigo, A.B.; Obuobie, E.; Kankam-Yeboah, K. Floodplain hydrodynamic modelling of the Lower Volta River in Ghana. J. Hydrol. 2017, 14, 1–9. [Google Scholar] [CrossRef]
- Yang, Y.Z.; Wu, Q.B.; Jin, H.J.; Wang, Q.F.; Huang, Y.D.; Luo, D.L.; Gao, S.H.; Jin, X.Y. Delineating the hydrological processes and hydraulic connectivities under permafrost degradation on Northeastern Qinghai-Tibet Plateau, China. J. Hydrol. 2019, 569, 359–372. [Google Scholar] [CrossRef]
- Zang, S.Y. Heilongjiang Province Geography; Beijing Normal University Publishing Group: Beijing, China, 2014; pp. 123–126. [Google Scholar]
- Na, X.D.; Zang, S.Y.; Wu, C.S.; Tian, Y.; Li, W.L. Hydrological Regime Monitoring and Mapping of the Zhalong Wetland through Integrating Time Series Radarsat-2 and Landsat Imagery. Remote Sens. 2018, 10, 702. [Google Scholar] [CrossRef]
- Dutta, D.; Alam, J.; Umeda, K.; Hayashi, M.; Hironaka, S. A two dimensional hydrodynamic model for flood inundation simulation: A case study in the Lower Mekong River basin. Hydrol. Process. 2007, 21, 1223–1237. [Google Scholar] [CrossRef]
- Cunge, J. Two dimensional modelling of flood plains. In Unsteady Flow in Open Channels; Mahmood, K., Yevjevich, V., Eds.; Water Resources Publications: Fort Collins, CO, USA, 1975; pp. 705–762. [Google Scholar]
- Warren, I.R.; Bach, H.K. MIKE 21: A modelling system for estuaries, coastal waters and seas. Environ. Softw. 1992, 7, 229–240. [Google Scholar] [CrossRef]
- Karim, F.; Dutta, D.; Marvanek, S.; Petheram, C.; Ticehurst, C.; Lerat, J.L.; Kim, S.; Yang, A. Assessing the impacts of climate change and dams on floodplain inundation and wetland connectivity in the wet–dry tropics of northern Australia. J. Hydrol. 2015, 522, 80–94. [Google Scholar] [CrossRef]
- Mo, B.; Chen, X.Y.; Yang, Y.C.; Luo, B.L.; Tang, J.; Gong, C.M.; Lin, Z.H.; Zhou, T.J.; Shen, Y.K. Research on soil infiltration capacity and its influencing factors in different land uses. Res. Soil Water Conserv. 2016, 23, 13–17. [Google Scholar]
- Wang, J.J.; Zhang, K.D.; Gong, J.G.; Fan, Y.; Xu, D. Overland flow resistance law under different vegetation coverage. J. Soil Water Conserv. 2015, 29, 1–6. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I–A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Piedra-Cueva, I.; Fossati, M. Residual currents and corridor of flow in the Rio de la Plata. Appl. Mathemat. Model. 2007, 31, 564–577. [Google Scholar] [CrossRef]
- Biancamaria, S.; Bates, P.D.; Boone, A.; Mognard, N.M. Large-scale coupled hydrologic and hydraulic modelling of the Ob river in Siberia. J. Hydrol. 2009, 379, 136–150. [Google Scholar] [CrossRef]
- Bowen, S.; Simpson, S. Changes in Extent and Condition of the Vegetation Communities of the Macquarie Marshes Floodplain 1991–2008; Environment Department of New South Wales: Sydney, Australia, 2010.
- Na, X.D.; Zhou, H.T.; Zang, S.Y.; Wu, C.S.; Li, W.L.; Li, M. Maximum Entropy modeling for habitat suitability assessment of Red-crowned crane. Ecol. Indic. 2018, 91, 439–446. [Google Scholar] [CrossRef]




| Type | Description | Application | Source |
|---|---|---|---|
| Topography | DEM derived from 1:10,000 topographical maps | 30 m DEM for 2D elevation | Mapping and Surveying Bureau of Heilongjiang Province |
| Soil thematic map | 1: 50,000 soil-type map with hydraulic properties | To obtain soil infiltration parameters | Heilongjiang Geography [19] |
| Land-cover thematic map | 2014 land-cover map derived from Radarsat-2 and Landsat-8 imagery | To develop the hydraulic roughness map for the 2D model | Land cover thematic map [20] |
| Climate data | Rainfall, temperature and evaporation | Input parameters | Daily data set of ground climate data in China (V3.0) in 2014. |
| River gauge records | Includes water levels and river discharge at the Long’an Bridge station, Dongsheng Reservoir, Kertai, and Tele | River gauge records were used to define the inflow and outflow boundaries | Onset HOBO U20-001-01 water level logger, Hydrology Bureau of Heilongjiang Province, China |
| Wetland gauge records | Includes water levels and water temperature in 2014 in Tumuke and Jiudaogou | Wetland gauge records were used to calibrate and validate the hydrodynamic models. | Onset HOBO U20-001-01 water level logger and Thermochron@ iButton temperature sensors. |
| Flood extent map | Inundation maps were derived from time-series Radarsat-2 SAR images | To calibrate and evaluate the hydrodynamic models | Flood extent map [20] |
| Field data | Obtained from 150 sample sites; include inundation levels and geographic coordinates | To evaluate the accuracy of flooding extent | Field survey conducted on 22 May, 2014 |
| Event Location | Start Date | End Date | Inundation Map Dates | Use |
|---|---|---|---|---|
| Tumuke | 1 May 2014 | 29 May 2014 | 1 May 2014, 22 May 2014 | Calibration |
| Tumuke | 10 June 2014 | 7 July 2014 | 10 June 2014, 6 July 2014 | Calibration |
| Tumuke | 15 July 2014 | 20 August 2014 | 24 July 2014, 17 August 2014 | Validation |
| Tumuke | 6 September 2014 | 6 October 2014 | 10 September 2014, 2 October 2014 | Validation |
| Jiudaogou | 1 May 2014 | 29 May 2014 | 1 May 2014, 22 May 2014 | Calibration |
| Jiudaogou | 10 June 2014 | 7 July 2014 | 10 June 2014, 6 July 2014 | Calibration |
| Jiudaogou | 15 July 2014 | 20 August 2014 | 24 July 2014, 17 August 2014 | Validation |
| Jiudaogou | 6 September 2014 | 6 October 2014 | 10 September 2014, 2 October 2014 | Validation |
| Locations | Calibration (1 May 2014–29 May 2014) Low Flow | Calibration (1 June 2014–7 July 2014) High Flow | Validation (6 September 2014–4 October 2014) Medium Flow | Validation (15 July 2014–12 August 2014) High Flow | ||||
|---|---|---|---|---|---|---|---|---|
| R2 | NSE | R2 | NSE | R2 | NSE | R2 | NSE | |
| Tumuke | 0.96 | 0.95 | 0.95 | 0.94 | 0.95 | 0.86 | 0.85 | 0.83 |
| Jiudaogou | 0.97 | 0.96 | 0.96 | 0.95 | 0.93 | 0.92 | 0.89 | 0.81 |
| Flood Extent | User’s Accuracy | Producer’s Accuracy | Overall Accuracy | Kappa | ||
|---|---|---|---|---|---|---|
| Flooded | Non-Flooded | Flooded | Non-Flooded | |||
| Remote sensing imagery | 99.88 | 90.50 | 93.79 | 99.55 | 94.30 | 0.91 |
| Hydrodynamic model | 97.70 | 72.02 | 81.16 | 87.15 | 87.86 | 0.83 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Na, X.; Li, W. Modeling Hydrological Regimes of Floodplain Wetlands Using Remote Sensing and Field Survey Data. Water 2022, 14, 4126. https://doi.org/10.3390/w14244126
Na X, Li W. Modeling Hydrological Regimes of Floodplain Wetlands Using Remote Sensing and Field Survey Data. Water. 2022; 14(24):4126. https://doi.org/10.3390/w14244126
Chicago/Turabian StyleNa, Xiaodong, and Wenliang Li. 2022. "Modeling Hydrological Regimes of Floodplain Wetlands Using Remote Sensing and Field Survey Data" Water 14, no. 24: 4126. https://doi.org/10.3390/w14244126
APA StyleNa, X., & Li, W. (2022). Modeling Hydrological Regimes of Floodplain Wetlands Using Remote Sensing and Field Survey Data. Water, 14(24), 4126. https://doi.org/10.3390/w14244126








