Mechanism and Control of Grout Propagation in Horizontal Holes in Fractured Rock
Abstract
:1. Introduction
2. Characteristics of Macroscopic Vertical Permeability at the Top of a Middle Ordovician Limestone Layer
- (1)
- Dongpang mine: The flushing fluid leakages of a total of 88 boreholes were recorded. The end position of the No. 3 water source hole was in the upper Majiagou formation were is under the Fengfeng formation; the end positions of the others were in the Fengfeng formation. Among the 88 holes, only two holes did not leak and the other holes had various degrees of flushing fluid leakage. Within 10 m from the top of the MOL, the leakage of 90% of the boreholes was less than 1.0 m3h−1, which is categorized as slight leakage and the leakage of only one hole was greater than 10 m3h−1. In addition, according to the statistics for every 10 m at the top of the MOL from 16 boreholes (Table 1), we found that the leakage within 40 m of the top of the MOL was minor and changed little, but the leakage of the flushing fluid increased markedly at deeper than 40 m. This indicates that the karst fracture rate in the upper 40 m of the MOL was relatively low, the water yield was weak and the water entered the strong aquifer part of the seventh section of the Fengfeng formation at a depth of 40 m.
- (2)
- Wutongzhuang mine: The leakages of 11 boreholes in the MOL strata of the Wutongzhuang mine were determined. Among them, the flushing fluid leakages of two boreholes decreased within 30 m of the top of the MOL; this is for 18% of the boreholes. The leakages were 5 m3h−1 and 40 m3h−1 when the lengths of the boreholes were 15 m and 24.5 m under the MOL, respectively, which indicates that the water yield property of the eighth section of the MOL was uneven but generally weak. The end positions of eight of the boreholes in the seventh section of the MOL, among which four boreholes had leakage of flushing fluid, accounted for 50% of the total boreholes. According to the analysis, there was a weathering crust at the top interface of the MOL and most of the cracks were filled with argillaceous components, so the water resistance was good. The MOL aquifer is zonal vertically. At 15 m below the top surface of the MOL, we found no leakage of flushing fluid from any boreholes; at 15 to 30 m, the water yield of the stratum was relatively weak and uneven; at more than 30 m, the water yield of the stratum was strong and uneven.
3. Analysis of Cement Grout Performance and Its Influencing Factors
3.1. Hydro-Chemical Characteristics of a Middle Ordovician Limestone Top
3.2. Test Scheme
3.3. Test Results
4. Grout Propagating Mechanism of Inclined Single Fracture in Horizontal Grouting Hole
4.1. Basic Assumptions of Model Construction
4.2. Grout Propagating Model of an Inclined Single Fracture
5. Grouting Control Method of Horizontal Grouting Hole at the Top of Middle Ordovician Limestone
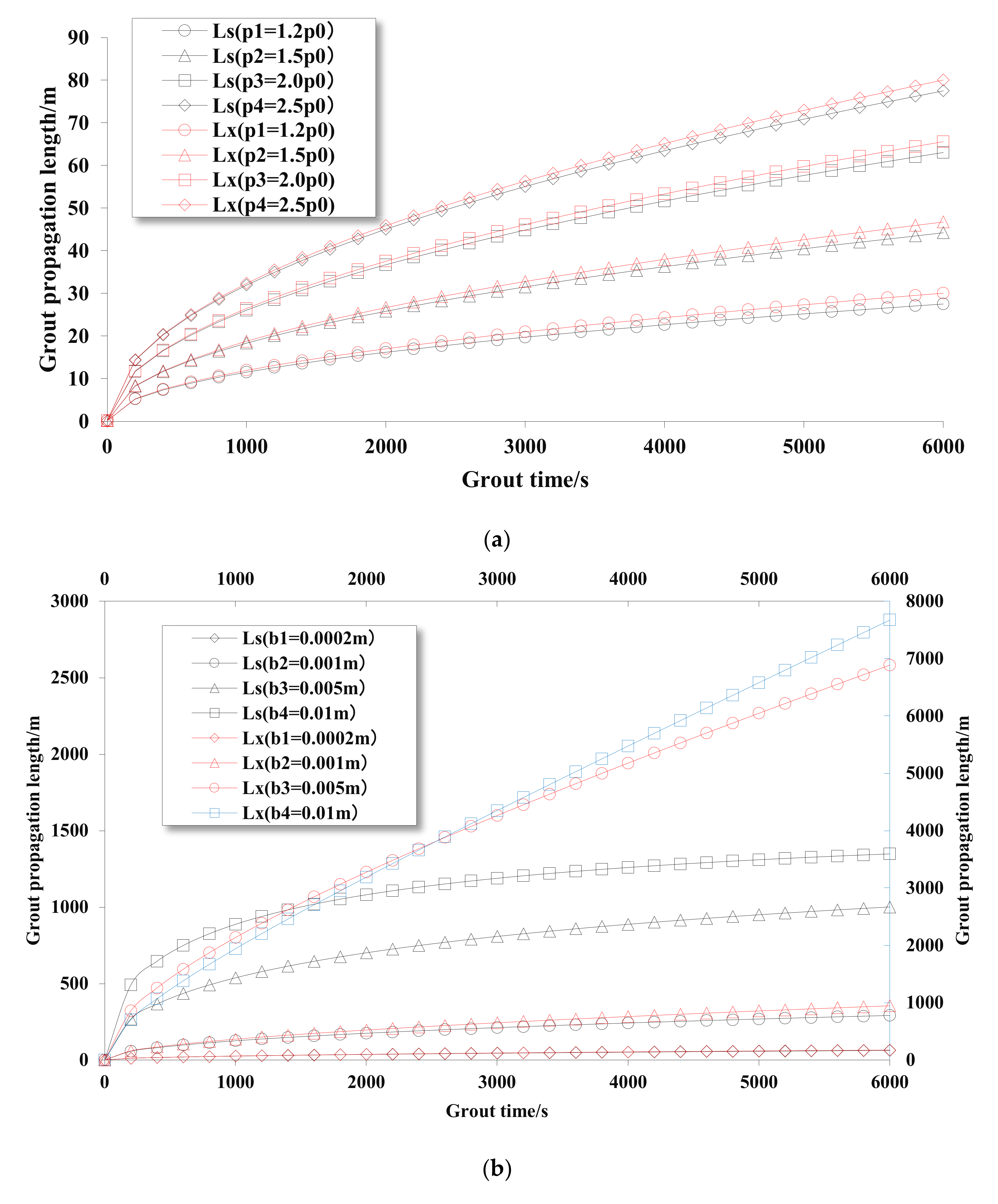
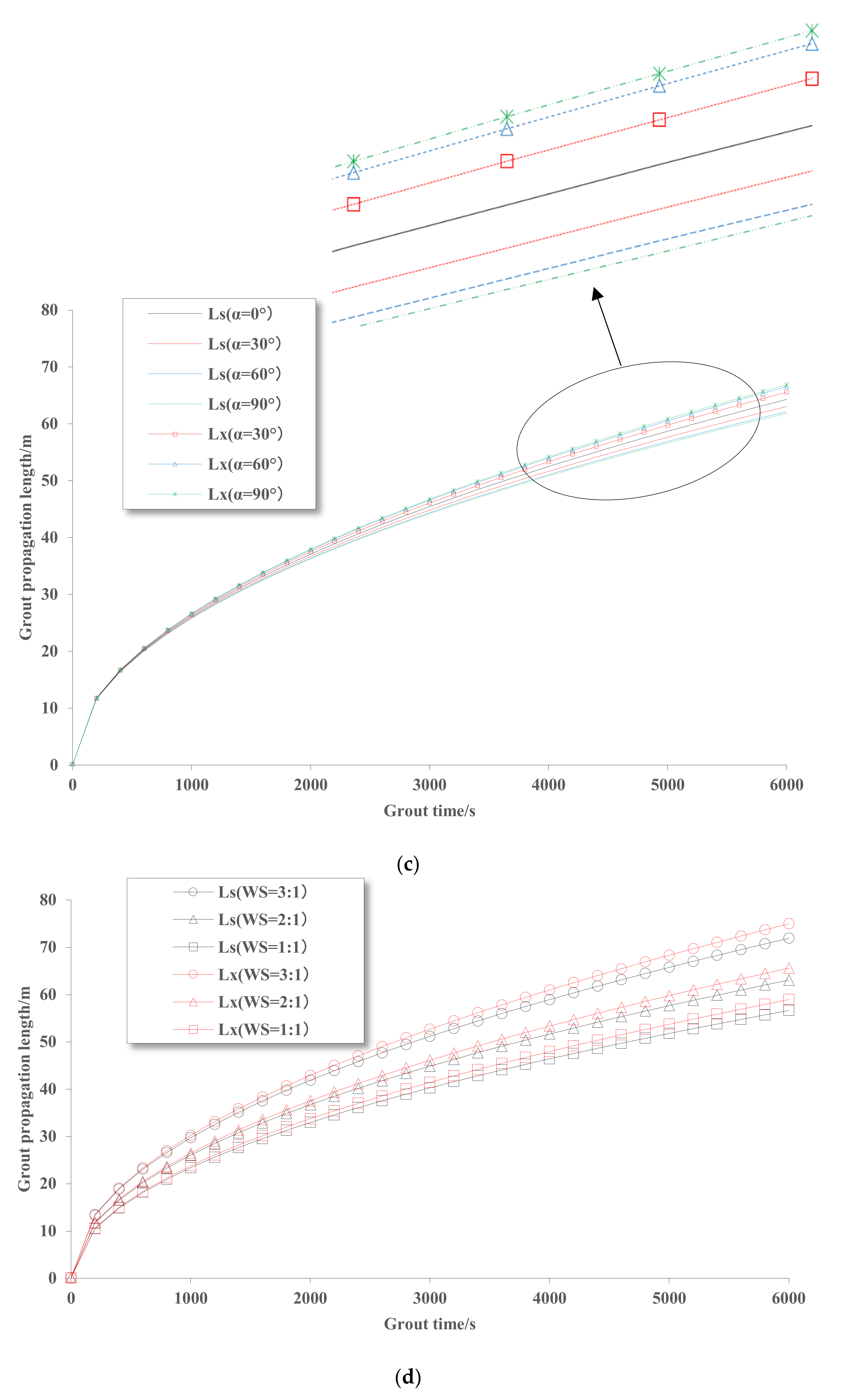
5.1. Analysis of Influencing Factors of Grout Propagation Length in a Single Fracture
5.2. Numerical Calculation of Grout Propagation Based on Orthogonal Test
5.3. Control Method of Grout Propagation Length
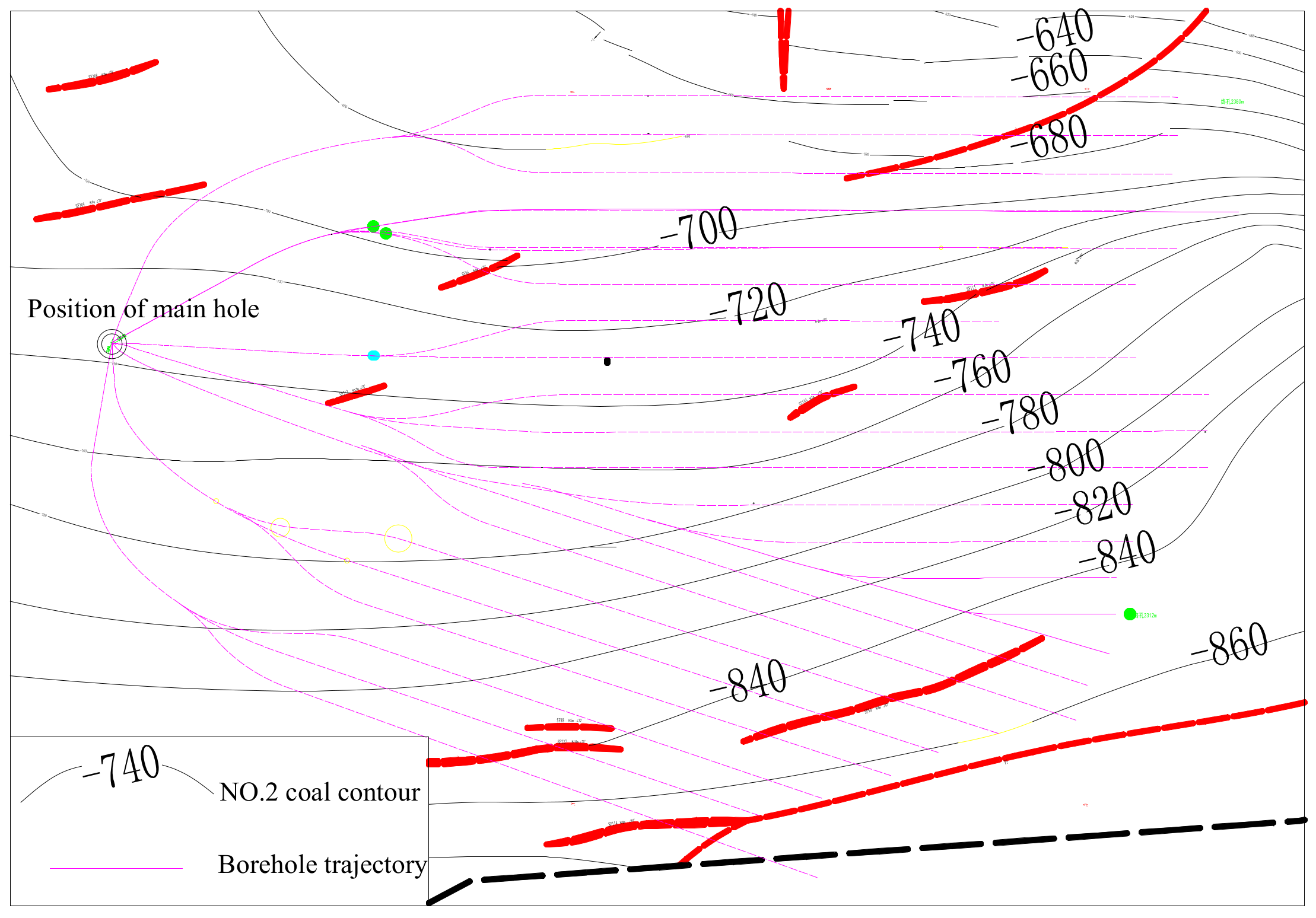
6. Engineering Application
7. Discussion
- (1)
- In the numerical calculation, there was no marked difference in the grout propagation length between the upper and lower fractures of the horizontal grouting holes under various working conditions. The main reason is that the grout propagation length was always in a small range. Relative to the previous theoretical analysis, the grout propagation lengths in the upper and lower fractures of the horizontal grouting holes differed only slightly, unless the grout propagation length was hundreds of meters or more. The phenomenon of a large difference in the range of the upper kilometer was consistent.
- (2)
- Under the condition of a wide-tension-fracture opening (0.01 m), there was a large gap between the numerical calculation results and the theoretical calculation results. The main reason was that the porosity of the rock mass was set in the numerical calculation and the fracture was filled with only water in the theoretical calculation. However, the spatial and temporal distribution characteristics of various factors on the grout propagation length could be accurately given by the numerical simulation calculation. The influence factors of distance had a good qualitative analysis effect.
8. Conclusions
- (1)
- Based on the factors of the grouting pressure, angle between crack and grouting hole, hydrostatic pressure, grouting volume, grout viscosity, fracture width, grout gravity and grouting duration, we established a mathematical model of Newtonian fluid slurry diffusion distance in the upper and lower cracks of horizontal grouting holes.
- (2)
- As determined by theoretical analysis, the slurry in an inclined single fracture of a horizontal grouting hole increases with an increase in grouting duration under various water–solid ratios, grouting pressure, crack opening and angle between crack and grouting hole and the increase rate decreases over time. However, the slurry diffusion distance in the fracture above the horizontal grouting hole is larger than that in the lower fracture when the grout propagation length is hundreds of meters or more and the difference increases multiple times under the wide fracture scale.
- (3)
- Based on the orthogonal design and numerical calculations, we obtained a sequence of the sensitivity of the factors affecting the diffusion distance of Newtonian grout in an inclined fracture of a horizontal grouting hole: from higher to lower, they were crack opening, fracture inclination angle, water–solid ratio and grouting pressure.
- (4)
- Based on the control equation of the grout diffusion distance of an inclined fracture in a horizontal grouting hole and grouting parameters for a mine in the fourth mining area, the horizontal spacing of branch holes was not more than 65.90 m and the interface distance between the branch holes and the Ordovician limestone roof was not more than 32.95 m, which is close to the engineering practice parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Liu, S.; Fei, Y.; Xu, Y.; Huang, L.; Guo, W. Full-floor Grouting Reinforcement for Working Faces with Large Mining Heights and High Water Pressure: A Case Study in China. Mine Water Environ. 2020, 39, 268–279. [Google Scholar] [CrossRef]
- Yin, S.; Zhang, J.; Liu, D. A study of mine water inrushes by measurements of in situ stress and rock failures. Nat. Hazards 2015, 79, 1961–1979. [Google Scholar] [CrossRef]
- Zhang, W.J.; Li, S.C.; Wei, J.C.; Zhang, Q.S.; Liu, R.T.; Li, Z.P.; Sun, Z.Z. Relative Impermeability of the Ordovician Top and Risk Assessment of Water Inrush from Coal Floor in Baode Coalfield. Adv. Mater. Res. 2013, 671, 85–89. [Google Scholar] [CrossRef]
- Qiu, M.; Huang, F.; Wang, J.; Shi, L.; Qu, X.; Liu, T. Characteristics of vertical karst development and grouting reinforcement engineering practice of the Ordovician top in the Feicheng coalfield, China. Carbonate Evaporite 2020, 35, 78. [Google Scholar] [CrossRef]
- Yin, S.; Han, Y.; Zhang, Y.; Zhang, J. Depletion control and analysis for groundwater protection and sustainability in the Xingtai region of China. Environ. Earth Sci. 2016, 75, 1246. [Google Scholar] [CrossRef]
- Yu, X.; Pei, F.; Han, J.; Gao, W.; Wang, X. Ordovician limestone karst development law in Feicheng coal field. Environ. Earth Sci. 2018, 77, 781. [Google Scholar] [CrossRef]
- Hässler, L.; Håkansson, U.; Stille, H. Computer-simulated flow of grouts in jointed rock. Tunn. Undergr. Space Technol. 1992, 7, 441–446. [Google Scholar] [CrossRef]
- El Tani, M. Grouting Rock Fractures with Cement Grout. Rock Mech. Rock Eng. 2012, 45, 547–561. [Google Scholar] [CrossRef]
- Gustafson, G.; Claesson, J.; Fransson, A. Steering Parameters for Rock Grouting. J. Appl. Math. 2013, 2013, 269594. [Google Scholar] [CrossRef]
- Li, S.; Han, W.; Zhang, Q.; Liu, R.; Weng, X. Research on time-dependent behavior of viscosity of fast curing grouts in underground construction grouting. Chin. J. Rock Mech. Eng. 2013, 32, 1–7. [Google Scholar]
- Zhang, Q.; Zhang, L.; Zhang, X.; Liu, R.; Zhu, M.; Zheng, D. Grouting diffusion in a horizontal crack considering temporaland spatialvariation of viscosity. Chin. J. Rock Mech. Eng. 2015, 34, 1198–1210. [Google Scholar]
- Zou, L.; Hakansson, U.; Cvetkovic, V. Yield-power-law fluid propagation in water-saturated fracture networks with application to rock grouting. Tunn. Undergr. Space Technol. 2020, 95, 103170. [Google Scholar] [CrossRef]
- Zou, L.; Hakansson, U.; Cvetkovic, V. Radial propagation of yield-power-law grouts into water-saturated homogeneous fractures. Int. J. Rock Mech. Min. 2020, 130, 104308. [Google Scholar] [CrossRef]
- Zhao, Z.H.; Zhou, D. Mechanical properties and failure modes of rock samples with grout-infilled flaws: A particle mechanics modeling. J. Nat. Gas Sci. Eng. 2016, 34, 702–715. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, W.; Shen, Z.; Gao, K.; Liang, D.; Cheng, S. Diffusion mechanism and sensitivity analysis of slurry while grouting in fractured aquifer with horizontal injection hole. Carbonate Evaporite 2020, 35, 49. [Google Scholar] [CrossRef]
- Nan, S. Technical feasibility of grouting reform for upper part of Ordovician limestone in Xingtai and Handan coal mining areas. Coal Geol. Explor. 2010, 38, 37–40. [Google Scholar] [CrossRef]
- Li, T.; Gao, Y.; Chen, W. Characteristics of deep Ordovician limestone water and its concentrated application in Ordovician limestone water disaster prevention. Mtan Xuebao/J. China Coal Soc. 2018, 43, 262–268. [Google Scholar]
- Pan, W.Y. Distribution regularities of the limestone and development of karst in North-China type coal fields. J. China Coal Soc. 1982, 3, 48–56. [Google Scholar]
- Zhao, Q.B. Ordovician limestone karst water disaster regional advanced governance technology study and application. J. China Coal Soc. 2014, 39, 1112–1117. [Google Scholar]
- Brebbia, C.A.; Connor, J.J. Boundary element formulation for viscous compressible flow. In Viscous Flow Applications; Springer: Berlin/Heidelberg, Germany, 1989; pp. 10–31. [Google Scholar]













| Leakage/m3·h−1 | Number of Boreholes at Different Depths | ||||
|---|---|---|---|---|---|
| ≤10 m | 10–20 m | 20–30 m | 30–40 m | >40 m | |
| ≤0.1 | 5 | 5 | 7 | 7 | 3 |
| 0.1–1.0 | 9 | 9 | 7 | 6 | 6 |
| 1.0–10.0 | 2 | 2 | 2 | 3 | 5 |
| >10.0 | 0 | 0 | 0 | 0 | 1 |
| Average leakage | 0.5 | 0.35 | 0.38 | 0.31 | 2.12 |
| Number | Mining | Borehole Number | Position | pH | Hydro-Chemical Type | Mineralization Degree/mg·L−1 |
|---|---|---|---|---|---|---|
| a | Xingmei | D3 | The eighth section of Fengfeng formation | 8.17 | HCO3-Ca·Mg | 336.07 |
| b | Xingdong | T3 | The seventh section of Fengfeng formation | 8.85 | SO4-Ca·Mg | 1690.37 |
| c | Wutongzhuang | WO3 | Fengfeng formation | 7.09 | Cl·SO4-Ca·Na | 5496.47 |
| d | Jiulong | / | The seventh section of Fengfeng formation | 7.75 | Cl·SO4-Ca·Na | 4333.30 |
| Level | Factors | ||
|---|---|---|---|
| Water–Cement Mass Ratio (A) | Content of Sodium Silicate/% (B) | Hydro-Chemical Type (Mining) (C) | |
| 1 | 0.6:1 | 0 | a (Xingmei) |
| 2 | 0.8:1 | 2 | b (Xingdong) |
| 3 | 1:1 | 5 | c (Wutongzhuang) |
| 4 | 2:1 | 8 | d (Jiulong) |
| Test Number | Water–Cement Mass Ratio (A) | Content of Sodium Silicate/% (B) | Hydro-Chemical Type (Mining) (C) |
|---|---|---|---|
| 1 | 0.6:1 | 0 | a |
| 2 | 0.6:1 | 2 | b |
| 3 | 0.6:1 | 5 | c |
| 4 | 0.6:1 | 8 | d |
| 5 | 0.8:1 | 0 | b |
| 6 | 0.8:1 | 2 | a |
| 7 | 0.8:1 | 5 | d |
| 8 | 0.8:1 | 8 | c |
| 9 | 1:1 | 0 | c |
| 10 | 1:1 | 2 | d |
| 11 | 1:1 | 5 | a |
| 12 | 1:1 | 8 | b |
| 13 | 2:1 | 0 | d |
| 14 | 2:1 | 2 | c |
| 15 | 2:1 | 5 | b |
| 16 | 2:1 | 8 | a |
| Test Number | Influencing Factors | Physical and Mechanical Property Parameters | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A | B | C | Viscosity/Pa.s | Density/g.cm−3 | Initial Setting Time/h | Final Setting Time/h | Stone Rate/% | Flexural Strength/MPa | Compressive Strength/MPa | |||||
| 3 d | 7 d | 28 d | 3 d | 7 d | 28 d | |||||||||
| 1 | 0.6:1 | 0 | a | 0.30 | 1.64 | 10.08 | 13.00 | 95.40 | 2.47 | 2.75 | 4.88 | 6.09 | 8.32 | 18.74 |
| 2 | 0.6:1 | 2 | b | 0.58 | 1.57 | 8.92 | 11.33 | 97.10 | 2.50 | 3.13 | 4.71 | 6.79 | 10.68 | 16.36 |
| 3 | 0.6:1 | 5 | c | 0.88 | 1.56 | 6.08 | 8.42 | 98.40 | 2.42 | 3.34 | 4.86 | 6.37 | 10.34 | 16.29 |
| 4 | 0.6:1 | 8 | d | 1.24 | 1.51 | 4.33 | 6.58 | 99.20 | 1.69 | 2.73 | 3.50 | 4.17 | 9.12 | 14.98 |
| 5 | 0.8:1 | 0 | b | 0.16 | 1.45 | 11.33 | 15.10 | 84.65 | 1.77 | 2.37 | 4.43 | 3.65 | 6.22 | 18.32 |
| 6 | 0.8:1 | 2 | a | 0.22 | 1.42 | 9.50 | 11.83 | 90.75 | 1.25 | 1.73 | 3.52 | 3.33 | 5.93 | 11.66 |
| 7 | 0.8:1 | 5 | d | 0.67 | 1.41 | 7.25 | 10.08 | 93.05 | 1.14 | 1.54 | 2.75 | 3.00 | 4.68 | 9.29 |
| 8 | 0.8:1 | 8 | c | 0.79 | 1.39 | 5.17 | 7.67 | 96.50 | 1.13 | 1.54 | 2.57 | 2.93 | 4.42 | 8.43 |
| 9 | 1:1 | 0 | c | 0.12 | 1.42 | 13.18 | 16.28 | 74.60 | 1.24 | 1.82 | 3.59 | 2.83 | 4.55 | 8.83 |
| 10 | 1:1 | 2 | d | 0.17 | 1.40 | 10.17 | 12.50 | 81.50 | 0.96 | 1.45 | 2.57 | 1.74 | 3.73 | 7.27 |
| 11 | 1:1 | 5 | a | 0.39 | 1.38 | 7.92 | 10.75 | 94.50 | 0.86 | 0.92 | 2.07 | 2.16 | 2.85 | 6.25 |
| 12 | 1:1 | 8 | b | 0.52 | 1.36 | 6.67 | 9.33 | 98.20 | 0.64 | 0.93 | 1.98 | 1.69 | 2.60 | 4.75 |
| 13 | 2:1 | 0 | d | 0.10 | 1.25 | 16.83 | 19.58 | 45.90 | 0.82 | 1.24 | 2.40 | 1.52 | 3.35 | 5.18 |
| 14 | 2:1 | 2 | c | 0.13 | 1.22 | 11.92 | 15.80 | 73.60 | 0.49 | 0.46 | 1.01 | 0.59 | 1.09 | 1.56 |
| 15 | 2:1 | 5 | b | 0.15 | 1.20 | 10.58 | 13.08 | 87.65 | 0.30 | 0.50 | 0.65 | 0.45 | 0.80 | 1.36 |
| 16 | 2:1 | 8 | a | 0.22 | 1.18 | 7.17 | 10.42 | 91.60 | 0.21 | 0.29 | 0.44 | 0.35 | 0.49 | 0.92 |
| Physical and Mechanical Property Parameters | Water–Cement Mass Ratio (A) | Content of Sodium Silicate (B) | Hydro-Chemical Type (Mining) (C) | Sensitivity Ranking | |
|---|---|---|---|---|---|
| density/Kg.m−3 | 0.36 | 0.08 | 0.01 | A > B > C | |
| viscosity/Pa.s | 0.60 | 0.52 | 0.26 | A > B > C | |
| Initial setting time/h | 4.27 | 7.02 | 0.98 | B > A > C | |
| Final setting time/h | 4.89 | 7.49 | 0.71 | B > A > C | |
| Stone rate/% | 22.84 | 21.24 | 13.15 | A > B > C | |
| Flexural strength/MPa | 3 d | 1.82 | 0.66 | 0.16 | A > B > C |
| 7 d | 2.36 | 0.67 | 0.36 | A > B > C | |
| 28 d | 3.37 | 1.70 | 0.28 | A > B > C | |
| Compressive strength/MPa | 3 d | 5.13 | 1.24 | 0.57 | A > B > C |
| 7 d | 8.18 | 2.11 | 1.45 | A > B > C | |
| 28 d | 14.34 | 8.02 | 1.42 | A > B > C | |
| Number | Level | Water–Cement Ratio | Viscosity/Pa·s | Density/Kg.m−3 | Width of Fracture/m | Angle/° | Grout Pressure/Pa |
|---|---|---|---|---|---|---|---|
| 1 | grout pressure | 2:1 | 0.0967 | 1248 | 0.0002 | 30 | 1.2 × 107 |
| 1.5 × 107 | |||||||
| 2.0 × 107 | |||||||
| 2.5 × 107 | |||||||
| 2 | width of fracture | 2:1 | 0.0967 | 1248 | 0.0002 | 30 | 2 × 107 |
| 0.001 | |||||||
| 0.005 | |||||||
| 0.01 | |||||||
| 3 | angle | 2:1 | 0.0967 | 1248 | 0.0002 | 0 | 2 × 107 |
| 30 | |||||||
| 60 | |||||||
| 90 | |||||||
| 4 | water–cement ratio | 3:1 | 1160 | 0.0742 | 0.0002 | 30 | 2 × 107 |
| 2:1 | 1248 | 0.0967 | |||||
| 1:1 | 1424 | 0.1198 |
| Factors | Levels | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| water–cement ratio | 1:1 | 2:1 | 3:1 |
| grouting pressure/MPa | 15 | 20 | 25 |
| width of fracture/mm | 1 | 5 | 10 |
| angle of fracture/° | 30 | 60 | 90 |
| Number | Water–Cement Ratio | Grouting Pressure/MPa | Width of Fracture/mm | Angle of Fracture/° |
|---|---|---|---|---|
| 1 | 1:1 | 15 | 1 | 30 |
| 2 | 1:1 | 20 | 5 | 60 |
| 3 | 1:1 | 25 | 10 | 90 |
| 4 | 2:1 | 15 | 5 | 90 |
| 5 | 2:1 | 20 | 10 | 30 |
| 6 | 2:1 | 25 | 1 | 60 |
| 7 | 3:1 | 15 | 10 | 60 |
| 8 | 3:1 | 20 | 1 | 90 |
| 9 | 3:1 | 25 | 5 | 30 |
| Factor | Grout Propagation Length/m | ||||
|---|---|---|---|---|---|
| A | B | C | D | ||
| 1 | 1:1 | 15 | 1 | 30 | 46 |
| 2 | 1:1 | 20 | 5 | 60 | 41.57 |
| 3 | 1:1 | 25 | 10 | 90 | 48 |
| 4 | 2:1 | 15 | 5 | 90 | 43 |
| 5 | 2:1 | 20 | 10 | 30 | 56 |
| 6 | 2:1 | 25 | 1 | 60 | 27.71 |
| 7 | 3:1 | 15 | 10 | 60 | 42.73 |
| 8 | 3:1 | 20 | 1 | 90 | 24.5 |
| 9 | 3:1 | 25 | 5 | 30 | 53 |
| mean value 1 | 45.19 | 43.91 | 32.74 | 51.67 | / |
| mean value 2 | 42.24 | 40.69 | 45.86 | 37.34 | / |
| mean value 3 | 40.08 | 42.90 | 48.91 | 38.50 | / |
| xmax-xmin | 5.11 | 3.22 | 16.17 | 14.33 | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Dong, S.; Wang, H.; Shang, H. Mechanism and Control of Grout Propagation in Horizontal Holes in Fractured Rock. Water 2022, 14, 4062. https://doi.org/10.3390/w14244062
Liu Z, Dong S, Wang H, Shang H. Mechanism and Control of Grout Propagation in Horizontal Holes in Fractured Rock. Water. 2022; 14(24):4062. https://doi.org/10.3390/w14244062
Chicago/Turabian StyleLiu, Zhaoxing, Shuning Dong, Hao Wang, and Hongbo Shang. 2022. "Mechanism and Control of Grout Propagation in Horizontal Holes in Fractured Rock" Water 14, no. 24: 4062. https://doi.org/10.3390/w14244062





