1. Introduction
The frequent occurrence of extreme hydrological events creates flood disasters causing more and more damage to people’s lives [
1], which has become an important issue affecting economic and social development. The complex and diverse topography and continental monsoon climate cause most of the rainfall in China to be concentrated within a period of time, which to a certain extent also exacerbates the frequency and extent of floods [
2]. In July 2021, the city of Zhengzhou, China, was hit by a once-in-a-millennium extraordinarily heavy rainfall [
3], with more than 200 mm of precipitation in just one hour from 16:00 to 17:00 on the 20th; and about 620 mm of precipitation in three days, from the 17th to the 20th. According to the “7.20 rainstorm disaster investigation report” released by the State Council Disaster Investigation Group in China, a total of 150 counties (cities and districts) in Henan Province, with a population of 14.78 million people, were affected, with direct economic losses amounting to RMB 120.6 billion. This shows that flood prevention and mitigation is of great significance to ensure people’s safety, social stability and economic development. Based on the available hydro-meteorological data, flood projection can qualitatively and quantitatively analyze and predict possible future floods [
4]. It is regarded as a very important non-engineering initiative to provide a reference for flood control and scheduling decisions. Timely and accurate flood projection is useful for making scientific flood control decisions to avoid risks, but the question of how to further improve flood projection accuracy above the current level is still a research focus for hydrologists.
Hydrological models can simulate a real system and predict changes in relevant variables [
5]. With the development of hydrology, more and more practical hydrological models have been put forward, such as the Stanford model [
6], API model [
7], Xinanjiang model [
8], SWAT model, etc. These models can be classified into three categories: empirical models, conceptual models, and physically based models [
5]. Of these, empirical models lack the relevant physical mechanism; they only obtain information from the existing data, resulting in a large randomness of prediction results. Physically based models are constructed based on the principles of physical processes. They require a large number of data, and the non-linear calculation process is complicated, causing their application to be limited. Compared with the above two types of models, conceptual models are both physical and empirical, and can describe the water cycle process in the basin with simplified equations. The conceptual models have good applicability to most basins in China because of their low requirements regarding the number of parameters and accuracy of the modeling data, and simple structure. Actually, the widely used Xinanjiang model is a conceptual model type. Considering that the Xun River in the Hanjiang River Basin belongs to the subtropical semi-humid climate zone, which meets the storage and flow production mechanism of the Xinanjiang model, this paper has chosen it as the appropriate flood prediction model.
Hydrological model parameters can quantify the characteristics of vegetation, soil, and stream channels in a watershed [
9]. In general, it is not easy to obtain their true values due to the numerous uncertainties in the models, but it is necessary to estimate the parameters in a practical study that takes into account the spatial and temporal heterogeneity of the watershed and the scale of the parameters. The parameter values affect the accuracy of the models. The mainstream method used by hydrologists to determine the parameters is to continuously tune them to obtain simulation results that are highly consistent with past observations, which is called parameter calibration [
10]. It is essentially a robust optimization problem under the model uncertainties from a mathematical point of view [
11]. Compared with manual calibration methods with certain subjectivity and experience, automatic calibration has been favored by many scholars because of its efficiency and objectivity. However, due to the randomness and uncontrollability of hydrological processes, predicting future floods by using parameters obtained from historical hydrological data calibration will lead to inestimable errors. Therefore, it is necessary to correct the hydrological state variables and model parameters by means of relevant technical methods. At present, the correction algorithms have been greatly enriched, such as feedback simulation technology, error autoregression algorithm (AR) [
12], recursive least squares algorithm (RLS) [
13,
14], Kalman filter (KF) [
15,
16] and dynamic system response curve algorithm (DSRC) [
17], etc. Generally, AR and RLS are more commonly used to estimate the model parameter, while KF is used to estimate the state.
The development of remote sensing observation technology has broadened the access to data and enriched the existing sources of observation data, which makes data assimilation more applicable to hydrological projection. Data assimilation takes into account both forecast and observational information, helps to quantify and reduce uncertainty in hydrological applications, and is effective in water level forecasting and/or flood forecasting [
18]. The assimilation methods currently used in hydrology are divided into two categories according to the optimization path: one is the variational assimilation for global fitting, and the other is the sequential assimilation for real-time optimization [
19]. Variational assimilation transforms the data assimilation process into a solution of extreme values by constructing a cost function to represent the difference between the analyzed and true values of the variables. After meeting the dynamic constraints, the state variable value that minimizes the difference between the observed and predicted values is taken as the optimal analysis value. However, the adjoint model established by variational assimilation requires continuous differentiability of the state variables, and the nonlinearity of the hydrological model makes it difficult to satisfy this, thus, limiting its application. Based on the error estimation theory, sequential assimilation updates the forecast in time sequence by adding new observations at each time step, generates the forecast background at the next moment, advances forward by time, and finally obtains the optimal estimation of parameters or state variables for the whole period. KF is the basic form of sequential assimilation, which was proposed by R.E. Kalman in 1960 [
20]. It has the advantages of simplicity, small dependence on initial values, and good convergence, but it can only have unbiased optimal estimation if the system is linear and the noise is Gaussian white noise [
21]. For nonlinear systems, some processing of KF is required.
Based on this, Evensen used the idea of ensemble projection in Kalman filtering and proposed the ensemble Kalman filter (EnKF) algorithm, which solved the shortcomings of the traditional KF when applied to a nonlinear system [
22]. EnKF adds Gaussian white noise disturbances to model state variables and observation data, calculates Kalman gain and generates analysis ensemble at that time. Assuming that the mean value of analysis is the truth, the errors of the members of the analysis ensemble are calculated, and the error covariance of the analysis can be obtained. The mean value of the analysis and the error covariance matrix at that moment are applied to initialize the background in the next moment, so that the simulation is more consistent with the real probability distribution of the state variables. Reichle et al. [
23] applied EnKF to the retrieval problem of soil moisture distributions and investigated the effect of ensemble size and non-Gaussian forecast errors on estimation accuracy, and the results showed that EnKF was a flexible and robust data assimilation option that could give satisfactory estimates. Reichle et al. [
24] assessed the performance of the extended Kalman filter (EKF) and EnKF for soil moisture estimation, and the results indicated that EnKF was a promising approach for soil moisture initialization problems. Zhang et al. [
25] investigated the ability to retrieve the true soil moisture profile by assimilating near-surface soil moisture into a soil moisture model with an EnKF assimilation scheme. Shen et al. [
26] analyzed the basic theory and steps for data assimilation by using EnKF with an example based on numerical modeling, and drew the conclusion that EnKF can be used in groundwater level forecasting and pre-warning. Li et al. [
27] applied a coupling model of support vector machines (SVM) and EnKF (SVM + EnKF) for rainfall–runoff simulation, and found that this model could substantially improve the accuracy of flood prediction compared with SVM. KF with state and parameter updating is the so-called adaptive Kalman filter (AKF). Additionally, there is the corresponding adaptive EnKF, e.g., [
28], which can accelerate the speed of convergence and significantly improve the identification accuracy and search efficiency.
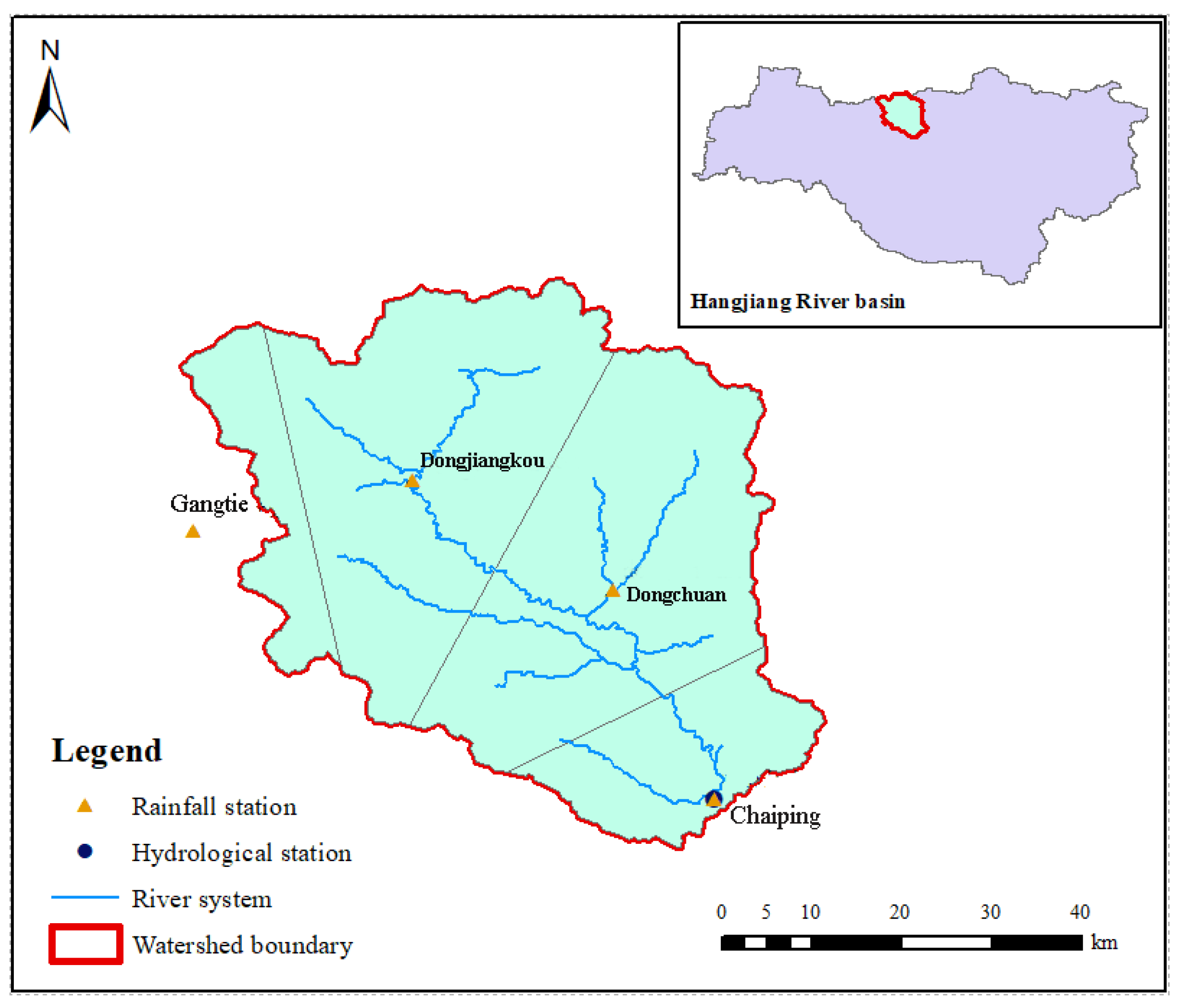
In this paper, the EnKF algorithm was applied to the Xinanjiang model to construct the EnKF data assimilation model, taking the Xun River of the Hanjiang River Basin as the study area. Combined with the measured data, WU and sensitive parameters (i.e., soil storage capacity curve index (B), and basin average free water storage capacity (SM)) of the model were assimilated and updated. The improvement of flood projection accuracy after assimilation was analyzed to assess the practicality of the data assimilation for flood projection for the Xun River, with a view to providing a reference basis and technical support for future flood prevention and mitigation, and flood projection. The paper is organized as follows:
Section 2 introduces an overview of Xun River and the data,
Section 3 describes the methods,
Section 4 provides the results, and
Section 5 is a summary.
5. Conclusions
The numerous uncertainties in flood projection models have limited the forecast accuracy, while data assimilation has been proved to improve the flood prediction accuracy by combining the prediction model with the actual observations. In addition, the development of remote sensing technology has broadened access to data, which provides more possibilities for the application of assimilation in flood projection. In this study, the Xun River of the Hanjiang River Basin was selected as the research object. The EnKF algorithm was applied to the Xinanjiang model, and a data assimilation scheme for the WU of the Xinanjiang model was proposed to explore the improvement effect of assimilation on the forecast accuracy. Thereafter, the WU assimilation scheme was further improved, and two novel assimilation schemes (AEnKF scheme and DEnKF scheme) were proposed to update the model-sensitive parameters and WU simultaneously. The main conclusions are as follows.
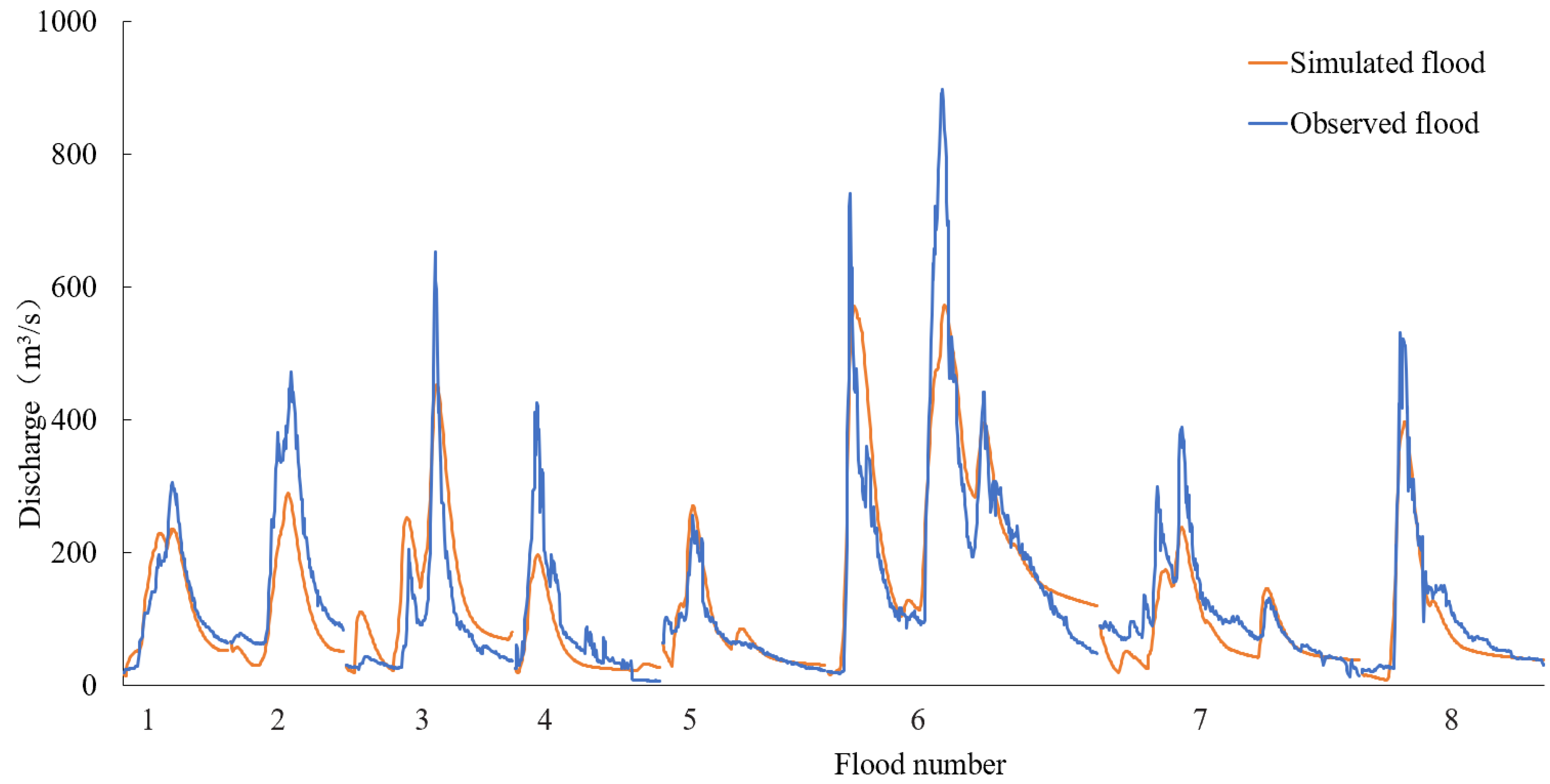
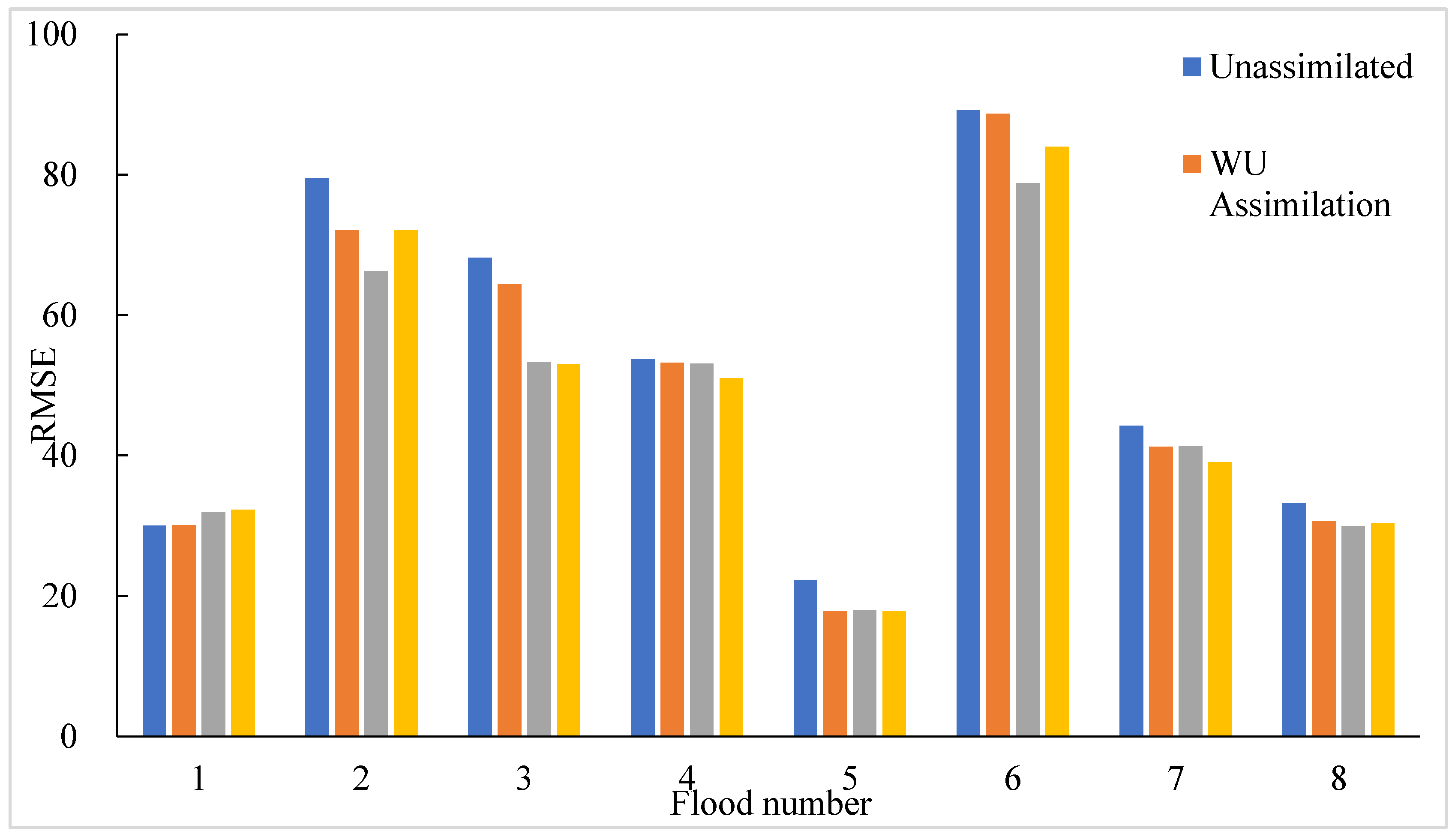
(1) Using SMAP remote-sensing soil moisture data, WU assimilation improved the flood forecast accuracy to some extent. The overall flood peak error of the eight floods in the validation period decreased from 0.32 to 0.3, the NSE improved from 0.725 to 0.758, and the peak time difference also improved to a certain extent. The flood peak error of flood no. 20170927, flood no. 20171004, flood no. 20190628, flood no. 20200819 and flood no. 20210424 improved, and the flood peak error decreased by 3% at most. The peak time difference of flood no. 20171004 and flood no. 20210424 were each reduced by 1 hour. In terms of the NSE, except for flood no. 20170927, whose NSE had a slight decrease (0.1%), all the other floods improved to some extent, and NSE was increased by 7.5%, at most;
(2) The dynamic update of model parameters during the projection process was more realistic than taking fixed values. Compared with the WU assimilation scheme, the simultaneous assimilation of parameters and WU effectively improved the prediction ability of the Xinanjiang model. The AEnKF scheme improved the overall NSE of flood from 0.725 for unassimilated, and 0.758 for assimilated WU, to 0.781. Compared with the unassimilated simulation results, NSE increased by 14.1%, at most. In comparison with the results of assimilating WU, NSE improved by 10.1% at most, and the number of floods with NSE above 0.7 increased by two. The overall NSE of flood in the DEnKF scheme was improved to 0.779, and it was close to that of the AEnKF scheme. Compared with the results of unassimilated and WU assimilation, the flood peak errors after considering the parameter update reduced by 13% and 12% at most, respectively, and the NSE improved by a maximum of 15% and 11%, respectively. The above results indicated that the two improved schemes with simultaneous assimilation of model parameters and WU performed better in terms of improvement of forecast accuracy compared with the assimilating WU scheme.