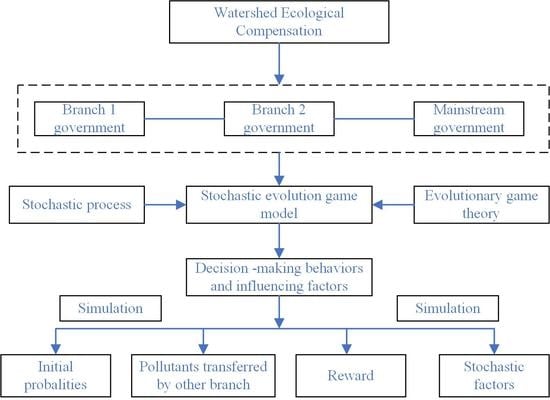
Watershed Ecological Compensation Mechanism for Mainstream and Branches Based on Stochastic Evolutionary Game: A Case of the Middle Yellow River
Abstract
:1. Introduction
2. Materials and Methods
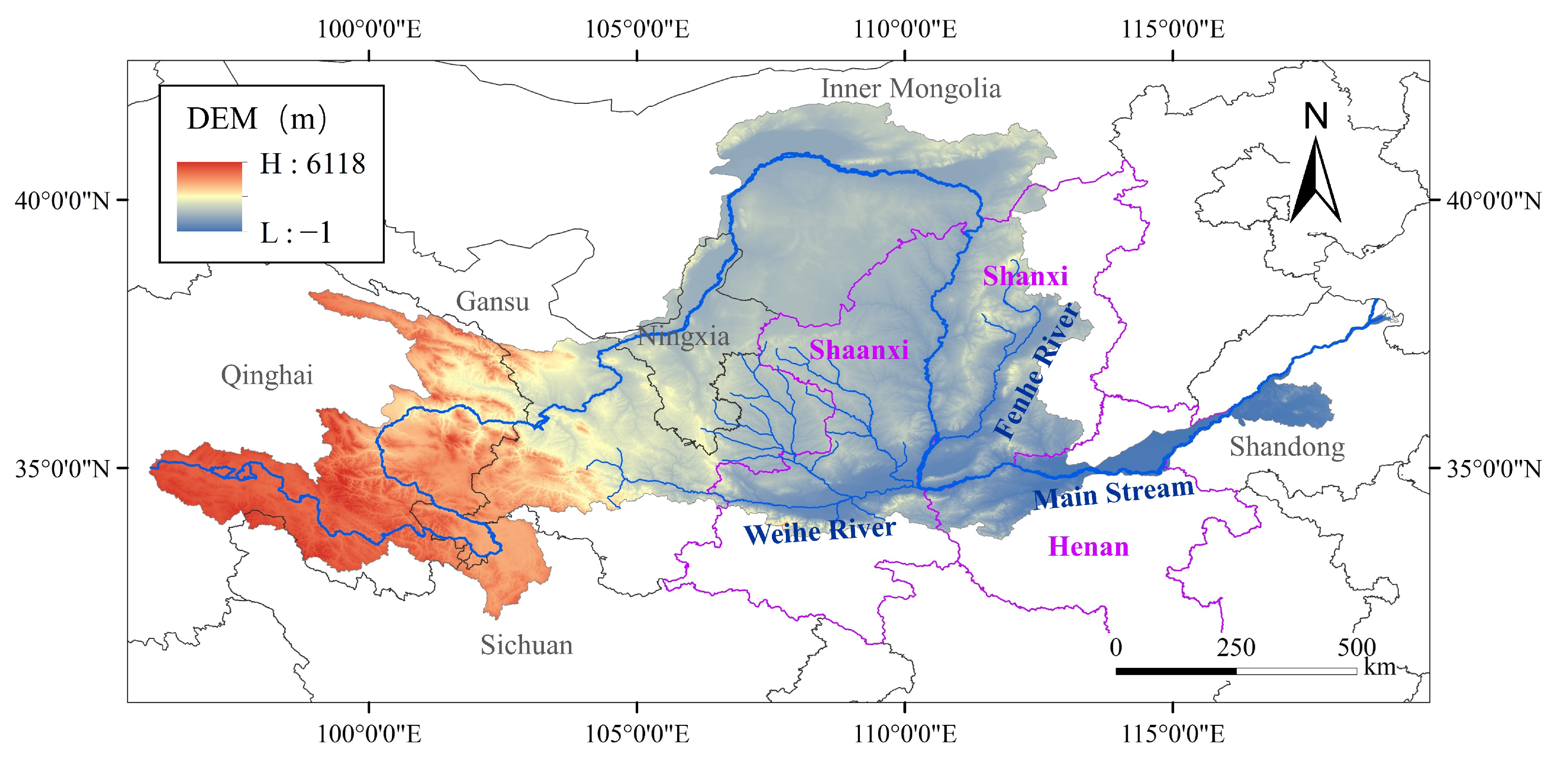
2.1. Overview of Research Region
2.2. Method
2.2.1. Model Assumptions
- Shanxi, Shaanxi and Henan provincial governments are all limited rational players, and it is difficult to determine individual optimal strategies in a single game. It takes multiple games to reach a consensus.
- With the goal of pollution control and emission reduction, Shanxi and Shaanxi governments have two strategies. The first is complete governance: that is, restricting the development of some local industries to achieve the goal of reducing pollutants. The second is incomplete governance: that is, not completely restricting the development of local industries. Thus, the goal of pollution control and emission reduction cannot be completely achieved, and the task of emission reduction will be transferred to the mainstream government and other branch governments.
- For the mainstream Henan provincial government, there are two strategies: one is compensation and reward. Since the Shanxi and Shaanxi provincial governments have given up on the development of local industries to improve the water environment, this has greatly reduced the pollution control cost of the Henan provincial government. Thus, the provincial government believes that compensation and reward should be given for the opportunities and benefits given up due to pollution control; the other is no compensation or reward. The Henan provincial government believes that it is the obligation of branch governments to eliminate pollutants without compensation or reward.
2.2.2. Mechanism Design
2.2.3. Model Construction
- (1)
- Definition of parameters
- (2)
- Certainty evolutionary system
2.2.4. Model Solution
- (1)
- Stability judgment of stochastic evolution system
- (1)
- If there is a positive constant , such that , the zero solution of Equation (19) p-order moment is exponentially stable and is achieved.
- (2)
- If there is a positive constant , such that , the zero solution of Equation (19) p-order moment is exponentially stable and is achieved.
- (2)
- System equilibrium
3. Results
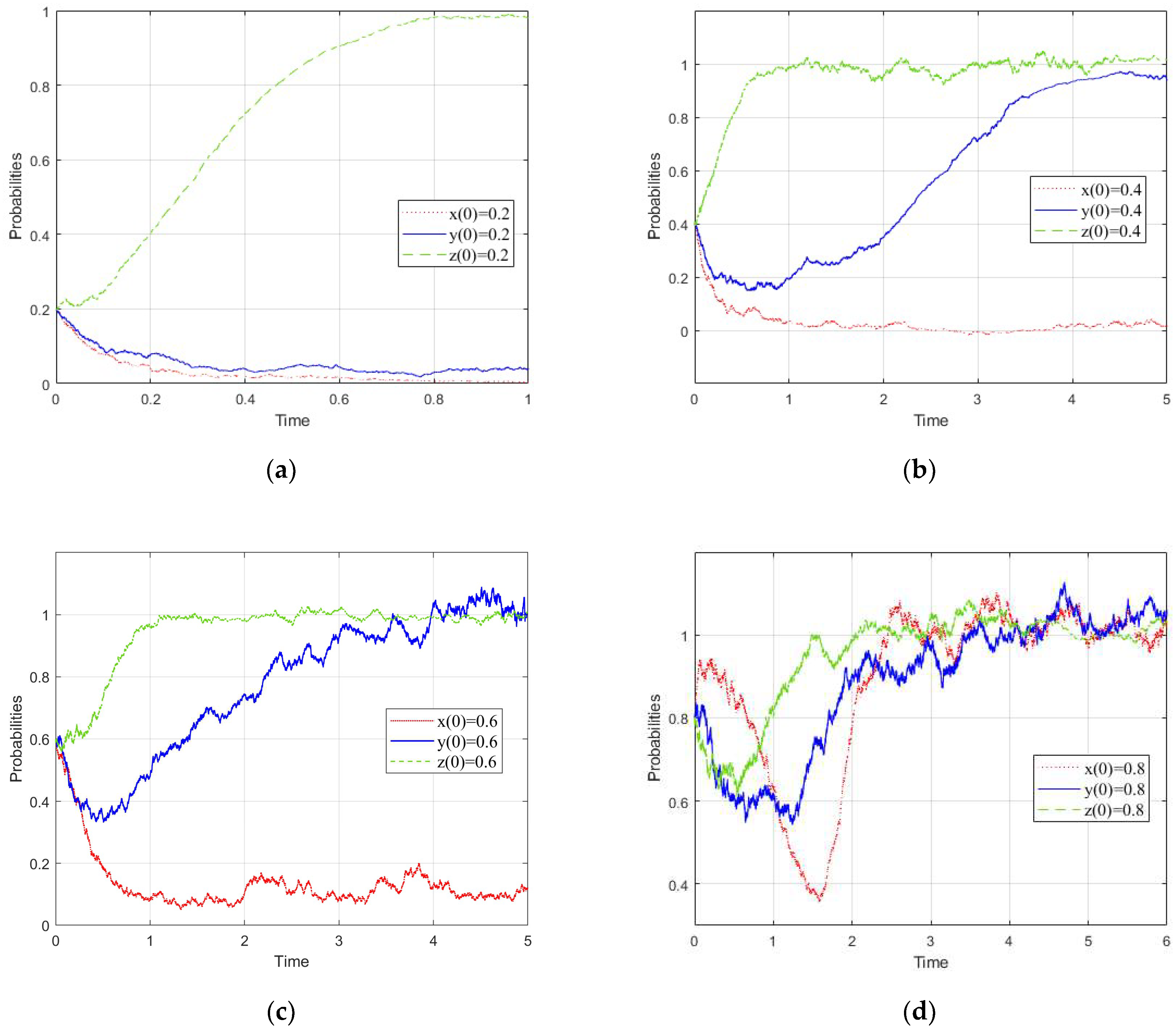
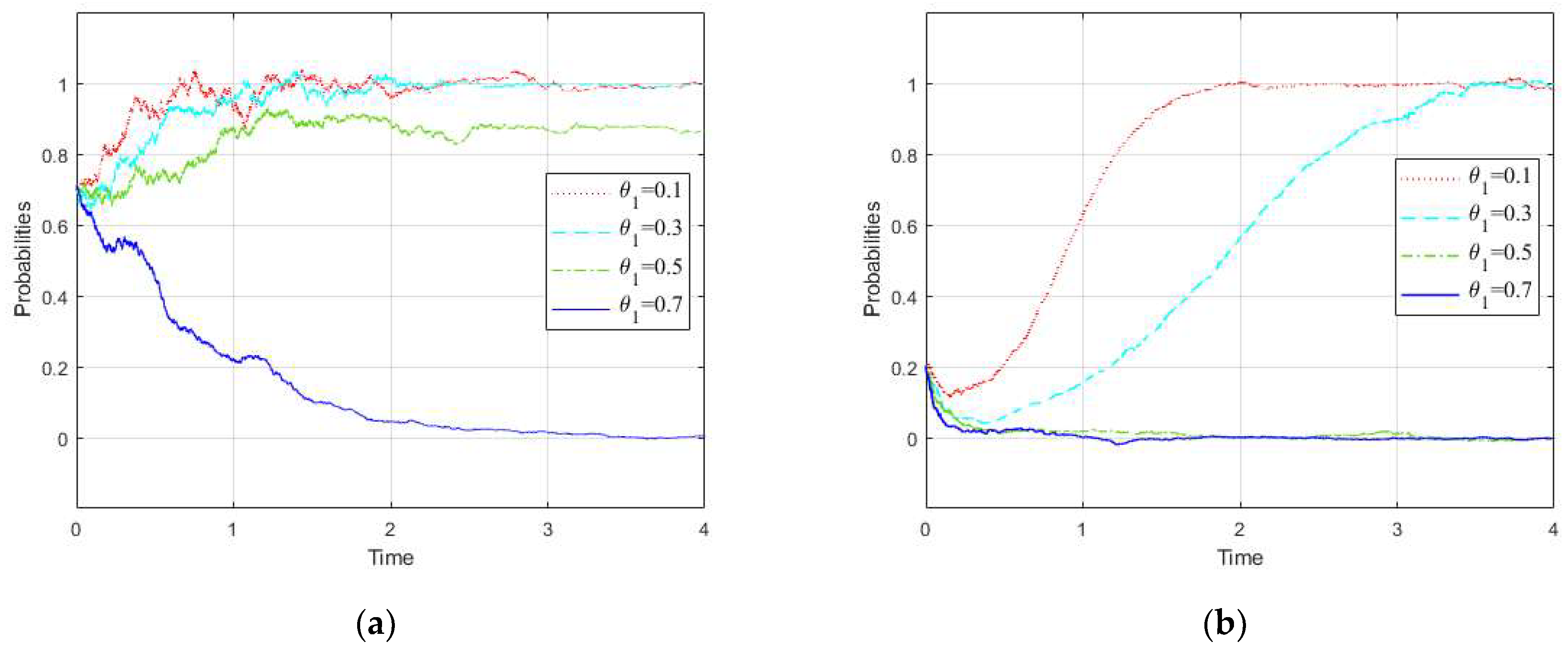
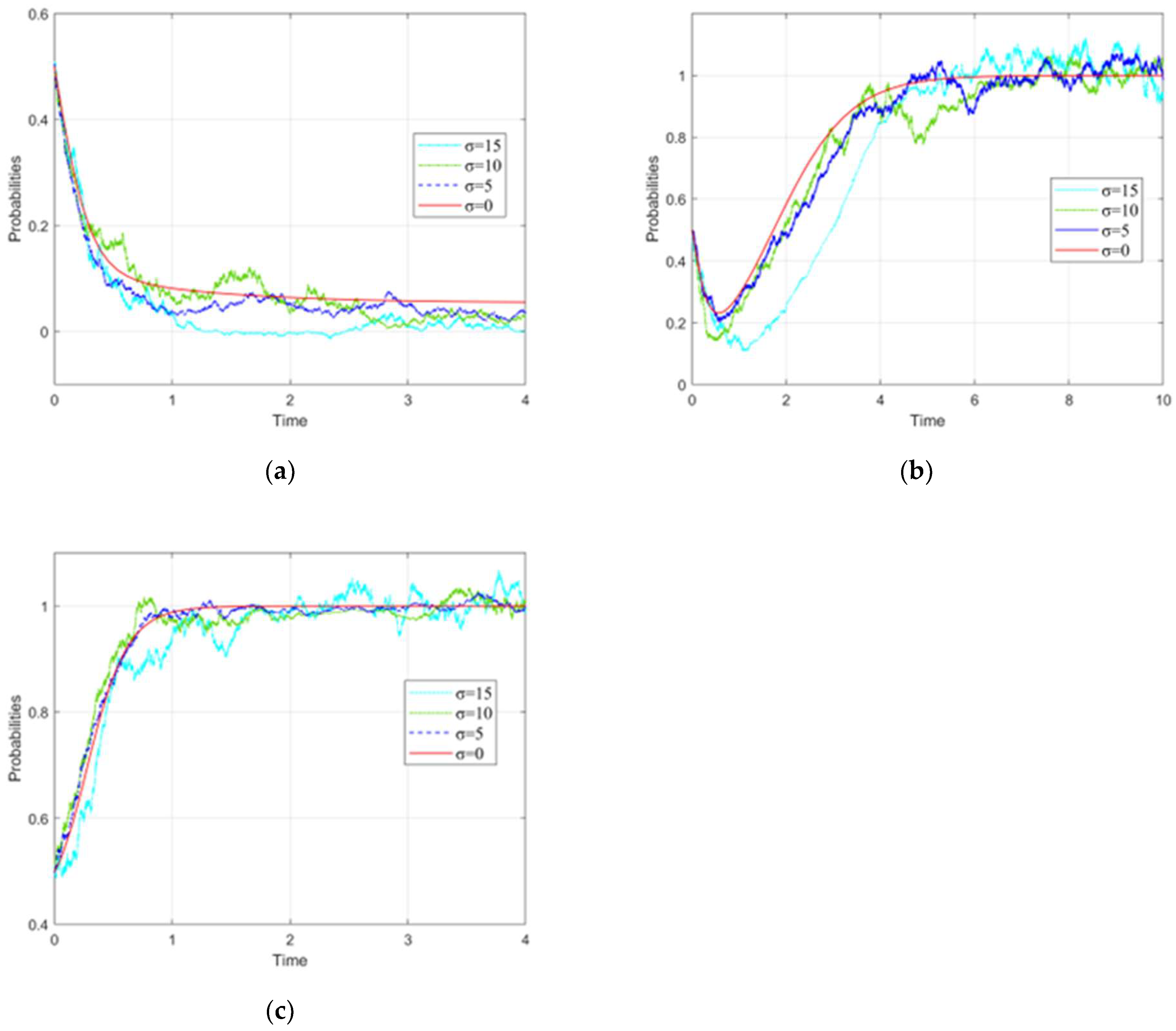
3.1. Influence Rule of the Initial Probability
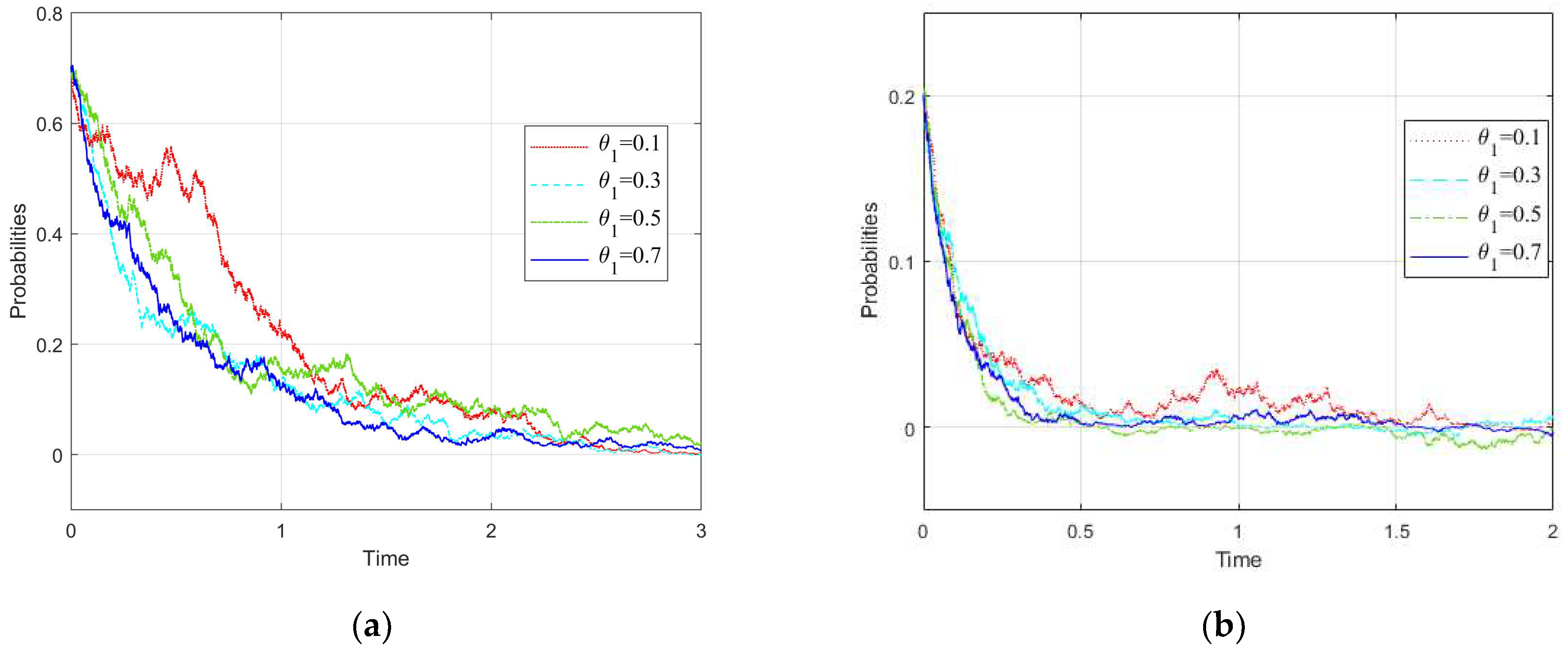
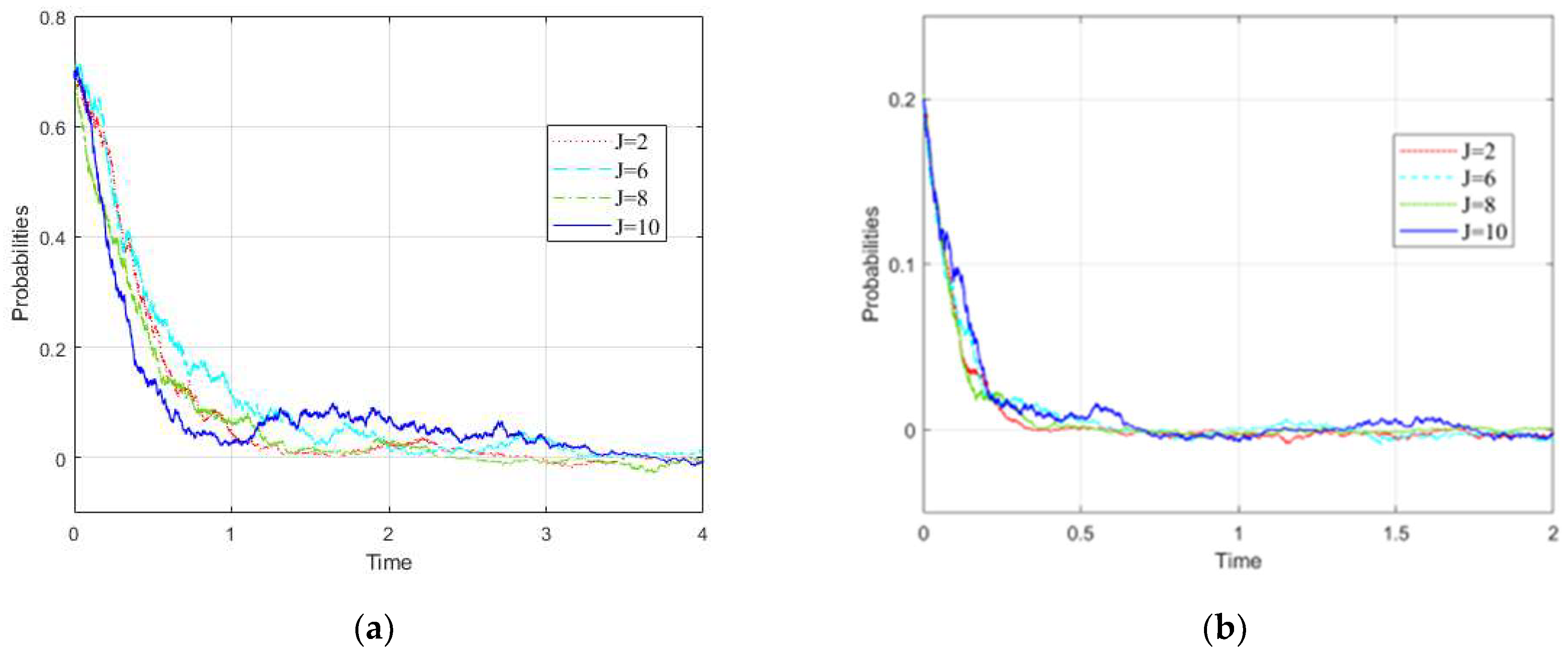
3.2. Influence Rule of
- (1)
- Influence rule of changes of on the Branch Government 1
- (2)
- Influence rule of the change of on Branch Government 2
- (3)
- Influence rule of change of on the mainstream government
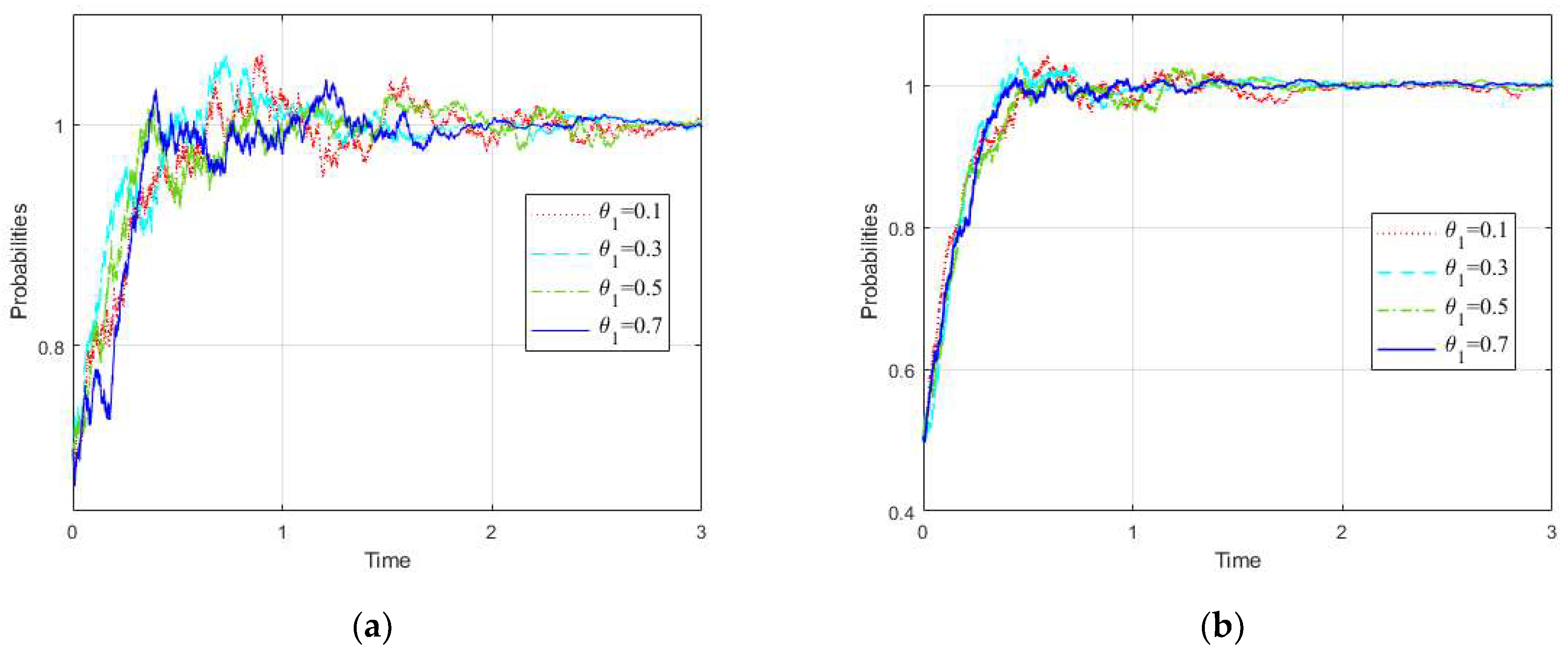
3.3. Influence Rule of
- (1)
- Influence rule of change on Branch Government 1
- (2)
- Influence rule of change on Branch Government 2
- (3)
- Influence rule of change on the mainstream government
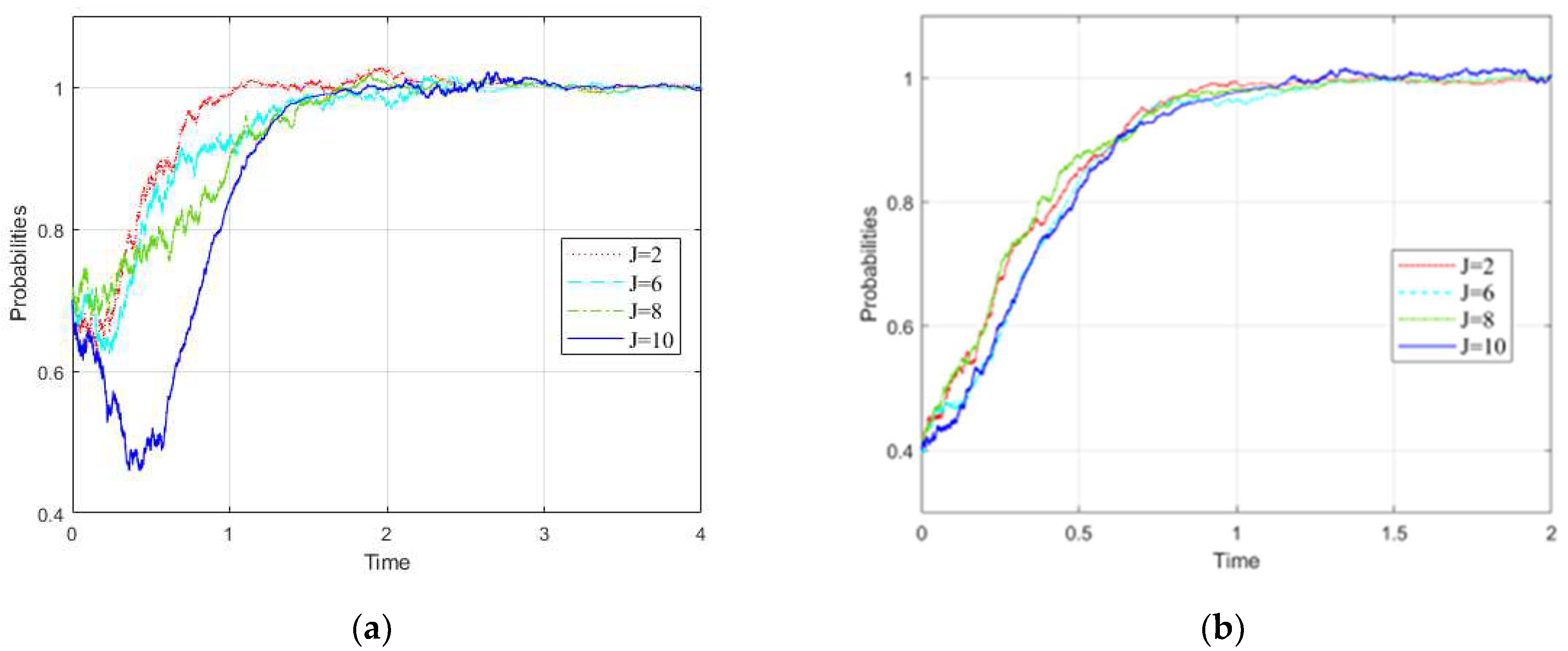
3.4. Influence Rule of Random Factors
4. Discussion
5. Conclusions and Suggestion
- (1)
- The initial probability affects the decisions of the three governments. With the increase of the initial probability, Branch Government 2 (the Shaanxi Provincial government) will first stabilize from the incomplete governance strategy to the complete governance strategy. In the case of high initial willingness, the three governments will stabilize to the optimal strategy (complete governance, complete governance, reward and compensation). As a result, strengthening the publicity of the ecological compensation policy and the guidance of the branch and mainstream governments plays an important role in the implementation of the ecological compensation mechanism.
- (2)
- With the increase of the transferred pollution amount of a branch, other branch governments are more unwilling to govern the pollution. When the proportion of transferred pollution amount exceeds a certain critical value, then other branch governments will choose the incomplete governance strategy. In addition, in the case of the high initial willingness of other branch governments to control pollution, the critical value of the proportion of transferred pollution will also increase. As a result, when carrying out the actual implementation of policies, it is essential to strengthen the supervision of a branch government on water pollution governance. When necessary, compensation mechanisms for watershed ecology can be combined with other policies, including China’s “The River Chief System” policy, to avoid a branch government’s “free-rider” phenomenon. This means that it is necessary to avoid the situation of a branch government transferring the pollution it shall treat to other branch governments.
- (3)
- The more the mainstream government (Henan provincial government) rewards the branch governments (Shanxi and Shaanxi provincial governments) for more pollution control, the more the branch governments will be encouraged to carry out pollution control. Thus, the mainstream government can increase the rewards to the branch governments within a certain range, to encourage them to increase pollution control efforts. To encourage the effective implementation of the mechanism, the central government can also offer some incentives to the river basin and branches where the ecological compensation mechanism is well implemented.
- (4)
- Branch governments (Shanxi and Shaanxi provincial governments) are greatly affected by random factors, and the greater random interference, the more unfavorable for the branch governments regarding pollution control. It is necessary to consider the influence of random factors when formulating the ecological compensation mechanism. According to the long time series data, the impact of random factors on branch governments should be quantified, and differentiated compensation standards should be set under different circumstances.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, X.M. Water stress, water transfer and social equity in Northern China—Implications for policy reforms. J. Environ. Manag. 2008, 87, 14–25. [Google Scholar] [CrossRef] [PubMed]
- Sadoff, C.W.; Hall, J.W.; Grey, D.; Aerts, J.C.J.H.; Ait-Kadi, M.; Brown, C.; Cox, A.; Dadson, S.; Garrick, D.; Kelman, J.; et al. Securing Water, Sustaining Growth: Report of the GWP/OECD Task Force on Water Security and Sustainable Growth; University of Oxford: Oxford, UK, 2015. [Google Scholar]
- Talukder, B.; Hipel, K.W. Diagnosis of sustainability of trans-boundary water governance in the Great Lakes basin. World Dev. 2020, 129, 104855. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Y.; Dai, J.; Zeng, Y. Cost sharing mechanism of water pollution control in main and sub basins based on Stackelberg game model. Math. Probl. Eng. 2022, 8, 6559840. [Google Scholar]
- Yang, Y.; Liu, Y.; Yuan, Z.; Dai, J.; Zeng, Y.; Khan, M.Y.A. Analyzing the Water Pollution Control Cost-Sharing Mechanism in the Yellow River and Its Two Tributaries in the Context of Regional Differences. Water 2022, 14, 1678. [Google Scholar] [CrossRef]
- Zhang, J.Y. Impacts of climate change on national water security and mitigation strategies. China Water Resour. 2022, 15, 3–5+14. [Google Scholar]
- Pan, X.; Xu, L.; Yang, Z.; Yu, B. Payments for ecosystem services in China: Policy, practice, and progress. J. Clean. Prod. 2017, 158, 200–208. [Google Scholar] [CrossRef]
- Farley, J.; Costanza, R. Payments for ecosystem services: From local to global. Ecol. Econ. 2010, 69, 2060–2068. [Google Scholar] [CrossRef]
- Gao, X.; Shen, J.; He, W.; Sun, F.; Zhang, Z.; Zhang, X.; Yuan, L.; An, M. Multilevel Governments’ Decision-Making Process and Its Influencing Factors in Watershed Ecological Compensation. Sustainability 2019, 11, 1990. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, Z.Y.; Zheng, H.; Yue, P. Establishment of ecological compensation mechanisms in China: Perspectives and strategies. Acta Ecol. Sin. 2013, 33, 686–692. [Google Scholar] [CrossRef] [Green Version]
- Wunder, S. Revisiting the concept of payments for environmental services. Ecol. Econ. 2015, 117, 234–243. [Google Scholar] [CrossRef]
- Fu, Y.; Zhang, J.; Zhang, C.; Zang, W.; Guo, W.; Qian, Z.; Liu, L.; Zhao, J.; Feng, J. Payments for Ecosystem Services for watershed water resource allocations. J. Hydrol. 2018, 556, 689–700. [Google Scholar] [CrossRef]
- Ma, J.; Cheng, C.; Tang, Y. Basin Eco-Compensation Strategy Considering a Cost-Sharing Contract. IEEE Access 2021, 9, 91635–91648. [Google Scholar] [CrossRef]
- Jiang, K.; You, D.; Li, Z.; Shi, S. A differential game approach to dynamic optimal control strategies for watershed pollution across regional boundaries under eco-compensation criterion. Ecol. Indic. 2019, 105, 229–241. [Google Scholar] [CrossRef]
- Yu, B.; Chen, L. Interventional Impacts of Watershed Ecological Compensation on Regional Economic Differences: Evidence from Xin’an River, China. Int. J. Environ. Res. Public Health 2020, 17, 6389. [Google Scholar] [CrossRef]
- Hu, D.B.; Lin, M.; Chen, X.H. Study on the effects of river basin horizontal ecological compensation on water environment benefits. China Environ. Sci. 2022, 1–12. [Google Scholar] [CrossRef]
- Qu, F.G.; Sun, Y.F. Study on payments for environmental services in basin area based on intergovernmental game. China Popul. Resour. Environ. 2014, 24, 83–88. [Google Scholar]
- Hu, Z.H.; Liu, J.Y.; Zhong, M.R.; Hong, K.R. Interests balance of trans-boundary river basin ecological compensation based on evolutionary game theory—Taking Lijiang Basin as a case. Econ. Geogr. 2016, 36, 42–49. [Google Scholar]
- Wang, Q.; Wang, N.; Wang, H.; Xiu, Y. Study on Influencing Factors and Simulation of Watershed Ecological Compensation Based on Evolutionary Game. Sustainability 2022, 14, 3374. [Google Scholar] [CrossRef]
- Gao, X.; Shen, J.; He, W.; Sun, F.; Zhang, Z.; Guo, W.; Zhang, X.; Kong, Y. An evolutionary game analysis of governments’ decision-making behaviors and factors influencing watershed ecological compensation in China. J. Environ. Manag. 2019, 251, 109592. [Google Scholar] [CrossRef]
- Sheng, J.; Webber, M. Using incentives to coordinate responses to a system of payments for watershed services: The middle route of South–North Water Transfer Project, China. Ecosyst. Serv. 2018, 32, 1–8. [Google Scholar] [CrossRef]
- Jiang, K.; Zhang, X.; Wang, Y. Stability and influencing factors when designing incentive-compatible payments for watershed services: Insights from the Xin’an River Basin, China. Mar. Policy 2021, 134, 104824. [Google Scholar] [CrossRef]
- Yang, Z.; Niu, G.M.; Lan, Z.R. Policy strategy of transboundary water pollution control in boundary rivers based on evolutionary game. China Environ. Sci. 2021, 41, 5446–5456. [Google Scholar]
- Jiang, E.H.; Wang, Y.J.; Tian, S.M.; Li, J.H.; Xu, L.J.; Zhang, X.P. Exploration of watershed system science. J. Hydraul. Eng. 2020, 51, 1026–1037. [Google Scholar]
- Gao, J.X.; Wang, Y.C.; Hou, P.; Wan, H.W.; Zhang, W.G. Temporal and spatial variation characteristics of land surface water area in the Yellow River basin in recent 20 years. J. Hydraul. Eng. 2020, 51, 1157–1164. [Google Scholar]
- Hu, D.X.; Liu, Z.C.; Liu, T.L.; Liu, Q.P.; Li, Y.J. Analysis on spatial-temporal difference of water use efficiency in Weihe River Basin of Shaanxi province. Yellow River 2020, 42, 56–61. [Google Scholar]
- Quan, J.; Xu, Y.; Ma, T.; Wilson, J.P.; Zhao, N.; Ni, Y. Improving surface water quality of the Yellow River Basin due to anthropogenic changes. Sci. Total Environ. 2022, 836, 155607. [Google Scholar] [CrossRef]
- Baker, C.T.H.; Buckwar, E. Exponential stability in p-th mean of solutions, and of convergent Euler-type solutions, of stochastic delay differential equations. J. Comput. Appl. Math. 2005, 184, 404–427. [Google Scholar] [CrossRef] [Green Version]
- Higham, D.J. An Algorithmic Introduction to Numerical Simulation of Stochastic Differential Equations. SIAM Rev. 2001, 43, 525–546. [Google Scholar] [CrossRef]
- Gao, X.; Song, Z.R.; Zeng, S.X.; Shen, J.Q. Ecological compensation of major water transfer project based on stochastic evolutionary game: A case of South-to-North Water Transfer Project. Front. Sci. Technol. Eng. Manag. 2022, 41, 26–34. [Google Scholar]
- Jiang, K.; Merrill, R.; You, D.; Pan, P.; Li, Z. Optimal control for transboundary pollution under ecological compensation: A stochastic differential game approach. J. Clean. Prod. 2019, 241, 118391. [Google Scholar] [CrossRef]

| Game Subject | Strategy | Selection Probability |
|---|---|---|
| Branch Government 1 (Shanxi Provincial Government) | Complete governance | |
| Incomplete governance | ||
| Branch Government 2 (Shaanxi Provincial Government) | Complete governance | |
| Incomplete governance | ||
| Mainstream Government (Henan Provincial Government) | Reward | |
| No reward |
| Mainstream Government Executes Reward and Compensation | Mainstream Government Does Not Execute Reward and Compensation | |||
|---|---|---|---|---|
| Branch Government 2 Achieves Complete Governance | Branch Government 2 Achieves Incomplete Governance | Branch Government 2 Achieves Complete Governance | Branch Government 2 Achieves Incomplete Governance | |
| Branch Government 1 achieves complete governance | ||||
| Branch Government 1 achieves incomplete governance | ||||
| 15 | 10 | 7 | 9 | 6 | 8 | 8 | 3 | 4 |
| 3 | 2 | 5 | 5 | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, E.; Qu, B.; Zhu, Y.; Liu, C. Watershed Ecological Compensation Mechanism for Mainstream and Branches Based on Stochastic Evolutionary Game: A Case of the Middle Yellow River. Water 2022, 14, 4038. https://doi.org/10.3390/w14244038
Liu Y, Jiang E, Qu B, Zhu Y, Liu C. Watershed Ecological Compensation Mechanism for Mainstream and Branches Based on Stochastic Evolutionary Game: A Case of the Middle Yellow River. Water. 2022; 14(24):4038. https://doi.org/10.3390/w14244038
Chicago/Turabian StyleLiu, Ying, Enhui Jiang, Bo Qu, Yongwei Zhu, and Chang Liu. 2022. "Watershed Ecological Compensation Mechanism for Mainstream and Branches Based on Stochastic Evolutionary Game: A Case of the Middle Yellow River" Water 14, no. 24: 4038. https://doi.org/10.3390/w14244038