Comparative Study of Coupling Models of Feature Selection Methods and Machine Learning Techniques for Predicting Monthly Reservoir Inflow
Abstract
:1. Introduction
2. Materials and Methods
2.1. Research Framework
2.2. Study Area
2.3. Data Used
2.4. Machine Learning Techniques
2.4.1. Multivariable Linear Regression (MLR)
2.4.2. Support Vector Regression (SVR)
2.4.3. Artificial Neural Networks (ANN)
2.4.4. Genetics Algorithm (GA)
2.4.5. Backward Eliminations (BE)
| Algorithm 1 Backward Elimination (BE) for Reservoir Inflow Forecasting |
| Input: Data set D, Target T. Output: Selected Variables SV |
| //D: Huai Nam Sai Reservoir, T: Inflow, SV: R, S, Inf., Climate Indices (10 parameters) |
| iterate until SV does not change |
| 1: while SV changes do |
| 2://Identify the worst variable Vworst out of all selected variables SV, according to Perf |
| 3: Vworst ← argmax (V∈SV) Perf(S\V) |
| 4://Remove Vworst if it does not decrease performance according to criterion C |
| 5: if Perf(SV\Vworst) ≥ Perf(SV) then |
| 6: SV ← SV\Vworst |
| 7: end if |
| 8: end while |
| 9: return SV |
2.5. Experimental Setup
2.6. Statistical Performance Measures
3. Results and Discussion
3.1. Results of Feature Selection
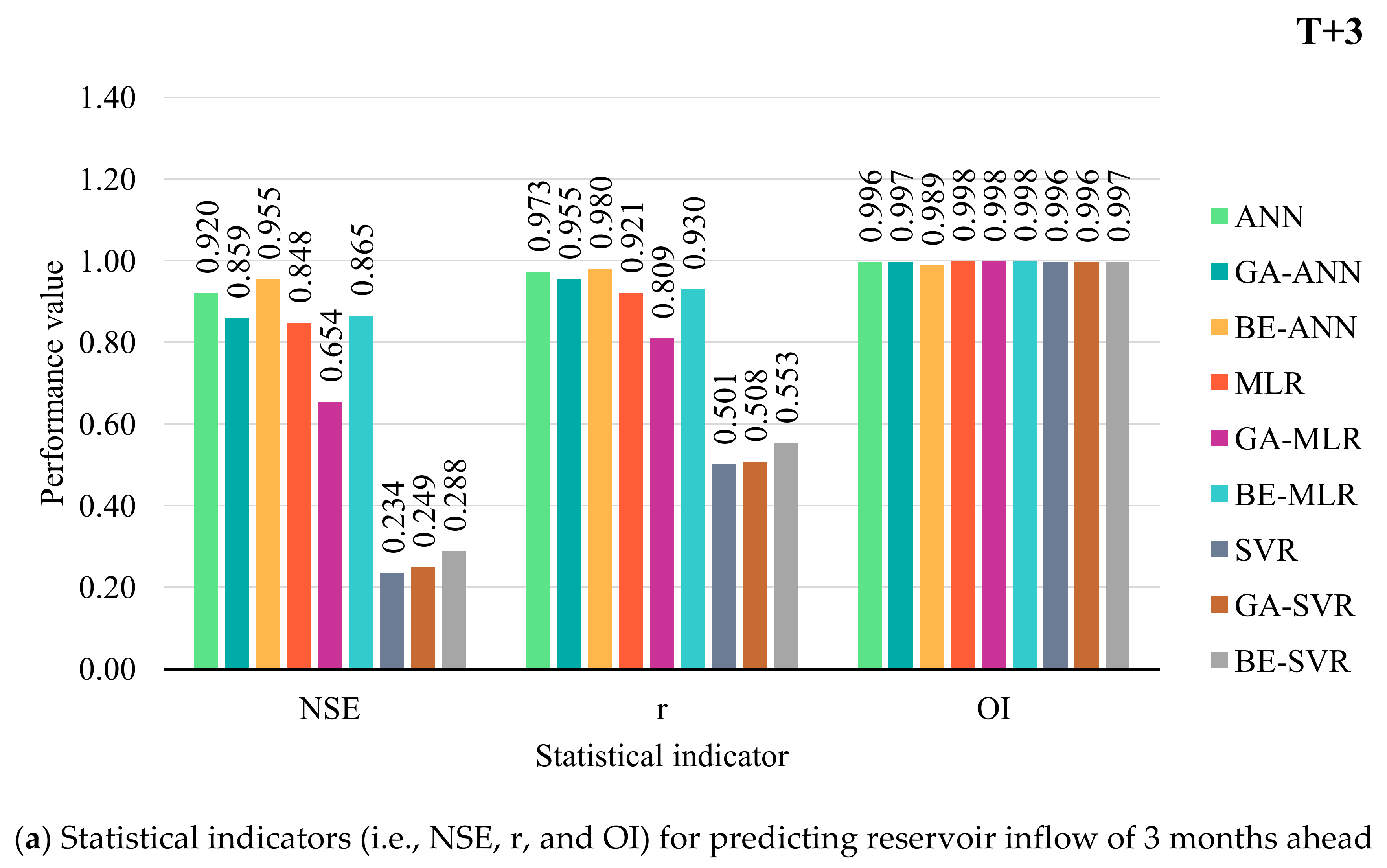
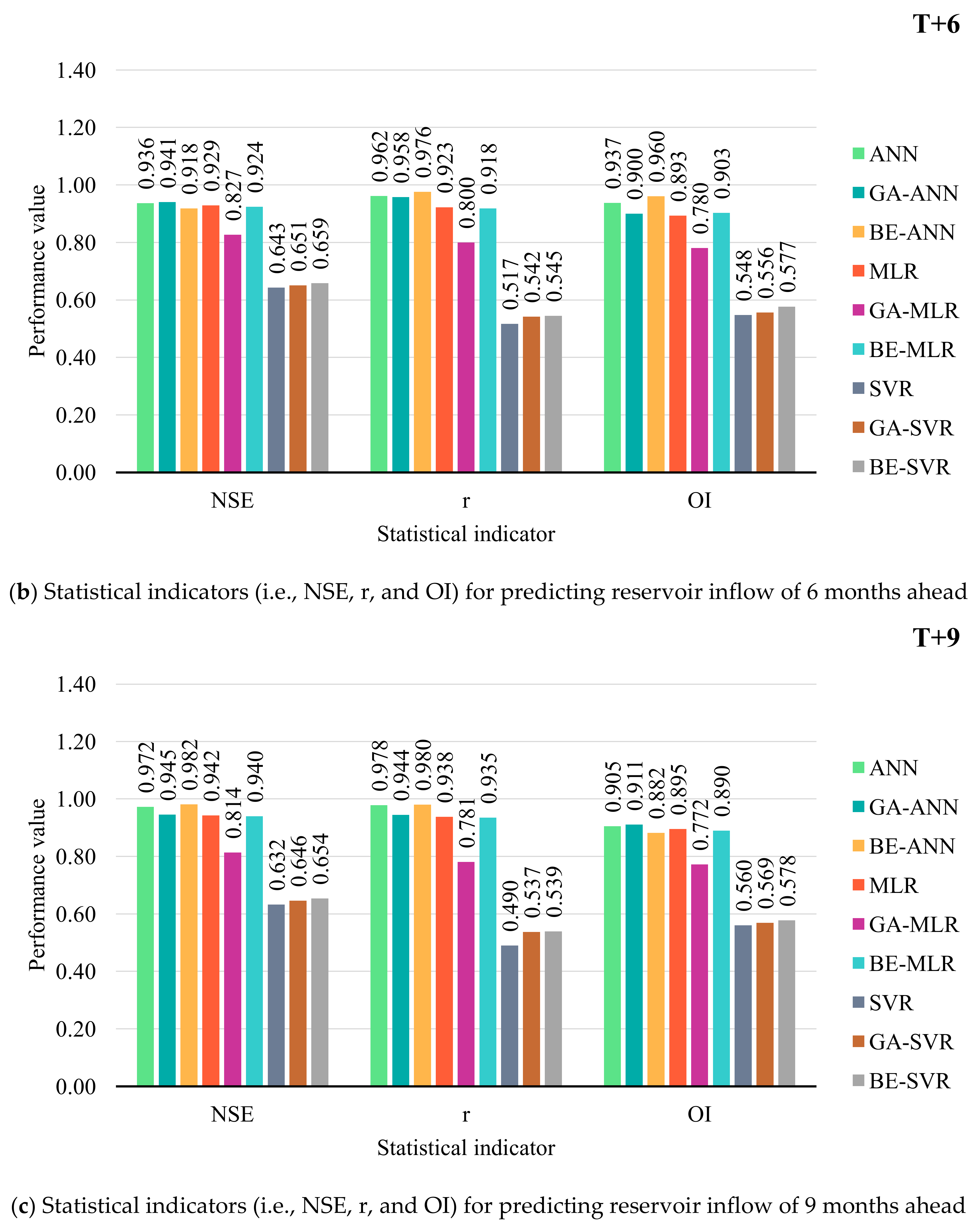
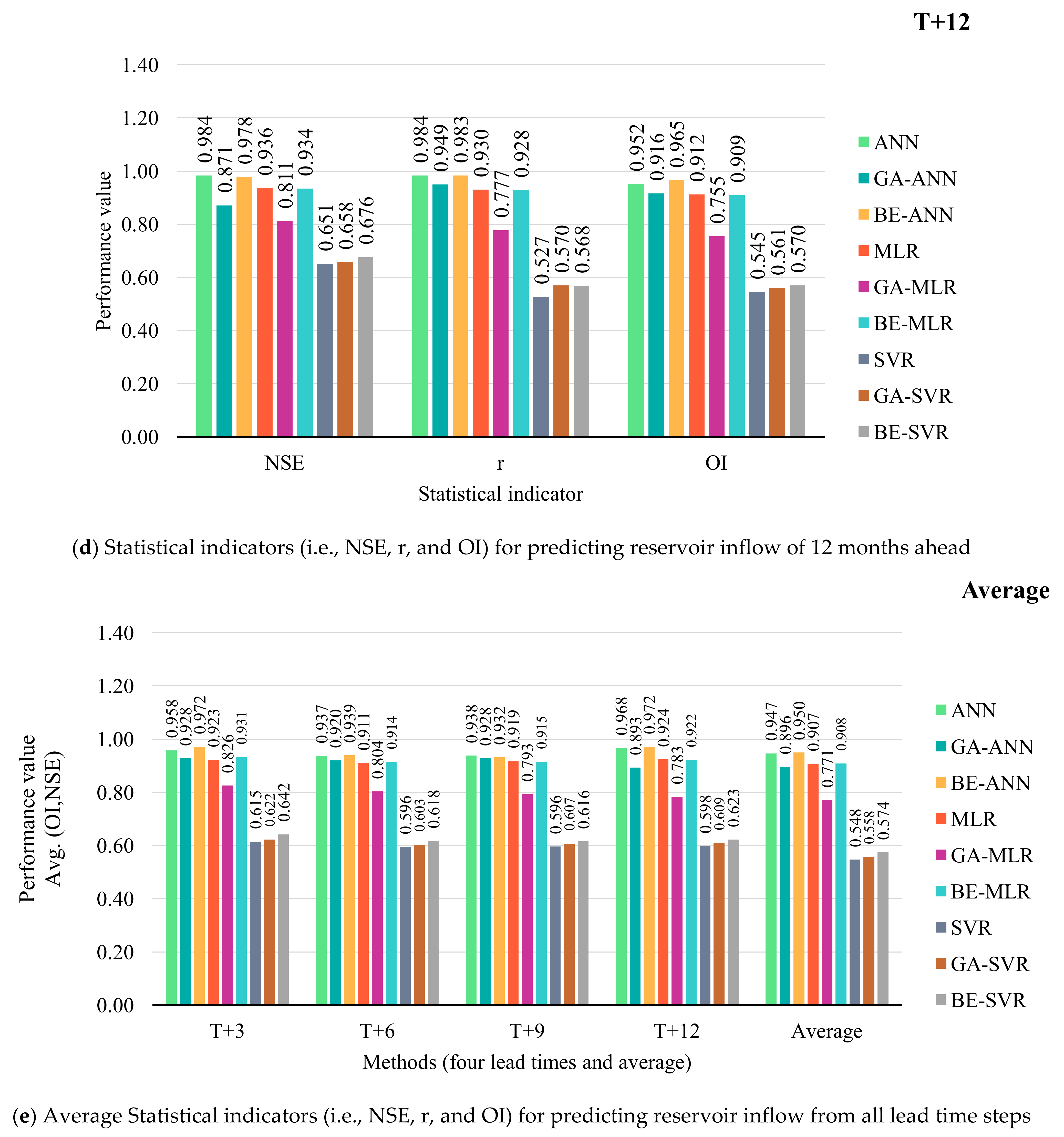
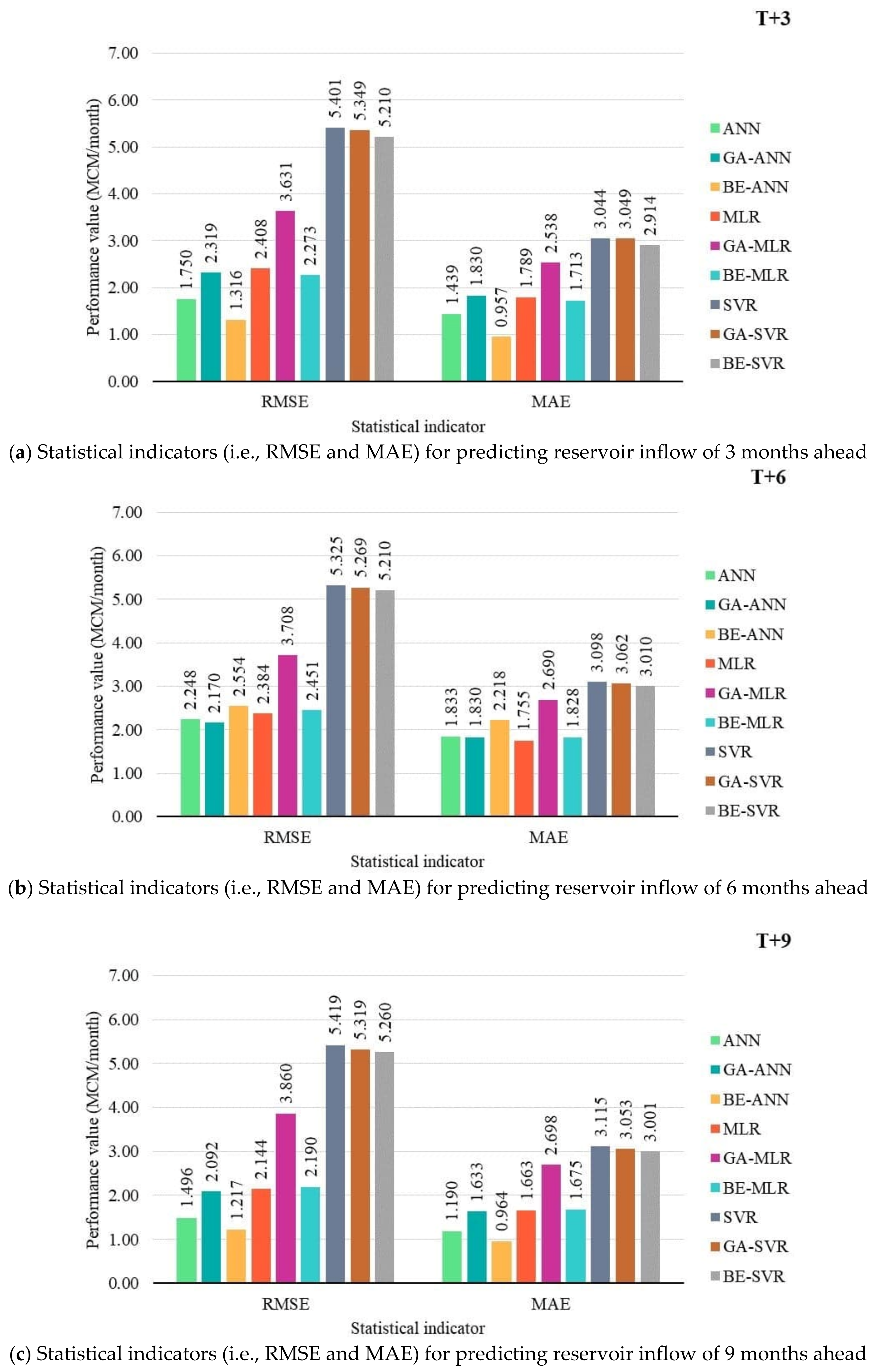
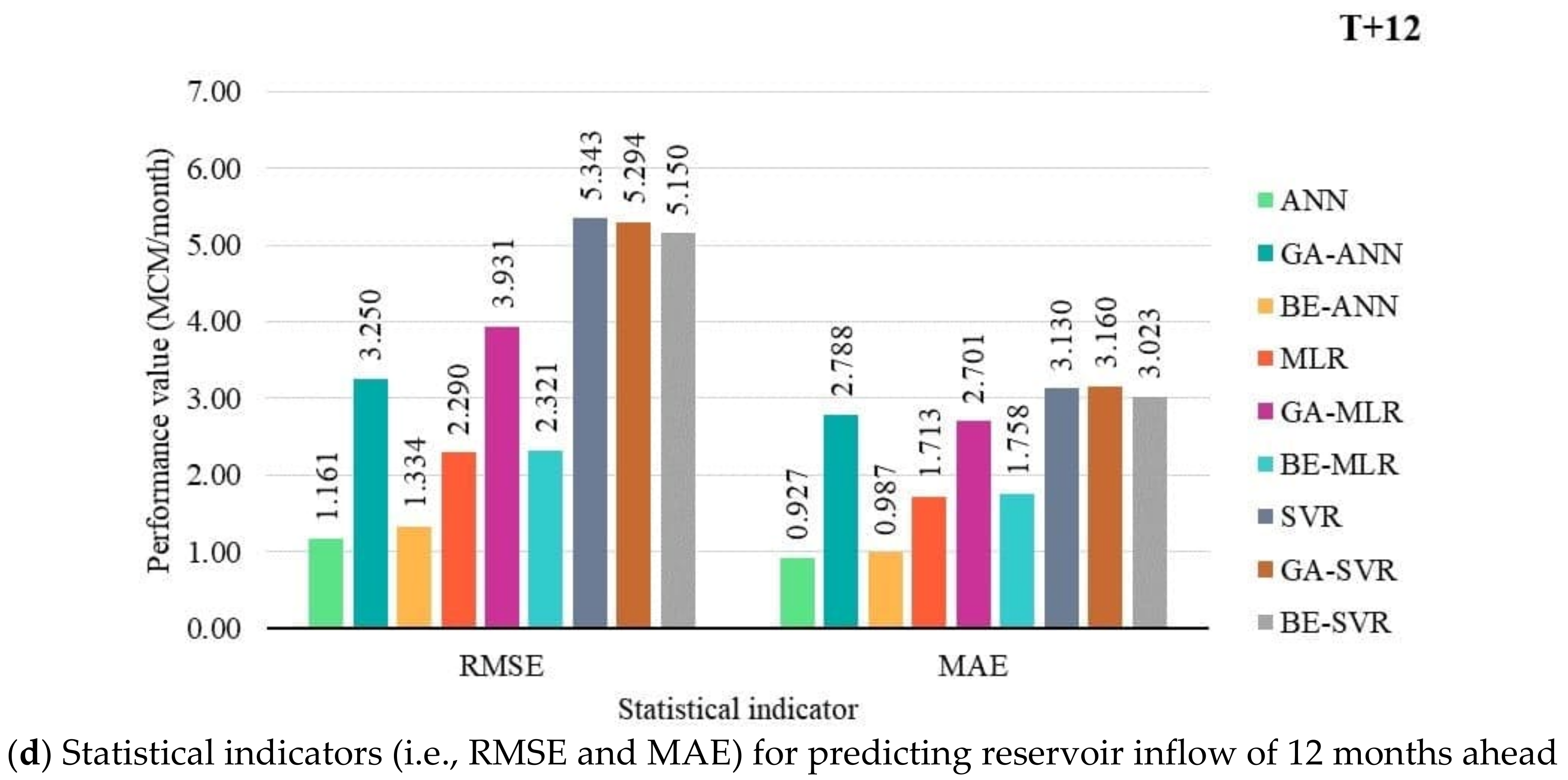
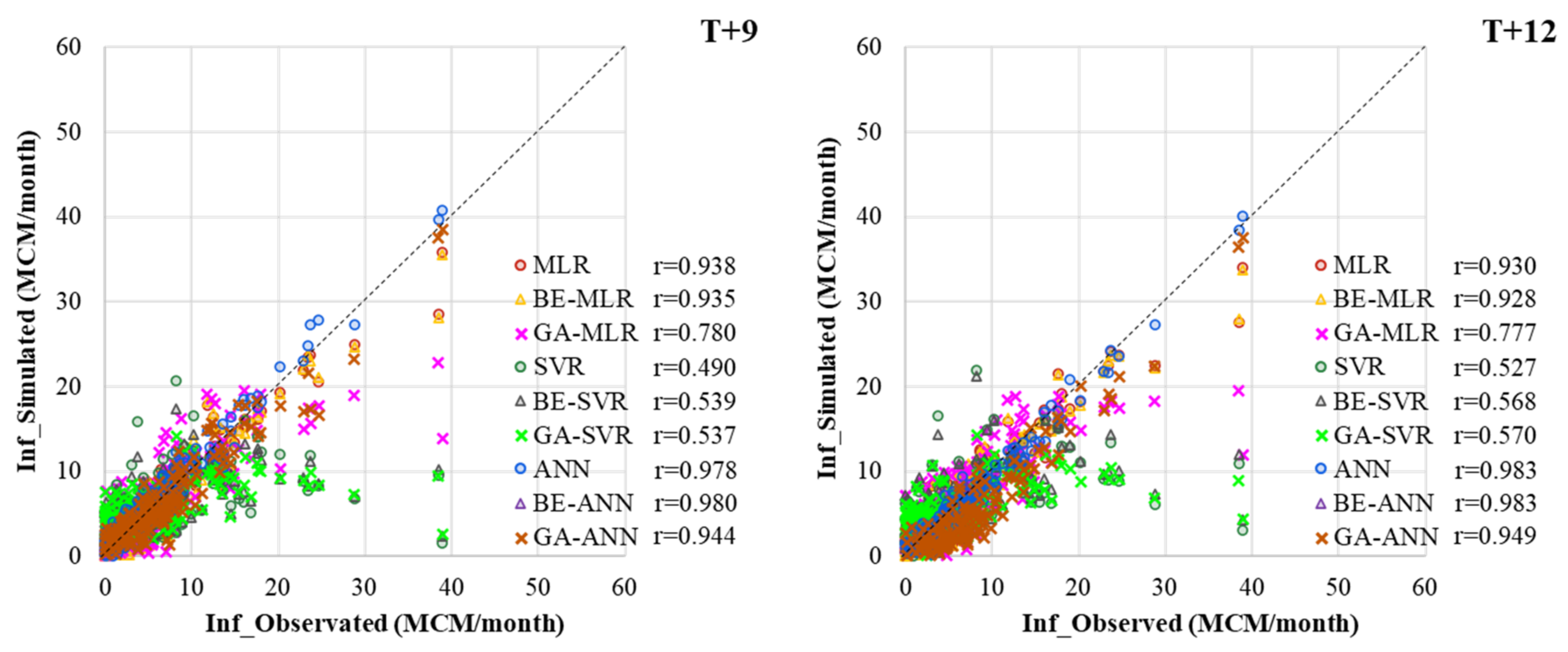
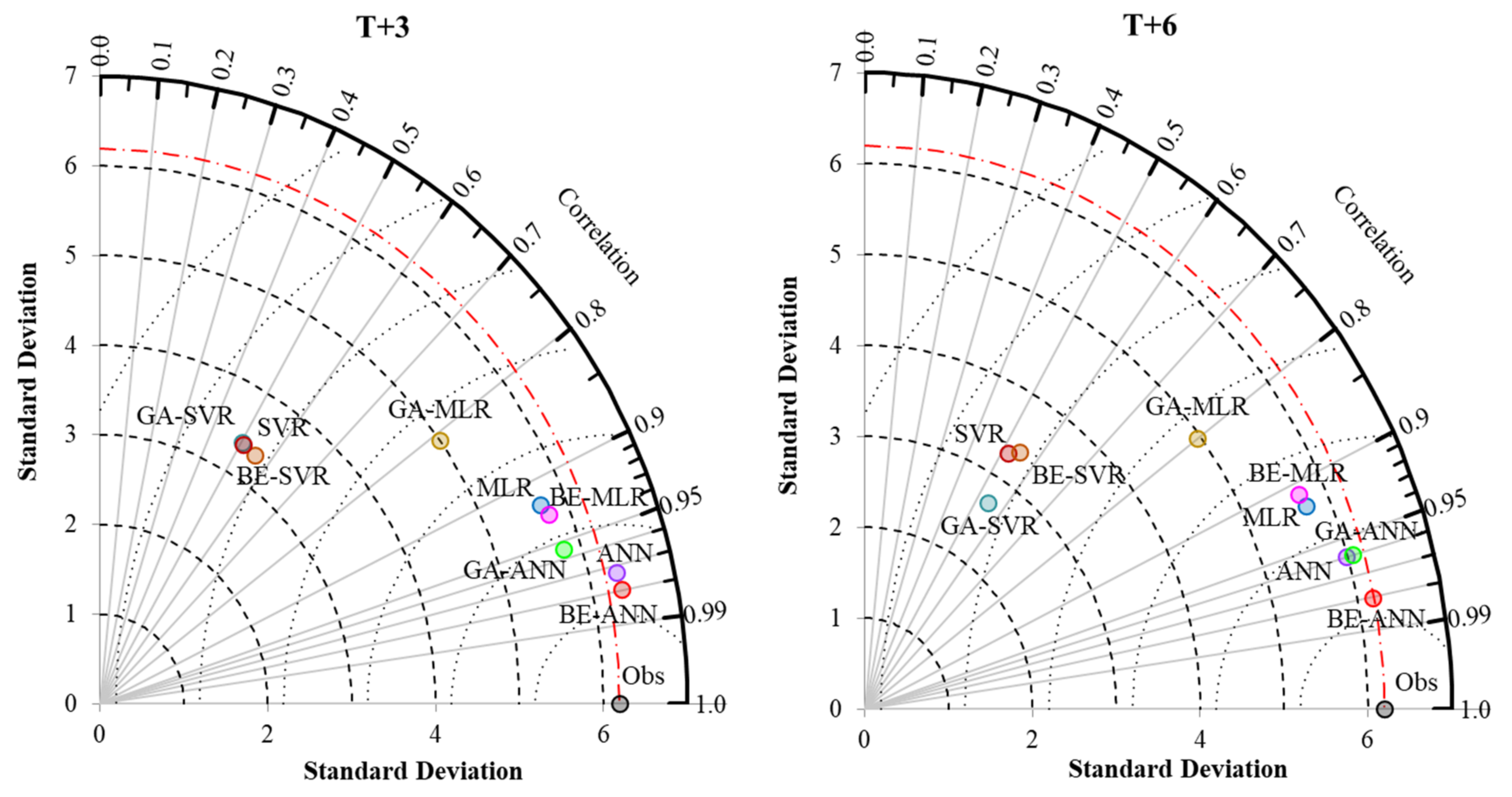
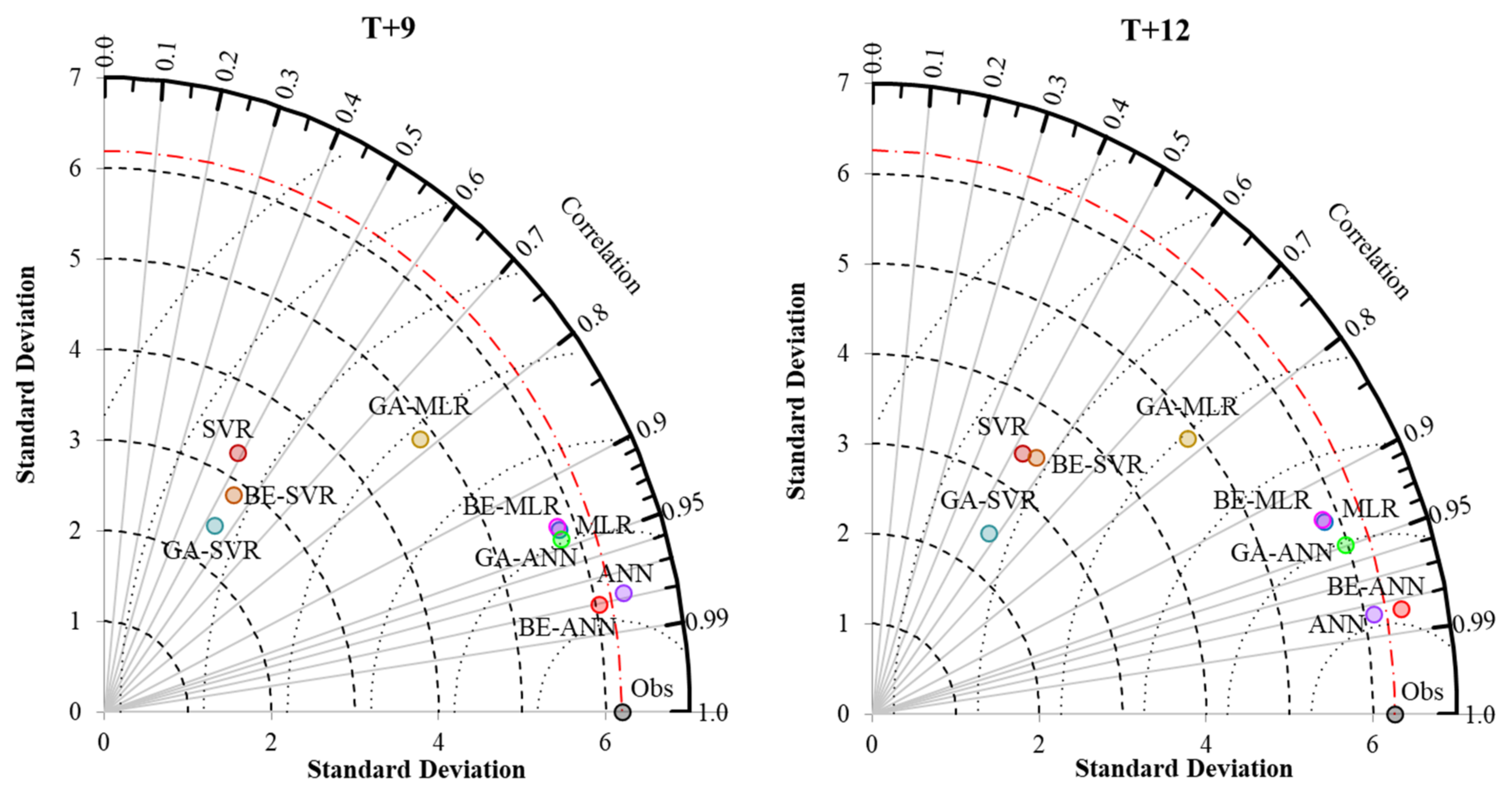
3.2. Performance Comparison of Prediction Models
MLR, ANN, SVR, and Hybrid with BE and GA
4. Conclusions
- Feature selection methods (i.e., GA and BE) could improve the performance of SVR and ANN for predicting monthly reservoir inflow forecasting, but they have no effects on MLR. GA and BE could select better features for SVR for all of the lead times. Only BE could make compelling selection features for ANN by improving its performance for almost all of the lead times (i.e., T + 3, T + 6, T + 9) except for twelve lead times (T + 12). GA could overwhelmingly reduce the number of features by more than 60% and 45% for ANN and SVR, respectively. Although BE could improve the ANN and SVR’s performance by approximately 1% over GA, it required a much higher number of features.
- With average an OI and NSE, BE-ANN provides the best performance for 3, 6, and 12 months ahead (T + 3, T + 6, and T + 12). While ANN was suitable for 9 months ahead only. SVR, GA-SVR, and BE-SVR, however, are the least effective of the top three prediction methods.
- Different developed forecasting models were suitable for different reservoir inflow forecasting time-step-ahead. That is, BE-ANN gave the best performance for 3 and 9 months ahead (T + 3 and T + 9), whilst GA-ANN was suitable for semi-annually reservoir inflow forecasting. Finally, ANN provided the best model for annual reservoir inflow forecasting. From the overall results, all SVR-based models (i.e., SVR, GA-SVR, and BE-SVR) gave the lowest performance by giving the lowest values of OI, NSE, and r and the highest values of RMSE and MAE.
- To increase the forecasting models’ performance on reservoir inflow, future studies would have to focus on the extreme events that are frequently happening presently due to climate change effects, i.e., very high peak reservoir inflow, crucially leading to helping reservoir regulators with optimal reservoir operations.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Chiamsathit, C.; Adeloye, A.J.; Bankaru-Swamy, S. Inflow forecasting using artificial neural networks for reservoir operation. Proc. Int. Assoc. Hydrol. Sci. 2016, 373, 209–214. [Google Scholar] [CrossRef] [Green Version]
- Liao, S.; Liu, Z.; Liu, B.; Cheng, C.; Jin, X.; Zhao, Z. Multistep-ahead daily inflow forecasting using the ERA-Interim reanalysis data set based on gradient-boosting regression trees. Hydrol. Earth Syst. Sci. 2020, 24, 2343–2363. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, K.; Li, Z.; Liu, Z.; Wang, J.; Huang, P. A hybrid runoff generation modelling framework based on spatial combination of three runoff generation schemes for semi-humid and semi-arid watersheds. J. Hydrol. 2020, 590, 125440. [Google Scholar] [CrossRef]
- Chen, Z.; Liu, Z.; Yin, L.; Zheng, W. Statistical analysis of regional air temperature characteristics before and after dam construction. Urban Clim. 2022, 41, 101085. [Google Scholar] [CrossRef]
- Yin, L.; Wang, L.; Keim, B.D.; Konsoer, K.; Zheng, W. Wavelet Analysis of Dam Injection and Discharge in Three Gorges Dam and Reservoir with Precipitation and River Discharge. Water 2022, 14, 567. [Google Scholar] [CrossRef]
- Lee, D.; Kim, H.; Jung, I.; Yoon, J. Monthly Reservoir Inflow Forecasting for Dry Period Using Teleconnection Indices: A Statistical Ensemble Approach. Appl. Sci. 2020, 10, 3470. [Google Scholar] [CrossRef]
- Allawi, M.F.; Hussain, I.R.; Salman, M.I.; El-Shafie, A. Monthly inflow forecasting utilizing advanced artificial intelligence methods: A case study of Haditha Dam in Iraq. Stoch. Hydrol. Hydraul. 2021, 35, 2391–2410. [Google Scholar] [CrossRef]
- Weekaew, J.; Ditthakit, P.; Kittiphattanabawon, N. Reservoir Inflow Time Series Forecasting Using Regression Model with Climate Indices. Recent Adv. Inf. Commun. Technol. 2021, 251, 127–136. [Google Scholar]
- Kim, T.; Shin, J.Y.; Kim, H.; Kim, S.; Heo, J.H. The use of large-scale climate indices in monthly reservoir inflow forecasting and its application on time series and artificial intelligence models. Water 2019, 11, 374. [Google Scholar] [CrossRef] [Green Version]
- Vadiati, M.; Rajabi Yami, Z.; Eskandari, E.; Nakhaei, M.; Kisi, O. Application of artificial intelligence models for prediction of groundwater level fluctuations: Case study (Tehran-Karaj alluvial aquifer). Environ. Monit. Assess. 2022, 194, 1–21. [Google Scholar] [CrossRef]
- Samani, S.; Vadiati, M.; Azizi, F.; Zamani, E.; Kisi, O. Groundwater Level Simulation Using Soft Computing Methods with Emphasis on Major Meteorological Components. Water Resour. Manag. 2022, 36, 3627–3647. [Google Scholar] [CrossRef]
- Ditthakit, P.; Pinthong, S.; Salaeh, N.; Binnui, F.; Khwanchum, L.; Pham, Q.B. Using machine learning methods for supporting GR2M model in runoff estimation in an ungauged basin. Sci. Rep. 2021, 11, 19955. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Guo, S.; Chang, F.J. Explore an evolutionary recurrent ANFIS for modelling multi-step-ahead flood forecasts. J. Hydrol. 2019, 570, 343–355. [Google Scholar] [CrossRef]
- Kao, I.F.; Liou, J.Y.; Lee, M.H.; Chang, F.J. Fusing stacked autoencoder and long short-term memory for regional multistep-ahead flood inundation forecasts. J. Hydrol. 2021, 598, 126371. [Google Scholar] [CrossRef]
- Chang, L.C.; Liou, J.Y.; Chang, F.J. Spatial-temporal flood inundation nowcasts by fusing machine learning methods and principal component analysis. J. Hydrol. 2022, 612, 128086. [Google Scholar] [CrossRef]
- Makridakis, S. Time series prediction: Forecasting the future and understanding the past. Int. J. Forecast. 1994, 10, 463–466. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, K.; Chao, L.; Li, D.; Tian, X.; Bao, H.; Chen, G.; Xia, Y. Exploring the utility of radar and satellite-sensed precipitation and their dynamic bias correction for integrated prediction of flood and landslide hazards. J. Hydrol. 2021, 603, 126964. [Google Scholar] [CrossRef]
- Tongsiri, J.; Kangrang, A. Prediction of Future Inflow under Hydrological Variation Characteristics and Improvement of Nam Oon Reservoir Rule Curve using Genetic Algorithms Technique. Mahasarakham Univ. J. Sci. Technol. 2018, 37, 775–788. [Google Scholar]
- Valipour, M.; Banihabib, M.E.; Behbahani, S.M.R. Parameters estimate of autoregressive moving average and autoregressive integrated moving average models and compare their ability for inflow forecasting. J. Math. Stat. 2012, 8, 330–338. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.F.; Chen, G.R.; Huang, P.Y. Effective typhoon characteristics and their effects on hourly reservoir inflow forecasting. Adv. Water Resour. 2010, 33, 887–898. [Google Scholar] [CrossRef]
- Yang, T.; Asanjan, A.A.; Welles, E.; Gao, X.; Sorooshian, S.; Liu, X. Developing reservoir monthly inflow forecasts using artificial intelligence and climate phenomenon information. Water Resour. Res. 2017, 53, 2786–2812. [Google Scholar] [CrossRef]
- Cheng, C.T.; Feng, Z.K.; Niu, W.J.; Liao, S.L. Heuristic methods for reservoir monthly inflow forecasting: A case study of xinfengjiang reservoir in pearl river, China. Water 2015, 7, 4477–4495. [Google Scholar] [CrossRef]
- Elbeltagi, A.; Kumar, M.; Kushwaha, N.L.; Pande, C.B.; Ditthakit, P.; Vishwakarma, D.K.; Subeesh, A. Drought indicator analysis and forecasting using data driven models: Case study in Jaisalmer, India. Stoch. Hydrol. Hydraul. 2022, 2022, 1–19. [Google Scholar] [CrossRef]
- Chang, F.; Hsu, K.; Chang, L. Flood Forecasting Using Machine Learning Methods; MDPI: Basel, Switzerland, 2019; ISBN 9783038975489. [Google Scholar]
- Salaeh, N.; Ditthakit, P.; Pinthong, S.; Hasan, M.A.; Islam, S.; Mohammadi, B.; Linh, N.T.T. Long-Short Term Memory Technique for Monthly Rainfall Prediction in Thale Sap Songkhla River Basin, Thailand. Symmetry 2022, 14, 1599. [Google Scholar] [CrossRef]
- Li, B.; Yang, G.; Wan, R.; Dai, X.; Zhang, Y. Comparison of random forests and other statistical methods for the prediction of lake water level: A case study of the Poyang Lake in China. Hydrol. Res. 2016, 47, 69–83. [Google Scholar] [CrossRef] [Green Version]
- Sarhani, M.; El Afia, A. Electric load forecasting using hybrid machine learning approach incorporating feature selection. In Proceedings of the International Conference on Big Data Cloud and Applications, Jeju Island, Republic of Korea, 20–23 October 2015. [Google Scholar]
- Ivanciuc, O. Applications of Support Vector Machines in Chemistry. Rev. Comput. Chem. 2007, 23, 291–400. [Google Scholar] [CrossRef]
- Domingos, S.; de Oliveira, J.F.L.; de Mattos Neto, P.S.G. An intelligent hybridization of ARIMA with machine learning models for time series forecasting. Knowledge Based Syst. 2019, 175, 72–86. [Google Scholar] [CrossRef]
- Bai, Y.; Chen, Z.; Xie, J.; Li, C. Daily reservoir inflow forecasting using multiscale deep feature learning with hybrid models. J. Hydrol. 2016, 532, 193–206. [Google Scholar] [CrossRef]
- Karagiannopoulos, M.; Anyfantis, D.; Kotsiantis, S.B.; Pintelas, P.E. Feature Selection for Regression Problems; Educational Software Development Laboratory, Department of Mathematics, University of Patras: Patras, Greece, 2007; pp. 20–22. [Google Scholar]
- Zhao, M.; Fu, C.; Ji, L.; Tang, K.; Zhou, M. Feature selection and parameter optimization for support vector machines: A new approach based on genetic algorithm with feature chromosomes. Expert Syst. Appl. 2011, 38, 5197–5204. [Google Scholar] [CrossRef]
- Hall, M.A. Correlation Based Feature Selection for Discrete and Numeric Class Machine Learning; University of Waikato: Hamilton, New Zealand, 2000. [Google Scholar]
- Alquraish, M.M.; Abuhasel, K.A.; Alqahtani, A.S.; Khadr, M. A comparative analysis of hidden markov model, hybrid support vector machines, and hybrid artificial neural fuzzy inference system in reservoir inflow forecasting (Case study: The king fahd dam, saudi arabia). Water 2021, 13, 1236. [Google Scholar] [CrossRef]
- Lima, C.H.R.; Lall, U. Climate informed monthly streamflow forecasts for the Brazilian hydropower network using a periodic ridge regression model. J. Hydrol. 2010, 380, 438–449. [Google Scholar] [CrossRef]
- Paper, C.; Cheng, H.; Scripps, J. Multistep-Ahead Time Series Prediction. Lect. Notes Comput. Sci. 2006, 765–774. [Google Scholar] [CrossRef]
- Pal, I.; Tularug, P.; Jana, S.K.; Pal, D.K. Risk assessment and reduction measures in landslide and flash flood-prone areas: A case of Southern Thailand (Nakhon Si Thammarat Province). In Integrating Disaster Science and Management: Global Case Studies in Mitigation and Recovery; Samui, P., Kim, D., Ghosh, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2018; pp. 295–308. ISBN 9780128120576. [Google Scholar]
- Langkulsen, U.; Rwodzi, D.T.; Cheewinsiriwat, P.; Nakhapakorn, K.; Moses, C. Socio-Economic Resilience to Floods in Coastal Areas of Thailand. Int. J. Environ. Res. Public Health 2022, 19, 7316. [Google Scholar] [CrossRef] [PubMed]
- The World Bank Group Thailand Climate Risk Country Profile. 2021. Available online: https://openknowledge.worldbank.org/handle/10986/36368 (accessed on 1 August 2022).
- Kotu, V.; Deshpande, B. Predictive Analytics and Data Mining Concepts and Practice with RapidMiner; Elliot, S., Ed.; Elsevier: Amsterdam, The Netherlands, 2015; ISBN 9780128014608. [Google Scholar]
- Kelleher, J.D.; Namee, B.; Mac D’Arcy, A. Fundamentals of Machine Learning for Predictive Data Analytics Algorithms, Worked Examples, and Case Studies; The MIT Press: London, England, 2015; ISBN 9780262029445. [Google Scholar]
- Awad, M.; Khanna, R. Efficient Learning Machines Theories, Concepts, and Applications for Engineers and System Designners; Apress: New York, NY, USA, 2015. [Google Scholar]
- Zhang, D.; Lin, J.; Peng, Q.; Wang, D.; Yang, T.; Sorooshian, S.; Liu, X.; Zhuang, J. Modeling and simulating of reservoir operation using the artificial neural network, support vector regression, deep learning algorithm. J. Hydrol. 2018, 565, 720–736. [Google Scholar] [CrossRef] [Green Version]
- Thomas, S.; Pillai, G.N.; Pal, K. Prediction of peak ground acceleration using ϵ-SVR, ν-SVR and Ls-SVR algorithm. Geomat. Nat. Hazards Risk 2017, 8, 177–193. [Google Scholar] [CrossRef] [Green Version]
- Neapolitan, R.E.; Neapolitan, R.E. Neural Networks and Deep Learning; Springer: Berlin/Heidelberg, Germany, 2018; ISBN 9783319944623. [Google Scholar]
- Swamynathan, M. Mastering Machine Learning with Python in Six Steps; Apress: New York, NY, USA, 2019; ISBN 9781484228654. [Google Scholar]
- Tyralis, H.; Papacharalampous, G.; Langousis, A. A Brief Review of Random Forests for Water Scientists and Practitioners and Their Recent History in Water Resources. Water 2019, 11, 910. [Google Scholar] [CrossRef] [Green Version]
- Noori, R.; Karbassi, A.R.; Moghaddamnia, A.; Han, D.; Zokaei-Ashtiani, M.H.; Farokhnia, A.; Gousheh, M.G. Assessment of input variables determination on the SVM model performance using PCA, Gamma test, and forward selection techniques for monthly stream flow prediction. J. Hydrol. 2011, 401, 177–189. [Google Scholar] [CrossRef]
- Valente, J.M.; Maldonado, S. SVR-FFS: A novel forward feature selection approach for high-frequency time series forecasting using support vector regression. Expert Syst. Appl. 2020, 160, 113729. [Google Scholar] [CrossRef]
- Chowdhury, M.Z.I.; Turin, T.C. Variable selection strategies and its importance in clinical prediction modelling. Fam. Med. Community Health 2020, 8, e000262. [Google Scholar] [CrossRef] [Green Version]
- Borboudakis, G.; Tsamardinos, I. Forward-backward selection with early dropping. J. Mach. Learn. Res. 2019, 20, 1–39. [Google Scholar]
- Nash, J.E.; Sutcliffe, J. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Hong, J.; Lee, S.; Bae, J.H.; Lee, J.; Park, W.J.; Lee, D.; Kim, J.; Lim, K.J. Development and evaluation of the combined machine learning models for the prediction of dam inflow. Water 2020, 12, 2927. [Google Scholar] [CrossRef]
- Bahrami, S. Global Ensemble Streamflow and Flood Modeling with Application of Large Data Analytics, Deep learning and GIS. Ph.D. Thesis, University of Nevada, Reno, NV, USA, 2019. [Google Scholar]
- Ditthakit, P.; Pinthong, S.; Salaeh, N.; Weekaew, J.; Thanh Tran, T.; Bao Pham, Q. Comparative study of machine learning methods and GR2M model for monthly runoff prediction. Ain Shams Eng. J. 2022, 2022, 101941. [Google Scholar] [CrossRef]
- Dehghani, M.; Salehi, S.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Ghamisi, P. Spatial Analysis of Seasonal Precipitation over Iran: Co-Variation with Climate Indices. ISPRS Int. J. Geo Inf. 2020, 9, 73. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Wang, H.; Lin, Y.; Jin, J.; Liu, W.; An, X. Reservoir inflow predicting model based on machine learning algorithm via multi-model fusion: A case study of Jinshuitan river basin. IET Cyber Syst. Robot. 2021, 3, 265–277. [Google Scholar] [CrossRef]



| Reference | ML Methods | Lead Time | CI | Parameter | Time Interval | ||||
|---|---|---|---|---|---|---|---|---|---|
| SVR/M | ANN | MLR | Hybrid | Other | |||||
| [19] | - | - | - | - | ARMA, ARIMA | - | - | reservoir inflow | monthly |
| [22] | SVM | 🗸 | - | GA-SVM | - | T + 1 | - | reservoir inflow | monthly |
| [9] | - | - | - | AR-ANN, ARX-ANN, AR-ANFIS, ARX-ANFIS, AR-RF, and ARX-RF | BE | T + 1, T + 2, …, T + 36 | NINO12, QBO, NTA, AMM 12, NINO4, AMO | reservoir inflow | monthly |
| [20] | SVM | 🗸 | - | - | BPN | T + 1, T + 2, …, T + 6 | - | rainfall, reservoir inflow | hourly |
| [6] | SVM | 🗸 | 🗸 | - | SMA, BMA | T + 1, T + 2, T + 3 | SOI, ENSO, SST | monthly | |
| [21] | SVR | 🗸 | - | RF | T + 1, T + 2 | SOI, Nino1+2, Nino3, Nino34, Nino4, ONI, MEI, PDO, WP, NAO, WHWP, TNI, AO, QBO, CENSO, EPO | inflow | daily | |
| [7] | - | 🗸 | - | - | CANFIS, ANFIS | T + 1, T + 2, …, T + 5 | - | inflow | monthly |
| [8] | SVR | - | - | - | RF | T + 1, T + 2, …, T + 12 | NINO1+2, ANOM1+2, NINO3, ANOM3, NINO4, ANOM4, NO3.4, ANOM3.4, SOI, DMI | inflow | monthly |
| Current Study | SVR | 🗸 | 🗸 | BE-ANN, BE-MLR, BE-SVR, GA-ANN, GA-MLR, GA-SVR | - | T + 3, T + 6, T + 9, T + 12 | NINO1+2, ANOM1+2, NINO3, ANOM3, NINO4, ANOM4, NO3.4, ANOM3.4, SOI, DMI | rainfall, reservoir inflow, reservoir storage | monthly |
| Data Used | Features (Monthly) | Types | Data Sources |
|---|---|---|---|
| Hydrological data | Reservoir inflow (Inf) | Input/Output | The Upper Pak Phanang Operation and Maintenance Project, Irrigation Office 15, Royal Irrigation Department (RID), Thailand |
| Rainfall (R) reservoir storage (S) | Input | ||
| Ocean indices | Dipole Mode Index (DMI) | Input | The Japan Agency for Marine-Earth Science and Technology (JAMSTEC) |
| Southern Oscillation Index (SOI) | Input | ||
| Sea surface temperature (SST) | NINO1+2, ANOM1+2, NINO3, ANOM3, NINO4, ANOM4, NO3.4, and ANOM3.4 | Input | The US National Oceanic and Atmospheric Administration (NOAA) |
| Data | Statistical Value | |||||
|---|---|---|---|---|---|---|
| Max | Min | Average | SD | Kurtosis | Skewness | |
| NINO1+2 | 27.53 | 18.57 | 22.89 | 2.33 | −1.17 | 0.15 |
| ANOM1+2 | 1.64 | −2.10 | −0.24 | 0.80 | −0.57 | 0.15 |
| NINO3 | 28.05 | 23.17 | 25.71 | 1.17 | −0.85 | −0.19 |
| ANOM3 | 1.53 | −1.81 | −0.17 | 0.70 | −0.38 | −0.05 |
| NINO4 | 29.88 | 26.43 | 28.49 | 0.82 | −0.55 | −0.62 |
| ANOM4 | 1.25 | −1.71 | −0.07 | 0.75 | −0.84 | −0.40 |
| NO3.4 | 28.43 | 24.65 | 26.85 | 0.93 | −0.57 | −0.52 |
| ANOM3.4 | 1.72 | −1.92 | −0.18 | 0.79 | −0.33 | −0.06 |
| SOI | 4.80 | −5.20 | 0.57 | 1.52 | 0.56 | 0.18 |
| DMI | 0.76 | −0.49 | 0.07 | 0.23 | 0.23 | 0.22 |
| R | 1017.40 | 0.00 | 172.71 | 164.86 | 7.25 | 2.27 |
| Inf | 38.93 | 0.00 | 6.59 | 6.26 | 7.28 | 2.26 |
| S | 34.58 | 0.00 | 5.87 | 5.59 | 7.25 | 2.27 |
| Methods | Feature Selection Techniques | Symbol |
|---|---|---|
| Multiple Linear Regression | - | MLR |
| Multiple Linear Regression | GA | GA-MLR |
| Multiple Linear Regression | BE | BE-MLR |
| Support Vector Regression | - | SVR |
| Support Vector Regression | GA | GA-SVR |
| Support Vector Regression | BE | BE-SVR |
| Artificial Neural Networks | ANN | |
| Artificial Neural Networks | GA | GA-ANN |
| Artificial Neural Networks | BE | BE-ANN |
| Methods | No. Selected Features | |||
|---|---|---|---|---|
| T + 3 | T + 6 | T + 9 | T + 12 | |
| ANN | 155 | 155 | 155 | 155 |
| GA-ANN | 70 | 67 | 59 | 71 |
| BE-ANN | 152 | 154 | 151 | 154 |
| MLR | 155 | 155 | 155 | 155 |
| GA-MLR | 154 | 154 | 154 | 154 |
| BE-MLR | 154 | 154 | 154 | 154 |
| SVR | 155 | 155 | 155 | 155 |
| GA-SVR | 82 | 90 | 72 | 79 |
| BE-SVR | 154 | 154 | 154 | 154 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Weekaew, J.; Ditthakit, P.; Pham, Q.B.; Kittiphattanabawon, N.; Linh, N.T.T. Comparative Study of Coupling Models of Feature Selection Methods and Machine Learning Techniques for Predicting Monthly Reservoir Inflow. Water 2022, 14, 4029. https://doi.org/10.3390/w14244029
Weekaew J, Ditthakit P, Pham QB, Kittiphattanabawon N, Linh NTT. Comparative Study of Coupling Models of Feature Selection Methods and Machine Learning Techniques for Predicting Monthly Reservoir Inflow. Water. 2022; 14(24):4029. https://doi.org/10.3390/w14244029
Chicago/Turabian StyleWeekaew, Jakkarin, Pakorn Ditthakit, Quoc Bao Pham, Nichnan Kittiphattanabawon, and Nguyen Thi Thuy Linh. 2022. "Comparative Study of Coupling Models of Feature Selection Methods and Machine Learning Techniques for Predicting Monthly Reservoir Inflow" Water 14, no. 24: 4029. https://doi.org/10.3390/w14244029






