Plain Stilling Basin Performance below 30° and 50° Inclined Smooth and Stepped Chutes

Abstract

Energy dissipators, such as stilling basins, are usually required at the toe of stepped chutes to achieve adequate and safe operation of the spillway. Stepped chute hydraulics has been extensively studied in last several decades, however, only limited knowledge is available on the stilling basin performance below stepped chutes. In particular, the effect of the chute slope remains unknown, despite being a central design issue. Therefore, an experimental campaign was performed using a 30° or 50° inclined smooth or stepped chute with an adjacent conventional plain stilling basin. The experimental results indicated that, within the stilling basin, the surface characteristics and the roller as well as hydraulic jump lengths are practically independent of the chute slope. This further strengthens the previous findings that stepped chutes require 17% longer dimensionless jump lengths and consequently stilling basin lengths. The experimental results also confirmed that stepped chutes generated increased extreme and fluctuating bottom pressure characteristics at the stilling basin entrance area. With increasing chute slope, the latter were found to significantly magnify. However, such increased magnitudes were not expected to provoke cavitation damage as stepped chute inflows induced bottom aeration at the basin entrance, irrespective of the chute slope.

1. Introduction

In recent decades, stepped spillways became one of the preferred options of flood releasing facilities implemented in dams. This is, among others, due to the development of the Roller Compacted Concrete (RCC) construction technique. The latter leads to reduced costs, increased energy dissipation along the stepped chute (compared to conventional smooth chutes) and consequently to smaller energy dissipation structures at the spillway end. Extensive research was conducted on stepped chute hydraulics and several guidelines [1,2,3,4] resulted, further giving confidence in implementing such flood releasing facilities.

In spite of having an increased energy dissipation rate along the chute (as compared to conventional smooth chutes), adequately sized energy dissipators however should be provided at the stepped chute end, given that they only provide partial energy dissipation of the conveyed flow. The dissipation is typically not sufficient for a safe release into the downstream river [5]. Stilling basins are usually implemented, primarily due to the diversity of flow conditions encountered at the stepped chute ends, making them efficient energy dissipation devices.

To date only few studies investigated stilling basin performance below stepped chutes and no comprehensive design guidelines for these structures exist. The majority of the conducted studies focused on tailwater requirements, mean invert pressures and energy dissipation in the plain and USBR type III stilling basins [6,7,8,9]. The dynamic pressures acting on the plain stilling basin invert were investigated in [5,10,11]. These studies showed that stepped chute inflows enhance dynamic pressures acting at the stilling basin begin. Using detailed measurements of the flow surface fluctuations along with dynamic pressure measurements at the invert, [5] revealed that up to 17% higher dimensionless stilling basin lengths are required below stepped chutes as compared to smooth chutes. The latter was further confirmed by [12], who studied internal macroscopic air-water flow properties of a plain stilling basin below smooth and stepped chutes. Moreover, they reported increased bottom air concentrations at the stilling basin entrance downstream of stepped chutes indicating that they were better protected against cavitation than stilling basins downstream of smooth chutes. All of the above-mentioned studies were typically performed for a single chute slope and, as such, the effect of the stepped chute slope on the stilling basin performance remains open.

The present paper reports a systematic experimental study on the effect of chute slope on the plain stilling basin performance downstream of smooth and stepped chutes. The experimental results on stilling basin performance below 30°degree stepped chutes reported in [5,12] are expanded herein by analyzing an additional set of experimental data collected in a similar plain stilling basin below 50° smooth and stepped chutes. The analysis on the effect of chute slope will primarily focus on flow surface, roller and jump lengths, bottom pressure and bottom air concentration characteristics along the stilling basin, given that they are the most relevant parameters for design.

2. Materials and Methods

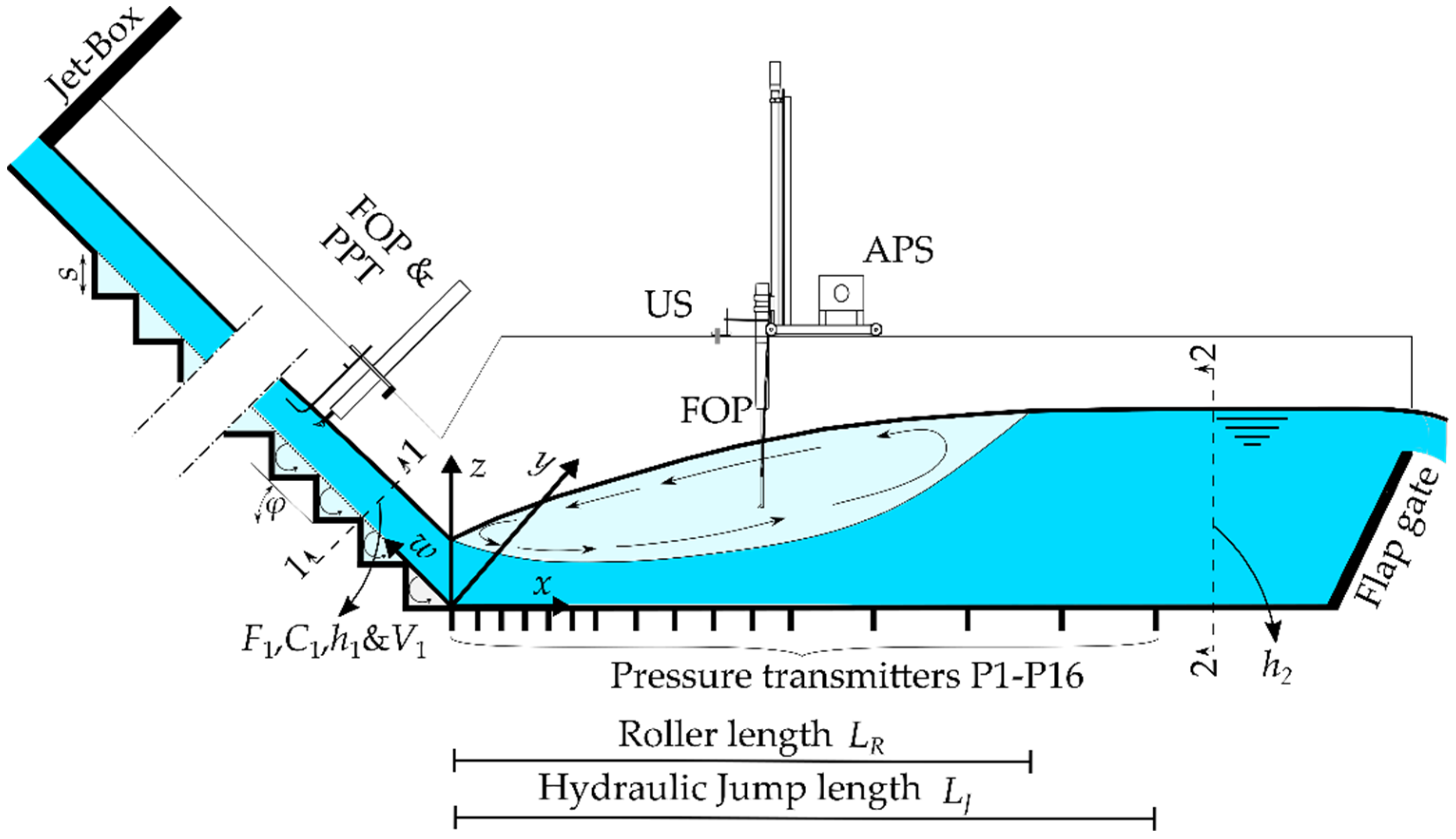
2.1. Physical Model

The spillway model, assembled at the Laboratory of Hydraulic Constructions (LCH) of the Ecole Polytechnique Fédérale de Lausanne (EPFL) in Switzerland, consisted of a: jet box at the chute inlet [13], prismatic smooth or stepped chute, and plain, prismatic, and horizontal stilling basin (Figure 1 and Figure 2).

The chute channel was 0.5 m wide and 0.6 m deep. Its slope φ was constant and adjustable. Two slopes were tested, namely φ = 30° and φ = 50° with 6.0 and 4.8 m long chutes, respectively. The chute consisted of aluminum (right) and glass (left) sidewalls allowing flow observation. Its bottom was equipped with s = 0.06 m or s = 0.03 m high steps made out of folded stainless-steel sheets. The total number of s = 0.06 m high steps was 45 for 30° and 60 and 50° stepped chutes. For the smaller step height s = 0.03 m the latter numbers were doubled. The smooth chutes were built by placing 0.01 m thick PVC plates on top of the steps.

As smooth chutes resulted in non-aerated flow along the entire chute, flow aeration at the chute end was provoked by: (a) increasing the bottom roughness by installing a 4.0 m (φ = 30°) or 3.5 m (φ = 50°) long, 0.496 m wide and 0.0015 m thick metal grid on the smooth chute bottom and (b) pre-aerating the flow by supplying air into the jet-box and conserving the metal grid.

The chute channel released the flow in a 6.0 m (φ = 30°) or 6.5 m (φ = 50°) long and 0.5 m wide stilling basin channel built with 0.015 m thick aluminum plates as bottom, and acrylic sidewalls for flow observation. The stilling basin end was equipped with a flap gate to control the tailwater and thus the position of the hydraulic jump.

2.2. Instrumentation

An electromagnetic flowmeter ABB FXE 4000 (Baden, Switzerland) of ±0.5% accuracy full scale (FS), installed on a DN300 supply conduit of the jet-box, was used to measure the discharge Q.

The stilling basin approach flow conditions, i.e., the air-water flow properties at the chute end centerline, were derived using a fiber-optical probe (FOP, Figure 1, RBI Instrumentation, Grenoble, France) featuring two optical fibers with inline tips. The air-water flow properties, namely the local air concentration C and velocity V, were measured in three profiles (some 15–20 points per profile) close to the chute end, perpendicular to its (pseudo) bottom. The measurements were conducted at w = 0.260, 0.460 and 0.660 m distance for the smooth chute ends, and at the step edges 2, 3 and 4 for φ = 30° (i.e., w = 0.240, 0.360 and 0.480 m) or 3, 4 and 5 (i.e., w = 0.235 0.313 0.391 m) for φ = 50° (Figure 1). The sampling duration was 30 s at a frequency of 1 MHz. In low air content flow regions (i.e., C < 0.03), the velocity measurements were completed with a Pitot–Prandtl tube (PPT, Figure 1) with a 0.003 m tip diameter, linked to a differential pressure transducer Keller PD-33X (Winterthur, Switzerland) with an accuracy of 0.02% FS. The sampling duration was 60 s at a frequency of 30 Hz.

The air-water flow properties in the stilling basin were measured with an additional FOP, fixed on an automatic positioning system (APS), moving with an accuracy of 0.0001 m (Figure 1). These measurements were performed perpendicular to the basin invert at 15 equidistant profiles (40 points per profile) along its centerline. The measurements ranged within 0.1 ≤ x/L_R ≤ 1.5, where L_R is the roller length derived from the flow depth measurements (Section 4.1.2). At each profile, the measurements were conducted from 0.006 m distance to the bottom up to the free surface. The sampling duration was 60 s per point at a frequency of 30 Hz.

Flow depths along the basin centerline were measured with an ultrasonic distance sensor (US) Baumer UNAM 30U9103/S14 (Frauenfeld, Switzerland) with an accuracy of ±0.0005 m (Figure 1). The US sensor was fixed on an APS. The flow depths were collected at 24 points, ranging between 0.2 m ≤ x ≤4.9 m, for 328 s per point at 12.5 Hz.

Fluctuating bottom pressures along the stilling basin centerline were measured using sixteen piezo-resistive transmitters with a flush diaphragm (Keller Series 25,Zurich, Switzerland) installed in the stilling basin invert (Figure 1). They had a measuring range of ±1 bar with an accuracy of 0.1% FS. Pressures were collected simultaneously during 393 s at a sampling rate of 1 kHz.

Further information about the instrumentation as well as the detailed measuring procedure can be found in [5,12,14].

3. Test Program and Inflow Conditions

Test program included eighteen runs with smooth and twelve with stepped chute inflows (

Table 1. Test program. SM = smooth chute; R = roughened with grid; PA = roughened with grid and pre-aeration; ST = stepped chute; s = step size.

Chute Configuration	Test Run	φ (°)	q (m2/s)	hc/s (-)	C1 (-)	h1 (m)	V1 (m/s)	α (-)	F1 (-)	R1 × 105 (-)	W1 (-)
SM + PA	1	30	0.198	/	0.32	0.031	6.47	1.09	11.8	1.98	133
	2	30	0.277	/	0.32	0.038	7.22	1.08	11.8	2.77	166
	3	30	0.358	/	0.32	0.046	7.79	1.09	11.6	3.58	196
SM + R	4	30	0.198	/	0.25	0.032	6.21	1.09	11.1	1.98	130
	5	30	0.277	/	0.26	0.040	6.86	1.08	10.9	2.77	162
	6	30	0.356	/	0.26	0.047	7.51	1.08	11.0	3.56	192
SM	7	30	0.198	/	0.16	0.029	6.95	1.08	13.1	1.98	137
	8	30	0.278	/	0.15	0.036	7.68	1.08	12.9	2.78	171
	9	30	0.356	/	0.15	0.042	6.38	1.08	13.0	3.56	202
ST s = 0.06 m	10	30	0.204	2.70	0.42	0.048	4.24	1.18	6.2	2.04	109
	11	30	0.284	3.36	0.42	0.058	4.91	1.18	6.5	2.84	138
	12	30	0.362	3.95	0.41	0.068	5.35	1.18	6.6	3.62	163
ST s = 0.03 m	13	30	0.204	5.40	0.41	0.047	4.34	1.19	6.4	2.04	110
	14	30	0.282	6.70	0.41	0.056	5.07	1.19	6.9	2.82	140
	15	30	0.364	7.94	0.41	0.066	5.54	1.18	6.9	3.64	166
SM + PA	16	50	0.198	/	0.37	0.028	7.16	1.08	13.8	1.98	140
	17	50	0.280	/	0.36	0.036	7.88	1.07	13.4	2.80	174
	18	50	0.358	/	0.35	0.043	8.38	1.07	13.0	3.58	203
SM + R	19	50	0.199	/	0.28	0.029	6.88	1.08	12.9	1.99	137
	20	50	0.278	/	0.29	0.038	7.41	1.07	12.2	2.78	168
	21	50	0.358	/	0.28	0.044	8.07	1.08	12.2	3.58	199
SM	22	50	0.199	/	0.16	0.026	7.61	1.08	15.0	1.99	144
	23	50	0.279	/	0.16	0.033	8.38	1.09	14.7	2.79	179
	24	50	0.356	/	0.15	0.040	8.99	1.08	14.4	3.56	210
ST s = 0.06 m	25	50	0.205	2.71	0.55	0.041	4.95	1.18	7.8	2.05	118
	26	50	0.284	3.36	0.53	0.051	5.52	1.19	7.8	2.84	147
	27	50	0.364	3.97	0.50	0.061	5.96	1.19	7.7	3.64	173
ST s = 0.03 m	28	50	0.205	5.51	0.50	0.040	5.10	1.18	8.1	2.05	120
	29	50	0.284	6.73	0.48	0.050	5.71	1.19	8.2	2.84	149
	30	50	0.364	7.94	0.46	0.060	6.08	1.19	7.9	3.64	174

). Based on the air-water flow measurements conducted at the chute end, the equivalent clear water flow parameters were deduced in order to quantify the approach flow conditions and subsequently use them for the stilling basin analysis. These included: (1) the inflow equivalent clear-water depth h₁ = (1 − C₁)y₉₀, (2) the inflow mean water velocity V₁ = q/h₁, (3) the inflow Froude number F₁ = V₁/(gh₁)^0.5, (4) the inflow Reynolds number R₁ = q/ν, (5) the inflow Weber number W₁ = (ρV₁²h₁)/σ, (6) critical flow depth h_{c =} (q²/h₁)^1/3, and (7) kinetic energy correction coefficient α, with C₁ as the mean (depth-averaged) air concentration at the inflow section as [15,16]:

$$C_1=\frac{1}{y_{90}}{\displaystyle {\int }_0^{y_{90}}C\mathrm{d}y}$$

(1)

where y₉₀ is the characteristic flow depth defined up to y(C = 0.90), g as gravitational acceleration, ν as the kinematic viscosity of water, ρ as the water density and σ as the air-water surface tension.

The reference section for the stilling basin analysis, i.e., inflow Section 1-1 (Figure 1), was the most downstream measured section near the chute end, namely step edge 3 (50°) or 2 (30°) for stepped chutes, and at w = 0.240 for smooth chutes (30° or 50°).

The smooth chute tests (Runs 1–9 and 16–24, Table 1) included two chute slopes of φ = 30° and 50°, each with three discharges of q ≈ 0.20, 0.28 and 0.36 m²/s. To assess the effect of approach flow aeration on the stilling basin performance, air concentrations C₁ at the inflow section were varied between 0.15 ≤ C₁ ≤0.37. The lowest values of C₁ ≈ 0.16 (Runs 6–9 and 22–24, Table 1) practically correspond to black-water at the stilling basin entrance. The latter was achieved for a smooth chute without bottom roughness or flow pre-aeration. Self-aeration of the flow upstream of the stilling basin entrance was provoked by roughening the bottom, resulting in C₁ ≈ 0.26 (φ = 30°, Runs 4–6, Table 1) and C₁ ≈ 0.28 (φ = 50°, Runs 19–21, Table 1). The highest approach flow aeration of C₁ ≈ 0.32 (φ = 30°, Runs 1–3, Table 1) and C₁ ≈ 0.36 (φ = 50°, Runs 16–18, Table 1) was achieved with a roughened smooth chute bottom combined with the jet-box pre-aeration. Detailed analysis of 30° smooth chute inflows is given in [5]. The air concentration profiles measured at the inflow section for 50° smooth chutes are shown in Figure 3a. They are compared with the advective diffusion model [17] and, similarly to 30° smooth chutes [5], showed a good agreement. The dimensionless velocity V/V₉₀ profiles, with V₉₀ as the velocity at y(C = 0.90), measured at the inflow section for 50° smooth chutes are shown in Figure 3b. They are approximated by:

$$\frac{V}{V_{90}}={\left(\frac{y}{y_{90}}\right)}^{1/N}\mathrm{for}y/y_{90}\le 1$$

(2)

with N = 12.9 and a coefficient of determination of R² = 0.92. The velocity profiles were almost similar to those measured for the 30° smooth chute inflows [5], as indicated by the similar exponent (N = 12.6 for the 30° smooth chutes).

The stepped chutes tests (Runs 10–15 and 25–30, Table 1) included two chute slopes of φ = 30° and 50° systematically investigated for three unit discharges q ≈ 0.20, 0.28 and 0.36 m²/s. They corresponded to skimming flow with 2.7 ≤ h_c/s ≤ 7.94. Quasi-uniform approach flow conditions were attained at the 30° stepped chute end with C₁ ≈ 0.41 [5]. Detailed analysis of 30° stepped chute approach flows is given in [5]. The air concentration profiles measured at the inflow section for 50° stepped chutes are shown in Figure 4a. The measured range of C₁ and the shape of the air concentration profiles for different tests at the inflow section (Figure 4a) suggest that quasi-uniform flow was not fully attained at the stepped chute end for all 50° stepped chutes tests. This is shown in Figure 5, where measured values of C₁ are compared to the quasi-uniform mean air concentration values C_u of [18] for the same chute slope and range of relative critical depths. For lower relative critical depths, i.e., h_c/s = 2.71 and 3.36 (Runs 25 and 26, Table 1), the flow conditions at the chute end were practically quasi-uniform with C₁/C_u ≈ 0.95 (Figure 5). On the other hand, for higher relative critical depths, i.e., for 3.97 ≤ h_c/s ≤ 7.94 (Runs 27–30, Table 1), gradually varied flow conditions were attained. The advection diffusion model [17] well described the measured air concentration profiles, excepted close to the pseudo-bottom (Figure 4a). The dimensionless velocity V/V₉₀ profiles at the inflow section (Figure 4b) follow Equation (2) with N = 4.9 (R² = 0.87). Similarly to the results of other studies on steep chutes (e.g., [18,19]), a lower N was obtained as compared to 30° stepped chutes (N = 5.5 [5]).

4. Results and Discussion

4.1. Free Surface Characteristics

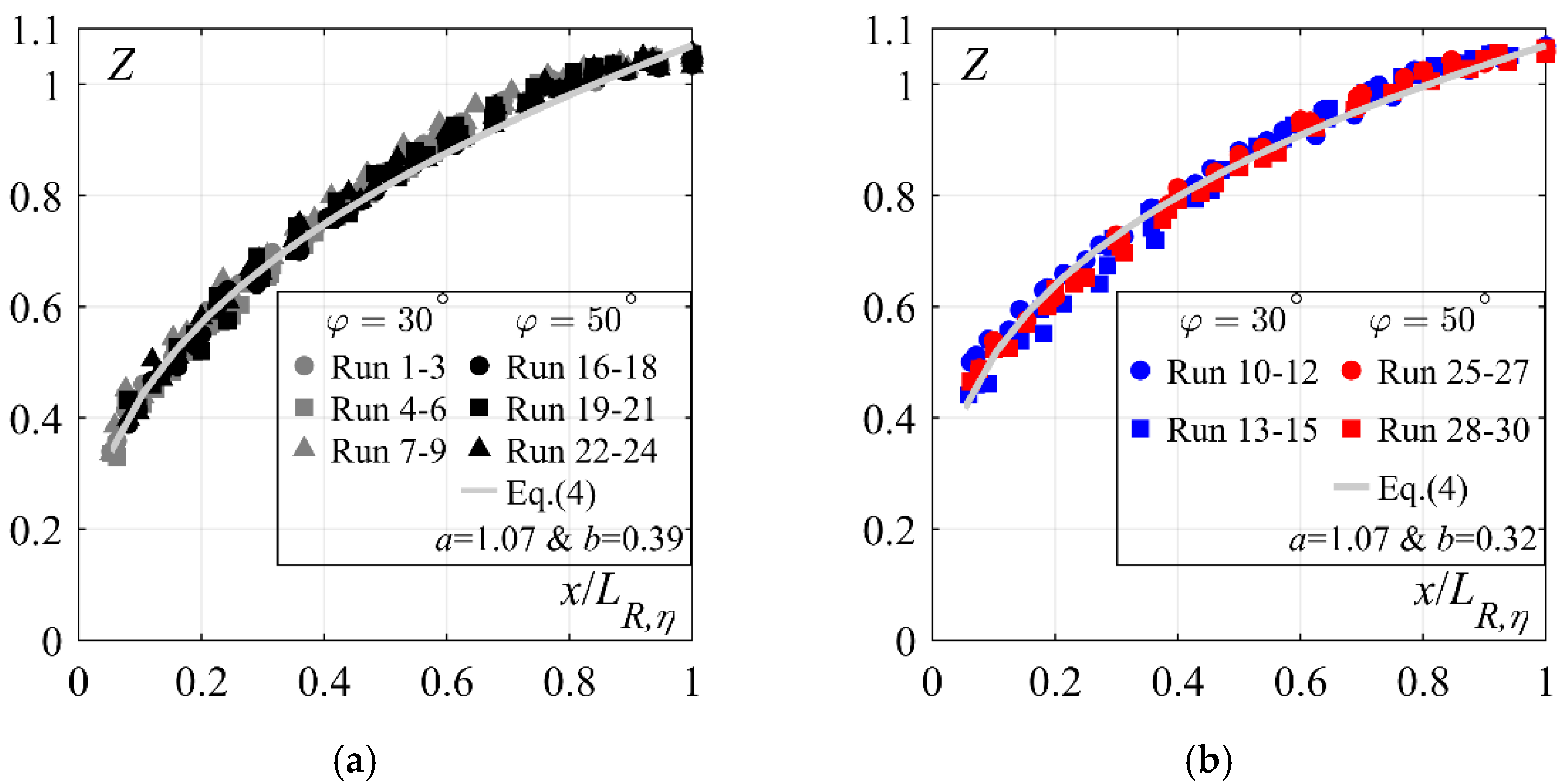
4.1.1. Mean Flow Depths

A typical streamwise development of the mean (time-averaged) flow depth η (from US measurements) along the stilling basin for 50° smooth (Run 22) and stepped (Run 25) chute inflows is shown in Figure 6a and compared to the mean flow depth development for 30° smooth (Run 7) and stepped (Run 10) inflows for similar unit discharge q, step size s and smooth chute inflow aeration C₁. The mean flow depths streamwise increased reaching a maximum in the “boiling” zone, herein defined as the roller length L_R,η (Figure 6a). Downstream of the roller end, i.e., at x > L_R,η, the flow depths decreased reaching a quasi-constant tailwater depth h₂. As one may expect, higher approach flow Froude numbers F₁ at the 50° smooth and stepped chute ends (as compared to 30° chutes) resulted in higher mean flow depths η and longer jump rollers L_R,η for quasi-similar unit discharge q.

In Figure 6b the measured sequent depth ratio h₂/h₁ is plotted against F₁, including the values for 30° and 50° chutes. They are compared to the basic solution of momentum conservation equation for classical hydraulic jumps:

$$h_2/h_1=0.5\left(\sqrt{1+8{\mathrm{F}}_1^2}-1\right)$$

(3)

showing a good agreement. Accordingly, for a given F₁, the sequent depth ratio is practically independent of the approach flow conditions (except F₁) or chute slope φ. These results further strengthen the conclusions [5] that using equivalent clear-water parameters at the chute end lead to a fairly accurate prediction of the sequent depth ratio using the classical momentum principle. As mentioned in [5], these results indicate that Equation (3) is applicable even if the flow enters at a significant angle with the horizontal, which would not be expected a priori, because Equation (3) was derived for horizontal approach flows. Nevertheless, these results are in line with observations [20] for smooth chute inflows.

The dimensionless mean flow depths Z = (η − h₁)/(h₂ − h₁) along the jump roller for 50° smooth and stepped chute approach flows are shown in Figure 7a,b, and compared to dimensionless flow depth data obtained with 30° smooth and stepped chute inflows. It can be seen that no major effect of the chute slope φ on the development of the mean flow depths Z occurred. Similarly to the 30° chutes [5], the dimensionless mean flow depths for 50° chutes are found to be higher below stepped chutes within the first half of the roller, i.e., x/L_R,η ≤ 0.5, as compared to smooth chutes, which is attributed to the relatively higher approach flow depth after stepped chutes. As such, the mean flow depths over the jump roller can be described with the self-similar function [5]:

$$Z=\frac{\eta -h_1}{h_2-h_1}=a{\left(\frac{x}{L_{R,\eta }}\right)}^b$$

(4)

with coefficients a = 1.07 and b = 0.39 for smooth chute approach flows and a = 1.07 and b = 0.32 for stepped chute approach flows, irrespective of the chute slope φ.

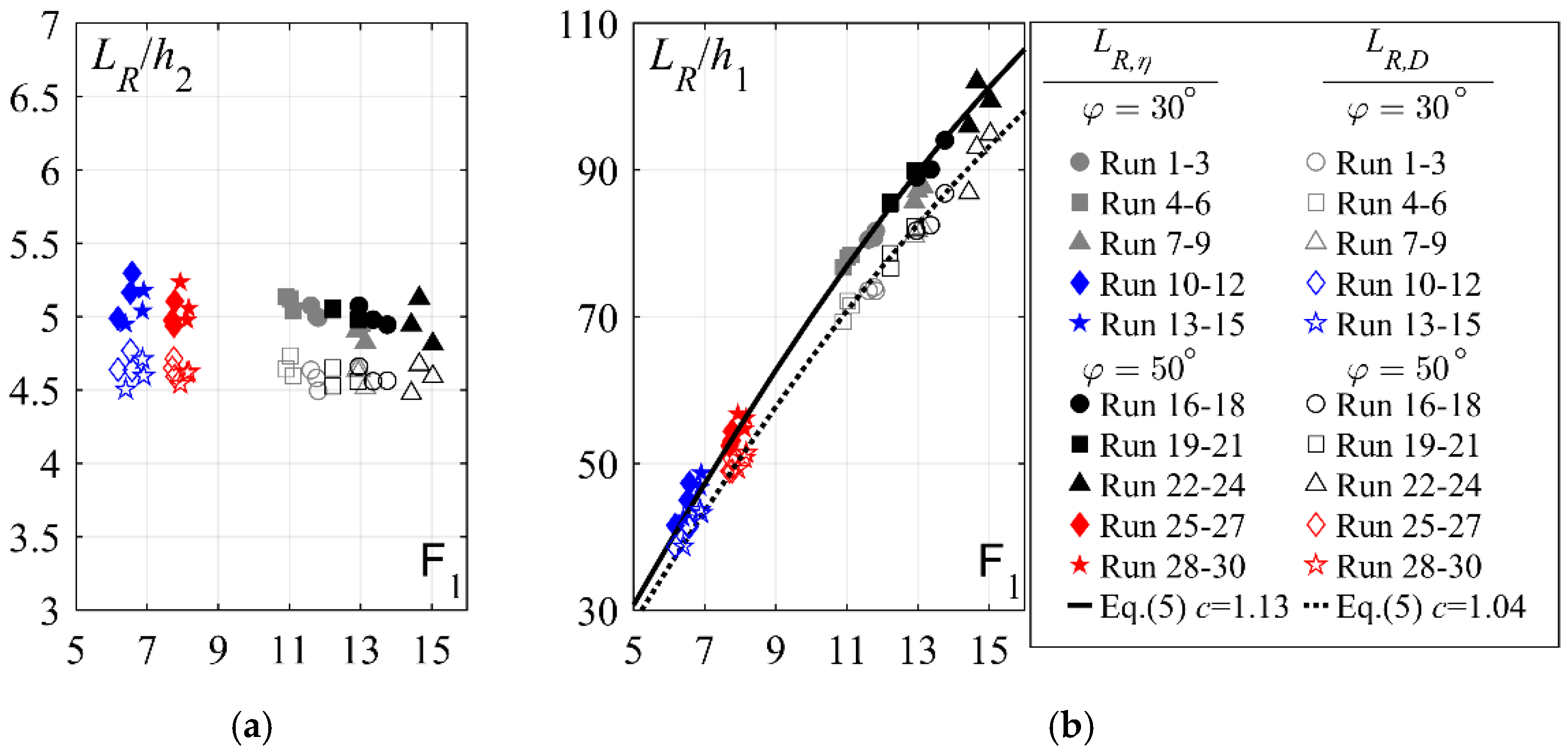
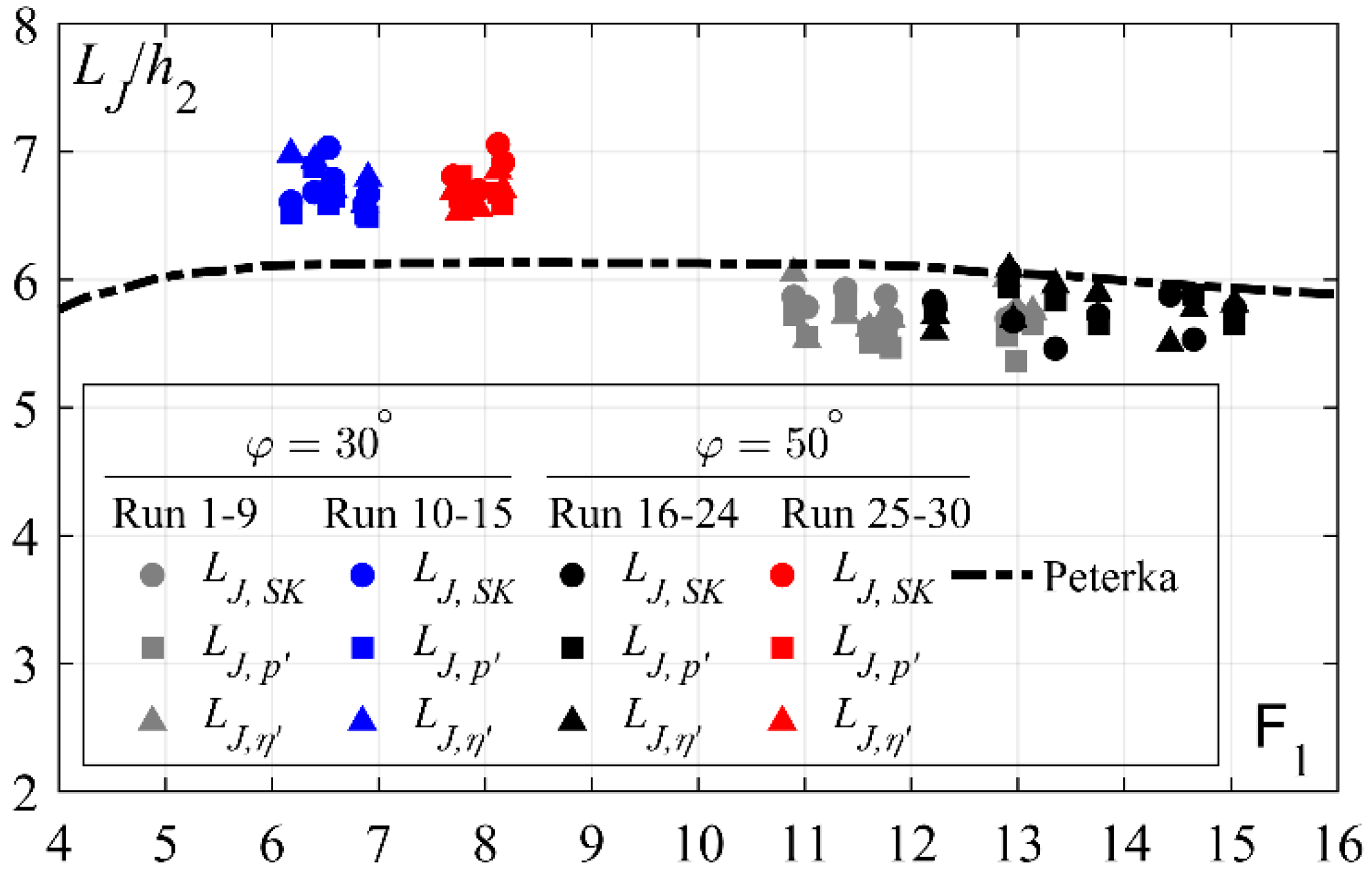
4.1.2. Roller Length

The dimensionless roller lengths L_R/h₂ for 50° (black symbols) smooth (Runs 16–24) and stepped (Runs 25–30) chute inflows, obtained from flow depth measurements L_R,η and visual observations L_R,D, are plotted against the F₁ in Figure 8a and compared to the dimensionless roller lengths obtained with 30° (gray symbols) smooth (Runs 1–9) and stepped (Runs 10–15) chute inflows. One can notice that the dimensionless roller lengths L_R,η/h₂ (full symbols) are practically independent of the approach flow conditions or chute slope φ with a typical value of L_R,η ≈ 5.0h₂. Similarly to the conclusions made in [5], the visually observed roller lengths (open symbols) are consistently shorter, with typical values of L_R,η ≈ 4.6h₂.

In Figure 8b the roller lengths are plotted in dimensionless form as L_R,η/h₁ and compared with the roller length prediction developed by [5]:

$$\frac{L_R}{h_1}=c\left(-12+160\tanh \left({\mathrm{F}}_1/20\right)\right)$$

(5)

with c = 1.13 and 1.04 for measured L_R,η and visually observed L_R,D roller lengths, respectively. As can be noticed, the agreement is good. The resulting coefficient of determination for measured L_R,η and visually observed L_R,D roller lengths are R² = 0.92 and R² = 0.99, respectively.

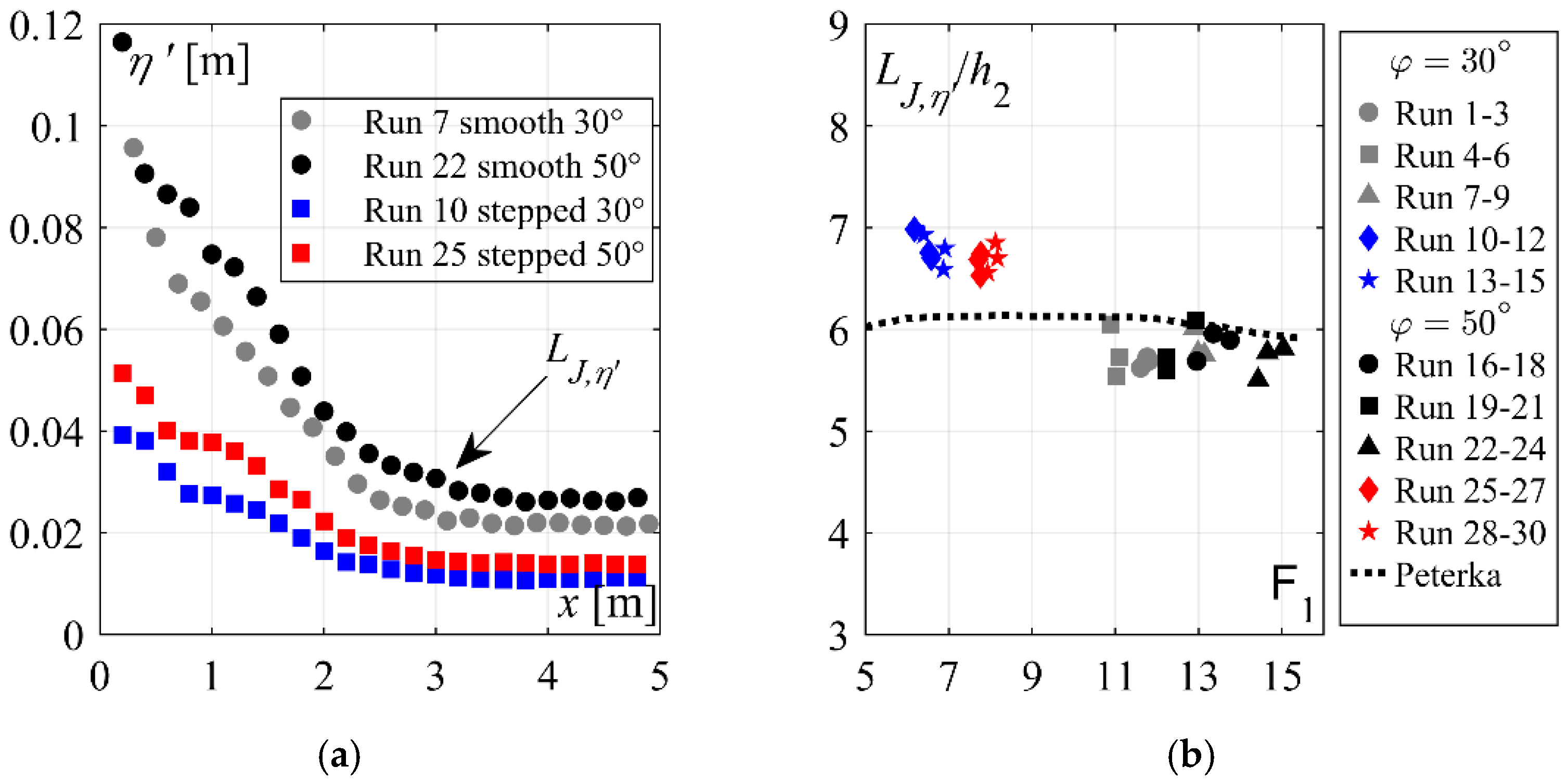
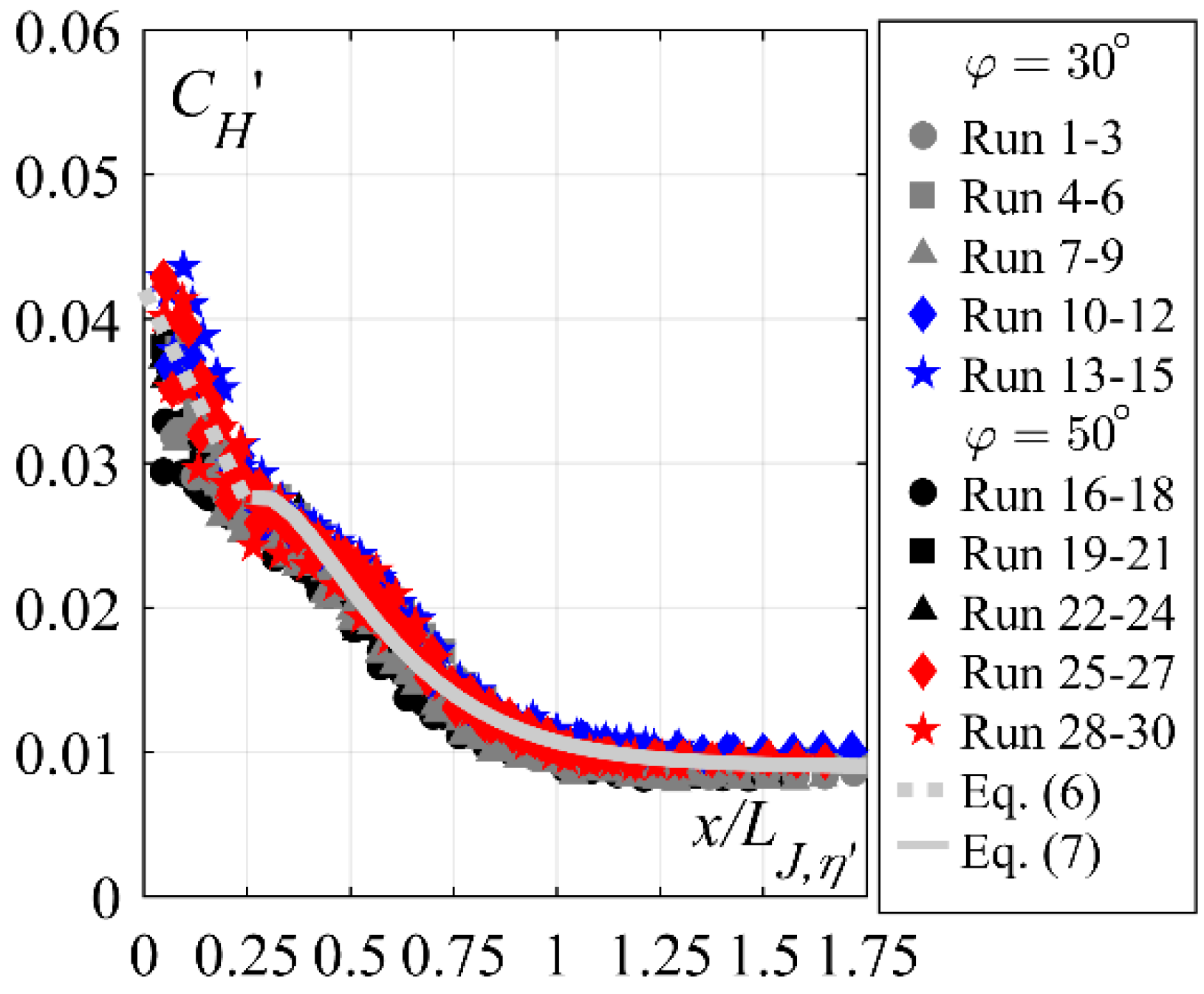
4.1.3. Flow Depth Fluctuations and Jump Length

A typical streamwise development of flow depth fluctuations η’ (characterized by the standard deviation of US readings) along the stilling basin for 50° smooth (Run 22) and stepped (Run 25) inflows are shown in Figure 9a, and compared to the flow depth fluctuation development for 30° sloping smooth (Run 7) and stepped (Run 10) approach flows for similar unit discharge q, step size s and smooth chute approach flow aeration C₁. Irrespective of the chute slope, the surface fluctuations along the hydraulic jump showed a monotonic decrease in the streamwise direction. As expected, higher approach F₁ at the 50° chute end, as compared to 30° chutes, resulted in higher flow depth fluctuations.

The hydraulic jump length with respect to the surface fluctuations L_J,η’ was deduced using the criteria introduced in [5], namely as the distance from the jump toe to the section where the surface fluctuations η’ are 1.1 times those measured in the tailwater zone. The resulting dimensionless jump lengths L_J,η’/h₂ downstream of 50° smooth and stepped chutes are plotted in Figure 9b against F₁, and compared with dimensionless jump length values obtained downstream of 30° smooth and stepped chutes and jump length prediction [20]. The jump lengths after smooth chutes were between 5.5 ≤ L_J,η’/h₂ ≤ 6.1, with an overall average value of L_J = 5.8h₂, in agreement with the recommendations of [20]. The hydraulic jumps occurring after stepped chutes consistently required an increased flow length x/h₂, namely 6.5 ≤ L_J,η’/h₂ ≤ 7.0 with an overall average value of L_J,η’/h₂ = 6.7h₂. The chute slope had no major effect on the dimensionless jump lengths L_J,η’/h₂. These results further support the conclusion [5] that hydraulic jumps formed below stepped chutes required a longer normalized distance x/h₂ than those formed below smooth chutes.

Figure 10 shows the streamwise development of the surface fluctuation coefficient C_H′ = η′/H_K with H_K = αV₁²/(2 g), plotted against the normalized streamwise coordinate x/L_J,η’ for all tests. The maximum fluctuation coefficients were observed in the vicinity of the jump toe, caused by the intense splashing [5]. Further downstream, the surface fluctuation coefficients tended to rapidly reduce, attaining quasi-constant values of C_H’ ≈ 0.01 in the tailwater zone. No major effect of approach flow conditions or chute slope φ on the streamwise development of C_H’ occurred. These results suggest that the surface fluctuations were mainly governed by the approach flow kinetic energy H_K. As such the streamwise development of C_H’ for 50° chutes can be described using the same equations developed for 30° chute inflows [5]:

$$C_H\prime =-0.059x/L_{J,\eta \prime }+0.042\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}0<x/L_{J,\eta \prime }\le 0.25$$

(6)

$$C_H\prime =1.009-\tanh {(2.8x/L_{J,\eta \prime })}^{0.26x/L_{J,\eta \prime }-0.028}x/L_{J,\eta \prime }>0.25$$

(7)

with R² = 0.57 and 0.97 for Equations (6) and (7), respectively.

4.2. Bottom Pressure Characteristics

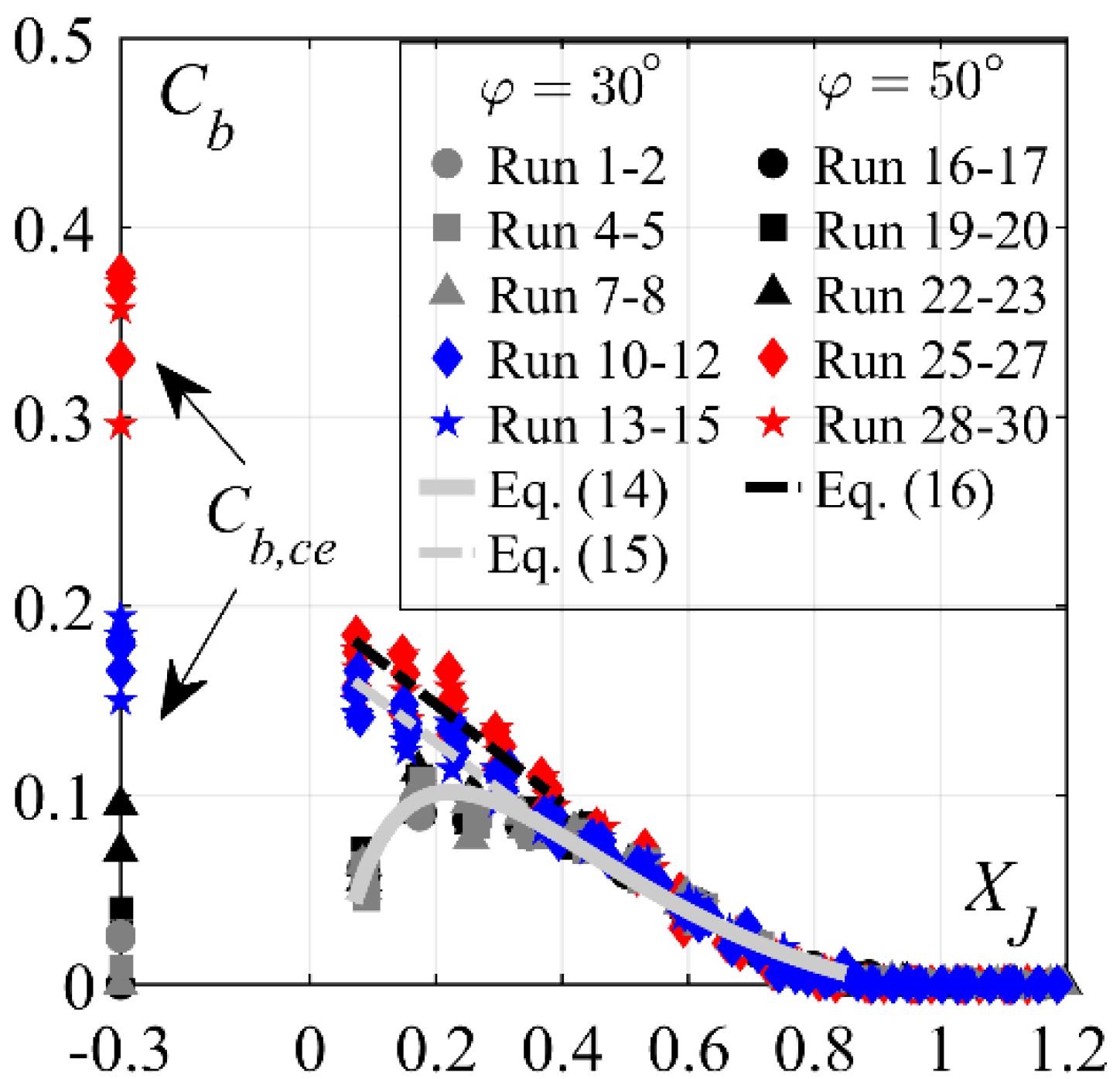
4.2.1. Streamwise Pressure Distribution and Jump Length

Based on the simultaneous pressure measurements conducted at 16 points (Figure 1), the dynamic pressure parameters used for assessment of hydrodynamic loads acting on the stilling basin invert [5] were derived. These include: (1) time-averaged pressure p_m, (2) fluctuating pressure characterized by standard deviation p’, (3) extreme maximum pressure p_max and corresponding 99.9th percentile p_99.9, (4) extreme minimum pressure p_min and corresponding 0.1th percentile p_0.1, (5) skewness as $S={{\displaystyle \sum \left(p_i-p_m\right)}}^3/\left(n{\left(p\prime \right)}^{-3}\right)$ where p_i is the pressure at a given instant and n is the number of samples, and (6) excess kurtosis defined as $K={{\displaystyle \sum \left(p_i-p_m\right)}}^4/\left(n{\left(p\prime \right)}^{-4}\right)-3$ A typical streamwise bottom pressure development for 50° chutes is shown in Figure 11 (Run 22, smooth chute).

Based on criteria established in [5], the hydraulic jump lengths L_J with respect to bottom pressures L_J,p′ and L_J,SK were derived, namely as: (1) L_J,p′ distance from the jump toe to the section where pressure fluctuations p′ are 1.1 times those measured in the tailwater zone, and (2) L_J,SK as a distance from the jump toe to the section where the pressure distribution followed a normal probability density function with skewness S and excess kurtosis K tending to zero (Figure 11b). The resulting jump lengths are plotted as L_J/h₂ in Figure 12 against F₁, along with jump lengths obtained with flow depth measurements L_J,η′/h₂ (Figure 9). The pressure measurements indicated a similar range of dimensionless jump lengths as the flow depth measurements. The overall average values for smooth and stepped chutes were L_J/h₂ = 5.8h₂ and L_J/h₂ = 6.7h₂, respectively. Moreover, if comparing the dimensionless jump lengths downstream of 30° and 50° chutes (Figure 12) it became noticeable that no major effect of the chute slope φ on the dimensionless jump length occurred. These results show that hydraulic jumps initiated below stepped chutes required an increased length x/h₂, as compared to those below smooth chutes.

To describe and conduct a comparative analysis of streamwise pressure distributions, the following pressure coefficients are introduced [5]: (1) mean coefficient P_m = (p_m − h₁)/(h₂ − h₁), (2) fluctuation coefficient C_P’ = p’H_k⁻¹, (3) extreme maximum coefficient C_P^max = (p_max − p_m)H_k⁻¹, (4), 99.9th percentile coefficient C_P^99.9 = (p_99.9 − p_m)H_k⁻¹, (5) extreme minimum coefficient C_P^min = (p_m − p_min)H_k⁻¹ and (6) 0.1th percentile coefficient C_P^0.1 = (p_m − p_0.1)H_k⁻¹. In Figure 13a–h, the streamwise development of bottom pressure coefficients P_m, C_P’, C_P^max, C_P^99.9, C_P^min, C_P^0.1, S and K downstream of 50° smooth and stepped chutes are plotted against the normalized streamwise coordinate X_J = x/L_J. The latter bottom pressure coefficient developments for 30° chutes can be found in [5]. In following sub-chapters, the effect of chute slope on the streamwise development of bottom pressure coefficients is detailed.

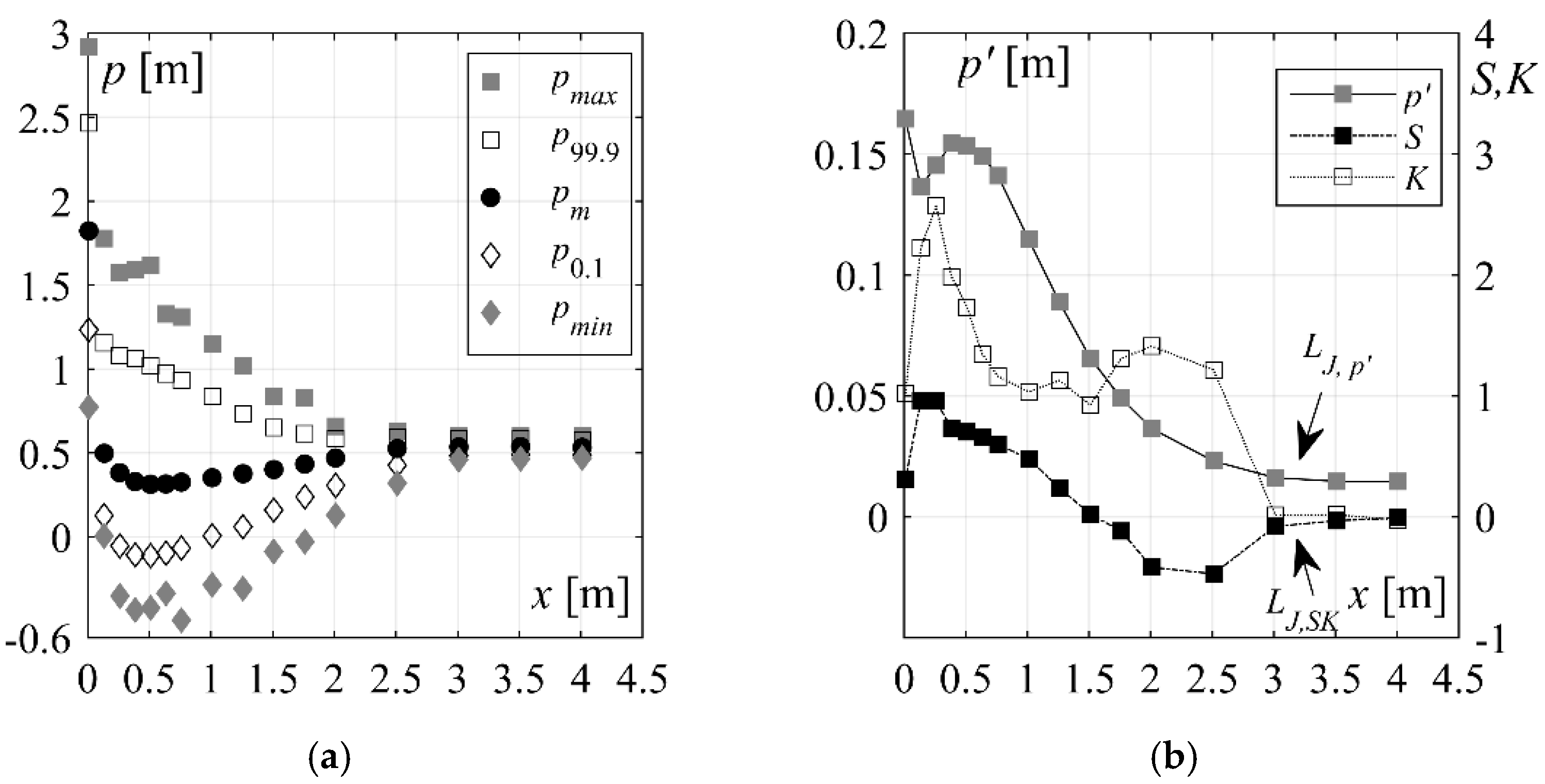
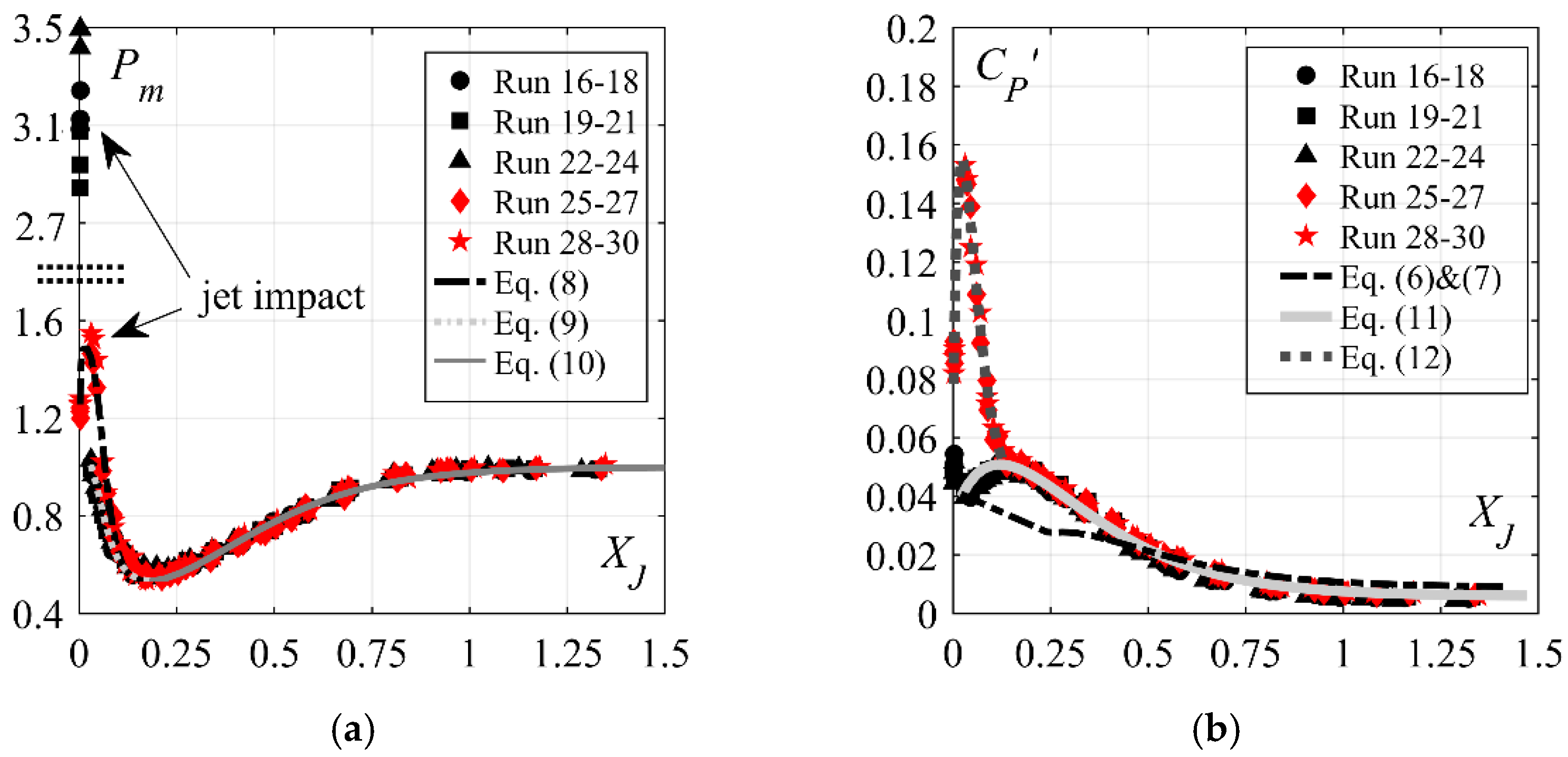
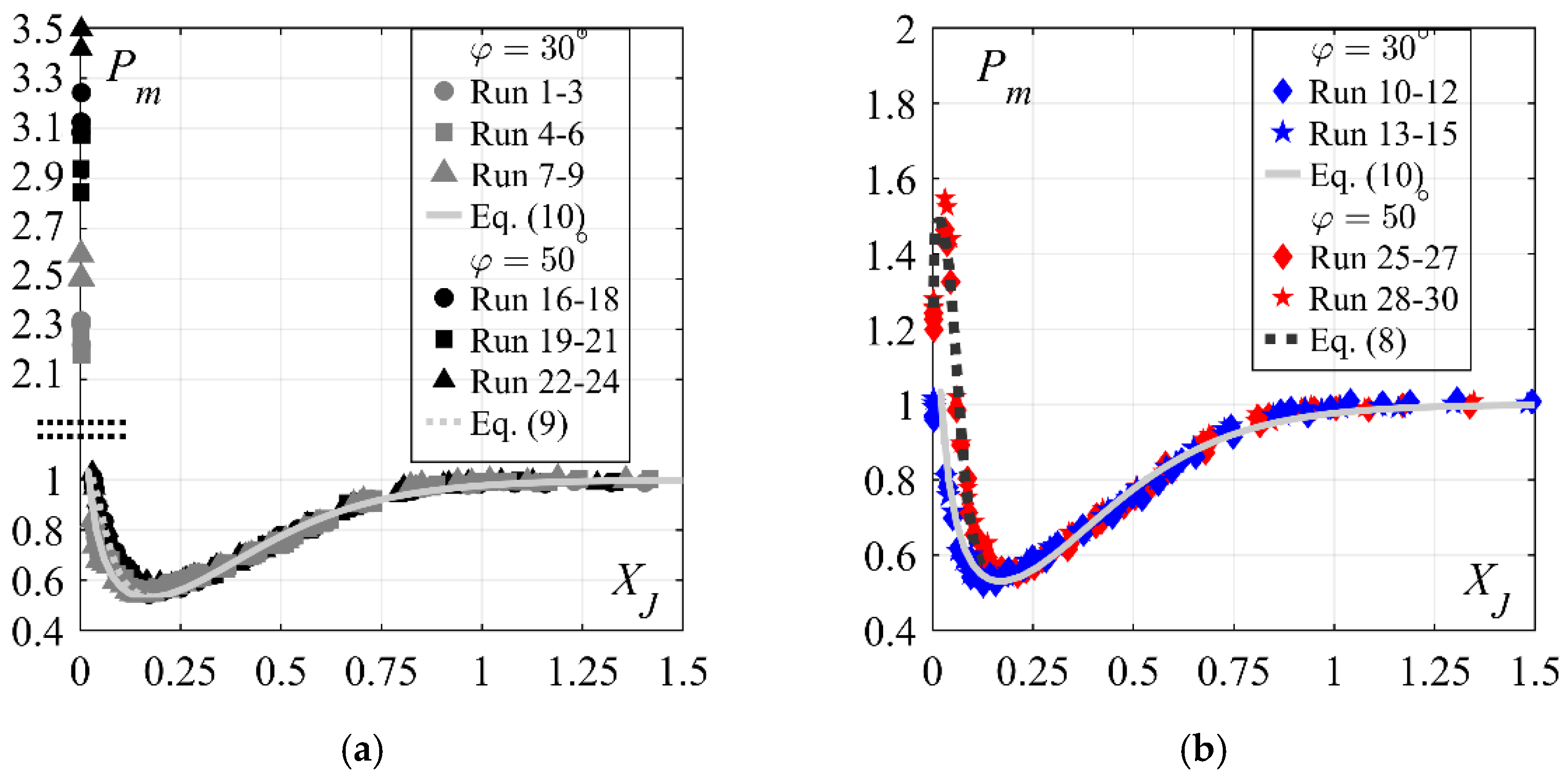
4.2.2. Streamwise Distribution of Mean Pressure

The streamwise development of dimensionless mean pressure P_m downstream of the 50° chutes, similarly to the 30° chutes [5], indicated the following flow zones (Figure 13a):

• deflection zone along 0 ≤ X_J ≤ 0.18, characterized by increased mean pressures due to the impact and flow curvature
• transition zone along 0.18 < X_J < 1, where mean pressures qualitatively follow the flow depths, and
• tailwater zone along X_J ≥ 1, where mean pressures are quasi-hydrostatic.

The development of the mean pressure coefficients P_m for 30° and 50° smooth and stepped chutes are compared in Figure 14a,b, respectively.

Comparing the mean pressure development for smooth chute inflows (Figure 14a), a clear effect of chute slope φ within the flow deflection zone was visible. At the flow deflection point, i.e., at the jump toe X_J ≈ 0, up to 60% higher dimensionless mean pressures P_m are observed downstream of 50° smooth chutes, as compared to those downstream of 30° smooth chutes.

Further downstream, within 0 ≤ X_J ≤ 0.18, the mean pressure with 50° smooth chutes decreases in a similar manner as on 30° smooth chutes, however, with slightly higher magnitudes caused by stronger flow curvature due to the more abrupt slope change. The local minimum below 50° smooth chutes is observed at X_J ≈ 0.18, where flow curvature greatly reduced, and beyond which the dimensionless mean pressure magnitudes coincide with those of 30° smooth chutes along the remaining part of the stilling basin, i.e., in the transition and tailwater zone. The influence reach of the flow curvature was thus somewhat longer below 50° smooth chutes, i.e., 0 ≤ X_J ≤ 0.18, as compared to those after 30° smooth chutes, i.e., 0 ≤ X_J ≤0.15 [5].

The effect of chute slope within the flow deflection zone was even more pronounced downstream of stepped chute inflows (Figure 14b). The streamwise position of the maximum mean pressures downstream of 50° stepped chutes was observed further downstream, i.e., at X_J ≈ 0.04, as compared to 30° stepped chute inflows at X_J ≈ 0. The maximum P_m magnitudes downstream of 50° stepped chutes were up to 60% higher than maximum P_m magnitudes observed downstream of 30° stepped chutes or two times higher for the similar streamwise position, i.e., X_J ≈ 0.04.

The relative downstream shift of the maximum mean pressure position after 50° stepped chute can be explained with the smaller impact area of the internal jet (typical of stepped chute flows) close to the jump toe. As observed by [18], the impact region of the internal jet decreased with increasing chute slope. Therefore, for the 30° chutes, a major portion of the incoming flow was “deflected” towards the inner part of the last step cavity (i.e., upstream of the first pressure sensor P1, Figure 1) resulting in a concentrated flow impact at the jump toe, i.e., at X_J ≈ 0. For the 50° chutes, only a small portion of the flow impacted near the jump toe (i.e., fictitious step edge) resulting in the more concentrated impact further downstream, i.e., at X_J ≈ 0.04. Downstream of the flow deflection point, within 0.04 < X_J ≤ 0.18, the mean pressures below 50° stepped chutes decreased in a similar manner as below 30° chutes, however with higher magnitudes caused by stronger flow curvature (Figure 14b). The mean pressure coefficients reached a local minimum at X_J ≈ 0.18, after which they coincide with 30° stepped chute inflows along the entire remaining stilling basin reach.

Comparing the maximum mean pressures coefficients downstream of the 50° chute (i.e., at X_J ≈ 0 for smooth and X_J ≈ 0.04 for stepped chutes), one can notice up to 2.5 times higher magnitudes below smooth chute as compared to those below stepped chute (Figure 13a). As the mean pressure at this point was mainly governed by the approach flow kinetic energy [5], the mean pressure at the flow deflection point p_def was normalized with the approach flow kinetic energy H_K. The resulting mean pressure coefficients C_P^def = p_def/H_K are shown in Figure 15, along with C_P^def values for 30° chute. In case of the 50° chute, the mean pressures at the flow deflection point were, on average, 41% and 58% of the corresponding approach flow kinetic energy for smooth and stepped chutes. As detailed in [5], the higher magnitudes downstream of smooth chutes were caused by its lower approach flow depth, resulting in a more concentrated impact. Furthermore, the pressure coefficients C_P^def are approximately 20% higher below 50° smooth and stepped chutes, as compared to the corresponding ones for 30° chutes (Figure 15). This is clearly caused by the “sharper” angle of the flow impact.

As a result of a slightly shifted flow deflection point, the 50° stepped chute indicated slightly higher P_m magnitudes within 0.05 ≤ X_J < 0.12, as compared to 50° smooth chute (Figure 13a). Further downstream, i.e., X_J ≥ 0.12, the mean pressure coefficients were practically independent of the approach flow conditions. The pronounced mean pressures in the flow deflection zone below 50° stepped (R² = 0.97) and smooth (R² = 0.95) chutes can be described as (Figure 13a):

$$\hspace{1em}{P}_m=1.53-\tanh {(30X_J)}^{260X_J-0.15}\hspace{1em}\phi =50{°}_{}^{}{\mathrm{stepped}}_{}^{}\mathrm{chute}\hspace{1em}{X}_J\le 0.18$$

(8)

$$\hspace{1em}\hspace{1em}{P}_m=1.53-\tanh {(22X_J)}^{40X_J}\hspace{1em}\phi =50{°}_{}^{}{\mathrm{smooth}}_{}^{}\mathrm{chute}\hspace{1em}0.03\le X_J\le 0.18$$

(9)

Further downstream, in the transition and tailwater zones, the streamwise distribution of mean pressures for 50° sloping smooth and stepped chutes can be estimated using the same equation developed for 30° smooth and stepped chutes by [5] (Figure 13a):

$$P_m=\tanh {(3.1X_J)}^{5.9X_J-0.14}\hspace{1em}30°\le \phi \le 50{°}_{}^{}\mathrm{smooth}/\mathrm{stepped}\hspace{1em}{X}_J>0.18$$

(10)

Finally, no major effect of the step size s or the smooth chute inflow aeration C₁ on the streamwise mean pressure distribution occurred.

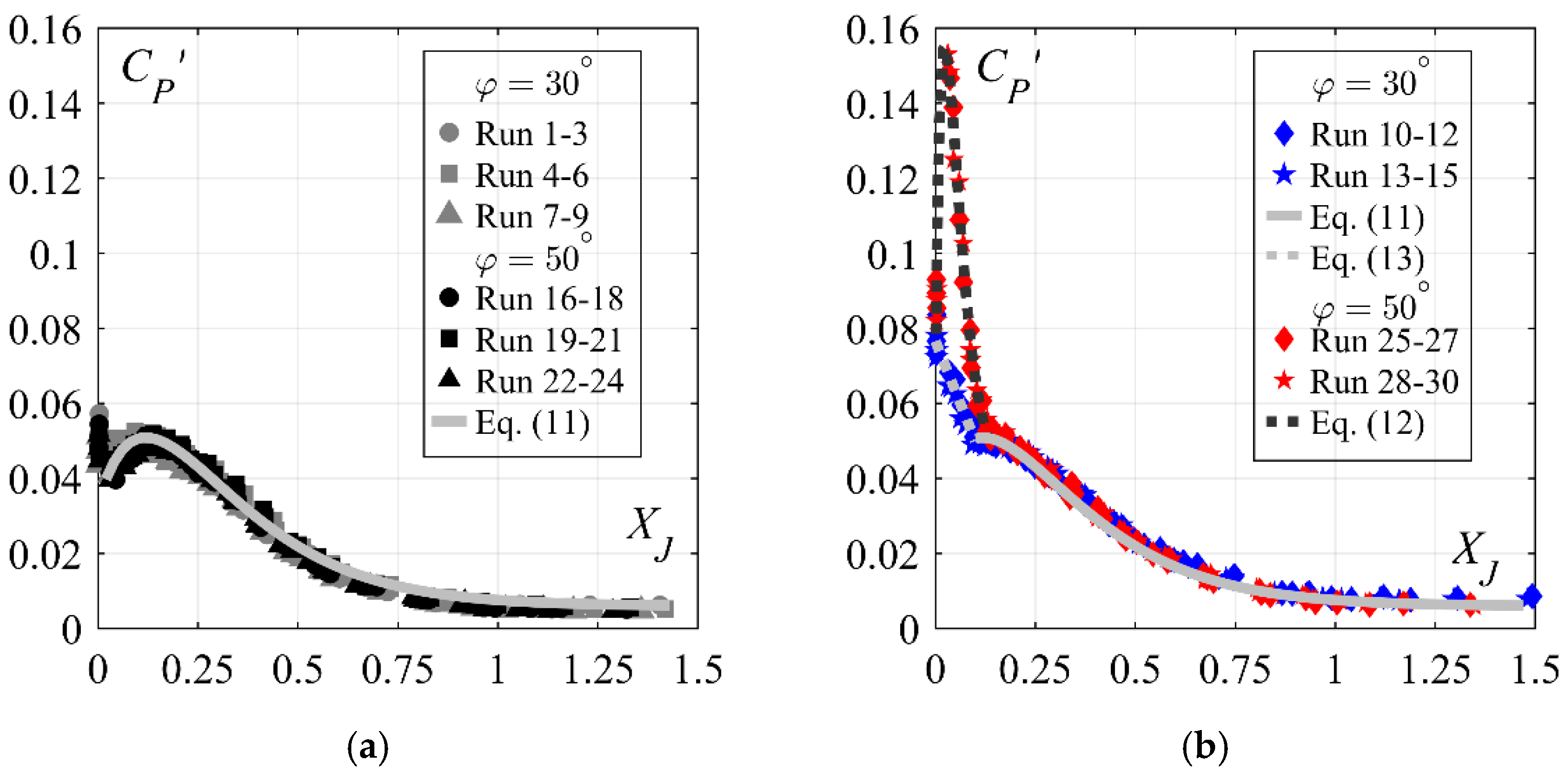
4.2.3. Streamwise Distribution of the Pressure Fluctuation

The 50° sloping smooth chute approach flows (Figure 13b) showed a typical streamwise pressure fluctuation C_P’ development (e.g., [21,22,23]). The pressure fluctuations increased downstream of the jump toe reaching maximum values of C_P’ ≈ 0.05 at X_J ≈ 0.12. Further downstream, they monotonically decreased towards quasi-constant tailwater magnitudes. Due to the flow deviation at the jump toe (X_J = 0), the pressure fluctuations reached or exceed the magnitudes observed at X_J ≈ 0.12. No major effect of approach flow aeration C₁ on the streamwise development of C_P’ occurred.

The streamwise development of the pressure fluctuation coefficients C_P’ for 50° and 30° smooth chutes are compared in Figure 16a. No considerable effect of the chute slope φ on the pressure fluctuation development occurred.

Comparing the pressure fluctuation development (Figure 13b), the effect of stepped chute approach flows becomes evident. At the jump toe, up to 40% higher pressure fluctuation coefficients could be observed, as compared to 50° smooth chute approach flows, reaching up to C_P’ = 0.09 (Figure 17). Downstream of the jump toe, the fluctuation magnitudes sharply increased reaching maximum values of C_P’ = 0.15 at X_J ≈ 0.04. These values are up to 3 times higher as compared to the maximum values observed for smooth chute approach flows (Figure 13b and Figure 17). To further illustrate the severeness of pressure fluctuations downstream of stepped chute at this location, the absolute values of the pressure fluctuations p′ are compared for smooth (Run 24) and stepped chute (Run 30) inflows in Figure 18 with similar unit discharge of q ≈ 0.360 m²/s. Despite the significantly higher inflow Froude number F₁ for the smooth chute inflow (F₁ ≈ 14), as compared to stepped chute inflow (F₁ ≈ 8), the absolute values of pressure fluctuations p′ downstream of stepped chute were about 50% higher at the flow deflection point, as compared to the maximum values observed with smooth chute approach flow (i.e., in the zone of maximum pressure fluctuations at X_J ≈ 0.12). This shows that pronounced pressure fluctuations downstream of stepped chute are caused by the higher turbulence levels of the approaching flow, as compared to smooth chute approach flows. Downstream of the flow deflection point, i.e., X_J > 0.04, the pressure fluctuation coefficients monotonically decreased up to X_J ≈ 0.13, after which they coincided with smooth chute approach flows magnitudes over the entire stilling basin reach (Figure 13b). No considerable effect of step size s occurred.

The streamwise development of C_P’ for 50° and 30° stepped chute approach flows are compared in Figure 16b. A major effect of the chute slope could be noticed. As a result of the relative downstream shift of the flow deflection point, the maximum pressure fluctuations for 50° stepped chutes occurred further downstream (X_J ≈ 0.04), as compared to the 30° chutes (X_J ≈ 0). At this point, up to 2 times higher C_P’ magnitudes were observed, as compared to those of 30° stepped chute at the flow deflection point (X_J ≈ 0) (Figure 16b and Figure 17). Apart from the flow deflection point, the 50° stepped chute tended to increase the pressure fluctuations at the jump toe as well, with up to 30% higher C_P’ magnitudes (Figure 16b and Figure 17). Downstream of the flow deflection point (X_J ≈ 0.04), as previously mentioned, the pressure fluctuations monotonically decreased and reached the 30° chute magnitudes at X_J ≈ 0.13, beyond which they coincided along the remaining downstream reach of the stilling basin.

The pressure C_P’ and surface fluctuation C_H′ are also compared in Figure 13b (only Equations (6) and (7) are included for clarity). As expected, the surface fluctuations were lower than the corresponding pressure fluctuations within the first half of the hydraulic jump, i.e., X_J < 0.5. As for the 30° chute inflows [5], they coincided at X_J ≈ 0.5. At this point, the skewness of the pressure readings reached negative values, indicating a detachment of the bottom jet flow [5] (Figure 13g). The skewness values attended minimal values at X_J ≈ 0.75, beyond which they tended towards zero in the tailwater zone.

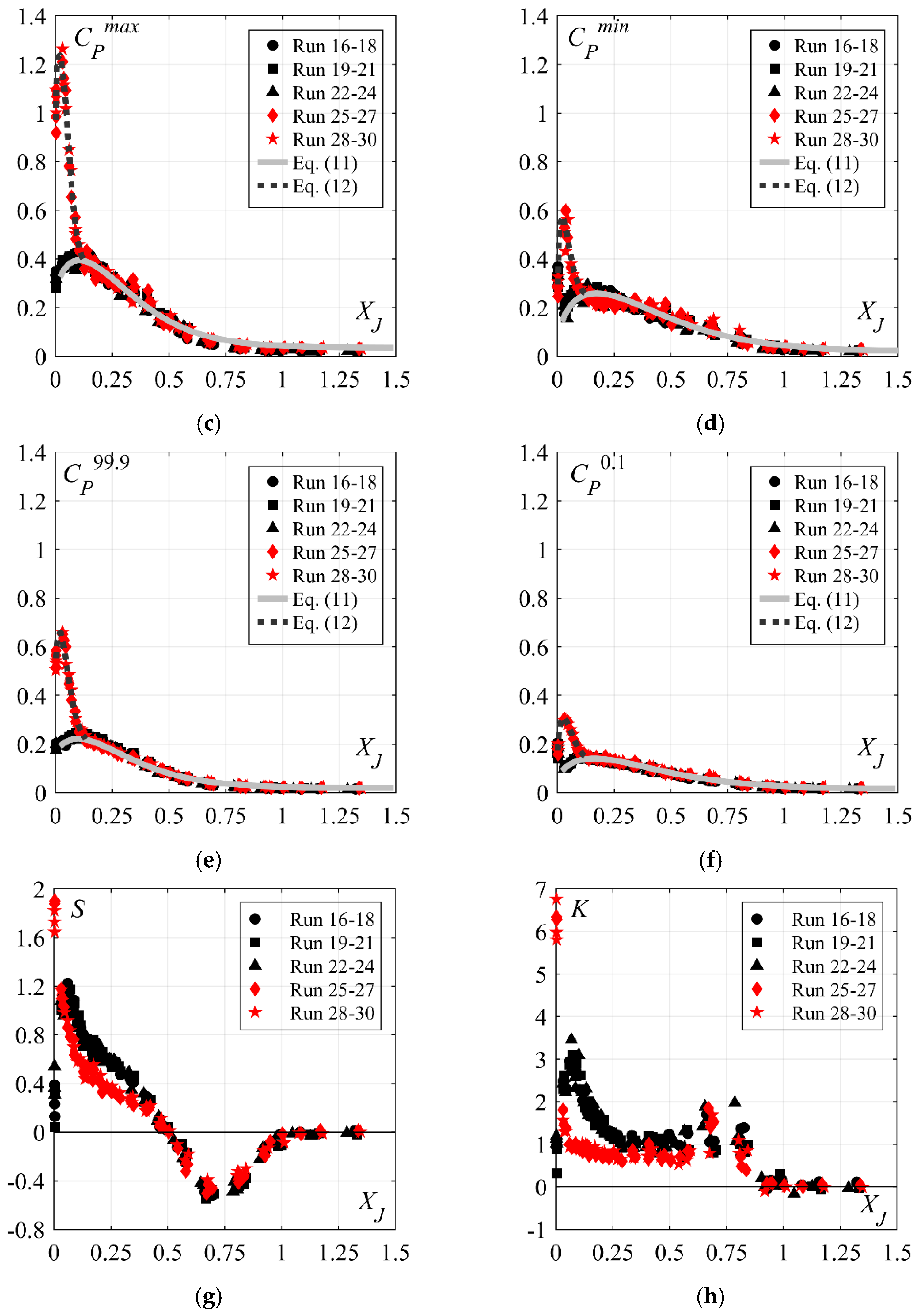
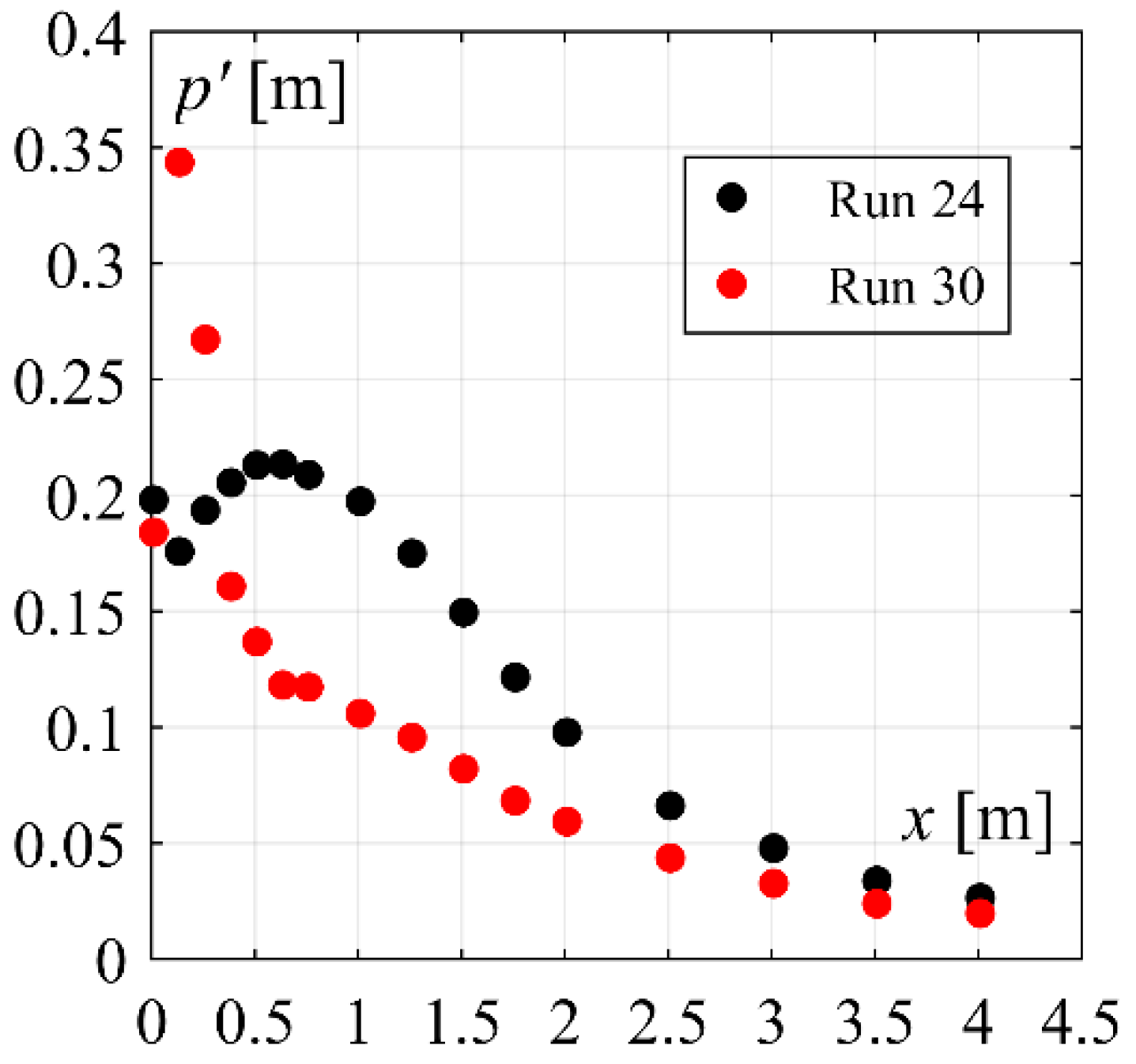
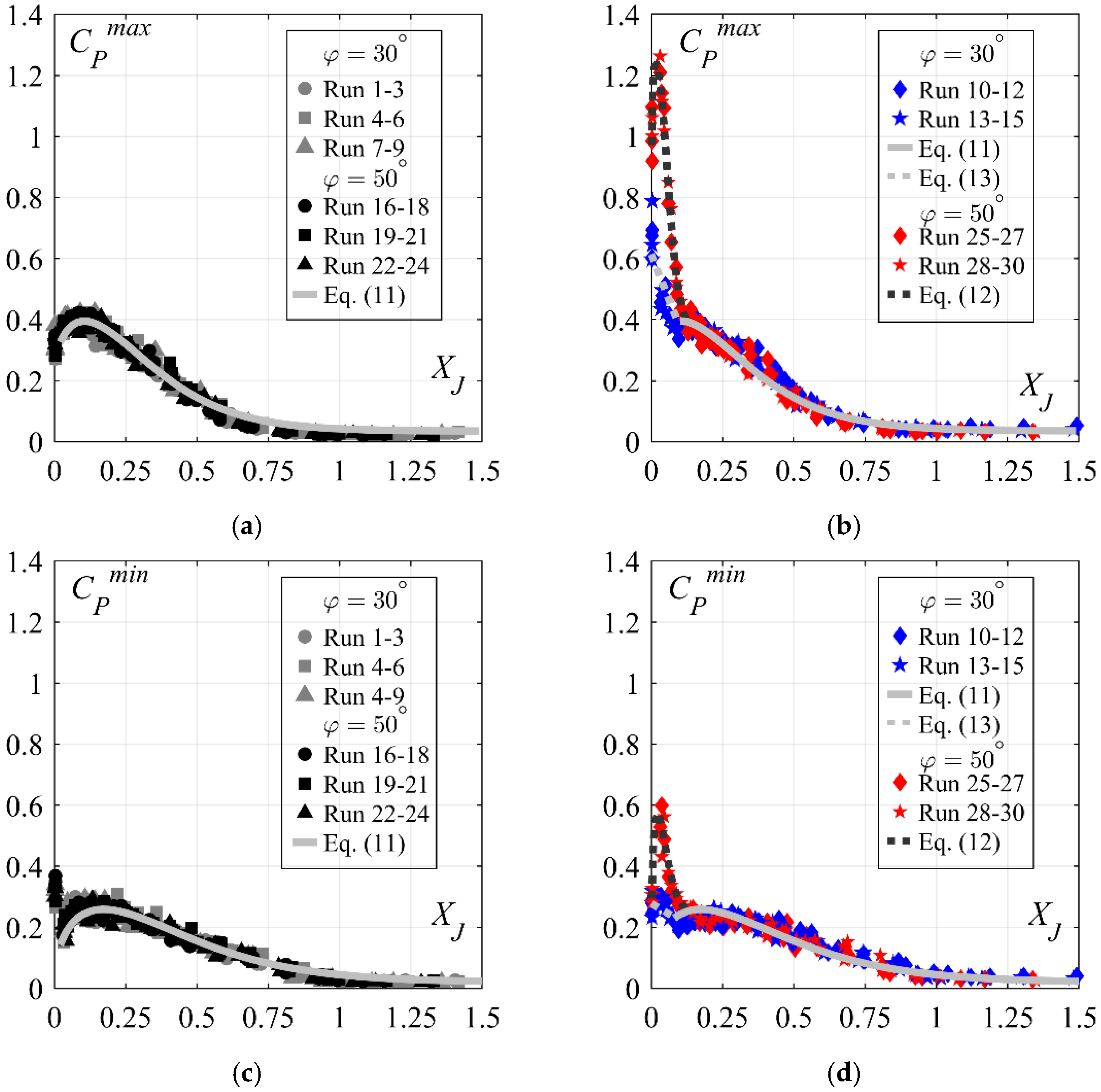
4.2.4. Streamwise Distribution of Extreme Pressures

The extreme pressure coefficients C_P^max and C_P^min downstream of 50° chute showed a similar streamwise distribution as the previously described pressure fluctuations (Figure 13c,d).

The 50° sloping smooth chute approach flows revealed an increase in extreme pressure coefficients downstream of the jump toe, reaching maximum magnitudes of C_P^max = 0.42 and C_P^min = 0.29 at X_J ≈ 0.12 and X_J ≈ 0.18, respectively. Further downstream, they decreased attaining quasi-constant tailwater magnitudes. As a result of the flow deflection, the extreme pressure coefficients were of the same order of magnitudes at the jump toe, i.e., C_P^max ≈ C_P^min ≈0.32 (Figure 13c and Figure 20). In Figure 19a,c, the streamwise development of extreme pressure coefficients for 30° and 50° smooth chutes are compared, showing that the chute slope φ had no considerable effect.

In Figure 19b,d, the streamwise development of extreme pressure coefficients for 30° and 50° stepped chutes are compared. The 50° stepped chute approach flows produced up to three times higher extreme maximum pressure coefficients C_P^max at the flow deflection point (i.e., X_J ≈ 0.04, Figure 13c), as compared to the 50° smooth chute, or up to two times higher compared to 30° stepped chute (Figure 19b). These values reached up to C_P^max ≈ 1.26 (Figure 13c and Figure 20). Similarly, to the pressure fluctuation coefficients, pronounced values were also observed at the jump toe, where they reached up to C_P^max ≈ 1.1 (Figure 13c and Figure 20). The peak in extreme negative pressures C_P^min was also observed at the flow deflection point, where they reached up C_P^min ≈ 0.6 (Figure 13d and Figure 20). These values were up to 2 times higher as compared to 50° smooth or 30° stepped chutes (Figure 13d, Figure 19d and Figure 20). At the jump toe, the extreme negative pressures were similar to those of 50° smooth or 30°stepped chutes (Figure 13c, Figure 19d and Figure 20). Downstream of the flow deflection point, i.e., X_J > 0.04, the extreme pressure coefficients for 50° stepped chutes decreased and were similar to 50° smooth chute approach flow magnitudes for X_J > 0.13. Similar conclusions can be drawn for extreme pressure coefficients with 99.9% and 0.1% percentiles, but with typically two times lower magnitudes (Figure 13e,f).

The fluctuation and extreme pressure coefficients for 50° smooth chute approach flows can be described with the same relation developed for 30° chutes [5] (Figure 13c,d):

$$C_P=d-\tanh {(e{X}_J)}^{f{X}_J-j}\hspace{1em}30°\le \phi \le 50{°}_{}^{}{\mathrm{smooth}}_{}^{}\mathrm{chute}\hspace{1em}{X}_J\ge 0.03$$

(11)

where coefficients d, e, f and j are given in

Table 2. Coefficients of Equations (11)–(13).

Equation	Coefficient	CP′ (-)	CPmax (-)	CP99.9 (-)	CPmin (-)	CP0.1 (-)
(11)	d	1.006	1.035	1.020	1.020	1.015
	e	3.00	3.41	3.31	2.52	2.46
	f	0.31	3.41	1.60	1.80	0.79
	j	0.006	0.060	0.037	0.010	0.010
	R2	0.99	0.97	0.98	0.91	0.97
(12)	k	1.04	1.36	1.19	1.24	1.12
	l	19	28	21	24	18
	m	6	154	31	28	10
	n	0.000	0.020	0.070	−0.050	−0.007
	R2	0.98	0.96	0.97	0.86	0.96
(13)	o	−0.266	−2.400	−1.650	−0.560	−0.375
	r	0.076	0.604	0.362	0.278	0.175
	R2	0.90	0.75	0.90	0.42	0.60

. The same equation can be used for 50° stepped chutes for X_J > 0.13 or 30° stepped chutes for X_J > 0.1. The pronounced pressure coefficients for 50° stepped chute inflows within X_J ≤ 0.13 are described as:

$$C_P=k-\tanh {(l{X}_J)}^{m{X}_J+n}\hspace{1em}\phi =50{°}_{}^{}{\mathrm{stepped}}_{}^{}\mathrm{chute}\hspace{1em}{X}_J\le 0.13\hspace{1em}\hspace{1em}$$

(12)

where coefficients k, l, m and n are listed in Table 2. The pronounced pressure coefficients for 30° stepped chute inflows within X_J ≤ 0.1 are described as [5]:

$$C_P=o{X}_J+r\hspace{1em}\phi =30{°}_{}^{}{\mathrm{stepped}}_{}^{}\mathrm{chute}\hspace{1em}{X}_J\le 0.1\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}$$

(13)

where coefficients o and r are listed in Table 2.

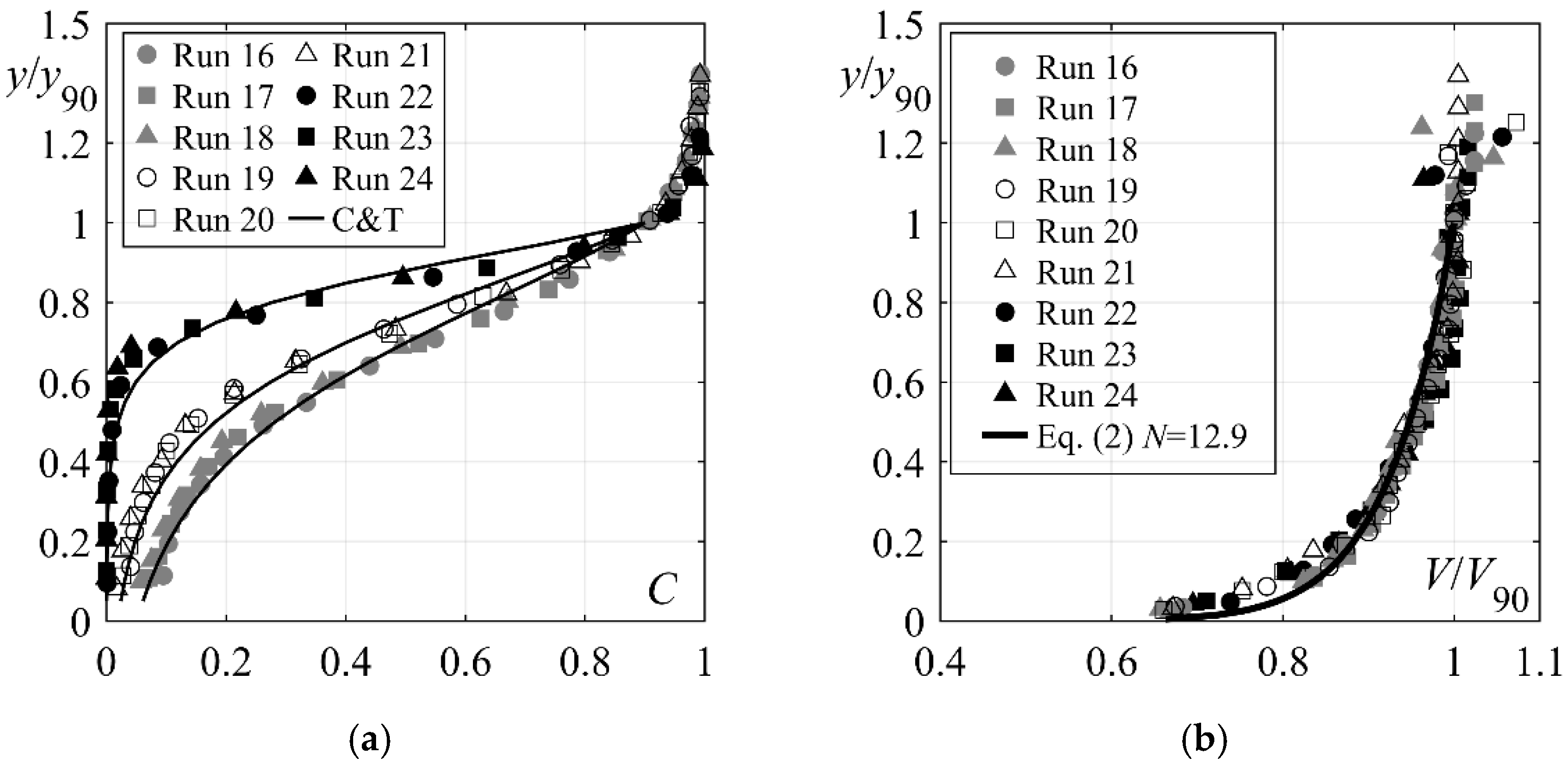
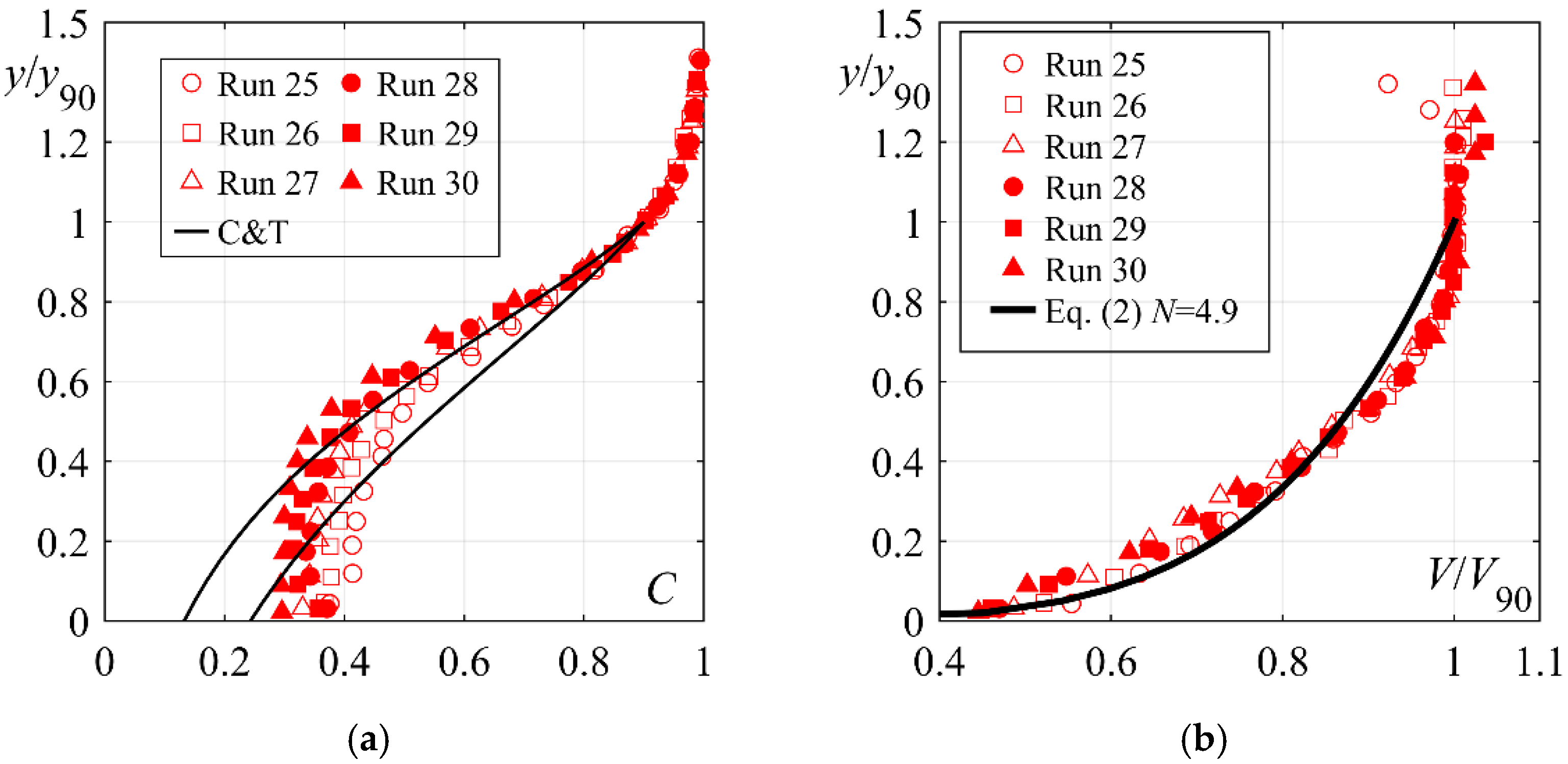
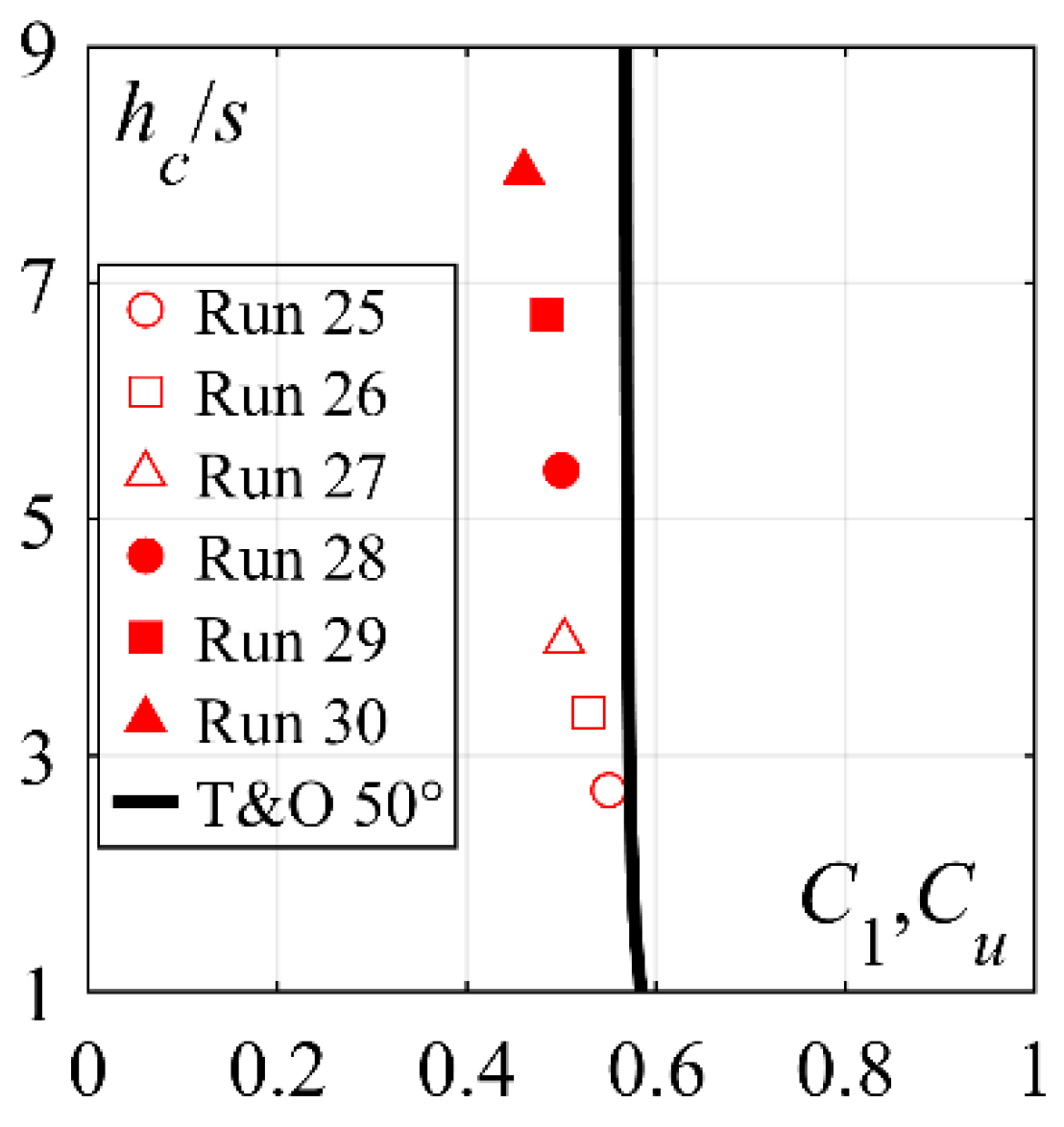
4.2.5. Streamwise Distribution of Bottom Air Concentration and Cavitation Damage Protection

Structures subjected to high velocity flows, such as stilling basins, are sensitive to cavitation formation and associated damage. The knowledge of the bottom air concentration development is essential, as even a relatively small quantity close to the concrete surface can provide protection [24]. In Figure 21 the streamwise development of the bottom air concentration C_b downstream of 30° and 50° smooth and stepped chutes are compared, including the bottom air concentration at the chute end, i.e., C_b,_ce, illustrated at X_J = −0.3.

Smooth chute inflows were characterized by a sharp rise in C_b in the downstream direction, reaching maxima C_b ≈ 0.11 at X_J ≈ 0.17, followed by a decrease towards zero at X_J ≈ 0.9. The bottom air concentration development was practically independent of the approach flow conditions or chute slope φ. The bottom air concentration development remained unaltered, despite the increased bottom air concentration at the 50° smooth chute end, i.e., C_b,_ce values. This further strengthens the conclusion made in [12] that the bottom air concentrations downstream of smooth chutes were not influenced by the approach flow aeration C₁ due to the flow deviation at the jump toe, that generated high pressures (Figure 14a) and thus promoted de-aeration of the flow at the basin entrance.

The 50° stepped chute approach flows had significantly higher bottom air concentrations within X_J ≤ 0.4, as compared to 50° smooth chute approach flows, with values reaching up to C_b = 0.18 at X_J = 0.08 (Figure 21). The increased values after 50° stepped chute approach flows, similarly to those after 30° stepped chutes, can be attributed to the significantly higher C_b,_ce and comparatively lower pressure magnitudes at the flow deviation point [12] (Figure 13a). Further downstream, the values of C_b decreased up to X_J ≈ 0.4, beyond which they coincide with smooth chute approach flow values. Comparing the 30° and 50° stepped chute approach flows (Figure 21), it was noticeable that 50° stepped chute had a slightly higher air concentration (on average 2% more) within X_J ≤ 0.4, as compared to 30° stepped chute, despite the significantly higher bottom air concentration at the 50° stepped chute end (18%, on average) This was caused by the higher pressure magnitudes at the flow deviation point downstream of 50° stepped chute (Figure 13a), which lead to higher de-aeration rates at the basin entrance. Further downstream, i.e., X_J > 0.4, the bottom air concentration development was independent of the chute slope φ

The streamwise development of the bottom air concentration C_b for 50° smooth chute approach flows was described by the equation developed for 30° [12] (Figure 21):

$$C_b=0.98-\tanh {(2.4X_J)}^{0.95X_J-0.03}\hspace{1em}30°\le \phi \le 50{°}_{}^{}{\mathrm{smooth}}_{}^{}\mathrm{chute}\hspace{1em}0.08\le X_J\le 0.9$$

(14)

The same equation can be used for 30° or 50° sloping stepped chute approach flows for X_J > 0.4. The pronounced bottom air concentrations for stepped chute approach flows can be approximated as (R² = 0.8, Figure 21):

$$C_b=-0.25X_J+0.178\hspace{1em}\phi =30{°}_{}^{}{\mathrm{stepped}}_{}^{}\mathrm{chute}\hspace{1em}0.08\le X_J\le 0.4$$

(15)

$$C_b=-0.26X_J+0.2\hspace{1em}\phi =50{°}_{}^{}{\mathrm{stepped}}_{}^{}\mathrm{chute}\hspace{1em}0.08\le X_J\le 0.4\hspace{1em}$$

(16)

In terms of cavitation protection, stilling basins downstream of 50° chutes had the same cavitation damage protection length with respect to bottom air concentration as 30° steep chutes [12]: (1) smooth chute inflows within 0.1 ≤ X_J ≤ 0.5 and 0.15 ≤ X_J ≤ 0.4 considering 5% and 8% bottom air concentration limit [24,25,26], and (2) stepped chute inflows within 0 ≤ X_J ≤ 0.5 and 0 ≤ X_J ≤ 0.4 considering 5% and 8% bottom air concentration limit [24,25,26]. The pronounced extreme pressures downstream of 30° or 50° sloping stepped chutes within X_J ≤ 0.13 (Figure 19b,d) do probably not present a risk in terms of cavitation damage.

5. Conclusions

The effect of chute slope (i.e., φ = 30° and 50°) on the performance of a plain stilling basin below smooth and stepped chutes was systematically investigated for several discharges, smooth chute approach flow aerations and two step heights. The following conclusions can be drawn:

• The use of equivalent clear water parameters at the chute end leads to a fairly accurate prediction of the sequent depth ratio using classical momentum principle, irrespective of the approach flow conditions or chute slope φ, for a given approach Froude number F₁.
• The free surface characteristics along the plain stilling basin, such as dimensionless flow depths Z and dimensionless flow depth fluctuations C_H’, are independent of the approach flow conditions or chute slope φ, either for smooth or stepped chutes.
• The dimensionless roller lengths L_R/h₂ are independent of the approach flow conditions or chute slope φ.
• The dimensionless hydraulic jump lengths L_R/h₂ are practically independent of the chute slope φ. Further, the results support the conclusions made by [5], stating that hydraulic jumps initiated below stepped chutes require an increased length x/h₂ as compared to those below smooth chutes.
• It is recommended that longer dimensionless plain stilling basin lengths are provided below stepped chutes irrespective of the chute slope, namely L_J ≈ 6.7h₂ as compared to L_J ≈ 5.8h₂ below smooth chutes, plus a safety margin.
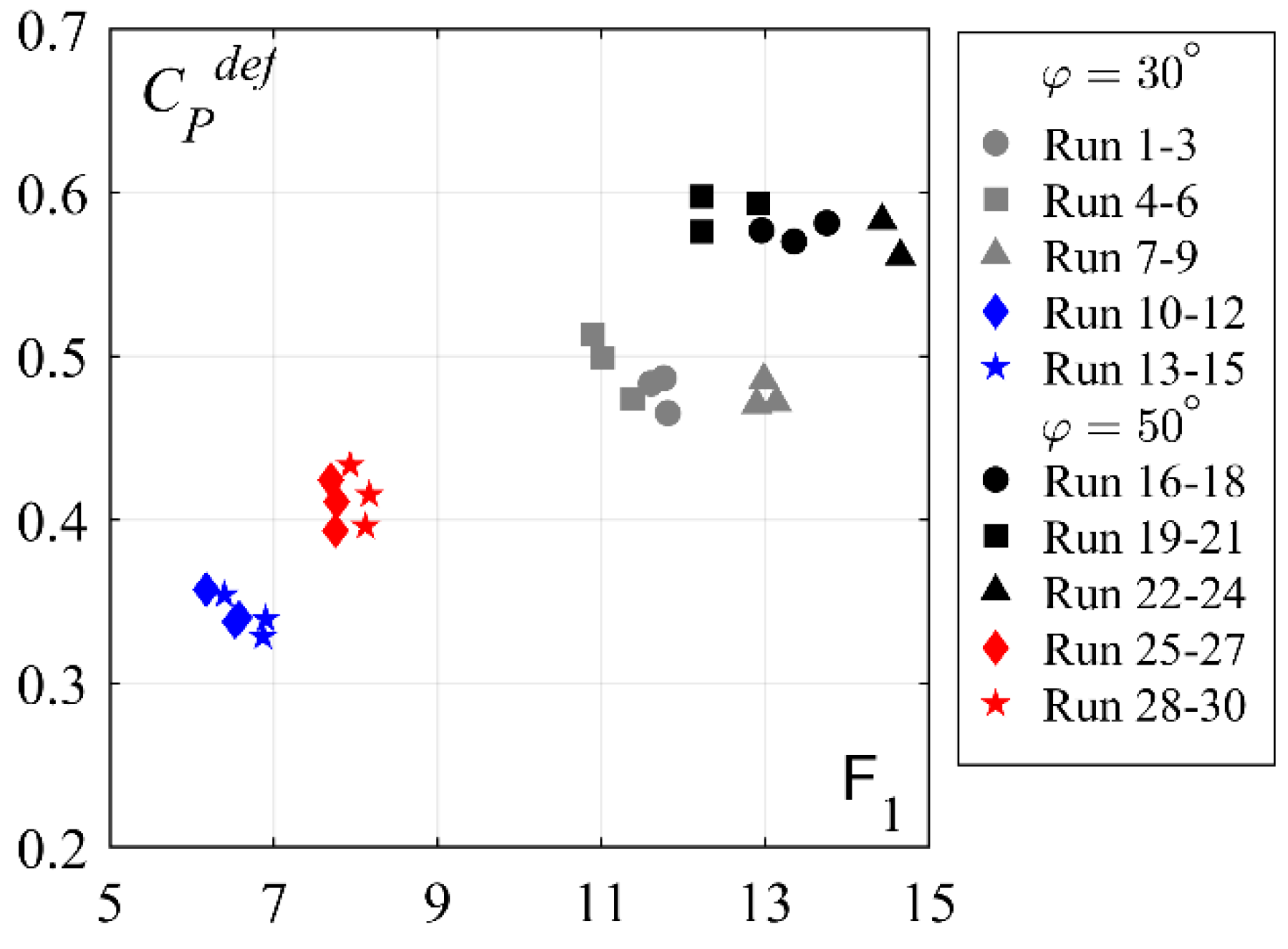
• Increasing chute slope pronounces dimensionless mean bottom pressures P_m, due to the stronger flow curvature, and slightly extends the influence reach of the flow curvature. The latter is more significant for stepped chute inflows.
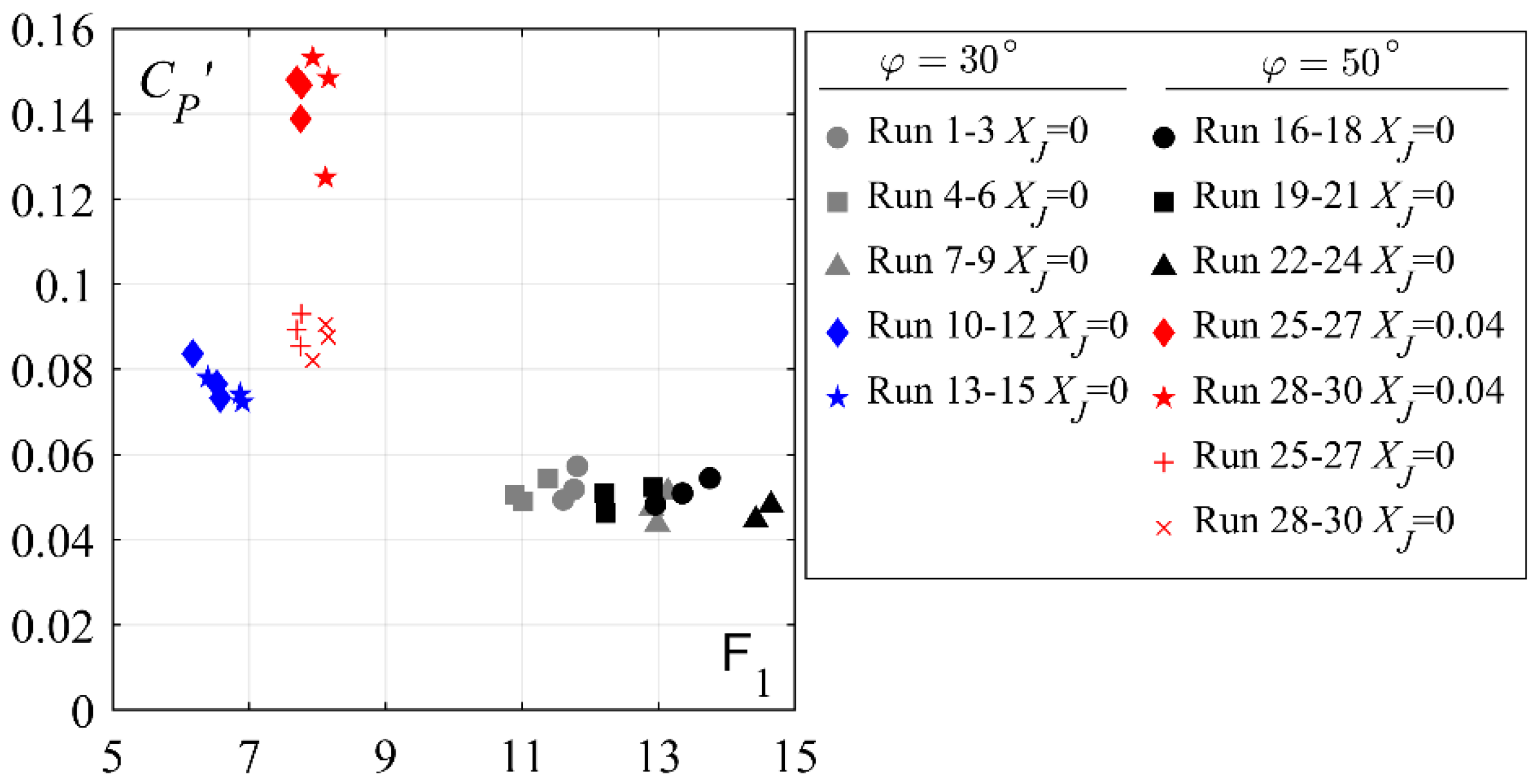
• Fluctuation and extreme pressure coefficients along the plain stilling basin invert are independent of the approach flow aeration C₁ or chute slope φ below smooth chutes.
• Stepped chute inflows increase the fluctuating and extreme pressure coefficients at the plain stilling basin entrance, as compared to smooth chute inflows. Increasing stepped chute slope increases the extreme and fluctuating pressure coefficients within X_J ≤ 0.13. For 50° stepped chutes, these coefficients can reach up to 3 times higher magnitudes compared to smooth chute inflows or up to 2 times higher compared to the 30° stepped chute inflows.
• The bottom air concentration development along the plain stilling basin below smooth chutes is independent of the chute slope φ, for X_J ≥ 0.08. Stepped chute inflows increase bottom air concentration within X_J ≤ 0.4. Increasing stepped chute slope slightly increases the bottom air concentration within the latter region, namely by some 2% for 50° stepped chute compared to 30° chutes.
• The cavitation protection length is independent of the chute slope, namely for: (1) smooth chute inflows within 0.1 ≤ X_J ≤ 0.5 and 0.15 ≤ X_J ≤ 0.4 considering 5% and 8% bottom air concentration limit, and (2) stepped chute inflows within 0 ≤ X_J ≤ 0.5 and 0 ≤ X_J ≤ 0.4 considering 5% and 8% bottom air concentration limit. Evidently, stepped chute approach flows provide better cavitation damage protection in the initial reach of the plain stilling basin.
• The increased extreme pressures below stepped chutes within X_J ≤ 0.13 are not expected to represent a danger in terms of cavitation. In spite of this, the increased bottom pressure coefficients below stepped chutes should be considered in the plain stilling basin slab design.

Empirical equations for predicting the roller length, mean and fluctuating flow depth development and bottom pressure characteristics along plain stilling basins below smooth and stepped chutes were proposed. The latter, including the results of the present study, strictly apply to 30° ≤ φ ≤ 50° gradually varied or quasi-uniform smooth (0.15 ≤ C₁ ≤ 0.37 and 10.9 ≤ F₁ ≤ 15) and skimming stepped (0.41 ≤ C₁ ≤ 0.55, 6.2 ≤ F₁ ≤ 8.2 and 2.70 ≤ h_c/s ≤ 7.94) chute inflows.