Hydrometeorological Forecast of a Typical Watershed in an Arid Area Using Ensemble Kalman Filter
Abstract
:1. Introduction
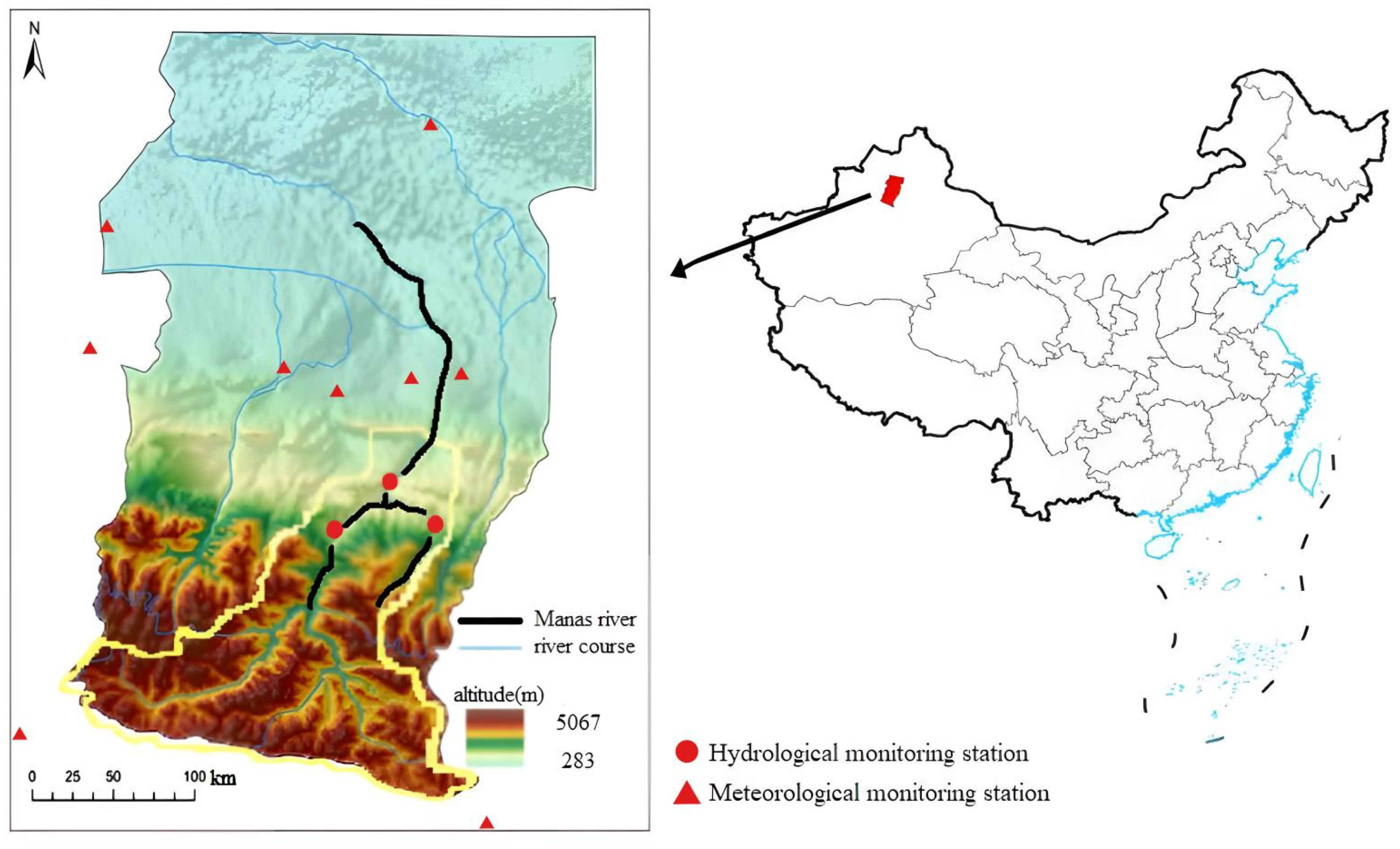
2. Overview of the Research Area
3. Data and Methods
3.1. Data
3.2. Algorithm
3.2.1. Stationarity Test
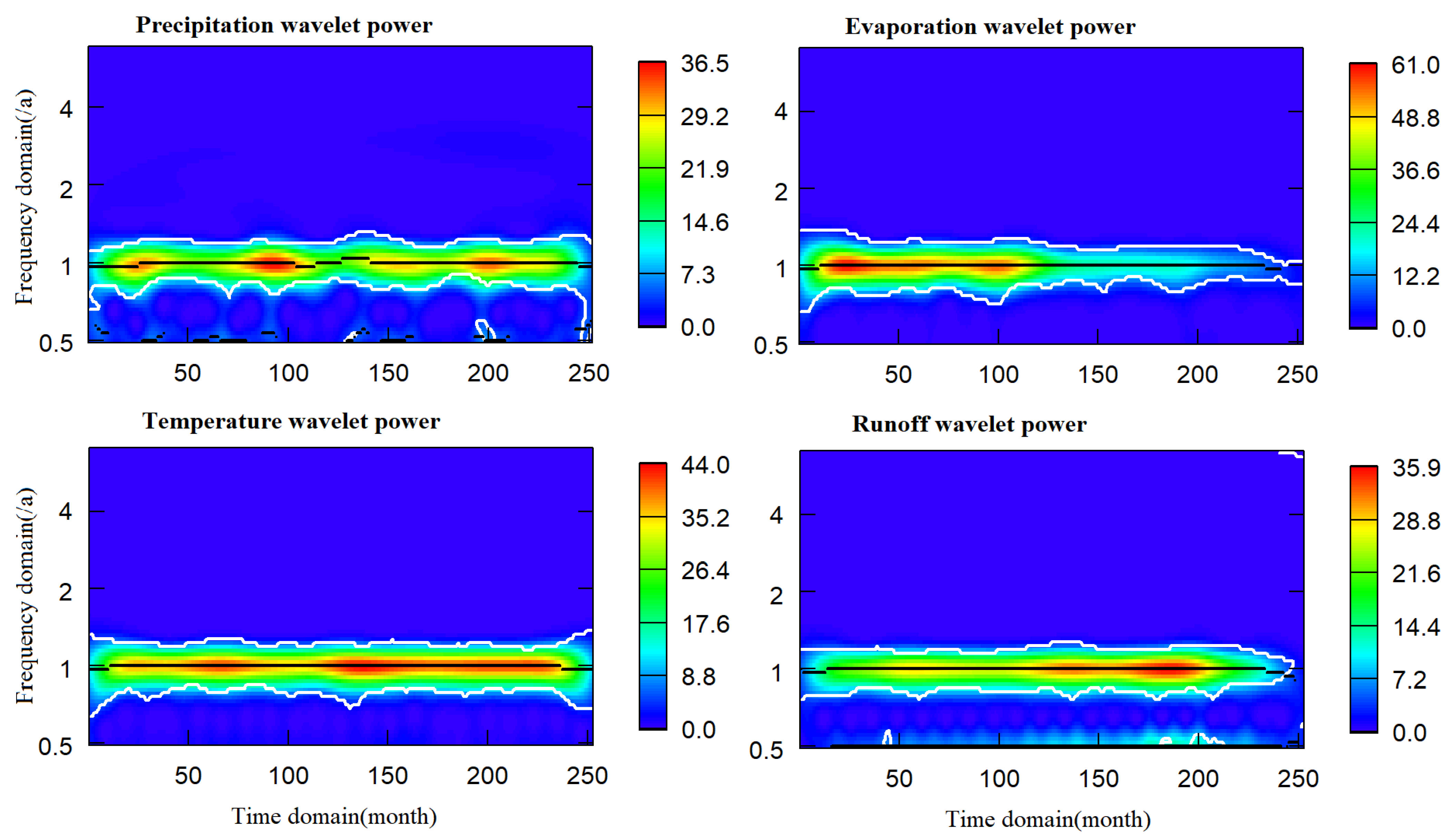
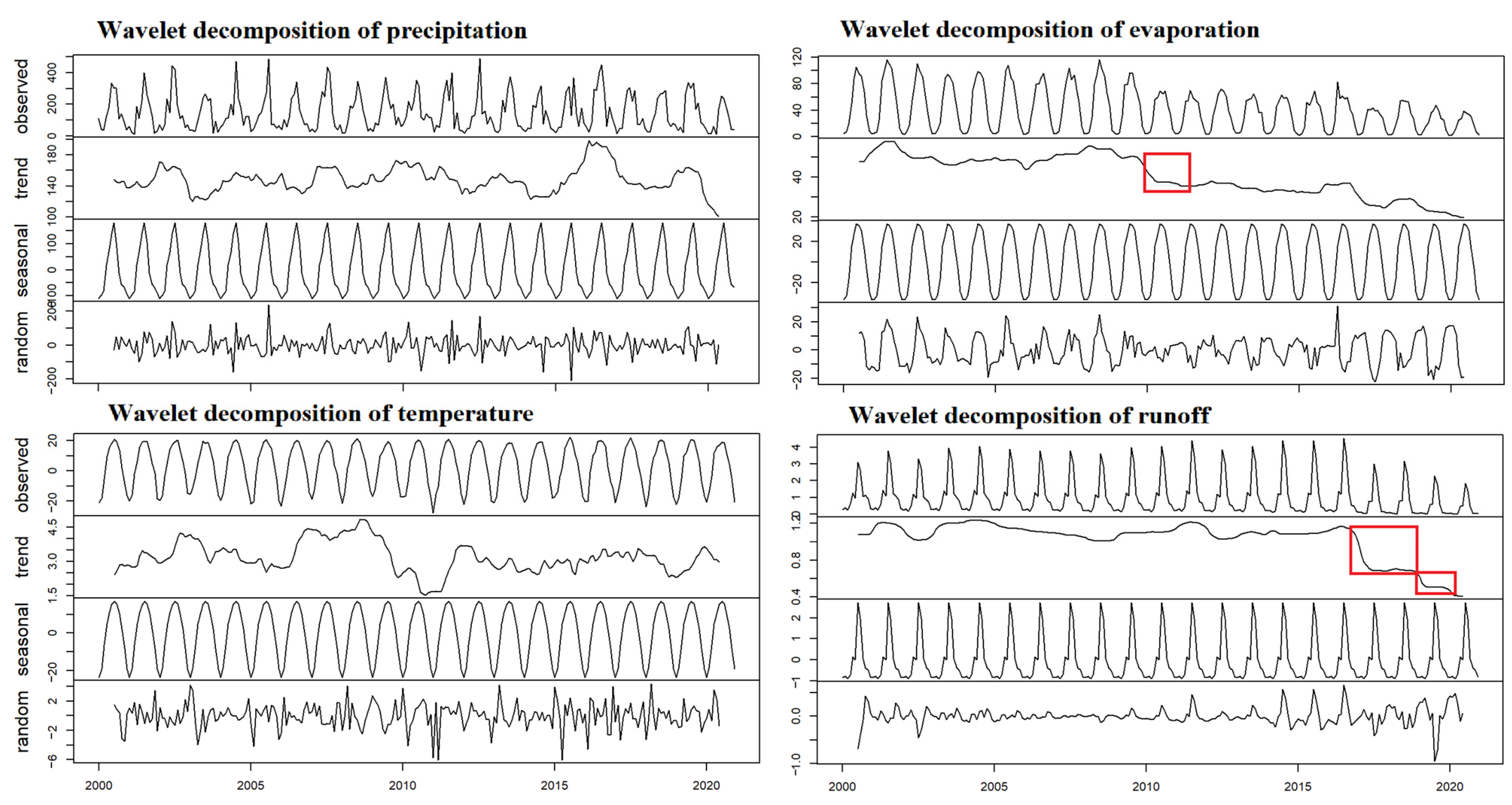
3.2.2. Wavelet Analysis and Wavelet Decomposition
3.2.3. Traditional Framework of EnKF (Ensemble Kalman Filter)
3.2.4. Preprocessing of Filter Input Data
3.2.5. Accuracy Verification
4. Results Analysis
4.1. Spatial and Temporal Distribution Characteristics of Parameters
4.2. Stationarity Test and Wavelet Decomposition
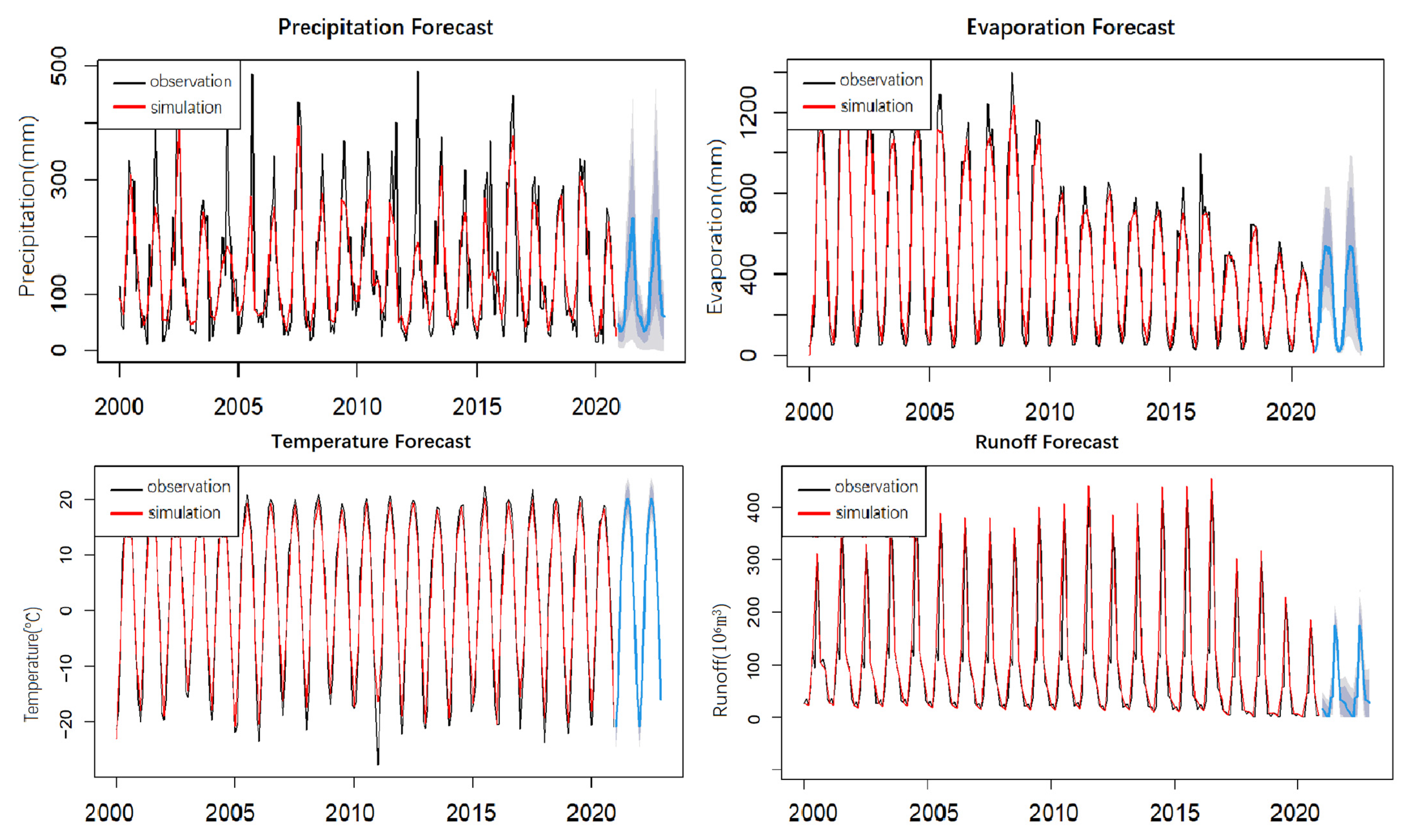
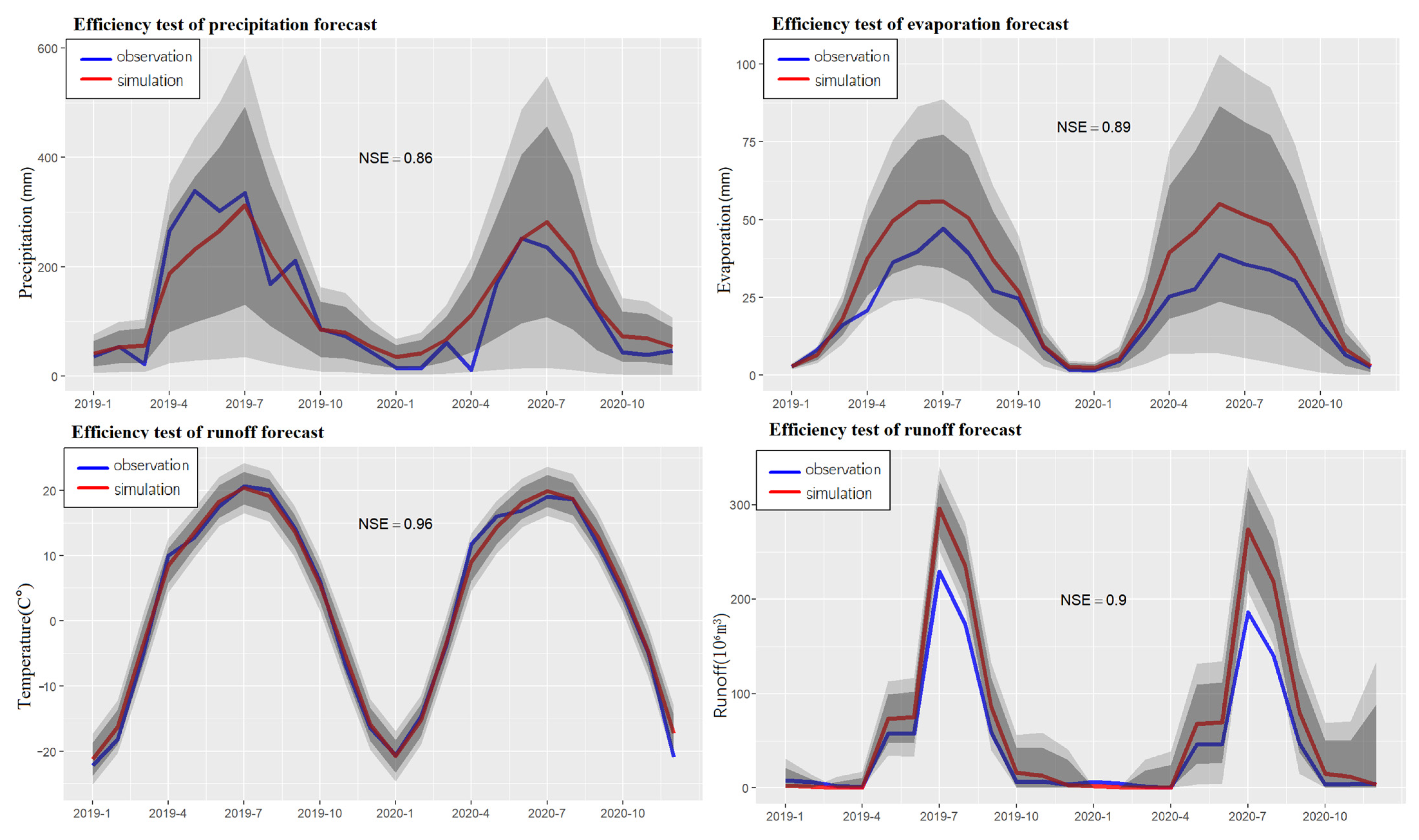
4.3. Prediction
4.4. Reducing Data Overreliance and Improving Prediction Ability
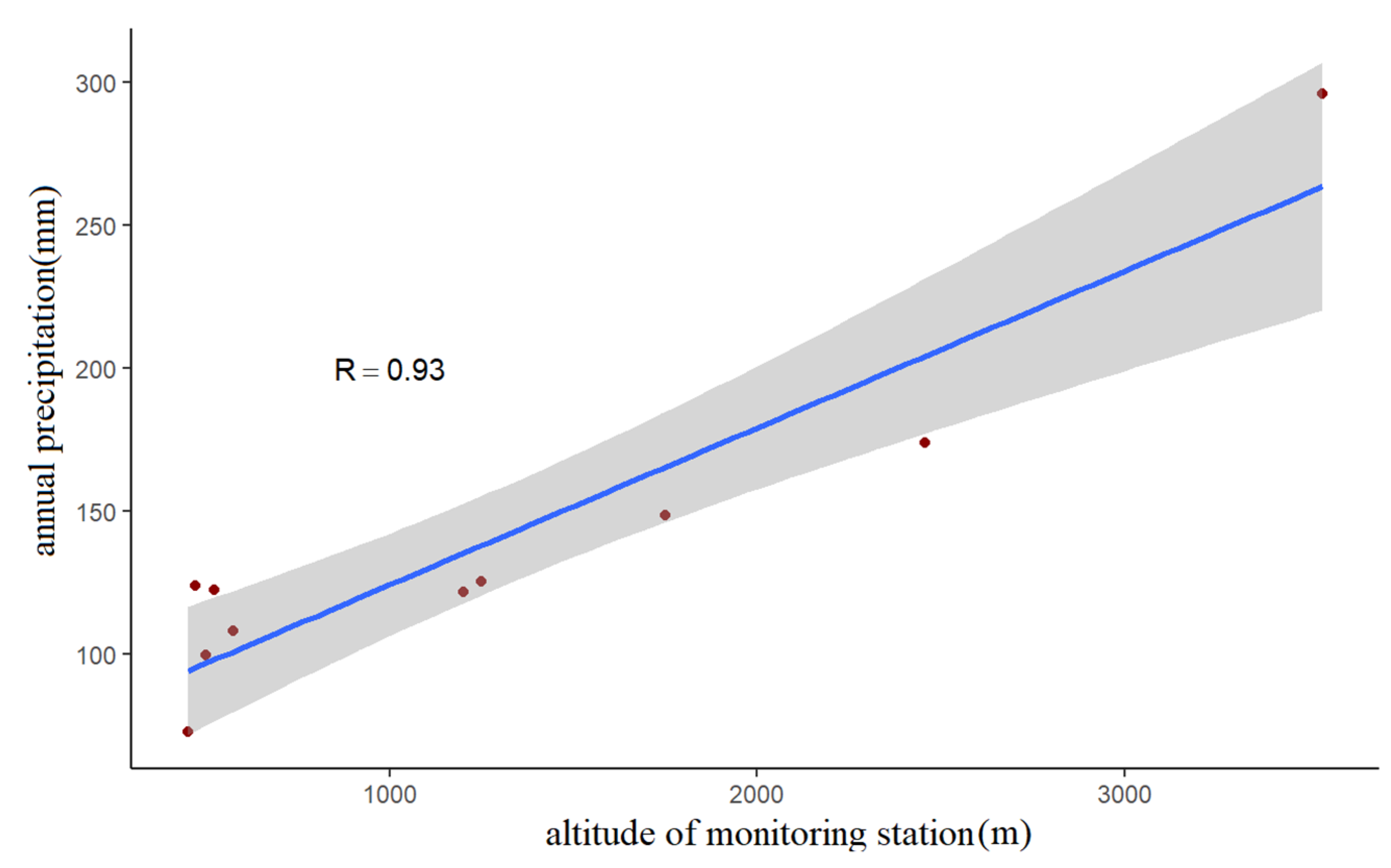
4.5. Relationship between Precipitation and Altitude
4.6. Relationship between Evaporation and Temperature
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
Appendix C
References
- Berghuijs, W.; RA, W.; Hrachowitz, M. A precipitation shift from snow towards rain leads to a decrease in streamflow. Nat. Clim. Change 2014, 4, 583–586. [Google Scholar] [CrossRef] [Green Version]
- Alemu, Z.; Dioha, M. Climate change and trend analysis of temperature: The case of Addis Ababa, Ethiopia. Environ. Syst. Res. 2020, 9, 27. [Google Scholar] [CrossRef]
- Stocker, T. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014; pp. 127–129. [Google Scholar]
- Chen, Y.; Li, Z.; Fan, Y.; Wang, H.; Deng, H. Progress and prospects of climate change impacts on hydrology in the arid region of northwest China. Environ. Res. 2015, 139, 11–19. [Google Scholar] [CrossRef] [PubMed]
- Kraft, B.; Jung, M.; Körner, M.; Koirala, S.; Reichstein, M. Towards hybrid modeling of the global hydrological cycle. Hydrol. Earth Syst. Sci. 2022, 36, 1576–1614. [Google Scholar] [CrossRef]
- Fang, G.; Yang, J.; Chen, Y.; Zammit, C. Comparing bias correction methods in downscaling meteorological variables for a hydrologic impact study in an arid area in China. Hydrol. Earth Syst. Sci. 2015, 19, 2547–2559. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Wang, H.; Wang, Z.; Zhang, H. Characteristics of extreme climatic/hydrological events in the arid region of northwestern China. Arid. Land Geogr. 2017, 40, 1–9. [Google Scholar]
- Chen, L.; Cao, Y.; Ma, L.; Zhang, J. A Deep Learning-Based Methodology for Precipitation Nowcasting with Radar. Earth Space Sci. 2020, 7, e2019EA000812. [Google Scholar] [CrossRef] [Green Version]
- Goodarzi, D.; Abolfathi, S.; Borzooei, S. Modelling solute transport in water disinfection systems: Effects of temperature gradient on the hydraulic and disinfection efficiency of serpentine chlorine contact tanks. J. Water Process Eng. 2020, 37, 101411. [Google Scholar] [CrossRef]
- Goodarzi, D.; Mohammadian, A.; Pearson, J.; Abolfathi, S. Numerical modelling of hydraulic efficiency and pollution transport in waste stabilization ponds. Ecol. Eng. 2022, 182, 106702. [Google Scholar] [CrossRef]
- Cazelles, B.; Chavez, M.; Berteaux, D.; Ménard, F.; Vik, J.; Jenouvrier, S.; Stenseth, N. Wavelet analysis of ecological time series. Oecologia 2008, 156, 287–304. [Google Scholar] [CrossRef] [PubMed]
- Hewlett, J.D.; Hibbert, A.R. Factors affecting the response of small watersheds to precipitation in humid areas. For. Hydrol. 1967, 1, 275–290. [Google Scholar]
- Abbott, M.; Bathurst, J.; Cunge, J.; O’connell, P.; Rasmussen, J. An introduction to the European Hydrological System—Systeme Hydrologique Europeen,“SHE”, 2: Structure of a physically-based, distributed modelling system. J. Hydrol. 1986, 87, 61–77. [Google Scholar] [CrossRef]
- Laio, F.; Di Baldassarre, G.; Montanari, A. Model selection techniques for the frequency analysis of hydrological extremes. Water Resour. Res. 2009, 45, W07416. [Google Scholar] [CrossRef]
- Chen, H.; Chen, Y.; Li, W.; Li, Z. Quantifying the contributions of snow/glacier meltwater to river runoff in the Tianshan Mountains, Central Asia. Glob. Planet. Change 2019, 174, 47–57. [Google Scholar] [CrossRef]
- Xie, X.; Zhang, D. Data assimilation for distributed hydrological catchment modeling via ensemble Kalman filter. Adv. Water Resour. 2010, 33, 678–690. [Google Scholar] [CrossRef]
- Clark, M.; Rupp, D.; Woods, R.; Zheng, X.; Ibbitt, R.; Slater, A.; Schmidt, J.; Uddstrom, M.J. Hydrological data assimilation with the ensemble Kalman filter: Use of streamflow observations to update states in a distributed hydrological model. Adv. Water Resour. 2008, 31, 1309–1324. [Google Scholar] [CrossRef]
- Vetra-Carvalho, S.; Van Leeuwen, P.J.; Nerger, L.; Barth, A.; Altaf, M.U.; Brasseur, P.; Kirchgessner, P.; Beckers, J.M. State-of-the-art stochastic data assimilation methods for high-dimensional non-Gaussian problems. Tellus A Dyn. Meteorol. Oceanogr. 2018, 70, 1–43. [Google Scholar] [CrossRef] [Green Version]
- Bannister, R.N. A review of operational methods of variational and ensemble-variational data assimilation. Q. J. R. Meteorol. Soc. 2017, 143, 607–633. [Google Scholar] [CrossRef] [Green Version]
- Houtekamer, P.L.; Zhang, F. Review of the Ensemble Kalman Filter for Atmospheric Data Assimilation. Mon. Weather. Rev. 2016, 144, 208–239. [Google Scholar] [CrossRef]
- Evensen, G. Sequential data assimilation with a nonlinear quasi-geostrophic model using Monte Carlo methods to forecast error statistics. J. Geophys. Res. Ocean. 1994, 99, 10143–10162. [Google Scholar] [CrossRef]
- Burgers, G.; Leeuwen, P.J.; Evensen, G. Analysis scheme in the ensemble Kalman filter. Mon. Weather. Rev. 1998, 126, 1719–1724. [Google Scholar] [CrossRef]
- Pham, D.T.; Verron, J.; Gourdeau, L. A singular evolutive Kalman filters for data assimilation in oceanography. J. Mar. Syst. 1998, 16, 323–340. [Google Scholar] [CrossRef]
- Kong, L.; Tang, X.; Zhu, J.; Wang, Z.; Pan, Y.; Wu, H.; Wu, L.; Wu, Q.; He, Y.; Tian, S. Improved inversion of monthly ammonia emissions in China based on the Chinese ammonia monitoring network and ensemble Kalman filter. Environ. Sci. Technol. 2019, 53, 12529–12538. [Google Scholar] [CrossRef] [PubMed]
- Chatrabgoun, O.; Karimi, R.; Daneshkhah, A.; Abolfathi, S.; Nouri, H.; Esmaeilbeigi, M. Copula-based probabilistic assessment of intensity and duration of cold episodes: A case study of Malayer vineyard region. Agric. For. Meteorol. 2020, 295, 108150. [Google Scholar] [CrossRef]
- Donnelly, J.; Abolfathi, S.; Pearson, J.; Chatrabgoun, O.; Daneshkhah, A. Gaussian process emulation of spatio-temporal outputs of a 2D inland flood model. Water Res. 2022, 225, 119100. [Google Scholar] [CrossRef] [PubMed]
- Naumann, G.; Cammalleri, C.; Mentaschi, L.; Feyen, L. Increased economic drought impacts in Europe with anthropogenic warming. Nat. Clim. Change 2021, 11, 485–491. [Google Scholar] [CrossRef]
- Hamid, A.; Hafeez, A.; Khan, M.; Alshomrani, A.; Alghamdi, M. Heat transport features of magnetic water–graphene oxide nanofluid flow with thermal radiation: Stability Test. Eur. J. Mech.-B/Fluids 2019, 76, 434–441. [Google Scholar] [CrossRef]
- Vishwanath, M. The recursive pyramid algorithm for the discrete wavelet transform. IEEE Trans. Signal Process. 1994, 42, 673–676. [Google Scholar] [CrossRef]
- Kalman, R.E. On the General Theory of Control Systems. IFAC Proceedings Volumes. 1960, 1, 491–502. [Google Scholar] [CrossRef]
- Sun, Y.; Bao, W.; Valk, K.; Brauer, C.C.; Sumihar, J.; Weerts, A.H. Improving forecast skill of lowland hydrological models using ensemble Kalman filter and unscented Kalman filter. Water Resour. Res. 2020, 56, e027468. [Google Scholar] [CrossRef]
- Farahani, A.V.; Abolfathi, S. Sliding Mode Observer Design for decentralized multi-phase flow estimation. Heliyon 2022, 8, e08768. [Google Scholar] [CrossRef] [PubMed]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part IA discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Sornette, D.; Davis, A.; Ide, K.; Vixie, K.; Pisarenko, V.; Kamm, J. Algorithm for model validation: Theory and applications. Proc. Natl. Acad. Sci. 2007, 104, 6562–6567. [Google Scholar] [CrossRef] [Green Version]
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Wu, K. Hydrological Characteristics of Manas River Basin in Xinjiang. Inn. Mong. Water Resour. 2011, 6, 2. Available online: http://qikan.cqvip.com/Qikan/Article/Detail?id=40642448 (accessed on 1 June 2022).
- Stone, M. Cross-validatory choice and assessment of statistical predictions. J. R. Stat. Soc. Ser. B (Methodol.) 1974, 36, 111–133. [Google Scholar] [CrossRef]
- Moradkhani, H.; Sorooshian, S.; Gupta, H.V.; Houser, P.R. Dual state–parameter estimation of hydrological models using ensemble Kalman filter. Adv. Water Resour. 2005, 28, 135–147. [Google Scholar] [CrossRef] [Green Version]
- Tiao, G.C.; Tsay, R.S. Model specification in multivariate time series. J. R. Stat. Soc. Ser. B (Methodol.) 1989, 51, 157–195. [Google Scholar] [CrossRef]
- Yao, F.; Qin, P.; Zhang, J. Uncertainties in agricultural impact assessment of climate change based on model simulation and treatment methods. Sci. Bull. 2011, 56, 9. [Google Scholar] [CrossRef] [Green Version]
- Walsh, J.E.; Chapman, W.L.; Romanovsky, V.; Christensen, J.H.; Stendel, M. Global climate model performance over Alaska and Greenland. J. Clim. 2008, 21, 6156–6174. [Google Scholar] [CrossRef]
- Lermusiaux, P.; Robinson, A. Data assimilation via error subspace statistical estimation. Part I: Theory and schemes. Mon. Weather. Rev. 1999, 127, 1385–1407. [Google Scholar] [CrossRef]
- Bishop, C.; Etherton, B.; Majumdar, S. Adaptive sampling with the ensemble transform Kalman filter. Part I: Theoretical aspects. Mon. Weather. Rev. 2001, 129, 420–436. [Google Scholar] [CrossRef]
- Ghiasi, B.; Noori, R.; Sheikhian, H.; Zeynolabedin, A.; Sun, Y.; Jun, C.; Hamouda, M.; Bateni, S.M.; Abolfathi, S. Uncertainty quantification of granular computing-neural network model for prediction of pollutant longitudinal dispersion coefficient in aquatic streams. Sci. Rep. 2022, 12, 4610. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Liu, Y.; Sun, H. Physics-informed learning of governing equations from scarce data. Nat. Commun. 2021, 12, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Luo, L.; Wang, X.; Yu, P. Comparative study on calculation formulas of saturated water vapor pressure. Meteorol. Hydrol. Mar. Instrum. 2003, 4, 4. Available online: http://qikan.cqvip.com/Qikan/Article/Detail?id=8938748 (accessed on 1 June 2022).
- Houtekamer, P.L.; Mitchell, H.L. Data assimilation using an ensemble Kalman filter technique. Mon. Weather. Rev. 1998, 126, 796–811. [Google Scholar] [CrossRef]
- Rodriguez-Iturbe, I.; Mejía, J.M. On the transformation of point rainfall to areal rainfall. Water Resour. Res. 1974, 10, 729–735. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, M.; Wang, S. Change of snowfall/rainfall ratio in the Tibetan Plateau based on a gridded dataset with high resolution during 1961–2013. Acta Geo-Graph. Sin. 2016, 71, 142–152. [Google Scholar]
| Site Name | Longitude | Latitude | Altitude (m) |
|---|---|---|---|
| Karamay | 84°51′ | 45°37′ | 449.5 |
| Shawan | 85°37′ | 44°20′ | 522.2 |
| Manas | 86°12′ | 44°19′ | 471.4 |
| Hutubi | 86°51′ | 44°10′ | 575.1 |
| Daxigou | 86°50′ | 43°06′ | 3539.0 |
| Bayanbulak | 84°09′ | 43°02′ | 2458.0 |
| Baluntai | 86°18′ | 44°19′ | 1739.0 |
| Ulan Wusu | 84°62′ | 44°45′ | 480.6 |
| Shihezi | 86°02′ | 44°18′ | 493.0 |
| Parameter | Test | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Precipitation | MK | 0.088 | 0.064 | 0.209 | −0.037 | 0.099 | −0.035 | −0.06 | 0.49 | −0.047 | −0.089 | −0.08 |
| ACF | 0.032 | 0.064 | 0.238 | −0.063 | 0.089 | 0.024 | −0.384 | −0.28 | −0.097 | −0.03 | −0.606 | |
| Evaporation | MK | −0.317 | −0.092 | 0.098 | −0.085 | 0.044 | 0.035 | 0.021 | −0.132 | 0.033 | 0.07 | −0.017 |
| ACF | −0.755 | −0.746 | −0.026 | −0.063 | 0.024 | 0.026 | −0.422 | −0.177 | −0.237 | 0.045 | −0.211 | |
| Temperature | MK | 0.07 | −0.099 | 0.037 | −0.037 | −0.094 | 0.082 | 0.064 | −0.363 | −0.039 | −0.033 | −0.251 |
| ACF | −0.048 | −0.068 | −0.074 | 0.002 | 0.099 | 0.054 | 0.034 | −0.46 | −0.195 | −0.27 | −0.256 | |
| Runoff | MK | 0.002 | −0.008 | 0.01 | −0.001 | −0.001 | 0.001 | −0.006 | 0.002 | 0.004 | 0.006 | 0.002 |
| ACF | 0.004 | −0.007 | −0.009 | 0 | 0.001 | 0 | 0 | 0.009 | 0.01 | −0.004 | 0.008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, G.; Chen, Y.; Fang, G.; Li, Z. Hydrometeorological Forecast of a Typical Watershed in an Arid Area Using Ensemble Kalman Filter. Water 2022, 14, 3970. https://doi.org/10.3390/w14233970
He G, Chen Y, Fang G, Li Z. Hydrometeorological Forecast of a Typical Watershed in an Arid Area Using Ensemble Kalman Filter. Water. 2022; 14(23):3970. https://doi.org/10.3390/w14233970
Chicago/Turabian StyleHe, Ganchang, Yaning Chen, Gonghuan Fang, and Zhi Li. 2022. "Hydrometeorological Forecast of a Typical Watershed in an Arid Area Using Ensemble Kalman Filter" Water 14, no. 23: 3970. https://doi.org/10.3390/w14233970











