Daily Streamflow Time Series Modeling by Using a Periodic Autoregressive Model (ARMA) Based on Fuzzy Clustering
Abstract
:1. Introduction
2. Materials and Methods
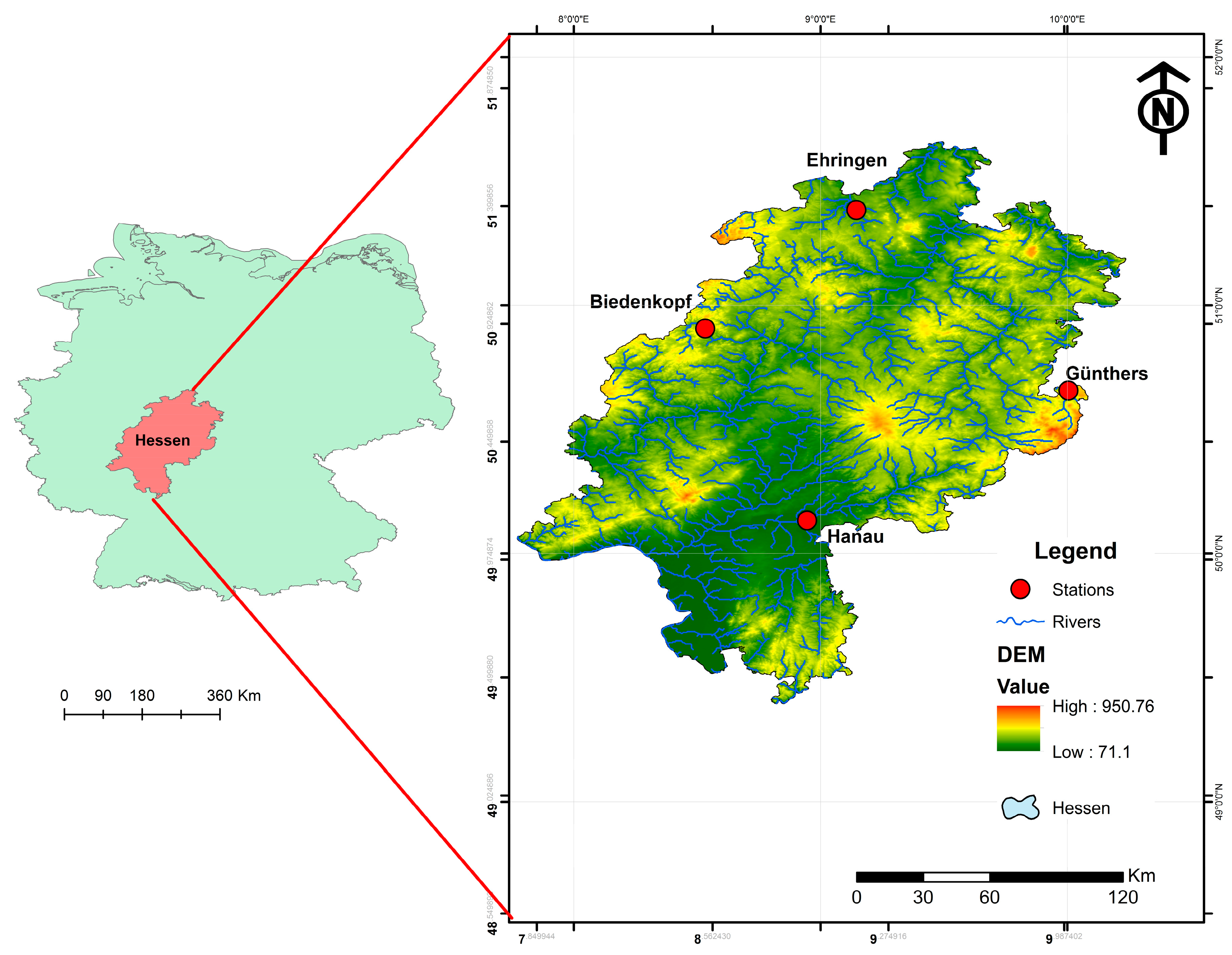
2.1. Study Site
2.2. Database
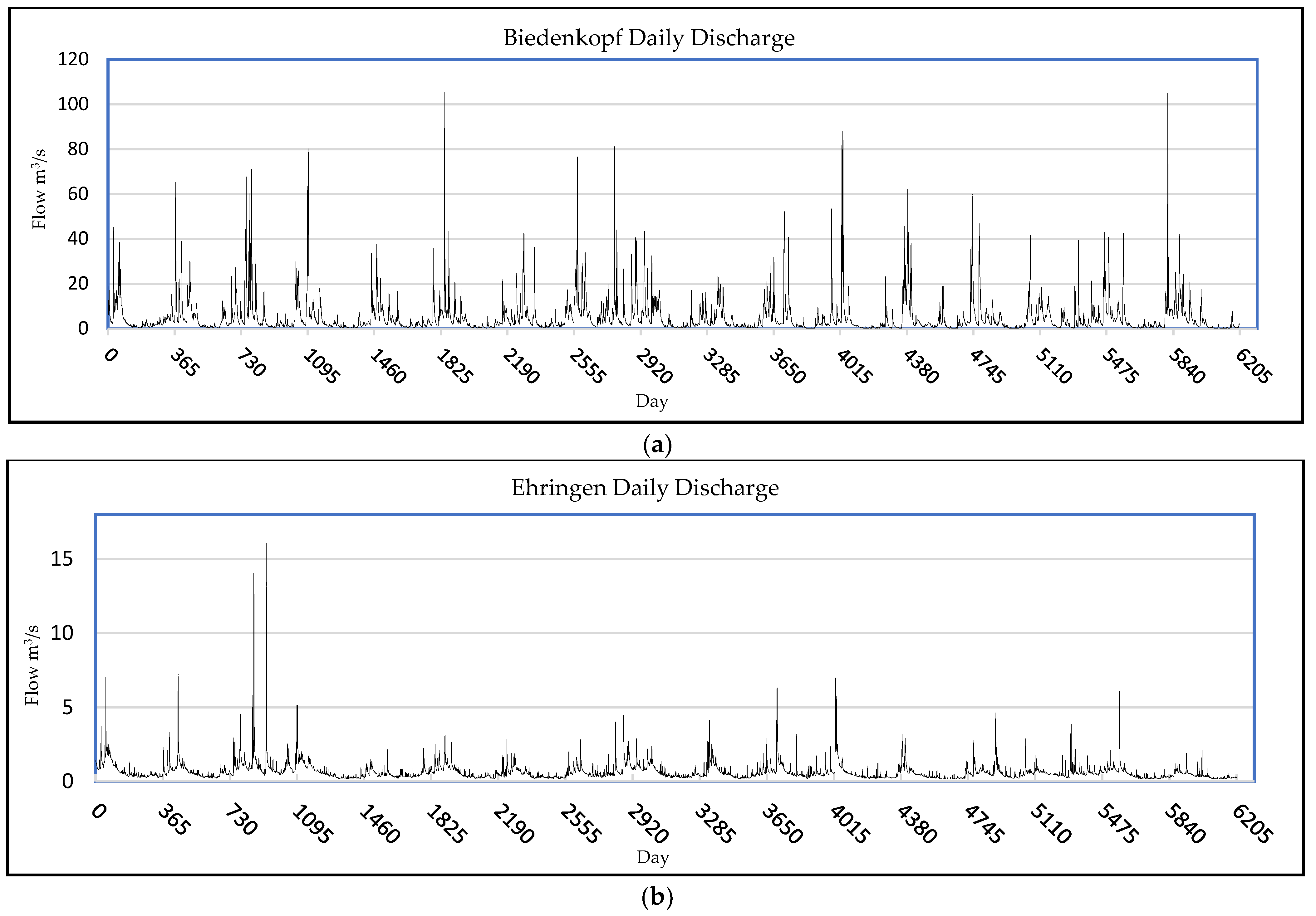
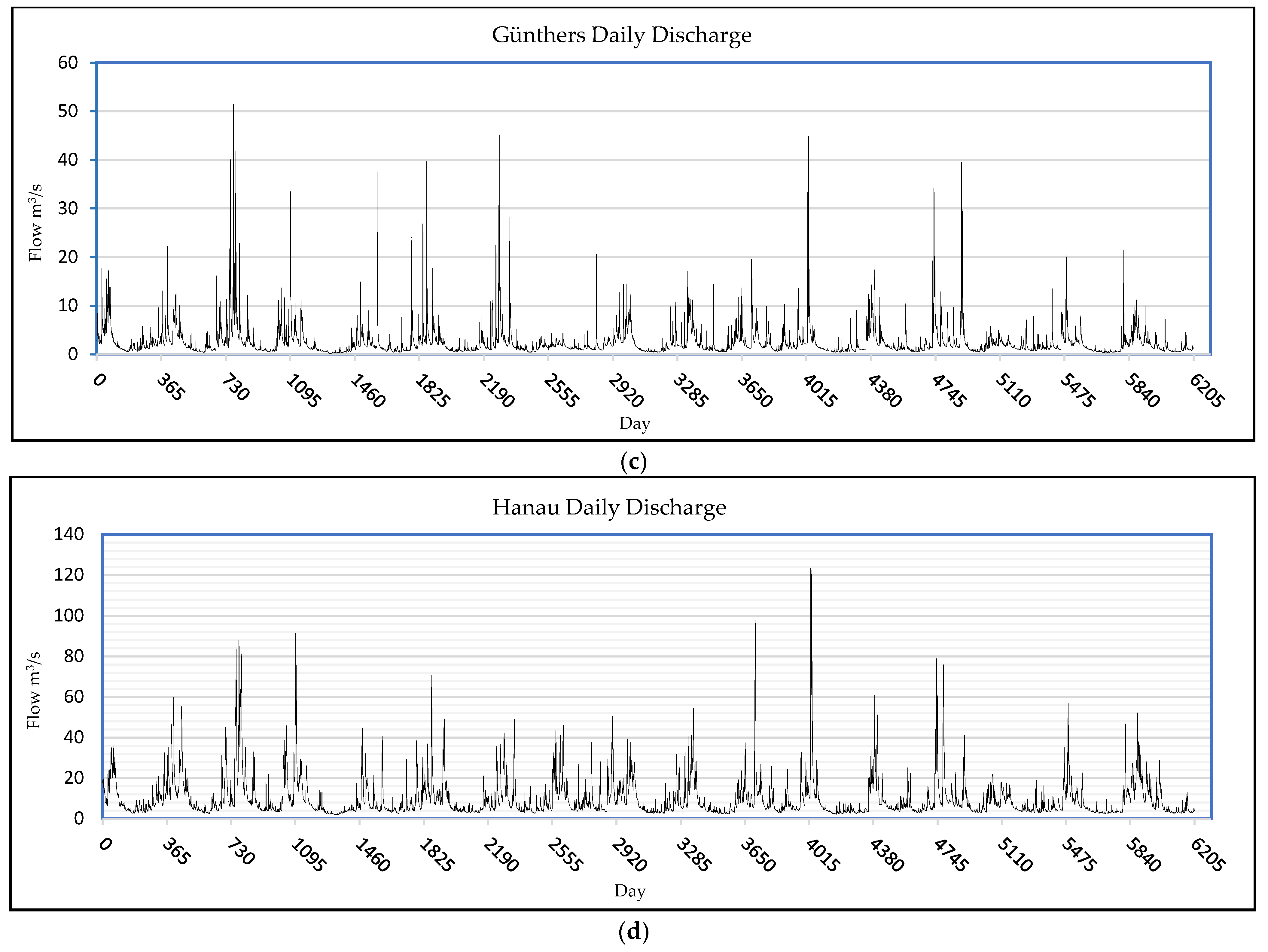
2.2.1. Description
2.2.2. Preprocessing
2.3. Methodology
2.3.1. Augmented Dickey Fuller Test (ADF)
2.3.2. Fuzzy C-Mean Cluster (FCM)
2.3.3. ARIMA Model
2.3.4. Performance Metric
3. Results
3.1. Normalization
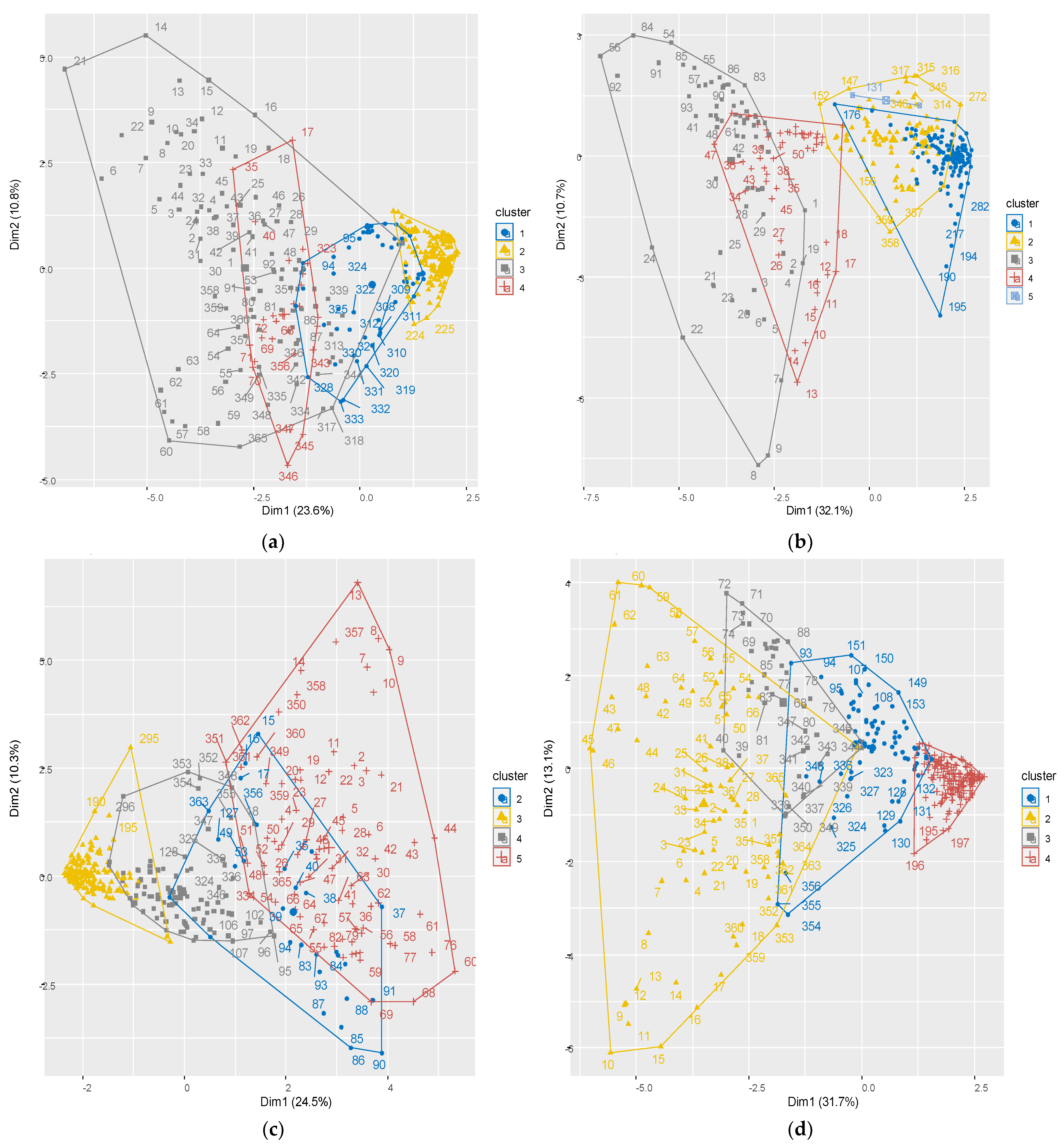
3.2. Clustering
3.3. Modeling
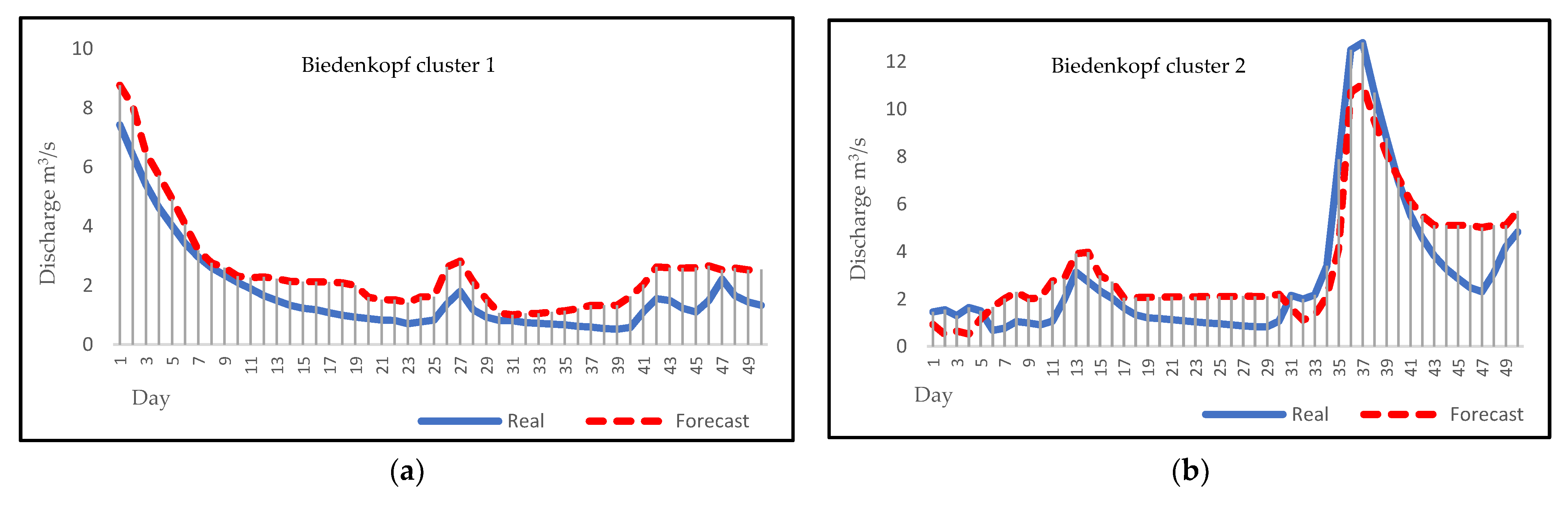
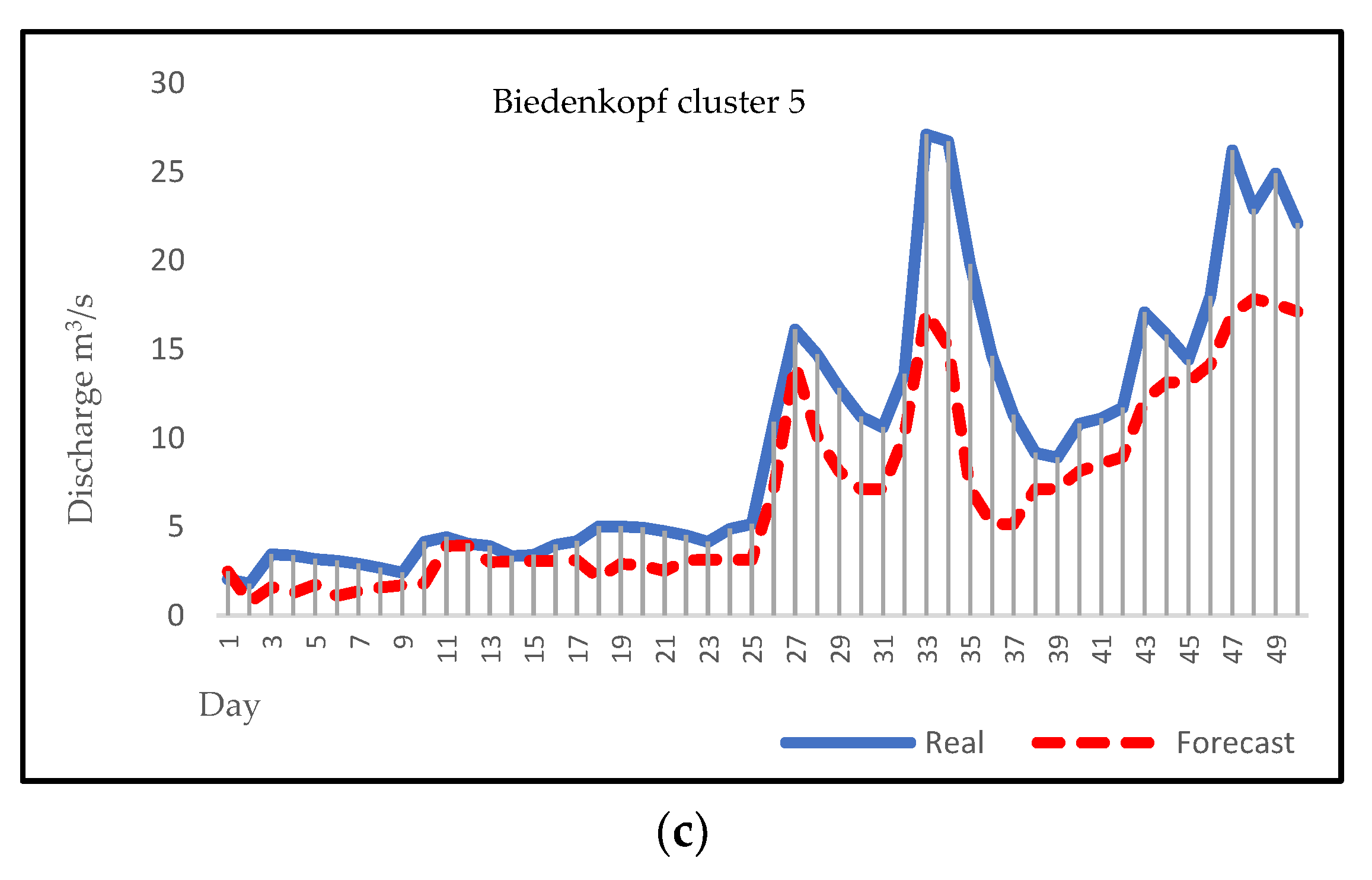
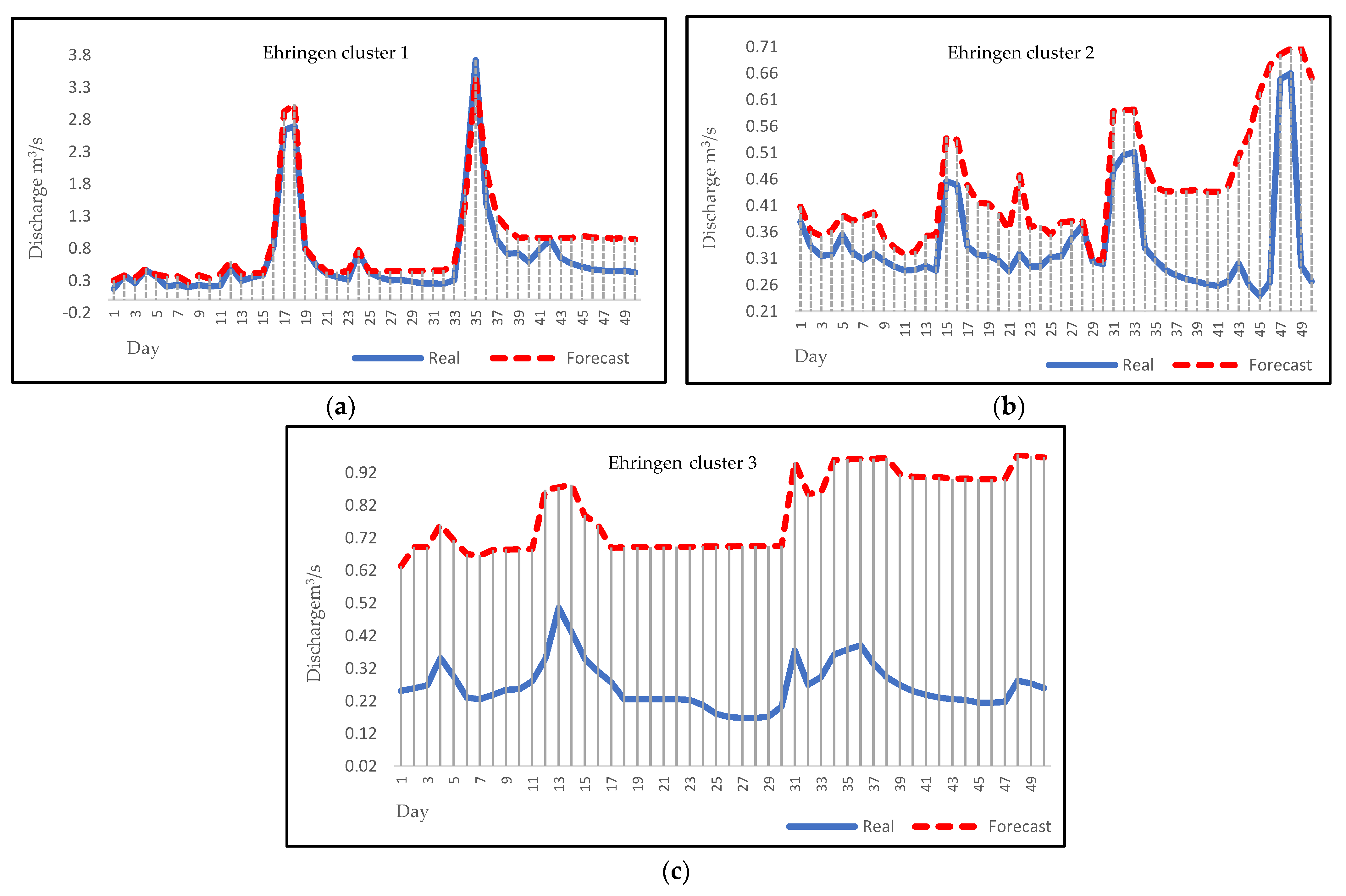
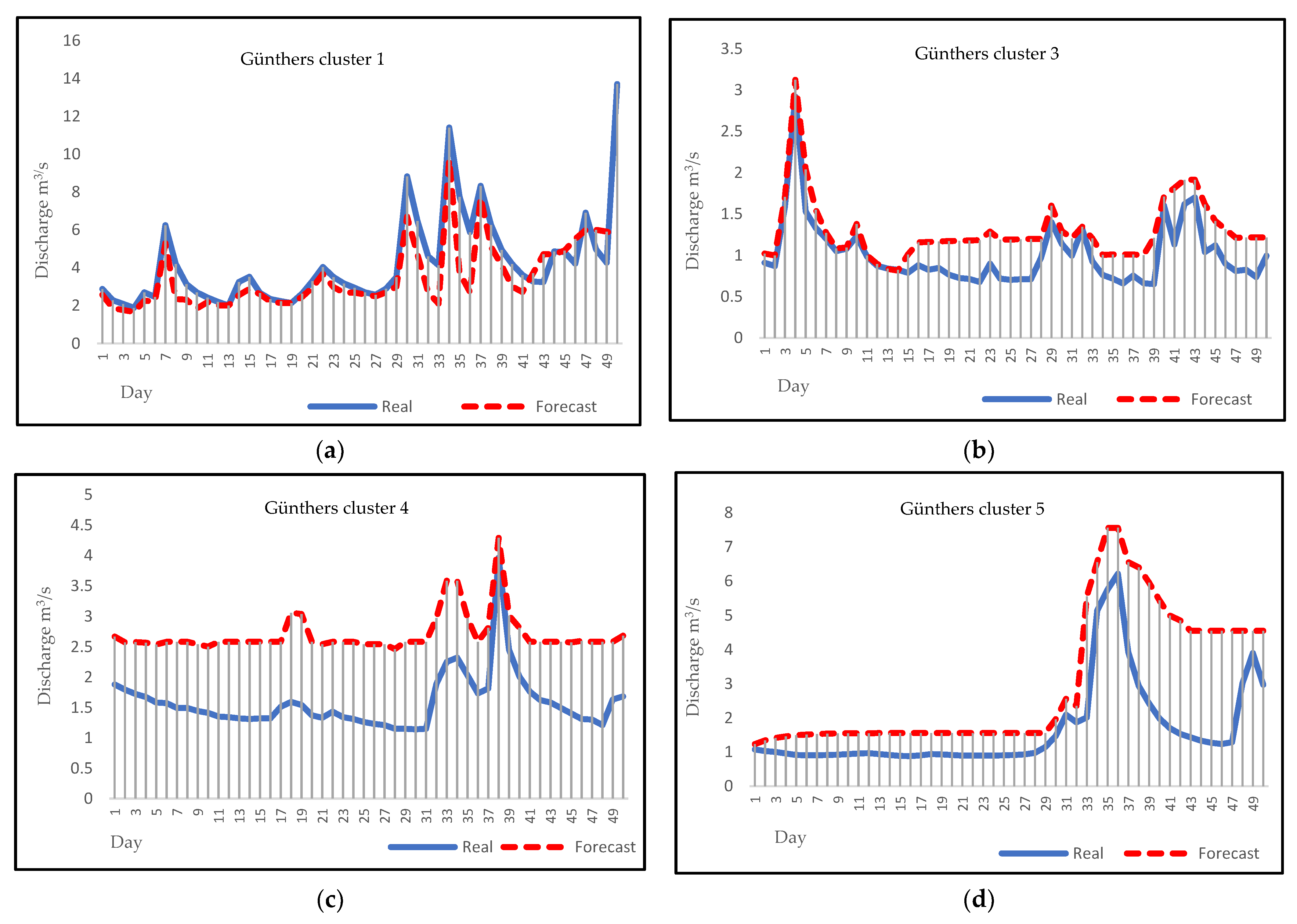
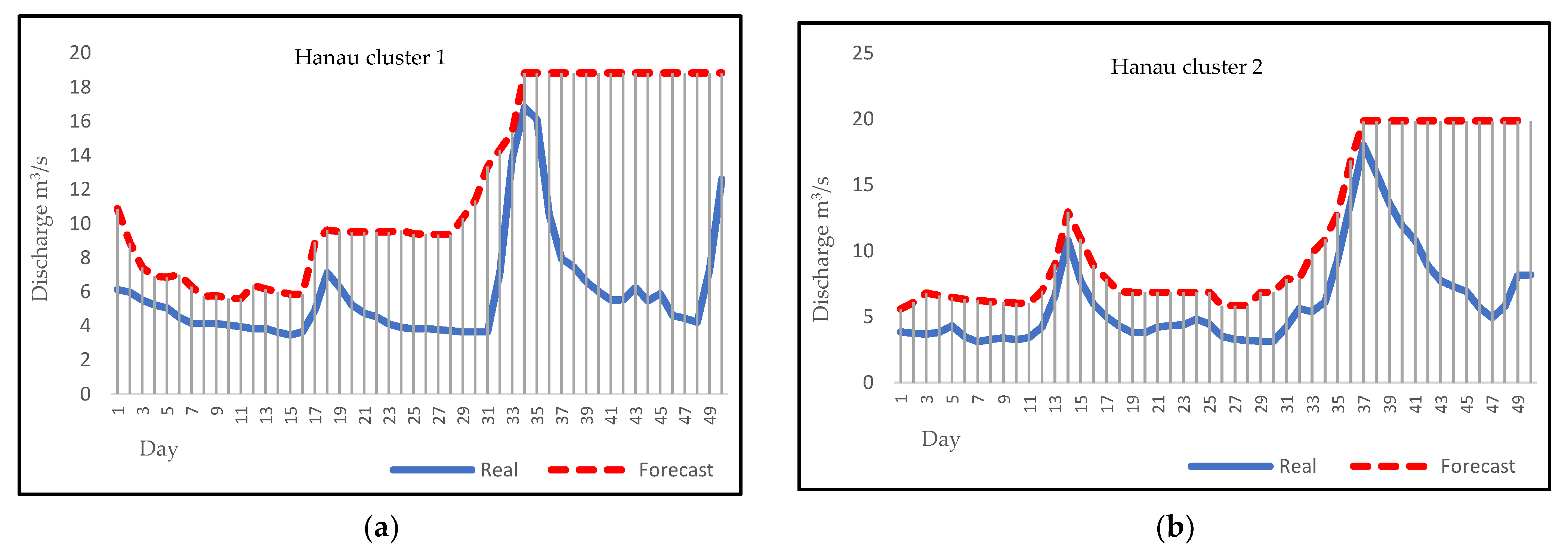
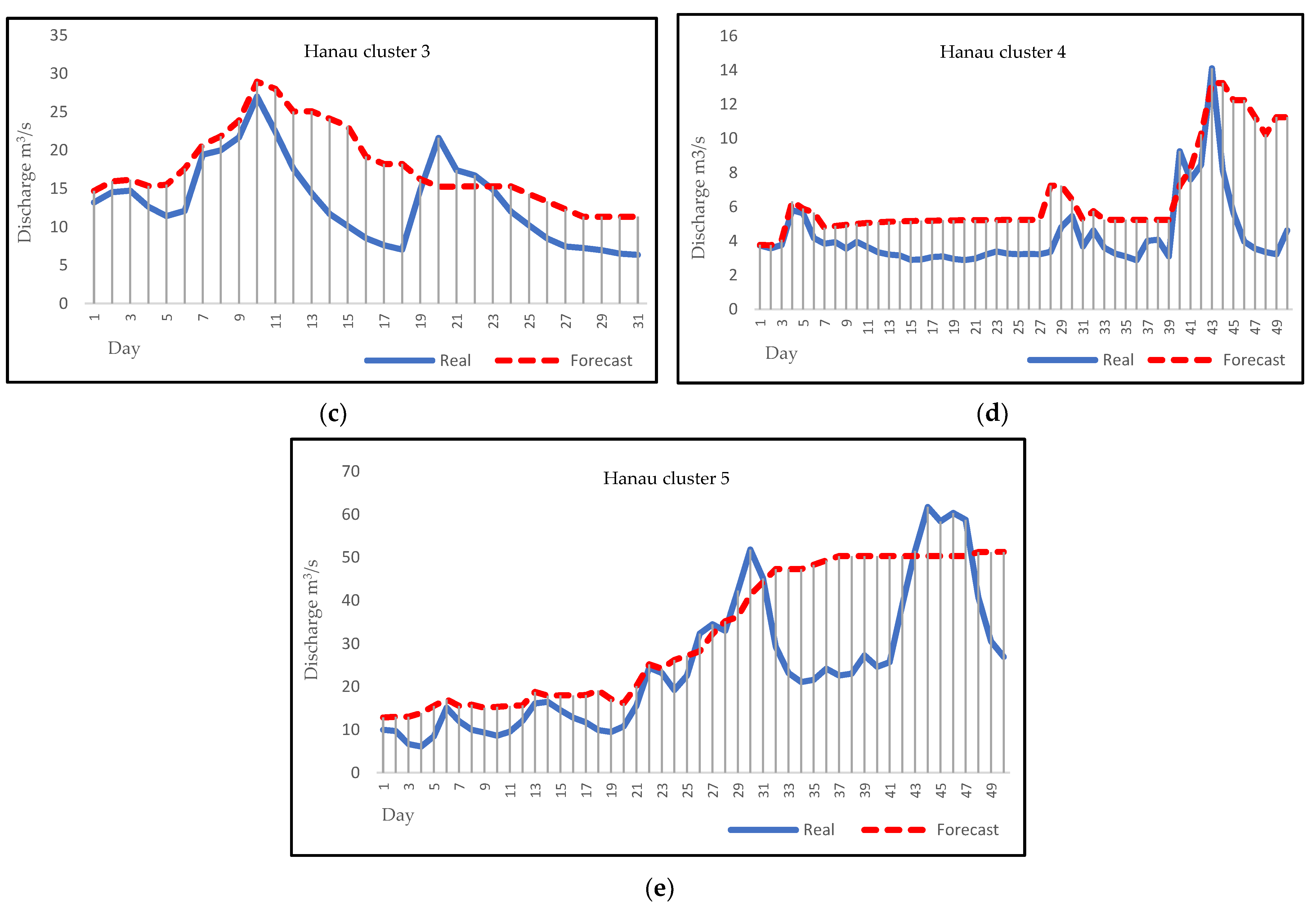
3.4. Forecasting
4. Discussion
5. Conclusions and Outlook
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bai, Y.; Wang, P.; Li, C.; Xie, J.; Wang, Y. A multi-scale relevance vector regression approach for daily urban water demand forecasting. J. Hydrol. 2014, 517, 236–245. [Google Scholar] [CrossRef]
- Abbaspour, K.C.; Faramarzi, M.; SeyedGhasemi, S.; Yang, H. Assessing the impact of climate change on water resources in Iran. Water Resour. Res. 2009, 45, W10434. [Google Scholar] [CrossRef] [Green Version]
- Tekieh, M.H.; Raahemi, B. Importance of data mining in healthcare: A survey. In Proceedings of the ACM International Conference on Advances in Social Networks Analysis and Mining, Paris, France, 25–28 August 2015. [Google Scholar]
- Lee, S.J.; Siau, K. A review of data mining techniques. Ind. Manag. Data Syst. 2001, 101, 41–46. [Google Scholar] [CrossRef] [Green Version]
- Weiss, S.M.; Indurkhya, N. Predictive Data Mining: A Practical Guide, 1st ed.; Morgan Kaufmann Publishers, Inc.: San Francisco, CA, USA, 1998; pp. 1–2. [Google Scholar]
- Fayyad, U.; Piatetsky-Shapiro, G.; Smyth, P. From Data Mining to knowledge Discovery in Databases. Al Mag. 1996, 17, 37–54. [Google Scholar] [CrossRef]
- Coenen, F. Data mining: Past, Present and Future. Knowl. Eng. Rev. 2011, 26, 25–29. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, S. Application Research of Data Mining Technology in Personal Privacy Protection and Material Data Analysis. Integr. Ferroelectr. 2021, 216, 29–42. [Google Scholar] [CrossRef]
- Ekasingh, B.; Ngamsomsuke, K.; Letcher, R.A.; Spate, J. A data mining approach to simulating farmers’ crop choices for integrated water resources management. J. Environ. Manag. 2005, 77, 315–325. [Google Scholar] [CrossRef]
- Habibipour, A.; Mahjoubi, J.; Dastourani, M.T. Investigation of ability of some data mining methods in studies related to water resources. In Proceedings of the First Regional Water Resources Development Conference, Azad University, Abar Kooh, Iran, 19 May 2011. [Google Scholar]
- Wei, W.; Watkins, D.W., Jr. Data Mining Methods for Hydro Climatic Forecasting. Adv. Water Resour. 2011, 34, 1390–1400. [Google Scholar] [CrossRef]
- Nourani, V.; Sattari, M.T.; Molajou, A. Threshold-Based Hybrid Data Mining Method for Long-Term Maximum Precipitation Forecasting. Water Resour. Manag. 2017, 31, 2645–2658. [Google Scholar] [CrossRef]
- Berkhin, P. Grouping Multidimensional Data, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2006; pp. 25–71. [Google Scholar]
- Luczak, A.; Kalinowski, S. Fuzzy Clustering Methods to Identify the Epidemiological Situation and Its Changes in European Countries during COVID-19. Entropy 2021, 24, 14. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, C.; Tang, W.J.; Wie, Z.W. Medical Image Segmentation Using Improved FCM. Sci. China Inf. Sci. 2012, 55, 1052–1061. [Google Scholar] [CrossRef] [Green Version]
- Aydogdu, M.; Firat, M. Estimation of Failure Rate in Water Distribution Network Using Fuzzy Clustering and LS-SVM Methods. Water Resour. Manag. 2014, 29, 1575–1590. [Google Scholar] [CrossRef]
- Mosavi, A.; Golshan, M.; Choubin, B.; Ziegler, A.D.; Sigaroodi, S.K.; Zhang, F.; Dineva, A.A. Fuzzy clustering and distributed model for streamflow estimation in ungauged watersheds. Sci. Rep. 2021, 11, 8243. [Google Scholar] [CrossRef] [PubMed]
- Latt, Z.Z.; Wittenberg, H.; Urban, B. Clustering Hydrological Homogeneous Regions and Neural Network Based Index Flood Estimation for Ungauged Catchments: An Example of the Chindwin River in Myanmar. Water Resour. Manag. 2015, 29, 913–928. [Google Scholar] [CrossRef]
- Maruyama, T.; Kawachi, T.; Singh, V.P. Entropy-based assessment and clustering of potential water resources availability. J. Hydrol. 2005, 309, 104–113. [Google Scholar] [CrossRef]
- Ebrahimi Varzane, A.; Zarei, H.; Tishehzan, P.; Akhondali, A.M. Evaluation of Groundwater-Surface Water Interaction by Using Cluster Analysis (Case Study: Western Part of Dezful-Andimeshk Plain). Iran-Water Resour. Res. 2019, 15, 246–257. [Google Scholar]
- Kottegoda, N.T. Stochastic Water Resources Technology, 1st ed.; The Macmillan Press Ltd.: London, UK, 1980; pp. 20–21. [Google Scholar]
- Jones, R.H.; Brelsford, W.M. Time Series with Periodic Structure. Biometrika 1967, 54, 403–408. [Google Scholar] [CrossRef]
- Pagano, M. On Periodic and Multiple Autoregression. Inst. Math. Stat. 1978, 6, 1310–1317. Available online: https://www.jstor.org/stable/2958718 (accessed on 20 October 2022). [CrossRef]
- Troutman, B.M. Some Results in Periodic Autoregression. Biometrika 1979, 66, 219–228. [Google Scholar] [CrossRef]
- Ula, T.A. Periodic covariance stationarity of multivariate periodic autoregressive moving average processes. Water Resour. Manag. 1990, 26, 855–861. [Google Scholar] [CrossRef]
- Ula, T.A. Forecasting of Multivariate Periodic Autoregressive Moving-Average Process. J. Time Ser. Anal. 1993, 14, 645–657. [Google Scholar] [CrossRef]
- Puech, T.; Boussard, M.; D’Amato, A.; Millerand, G. A Fully Automated Periodicity Detection in Time Series. In Proceedings of the International Workshop on Advanced Analysis and Learning on Temporal Data, Cham, Germany, 23 January 2020. [Google Scholar]
- Brittanica. Available online: https://www.britannica.com/place/Hessen (accessed on 20 October 2022).
- Deutscher Wetterdienst (German Weather Service). DWD (2022): Nationaler Klimareport (National Climate Report), 6th ed.; Deutscher Wetterdienst (German Weather Service): Offenbach, Germany, 2022; 53p, ISBN 978-3-88148-536-4. [Google Scholar]
- DGJ (2017): Deutsche Gewässerkundliche Jahrbücher des Bundes und der Länder (German Hydrographic Yearbook), with Ehringen/Erpe ID 44480552 (Wesergebiet), Hanau/Kinzig ID 24784259 (Rheingebiet, Teil II, Main), Biedenkopf/Lahn ID 25810558 (Rheingebiet, Teil III), Günthers/Ulster ID 41450056 (Wesergebiet). Available online: https://www.lfu.bayern.de/wasser/wasserstand_abfluss/dgj/index.htm#:~:text=Das%20Deutsche%20Gew%C3%A4sserkundliche%20Jahrbuch%20(DGJ,und%20K%C3%BCstengebiete%20in%2010%20Teilb%C3%A4nden.&text=werden%20vom%20Bayerischen%20Landesamt%20f%C3%BCr,hydrologische%20Kenngr%C3%B6%C3%9Fen%20ausgew%C3%A4hlter%20Messstellen%20ver%C3%B6ffentlicht (accessed on 22 October 2022).
- RP Kassel (2013): Hochwasserrisikomanagementplan für das Hessische Einzugsgebiet der Diemel und Weser; Regierungspräsidium (Regional Commission): Kassel, Germany, 2013; 171p.
- Kakouei, K.; Domisch, S.; Kiesel, J.; Kail, J.; Jähnig, S.C. Climate model variability leads to uncertain predictions of the future abundance of stream macroinvertebrates. Sci. Rep. 2020, 10, 2520. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Herrig, I.M.; Böer, S.I.; Brennholt, N.; Manz, W. Development of multiple linear regression models as predictive tools for fecal indicator concentrations in a stretch of the lower Lahn River, Germany. Water Res. 2015, 85, 148–157. [Google Scholar] [CrossRef] [PubMed]
- Trabert, A.; Opp, C. Long-term trends in flood discharges of the Ulster and Upper Fulda (Germany): A statistical review. Environ. Earth Sci. 2016, 75, 1363. [Google Scholar] [CrossRef]
- Khazaiee, M.; Khalili, K.; Behmanesh, J. Investigating the relationship between physical characteristics of watersheds and nonlinearity of daily streamflow processes. Int. J. Water 2018, 12, 141–157. [Google Scholar] [CrossRef]
- Wang, W.; Wriggling, J.K.; Van Gelder, P.H.A.J.M.; Ma, J. Testing for nonlinearity of streamflow process at different time scale. J. Hudrol. 2006, 322, 247–268. [Google Scholar] [CrossRef]
- Khalili, K. Comparison pf geostatistical methods for interpolation ground water level (Case Study: Lake Urmia basin). J. Appl. Environ. Biol. Sci. 2014, 4, 15–23. [Google Scholar]
- Jarvis, D.; Stoeckl, N.; Chaiechi, T. Applying econometric Techniques to hydrological problems in a large basin: Quantifying the rainfall-discharge relationship in the Burdekin, Queensland, Australia. J. Hydrol. 2013, 496, 107–121. [Google Scholar] [CrossRef]
- Khalili, K.; Nazeri Tahrudi, M.; Khanmohammadi, N. Trend Analysis of precipitation in recent two decades over Iran. J. Appl. Environ. Biol. Sci. 2014, 4, 5–10. [Google Scholar]
- Khalili, K.; Nazeri Tahrudi, M.; Abbaszadeh Afshar, M.; Nazeri Tahroudi, Z. Modeling monthly mean air temperature using SAMS2007 (case study: Urmia synoptic station). J. Middle East Appl. Sci. Technol. 2014, 15, 578–583. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Distribution of the estimators for autoregressive time series with a unit root. J. Am. Stat. Assoc. 1979, 74, 423–431. [Google Scholar] [CrossRef]
- Said, S.E.; Dickey, D. Testing for unit roots in autoregressive moving average models with unknown order. Biometrica 1984, 71, 599–607. [Google Scholar] [CrossRef]
- Patil, S.D.; Steiglitz, M. Comparing Spatila and Temporal Transferability of Hydrological Model Parameters. J. Hydrol. 2015, 525, 409–417. [Google Scholar] [CrossRef] [Green Version]
- Choubin, B.; Solaimani, K.; Habibnejad Roshan, M.; Malekian, A. Watershed Classification by remote sensing indices: A Fuzzy C-mean Clustering Approach. J. Mt. Sci. 2017, 14, 2053–2063. [Google Scholar] [CrossRef]
- Li, Q.; Wu, X.; Zheng, J.; Wu, B.; Jian, H.; Sun, C.; Tang, Y. Determination of Pork Meat Storage Time Using Near-Infrared Spectroscopy Combined with Fuzzy Clustering Algorithms. Foods 2022, 11, 2101. [Google Scholar] [CrossRef]
- Atashi, V.; Taheri Gorji, H.; Shahabi, S.M.; Kardan, R.; Howe Lim, Y. Water Level Forecasting Using Deep Learning Time-Series Analysis: A Case Study of Red River of the North. Water 2022, 14, 1971. [Google Scholar] [CrossRef]
- Hadizadeh, R.; Eslamian, S. Hand Book of Drought and Water Scarcity, 1st ed.; CRC Press: Boka Raton, FL, USA, 2017; pp. 569–588. [Google Scholar]
- Attar, N.F.; Khalili, K.; Behmanesh, J.; Khanmohammadi, N. On the reliability of soft computing methods in the estimation of dew point temperature: The case of arid regions of Iran. Comput. Electron. Agric. 2018, 153, 334–346. [Google Scholar] [CrossRef]
- Khalili, K.; Ahmadi, F.; Dinpashoh, Y.; Behmanesh, J. Linear and Non-linear Behavior Analysis of Hydrological Time Series (Case study: Western Rivers of Lake Urmia). Iran. Water Resour. Res. 2014, 10, 12–20. [Google Scholar]
- Ho, S.L.; Xie, M.; Goh, T.N. A Comparative Study of Neural Network and Box-Jenkins ARIMA Modeling in Time Series Prediction. Comput. Ind. Eng. 2002, 42, 371–375. [Google Scholar] [CrossRef]
- Hadizade, R.; Eslamian, S.; Chinipardaz, R. Investigation of long memory properties in stream flow time series in Gamasiab River, Iran. Int. J. Hydrol. Sci. Technol. 2013, 3, 319–350. [Google Scholar] [CrossRef]
- Ghimire, B.N. Application of ARIMA model for River Discharge Analysis. Nepal Phys. Soc. 2017, 4, 27–32. [Google Scholar] [CrossRef] [Green Version]
- Yürekli, K.; Kurunç, A.; Öztürk, F. Testing the residuals of an ARIMA model on the Cekerek Stream Watershed in Turkey. Turk. J. Eng. Environ. Sci. 2005, 29, 61–74. [Google Scholar]
- Mancini, S.; Francavilla, A.B.; Longobardi, A.; Viccione, G.; Guarnaccia, C. Predicting Daily Water Tank Level Fluctuations by Using ARIMA Model, A Case Study. In Proceedings of the 5th International Conference on Applies Physics, Simulation and Computing (APSAC 2021), Salerno, Italy, 3–5 September 2021. [Google Scholar]
- Kumar, R.; Kumar, P.; Kumar, Y. Multi-Step Time Series Analysis and Forecasting Strategy Using ARIMA and Evolutionary Algorithms. Int. J. Inf. Technol. 2022, 14, 359–373. [Google Scholar] [CrossRef]
- Gui, H.; Wu, Z.; Zhang, C. Comparative Study of Different Types of Hydrological Models Applied to Hydrological Simulation. Clean Soli Air Water 2021, 49, 2000381. [Google Scholar] [CrossRef]
- Al Sayah, M.J.; Abdallah, C.; Khouri, M.; Nedjai, R.; Darwich, T. A Framework for Climate Change Assessment in Mediterranean Data-Sparse Watershed Using Remote Sensing and ARIMA Modeling. Theor. Appl. Climatol. 2021, 143, 639–658. [Google Scholar] [CrossRef]
- Ren, H.; Cromwell, E.; Chen, X. Technical Note: Using Long Short-Term Memory Models to Fill Data Gaps in Hydrological Monitoring Networks. Hydrol. Earth Syst. Sci. 2022, 26, 1727–1743. [Google Scholar] [CrossRef]
- Mehdi, H.; Pooranian, Z.; Vinueza Naranjo, P.G. Cloud Traffic Prediction Based on Fuzzy ARIMA Model with Low Dependence on Historical Data. Emerg. Telecommun. Technol. 2019, 33, e3731. [Google Scholar] [CrossRef]
- Yu, Z.; Jiang, Z.; Lei, G.; Liu, F. ARIMA Modeling and Forecasting of Water Level in the Middle Reach of the Yangtze River. In Proceedings of the 4th International Conference on Transportation Information and Safety (ICTIS), Banff, AB, Canada, 8–10 August 2017. [Google Scholar]

| Station | Period | Samples | Average (m3/s) | Standard Deviation (m3/s) | Skewness (m3/s) | Kurtosis (m3/s) |
|---|---|---|---|---|---|---|
| Biedenkopf | 2000–2017 | 6570 | 5.11 | 7.91 | 4.24 | 27.38 |
| Ehringen | 2000–2017 | 6570 | 0.64 | 0.59 | 7.57 | 128.89 |
| Günthers | 2000–2017 | 6570 | 2.56 | 3.29 | 5.51 | 47.01 |
| Hanau | 2000–2017 | 6570 | 9.91 | 10.20 | 3.55 | 19.65 |
| Station | Lag | ADF Unit Root | Result | |
|---|---|---|---|---|
| ADF Statistic | p-Value | |||
| Biedenkopf | 4 | −14.42241 | 0 | Stationary |
| Ehringen | 13 | −7.734843 | 0 | Stationary |
| Günthers | 10 | −11.47729 | 0 | Stationary |
| Hanau | 6 | −12.90913 | 0 | Stationary |
| Station | Clusters | No of Cluster | Days | Average (m3/s) | Standard Deviation (m3/s) | Skewness (m3/s) | Kurtosis (m3/s) | |
|---|---|---|---|---|---|---|---|---|
| Before Editing | After Editing | |||||||
| Biedenkopf | 4 | 3 | 2 | 1–81 | 9.91 | 11.31 | 3.04 | 12.66 |
| 1 | 82–299 | 2.63 | 4.14 | 5.86 | 59.38 | |||
| 5 | 300–365 | 7.42 | 8.84 | 3.43 | 20.55 | |||
| Ehringen | 5 | 3 | 3 | 1–107 | 0.95 | 0.67 | 3.66 | 22.57 |
| 2 | 108–189 | 0.60 | 0.54 | 12.64 | 265.76 | |||
| 1 | 190–365 | 0.48 | 0.48 | 13.61 | 365.05 | |||
| Günthers | 4 | 4 | 5 | 1–90 | 4.46 | 4.67 | 4.21 | 25.73 |
| 4 | 91–151 | 2.52 | 2.86 | 6.85 | 65.60 | |||
| 3 | 152–295 | 1.26 | 1.44 | 9.87 | 161.24 | |||
| 1 | 296–365 | 2.85 | 2.93 | 4.50 | 33.55 | |||
| Hanau | 4 | 5 | 2 | 1–59 | 18.19 | 15.74 | 2.73 | 9.97 |
| 3 | 60–90 | 15.18 | 11.09 | 2.11 | 6.31 | |||
| 1 | 91–151 | 8.57 | 6.70 | 2.68 | 9.08 | |||
| 4 | 152–304 | 5.34 | 3.95 | 4.04 | 22.39 | |||
| 5 | 305–365 | 12.02 | 9.90 | 2.24 | 6.91 | |||
| Station | Cluster | Model | Coefficients | AIC | RMSE | |
|---|---|---|---|---|---|---|
| p | q | |||||
| Biedenkopf | 1 | ARMA (2,2) | 1.7309 | −0.6591 | 2948.53 | 0.351 |
| −0.7386 | −0.1691 | |||||
| 2 | ARMA (2,2) | 1.5614 | −0.2682 | −793.42 | 0.183 | |
| −0.6116 | −0.1553 | |||||
| 5 | ARMA (1,2) | 0.9088 | 0.3375 | 855.98 | 0.345 | |
| 0.0663 | ||||||
| Ehringen | 1 | ARMA (3,1) | 1.5526 | −0.8009 | 3409.21 | 0.413 |
| −0.6217 | ||||||
| 0.0598 | ||||||
| 2 | ARMA (1,2) | 0.9713 | −0.5694 | 2859.04 | 0.634 | |
| −0.1744 | ||||||
| 3 | ARMA (2,2) | 1.5592 | −0.4584 | 871.71 | 0.302 | |
| −0.5718 | −0.3568 | |||||
| Günthers | 1 | ARMA (1,2) | 0.8925 | 0.0967 | 952.29 | 0.351 |
| −0.1803 | ||||||
| 3 | ARMA (2,2) | 1.5167 | −0.6099 | −0.04 | 0.241 | |
| −0.5324 | −0.135 | |||||
| 4 | ARMA (1,1) | 0.8952 | −0.5683 | 2718.4 | 0.831 | |
| 5 | ARMA (1,1) | 0.8292 | 0.2832 | 861.77 | 0.314 | |
| Hanau | 1 | ARMA (1,3) | 0.9226 | 0.1881 | 1092.25 | 0.395 |
| −0.2797 | ||||||
| −0.1445 | ||||||
| 2 | ARMA (2,1) | 1.2575 | 0.1114 | −2045.8 | 0.091 | |
| −0.3416 | ||||||
| 3 | ARMA (2,0) | 1.2172 | 0 | −541.66 | 0.147 | |
| −0.276 | ||||||
| 4 | ARMA (2,2) | 1.6488 | −0.6361 | −9711.9 | 0.413 | |
| −0.6589 | −0.2077 | |||||
| 5 | ARMA (1,2) | 0.8849 | 0.3871 | −73.8 | 0.232 | |
| 0.0541 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khazaeiathar, M.; Hadizadeh, R.; Fathollahzadeh Attar, N.; Schmalz, B. Daily Streamflow Time Series Modeling by Using a Periodic Autoregressive Model (ARMA) Based on Fuzzy Clustering. Water 2022, 14, 3932. https://doi.org/10.3390/w14233932
Khazaeiathar M, Hadizadeh R, Fathollahzadeh Attar N, Schmalz B. Daily Streamflow Time Series Modeling by Using a Periodic Autoregressive Model (ARMA) Based on Fuzzy Clustering. Water. 2022; 14(23):3932. https://doi.org/10.3390/w14233932
Chicago/Turabian StyleKhazaeiathar, Mahshid, Reza Hadizadeh, Nasrin Fathollahzadeh Attar, and Britta Schmalz. 2022. "Daily Streamflow Time Series Modeling by Using a Periodic Autoregressive Model (ARMA) Based on Fuzzy Clustering" Water 14, no. 23: 3932. https://doi.org/10.3390/w14233932







