Numerical Analysis of Wind Effect on Wave Overtopping on a Vertical Seawall
Abstract
:1. Introduction
- -
- to verify the ability of these numerical models to correctly reproduce the influence of wind on the overtopping rate, even though simplified wind modelling has been used;
- -
- to clarify how the wind acts and how its effect on the enhancement of the overtopping rate changes depending on the overtopping regime.
2. Literature
3. Numerical Models
3.1. FLOW-3D
The CFD Wind Stress Model
- ρa is the density of air (1.225 kg m−3),
- U10 is the wind velocity at 10 m above the water surface,
- CD10 is the wind shear coefficient (or drag coefficient).
3.2. SWASH
The SWASH Wind Stress Model
4. Experiments
4.1. Geometry of the Structure and Foreshore
4.2. Wind Model Implementation
4.3. CFD Numerical Setup
4.4. SWASH Numerical Setup
5. Results
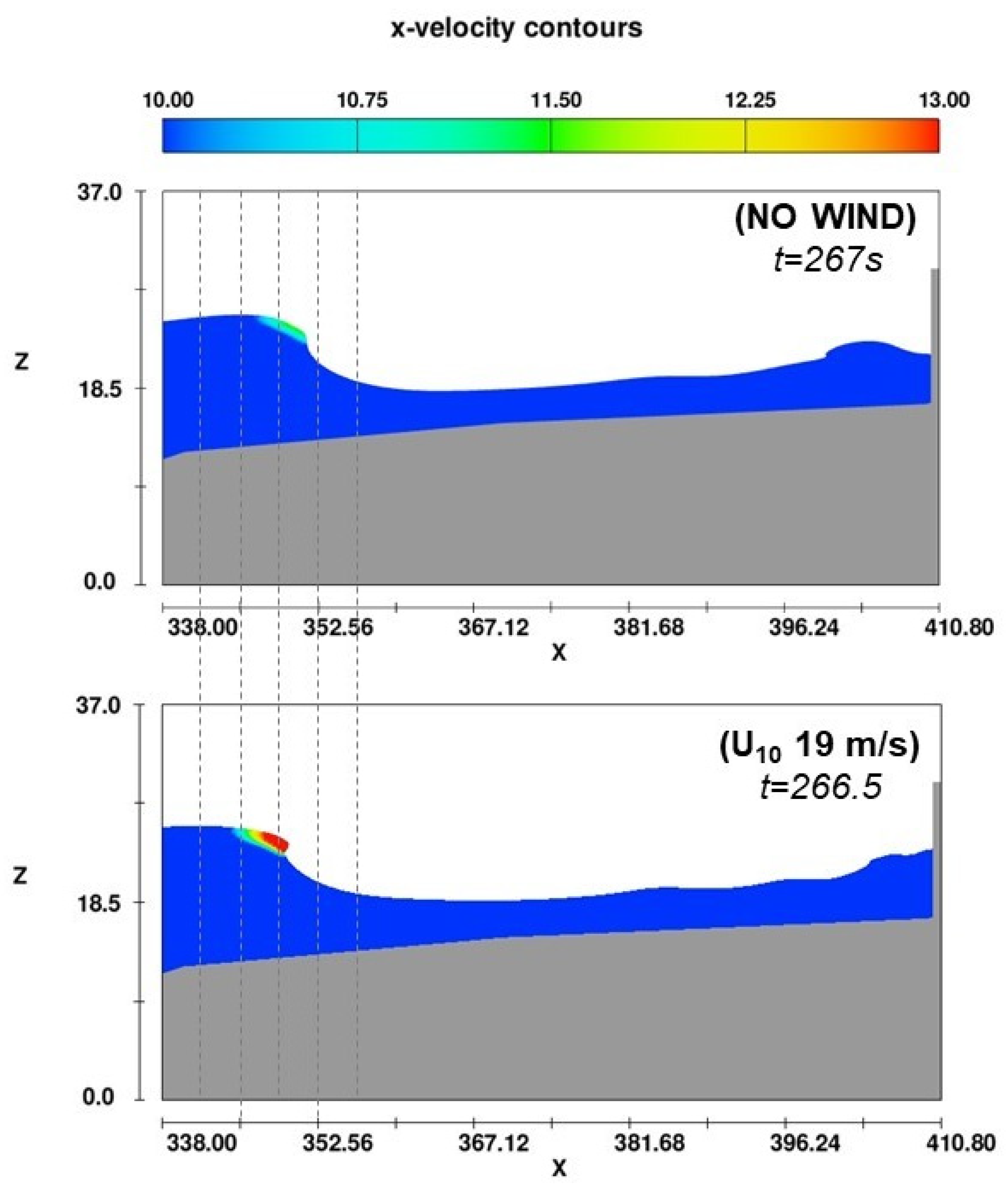
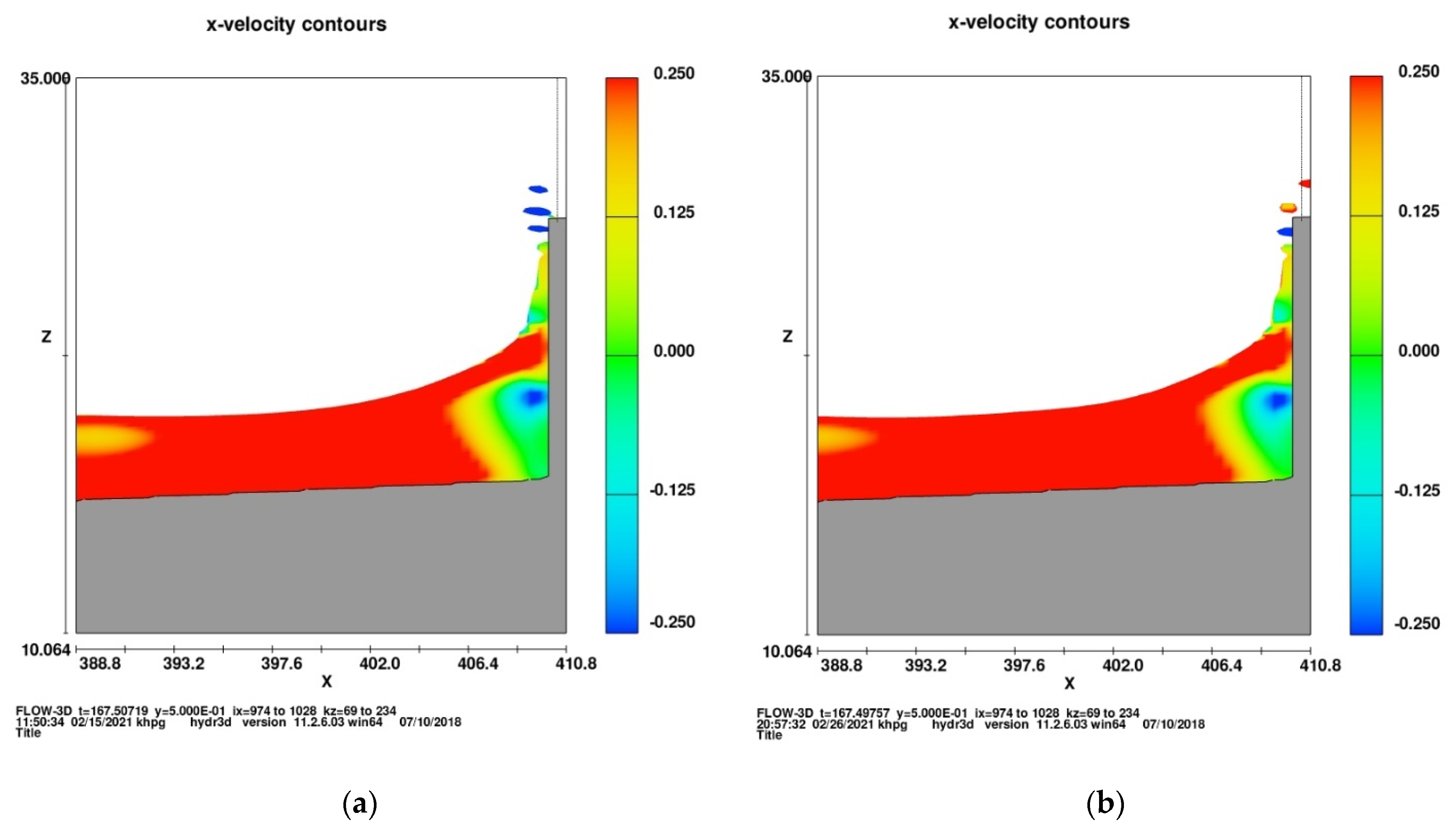
5.1. Physical Processes and Basic Definitions
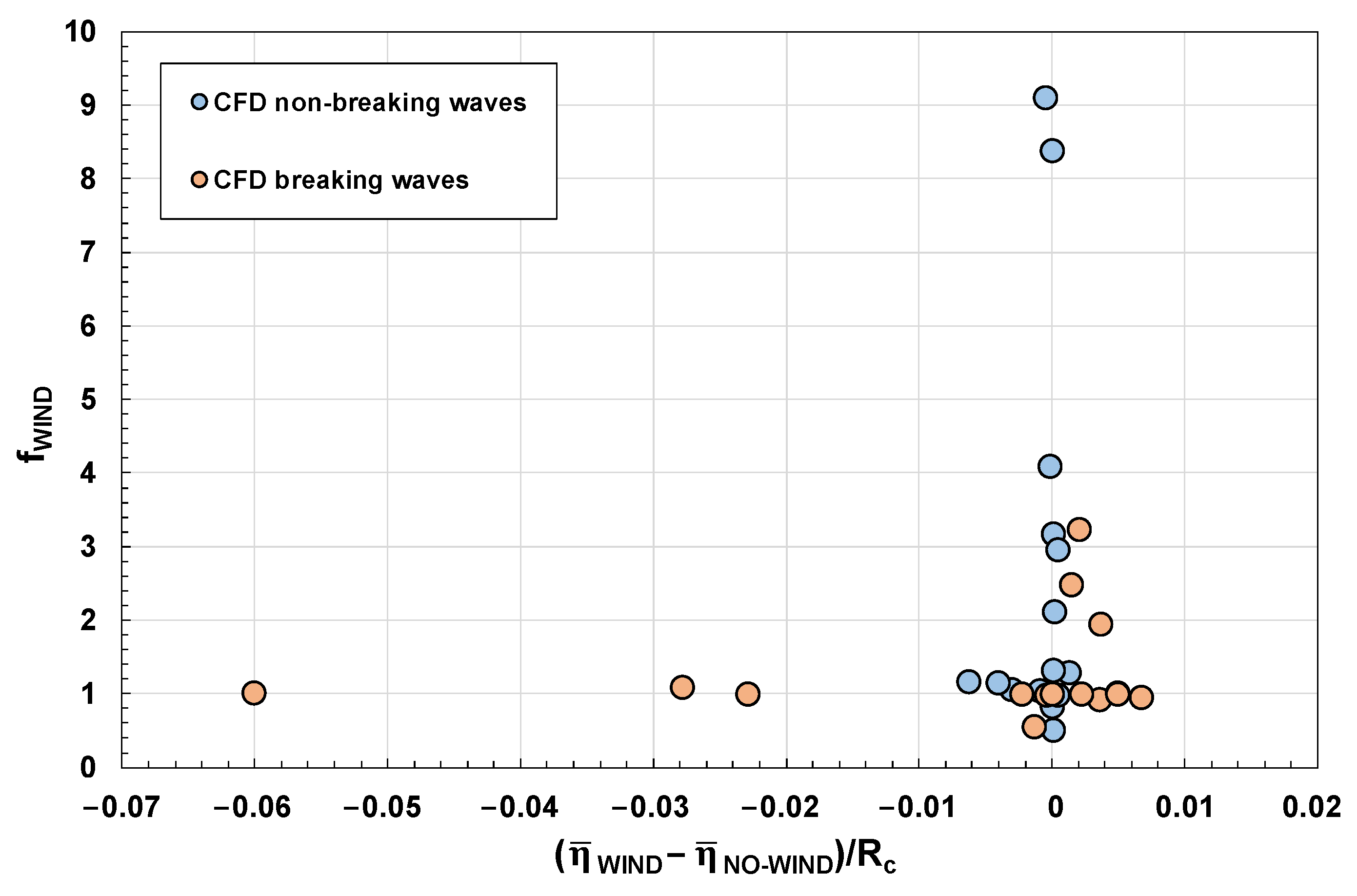
5.2. On the Role of the Mean Water Level
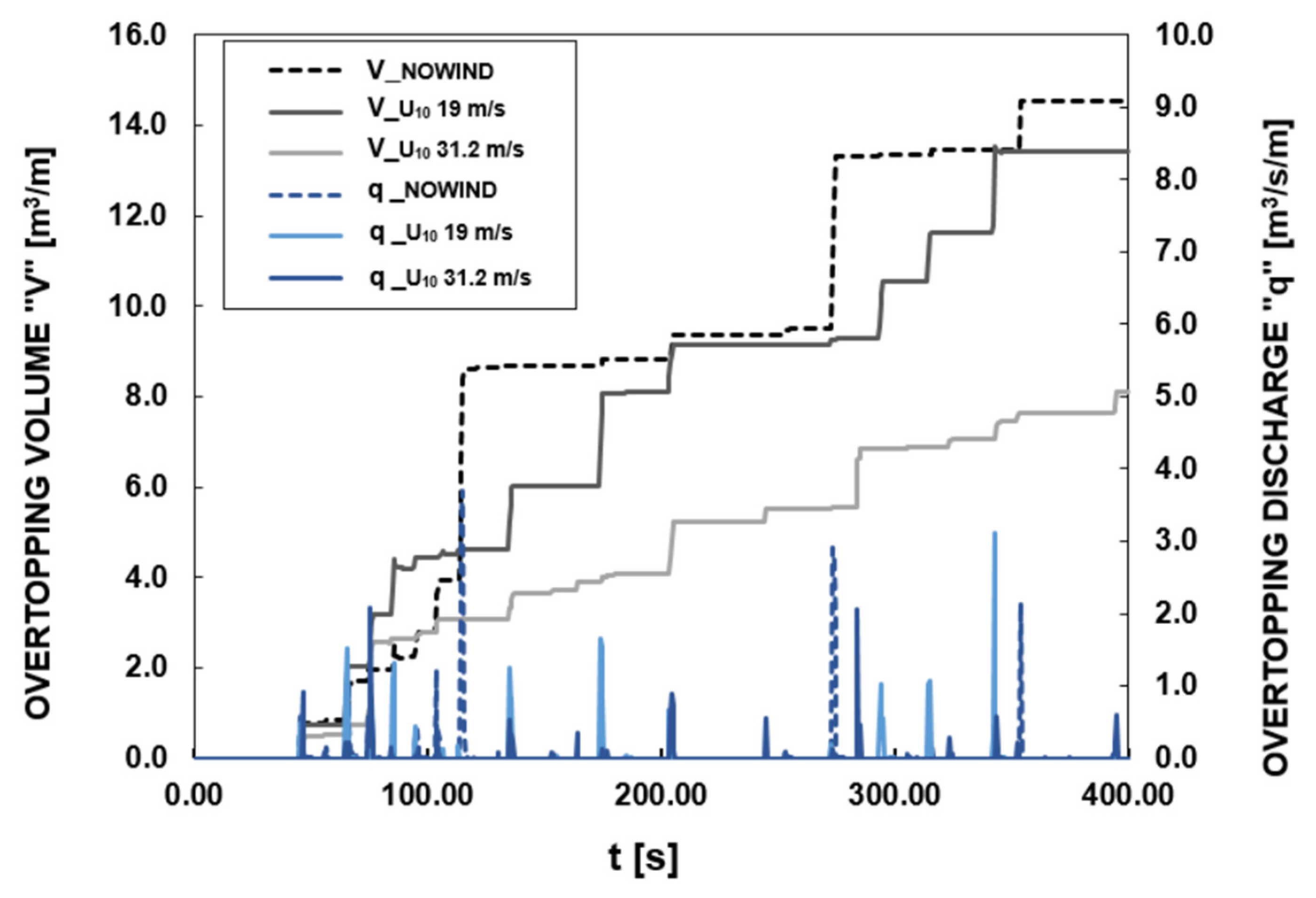
5.3. Wind Stress, Wave Profiles and Overtopping Rates
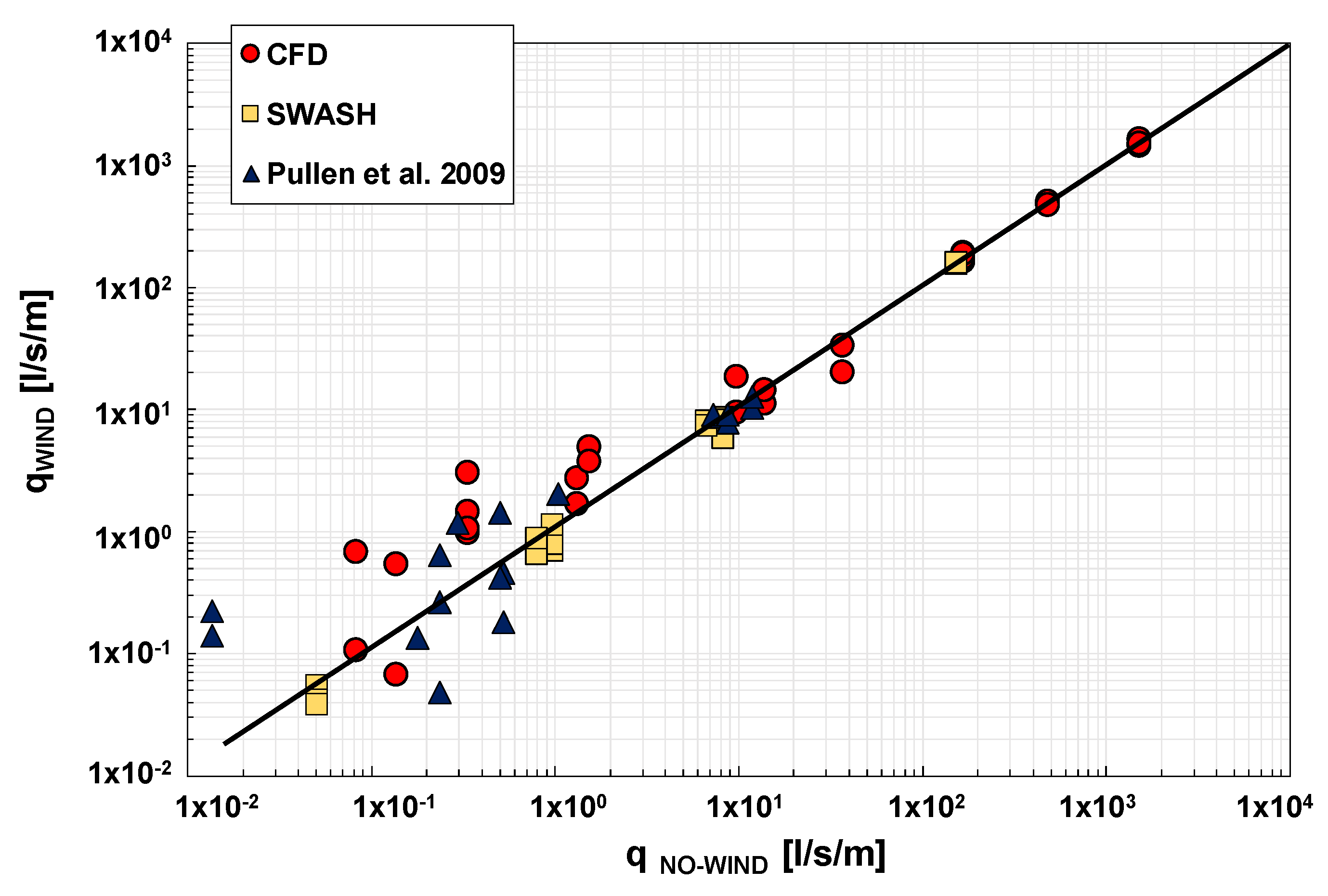
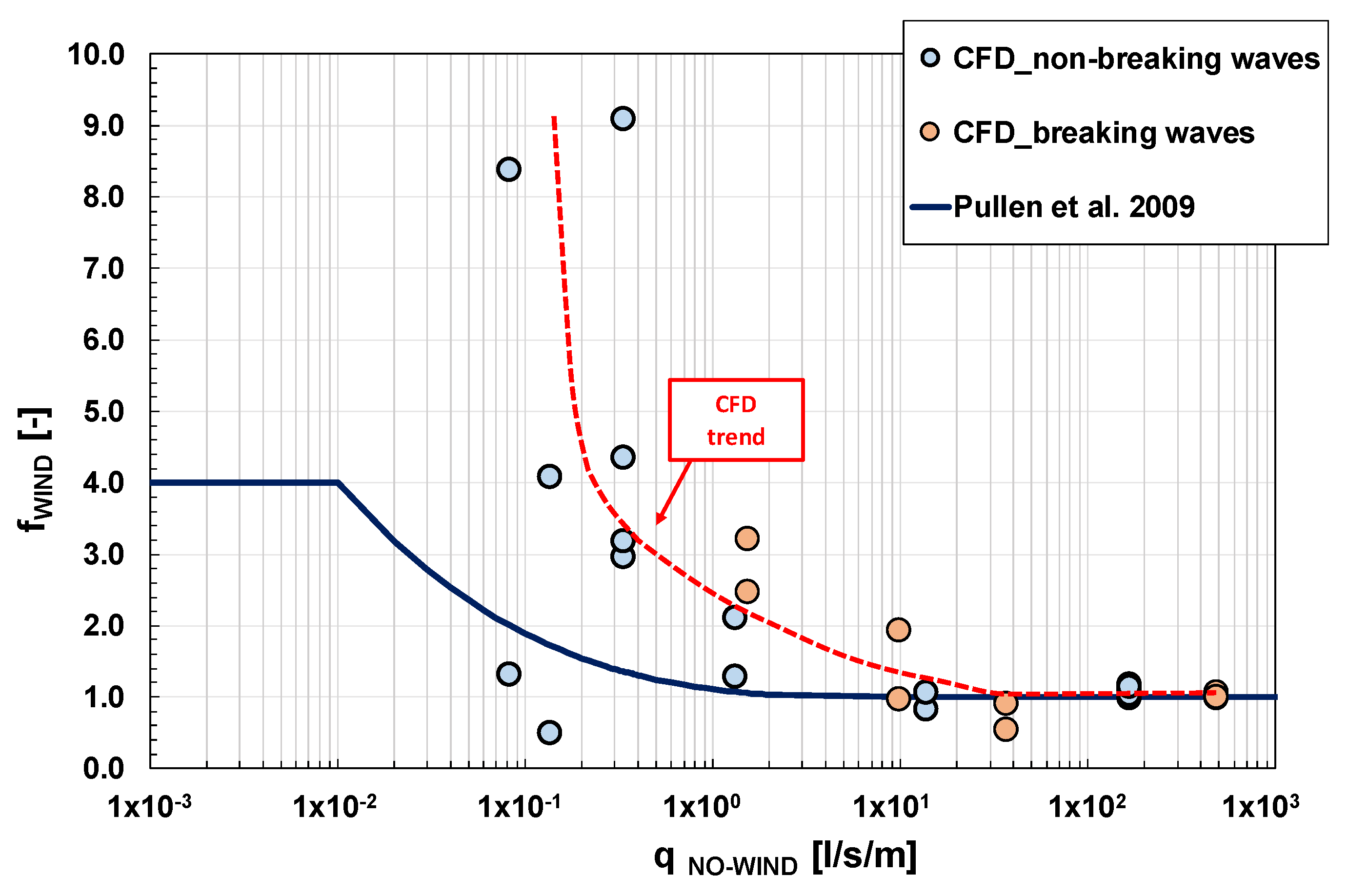
5.4. Numerical Experiments vs. Pullen et al.’s Physical Model Data
5.5. The Wind Factor fWIND
5.6. Quantitative Analysis
6. Discussion and Conclusions
- -
- Deformation of the run-up wedge;
- -
- Advection of the droplets formed in the uprush phase;
- -
- Variation in the breaking point with wind.
- -
- the wind enhancement factor reaches the value of 10 rather than a maximum of 4;
- -
- The effect of wind keeps on resenting for overtopping regimes as intense as 100 l/s/m, rather than vanishing at 1 l/s/m.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Van der Werf, I.M.; Van Gent, M.R.A. Wave Overtopping over Coastal Structures with Oblique Wind and Swell Waves. J. Mar. Sci. Eng. 2018, 6, 149. [Google Scholar] [CrossRef] [Green Version]
- EurOtop. Manual on Wave Overtopping of Sea Defences and Related Structures; Van der Meer, J.W., Allsop, N.W.H., Bruce, T., De Rouck, J., Kortenhaus, A., Pullen, T., Schüttrumpf, H., Troch, P., Zanuttigh, B., Eds.; 2018; Available online: www.overtopping-manual.com (accessed on 10 December 2018).
- de Waal, J.P.; Tönjes, P.; van der Meer, J. Wave overtopping of vertical structures including wind effect. In Proceedings of the 25th International Conference on Coastal Engineering, ASCE, Orlando, FL, USA, 2–6 September 1996. [Google Scholar] [CrossRef]
- De Rouck, J.; Geeraerts, J.; Troch, P.; Kortenhaus, A.; Pullen, T.; Franco, L. New results on scale effects for wave overtopping at coastal structures. In Proceedings of the International Conference on Coastlines, Structures and Breakwaters, London, UK, 19–21 April 2005. [Google Scholar]
- Pullen, T.; Allsop, W.; Bruce, T.; Pearson, J. Field and laboratory measurements of mean overtopping discharges and spatial distributions at vertical seawalls. Coast. Eng. 2009, 56, 121–140. [Google Scholar] [CrossRef]
- Murakami, K.; Maki, D.; Ogino, K. Effect of Wind Velocity on Wave Overtopping. In Proceedings of the 10th International Conference on Asian and Pacific Coasts (APAC 2019), Hanoi, Vietnam, 25–28 September 2019. [Google Scholar]
- Kiku, M.; Kawasaki, K. Proposal of numerical wave flume for wave overtopping computation considering wind external force. In Proceedings of the 34th Conference on Coastal Engineering, Seoul, Republic of Korea, 15–20 June 2014. [Google Scholar]
- De Chowdhury, S.; Causon, D.; Qian, L.; Mingham, C.; Chen, H.; Lin, Z.; Zhou, J.G.; Pullen, T.; Silva, E.; Hu, K.; et al. Investigation of Wind Effects on Wave Overtopping at Sea Defences. In Proceedings of the Coastal Structures 2019, Hannover, Germany, 29 September–2 October 2019; Bundesanstalt für Wasserbau. S: Karlsruhe, Germany, 2019; pp. 841–850. [Google Scholar] [CrossRef]
- Xie, Z. Numerical modelling of wind effects on breaking solitary waves. Eur. J. Mech. B-Fluid 2014, 43, 135–147. [Google Scholar] [CrossRef]
- Malara, G.; Kougioumtzoglou, I.A.; Arena, F. Extrapolation of random wave field data via compressive sampling. Ocean Eng. 2018, 157, 87–95. [Google Scholar] [CrossRef]
- Bayındır, C.; Namlı, B. Efficient sensing of the von Karman vortices using compressive sensing. Comput. Fluids 2021, 226, 104975. [Google Scholar] [CrossRef]
- Alan, A.R.; Bayindir, C. Analysis of Wave Runup, Overtopping and Overwash Parameters via Compressive Sensing. In Proceedings of the International Conference on Applied Mathematics in Engineering (ICAME), Balikesir, Turkey, 1–3 September 2021. [Google Scholar]
- Flow Science, Inc. FLOW-3D User’s Manual, HYDRO ed.; Flow Science, Inc.: Santa Fe, NM, USA, 2022. [Google Scholar]
- Zijlema, M.; Stelling, G.; Smit, P. SWASH: An operational public domain code for simulating wave fields and rapidly varied flows in coastal waters. Coast. Eng. 2011, 58, 992–1012. [Google Scholar] [CrossRef]
- Vicinanza, D.; Dentale, F.; Salerno, D.; Buccino, M. Structural response of seawave slot-cone generator (SSG) from random wave CFD simulations. In Proceedings of the Twenty-fifth International Ocean and Polar Engineering Conference, Kona, HI, USA, 21–26 June 2015. [Google Scholar]
- Di Leo, A.; Reale, F.; Dentale, F.; Viccione, G.; Carratelli, E.P. Wave-structure interactions a 2d innovative numerical methodology. In Proceedings of the 23rd Conference of the Italian Association of Theoretical and Applied Mechanics, Salerno, Italy, 4–7 September 2017; Volume 2, pp. 1699–1708. [Google Scholar]
- Dentale, F.; Reale, F.; Di Leo, A.; Pugliese Carratelli, E. A CFD approach to rubble mound breakwater design. Int. J. Nav. Archit. Ocean. Eng. 2018, 10, 644–650. [Google Scholar] [CrossRef]
- Buccino, M.; Daliri, M.; Dentale, F.; Di Leo, A.; Calabrese, M. CFD experiments on a low crested sloping top caisson breakwater. Part 1. nature of loadings and global stability. Ocean Eng. 2019, 182, 259–282. [Google Scholar] [CrossRef]
- Buccino, M.; Daliri, M.; Dentale, F.; Calabrese, M. CFD experiments on a low crested sloping top caisson breakwater. Part 2. Analysis of plume impact. Ocean Eng. 2019, 173, 345–357. [Google Scholar] [CrossRef]
- Di Leo, A. CFD Analysis of Coastal Flood Risk: Overtopping Related Phenomena. Ph.D. Thesis, University of Salerno, Department of Civil Engineering, Fisciano, Italy, 2021. [Google Scholar]
- Hieu, P.D.; Vinh, P.N.; Toan, D.V.; Son, N.T. Study of Wave-wind Interaction at a Seawall Using a Numerical Wave Channel. Appl. Math. Model. 2014, 38, 5149–5159. [Google Scholar] [CrossRef]
- Di Leo, A.; Buccino, M.; Dentale, F.; Pugliese Carratelli, E. CFD Analysis of Wind Effect on Wave Overtopping. In Proceedings of the 32nd International Ocean and Polar Engineering Conference, Shanghai, China, 5–10 June 2022. [Google Scholar]
- Zhang, N.; Zhang, Q.; Wang, K.H.; Zou, G.; Jiang, X.; Yang, A.; Li, Y. Numerical simulation of wave overtopping on breakwater with an armor layer of accropode using SWASH model. Water 2020, 12, 386. [Google Scholar] [CrossRef] [Green Version]
- Suzuki, T.; Altomare, C.; Veale, W.; Verwaest, T.; Trouw, K.; Troch, P.; Zijlema, M. Efficient and robust wave overtopping estimation for impermeable coastal structures in shallow foreshores using SWASH. Coast. Eng. 2017, 122, 108–123. [Google Scholar] [CrossRef]
- Ward, D.L.; Zhang, J.; Wibner, C.G.; Cinotto, C.M. Wind effects on runup and overtopping. In Proceedings of the 25th International Conference on Coastal Engineering (ICCE 1996), Orlando, FL, USA, 2–6 September 1996; ASCE: New York, NY, USA, 1996; pp. 2206–2215. [Google Scholar]
- Wolters, G.; van Gent, M.R.A. Maximum wind effect on wave overtopping of sloped coastal structures with crest elements. In Proceedings of the 5th International Coastal Structures, Venice, Italy, 2–4 July 2007; pp. 1263–1274. [Google Scholar]
- Durbridge, S. The effect of onshore wind on wave overtopping of a vertical sea wall. Plymouth Stud. Sci. 2021, 14, 311–355. [Google Scholar]
- Bradford, S.F. Numerical simulation of surf-zone dynamics. J. Waterw. Port Coast. Ocean Eng. 2000, 126, 1–13. [Google Scholar] [CrossRef]
- Hirt, C.W.; Nichols, B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 1981, 39, 201–225. [Google Scholar] [CrossRef]
- Hirt, C.W.; Sicilian, J.M. A porosity technique for the definition of obstacles in rectangular cell meshes. In Proceedings of the Fourth International Conference of Ship Hydrodynamics, National Academy of Science, Washington, DC, USA, 24–27 September 1985. [Google Scholar]
- Smit, P.; Zijlema, M.; Stelling, G. Depth-induced wave breaking in a non-hydrostatic, near-shore wave model. Coast. Eng. 2013, 76, 761–816. [Google Scholar] [CrossRef]
- Delft University of Technology. SWASH User’s Manual, Version 8.01; GA: Delft, The Netherlands, 2021–2022. [Google Scholar]
- Chen, Q.; Kaihatu, J.M.; Hwang, P.A. Incorporation of wind effects into Boussinesq wave models. J. Waterw. Port Coast. Ocean Eng. 2004, 130, 312–321. [Google Scholar] [CrossRef]
- Lopez, L.F.C.; Salerno, D.; Dentale, F.; Capobianco, A.; Buccino, M. Experimental campaign on the overtopping of the seawall Malecon Traditional. In Proceedings of the 25th International Ocean and Polar Engineering Conference (ISOPE), Kona, HI, USA, 21–26 June 2015. [Google Scholar]
- Bretschneider, C.L. Generation of Waves by Wind: State of Art; International Summer Course: Lunteren, The Netherlands, 1–18 September 1964. [Google Scholar]
- Andreas, E.L.; Mahrt, L.; Vickers, D. A New Drag Relation for Aerodynamically Rough Flow over the Ocean. J. Atmos. Sci. 2012, 69, 2520–2537. [Google Scholar] [CrossRef]
- Wu, J. Wind-stress coefficients over sea surface from breeze to hurricane. J. Geophys. Res. 1982, 87, 9704–9706. [Google Scholar] [CrossRef]
- Buccino, M.; Daliri, M.; Calabrese, M.; Somma, R. A numerical study of arsenic contamination at the Bagnoli bay seabed by a semi-anthropogenic source. Analysis of current regime. Sci. Total Environ. 2021, 782, 146811. [Google Scholar] [CrossRef]
- Buccino, M.; Daliri, M.; Buttarazzi, M.N.; Del Giudice, G.; Calabrese, M.; Somma, R. Arsenic contamination at the Bagnoli Bay seabed (South Italy) via particle tracking numerical modeling: Pollution patterns from stationary climatic forcings. Chemosphere 2022, 303, 134955. [Google Scholar] [CrossRef]
- Fenton, J.D. Numerical Methods for Nonlinear Waves. In Advances in Coastal and Ocean Engineering; Liu, P.L.-F., Ed.; World Scientific: Singapore, 1999; Volume 5, pp. 241–324. [Google Scholar]
- USACE (U.S. Army Corps of Engineers). Coastal Engineering Manual, EM 1110-2-1100; USACE: Washington, DC, USA, 2006.
- Symonds, G.; Huntley, D.A.; Bowen, A.J. Two-dimensional surf beat: Long wave generation by a time-varying breakpoint. J. Geophys. Res. Oceans 1982, 87, 492–498. [Google Scholar] [CrossRef] [Green Version]
- Durbin, P.A. On the k-3 stagnation point anomaly. Int. J. Heat Fluid Flow 1996, 17, 89–90. [Google Scholar] [CrossRef]
- Larsen, B.E.; Fuhrman, D.R. On the over-production of turbulence beneath surface waves in Reynolds-averaged Navier-Stokes models. J. Fluid Mech. 2018, 853, 419–460. [Google Scholar] [CrossRef] [Green Version]
- Zelt, J.A.; Skjelbreia, J.E. Estimating incident and reflected wave fields using an arbitrary number of wave gauges. In Proceedings of the 23rd International Conference on Coastal Engineering (ICCE), Venice, Italy, 4–9 October 1992; ASCE: Reston, VA, USA, 1992; Volume 1, pp. 777–789. [Google Scholar] [CrossRef]
- Resio, D.T. Assesment of Wind Effects on Wave Overtopping of Proposed Virginia Beach Seawall. Technical Memorandum to CERC, OCTI. 1987. [Google Scholar]
- Dean, R.G.; Dalrymple, R.A. Coastal Processes with Engineering Applications; Cambridge University Press: New York, NY, USA, 2001. [Google Scholar]
- Longuet-Higgins, M.S.; Stewart, R.W. Radiation stress and mass transport in gravity waves, with application to ‘surf beats’. J. Fluid Mech. 1962, 13, 481–504. [Google Scholar] [CrossRef]
- Galvin, C.J., Jr. Breaker type classification on three laboratory beaches. J. Geophys. Res. 1968, 73, 3651–3659. [Google Scholar] [CrossRef]
- Basco, D.R. A qualitative description of wave breaking. J. Waterw. Port Coast. Ocean Eng. 1985, 111, 171–188. [Google Scholar] [CrossRef]
- Calabrese, M.; Buccino, M.; Pasanisi, F. Wave breaking macrofeatures on a submerged rubble mound breakwater. J. Hydro-Environ. Res. 2008, 1, 216–225. [Google Scholar] [CrossRef]
- Nagai, S.; Ueda, S. Study on the shape and structure of seawall considering wind and waves. In Proceedings of the Coastal Engineering, JSCE, The Hague, The Netherlands, 29 January 1960. [Google Scholar]
- Perlin, M.; Wooyoung, C.; Zhigang, T. Breaking Waves in Deep and Intermediate Waters. Annu. Rev. Fluid Mech. 2013, 45, 115–145. [Google Scholar] [CrossRef] [Green Version]
- Romano, A.; Bellotti, G.; Briganti, R.; Franco, L. Uncertainties in the physical modelling of the wave overtopping over a rubble mound breakwater: The role of the seeding number and of the test duration. Coast. Eng. 2015, 103, 15–21. [Google Scholar] [CrossRef]



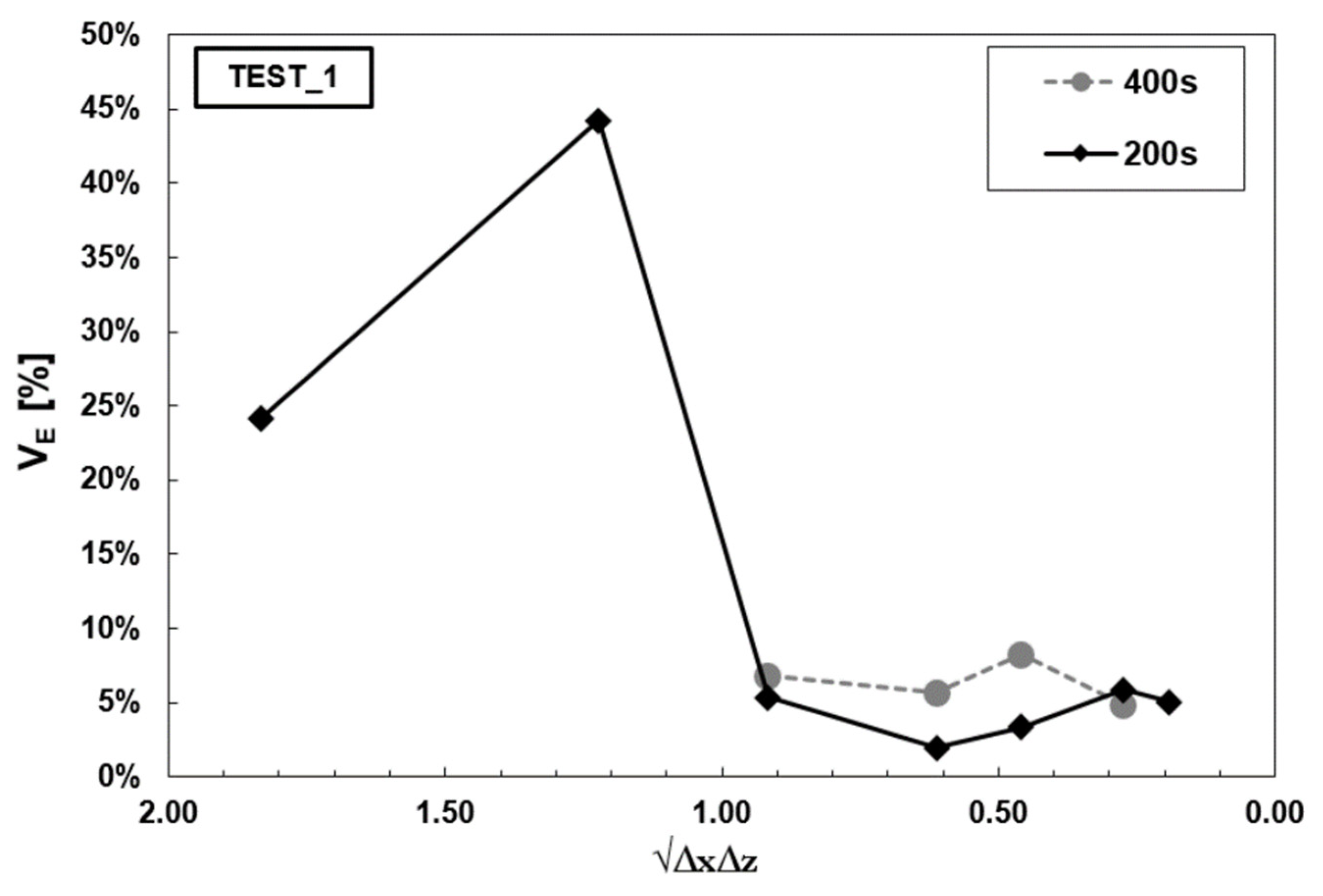

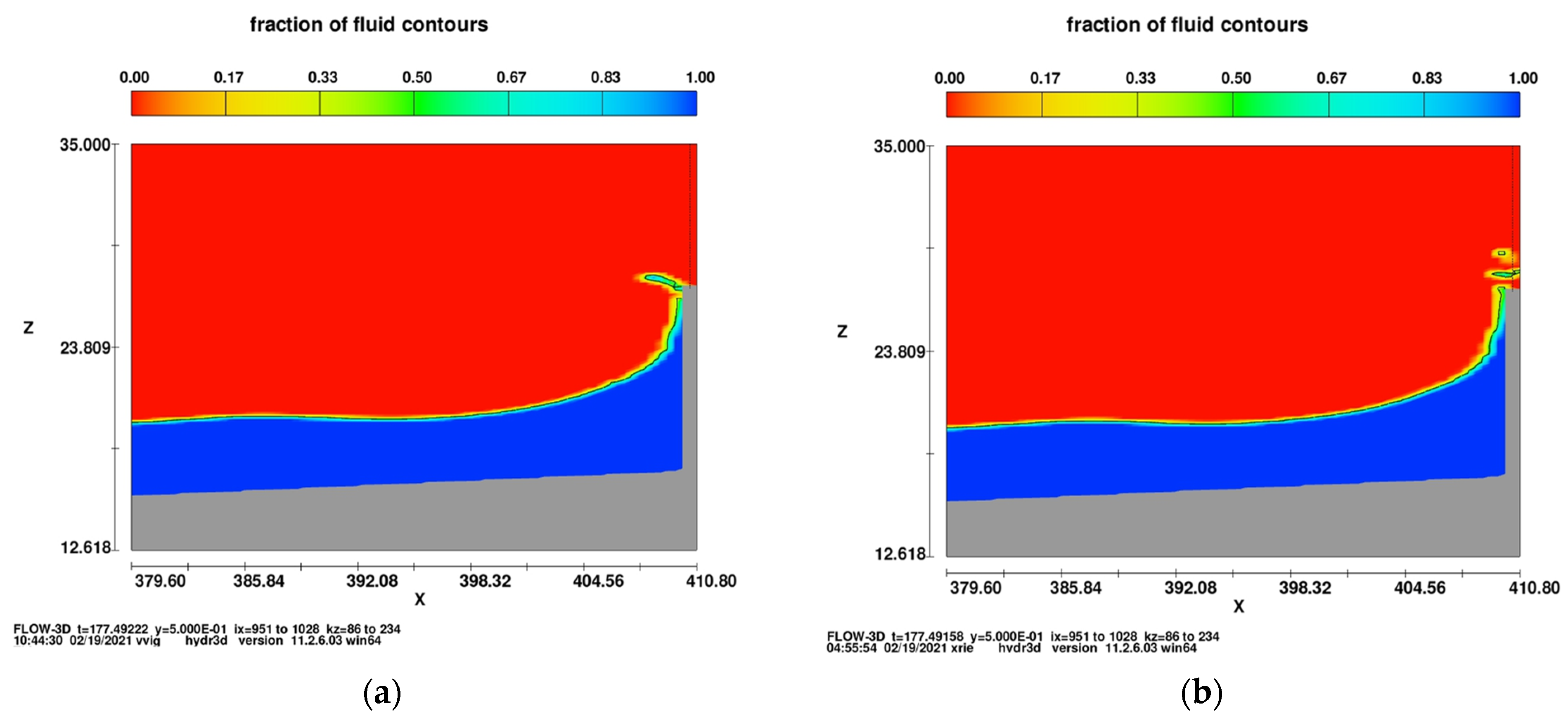
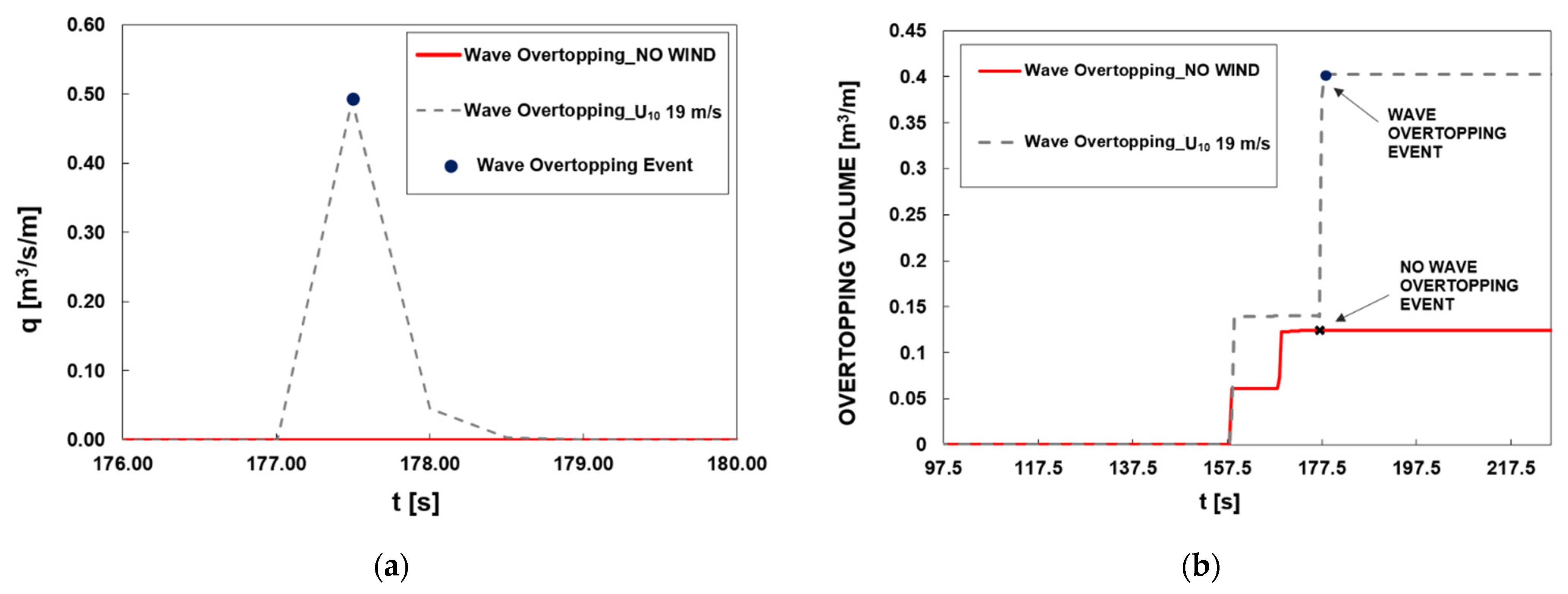
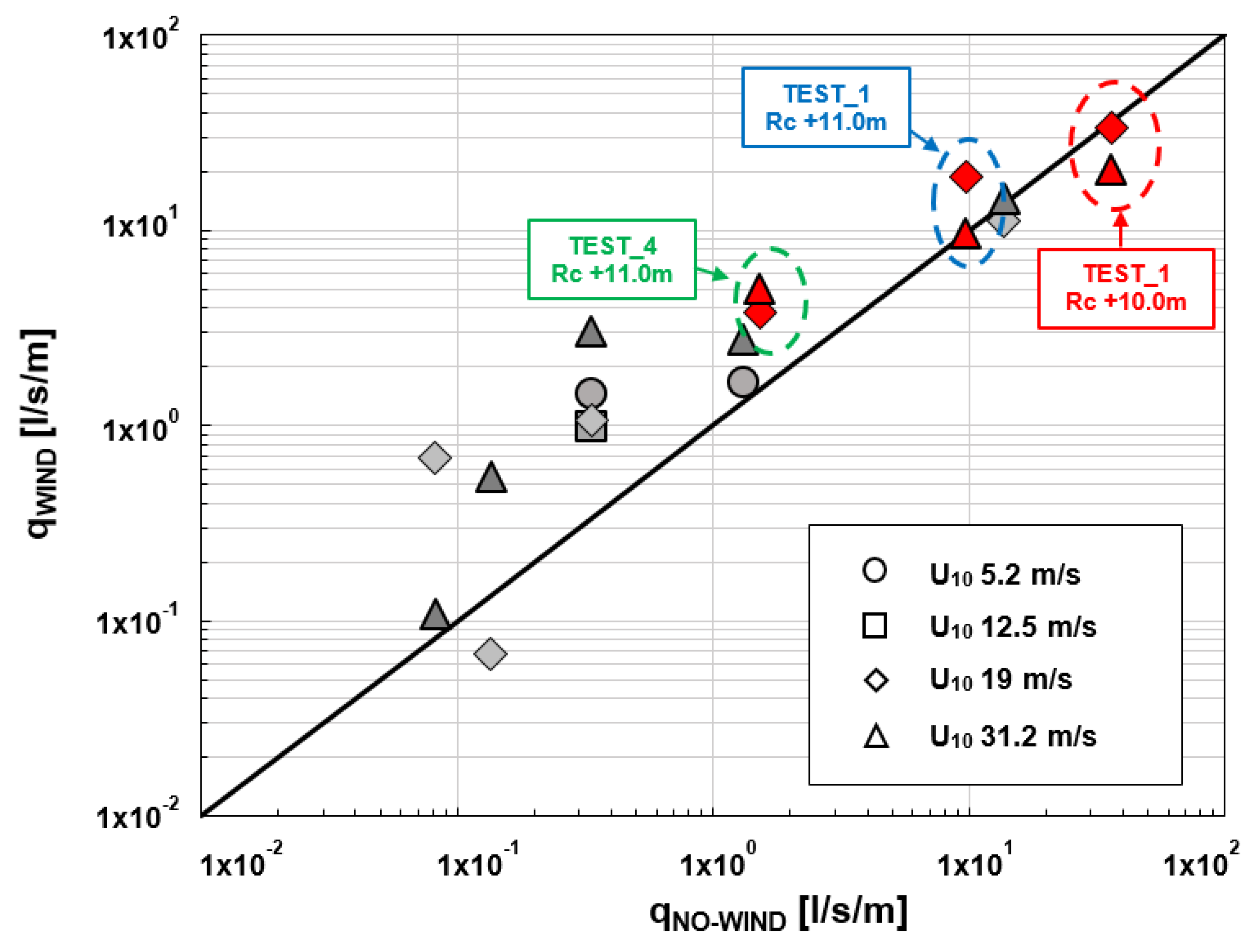





| ID | H (m) | T (s) | Wave Celerity c (m/s) | |
|---|---|---|---|---|
| Deep Water c0 | On 20.45 m Water Depth c | |||
| TEST_1 | 8 | 10 | 15.61 | 12.21 |
| TEST_2 | 8 | 12 | 18.74 | 12.81 |
| TEST_3 | 1.5 | 10 | 15.61 | 12.21 |
| TEST_4 | 5.4 | 10 | 15.61 | 12.21 |
| U10 | CD10 | β |
|---|---|---|
| 30 | 0.0025 | 0.62 |
| 18.7 | 0.0021 | 1.00 |
| 9.4 | 0.0011 | 1.99 |
| 6.1 | 0.0009 | 3.07 |
| 1.9 | 0.0010 | 9.86 |
| U10 | CD10 | β |
|---|---|---|
| 31.2 | 0.0026 | 0.50 |
| 19 | 0.0021 | 0.82 |
| 12.5 | 0.0015 | 1.25 |
| 5.2 | 0.0009 | 3.00 |
| 3.1 | 0.0009 | 5.04 |
| Parameter | Setting |
|---|---|
| Fluid | Water (20 °C), incompressible |
| Turbulence | RNG |
| Pressure Solver | GMRES |
| VOF advection | Split Lagrangian method (TruVof) |
| Time step control | Automatic (stability and convergence) |
| ID GRID | Δx (m) | Δz (m) |
|---|---|---|
| A20 | 2.9 | 1.2 |
| A30 | 1.9 | 0.8 |
| A40 | 1.5 | 0.6 |
| A60 | 1.0 | 0.4 |
| A80 | 0.7 | 0.3 |
| A160 | 0.4 | 0.15 |
| C278 | 0.25 | 0.30 |
| M278 | 0.25 | 0.15 |
| ID | H (m) | T (s) |
|---|---|---|
| TEST_1S | 0.95 | 10 |
| TEST_2S | 0.8 | 10 |
| TEST_3S | 0.7 | 10 |
| TEST_4S | 0.6 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Leo, A.; Dentale, F.; Buccino, M.; Tuozzo, S.; Pugliese Carratelli, E. Numerical Analysis of Wind Effect on Wave Overtopping on a Vertical Seawall. Water 2022, 14, 3891. https://doi.org/10.3390/w14233891
Di Leo A, Dentale F, Buccino M, Tuozzo S, Pugliese Carratelli E. Numerical Analysis of Wind Effect on Wave Overtopping on a Vertical Seawall. Water. 2022; 14(23):3891. https://doi.org/10.3390/w14233891
Chicago/Turabian StyleDi Leo, Angela, Fabio Dentale, Mariano Buccino, Sara Tuozzo, and Eugenio Pugliese Carratelli. 2022. "Numerical Analysis of Wind Effect on Wave Overtopping on a Vertical Seawall" Water 14, no. 23: 3891. https://doi.org/10.3390/w14233891
APA StyleDi Leo, A., Dentale, F., Buccino, M., Tuozzo, S., & Pugliese Carratelli, E. (2022). Numerical Analysis of Wind Effect on Wave Overtopping on a Vertical Seawall. Water, 14(23), 3891. https://doi.org/10.3390/w14233891








