Numerical Simulation of Boulder Fluid–Solid Coupling in Debris Flow: A Case Study in Zhouqu County, Gansu Province, China
Abstract
:1. Introduction
2. Background
3. Numerical Model of the Zhouqu Debris Flow
4. Results of the Simulation
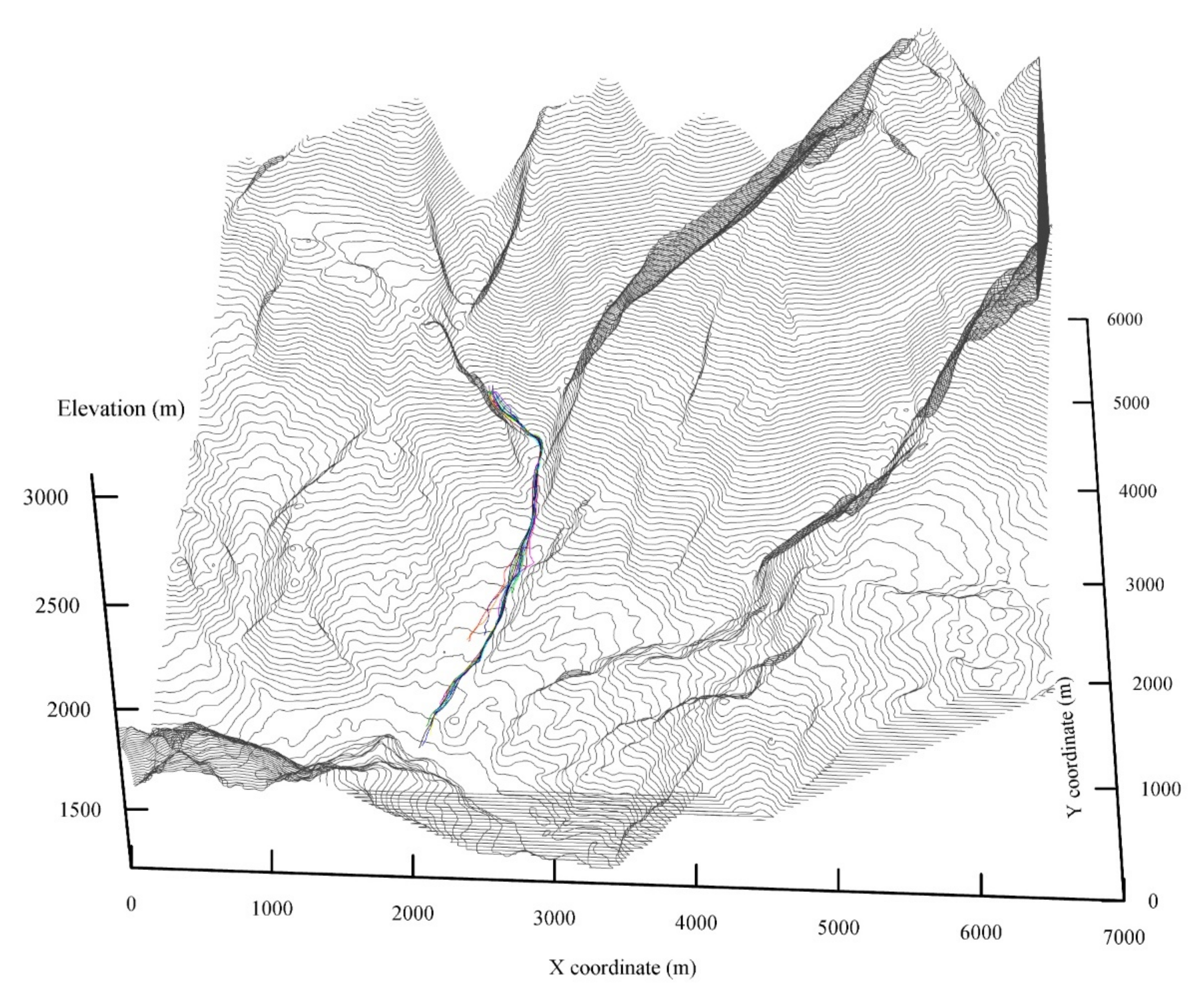
4.1. Movement Process of the Boulders
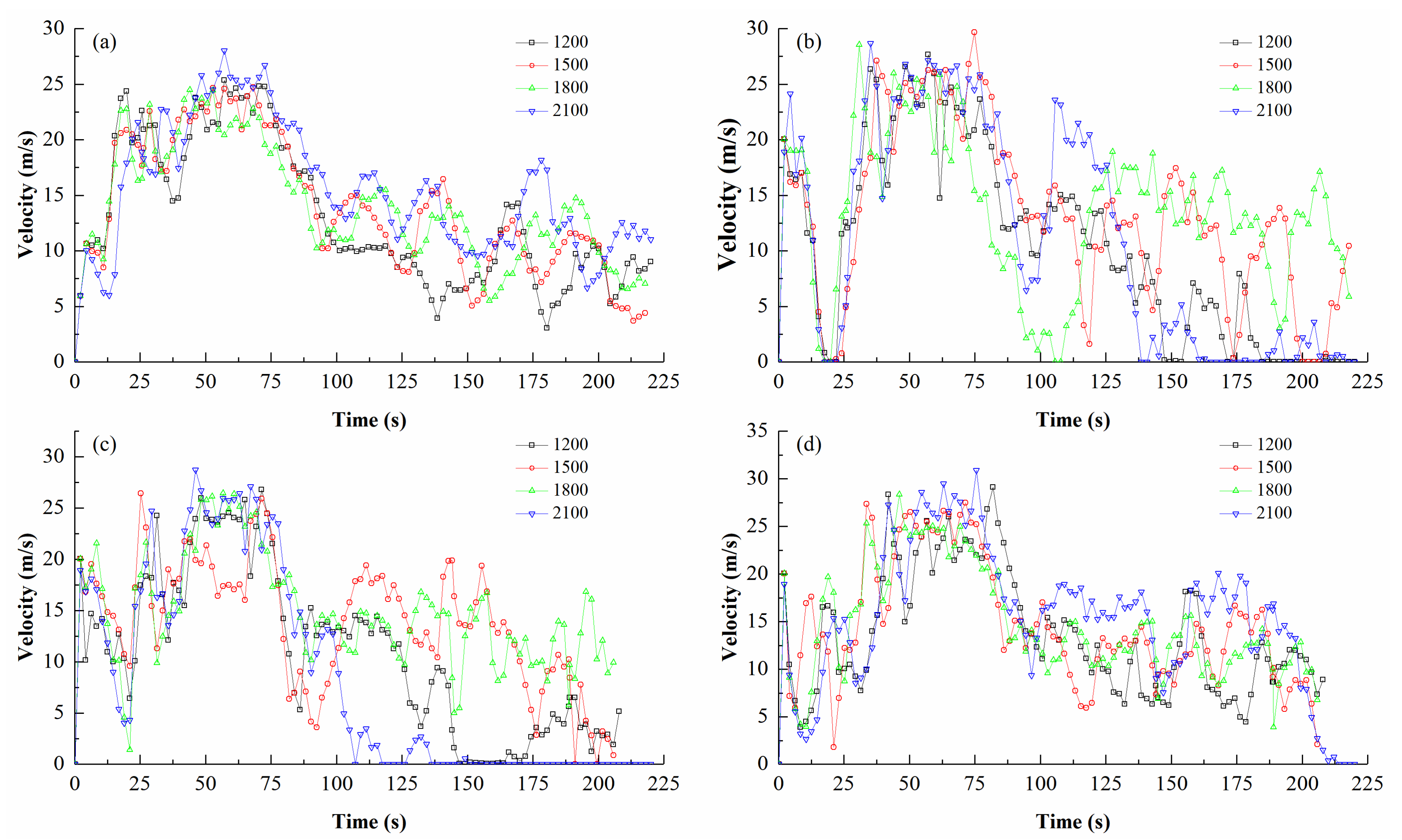
4.2. Velocity Variation Characteristics of Boulders
4.2.1. Influence of Density
4.2.2. Influence of Shape
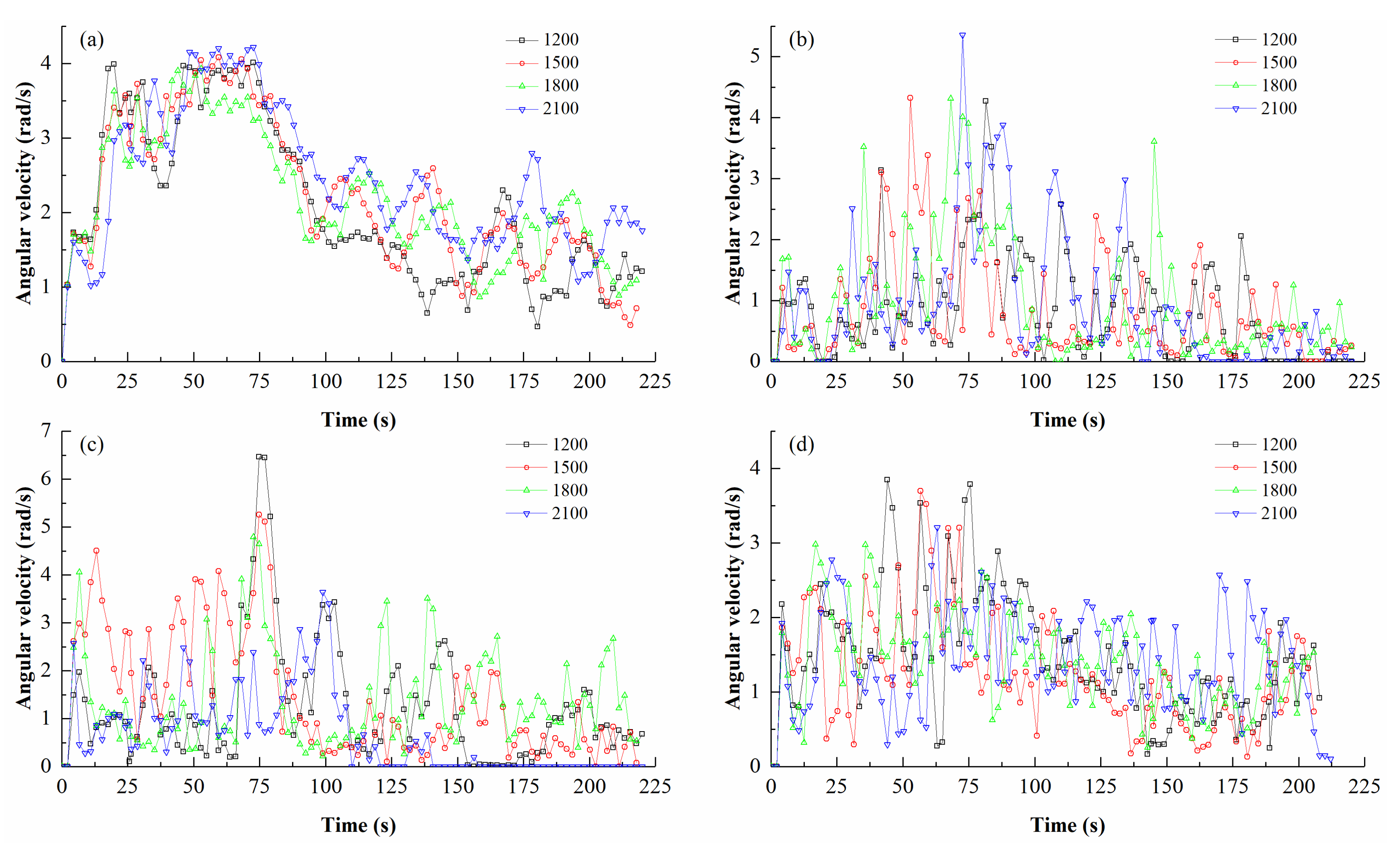
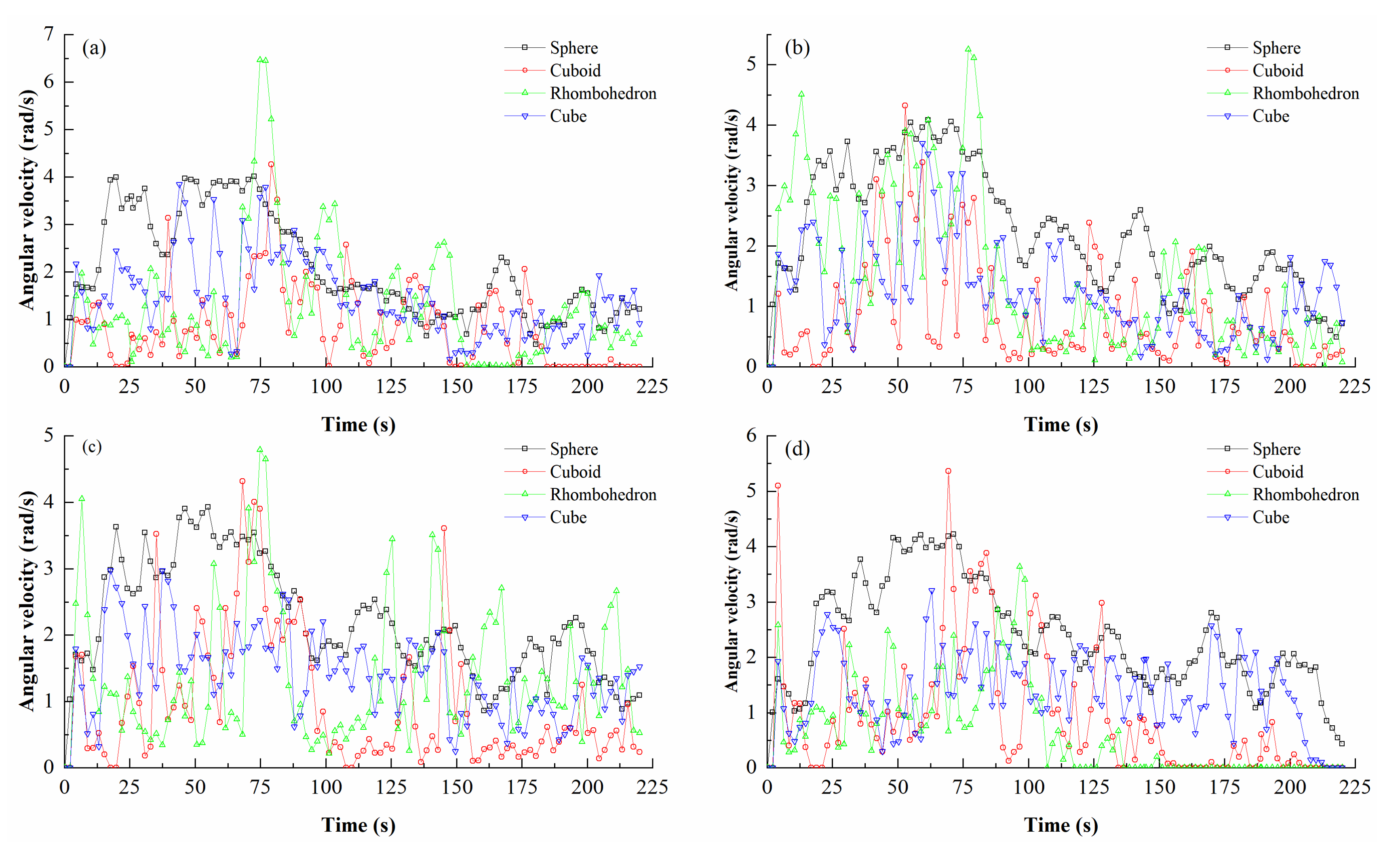
4.3. Angular Velocity Variation Characteristics of Boulders
4.3.1. Influence of Density
4.3.2. Influence of Shape
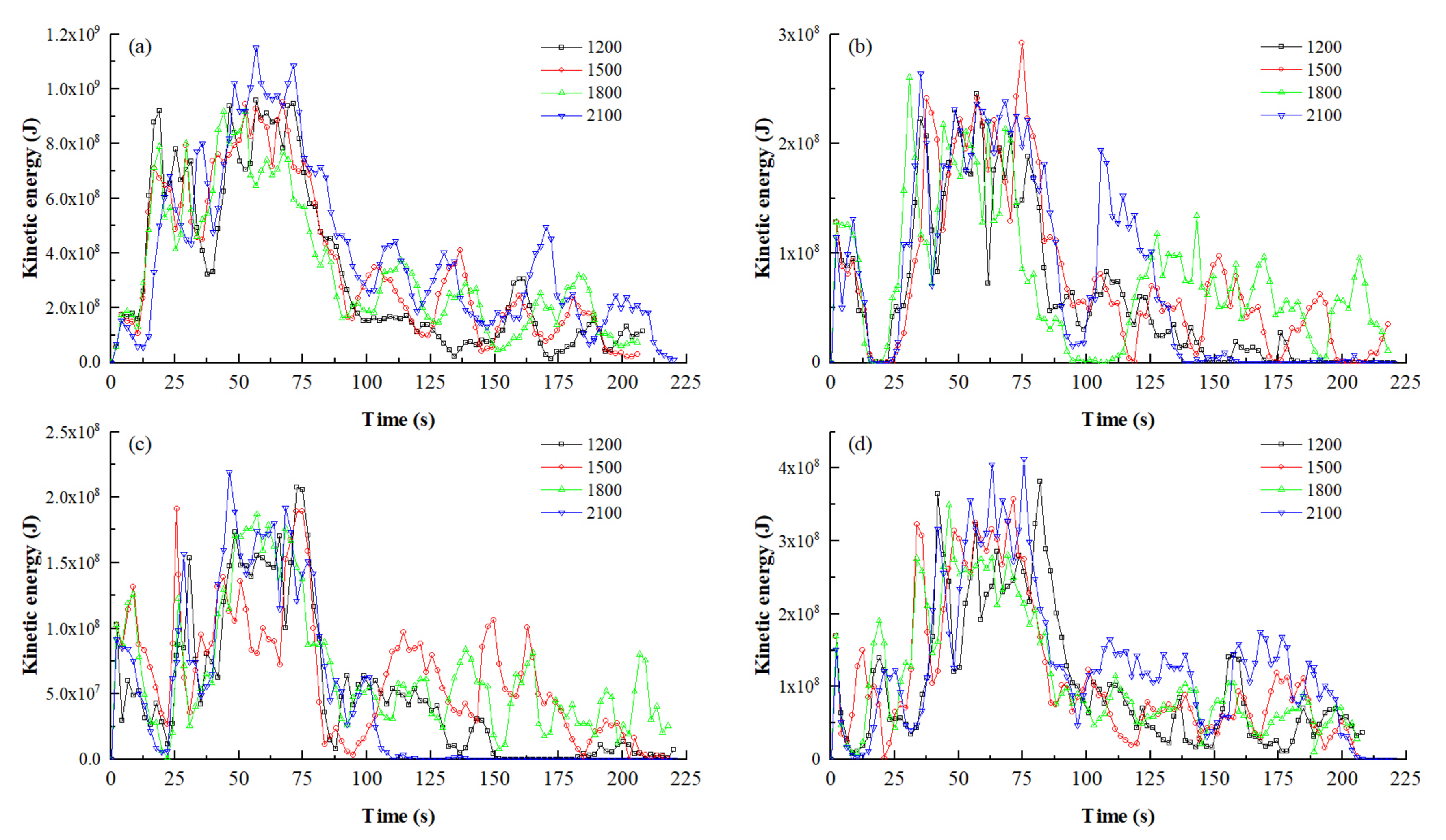
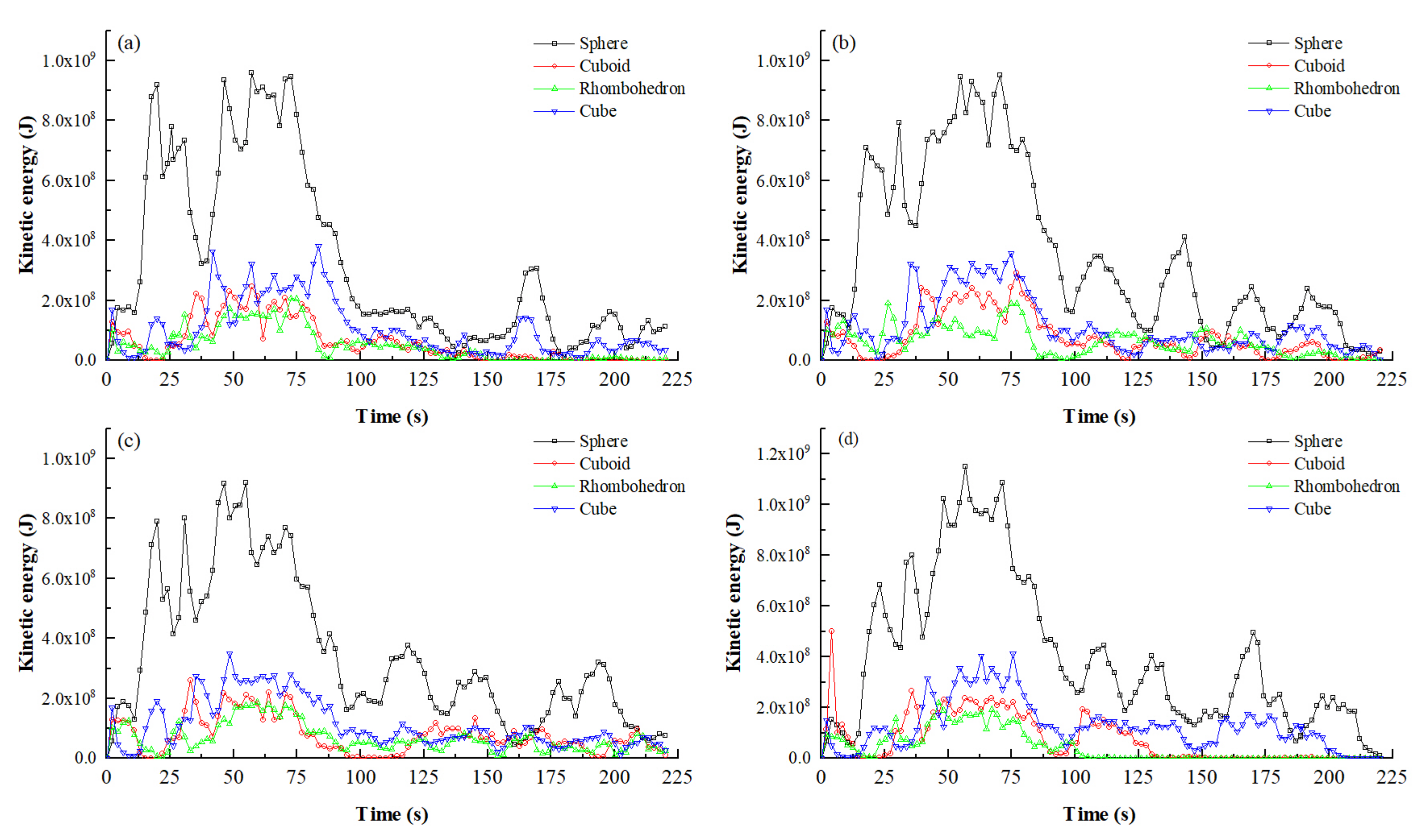
4.4. Kinetic Energy Variation Characteristics of Boulders
4.4.1. Influence of Density
4.4.2. Influence of Shape
5. Discussion
5.1. Boulder Movement Range
5.2. Boulder Movement Distance
5.2.1. Influence of Density
5.2.2. Influence of Shape
5.3. Dynamic Impact Force of the Boulders
5.4. Limitation of the Study
6. Conclusions
- (1)
- The motion characteristics of boulders in the 8.7 Zhouqu debris flow were simulated using FLOW-3D software with the GMO and RNG coupled models. The simulation results can be used to obtain various motion parameters of the boulders that interact with the debris flow slurry, such as the centroid velocity, angular velocity, kinetic energy, and motion trajectory. This method has a certain reference for studying the movement mechanism of debris flow.
- (2)
- The simulation results show that the movement velocity of boulders is affected by many factors such as terrain conditions, debris flow densities, and shapes of the boulders. When the terrain slope is relatively large, the boulders have greater potential energy, and the influence of terrain on the movement velocity of boulders is greater than that of debris flow density and boulder shape. When the slope is less, the appearance of boulders has a great influence on its movement. The velocity of a spherical boulder increases with debris flow density. However, the movement of cuboid, rhombohedron, and cube boulders presents a complex motion state, and it is difficult to predict the change law of their velocity.
- (3)
- The simulation results show that the angular velocity of the spherical boulder fluctuates slightly with time during the whole movement progress, whereas the angular velocity of the cuboid, rhombohedron, and cube boulders fluctuates continuously during the movement, presenting a peak form of “increasing-decreasing.” In addition, in most cases, the angular velocity of the spherical and cube boulders is larger than that of the cuboid and rhombohedron boulders. This indicates that the angular velocity variation law of boulder motion is related to whether the shape of the boulder is spherically symmetric, as well as the smoothness of the surface.
- (4)
- The simulation results show that motion distance is greatly influenced by the terrain slope and shape of the boulders. When the topographic slope is relatively large, the debris flow density and appearance characteristics of boulders have little influence. As the slope decreases, the boulders will gradually stop owing to insufficient dynamics. Moreover, the movement distance of the spherical and the approximately spherically symmetric cube boulders are greater than those of the cuboid and rhombohedron boulders. The accumulation characteristics of boulders in the simulation are generally consistent with the field investigation results.
- (5)
- Although the results of this study have simulated the coupled motion of debris flow and boulders under the influence of multiple factors, there are still some deficiencies in this study, such as the inaccuracy of the topographic map, limited computational resources, and boulder modeling. Further improvements can be made in subsequent studies.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Iverson, R.M. The physics of debris flows. Rev. Geophys. 1997, 35, 245–296. [Google Scholar] [CrossRef] [Green Version]
- Cui, P.; Chen, X.Q.; Zhu, Y.Y.; Su, F.H.; Wei, F.Q.; Han, Y.S.; Liu, H.J.; Zhuang, J.Q. The Wenchuan earthquake (May 12, 2008), Sichuan province, China, and resulting geohazards. Nat. Hazards. 2011, 56, 19–36. [Google Scholar] [CrossRef]
- Tang, C.; van Asch, T.; Chang, M.; Chen, G.; Zhao, X.; Huang, X. Catastrophic debris flows on 13 August 2010 in the Qingping area, southwestern China: The combined effects of a strong earthquake and subsequent rainstorms. Geomorphology 2012, 139–140, 559–576. [Google Scholar] [CrossRef]
- Cui, P.; Zhou, G.G.; Zhu, X.; Zhang, J. Scale amplification of natural debris flows caused by cascading landslide dam failures. Geomorphology 2013, 182, 173–189. [Google Scholar] [CrossRef]
- Chen, X.; Cui, P.; You, Y.; Chen, J.; Li, D. Engineering measures for debris flow hazard mitigation in the Wenchuan earthquake area. Eng. Geol. 2015, 194, 73–85. [Google Scholar] [CrossRef]
- Choi, S.-K.; Lee, J.-M.; Kwon, T.-H. Effect of slit-type barrier on characteristics of water-dominant debris flows: Small-scale physical modeling. Landslides 2018, 15, 111–122. [Google Scholar] [CrossRef]
- Wang, J.; Xu, Y.; Ma, Y.; Qiao, S.; Feng, K. Study on the deformation and failure modes of filling slope in loess filling engineering: A case study at a loess mountain airport. Landslides 2018, 15, 2423–2435. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, D.; Wang, N.; Gu, T. Mechanisms of wetting-induced loess slope failures. Landslides 2019, 16, 937–953. [Google Scholar] [CrossRef]
- Qiu, H.; Zhu, Y.; Zhou, W.; Sun, H.; He, J.; Liu, Z. Influence of DEM resolution on landslide simulation performance based on the Scoops3D model. Geomat. Nat. Hazards Risk 2022, 13, 1663–1681. [Google Scholar] [CrossRef]
- Cui, Y.-F.; Zhou, X.-J.; Guo, C.-X. Experimental study on the moving characteristics of fine grains in wide grading unconsolidated soil under heavy rainfall. J. Mt. Sci. 2017, 14, 417–431. [Google Scholar] [CrossRef]
- Liu, D.; Cui, Y.; Guo, J.; Yu, Z.; Chan, D.; Lei, M. Investigating the effects of clay/sand content on depositional mechanisms of submarine debris flows through physical and numerical modeling. Landslides 2020, 17, 1863–1880. [Google Scholar] [CrossRef]
- Cui, P.; Zeng, C.; Lei, Y. Experimental analysis on the impact pressure of viscous debris flow. Earth Surf. Process. Landf. 2015, 12, 1644–1655. [Google Scholar] [CrossRef] [Green Version]
- Armanini, A. On the Dynamic Impact of Debris Flows. In Recent Developments on Debris Flows; Lecture Notes in Earth Sciences; Armanini, A., Michiue, M., Eds.; Springer: Berlin, Heidelberg, 1997; Volume 64, pp. 208–226. [Google Scholar]
- Liu, Z.; Qiu, H.; Zhu, Y.; Liu, Y.; Yang, D.; Ma, S.; Zhang, J.; Wang, Y.; Wang, L.; Tang, B. Efficient Identification and Monitoring of Landslides by Time-Series InSAR Combining Single- and Multi-Look Phases. Remote. Sens. 2022, 14, 1026. [Google Scholar] [CrossRef]
- Bugnion, L.; McArdell, B.W.; Bartelt, P.; Wendeler, C. Measurements of hillslope debris flow impact pressure on obstacles. Landslides 2012, 2, 179–187. [Google Scholar] [CrossRef] [Green Version]
- Choi, C.; Ng, C.; Song, D.; Kwan, J.; Shiu, H.; Ho, K.; Koo, R. Flume investigation of landslide debris–resisting baffles. Can. Geotech. J. 2014, 5, 658–662. [Google Scholar] [CrossRef]
- He, S.M.; Liu, W.; Li, X.P. Prediction of impact pressure of debris flows based on distribution and size of particles. Environ. Earth Sci. 2016, 4, 298. [Google Scholar] [CrossRef]
- Wang, D.; Chen, Z.; He, S.; Liu, Y.; Tang, H. Measuring and estimating the impact pressure of debris flows on bridge piers based on large-scale laboratory experiments. Landslides 2018, 15, 1331–1345. [Google Scholar] [CrossRef]
- Hu, G.S.; Chen, N.S.; Deng, M.F.; Lu, Y. Analysis of the Characteristics of Impact Force of Massive Stones of the Sanyanyu Debris Flow Gully in Zhouqu, Gansu Province. Earth Env. 2011, 4, 478–484. (In Chinese) [Google Scholar]
- Tan, D.-Y.; Yin, J.-H.; Feng, W.-Q.; Qin, J.-Q.; Zhu, Z.-H. New simple method for measuring impact force on a flexible barrier from rockfall and debris flow based on large-scale flume tests. Eng. Geol. 2020, 279, 105881. [Google Scholar] [CrossRef]
- Su, Y.; Choi, C.; Ng, C.; Lam, H.; Wong, L.A.; Lee, C. New light-weight concrete foam to absorb debris-flow-entrained boulder impact: Large-scale pendulum modelling. Eng. Geol. 2020, 275, 105724. [Google Scholar] [CrossRef]
- Toshiyuki, H.; Vincent, R. Post-analysis simulation of the collapse of an open sabo dam of steel pipes subjected to boulder laden debris flow. Int. J. Sediment Res. 2020, 6, 621–635. [Google Scholar]
- Pudasaini, S.P. A fully analytical model for virtual mass force in mixture flows. Int. J. Multiph. Flow 2019, 113, 142–152. [Google Scholar] [CrossRef]
- Paris, R.; Fournier, J.; Poizot, E.; Etienne, S.; Morin, J.; Lavigne, F.; Wassmer, P. Boulder and fine sediment transport and deposition by the 2004 tsunami in Lhok Nga (western Banda Aceh, Sumatra, Indonesia): A coupled offshore–onshore model. Mar. Geol. 2010, 268, 43–54. [Google Scholar] [CrossRef]
- Imamura, F.; Goto, K.; Ohkubo, S. A numerical model for the transport of a boulder by tsunami. J. Geophys. Res.-Oceans 2008, 113, C01008. [Google Scholar] [CrossRef]
- Goto, K.; Okada, K.; Imamura, F. Numerical analysis of boulder transport by the 2004 Indian Ocean tsunami at Pakarang Cape, Thailand. Mar. Geol. 2010, 268, 97–105. [Google Scholar] [CrossRef]
- Nandasena, N.; Paris, R.; Tanaka, N. Reassessment of hydrodynamic equations: Minimum flow velocity to initiate boulder transport by high energy events (storms, tsunamis). Mar. Geol. 2011, 281, 70–84. [Google Scholar] [CrossRef]
- Nandasena, N.; Tanaka, N. Boulder transport by high energy: Numerical model-fitting experimental observations. Ocean Eng. 2013, 57, 163–179. [Google Scholar] [CrossRef]
- Istrati, D.; Hasanpour, A.; Buckle, I. Numerical Investigation of Tsunami-Borne Debris Damming Loads on a Coastal Bridge. In Proceedings of the 17th World Conference on Earthquake Engineering, Sendai, Japan, 13–18 September 2020. [Google Scholar]
- Hasanpour, A.; Istrati, D.; Buckle, I. Coupled SPH–FEM Modeling of Tsunami-Borne Large Debris Flow and Impact on Coastal Structures. J. Mar. Sci. Eng. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Buckle, I.G. Multi-Physics Modeling of Tsunami Debris Impact on Bridge Decks. In Proceedings of the 3rd International Conf on Natural Hazards & Infrastructure, Athens, Greece, 5–7 July 2022. [Google Scholar]
- Haehnel, R.B.; Daly, S.F. Maximum Impact Force of Woody Debris on Floodplain Structures. J. Hydraul. Eng. 2004, 130, 112–120. [Google Scholar] [CrossRef]
- Liu, H.; Sakashita, T.; Sato, S. AN Experimental Study On The Tsunami Boulder Movement. Coast. Eng. Proc. 2014, 1, 16. [Google Scholar] [CrossRef] [Green Version]
- Oetjen, J.; Engel, M.; Brückner, H.; Pudasaini, S.P.; Schã¼Ttrumpf, H. Enhanced field observation based physical and numerical modelling of tsunami induced boulder transport phase 1: Physical experiments. Coast. Eng. Proc. 2017, 1, 4. [Google Scholar] [CrossRef] [Green Version]
- Lodhi, H.A.; Hasan, H.; Nandasena, N. The role of hydrodynamic impact force in subaerial boulder transport by tsunami—Experimental evidence and revision of boulder transport equation. Sediment. Geol. 2020, 408, 105745. [Google Scholar] [CrossRef]
- Hastewell, L.; Inkpen, R.; Bray, M.; Schaefer, M. Quantification of contemporary storm-induced boulder transport on an intertidal shore platform using radio frequency identification technology. Earth Surf. Process. Landf. 2020, 45, 1601–1621. [Google Scholar] [CrossRef]
- Istrati, D.; Hasanpour, A. Advanced Numerical Modelling of Large Debris Impact on Piers During Extreme Flood Events. In Proceedings of the 7th IAHR Europe Congress, Athens, Greece, 7–9 September 2022. [Google Scholar]
- Oetjen, J.; Engel, M.; Pudasaini, S.P.; Schuettrumpf, H. Significance of boulder shape, shoreline configuration and pre-transport setting for the transport of boulders by tsunamis. Earth Surf. Process. Landf. 2020, 9, 2118–2133. [Google Scholar] [CrossRef] [Green Version]
- Zainali, A.; Weiss, R. Boulder dislodgement and transport by solitary waves: Insights from three-dimensional numerical simulations. Geophys. Res. Lett. 2015, 42, 4490–4497. [Google Scholar] [CrossRef]
- Yin, Y.-P.; Huang, B.; Chen, X.; Liu, G.; Wang, S. Numerical analysis on wave generated by the Qianjiangping landslide in Three Gorges Reservoir, China. Landslides 2015, 2, 355–364. [Google Scholar] [CrossRef]
- Ataie-Ashtiani, B.; Yavari, S. Numerical simulation of wave generated by landslide incidents in dam reservoirs. Landslides 2011, 4, 417–432. [Google Scholar] [CrossRef]
- Zhou, J.-W.; Xu, F.-G.; Yang, X.-G.; Yang, Y.-C.; Lu, P.-Y. Comprehensive analyses of the initiation and landslide-generated wave processes of the 24 June 2015 Hongyanzi landslide at the Three Gorges Reservoir, China. Landslides 2016, 13, 589–601. [Google Scholar] [CrossRef]
- Hu, Y.-X.; Yu, Z.-Y.; Zhou, J.-W. Numerical simulation of landslide-generated waves during the 11 October 2018 Baige landslide at the Jinsha River. Landslides 2020, 10, 2317–2328. [Google Scholar] [CrossRef]
- Tang, C.; Rengers, N.; Asch, T.W.J.; Yang, Y.H.; Wang, G.F. Triggering conditions and depositional characteristics of a disastrous debris-flow event in Zhouqu city, Gansu Province, northwestern China. Nat. Hazards Earth Syst. Sci. 2011, 11, 2903–2912. [Google Scholar] [CrossRef] [Green Version]
- Hu, K.H.; Ge, Y.G.; Cui, P.; Guo, X.J.; Yang, W. Preliminary analysis of extra-large-scale debris flow disaster in Zhouqu County of Gansu Province. J. Mt. Sci. 2010, 5, 628–634. [Google Scholar]
- Xiong, M.; Meng, X.; Wang, S.; Guo, P.; Li, Y.; Chen, G.; Qing, F.; Cui, Z.; Zhao, Y. Effectiveness of debris flow mitigation strategies in mountainous regions. Prog. Phys. Geogr. Earth Environ. 2016, 40, 768–793. [Google Scholar] [CrossRef]
- Fan, S. Internal Characteristics of Loose Solid Source of Debris Flow in Zhouqu. Sains Malays. 2017, 46, 2179–2186. [Google Scholar] [CrossRef]
- Flow Science. FLOW-3D V11.2 User’s Manual; Flow Science Inc.: Santa Fe, NM, USA, 2016. [Google Scholar]
- GB 50007-2002Code for Design of Building Foundation; The National Standard of the People’s Republic of China: Beijing, China, 2002; p. 44.
- Bagnold, R.A. Experiments on a gravity-free dispersion of large solid spheres in a Newtonian fluid under shear. P. Roy. Soc. A. 1954, 1160, 49–63. [Google Scholar]
- Iverson, R.M.; Denlinger, R.P. Flow of variably fluidized granular masses across three-dimensional terrain: 1. coulomb mixture theory. J. Geophys. Res.-Solid Earth. 2001, 106, 537–552. [Google Scholar] [CrossRef]
- Wu, J.S.; Zhang, J.; Cheng, Z.L. Relation and Its Determination of Residual Layer and Depth of Viscous Debris Flow. Int. J. Sediment Res. 2003, 6, 7–12. (In Chinese) [Google Scholar]
- Yang, H.J.; Hu, K.H.; Wei, F.Q. Methods for computing rheological parameters of debris-flow slurry and their extensibilities. J. Hydraul. Eng. 2013, 11, 1338–1346. (In Chinese) [Google Scholar]
- Hu, X.D.; Wang, G.L.; Zhao, C.; Zhu, L.F.; Wei, J.; Li, H. Analyses of Characteristic Values for Sanyanyu Debris Flow in Zhouqu County on August 8, 2010. Northwest. Geol. 2011, 3, 44–52. (In Chinese) [Google Scholar]
- Wang, F.; Chen, X.; Li, Y.; Li, K.; Yu, X. Fluid-solid Coupling Analysis of Boulder Rolling in Channel after Silt Dam Filled Based on Flow-3d. Sci. Technol. Eng. 2015, 10, 1671–1815. (In Chinese) [Google Scholar]
- Wang, F.; Chen, X.; Chen, J.; You, Y. Experimental study on a debris-flow drainage channel with different types of energy dissipation baffles. Eng. Geol. 2017, 220, 43–51. [Google Scholar] [CrossRef]
- Oetjen, J.; Engel, M.; Schüttrumpf, H. Experiments on tsunami induced boulder transport—A review. Earth-Sci. Rev. 2021, 220, 103714. [Google Scholar] [CrossRef]
- Lichtenhahn, C. Berechnung von Sperren in Beton und Eisenbeton. Mitt. Forstl. Bundensanstalt Wien. Heft 1973, 102, 91–127. [Google Scholar]
- Liu, X.; Ma, J.; Tang, H.; Zhang, S.; Huang, L.; Zhang, J. A novel dynamic impact pressure model of debris flows and its application on reliability analysis of the rock mass surrounding tunnels. Eng. Geol. 2020, 273, 105694. [Google Scholar] [CrossRef]
- Li, D.J. Debris Flow Mitigation Theory and Practices; Science Press: Beijing, China, 1997; pp. 65–70. (In Chinese) [Google Scholar]
- Chehade, R.; Chevalier, B.; Dedecker, F.; Breul, P.; Thouret, J.-C. Effect of Boulder Size on Debris Flow Impact Pressure Using a CFD-DEM Numerical Model. Geosciences 2022, 12, 188. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, Y. Seismic shaking-enhanced impact effect of granular flow challenges the barrier design strategy. Soil Dyn. Earthq. Eng. 2021, 143, 11. [Google Scholar] [CrossRef]
- Zhang, B.; Huang, Y. Impact behavior of superspeed granular flow: Insights from centrifuge modeling and DEM simulation. Eng. Geol. 2022, 299, 106569. [Google Scholar] [CrossRef]



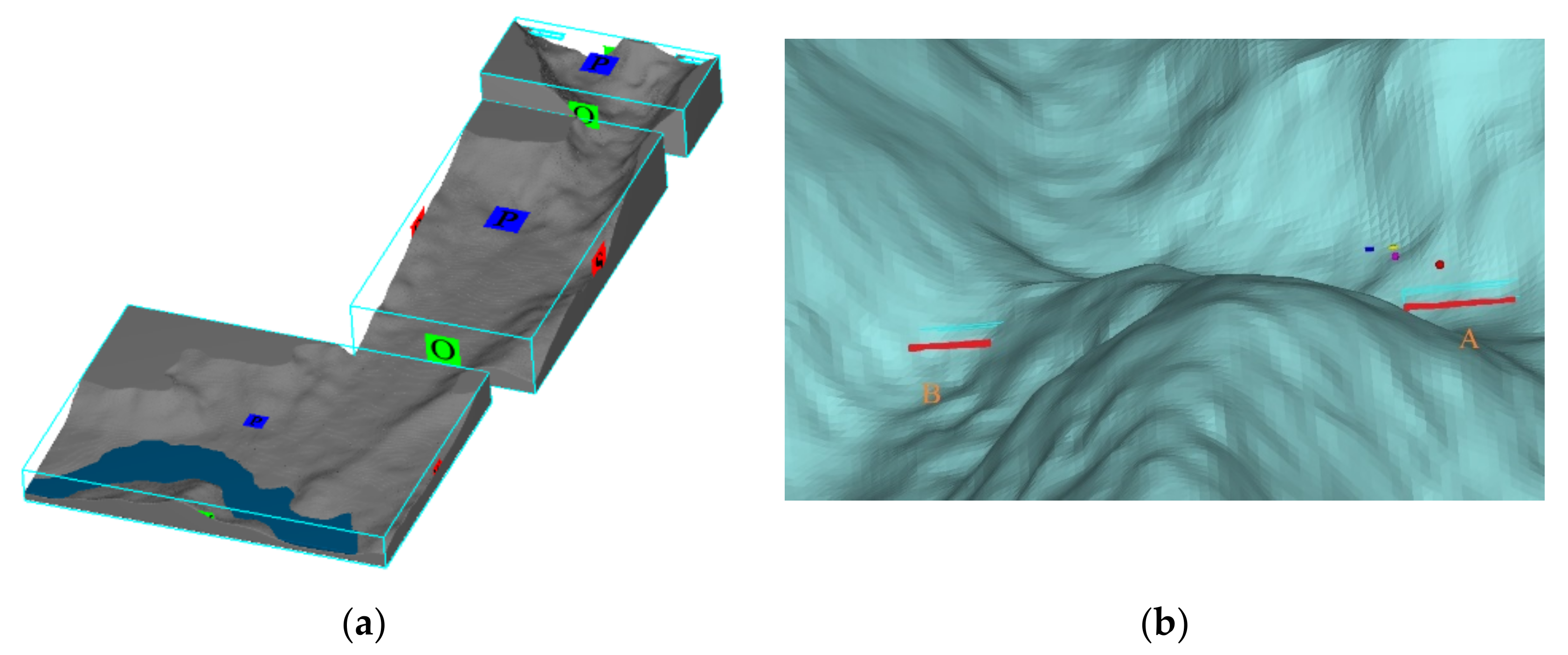



| Condition | Debris Flow Density (kg/m3) | Yield Stress η (Pa) | Viscosity Coefficient (Pa·s) |
|---|---|---|---|
| 1 | 1200 | 4.706 | 0.023 |
| 2 | 1500 | 18.900 | 0.091 |
| 3 | 1800 | 75.900 | 0.364 |
| 4 | 2100 | 304.770 | 1.463 |
| Debris Flow Inlet | Extent of the Rectangular Inlet (m) | Inlet Width (m) | Depth of Debris Flow (m) | Debris Flow Velocity (m/s) |
|---|---|---|---|---|
| A | x direction: 2062–2200 z direction: 1724–1732 | 138 | 8.0 | 7.10 |
| B | X direction: 2734–2832 z direction: 1730–1736 | 98 | 6.0 | 5.80 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, F.; Wang, J.; Chen, X.; Zhang, S.; Qiu, H.; Lou, C. Numerical Simulation of Boulder Fluid–Solid Coupling in Debris Flow: A Case Study in Zhouqu County, Gansu Province, China. Water 2022, 14, 3884. https://doi.org/10.3390/w14233884
Wang F, Wang J, Chen X, Zhang S, Qiu H, Lou C. Numerical Simulation of Boulder Fluid–Solid Coupling in Debris Flow: A Case Study in Zhouqu County, Gansu Province, China. Water. 2022; 14(23):3884. https://doi.org/10.3390/w14233884
Chicago/Turabian StyleWang, Fei, Jiading Wang, Xiaoqing Chen, Shaoxiong Zhang, Haijun Qiu, and Canyun Lou. 2022. "Numerical Simulation of Boulder Fluid–Solid Coupling in Debris Flow: A Case Study in Zhouqu County, Gansu Province, China" Water 14, no. 23: 3884. https://doi.org/10.3390/w14233884
APA StyleWang, F., Wang, J., Chen, X., Zhang, S., Qiu, H., & Lou, C. (2022). Numerical Simulation of Boulder Fluid–Solid Coupling in Debris Flow: A Case Study in Zhouqu County, Gansu Province, China. Water, 14(23), 3884. https://doi.org/10.3390/w14233884







