Study on Waterlogging Reduction Effect of LID Facilities in Collapsible Loess Area Based on Coupled 1D and 2D Hydrodynamic Model
Abstract
:1. Introduction
- (1)
- What are the reasonable infiltration parameters for the hydrodynamic model in collapsible loess regions;
- (2)
- How to effectively evaluate the effects of LID facilities on the degree of waterlogging and the drainage capacity of pipelines;
- (3)
- What are the changes in waterlogging levels before and after LID facility construction in the collapsible loess region;
- (4)
- What are the changes in the surface runoff, waterlogged area, and drainage network indicators under different rainfall patterns.
2. Materials and Methods
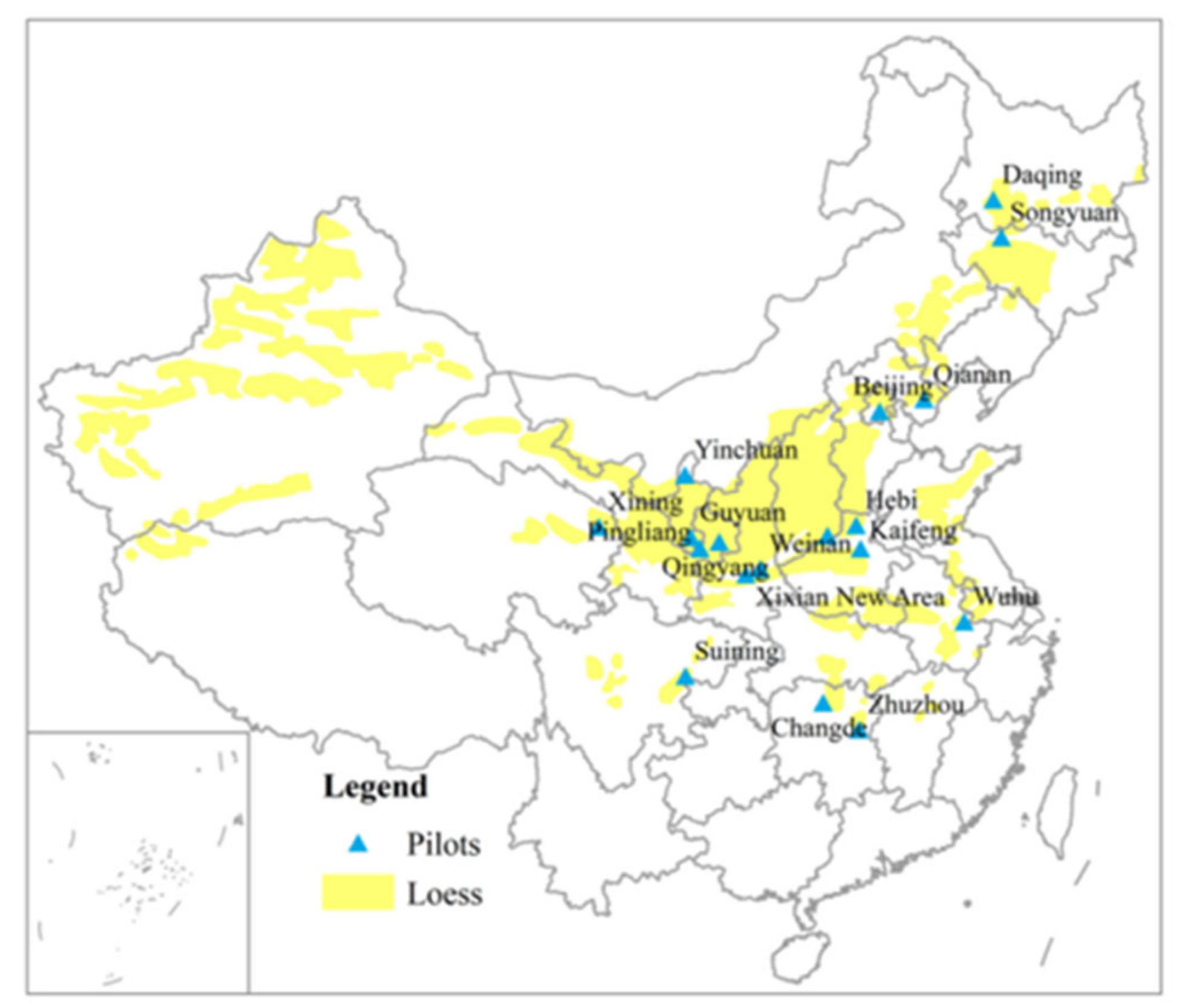
2.1. Study Site
2.2. Data Collection and Preprocessing
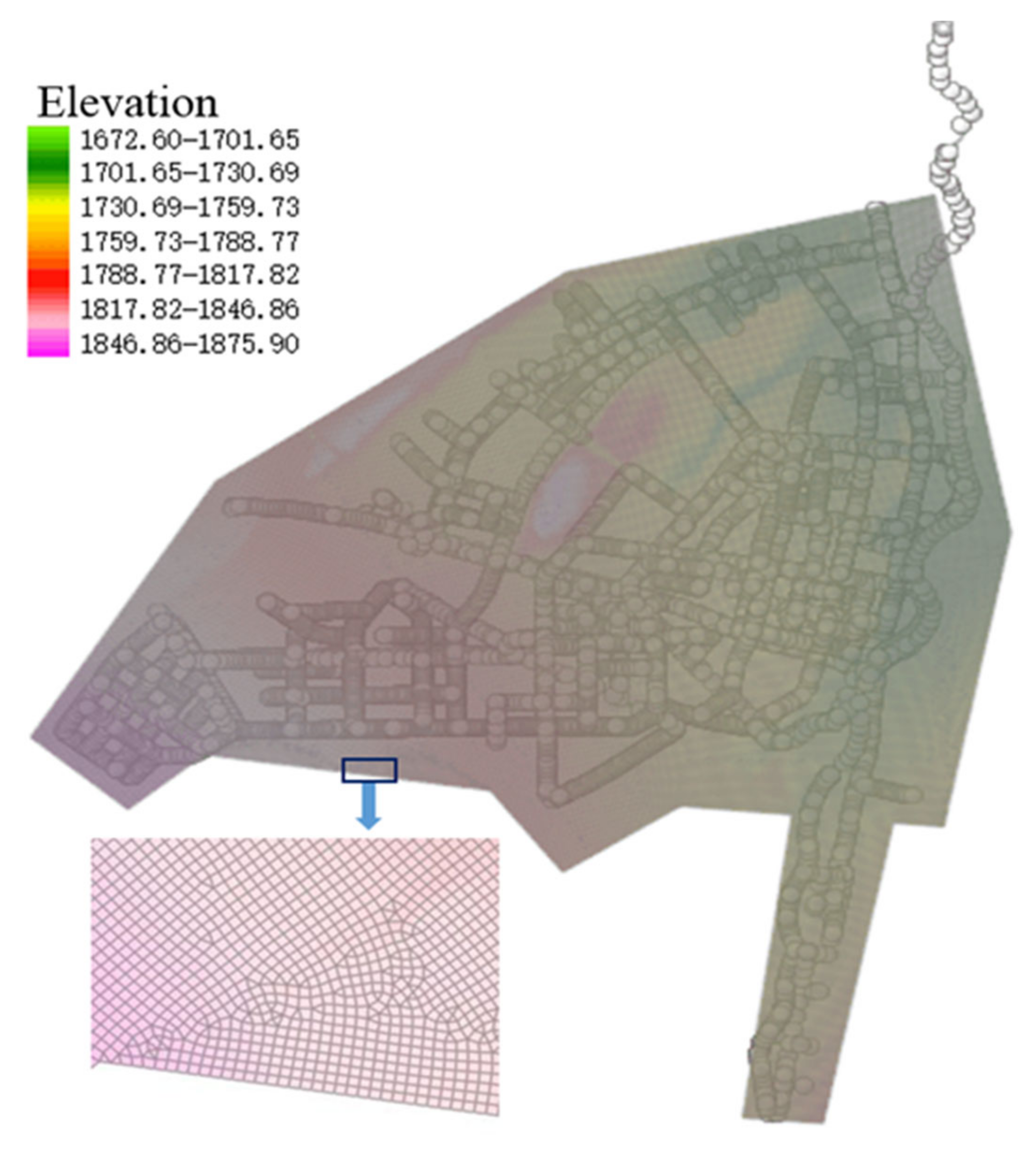
2.2.1. Topographic Data
2.2.2. Drainage Network Data
2.2.3. Rainstorm Data
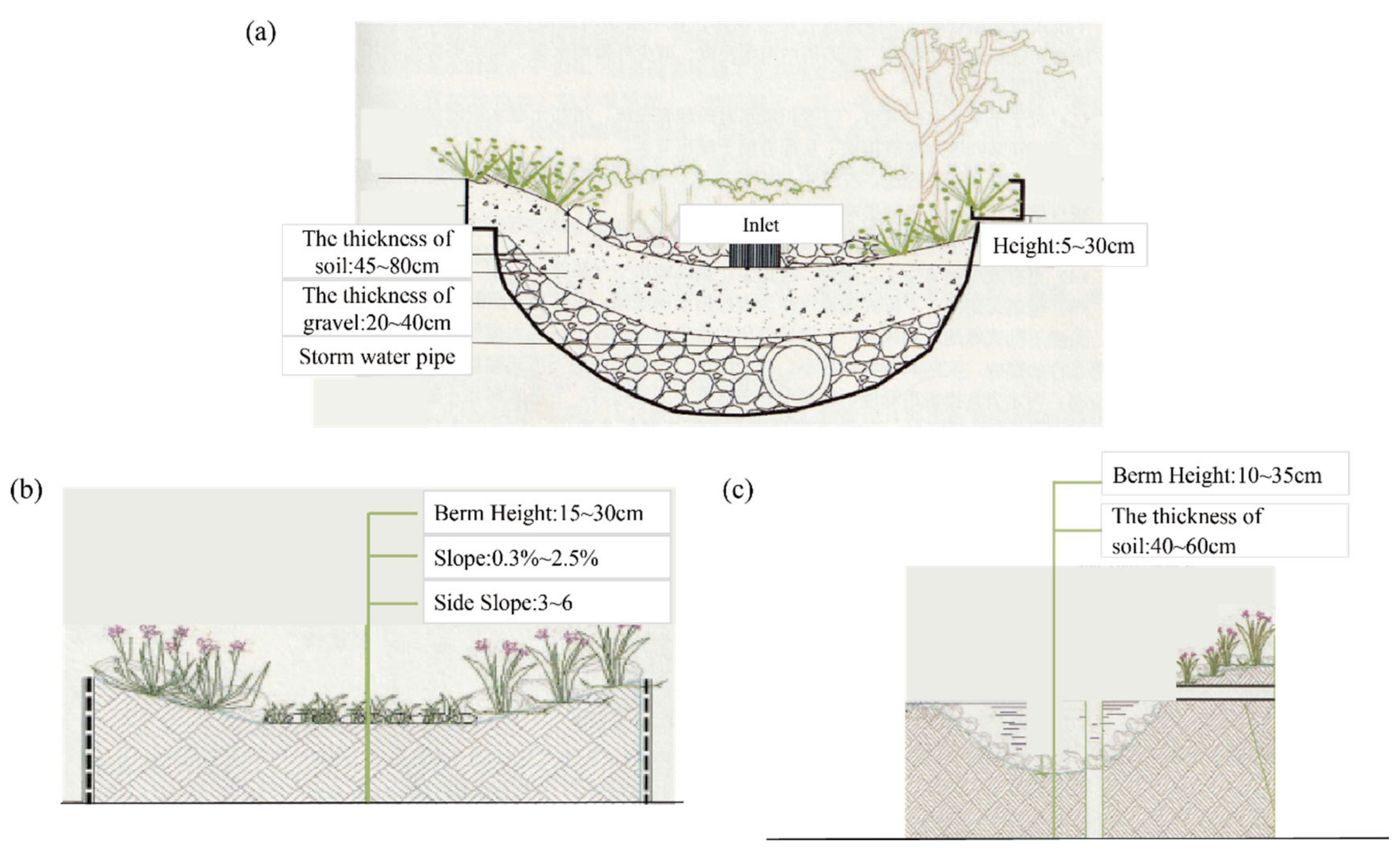
2.2.4. LID Data
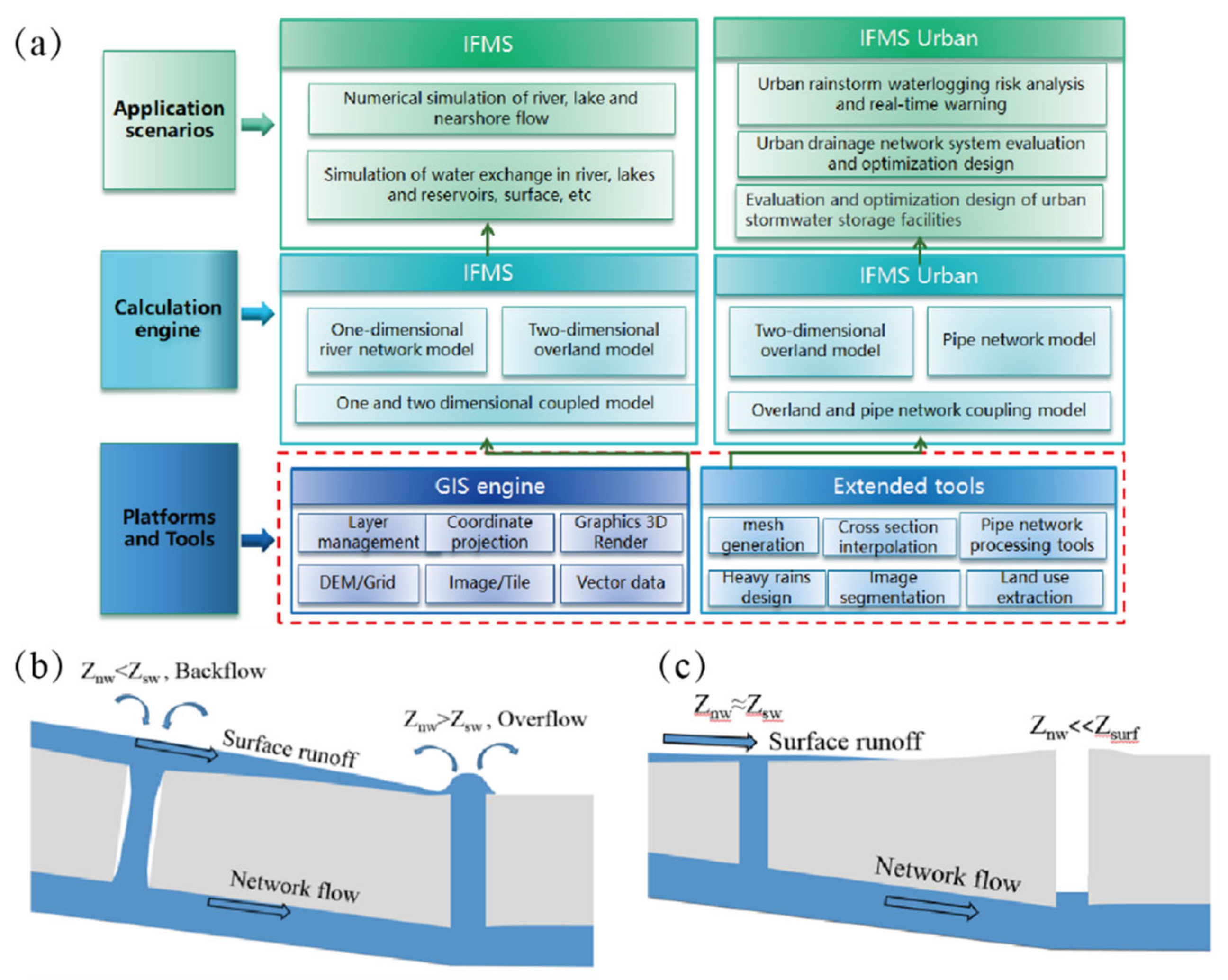
2.3. Model Theory
3. Results and Discussion
3.1. Model Calibration and Validation
3.2. Waterlogging Reduction Effect of LID Facilities
3.2.1. Rainfall Return Period
3.2.2. Rainfall Peak Coefficient
3.2.3. Rainfall Duration
3.3. Impact Analysis of Waterlogging Reduction Indicators
4. Conclusions
- (1)
- The coupled 1D and 2D hydrodynamic model is suitable for evaluating the effects of LID facilities on the degree of waterlogging and the drainage capacity of pipelines. The infiltration parameters of the hydrodynamic model in the collapsible loess area are relatively high, as compared with other cities in humid regions.
- (2)
- After due measures are taken in the collapsible loess area, the total runoff quantity, peak flood flow, waterlogged area, runoff coefficient, and drainage pipeline pressure have all decreased under different rainfall patterns. As the rainfall return period goes up, the waterlogging reduction effect and improvement of drainage capacity of the sponge city measures were gradually weakened. The reduction rates of waterlogged area in the case of rainstorms that occur once in every 2 years, 10 years and 50 years were 19.9%, 14.9% and 12.2%, respectively.
- (3)
- The implementation of LID measures has the more significant effect on the reduction in moderate waterlogged areas, as compared with the reduction in severely and mildly waterlogged area. For smaller storms, with LID measures in place, when the rainfall peak comes later, there would be larger amount of pre-peak stormwater infiltration and retention, resulting in slightly lower runoff coefficient.
- (4)
- The rainfall return period has a great impact on the indicators of surface runoff, waterlogged area, and drainage capacity; the position of rainfall peak has a relatively big impact on the proportion of overflow nodes, proportion of fully loaded pipelines, and average full-load duration; the rainfall duration has relatively big impact on the total runoff quantity, runoff coefficient, and average full-load duration.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Na, L.I.; Yuting, M.; Jing, W.; Qian, Y.U.; Nianqiang, Z. Effect of low impact development measures on inundation reduction—Taking Jinan pilot area as example. J. Hydraul. Eng. 2018, 49, 1489–1502. [Google Scholar]
- National Statistics Bureau. The Statistical Bulletin on National Economic and Social Development; China Statistics Press: China, Beijing, 2021. [Google Scholar]
- You, Q.; Kang, S.; Aguilar, E.; Pepin, N.; Flügel, W.; Yan, Y.; Xu, Y.; Zhang, Y.; Jie, H. Changes in daily climate extremes in China and their connection to the large scale atmospheric circulation during 1961–2003. Clim. Dyn. 2011, 36, 2399–2417. [Google Scholar] [CrossRef]
- Mahmoud, S.H.; Gan, T.Y. Urbanization and climate change implications in flood risk management: Developing an efficient decision support system for flood susceptibility mapping. Sci. Total Environ. 2018, 636, 152–167. [Google Scholar] [CrossRef]
- Ning, Y.-F.; Dong, W.-Y.; Lin, L.-S.; Zhang, Q. Analyzing the causes of urban waterlogging and sponge city technology in China. IOP Conf. Series Earth Environ. Sci. 2017, 59, 012047. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Hu, Q.; He, R. Discussion and views on some issues of the sponge city construction in China. Adv. Water Sci. 2016, 27, 793–799. [Google Scholar]
- Technical Guidelines for Sponge City Construction-Construction of Stormwater System with Low Impact Development (Trial); Ministry of Housing and Urban-Rural Development of the People’s Republic of China; China Architecture & Building Press: Beijing, China, 2014.
- State Council of the People’s Republic of China. Guidance on Promoting the Construction of Sponge Cities; State Council of the People’s Republic of China: Beijing, China, 2015.
- Li, H.; Ding, L.; Ren, M.; Li, C.; Wang, H. Sponge city construction in China: A survey of the challenges and opportunities. Water 2017, 9, 594. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Jia, Y.; Niu, C. “Sponge city” concept helps solve China’s urban water problems. Environ. Earth Sci. 2017, 76, 473. [Google Scholar] [CrossRef]
- Wang, H.; Mei, C.; Liu, J.H.; Shao, W.W. A new strategy for integrated urban water management in China: Sponge city. Sci. China Technol. Sci. 2018, 61, 317–329. [Google Scholar] [CrossRef]
- Zhou, M.; Köster, S.; Zuo, J.; Wu, C.; Wang, X. Cross-Boundary Evolution of Urban Planning and Urban Drainage Towards the Water Sensitive “Sponge City”: Technical and Institutional Aspects from Chinese and German Perspective. In Urban Water Management for Future Cities; Springer: Cham, Switzerland, 2019. [Google Scholar]
- Chang, N.-B.; Lu, J.-W.; Chui, T.F.M.; Hartshorn, N. Global policy analysis of low impact development for stormwater management in urban regions. Land Use Policy 2018, 70, 368–383. [Google Scholar] [CrossRef]
- Fiori, A.; Volpi, E. On the effectiveness of LID infrastructures for the attenuation of urban flooding at the catchment scale. Water Resour. Res. 2020, 56, e2020WR027121. [Google Scholar] [CrossRef]
- Behrouz, M.S.; Zhu, Z.; Matott, L.S.; Rabideau, A.J. A new tool for automatic calibration of the Storm Water Management Model (SWMM). J. Hydrol. 2020, 581, 124436. [Google Scholar] [CrossRef]
- Kang, Z.; Guo, Q.; Lian, J.; Cheng, L. Advances in simulation models for whole-life-cycle effectiveness of sponge city construction. J. Hydroelectr. Eng. 2017, 36, 82–93. [Google Scholar]
- Wei, D.; Urich, C.; Liu, S.; Gu, S. Application of CityDrain3 in flood simulation of sponge polders: A case study of Kunshan, China. Water 2018, 10, 507. [Google Scholar] [CrossRef]
- Chen, Q. Systematically Design of Sponge City Road Based on the SWMM Model. In Proceedings of the Sixth International Forum on Decision Sciences; Springer: Cham, Switzerland, 2020; pp. 29–34. [Google Scholar]
- Peng, J.; Yu, L.; Zhong, X.; Dong, T. Study on Runoff Control Effect of Different Drainage Schemes in Sponge Airport. Water Resour. Manag. 2022, 36, 1043–1055. [Google Scholar] [CrossRef]
- Sin, J.; Jun, C.; Zhu, J.; Yoo, C. Evaluation of flood runoff reduction effect of LID (Low Impact Development) based on the decrease in CN: Case studies from Gimcheon Pyeonghwa district, Korea. Procedia Eng. 2014, 70, 1531–1538. [Google Scholar] [CrossRef] [Green Version]
- Yuan, Y.; Gan, Y.; Xu, Y.; Xie, Q.; Shen, Y.; Yin, Y.J.W. SWMM-Based Assessment of Urban Mountain Stormwater Management Effects under Different LID Scenarios. Water 2022, 14, 78. [Google Scholar] [CrossRef]
- Lee, S.; Kim, D.; Maeng, S.; Azam, M.; Lee, B. Runoff Reduction Effects at Installation of LID Facilities under Different Climate Change Scenarios. Water 2022, 14, 1301. [Google Scholar] [CrossRef]
- Huang, C.-L.; Hsu, N.-S.; Liu, H.-J.; Huang, Y.-H. Optimization of low impact development layout designs for megacity flood mitigation. J. Hydrol. 2018, 564, 542–558. [Google Scholar] [CrossRef]
- Cui, T.; Long, Y.; Wang, Y. Choosing the LID for urban storm management in the south of taiyuan basin by comparing the storm water reduction efficiency. Water 2019, 11, 2583. [Google Scholar] [CrossRef] [Green Version]
- Mei, C.; Liu, J.; Wang, H.; Li, Z.; Yang, Z.; Shao, W.; Ding, X.; Weng, B.; Yu, Y.; Yan, D. Urban flood inundation and damage assessment based on numerical simulations of design rainstorms with different characteristics. Sci. China Technol. Sci. 2020, 63, 2292–2304. [Google Scholar] [CrossRef]
- Chen, W.; Huang, G.; Zhang, H.; Wang, W. Urban inundation response to rainstorm patterns with a coupled hydrodynamic model: A case study in Haidian Island, China. J. Hydrol. 2018, 564, 1022–1035. [Google Scholar] [CrossRef]
- Liu, Z.; Li, W.; Wang, L.; Li, L.; Xu, B. The scenario simulations and several problems of the Sponge City construction in semi-arid loess region, Northwest China. Landsc. Ecol. Eng. 2022, 18, 95–108. [Google Scholar] [CrossRef]
- Jia, L.; Xu, G.; Huang, M.; Li, Z.; Li, P.; Zhang, Z.; Wang, B.; Zhang, Y.; Zhang, J.; Cheng, Y. Effects of Sponge City Development on Soil Moisture and Water Quality in a Typical City in the Loess Plateau in China. Front. Earth Sci. 2020, 8, 125. [Google Scholar] [CrossRef] [Green Version]
- Huang, M.; Yang, S.; Qi, W.; Hou, J.; Zhang, Y. Numerical simulation of urban waterlogging reduction effect in Guyuan sponge city. Water Resour. Prot. 2019, 35, 13–18. [Google Scholar]
- Shao, Y.; Shao, D. A New Generation of Urban Rainstorm Intensity Formula in China; China Architecture & Building Press: Beijing, China, 2014. [Google Scholar]
- Yu, H.; Ma, J.; Zhang, D.; Mu, J. Application of IFMS Urban software in the preparation of urban flood risk maps. China Flood Drought Manag. 2018, 28, 13–17. [Google Scholar] [CrossRef]
- Ma, J.; Yu, H.; Zhang, D.; Zhang, H.; Wu, B.; Mu, J. Adoption of evaluation software in flood risk map drawing. China Water Resour. 2017, 5, 17–20. [Google Scholar]
- Yu, H.; Fan, Y.; Ma, J.; Wu, B.; Mu, J.; Zhang, D.; Cao, D.; Zhang, H. A 2D Flood Simulation Method Based on High-Precision Terrain Generalization; CNIPA: Beijing, China, 2019. [Google Scholar]
- Ma, J.; Wang, C.; Zhang, D.; Yu, H.; Zhang, H.; Wu, B.; Mu, J.; Ma, T.; Zeng, X.; Nie, W.; et al. An Object-Oriented Approach to Element Management in Hydrodynamic Modeling; CNIPA: Beijing, China, 2017. [Google Scholar]
- Yu, H.; Fan, Y.; Ma, J.; Wu, B.; Mu, J.; Zhang, D.; Cao, D.; Zhang, H. A Simulation Method of Urban Surface Building Hydrodynamics Based on Area Correction Rate; CNIPA: Beijing, China, 2019. [Google Scholar]
- Zhang, H.; Ma, J.; Yu, H.; Zhang, D.; Mu, J.; Wu, B.; Wang, C.; Zeng, X.; Cao, D.; Nie, W.; et al. A Hydrodynamic Coupling Method for Surface Two-Dimensional Underground Pipe Network Based on Spatial Topology; CNIPA: Beijing, China, 2018. [Google Scholar]
- Ma, J.; Yu, H.; Zhang, H.; Wang, C.; Zhang, D.; Mu, J.; Wu, B.; Zeng, X.; Cao, D.; Nie, W.; et al. The Utility Model Relates to a Risk Warning Method for Urban Rainstorm Waterlogging and Waterlogging; CNIPA: Beijing, China, 2018. [Google Scholar]
- Yu, H.; Huang, G.; Wu, C. Efficient finite-volume model for shallow-water flows using an implicit dual time-stepping method. J. Hydraul. Eng. 2015, 141, 04015004. [Google Scholar] [CrossRef]
- Zhang, D.; Quan, J.; Wang, Z.; Zhang, H.; Ma, J. Numerical Simulation of Overland Flows Using Godunov Scheme Based on Finite Volume Method. EPiC Ser. Eng. 2018, 3, 2425–2432. [Google Scholar]
- Fan, Y.; Ao, T.; Yu, H.; Huang, G.; Li, X. A coupled 1D-2D hydrodynamic model for urban flood inundation. Adv. Meteorol. 2017, 2017, 1–12. [Google Scholar] [CrossRef] [Green Version]
- Krebs, G.; Kokkonen, T.; Valtanen, M.; Koivusalo, H.; Setälä, H. A high-resolution application of a stormwater management model (SWMM) using genetic parameter optimization. Urban Water J. 2013, 10, 394–410. [Google Scholar] [CrossRef]



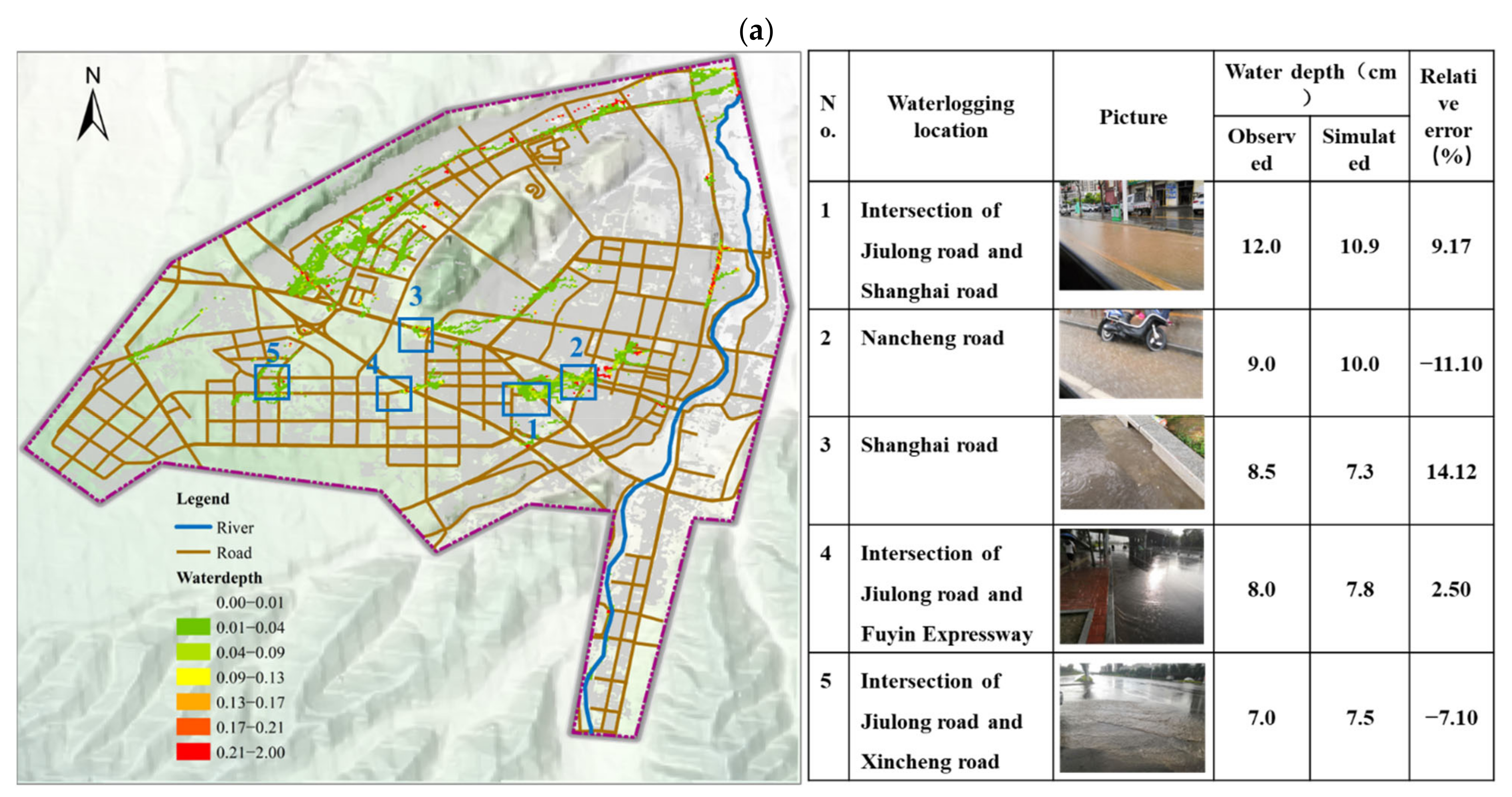

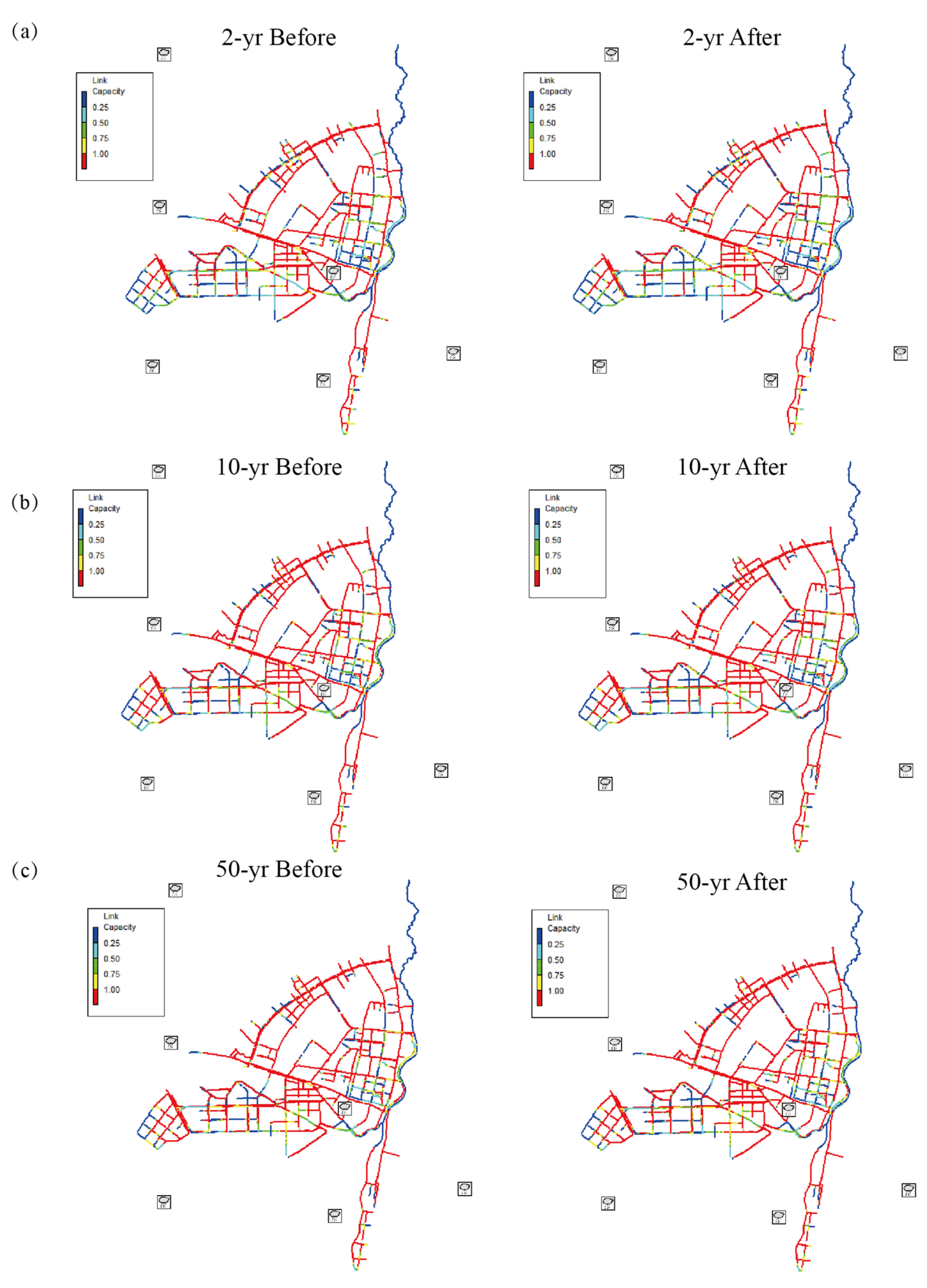
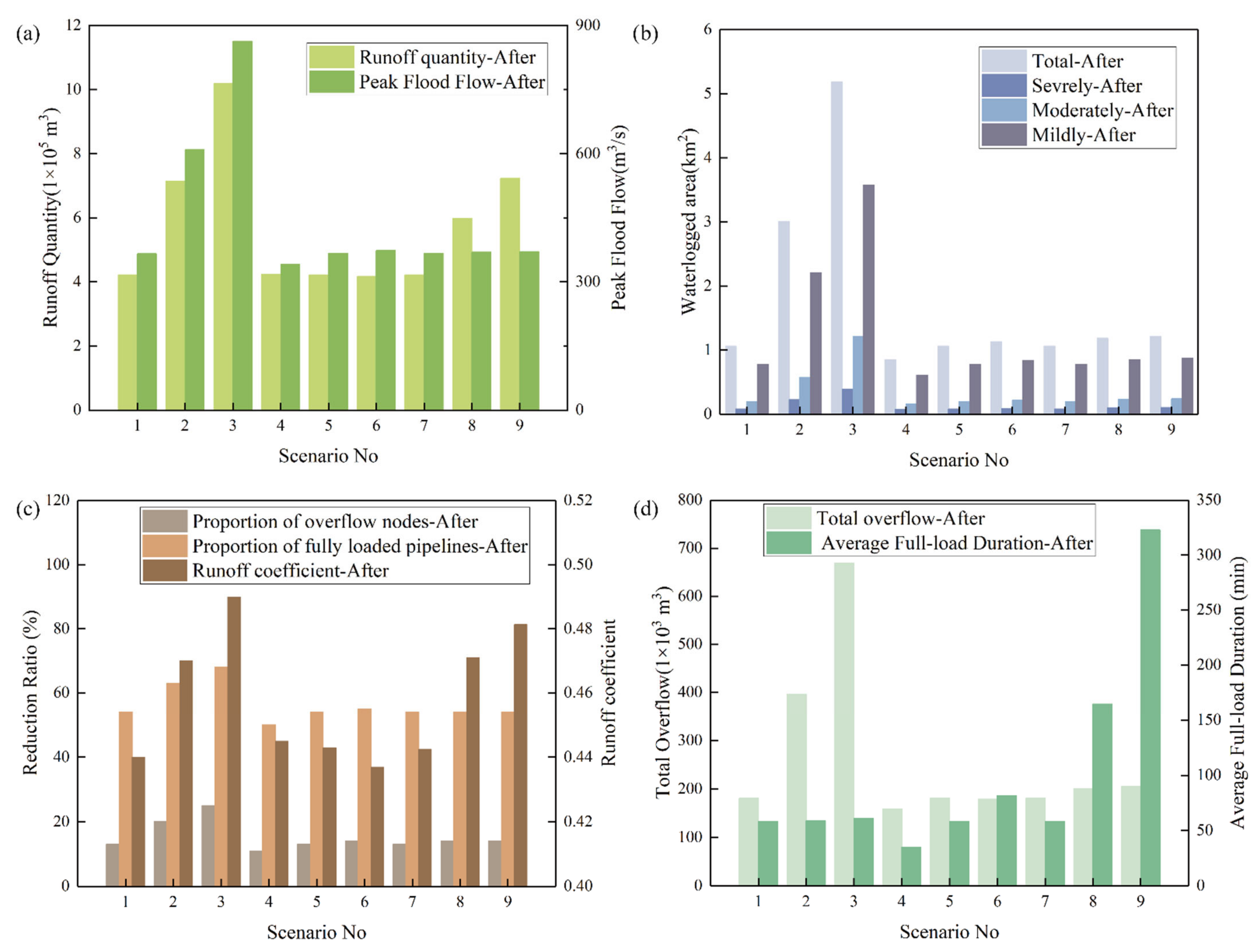
| Rain Gauge | Maximum Rainfall Intensity (mm/h) | 6 h Cumulative Rainfall (mm) | 24 h Cumulative Rainfall (mm) | |||
|---|---|---|---|---|---|---|
| Rainfall events | 20170727 | 20180821 | 20170727 | 20180821 | 20170727 | 20180821 |
| 1 | 7.1 | 17.3 | 19.3 | 35.5 | 25.5 | 57.9 |
| 2 | 10.2 | 21.6 | 32.9 | 38 | 33.9 | 76 |
| 3 | 12.6 | 17.5 | 41.1 | 31.8 | 49.6 | 59.7 |
| 4 | 4.4 | 14.9 | 14.8 | 19.6 | 23.7 | 48.8 |
| 5 | 10.7 | 10.5 | 38.2 | 39.4 | 44.6 | 68 |
| 6 | 6.3 | 12.5 | 22.7 | 36.5 | 30.3 | 67.9 |
| Scenario No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| Return period | 2 | 10 | 50 | 2 | 2 | 2 | 2 | 2 | 2 |
| Peak Position Coefficient | 0.5 | 0.5 | 0.5 | 0.25 | 0.5 | 0.75 | 0.5 | 0.5 | 0.5 |
| Duration | 2 h | 2 h | 2 h | 2 h | 2 h | 2 h | 2 h | 6 h | 12 h |
| Sponge City Measures | Rainwater Garden (km2) | Vegetative Swale (km) | Rain Barrel (m3) | Sunken Green Space (km2) |
|---|---|---|---|---|
| Scale | 0.2 | 5.51 | 17,585.00 | 2.60 |
| Layer | Parameter | Sunken Green Space | Vegetative Swale | Rain Barrel | Rainwater Garden |
|---|---|---|---|---|---|
| Surface | Berm height (mm) | 200 | 200 | 300 | |
| Vegetation volume fraction | 0.2 | 0.2 | 0.2 | ||
| Surface roughness | 0.15 | 0.15 | 0.15 | ||
| Surface slope (%) | 1 | 1 | 1 | ||
| Swale side slope | 5 | ||||
| Soil | Thickness (mm) | 500 | 500 | ||
| Porosity | 0.45 | 0.45 | |||
| Field capacity | 0.2 | 0.2 | |||
| Wilting point | 0.2 | 0.2 | |||
| Conductivity (mm/h) | 100 | 100 | |||
| Conductivity slope | 10 | 10 | |||
| Suction head (mm) | 90 | 90 | |||
| Storage | Thickness (mm) | 300 | 900 | ||
| Void ratio (voids/solids) | 0.75 | ||||
| Seepage rate (mm/h) | 250 | ||||
| Clogging factor | 0 |
| Parameter | Type | Value |
|---|---|---|
| Infiltration parameter | Maximum rate | 120 mm/h |
| Minimum rate | 5 mm/h | |
| Decay constant | 3/h | |
| Drying time | 7 days | |
| Manning coefficient | River | 0.03 s/m1/3 |
| Pipe | 0.013 s/m1/3 | |
| Grassland | 0.2 s/m1/3 | |
| Residential area | 0.015 s/m1/3 | |
| Street | 0.015 s/m1/3 | |
| Depression storage depth | Impervious | 2.0 mm |
| Previous | 4.5 mm |
| Rainfall Return Period | Amount of Rainfall /mm | Runoff Quantity (1 × 105 m3) | Peak Flood Flow (m3/s) | ||||
|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | ||
| 2-yr | 20.266 | 4.70 | 4.22 | 10.2% | 408.20 | 366.10 | 10.3% |
| 10-yr | 32.263 | 7.90 | 7.14 | 9.6% | 678.20 | 609.10 | 10.2% |
| 50-yr | 44.261 | 11.24 | 10.19 | 9.3% | 956.90 | 863.10 | 9.8% |
| Rainfall Return Period | Severely Waterlogged Area | Moderately Waterlogged Area | Mildly Waterlogged Area | Total Waterlogged Area | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | |
| 2-yr | 0.101 | 0.082 | 18.5% | 0.271 | 0.201 | 25.9% | 0.952 | 0.778 | 18.3% | 1.325 | 1.06 | 19.9% |
| 10-yr | 0.261 | 0.226 | 13.6% | 0.719 | 0.577 | 19.8% | 2.557 | 2.208 | 13.7% | 3.537 | 3.01 | 14.9% |
| 50-yr | 0.484 | 0.394 | 18.7% | 1.415 | 1.211 | 14.4% | 3.999 | 3.575 | 10.6% | 5.898 | 5.18 | 12.2% |
| Rainfall Return Periods | Runoff Coefficient | Proportion of Overflow Nodes | Total Overflow Quantity (1 × 103m3) | Proportion of Fully Loaded Pipelines | ||||
|---|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Before Measure | After Measure | Before Measure | After Measure | Before Measure | After Measure | |
| 2-yr | 0.49 | 0.44 | 15% | 13% | 218.69 | 181.02 | 57% | 54% |
| 10-yr | 0.52 | 0.47 | 22% | 20% | 472.26 | 395.70 | 65% | 63% |
| 50-yr | 0.54 | 0.49 | 27% | 25% | 766.02 | 669.24 | 71% | 68% |
| Rainfall Return Period | Rainfall Peak Coefficient | Runoff Quantity (1 × 105 m3) | Peak Flood Flow (m3/s) | ||||
|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | ||
| 2-yr | 0.25 | 4.73 | 4.24 | 10.4% | 375.10 | 341.00 | 9.1% |
| 2-yr | 0.50 | 4.70 | 4.22 | 10.2% | 408.20 | 366.40 | 10.2% |
| 2-yr | 0.75 | 4.64 | 4.17 | 10.1% | 410.10 | 373.40 | 8.9% |
| Rainfall Peak Coefficient | Severely Waterlogged Area | Moderately Waterlogged Area | Mildly Waterlogged Area | Total Waterlogged Area | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | |
| 0.25 | 0.093 | 0.076 | 18.5% | 0.204 | 0.162 | 20.9% | 0.725 | 0.610 | 15.9% | 1.023 | 0.848 | 17.1% |
| 0.50 | 0.101 | 0.082 | 18.5% | 0.271 | 0.201 | 25.9% | 0.952 | 0.778 | 18.3% | 1.325 | 1.062 | 19.9% |
| 0.75 | 0.098 | 0.083 | 15.3% | 0.292 | 0.215 | 26.2% | 1.033 | 0.836 | 19.1% | 1.423 | 1.134 | 20.3% |
| Rainfall Peak Coefficient | Runoff Coefficient | Proportion of Overflow Nodes | Total Runoff Quantity (1 × 103 m3) | Proportion of Fully Loaded Pipelines | Average Full-Load Duration (min) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Before Measure | After Measure | Before Measure | After Measure | Before Measure | After Measure | Before Measure | After Measure | |
| 0.25 | 0.495 | 0.445 | 13% | 11% | 193.25 | 159.11 | 53% | 50% | 35.34 | 34.91 |
| 0.50 | 0.493 | 0.443 | 15% | 13% | 218.69 | 181.02 | 57% | 54% | 58.72 | 58.20 |
| 0.75 | 0.486 | 0.437 | 15% | 14% | 213.90 | 179.19 | 57% | 55% | 81.73 | 81.60 |
| Rainfall Return Period | Rainfall Duration/h | Total Runoff Quantity (1 × 105 m3) | Peak Flood Flow (m3/s) | ||||
|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | ||
| 2-yr | 2 | 4.70 | 4.22 | 10.2% | 408.20 | 366.40 | 10.2% |
| 2-yr | 6 | 6.66 | 5.98 | 10.2% | 411.6 | 369.57 | 10.2% |
| 2-yr | 12 | 8.04 | 7.23 | 10.1% | 412.56 | 370.78 | 10.1% |
| Rainfall Return Period | Rainstorm Duration/h | Severely Waterlogged Area | Moderately Waterlogged Area | Mildly Waterlogged Area | Total Waterlogged Area | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | Before Measure | After Measure | Reduction Rate | ||
| 2-yr | 2 | 0.101 | 0.082 | 18.5% | 0.271 | 0.201 | 25.9% | 0.952 | 0.778 | 18.3% | 1.325 | 1.062 | 19.9% |
| 2-yr | 6 | 0.123 | 0.100 | 18.3% | 0.311 | 0.234 | 24.7% | 1.054 | 0.848 | 19.6% | 1.488 | 1.182 | 20.6% |
| 2-yr | 12 | 0.125 | 0.103 | 17.4% | 0.318 | 0.239 | 25.0% | 1.060 | 0.870 | 17.9% | 1.503 | 1.212 | 19.4% |
| Rainfall Duration/h | Runoff Coefficient | Proportion of Overflow Nodes | Total Overflow Quantity (1 × 103 m3) | Proportion of Fully Loaded Pipelines | Average Full-Load Duration (min) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Before Measure | After Measure | Before Measure | After Measure | Before Measure | After Measure | Before Measure | After Measure | Before Measure | After Measure | |
| 2 | 0.493 | 0.443 | 15% | 13% | 218.69 | 181.02 | 57% | 54% | 58.72 | 58.20 |
| 6 | 0.524 | 0.471 | 15% | 14% | 241.15 | 201.35 | 57% | 54% | 165.92 | 164.40 |
| 12 | 0.535 | 0.481 | 15% | 14% | 245.28 | 205.33 | 57% | 54% | 324.890 | 322.87 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mu, J.; Huang, M.; Hao, X.; Chen, X.; Yu, H.; Wu, B. Study on Waterlogging Reduction Effect of LID Facilities in Collapsible Loess Area Based on Coupled 1D and 2D Hydrodynamic Model. Water 2022, 14, 3880. https://doi.org/10.3390/w14233880
Mu J, Huang M, Hao X, Chen X, Yu H, Wu B. Study on Waterlogging Reduction Effect of LID Facilities in Collapsible Loess Area Based on Coupled 1D and 2D Hydrodynamic Model. Water. 2022; 14(23):3880. https://doi.org/10.3390/w14233880
Chicago/Turabian StyleMu, Jie, Miansong Huang, Xiaoli Hao, Xiaolan Chen, Haijun Yu, and Binbin Wu. 2022. "Study on Waterlogging Reduction Effect of LID Facilities in Collapsible Loess Area Based on Coupled 1D and 2D Hydrodynamic Model" Water 14, no. 23: 3880. https://doi.org/10.3390/w14233880






