Experimental and Numerical Analysis of Forced Convection in a Horizontal Tube Partially Filled with a Porous Medium under Local Thermal Equilibrium Conditions

Abstract

The objective of the present work is to analyze experimentally and numerically the laminar forced convection flow in a horizontal pipe partially filled with a porous medium under constant heat flux and to study the influence of the eccentricity of the porous medium on the results. In a numerical analysis, the governing equations are solved in three dimensions. To simplify the grid generation and the satisfaction of the boundary conditions, conformal mapping is applied to convert the cross-section of the tube in the fluid domain (space between two eccentric circles) into a rectangle, and the equations are solved in a computational domain in this domain. The Darcy–Brinkman–Forchheimer model is applied to simulate the hydrodynamic behavior of the flow in the porous region. Thermal equilibrium between solid and fluid is assumed for the energy equation. A FORTRAN program was developed to solve the equations using the finite volume method and the SIMPLE algorithm. Velocity profile, pressure drop and average Nusselt number are studied in a wide range of Darcy numbers, thickness of porous mediums and eccentricities. The results show that the eccentricity of the porous material reduces the heat transfer coefficient and the pressure drop simultaneously; of course, the reduction in the heat transfer coefficient is less noticeable when the thickness of the porous medium is smaller. For example, at R_P = 0.5, when the eccentricity of the porous medium increases up to E = 0.4, the average Nusselt number decreases by 66%, and this reduction for a smaller porous thickness decreases to 11%. The maximum pressure drop reduction for Da = 10⁻⁵ and E = 0.4 is 25%.

1. Introduction

In the last two decades, convection heat transfer in porous media has been widely studied because it has a wide range of applications in a variety of fields, such as geothermal energy [1], chemical engineering [2], microscale engineering [3,4], etc. Actually, porous media has brought significant changes to heat transfer enhancement [5,6,7].

The effect of applying porous media on the heat transfer rate in turbulent flow has been studied by many researchers [8,9,10]. Mohamad [11] employed porous media between two parallel plates and in tubes for heat transfer enhancement. It was depicted that a tube partially filled with porous media brings a higher heat transfer rate and lower pressure drop compared to a tube fully filled and saturated with a porous medium. The optimum thickness was obtained at a fixed Darcy number, which resulted in a maximum heat transfer rate.

Pavel and Mohmmad [12] experimentally and numerically studied the convection heat transfer enhancement in a tube partially and fully filled with a porous medium in the range of 1000 to 4500 Reynolds numbers. They concluded that, in both laminar and turbulent flow, the partially filled tube has further heat transfer enhancement and a lower pressure drop. Huang et al. [13] numerically investigated turbulent flow through a heat exchanger, which was filled with a porous medium, and studied the influence of Darcy and Reynolds numbers on heat transfer enhancement. They indicated that the increase in Darcy and Reynolds numbers leads to an increased Nusselt number.

Local thermal equilibrium (LTE) and local thermal non-equilibrium (LTNE) are two different attitudes towards energy equation analysis in porous media, which stand for the local thermal equilibrium and local thermal non-equilibrium of the solid and fluid phase. These two methods have attracted the attention of many researchers, who have studied the effect of a porous medium insert on the heat transfer coefficient in a channel partially filled with the porous medium [14,15,16,17,18,19]. The physics of the solid–fluid boundary condition plays a key role in the LTNE method, while there are no differences between the boundary condition of the solid and fluid phases under LTE conditions. Some works have been conducted that consider both LTNE and LTE methods [16,17]. Torabi et al. [20] modeled force convection in a channel partially filled with a porous medium in the existence of internal heat through both LTNE and LTE approaches. The governing equations were solved and the velocity and temperature fields were compared for both models. They found that the differences in the Nusselt numbers between these two conditions, which increase at a high porous thickness, are non-negligible. The effects of a number of parameters (which include porous media thickness, thermal conductivity ratio and two different positions of porous media) on the quantity and quality of the heat transfer rate have been taken into consideration by Shokouhmand et al. [21]. It is observed that the position of the porous media inside the pipe and the thermal conductivity ratio are two of the factors that most affect the heat transfer rate. Lu et al. [17] utilized the LTNE method to solve the governing equations for a parallel-plate channel partially filled with metallic foams. The results are compared with experimental results for a parallel-plate channel fully filled with metal foam, which are available in other studies. They concluded that a parallel-plate channel completely filled with metal foam experiences a higher pressure drop than partially filled channels. The effects of a wide range of parameters on the heat transfer rate were discussed. It was indicated that the heat transfer rate grows smoother at a higher value of the thermal conductivity ratio [17].

Alkam and Al-Nimr [22] numerically carried out the analysis of an unsteady forced convection in a tube partially filled with a porous medium. They assessed the influence of porous medium thickness, Darcy number and Forchheimer factor on flow properties and found that the time required to reach a steady state increases when the thickness of the porous medium increases to a certain extent, and with a further increase in its thickness, the time taken to reach a steady state reduces. An analysis was conducted by Minkowycz and Haji-Sheikh [23] to determine the hydrodynamically developed and thermally developing flow between parallel plates fully filled with a porous medium. The separation of variables method was employed to solve the energy equation. The temperature field was reported with mathematical series.

Zhao and Song [24] experimentally and analytically studied a forced convection flow inside a porous medium that was under heat flux normal to the flow direction of a permeable wall and obtained a linear relation between Peclet and Nusselt numbers. Alazmi and Vafai [25] considered different transport phenomena models inside a porous medium. They studied models derived from four assumptions, which are constant porosity, variable porosity, thermal dispersion and local thermal non-equilibrium conditions, and concluded that these changes in models are generally more effective in the velocity field than the temperature field.

Shokouhmand et al. [26] evaluated the effect of porous insert position on the enhanced heat transfer in channels partially filled with a porous medium. They simulated a fully developed laminar flow with the Lattice Boltzmann method and concluded that the position of the porous medium in the system has a significant effect on system thermal performance. Haji-Sheikh and Vafai [27] analyzed flow and heat transfer in different-shaped ducts filled with a porous medium using the Brinkman model.

In the present work, the influence of the geometric parameters of the porous media, such as its thickness and eccentricity, were analyzed in the forced convection inside a horizontal tube that is partially filled with a porous medium. Since the porous medium eccentricity disturbs the axial symmetry, a two-dimensional model with an axial symmetry assumption cannot be applied for this problem. Therefore, a three-dimensional model was utilized. In order to access simpler meshing and avoid using complex equations in writing the code of boundary conditions, an analytical conformal mapping was employed to convert the space between two concentric circles (clear fluid region) to a rectangular space. It should be noted that the two-dimensional mapping transforms the cross-section geometry from a physical space to a computational space and the geometry does not change in the axial direction.

2. Materials and Methods

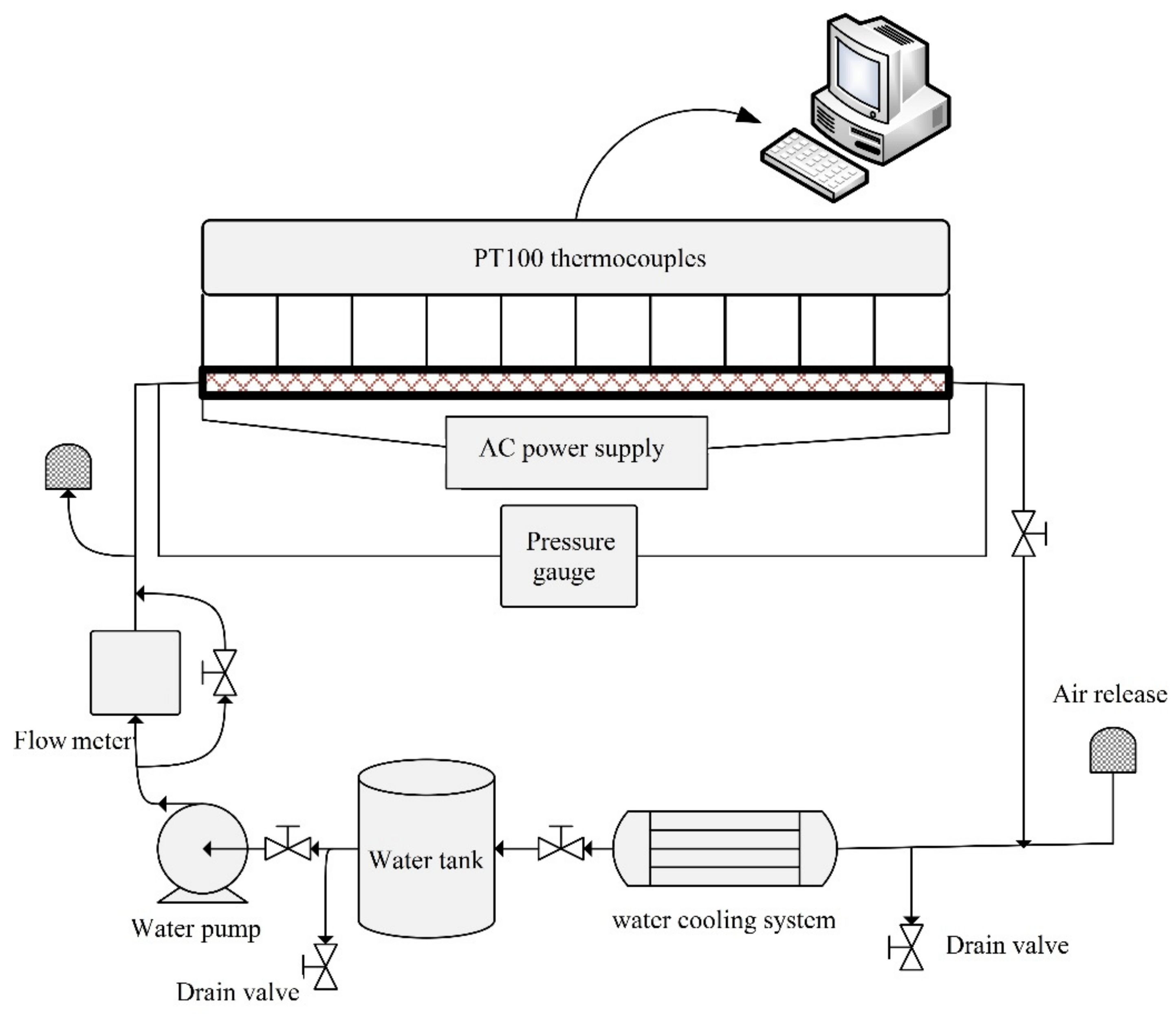
2.1. Experimental Setup

In the experimental setup, as shown in Figure 1, some instrumentation devices were used; their specifications are presented in

Table 1. Instrumentation and apparatuses with their resolution [28,29,30].

Instrumentation	Specifications	Sensed Parameter	Accuracy
Type-K, thermocouple	Testo, flexible	Tw	±1.0 ℃
PT100	Testo, highly accurate immersion	Tin, Tout	±0.03 ℃
PT100 Data logger	Testo 454	-	-
Differential Pressure (dP) Gauge	Model: 3051C, Rosemount, USA, Range: ±6.21 kPa	Differential pressure, ΔP	±0.015% Range = 1.8 Pa
Scaled decanter	2 Lit, 100 cc scaled	Volume	-
Type-K Data acquisition	USB 4718, Advantech	-	-
Ultrasonic Flowmeter	Flownetix, 100 series (0.5–25 L/min)	Flow rate, Q	3% (reading value)

. Water as working fluid was pumped into the test section, where an electrical heater element uniformly wrapped the pipe and thick insulation covered the whole pipe. Data from the inlet and outlet temperatures, as well as the wall temperature, were acquired by the thermocouples in order to calculate the HTC. Additionally, a differential pressure (ΔP) gauge measured the pressure drop along the test section in order to compute the friction coefficient along the test section. Copper foam was employed as a porous media with porosity ε = 0.75 and radius ratio r*_P = r_Porous/r₁ = 0.625. Additionally, after the test section, the water as working fluid entered the heat exchanger to reach its initial temperature again. Some properties, such as dynamic viscosity and thermal conductivity, directly used their corresponding experimental measurements.

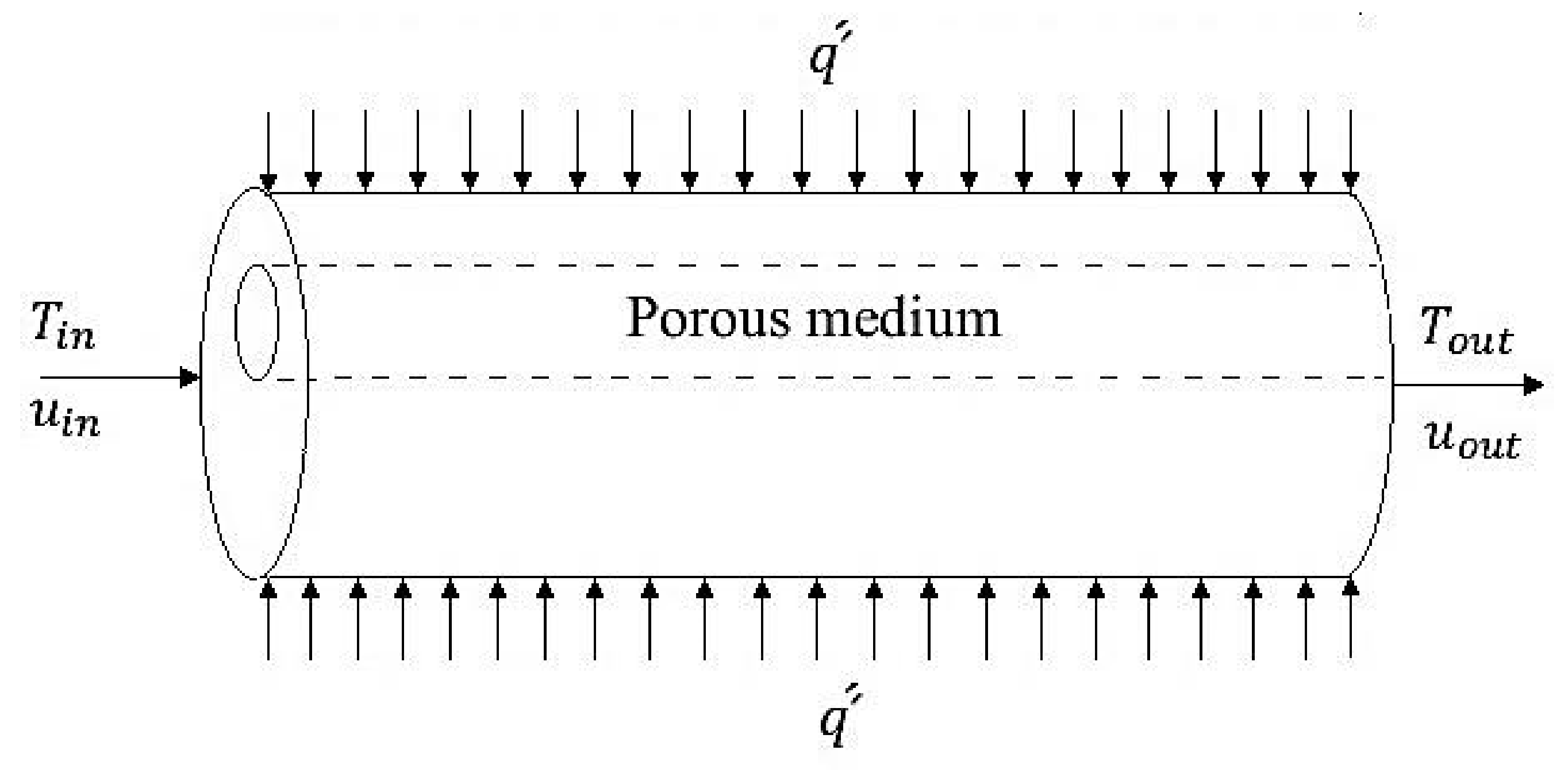
2.2. Governing Equations

The flow is considered laminar, steady, incompressible and three-dimensional. The porous media are supposed to be homogenous and isotropic. Viscous dissipation in energy equation and thermal non-equilibrium between fluid and solid zone in porous media are neglected. Navier–Stokes equations and Darcy–Brinkman–Forchheimer equations are implemented in the clear fluid region and porous region, respectively [31,32]. The geometry of the problem is shown in Figure 2. The non-dimensional parameters used in the governing equations are introduced in Equations (1)–(17).

The non-dimensional governing equations can be written as:

Continuity:

$$U=\frac{u}{w_{in}}$$

(1)

$$V=\frac{v}{w_{in}}$$

(2)

$$W=\frac{w}{w_{in}}$$

(3)

$$X=\frac{x}{r_i}$$

(4)

$$Y=\frac{y}{r_i}$$

(5)

$$Z=\frac{z}{r_i}$$

(6)

$$E=\frac{e}{r_i}$$

(7)

$$T^{*}=\frac{T-T_{in}}{\acute{\stackrel{´}{q}}{r}_i/k_{eff}}$$

(8)

$$P=\frac{p}{{\rho }_f{w}_{in}^2}$$

(9)

$$\left|V_{dl}\right|=\frac{\left|V\right|}{w_{in}}=\sqrt{U^2+V^2+W^2}$$

(10)

$$\mathrm{Re}=\frac{\rho w_{in}{r}_i}{{\mu }_f}$$

(11)

$$\mathrm{Pr}=\frac{\nu }{\alpha }$$

(12)

$$\mathrm{Da}=\frac{K}{r_i^2}$$

(13)

$${\mathrm{R}}_{\mathrm{k}}=\frac{k_{eff}}{k_f}$$

(14)

$$\mathrm{RR}=\frac{r_s}{r_i}$$

(15)

$$\mathrm{Br}=\frac{{\mu }_f{w}_{in}^2}{\acute{\stackrel{´}{q}}{r}_i}$$

(16)

$$\mathrm{M}=\frac{{\mu }_{eff}}{{\mu }_f}$$

(17)

$$\frac{\partial U}{\partial X}+\frac{\partial V}{\partial Y}+\frac{\partial W}{\partial Z}=0$$

(18)

Momentum:

$$\left(\frac{\partial \left(UU\right)}{\partial X}+\frac{\partial \left(UV\right)}{\partial Y}+\frac{\partial \left(UW\right)}{\partial Z}\right)=-{\phi }^2\frac{\partial P}{\partial Y}+\frac{\mathrm{M}.\phi }{\mathrm{Re}}\left[\frac{\partial }{\partial X}\left(\frac{\partial U}{\partial X}\right)+\frac{\partial }{\partial Y}\left(\frac{\partial U}{\partial Y}\right)+\frac{\partial }{\partial Z}\left(\frac{\partial U}{\partial Z}\right)\right]-k\frac{{\phi }^2}{\mathrm{Re}.\mathrm{Da}}U-k\frac{C_F{\phi }^2}{\sqrt{\mathrm{Da}}}\left|V_{dl}\right|U$$

(19)

$$\left(\frac{\partial \left(VU\right)}{\partial X}+\frac{\partial \left(VV\right)}{\partial Y}+\frac{\partial \left(VW\right)}{\partial Z}\right)=-{\phi }^2\frac{\partial P}{\partial Y}+\frac{\mathrm{M}.\phi }{\mathrm{Re}}\left[\frac{\partial }{\partial X}\left(\frac{\partial V}{\partial X}\right)+\frac{\partial }{\partial Y}\left(\frac{\partial V}{\partial Y}\right)+\frac{\partial }{\partial Z}\left(\frac{\partial V}{\partial Z}\right)\right]-k\frac{{\phi }^2}{\mathrm{Re}.\mathrm{Da}}V-k\frac{C_F{\phi }^2}{\sqrt{\mathrm{Da}}}\left|V_{dl}\right|V$$

(20)

$$\left(\frac{\partial \left(WU\right)}{\partial X}+\frac{\partial \left(WV\right)}{\partial Y}+\frac{\partial \left(WW\right)}{\partial Z}\right)=-{\phi }^2\frac{\partial P}{\partial Y}+\frac{\mathrm{M}.\phi }{\mathrm{Re}}\left[\frac{\partial }{\partial X}\left(\frac{\partial W}{\partial X}\right)+\frac{\partial }{\partial Y}\left(\frac{\partial W}{\partial Y}\right)+\frac{\partial }{\partial Z}\left(\frac{\partial W}{\partial Z}\right)\right]-k\frac{{\phi }^2}{\mathrm{Re}.\mathrm{Da}}W-k\frac{C_F{\phi }^2}{\sqrt{\mathrm{Da}}}\left|V_{dl}\right|W$$

(21)

Energy in fluid zone:

$$\frac{\partial \left(T^{*}U\right)}{\partial X}+\frac{\partial \left(T^{*}V\right)}{\partial Y}+\frac{\partial \left(T^{*}W\right)}{\partial Z}=\frac{{\mathrm{R}}_{\mathrm{k}}}{\mathrm{Re}.\mathrm{Pr}}\left[\frac{\partial }{\partial X}\left(\frac{\partial T^{*}}{\partial X}\right)+\frac{\partial }{\partial Y}\left(\frac{\partial T^{*}}{\partial Y}\right)+\frac{\partial }{\partial Z}\left(\frac{\partial T^{*}}{\partial Z}\right)\right]$$

(22)

Equation (18) is mass balance for an incompressible flow. If k = 0 and φ = 1, the Equations (19)–(21) belong to the clear zone, and if k = 1, it belongs to the porous zone. In Equation (22), R_k is the thermal conductivity ratio that is introduced in Equation (14). For the clear zone, R_k is equal to unity. In Equation (14),$k_{eff}$ is the effective thermal conductivity of porous media, which is defined as below:

$$k_{eff}=\phi k_f+\left(1-\phi \right)k_s$$

(23)

Boundary conditions of governing equations are defined as follows:

• Inlet: uniform profile; Z = 0, W = 1, U = V = 0, and T* = 0.
• Outlet: hydrodynamically and thermally fully development.

$$at Z=\frac{l}{r_i}: \frac{\partial U}{\partial Z}=\frac{\partial V}{\partial Z}=\frac{\partial W}{\partial Z}=0$$

(24)

$$at Z=\frac{l}{r_i}: \frac{\partial T^{*}}{\partial Z}=\frac{\partial T_s^{*}}{\partial Z}=\frac{\partial T_m^{*}}{\partial Z}=\frac{2{\mathrm{R}}_{\mathrm{k}}}{\mathrm{Re}.\mathrm{pr}.\sigma }$$

(25)

In Equation (25), ${\mathrm{R}}_{\mathrm{k}}$ and σ are equal to one for the clear zone. σ is defined as the ratio of thermal capacity, which is evaluated as follows:

$$\sigma =\frac{\phi {\rho }_f{C}_{p_f}+\left(1-\phi \right){\rho }_s{C}_s}{{\rho }_f{C}_{p_f}}$$

(26)

Wall (at X² + Y² = 1):

$$\mathrm{U}=\mathrm{V}=\mathrm{W}=0$$

(27)

$$\frac{\partial {\mathrm{T}}^{*}}{\partial \mathrm{X}}={\mathrm{R}}_{\mathrm{k}}\mathrm{X}$$

(28)

$$\frac{\partial {\mathrm{T}}^{*}}{\partial \mathrm{Y}}={\mathrm{R}}_{\mathrm{k}}\mathrm{Y}$$

(29)

Equations (28) and (29) are derived from Equations (30)–(33).

$$\mathrm{at} \mathrm{r}={\mathrm{r}}_{\mathrm{i}} : -{\mathrm{q}}^{’’}{\mathrm{e}}_{\mathrm{r}}=-{\mathrm{k}}_{\mathrm{f}}\nabla \mathrm{T}$$

(30)

$$at x^2+y^2=r_i^2: q^{″}\cos \mathsf{\theta }i+q^{″}\sin \mathsf{\theta }j=k_f\left(\frac{\partial T}{\partial x}i+\frac{\partial T}{\partial y}j\right)$$

(31)

The sin and cos Cartesian forms are within Equation (31):

$$q^{″}\left(\frac{x}{r_i}\right)=k_f\left(\frac{\partial T}{\partial y}\right)$$

(32)

$$q^{″}\left(\frac{y}{r_i}\right)=k_f\left(\frac{\partial T}{\partial y}\right)$$

(33)

Non-dimensional forms of Equations (32) and (33) are Equations (28) and (29).

The interface between porous medium (+) and fluid (−) [16] at ${\left(X-E\right)}^2+Y^2={(\mathrm{RR})}^2$:

$$U_{+}=U_{-}$$

(34)

$$V_{+}=V_{-}$$

(35)

$$W_{+}=W_{-}$$

(36)

$$P_{+}=P_{-}$$

(37)

$$T_{+}^{*}=T_{-}^{*}$$

(38)

The Equations (34)–(38) specify the interface between porous medium and fluid boundary condition.

2.2.1. Using Conformal Mapping in Numerical Analysis

In order to simplify grid generation and boundary condition satisfaction, conformal mapping is used to transform the cross-section of the pipe in the clear region to a rectangle, and equations are solved in a computational domain in this region. According to Figure 3, conformal mapping is defined as follows:

$$\zeta +i\eta =-i \mathrm{Ln}\left(\frac{a{r}_i-Z}{aZ-r_i}\right)$$

(39)

Required parameters in Equations (19)–(21) and Figure 2 are evaluated in Equations (40) and (41):

$$a=\frac{r_i^2+e^2-r_s^2}{2e{r}_i}-{\left[{\left(\frac{r_i^2+e^2-r_s^2}{2e{r}_i}\right)}^2-1\right]}^{\frac{1}{2}}$$

(40)

$$R_s={\left[\frac{e-a{r}_i}{a\left(ea-r_i\right)}\right]}^{\frac{1}{2}}$$

(41)

The transformed conservation equation in the computational domain can be written as Equation (42):

$$\frac{\partial \left(G{U}^{*}J\right)}{\partial \xi }+\frac{\partial \left(G{V}^{*}J\right)}{\partial \eta }+\frac{\partial \left(GWJ\right)}{\partial Z}={\Gamma }_G\left[\frac{\partial }{\partial \xi }\left(\frac{\partial G}{\partial \xi }\right)+\frac{\partial }{\partial \eta }\left(\frac{\partial G}{\partial \eta }\right)+J\frac{\partial }{\partial Z}\left(\frac{\partial G}{\partial Z}\right)\right]+J{S}_G$$

(42)

Parameters used in the conservation equation in the computational domain are defined as Equations (43)–(47):

$$Y_{\xi }=\frac{\left(1-a^2\right)e^{-\eta }\left(\cos \xi +a^2{e}^{-2\eta }\cos \xi +2a{e}^{-\eta }\right)}{{\left(1+a^2{e}^{-2\eta }+2a{e}^{-\eta }\cos \xi \right)}^2}$$

(43)

$$Y_{\eta }=\frac{e^{-\eta }\left(1-a^2\right)\sin \xi \left(a^2{e}^{-2\eta }-1\right)}{{\left(1+a^2{e}^{-2\eta }+2a{e}^{-\eta }\cos \xi \right)}^2}$$

(44)

$$J=Y_{ \xi }^2+Y_{\eta }^2$$

(45)

$$U^{*}=\frac{\left(V.Y_{ \xi }+U.Y_{\eta }\right)}{J}$$

(46)

$$V^{*}=\frac{\left(V.Y_{\eta }-U.Y_{\xi }\right)}{J}$$

(47)

$Y_{\xi }$ and $Y_{\eta }$ are the metric forms of the physical domain transform into the computational domain.$J$ is the jacobin, and $U^{*}$ and $V^{*}$ are defined velocity in the computational domain. The values of $G$ and ${\Gamma }_G$ and $S_G$ are shown in

Table 2. Conservation equation parameters in computational domain.

Equations	${\mathit{S}}_{\mathit{G}}$	${\mathit{\Gamma }}_{\mathit{G}}$	$\mathit{G}$
Continuity	$0$	$0$	$1$
Momentum in$\xi$direction	$\frac{1}{J}\left[-\frac{\partial }{\partial \xi }\left(P{Y}_{\eta }\right)+\frac{\partial }{\partial \eta }\left(P{Y}_{\xi }\right)\right]$	$\frac{2}{\mathrm{Re}}$	$U$
Momentum in$\eta$direction	$\frac{1}{J}\left[-\frac{\partial }{\partial \xi }\left(P{Y}_{\xi }\right)-\frac{\partial }{\partial \eta }\left(P{Y}_{\eta }\right)\right]$	$\frac{2}{\mathrm{Re}}$	$V$
Momentum in$Z$direction	$-\frac{\partial P}{\partial Z}$	$\frac{2}{\mathrm{Re}}$	$W$
Energy	$0$	$\frac{2}{\mathrm{Re}.\mathrm{Pr}}$	$\theta$

. In order to evaluate the conservation equation in the computational domain, the Cauchy–Riemann equations used in analytical conformal mapping are applied. The Cauchy–Riemann equations are shown as follows.

$$X_{ \xi }=Y_{\eta }$$

(48)

$$X_{\eta }=-Y_{ \xi }$$

(49)

For the evaluation of the thermo-hydraulic characteristics of the flow in the computational domain, there are several parameters, such as cross-sectional area, average temperature, local Nusselt number and average Nusselt number, which are shown in Equations (50) and (51).

$$T_m^{*}=\frac{{{\displaystyle \int }}_0^{\pi }{{\displaystyle \int }}_0^{1}W{T}^{*}R.dR.d\theta +{{\displaystyle \int }}_0^{-\ln \left(R_s\right)}{{\displaystyle \int }}_0^{\pi }W{T}^{*}R.d\xi .d\eta }{{{\displaystyle \int }}_0^{\pi }{{\displaystyle \int }}_0^{1}WR.dR.d\theta +{{\displaystyle \int }}_0^{-\ln \left(R_s\right)}{{\displaystyle \int }}_0^{\pi }WR.d\xi .d\eta }$$

(50)

To define average temperature, the relevant parameters in any domain of each cross-section should be calculated separately, and then the sum of the parameters is divided by each individual parameter.

$$\mathrm{Nu}\left(X.Y.Z\right)=\frac{2}{T_s^{*}\left(X.Y.Z\right)-T_m^{*}\left(Z\right)}$$

(51)

Since there is no symmetry in circumferential direction, the outside wall temperature is a function of X, Y and Z. In addition, as it is located on the circle, where there is a relationship between X and Y, one of the variables can be eliminated and Equation (51) may be written in the form of Equation (52):

$$\mathrm{Nu}\left(\theta .Z\right)=\frac{2}{T_s^{*}\left(\theta .Z\right)-T_m^{*}\left(Z\right)}$$

(52)

The average Nusselt number can be written as follows:

$${\mathrm{Nu}}_{\mathrm{ave}}=\frac{{{\displaystyle \int }}_0^{\pi }{{\displaystyle \int }}_0^{L_{dl}}\mathrm{Nu}\left(\theta .Z\right)dZ.d\theta }{{{\displaystyle \int }}_0^{\pi }{{\displaystyle \int }}_0^{L_{dl}}dZ.d\theta }$$

(53)

2.2.2. Numerical Solution Details

Figure 4 schematically shows domains 1 and 2 in the tube cross-section. Numerical solution of domains 1 and 2 is calculated with two different grids, and the interface between the fluid and porous media is coupled together using boundary condition.

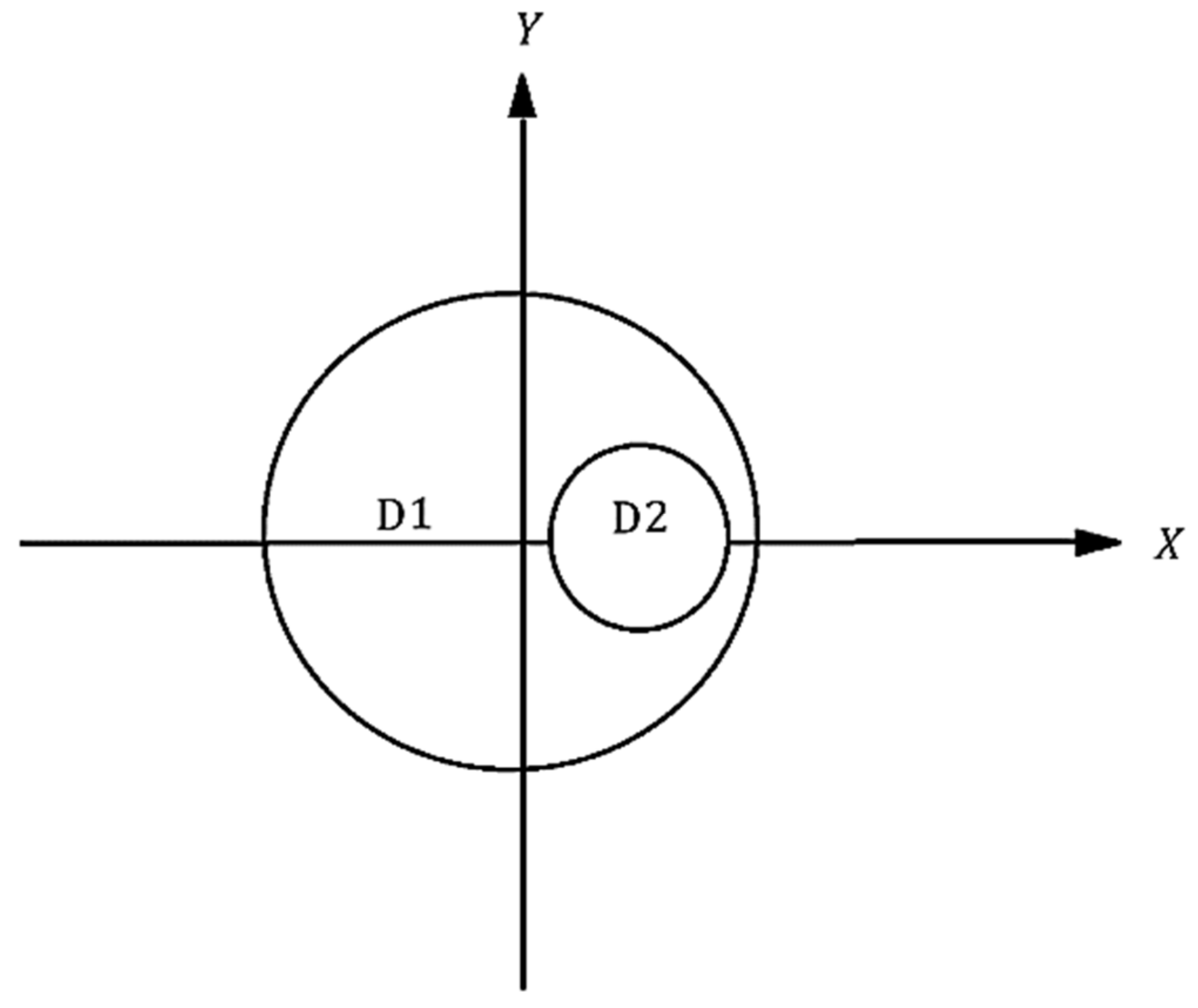
2.2.3. Mesh Domain 1 in Computational Space

When complex mapping is used to convert domain 1, the formed image is rectangular in computational space. According to Figure 5, a structured quadrilateral grid is used for meshing.

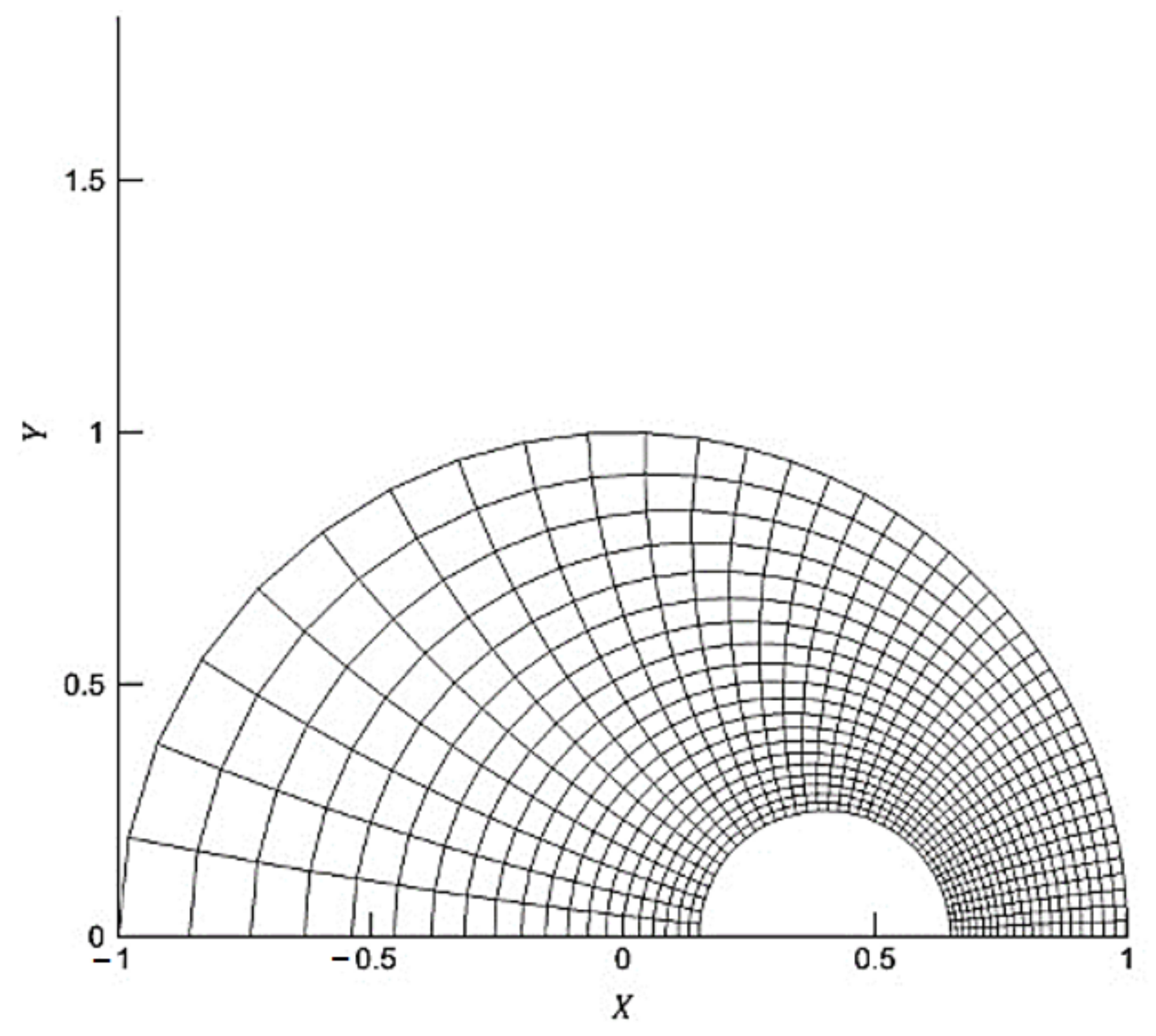
2.2.4. Mesh Domain 1 in Physical Space

Figure 6 shows the generated mesh of domain 1 in a physical space. As can be seen, it is an unstructured grid, which is obtained by applying a reverse mapping on a structure grid.

2.2.5. Mesh Domain 2

Cylindrical coordinates are the best coordinates for domain 2. The grid of this domain is shown in Figure 7.

2.2.6. Solution Methodology

With the finite volume method in the converted grid, discrete equations are solved using a simple algorithm. In the converted grid, velocity is considered at the cell boundaries, and temperature and pressure are considered at the center of a cell. Discrete momentum and energy equations are solved using a tridiagonal matrix algorithm that is based on backward elimination and forward substitution. The convergence criterion for the numerical solution is defined as follows:

$$\sum \left|A_P{G}_P-\sum A_{nb}{G}_{nb}-SS\right|<{10}^{-3}$$

(54)

As the above equation shows the absolute value of differences between total flux of the central point and total flux of neighboring points, as well as the source term for all points in the mesh, the presented convergence criterion is very large. Thus, 0.001 is a reasonable value for the convergence limit.

3. Results and Discussion

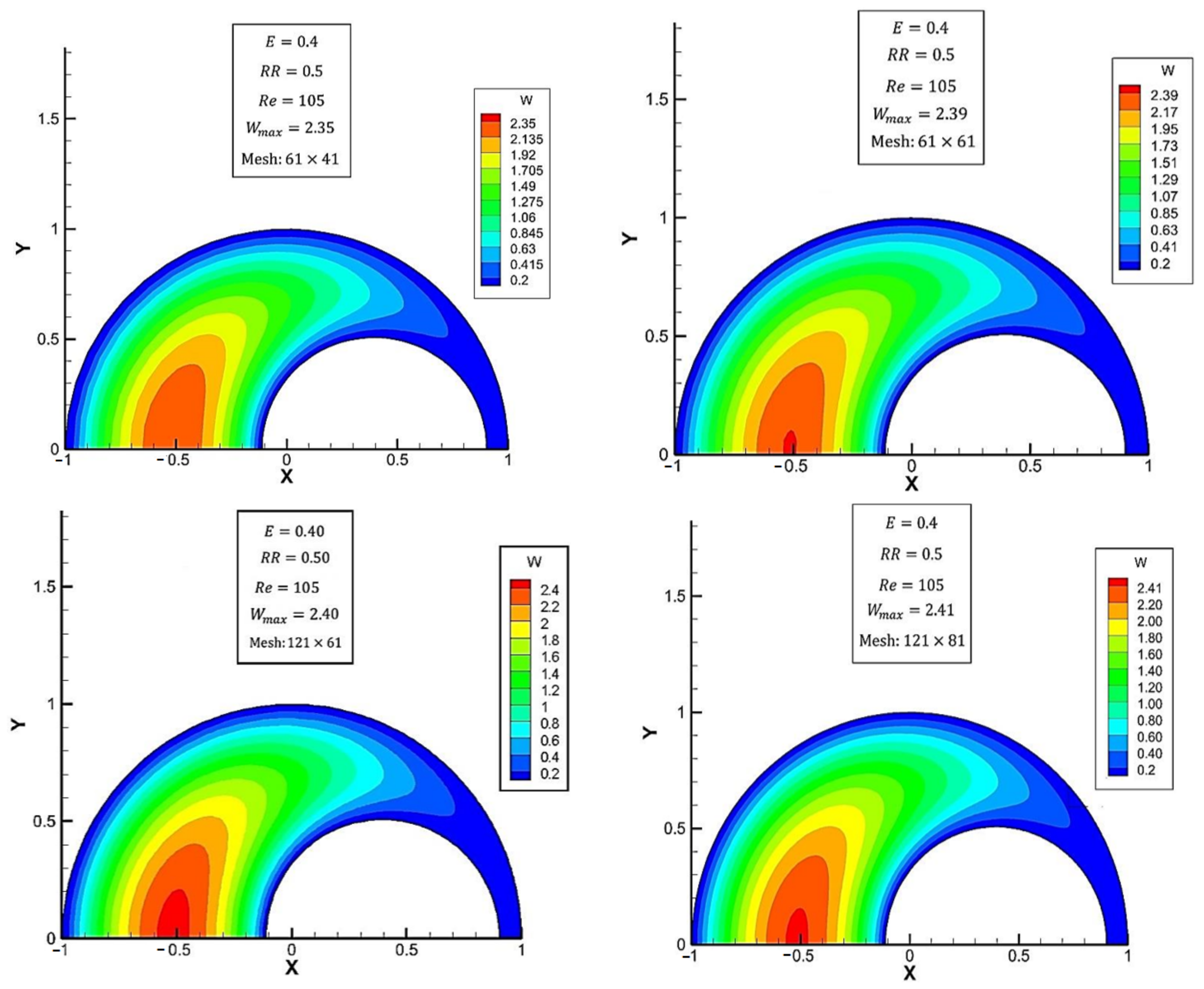
3.1. Grid Independency Analysis

Since in the present study, the solution is performed in two separate domains with two different grids, grid independence should be checked for both meshes. The optimum mesh for each domain is obtained by evaluating the average Nusselt number for the different meshes of domains 1 and 2. As shown in

Table 3. Average Nusselt number for eccentric state with several axial grid number for RR = 0.5.

Grid Dimension	$61\times 41$	$61\times 61$	$121\times 61$	$121\times 81$
$N{u}_{avg}$	2.50	2.39	2.37	2.37

and

Table 4. Average Nusselt number for a tube fully filled with porous medium in Da = 10⁻³.

Grid Dimension	$61\times 21$	$61\times 41$
$N{u}_{avg}$	8.19	8.20

, the optimum mesh for domains 1 and 2 can be considered as $121\times 61$ and $61\times 41$, respectively. For grid in z direction, according to

Table 5. Average Nusselt number for concentric state with several axial grid number.

Grid Number in z Direction	100	130	160	190
$N{u}_{avg}$	12.61	12.10	12.08	12.08

, the average Nusselt of the total geometry is compared for four different axial meshes. Therefore, the optimum mesh node number in z direction is 130.

Before extracting the results from the numerical solution, the non-dependence of the results from the created grid should be investigated. So, in this work, the solution was made in two different computational domains with two various grids. The mesh independence analysis was carried out for both computational domains. For this purpose, the developed velocity contours and the maximum velocity values for four different grids in domains 1 and 2 are presented in order to obtain the best grid for each of the domains.

The developed velocity contours in the space of two cylinders with various grid numbers are illustrated in Figure 8. Accordingly, it can be seen that the velocity contours for the two cases with 121 × 61 and 121 × 81 grids are similar, and the maximum velocities in these two cases are very close to each other. Therefore, the best grid in the case of space between two eccentric cylinders (domain 1) is 121 × 81.

The same analysis was carried out for the second computational domain: the case of a tube completely filled with a porous medium for two different grids. The developed velocity contours in this case are shown in Figure 9. As can be seen, the fluid flow gives exactly the same answer for the two different grids. Of course, these results were obtained for grids with a larger first component, and there was no difference in the shape of the contours and the maximum velocity; therefore, the best grid in domain 2 (related to the porous area) is considered to be 61 × 41. However, as the peripheral components of the grids in the computational domains 1 and 2 must be equal, we ultimately applied the 121 × 41 grid.

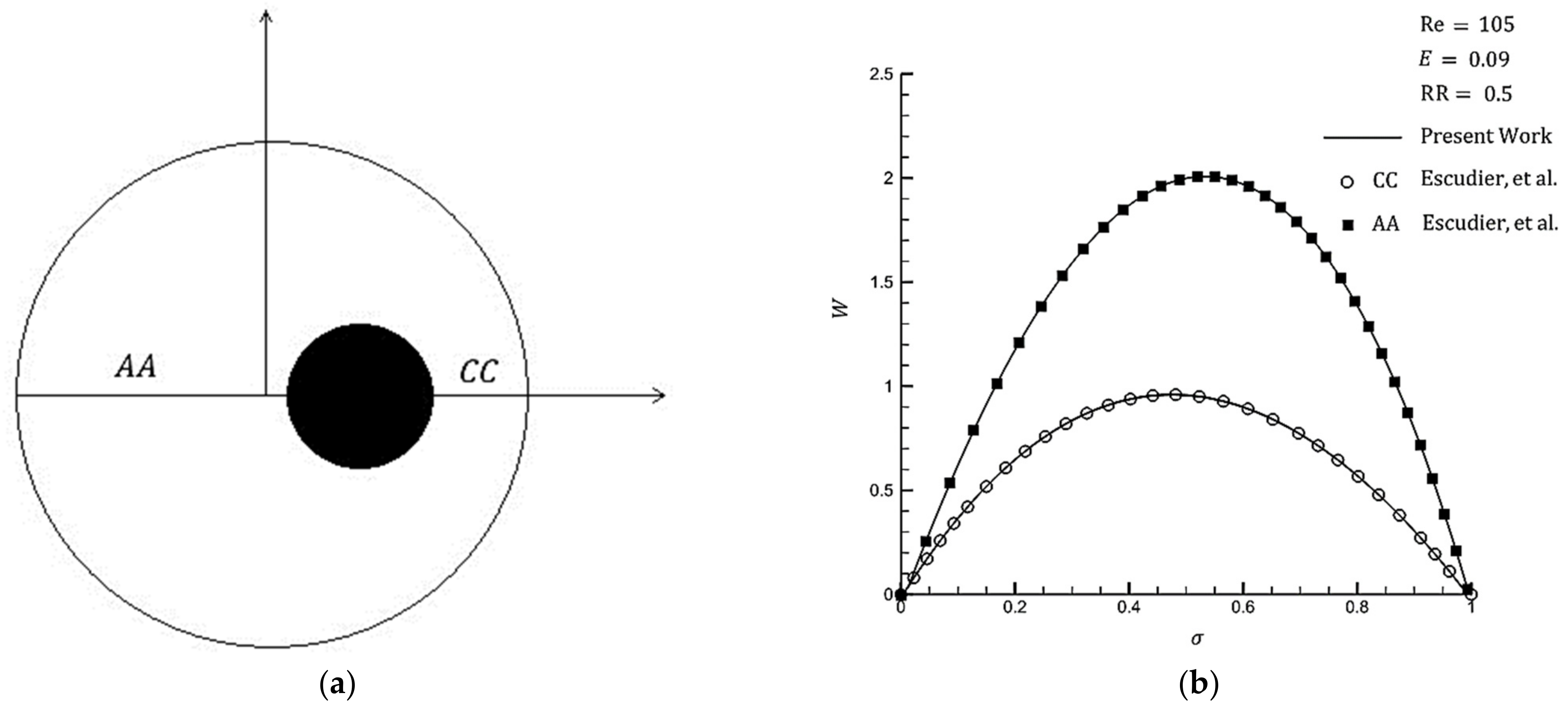
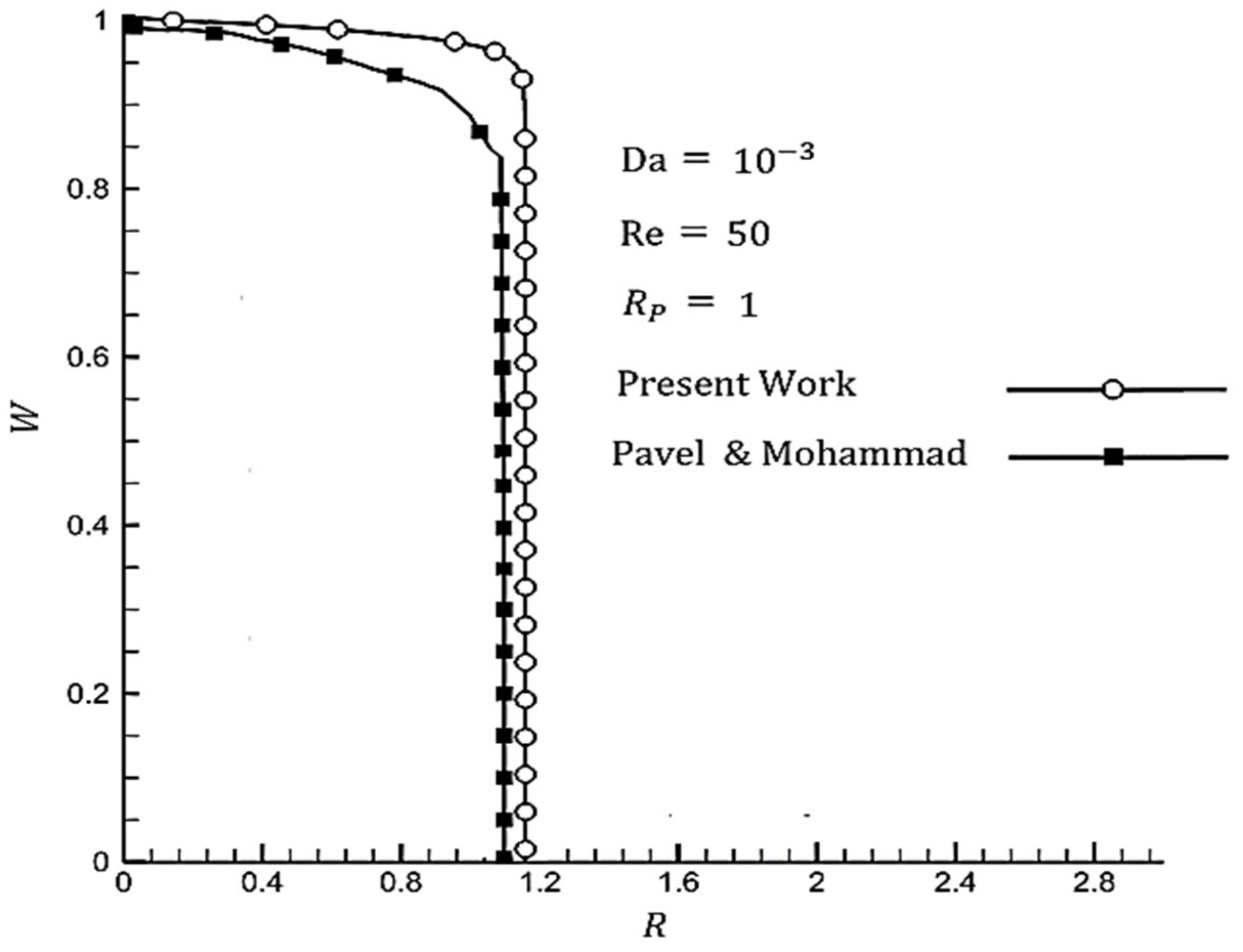
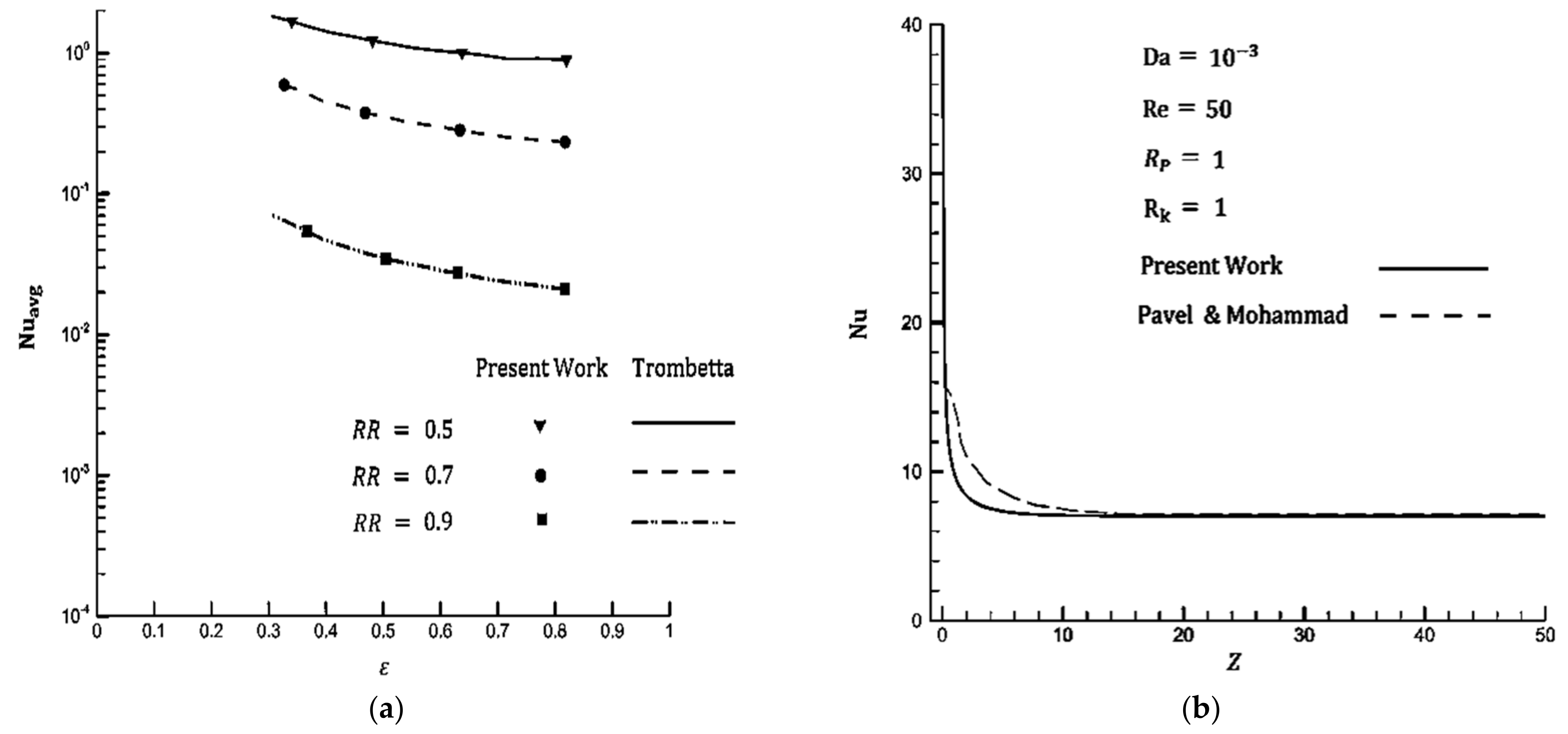
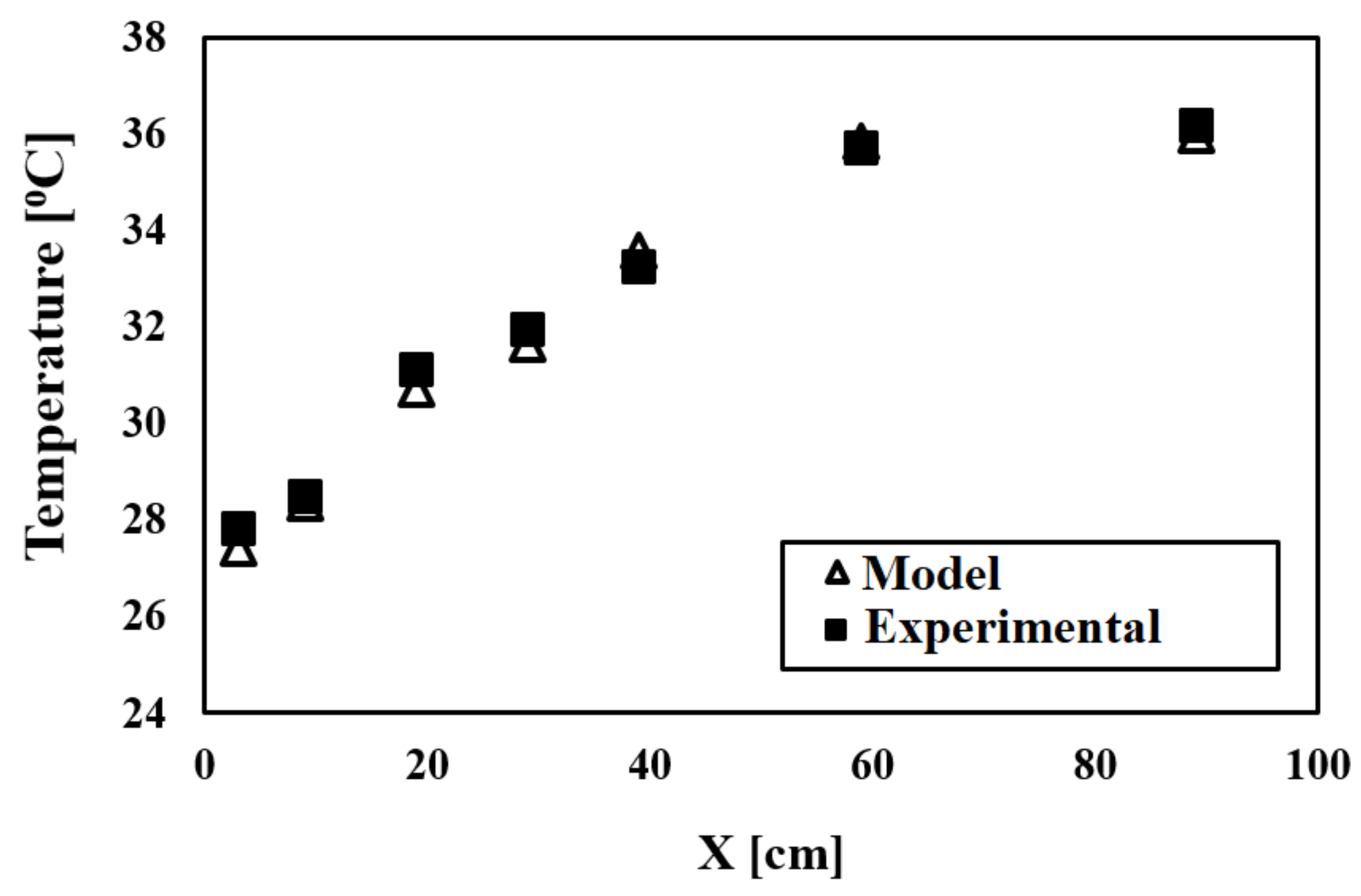
3.2. Validation of Present Study

The momentum equation for axial flow between two eccentric cylinders is compared with the results of Escudier et al. [33]. The geometry of the specific cross-section of the previous study is schematically shown in Figure 10a. The axial velocity obtained is compared with the results of [33] presented in Figure 10b. It can be seen from Figure 10b that good agreement exists between the model calculation results and the literate values. Figure 11 compares the velocity profile for the fully filled porous medium in the present paper and the experimental values of Pavel and Mohmmad [12]. Due to this symmetry, only half of the full geometry is calculated.

The average Nusselt number in annuls calculated for various eccentricities is compared with the results of [34] in Figure 12a. It is evident that the present model provides consistent results with the literature. In addition, a comparison between the local Nusselt numbers in a tube fully filled with a porous medium with Pavel and Mohmmad [12] is shown in Figure 12b.

To validate the employed numerical model with the results of the present experimental setup, the temperature values for the various positions of the sensors, according to Figure 1, were compared with the obtained results of the employed model in the Figure 13. Accordingly, it can be concluded that the utilized model has an acceptable accuracy.

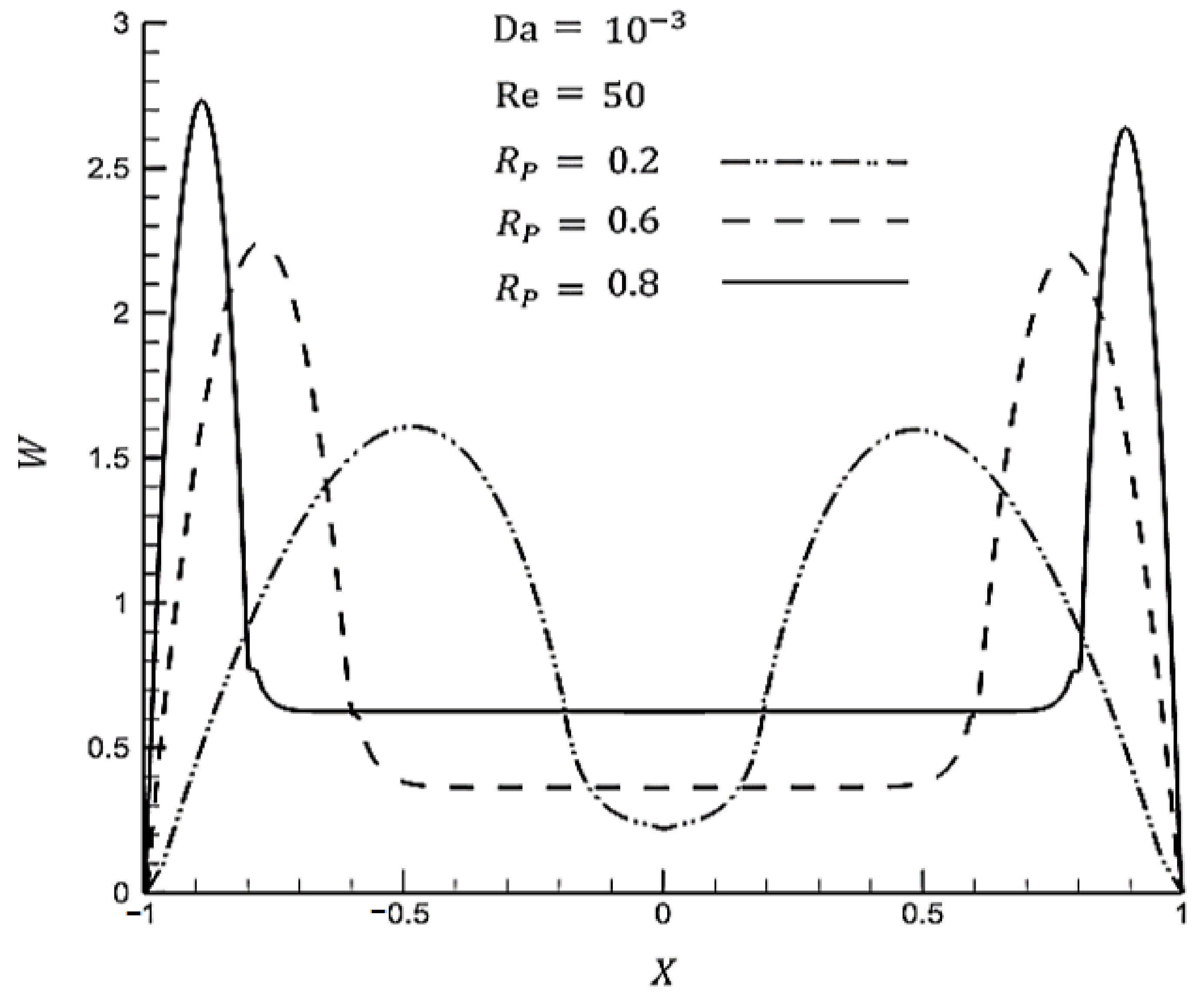
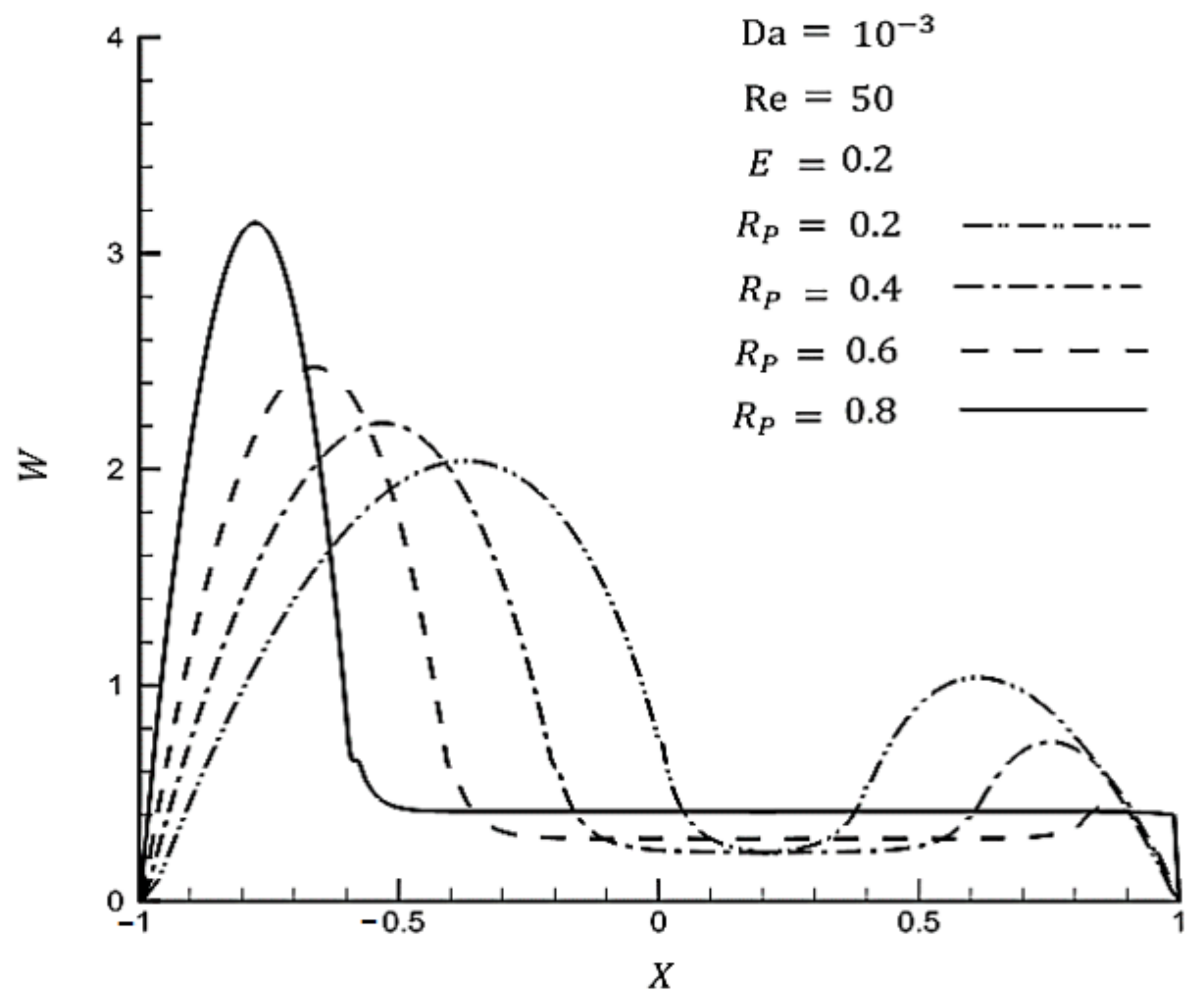
3.3. Impact of Various Parameters on the Hydrothermal Behavior of Fluid Flow

Figure 14 depicts the maximum velocity increase as the thickness of the porous medium increases. This is due to the fact that by increasing thickness, the net area and radius become smaller, which will, in turn, lead to a higher maximum velocity in the constant mass flow rate. Furthermore, a larger thickness of the porous medium causes a smoother velocity profile in the porous media. As seen in Figure 15, the average Nusselt number reaches a peak at optimum thickness, which varies between 0.7 and 0.9, before falling dramatically at a constant Darcy number. At a smaller Darcy number, the optimum thickness is higher.

Figure 16 depicts that the fully developed velocity profile becomes more symmetrical at a smaller eccentricity. As the boundary layer grows to have a larger net area, the velocity reaches a higher value. The effect of thickness on the velocity profile is illustrated in Figure 17. It can be said that thickness has the same impacts on velocity in both the eccentric and concentric cases.

It is evident from Figure 18 that the pressure drop increases while the Darcy number falls. This is because the permeability of the porous medium decreases at smaller Darcy numbers. In addition, Figure 18 illustrates that, while eccentricity grows, the pressure drop decreases, with a greater decrease in lower Darcy numbers. For instance, pressure drop decreases $25\%$ at $Da={10}^{-5}$ and $E=0.4$. Therefore, a large pressure drop, which is one of the main problems of using porous media, can be reduced by applying an eccentric porous medium inside. Figure 19 shows that by increasing the thickness of the porous medium in the pipe, the pressure drop increases. This is due to the resistance that the solid part of the porous material creates against fluid motion.

Figure 20 shows that the eccentricity of the porous media has a significant effect on the average Nusselt number. It should be noted that the average Nusselt number experiences a significant decrease when an eccentric porous media is employed, with an even higher decrease in larger thicknesses. For example, a $50\%$ reduction in the average Nusselt number is caused by adding $0.1$ eccentric porous media, where $\mathrm{E}=0.5$. Accordingly, it is not recommended to employ eccentric porous media at large thicknesses. As shown in Figure 20, at larger values of eccentricity, the average Nusselt number decreases at a smaller rate. Thus, it is beneficial to increase the eccentricity of porous media, as this leads to a smaller pressure drop and has an insignificant impact on the average Nusselt number, according to Figure 18, where eccentricity is greater than 0.3 of the outer pipe radius.

4. Conclusions

• In the present work, force convection flow in a tube partially filled with a porous medium at eccentric posture is investigated numerically. In addition, the effects of various parameters, including eccentricity, thickness and permeability of the porous media, are studied and the following conclusions are obtained.
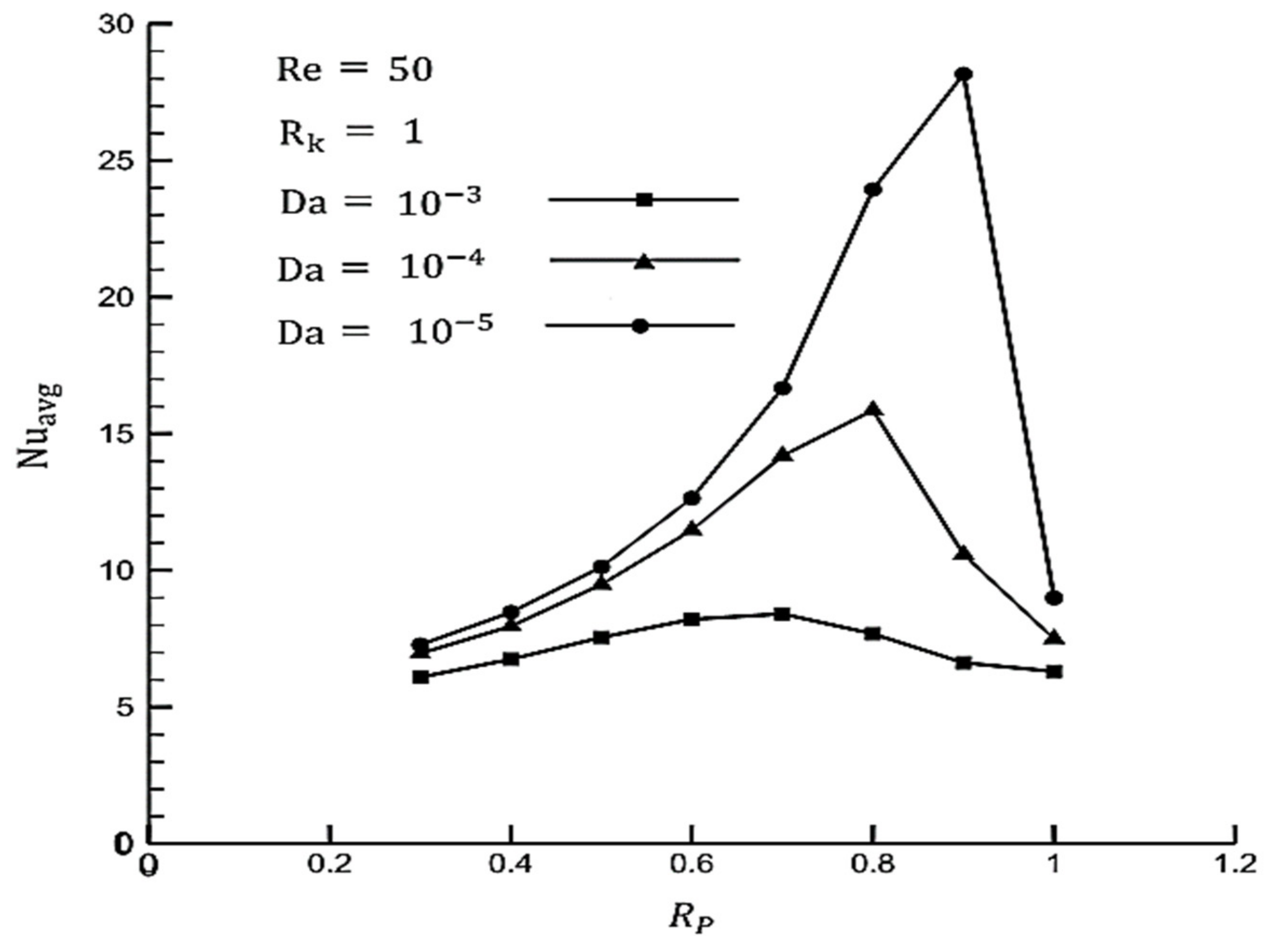
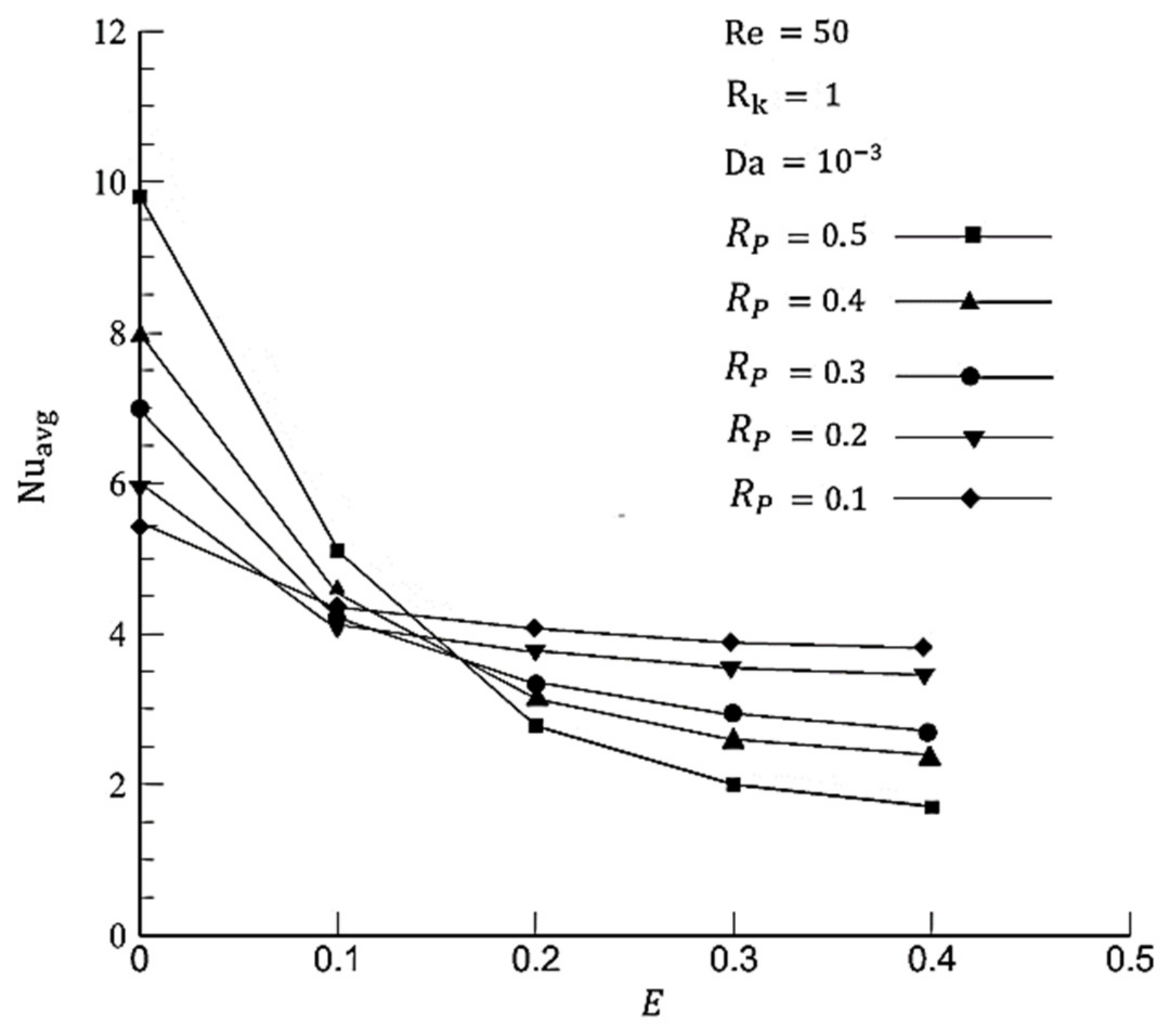
• A smaller Darcy number leads to a higher heat transfer rate in the concentric position. In addition, the highest average Nusselt number can be achieved at a specific thickness, which is considered to be the optimum thickness for a given Darcy number. Optimum thicknesses in the range of 0.7–0.9 increase with a decreasing Darcy number.
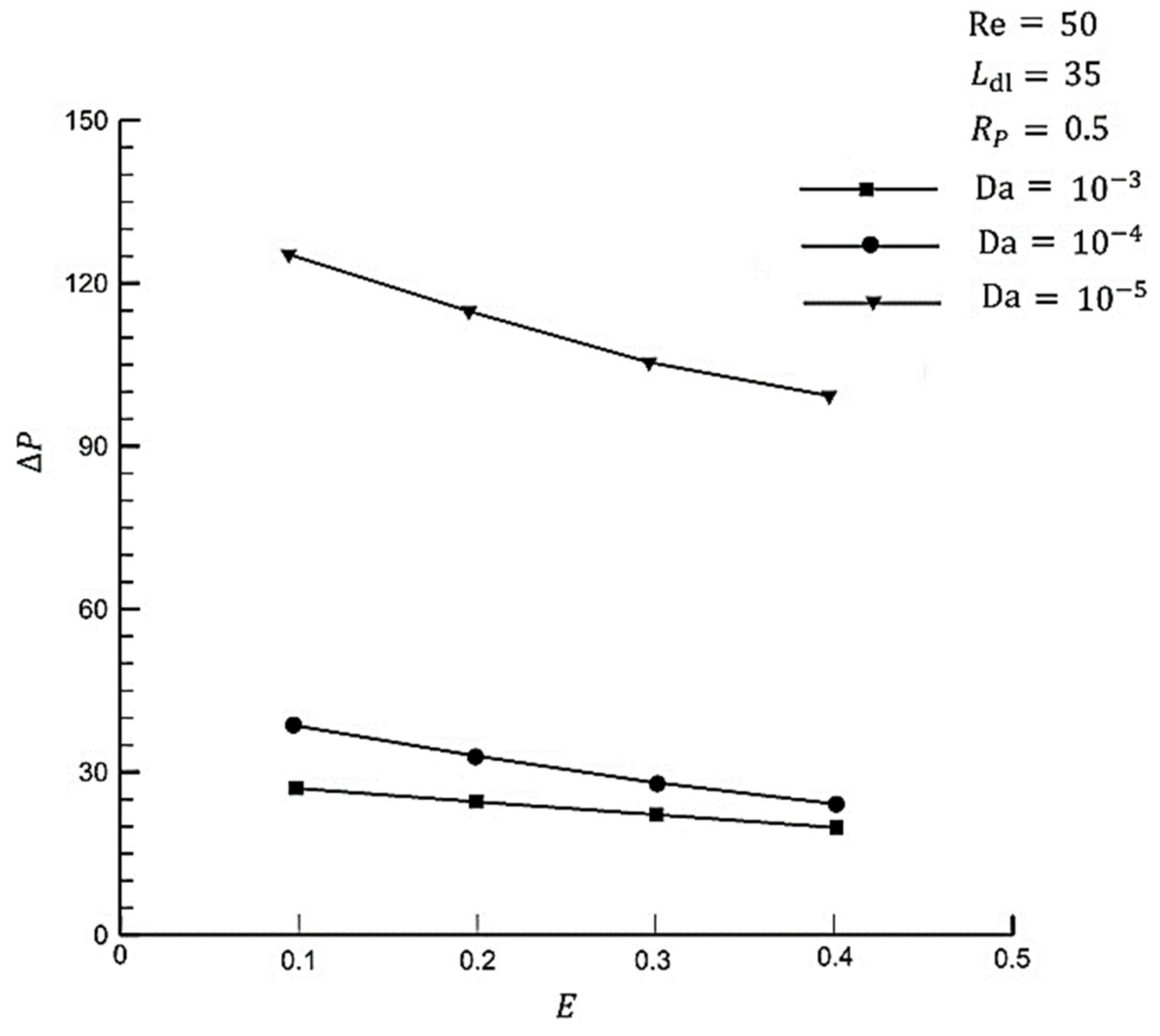
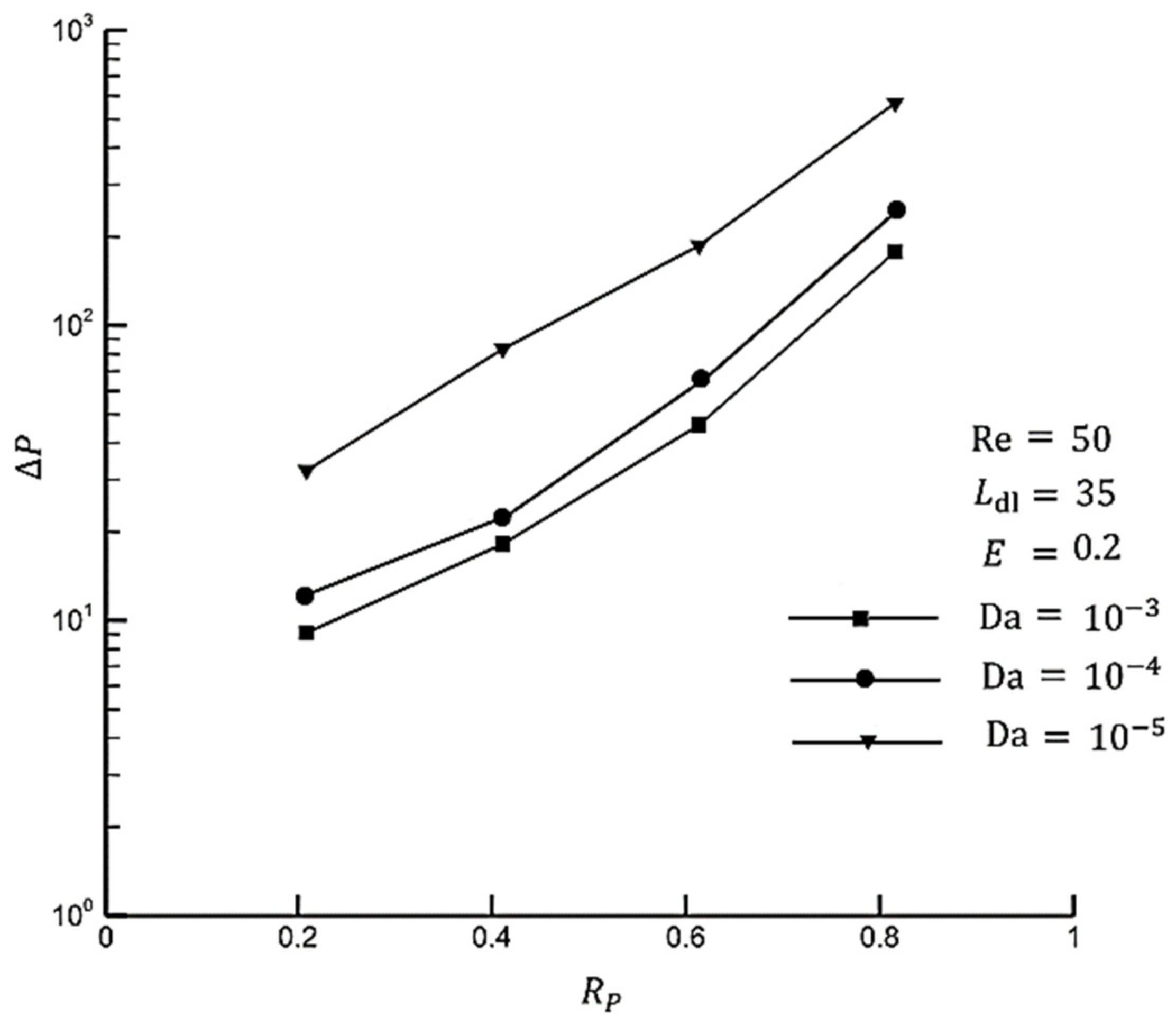
• A decreasing Darcy number gives rise to a pressure drop. This is due to a smaller Darcy number leading to a decline in permeability. On the other hand, rising eccentricity results in a decreasing pressure drop. In addition, the reduction rate grows while the Darcy number decreases. Pressure drop falls at the fastest rate to about $25\%$ at $Da={10}^{-5}$ and $E=0.4$. Applying eccentricity can be considered as a solution to reduce the pressure drop in porous media.
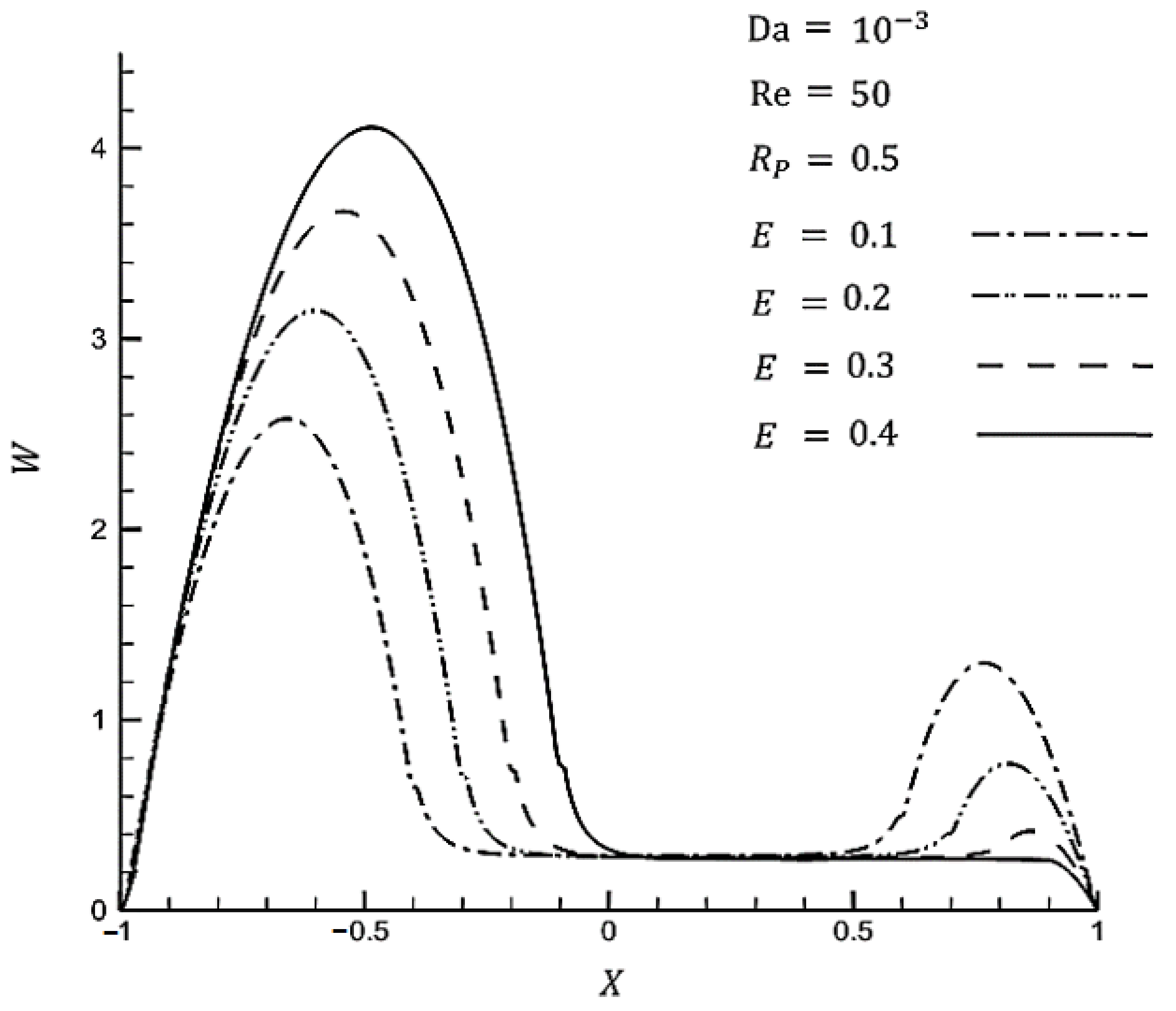
• The average Nusselt number decreases sharply with increasing eccentricity at a high radius ratio. By way of illustration, by increasing eccentricity from 0.1 to 0.4, the Nusselt number reduces by $66\%$ and $11\%$ at $R_P=0.5, 0.1,$ respectively. Although there is a smaller reduction at a larger eccentricity, it is not effective to apply eccentric porous media inside at a high radius ratio.
• The average Nusselt number decreases slower in small values of thickness. As there is a slower decreasing rate for the average Nusselt number and a small pressure drop, using eccentricity is beneficial for a small range of thicknesses.