On Bed Form Resistance and Bed Load Transport in Vegetated Channels
Abstract
:1. Introduction
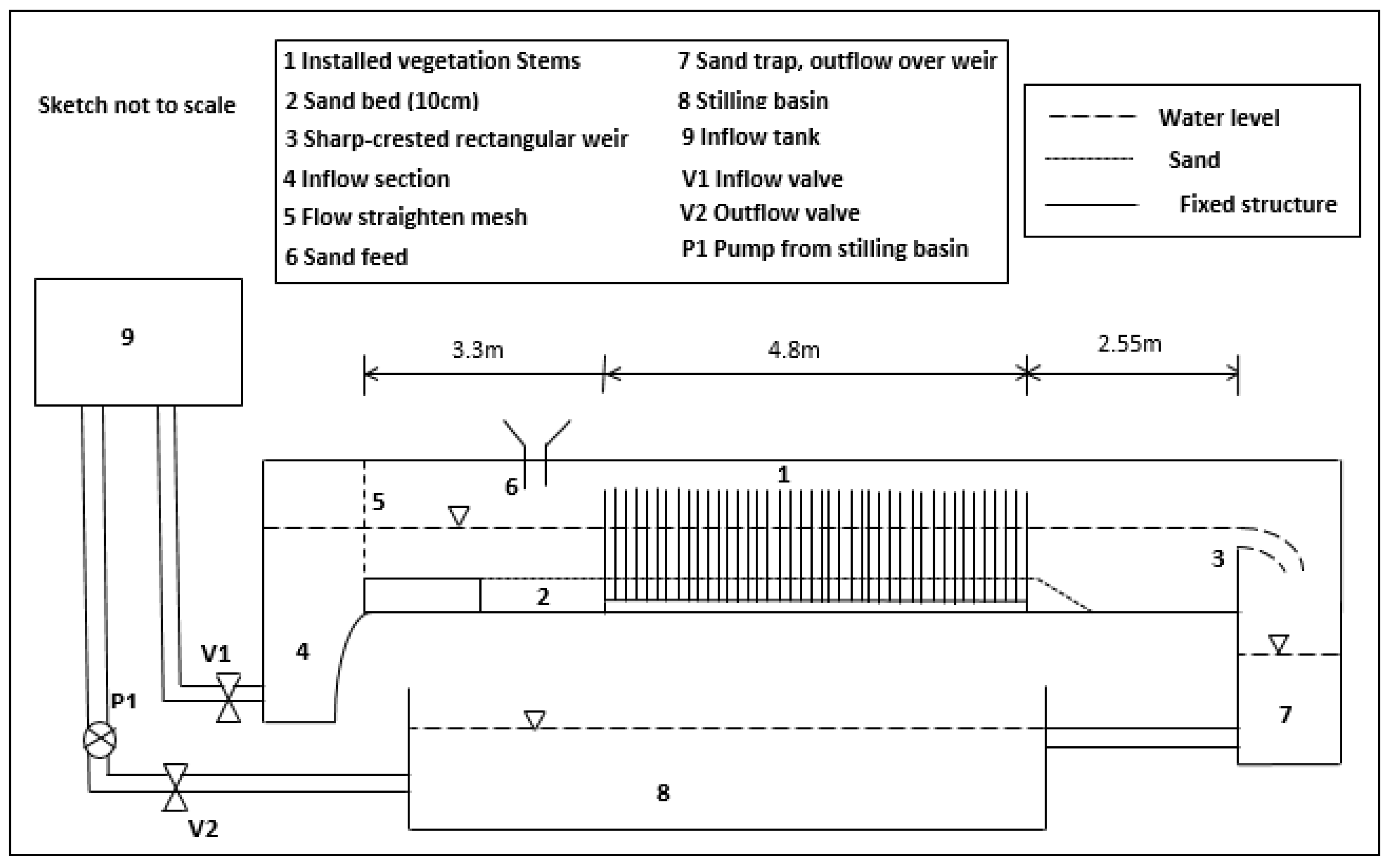
2. Experimental Setup
2.1. Flume Setup
2.2. Water and Bed Slopes
2.3. Bed Load Transport Rate
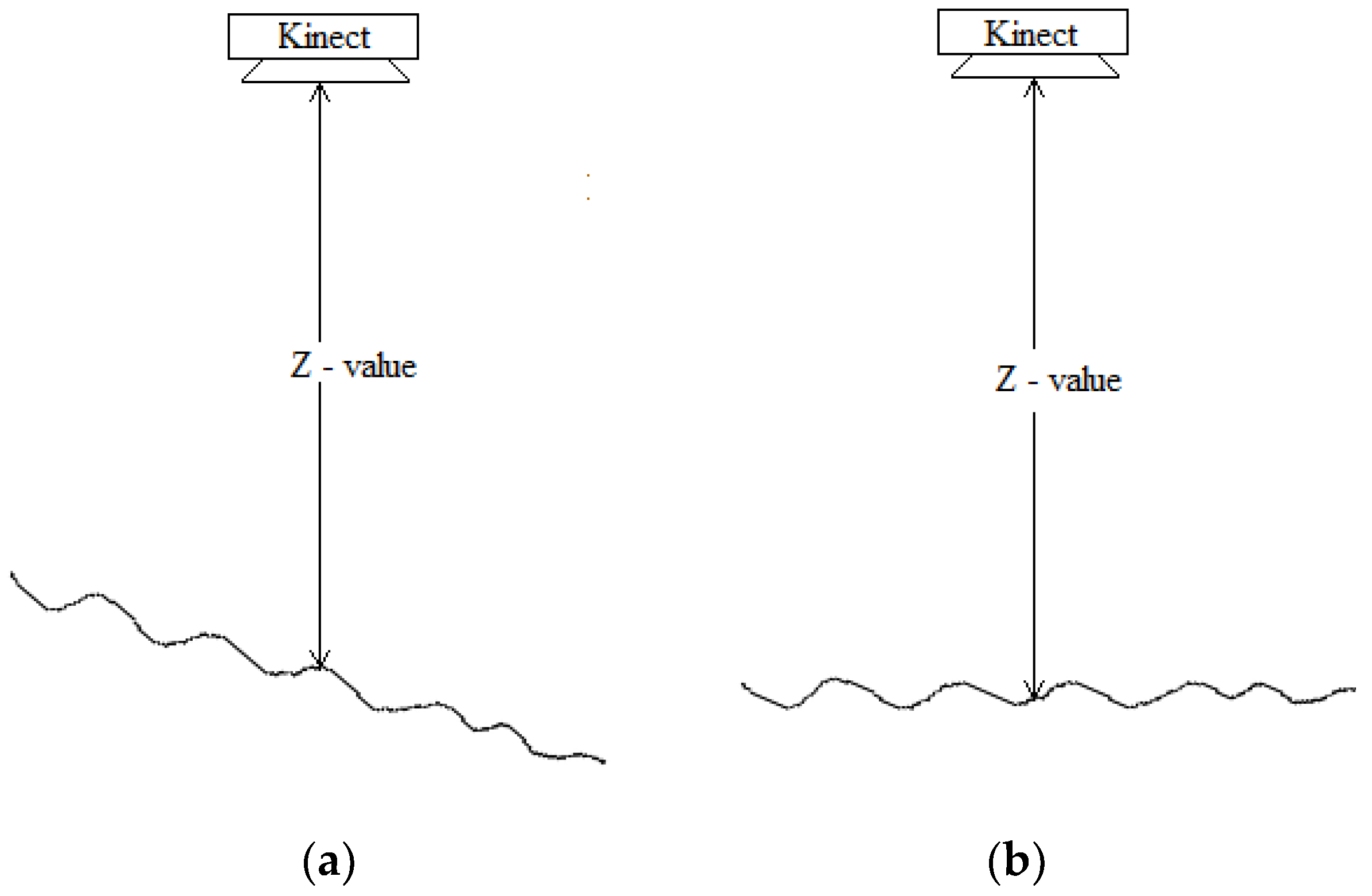
2.4. Bed Surface Elevation
3. Data Processing
3.1. Grain Resistance
3.2. Sidewall Resistance
3.3. Bed Form Resistance
- 1.
- Calculate the modified vegetation-related hydraulic radius, , using Equation (9).
- 2.
- Calculate Reynolds number for the pseudo-fluid model, , using Equation (8).
- 2.
- Calculate the drag coefficient for the pseudo-fluid model, , using Equation (7).
- 4.
- Calculate the vegetation drag coefficient, , using Equation (6).
- 5.
- Calculate the vegetation drag force, , using Equation (5).
- 6.
- Calculate the bed form resistance, , using Equation (4).
- 7.
- Calculate the Darcy–Weisbach bed form friction coefficient using .
- 8.
- Recalculate the Darcy–Weisbach bed friction coefficient using .
- 9.
- Repeat step #4 until the difference between the calculated and the assumed values of is within a desired tolerance.
3.4. Bed Form Height
4. Empirical Relations and Methods
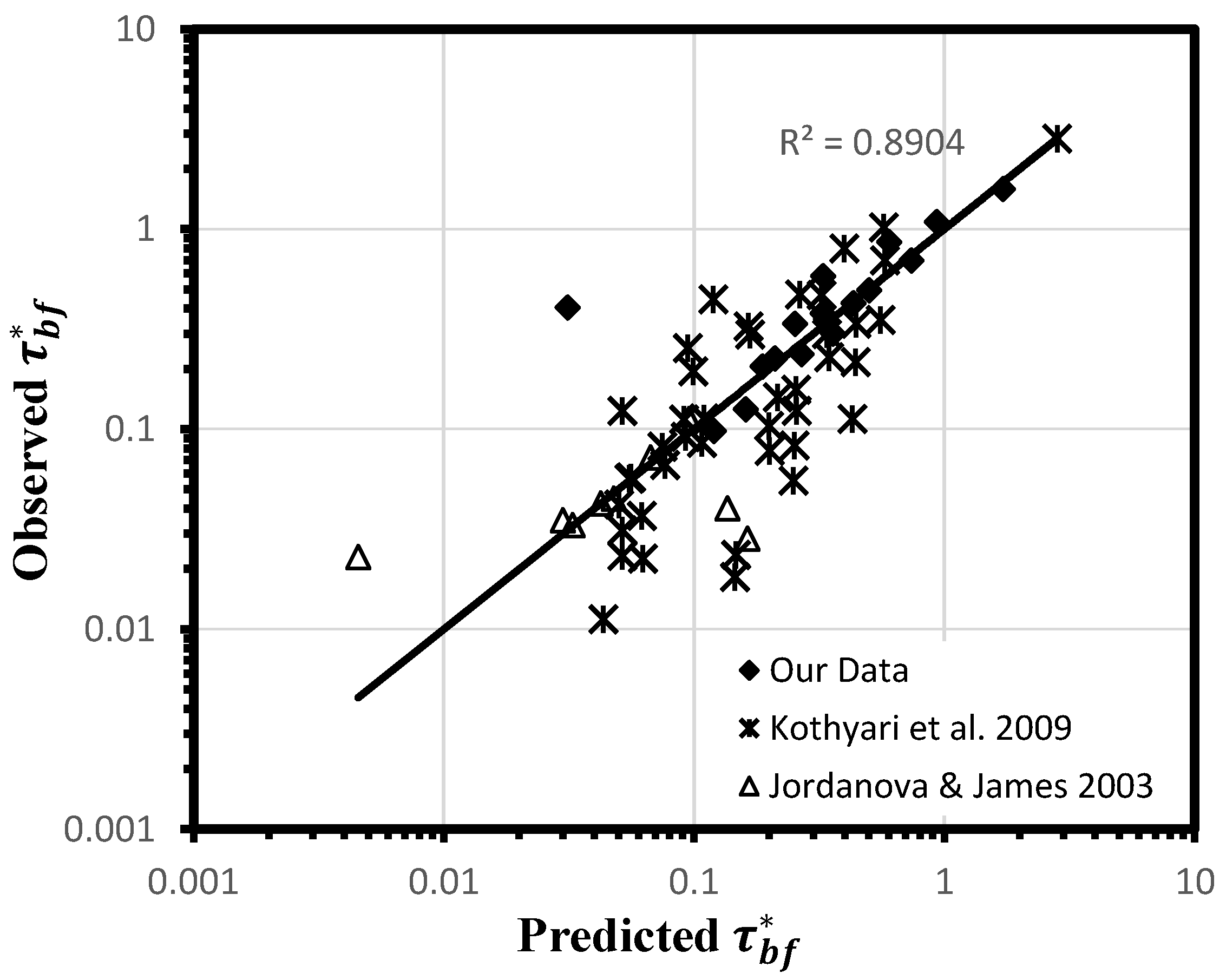
4.1. Bed Form Resistance Relation
4.2. Bed Load Transport Relation
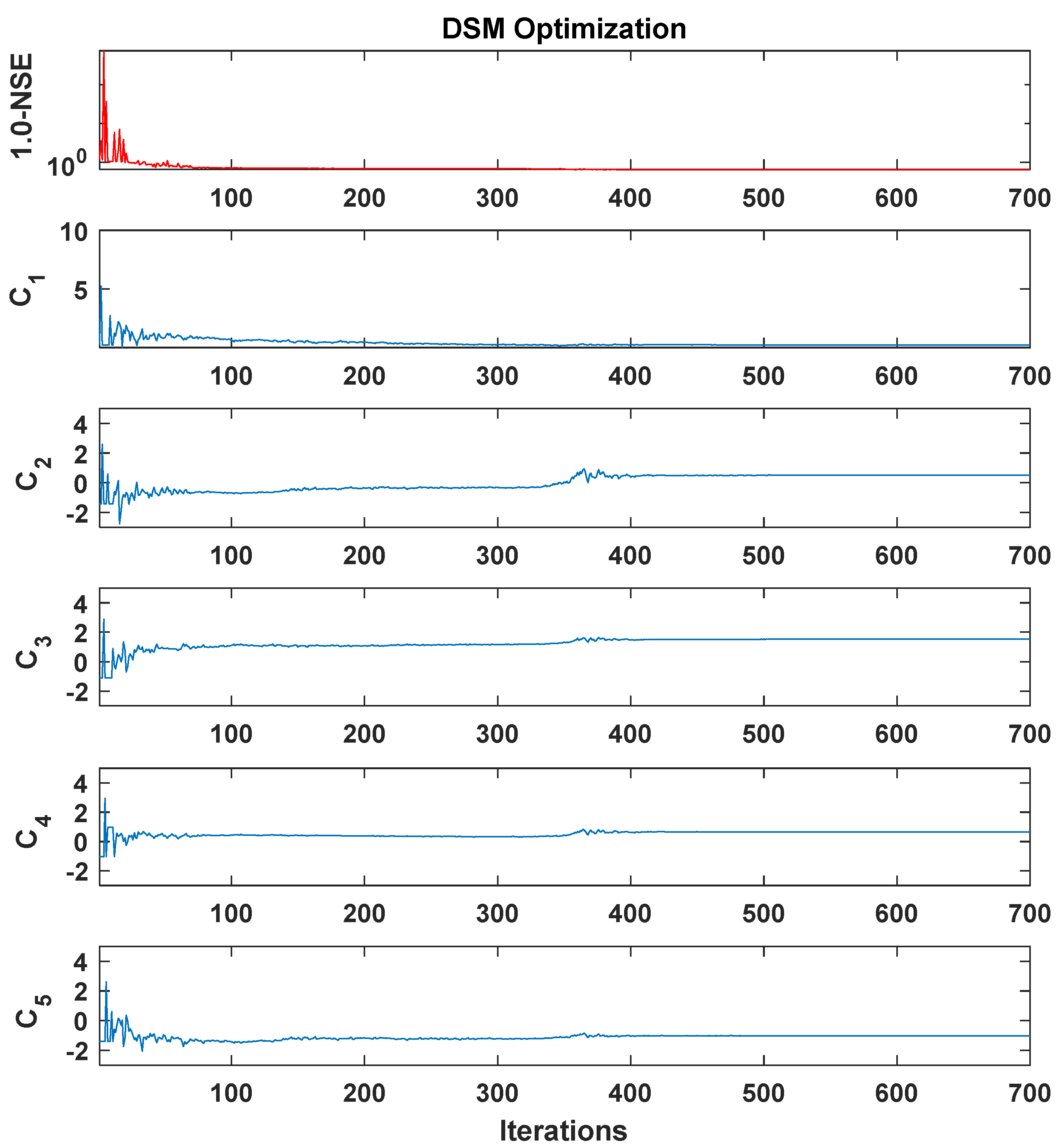
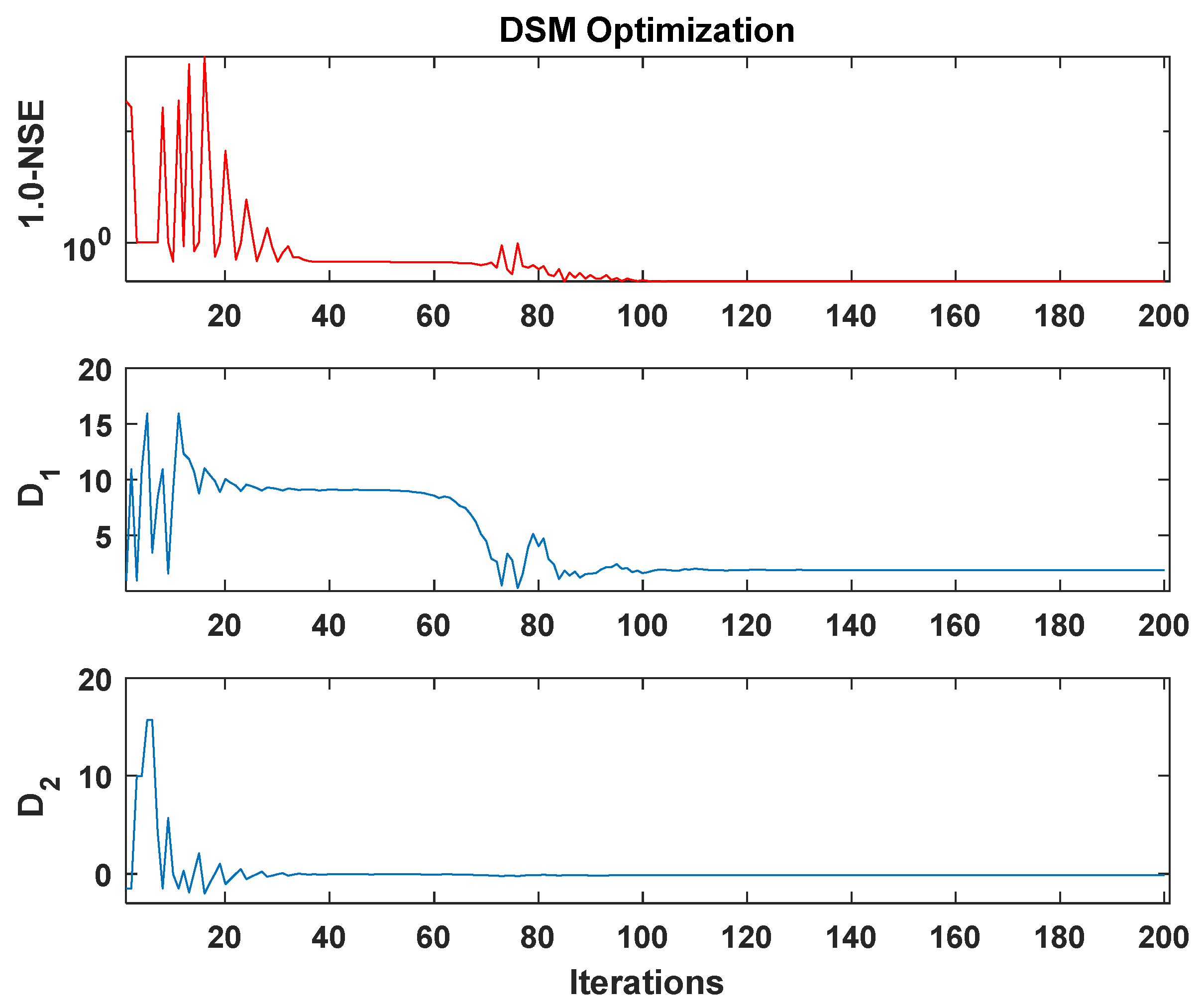
5. Downhill Simplex Method to Determine the Coefficients
5.1. Optimal Coefficient Set in Bed Form Resistance Relation
5.2. Optimal Coefficient Set for Bed Load Transport Relation
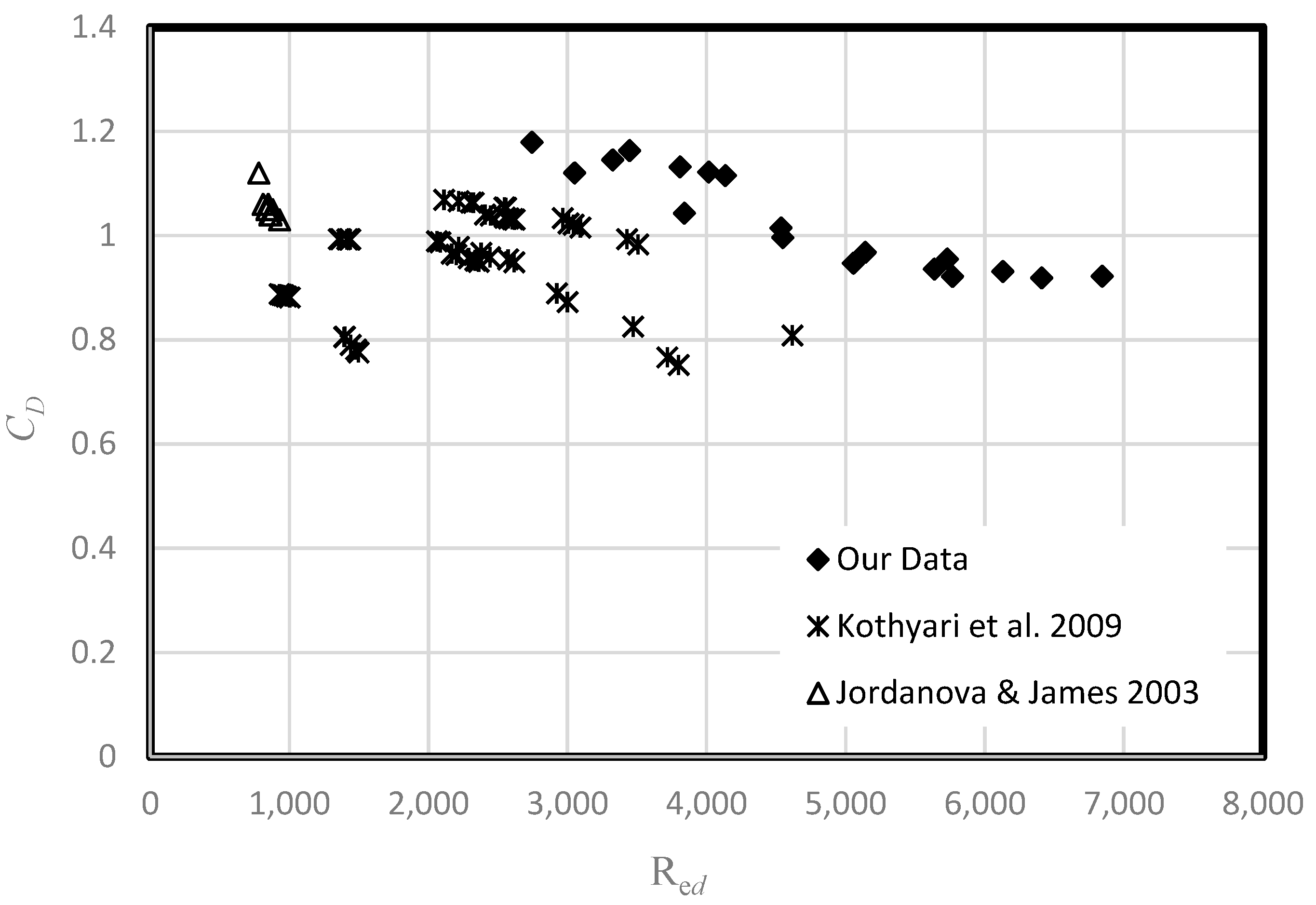
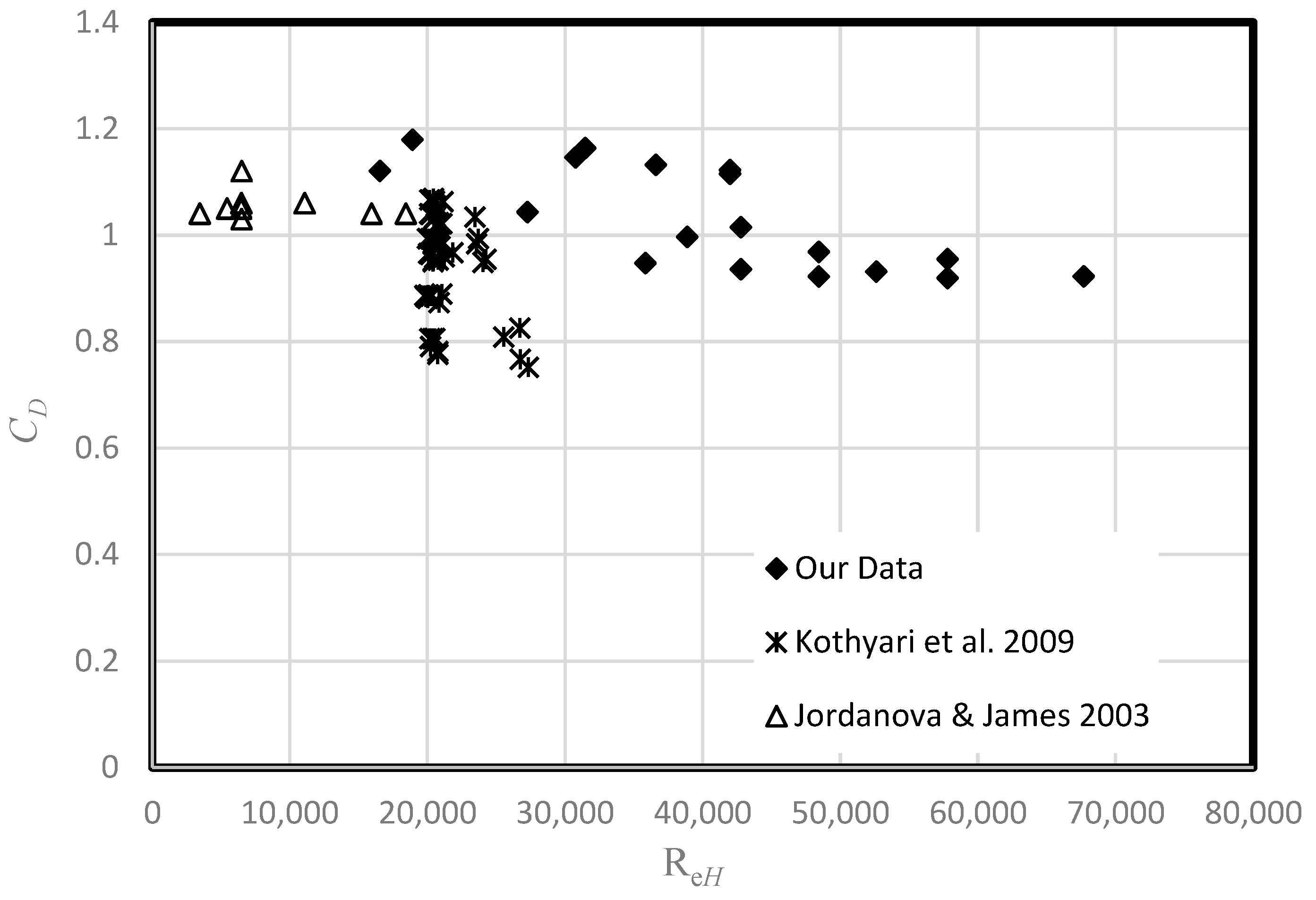
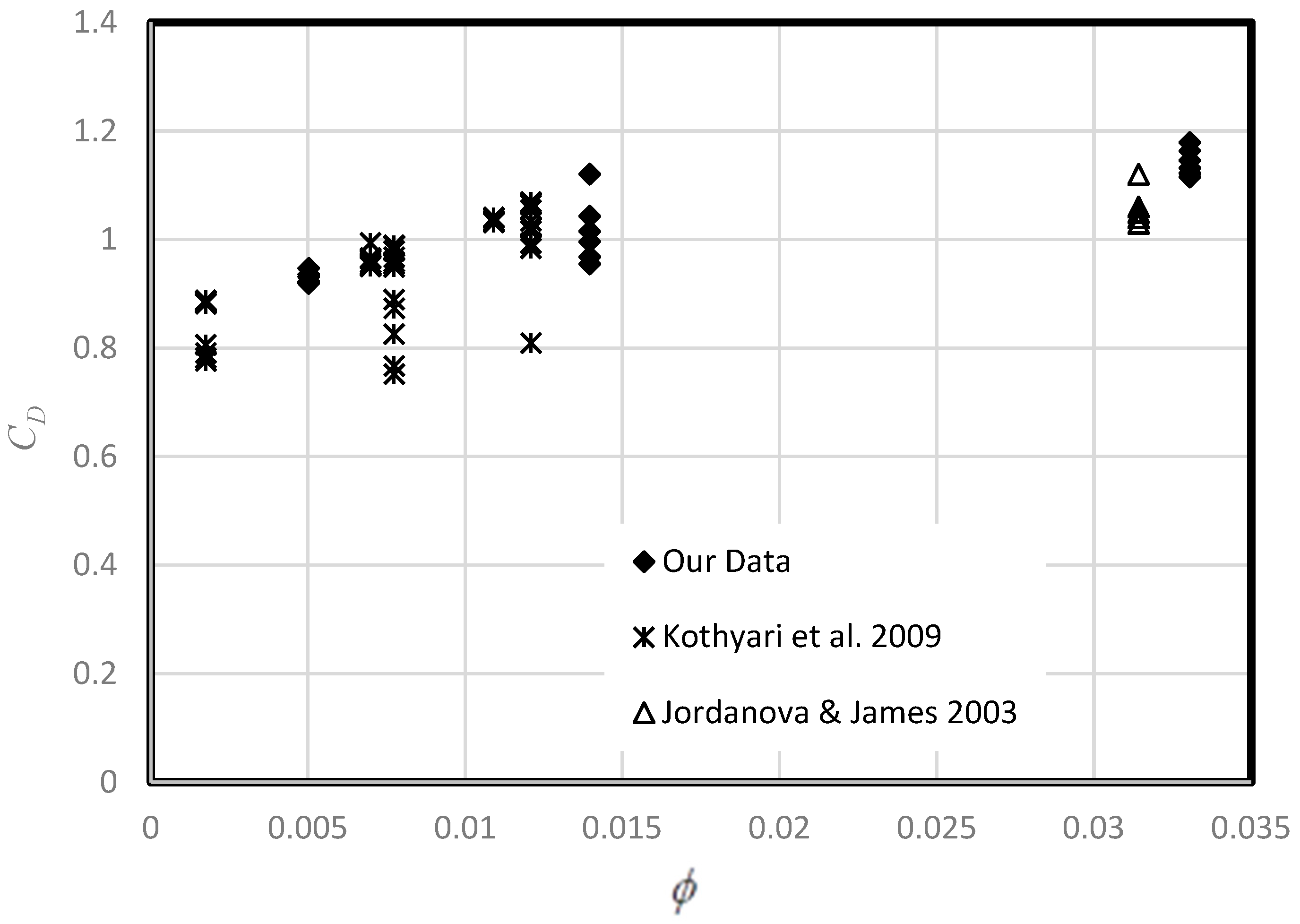
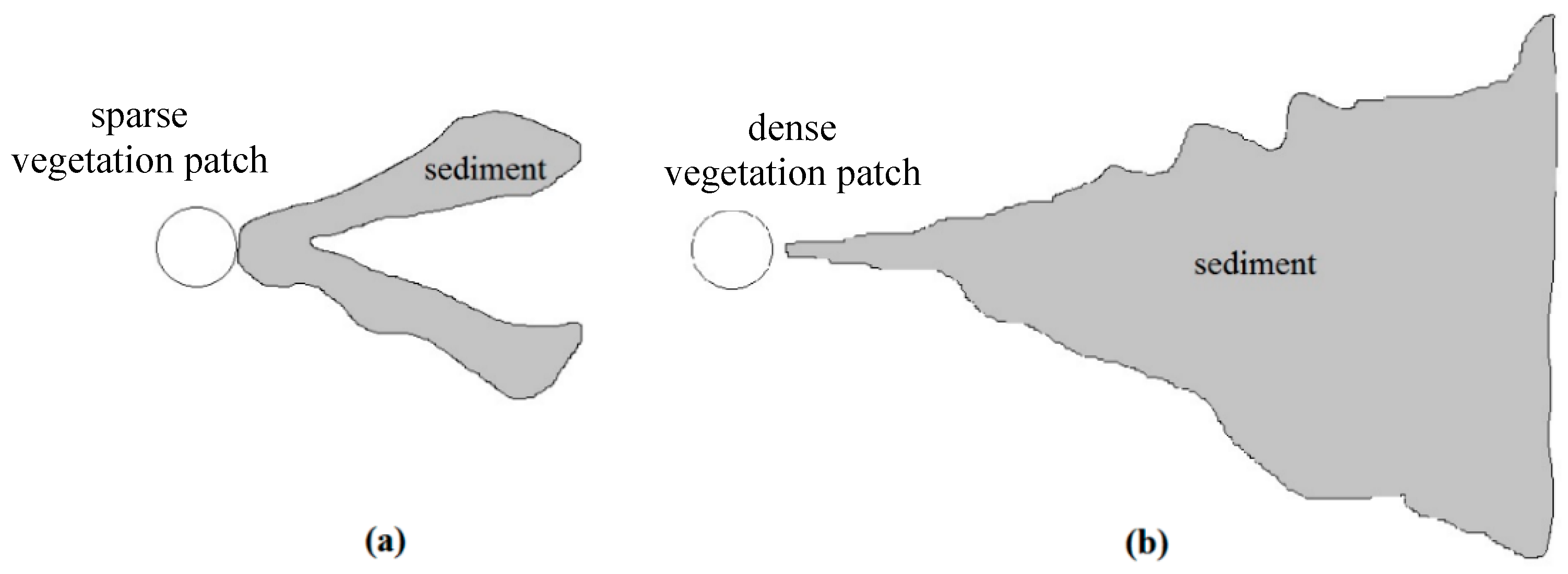
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Notation
| a | vegetation frontal area per unit volume (m−1); |
| vegetation roughness density (-); | |
| bed surface area (m2); | |
| B | channel width (m); |
| drag coefficient for a cylindrical emergent stem; | |
| drag coefficient for the pseudo-fluid model; | |
| Cbf | bed form drag coefficient (-); |
| d | vegetation stem diameter (mm); |
| d16,d84 | sizes for which 16% and 84% of the sediment are finer than d16 and d84, respectively (mm); |
| d50 | median sediment size (mm); |
| FD | vegetation drag force (N); |
| Fr | Froude number (-); |
| g | gravity acceleration (m/s2); |
| Gs | specific gravity of the sediment (-); |
| H | flow depth (m); |
| Hs | equilibrium flow depth (m); |
| m | total number of data; |
| N | number of stems per unit bead area (m−2); |
| NSE | Nash–Sutcliffe efficiency coefficient (-); |
| n | total number of bed elevation points; |
| O | observed value of non-dimensional bed form resistance or non-dimensional bed load transport rate; |
| P | predicted value of non-dimensional bed form resistance or non-dimensional bed load transport rate; |
| Q | flow rate (m3/s); |
| bed load transport rate (m2/s); | |
| non-dimensional bed load transport; | |
| R2 | coefficient of determination (-); |
| Reynolds number for the pseudo-fluid model (-); | |
| flow Reynolds number (-); | |
| vegetation stem Reynolds number (-); | |
| r | total hydraulic radius (m); |
| and | vegetation-related, and modified vegetation-related hydraulic radii respectively (m); |
| S | bed slope (-); |
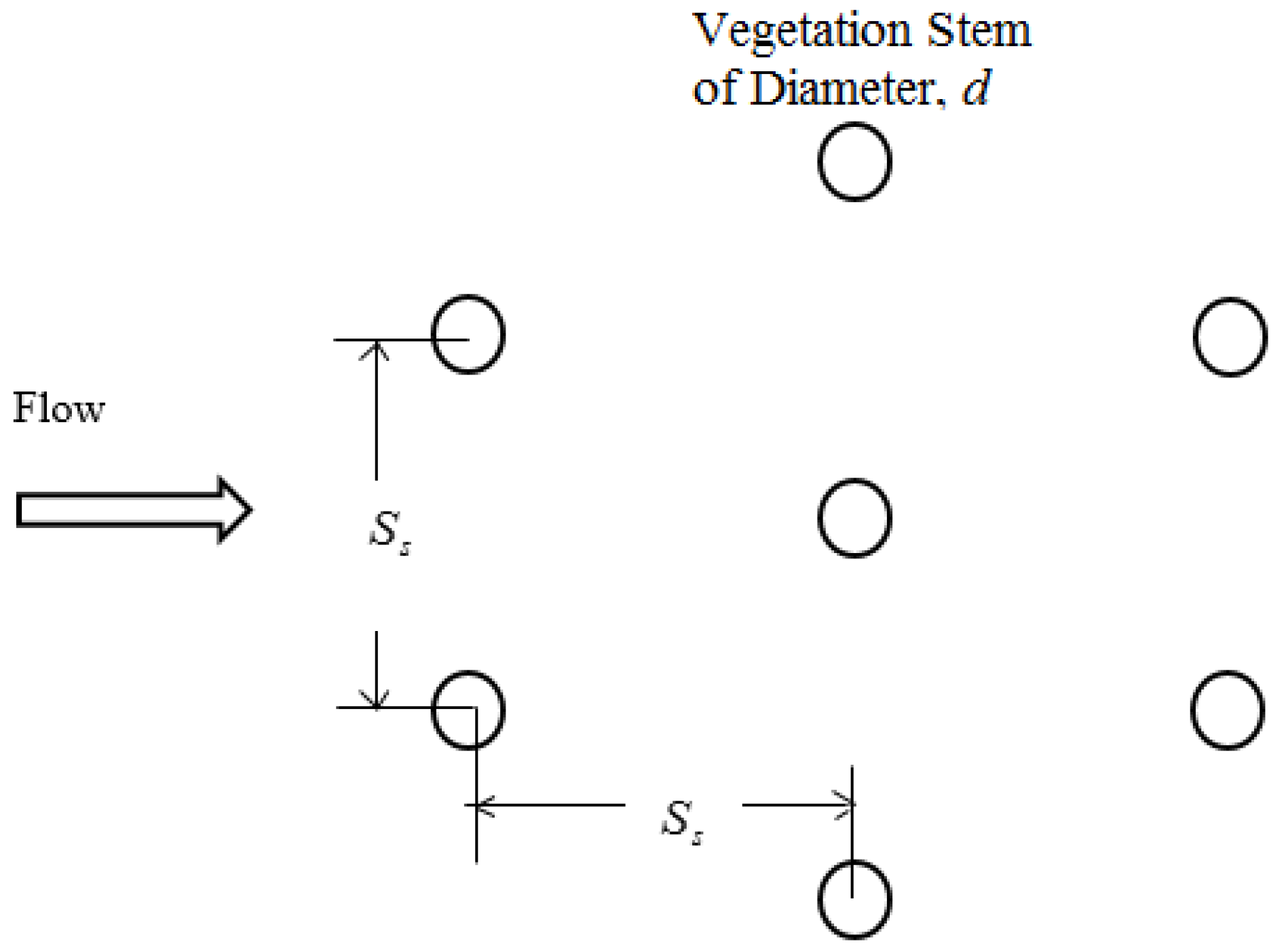
| Ss | vegetation stem spacing (mm); |
| T | bed mobility factor (-); |
| mean flow velocity (m/s); | |
| Ubf | mean velocity within the height of bed form (m/s); |
| ub | bed load particle velocity in non-vegetated channel (m/s); |
| ub-veg | bed load particle velocity in vegetated channel (m/s); |
| Vv | mean pore velocity (m/s); |
| X, Y, and Z | position of the bed points (points clouds) in space and distance (depth) (m); |
| bed elevation at any point i (m); | |
| mean bed elevation of original bed surface (m); | |
| Δ | height of bed form; |
| ΔZ | bed form height (mm); |
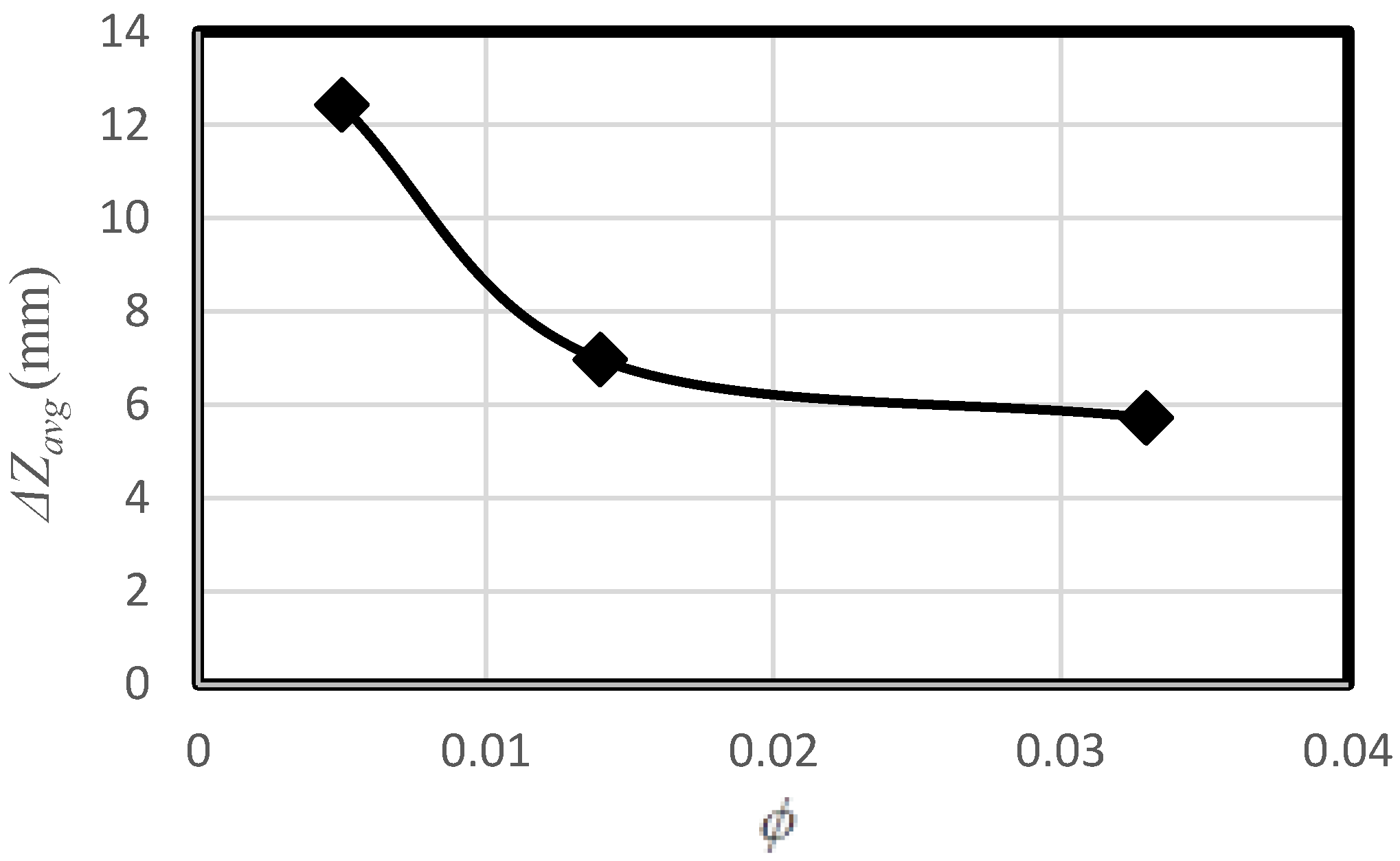
| ΔZavg | average of the bed form height for each ϕ value (mm); |
| ζb | bed load layer thickness in non-vegetated channel; |
| ζb-veg | bed load layer thickness in vegetated channel; |
| total Darcy–Weisbach friction coefficient (-); | |
| bed Darcy–Weisbach friction coefficient=(-); | |
| grain and bed form Darcy–Weisbach friction coefficients, respectively (-); | |
| ϕ | vegetation concentration (-); |
| ϕd | dynamic friction angle; |
| specific weight of water (N/m3); | |
| λ | length of bed form; |
| water dynamic viscosity (Ns/m2); | |
| kinematic viscosity of water (m2/s); | |
| grain, glass, and stainless steel roughness heights (m) | |
| von Karman constant = 0.41 (-); | |
| water and sediment density, respectively (kg//m3); | |
| standard deviation of sediment mixture; | |
| total bed resistance (N/m2) = ; | |
| grain and bed form resistances, respectively (N/m2); | |
| , | glass and stainless steel sidewall resistances, respectively (N/m2); |
| , , | non-dimensional bed form, grain, and critical resistances, respectively; |
| volume of water (m3); | |
| β1, β2, α1, α2, α3, α4, C1, C2, C3, C4, C5, η, D1, D2, ω1, ω2 | coefficients. |
References
- Fenzl, R.N. Hydraulic Resistance of Broad Shallow Vegetated Channels. Ph.D. Thesis, University of California, Davis, CA, USA, 1962. [Google Scholar]
- Temple, D.M.; Robinson, K.M.; Ahring, R.M.; Davis, A.G. Stability Design of Grassed-Lined Open Channels; US Department of Agriculture, Agricultural Research Service: Washington, DC, USA, 1987. [Google Scholar]
- Shi, Z.; Pethick, J.S.; Pye, K. Flow structure in and above the various heights of a saltmarsh canopy: A laboratory flume study. J. Coast. Res. 1995, 11, 1204–1209. [Google Scholar]
- Zhang, M.-L.; Li, C.; Shen, Y.-M. A 3D non-linear k–ε turbulent model for prediction of flow and mass transport in channel with vegetation. Appl. Math. Model. 2009, 34, 1021–1031. [Google Scholar] [CrossRef]
- Yang, J.Q.; Chung, H.; Nepf, H.M. The onset of sediment transport in vegetated channels predicted by turbulent kinetic energy. Geophys. Res. Lett. 2016, 43, 11261–11268. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.Q.; Nepf, H.M. A Turbulence-Based Bed-Load Transport Model for Bare and Vegetated Channels. Geophys. Res. Lett. 2018, 45, 10428–10436. [Google Scholar] [CrossRef]
- Yang, J.Q.; Nepf, H.M. Impact of Vegetation on Bed Load Transport Rate and Bedform Characteristics. Water Resour. Res. 2019, 55, 6109–6124. [Google Scholar] [CrossRef]
- Zhao, T.; Nepf, H.M. Turbulence Dictates Bedload Transport in Vegetated Channels Without Dependence on Stem Diameter and Arrangement. Geophys. Res. Lett. 2021, 48, e2021GL095316. [Google Scholar] [CrossRef]
- Zanke, U.; Roland, A.; Wurpts, A. Roughness Effects of Subaquaeous Ripples and Dunes. Water 2022, 14, 2024. [Google Scholar] [CrossRef]
- Engelund, F. Hydraulic Resistance for Flow over Dunes. In Progress Report 44; Institute of Hydrodynamics and Hydraulic Engineering, Technical University of Denmark: Lyngby, Denmark, 1977. [Google Scholar]
- Jordanova, A.A.; James, C.S. Experimental Study of Bed Load Transport through Emergent Vegetation. J. Hydraul. Eng. 2003, 129, 474–478. [Google Scholar] [CrossRef]
- Kothyari, U.C.; Hashimoto, H.; Hayashi, K. Effect of tall vegetation on sediment transport by channel flows. J. Hydraul. Res. 2009, 47, 700–710. [Google Scholar] [CrossRef]
- López, F.; García, M. Open-channel flow through simulated vegetation: Suspended sediment transport modeling. Water Resour. Res. 1998, 34, 2341–2352. [Google Scholar] [CrossRef]
- Al-Asadi, K.; Duan, J.G. Three-Dimensional Hydrodynamic Simulation of Tidal Flow through a Vegetated Marsh Area. J. Hydraul. Eng. 2015, 141, 06015014. [Google Scholar] [CrossRef]
- Al-Asadi, K.; Duan, J.G. Assessing methods for estimating roughness coefficient in a vegetated marsh area using Delft3D. J. Hydroinformatics 2017, 19, 766–783. [Google Scholar] [CrossRef] [Green Version]
- Wang, X.; Huai, W.; Cao, Z. An improved formula for incipient sediment motion in vegetated open channel flows. Int. J. Sediment Res. 2021, 37, 47–53. [Google Scholar] [CrossRef]
- Wang, X.; Li, S.; Yang, Z.-H.; Huai, W.-X. Incipient sediment motion in vegetated open-channel flows predicted by critical flow velocity. J. Hydrodyn. 2022, 34, 63–68. [Google Scholar] [CrossRef]
- Hashimoto, H.; Hirano, M. Gravity Flow of Sediment-Water Mixtures in a Steep Open Channel. Doboku Gakkai Ronbunshu 1996, 1996, 33–42. [Google Scholar] [CrossRef] [Green Version]
- Specht, F.-J. Einfluß von Gerinnebreite und Uferbewuchs auf die Hydraulisch-Edimentologischen Verhältnisse Naturnaher Fließgewässer; TU Braunschweig: Braunschweig, Germany, 2002. [Google Scholar]
- Nepf, H.M. Hydrodynamics of vegetated channels. J. Hydraul. Res. 2012, 50, 262–279. [Google Scholar] [CrossRef] [Green Version]
- Follett, E.M.; Nepf, H.M. Sediment patterns near a model patch of reedy emergent vegetation. Geomorphology 2012, 179, 141–151. [Google Scholar] [CrossRef] [Green Version]
- Cheng, N.-S.; Nguyen, H.T. Hydraulic Radius for Evaluating Resistance Induced by Simulated Emergent Vegetation in Open-Channel Flows. J. Hydraul. Eng. 2011, 137, 995–1004. [Google Scholar] [CrossRef]
- Cheng, N.-S. Calculation of drag coefficient for arrays of emergent circular cylinders with pseudofluid model. J. Hydraul. Eng. 2013, 139, 602–611. [Google Scholar] [CrossRef]
- Parker, G. Transport of gravel and sediment mixtures. In Sedimentation Engineering: Processes, Measurements, Modelling and Practice; Garcia, M., Ed.; ASCE: Reston, VA, USA, 2008; pp. 165–251. [Google Scholar]
- Mankoff, K.D.; Russo, T.A. The Kinect: A low-cost, high-resolution, short-range 3D camera. Earth Surf. Process. Landforms 2012, 38, 926–936. [Google Scholar] [CrossRef]
- Caviedes-Voullième, D.; Juez, C.; Murillo, J.; García-Navarro, P. 2D dry granular free-surface flow over complex topography with obstacles. Part I: Experimental study using a consumer-grade RGB-D sensor. Comput. Geosci. 2014, 73, 177–197. [Google Scholar] [CrossRef]
- Kahn, S.; Bockholt, U.; Kuijper, A.; Fellner, D.W. Towards precise real-time 3D difference detection for industrial applications. Comput. Ind. 2013, 64, 1115–1128. [Google Scholar] [CrossRef]
- Azzari, G.; Goulden, M.L.; Rusu, R.B. Rapid Characterization of Vegetation Structure with a Microsoft Kinect Sensor. Sensors 2013, 13, 2384–2398. [Google Scholar] [CrossRef] [Green Version]
- Andersen, M.R.; Jensen, T.; Lisouski, P.; Mortensen, A.K.; Hansen, M.K.; Gregersen, T.; Ahrendt, P.J.A.U. Kinect depth sensor evaluation for computer vision applications. In Electrical and Computer Engineering, Tech. Rep.; ECE-TR-6, Department of Engineering, Aarhus University: Aarhus, Denmark; Available online: http://eng.au.dk/fileadmin/DJF/ENG/PDF-filer/Tekniske_rapporter/Technical_Report_ECE-TR-6-samlet.pdf (accessed on 11 October 2022).
- Le Bouteiller, C.; Venditti, J.G. Sediment transport and shear stress partitioning in a vegetated flow. Water Resour. Res. 2015, 51, 2901–2922. [Google Scholar] [CrossRef]
- Einstein, H.A.; Banks, R.B. Fluid resistance of composite roughness. Trans. Am. Geophys. Union 1950, 31, 603–610. [Google Scholar] [CrossRef]
- Bai, Y.; Duan, J.G. Simulating unsteady flow and sediment transport in vegetated channel network. J. Hydrol. 2014, 515, 90–102. [Google Scholar] [CrossRef]
- Sturm, T. Open Channel Hydraulics; McGraw-Hill: Boston, MA, USA, 2001. [Google Scholar]
- Zanke, U.; Roland, A. Sediment Bed-Load Transport: A Standardized Notation. Geosciences 2020, 10, 368. [Google Scholar] [CrossRef]
- Zhang, S.; Duan, J.G.; Strelkoff, T.S. Grain-Scale Nonequilibrium Sediment-Transport Model for Unsteady Flow. J. Hydraul. Eng. 2013, 139, 22–36. [Google Scholar] [CrossRef]
- Shim, J.; Duan, J.G. Experimental study of bed-load transport using particle motion tracking. Int. J. Sediment Res. 2017, 32, 73–81. [Google Scholar] [CrossRef]
- Shim, J.; Duan, J. Experimental and theoretical study of bed load particle velocity. J. Hydraul. Res. 2018, 57, 62–74. [Google Scholar] [CrossRef]
- Fernandez-Luque, R.; van Beek, R. Erosion and transport of bed-load sediment. J. Hydraul. Res. 1976, 14, 127–144. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Xu, B.; Heidari, A.A.; Kuang, F.; Zhang, S.; Chen, H.; Cai, Z. Quantum Nelder-Mead Hunger Games Search for optimizing photovoltaic solar cells. Int. J. Energy Res. 2022, 46, 12417–12466. [Google Scholar] [CrossRef]
- Al-Asadi, K.; Abbas, A.A.; Hamdan, A.N. Optimization of the Hydrological Tank Model by Downhill Simplex Method. Int. J. Civ. Eng. 2020, 18, 1433–1450. [Google Scholar] [CrossRef]
- Alvarez-Vázquez, L.J.; Júdice, J.J.; Martínez, A.; Rodríguez, C.; Vázquez-Méndez, M.E.; Vilar, M.A. On the optimal design of river fishways. Optim. Eng. 2011, 14, 193–211. [Google Scholar] [CrossRef]
- Han, L.; Neumann, M. Effect of dimensionality on the Nelder–Mead simplex method. Optim. Methods Softw. 2006, 21, 1–16. [Google Scholar] [CrossRef]
- ASCE Committee on Sedimentation. Sedimentation Engineering: Processes, Measurements, Modeling, and Practice; ASCE Manuals and Reports on Engineering Practice No. 110; Garcia, M.H., Ed.; American Society of Civil Engineers: Reston, VA, USA, 2008; ISBN 13:978-0-7844-0814-8. [Google Scholar]
- Einstein, H.A. Formulas for the Transportation of Bed Load. Trans. Am. Soc. Civ. Eng. 1942, 107, 561–577. [Google Scholar] [CrossRef]
- Meyer-Peter, E.; Muller, R. Formulas for bed load transport. In Proceedings of the second Meeting of International Association for Hydraulic Structures Research, Stockholm, Sweden, 7 June 1948; pp. 39–64. [Google Scholar]
- Bagnold, R.A. An Approach to the Sediment Transport Problem from General Physics; U.S. Geological Survey Professional Paper 4221; U.S. Government Printing Office: Washington, DC, USA, 1966. [Google Scholar]
- Parker, G. Surface-based bedload transport relation for gravel rivers. J. Hydraul. Res. 1990, 28, 417–436. [Google Scholar] [CrossRef]
- Duan, J.G.; Scott, S. Selective bed-load transport in Las Vegas Wash, a gravel-bed stream. J. Hydrol. 2007, 342, 320–330. [Google Scholar] [CrossRef]
- Wilcock, P.R.; Crowe, J.C. Surface-based Transport Model for Mixed-Size Sediment. J. Hydraul. Eng. 2003, 129, 120–128. [Google Scholar] [CrossRef]


| Run | d (mm) | d50 (mm) | Stem Spacing (Ss) (mm) | N | S (%) | H (cm) | Q × 103 (m3/s) | qb × 106 (m2/s) | |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 16 | 0.45 | 78 | 164.366 | 0.033 | 0.805 | 11.4 | 11.34 | 0.95 |
| 2 | 16 | 0.45 | 78 | 164.366 | 0.033 | 1.14 | 15.3 | 18.44 | 2.77 |
| 3 | 16 | 0.45 | 78 | 164.366 | 0.033 | 1.705 | 17.3 | 25.18 | 7.68 |
| 4 | 16 | 1.6 | 78 | 164.366 | 0.033 | 1.4 | 15.1 | 18.87 | 0.51 |
| 5 | 16 | 1.6 | 78 | 164.366 | 0.033 | 1.55 | 15.9 | 21.95 | 3.02 |
| 6 | 16 | 1.6 | 78 | 164.366 | 0.033 | 1.78 | 16.8 | 25.18 | 6.17 |
| 7 | 16 | 0.45 | 120 | 69.4444 | 0.014 | 0.62 | 8.8 | 9.92 | 0.38 |
| 8 | 16 | 0.45 | 120 | 69.4444 | 0.014 | 0.77 | 11.52 | 16.36 | 2.02 |
| 9 | 16 | 0.45 | 120 | 69.4444 | 0.014 | 1.05 | 15.3 | 25.66 | 4.99 |
| 10 | 16 | 1.6 | 120 | 69.4444 | 0.014 | 0.94 | 13.87 | 23.32 | 1.47 |
| 11 | 16 | 1.6 | 120 | 69.4444 | 0.014 | 1.08 | 15.29 | 29.05 | 2.57 |
| 12 | 16 | 1.6 | 120 | 69.4444 | 0.014 | 1.3 | 16.36 | 34.67 | 12.65 |
| 13 | 16 | 0.45 | 200 | 25 | 0.005 | 0.51 | 11.4 | 21.50 | 3.53 |
| 14 | 16 | 0.45 | 200 | 25 | 0.005 | 0.62 | 12.2 | 25.66 | 4.14 |
| 15 | 16 | 0.45 | 200 | 25 | 0.005 | 0.74 | 13.8 | 31.57 | 8.19 |
| 16 | 16 | 1.6 | 200 | 25 | 0.005 | 0.54 | 13.5 | 29.05 | 1.58 |
| 17 | 16 | 1.6 | 200 | 25 | 0.005 | 0.65 | 14.5 | 34.67 | 3.82 |
| 18 | 16 | 1.6 | 200 | 25 | 0.005 | 0.85 | 15.9 | 40.61 | 5.74 |
| Run | (N/m2) | (N/m2) | (N/m2) | Vv (cm/s) | CD | (N/m2) | ΔZ (mm) | Fr |
|---|---|---|---|---|---|---|---|---|
| 1 | 0.334 | 0.079 | 0.081 | 17.15 | 1.18 | 3.264 | 5.5 | 0.162 |
| 2 | 0.484 | 0.107 | 0.110 | 20.78 | 1.15 | 6.279 | 5.4 | 0.170 |
| 3 | 0.712 | 0.148 | 0.153 | 25.09 | 1.12 | 11.513 | 5.6 | 0.193 |
| 4 | 0.884 | 0.114 | 0.118 | 21.54 | 1.16 | 8.708 | 6.1 | 0.177 |
| 5 | 1.037 | 0.136 | 0.140 | 23.80 | 1.13 | 9.204 | 5.2 | 0.191 |
| 6 | 1.209 | 0.156 | 0.162 | 25.84 | 1.12 | 11.029 | 6.5 | 0.201 |
| 7 | 0.360 | 0.096 | 0.099 | 19.06 | 1.12 | 2.944 | 7.7 | 0.205 |
| 8 | 0.528 | 0.139 | 0.143 | 24.00 | 1.04 | 4.220 | 7.3 | 0.226 |
| 9 | 0.731 | 0.180 | 0.186 | 28.35 | 1.01 | 7.905 | 7.8 | 0.231 |
| 10 | 1.089 | 0.183 | 0.190 | 28.42 | 1.00 | 5.324 | 6.3 | 0.244 |
| 11 | 1.339 | 0.225 | 0.234 | 32.12 | 0.97 | 6.138 | 5.7 | 0.262 |
| 12 | 1.646 | 0.271 | 0.283 | 35.82 | 0.96 | 7.770 | 7.0 | 0.283 |
| 13 | 0.691 | 0.224 | 0.233 | 31.60 | 0.95 | 2.759 | 9.2 | 0.299 |
| 14 | 0.853 | 0.270 | 0.282 | 35.23 | 0.94 | 3.607 | 13.0 | 0.322 |
| 15 | 1.012 | 0.308 | 0.323 | 38.32 | 0.93 | 5.069 | 15.0 | 0.329 |
| 16 | 1.245 | 0.277 | 0.289 | 36.05 | 0.92 | 2.527 | 5.4 | 0.313 |
| 17 | 1.524 | 0.332 | 0.347 | 40.05 | 0.92 | 3.260 | 10.3 | 0.336 |
| 18 | 1.818 | 0.369 | 0.387 | 42.78 | 0.92 | 5.844 | 21.7 | 0.343 |
| Investigator | d (mm) | d50 (mm) | S (%) | H (cm) | Vv (cm/s) | (N/m2) | Fr | qb × 106 (m2/s) | |
|---|---|---|---|---|---|---|---|---|---|
| Kothyari et al. [12] | 2.0 to 5.0 | 0.55 to 5.9 | 0.002 to 0.012 | 1.7 to 20.8 | 2.78 to 6.08 | 33.8 to 94.9 | 1.70 to 59.43 | 0.44 to 1.78 | 0.5 to 8121 |
| Jordanova & James [11] | 5.0 | 0.45 | 0.0314 | 1.18 to 1.84 | 2.05 to 11.1 | 15.5 to 18.5 | 0.51 to 1.32 | 0.16 to 0.37 | 1.89 to 6.94 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Duan, J.G.; Al-Asadi, K. On Bed Form Resistance and Bed Load Transport in Vegetated Channels. Water 2022, 14, 3794. https://doi.org/10.3390/w14233794
Duan JG, Al-Asadi K. On Bed Form Resistance and Bed Load Transport in Vegetated Channels. Water. 2022; 14(23):3794. https://doi.org/10.3390/w14233794
Chicago/Turabian StyleDuan, Jennifer G., and Khalid Al-Asadi. 2022. "On Bed Form Resistance and Bed Load Transport in Vegetated Channels" Water 14, no. 23: 3794. https://doi.org/10.3390/w14233794