1. Introduction
Xi’an is the center of the Guanzhong-Tianshui Economic Development Zone and the Xi-Xian New Area. Due to extensive construction and rapid urbanization, the city has become larger, the water resources have decreased, and the climate has become warm and dry [
1]. This is an important grain-producing area where groundwater is used for agriculture. Thus, the groundwater in this area has been overexploited for a long time, and the regional groundwater level has decreased, forming many groundwater depression cones, and resource and environmental problems, such as land subsidence, ground subsidence, and ground fissures. These problems have drawn the attention of the international community and severely restricted the healthy development of the regional economy. ‘What is the upper limit of the carrying capacity of groundwater resources for the social economy? Is there still room for regulation?‘ Such issues have become a concern of the Chinese government, the public, and even the international community. Hence, these issues need to be addressed. Evaluating the carrying capacity of groundwater resources is the key to answering the above questions. This is not only an important issue concerning the study of the water cycle and sustainable development of groundwater resources in Xi’an, but it also has significance in ensuring the coordinated and sustainable development of water resources, ecology, social economy, and food security. The serious and highly integrated water problem has shown that the groundwater resource carrying capacity needs to be studied urgently.
Developed countries neglected the study of the carrying capacity of water resources because they were abundant. Therefore, studies on the carrying capacity of water resources in the world are limited, and most discussions are included in the theory of sustainable development [
2,
3,
4,
5,
6]. The North American Lakes Association has defined the carrying capacity of lakes. The URS company in the United States has studied the carrying capacity of the Keys River Basin in Florida. Some studies by researchers such as Falkenmark have also involved the carrying limit of water resources. However, in China, a country with less than one-third of the world’s per capita water resources, the study of the carrying capacity of water resources is necessary. In China, many studies have investigated the carrying capacity of water resources, especially since the 1990s [
7,
8,
9,
10,
11,
12], and many concepts and research methods have been proposed. The water carrying capacity can be elaborated by two main theories: the scale of water resources development and the largest scale of the carrying capacity of water resources. The representative studies were performed by Yanchun Gao [
13] and Benqing Ruan [
14], and many other researchers, who hold the second theory [
15,
16]. The research methods of the carrying capacity of water resources include the conventional trend method, background analysis method, analytic hierarchy process, dynamic simulation recursive algorithm, state space method, fuzzy evaluation method, principal component analysis method, system dynamics method, etc. These methods can be mainly classified into three categories, including the empirical estimation method, the index system evaluation method, and the complex system analysis method. Among them, the empirical estimation method generally has low accuracy, the selection of the evaluation index of the index system method has certain limitations, and the complex system method has many parameters that are not easy to understand and explain.
Studies on the carrying capacity of groundwater resources are limited, and they are in the exploratory stage. It was not until 2000 that the correlation of the carrying capacity of groundwater resources was established [
17,
18,
19,
20,
21], and various methods and indicators were also quite abundant. Advancements in these methods and indicators encouraged studies on the carrying capacity of water resources. The concept and method of determining the carrying capacity of groundwater resources were followed by the method of determining the carrying capacity of water resources. There is no unified and clear definition and well-established method to determine the carrying capacity. Commonly used methods can be roughly divided into qualitative and quantitative evaluation methods. These methods assume a linear relationship between each index and the evaluation results, which cannot accurately reflect the complex and non-linear relationship between the factors of the groundwater system. The index classification is arbitrary and cannot reflect the influence of continuous change in each evaluation index value on the carrying capacity of groundwater. Additionally, the weight of such methods is generally estimated directly. Subjective factors have a greater impact on the results, and thus, evaluating the carrying capacity of groundwater from the same area at the same time might show different results.
The evaluation of groundwater carrying capacity follows the method for evaluating the carrying capacity of water resources. The indicators are comprehensively considered based on the society, economy, environment, and groundwater conditions. The methods cannot easily separate the influence of surface water and groundwater, and there are certain limitations and differences in the determination of the threshold of the carrying capacity of groundwater. This study considers that the bearing capacity of groundwater is the attribute of groundwater and its storage medium-aquifer. Society, the environment, and the economy are only the external factors that affect groundwater. They do not affect the bearing capacity of groundwater. For example, the load capacity of a car is only related to its performance, regardless of the object it carries. Therefore, in this study, all social, economic, environmental, and other external indicators are unified with the groundwater overexploitation coefficient as the external force object carried by groundwater. The evaluation index of the carrying capacity of groundwater only considers the characteristics of underground aquifers and groundwater.
Based on the above-mentioned background, in this study, we proposed a new method to determine the carrying capacity of groundwater resources in Xi’an, using the probabilistic neural network method based on the ‘W–F extension law’. The probabilistic neural network method of the ‘W–F extension law’ does not assign weights but calculates the clustering center, so it does not need to add weights to the parameters to avoid subjectivity. The method is not subject to regional restrictions. It can reflect the non-linear relationship between the groundwater system and the sensitivity and recovery ability of groundwater under the same future exploitation load. The evaluation and analysis of the carrying capacity of groundwater resources in Xi’an provided a reference for the rational development, utilization, and distribution of groundwater resources.
3. ‘W–F Extension Law’ Standard
The Weber–Fechner law (W–F law) was proposed by the German physiologists Weber and Fechner, who showed the relationship between psychological quantity and physical quantity and considered the influence of subjective and objective factors. Zhayong et al. applied it to the formulation of ambient air quality standards [
24], and the evaluation results were similar to those of national standards. In this study, we used it to determine the evaluation criteria of groundwater carrying capacity.
3.1. W–F Law (Weber–Fechner Law)
The Weber–Fechner Law represents the relationship between psychological quantities and physical quantities and is at the base of the foundation of psychophysics as a new discipline. The German physiologist Weber found that the difference of the same stimulus must reach a certain proportion to cause the sense of difference. This ratio is a constant, and its expression is known as Weber’s law.
In the formula, K represents a constant, also known as the Weber rate; ∆r represents the threshold of difference, also known as the minimum detectable difference; r represents the amount of stimulation.
To describe the relationship between sensory quantities and physical quantities in a continuous sense, the German physicist Fechner, based on Weber’s research, proposed a hypothesis in 1860 regarding the minimal perceptible difference (continuous differential threshold) as a unit of sensory quantities. For each additional differential threshold, the sensory quantity is increased by one unit, which can be expressed as follows:
In the formula, S represents the sensory quantity, also known as sensory intensity; R represents a physical quantity, also known as stimulus intensity; C represents the integral constant.
The sensory quantity is proportional to the logarithm of the physical quantity, i.e., the increase in the sensory quantity lags behind the increase in the physical quantity. The physical quantity increases in geometric progression, while the sensory quantity increases in arithmetic progression. This empirical formula is called the Weber–Fechner law (W–F law), which is suitable for medium-intensity stimulation.
The W–F law shows that all human senses, including vision, hearing, skin sense (including pain, itching, touch, and temperature), taste, smell, electric shock, etc., are proportional to the common logarithm of the intensity of the corresponding physical quantity, rather than the intensity of the corresponding physical quantity.
3.2. Extension of the W–F Law
The evaluation of the carrying capacity of groundwater can be regarded as the relationship between human feeling and each carrying capacity index. To apply the ‘W–F law’ for evaluating the carrying capacity of groundwater, it is necessary to extend the ‘W–F law’. The degree of influence of the index on the groundwater carrying capacity also satisfies Equation (2). The objective stimulus R can be regarded as the index value of the carrying capacity, and the human response S can be regarded as the measure of the carrying capacity of the index. Equation (2) describes the influence of the evaluation index on the carrying capacity of groundwater.
The difference on both sides of Equation (2) can be expressed as follows:
As shown in Equation (3), when the index value changes in equal proportion, its impact on the carrying capacity of groundwater changes in equal difference.
Therefore, when formulating the grading standard limit of a certain index, although the index limit between the adjacent standard levels of the index changes in an equal ratio, the degree of influence of this change on the carrying capacity of groundwater should be graded. The range of variation between the minimum value R
imin and the maximum value R
imax of the i
th index can be divided into 11 levels, such as n = 0, 1, 2, …, 10, where n = 0 and n = 10 correspond to the levels of R
imin and R
imax, respectively. The objective importance ratio between n and m of any two levels of the i index is:
When m = 0, the above equation can be expressed as:
In the formula, Ki = (Rimax/Rimin)1/10 indicates the ratio of the ith index to the two adjacent standards affecting the groundwater carrying capacity, i.e., the Weber rate in Formula (1).
In the classification standard, the classification number can be changed according to the requirements; the determination of its standard limits depends on the minimum and maximum values of the evaluation of sample data. Samples with different minimum and maximum values have different standard limits for classification.
According to the number of classifications, different n can be selected to divide the carrying capacity of groundwater into four categories, including extremely low, low, medium, and high. The standard limits when n = 0, 2, 5, and 8 correspond to levels VL (very low), L (low), M (medium), and H (high), and the corresponding levels are VL = 1, L = 2, M = 3, and H = 4. Each index has four standard limits corresponding to four levels, which constitute the standard model of probabilistic neural network learning. According to the Rimin and Rimax values and Formula (5) of the index values in the evaluation area, different n values can be used to calculate the corresponding standard limits R of each index of the very low, low, medium, and high bearing capacity levels.
For the indices with a higher evaluation index value, a higher bearing capacity, and a higher level, such as precipitation, the permeability coefficient of the phreatic aquifer, the thickness of the phreatic aquifer, the permeability coefficient of the confined aquifer, and confined aquifer thickness, the 0, 2, 5, and 8 levels in the standard ‘W–F extension law’ correspond to the VL, L, M, and H levels of the evaluation results, respectively. The smaller the index value, the higher the bearing capacity, and the higher the level of the index, such as phreatic water level depth, phreatic water level drop, and the buried depth of the confined water level. The 10, 8, 5, and 2 levels in the ‘W–F extension law’ correspond to the VL, L, M, and H levels of the evaluation results. The standard limits of the eight bearing capacity indices of groundwater were calculated, as shown in
Table 1.
3.3. Probabilistic Neural Network (PNN)
The probabilistic neural network (PNN) is a variant of the radial basis network, which is a feedforward neural network with a radial basis function layer and a competitive output layer. The network can use a linear learning algorithm to complete the work of a non-linear learning algorithm with high precision. This network is used for classification. It has been widely used in the field of pattern recognition classification [
25], but it has not been used for evaluating the carrying capacity of groundwater.
The probabilistic neural network method does not need to determine the weight of the evaluation index, and can be classified, which reduces the subjectivity of the evaluation. It is specifically used for recognition classification, and the evaluation of the carrying capacity of groundwater is a typical pattern classification problem. Because the artificial neural network (ANN) can express any non-linear relationship and learning, it can also reflect the non-linear relationship between the groundwater system evaluation index and the evaluation results. These two features are not available in the overlapping index method and fuzzy comprehensive evaluation method, and thus, the probabilistic neural network method is better for evaluating the carrying capacity of groundwater. However, there is a problem with determining the index limit in the groundwater carrying capacity. While evaluating the carrying capacity of groundwater, the selection of indicators has a certain subjectivity, and cannot reflect the mutation between the various levels of evaluation criteria [
26,
27,
28,
29,
30]. Therefore, the ‘W–F extension law’ needs to be used to improve the evaluation criteria, and then, evaluate the groundwater carrying capacity based on the probabilistic neural network.
3.4. Probabilistic Neural Network Method Based on the ‘W–F Extension Law’
After analysis, the ‘W–F extension law’ standard can be used to evaluate the bearing capacity of groundwater, which is not limited by regional restrictions, avoids subjectivity, reflects the abrupt relationship between various levels of the evaluation standard, and can determine any number of classifications as needed. The probabilistic neural network can avoid subjectivity in the process of weight determination and can reflect the non-linear relationship between the evaluation index and the evaluation result. The probabilistic neural network is specially used for classification because of its fast operation speed and no local minima.
Therefore, a probabilistic neural network method based on the ‘W–F extension law’ is proposed by combining the ‘W–F extension law’ with a probabilistic neural network. The W–F extension law is used to determine the index standard limit of the evaluation of groundwater carrying capacity, and the probabilistic neural network method is used to classify groundwater carrying capacity. The new evaluation method can avoid subjectivity while determining the index standard and weight, and the index standard is not limited by regional restrictions. It can broaden the scope of evaluation and evaluate the bearing capacity of groundwater. It can reflect the non-linear relationship between different levels and also between evaluation indices and evaluation results, improve the operation speed, and determine the number of classifications according to requirements. The method is verified below.
4. Xi’an Groundwater Carrying Capacity Evaluation Process
4.1. Division of the Evaluation Area
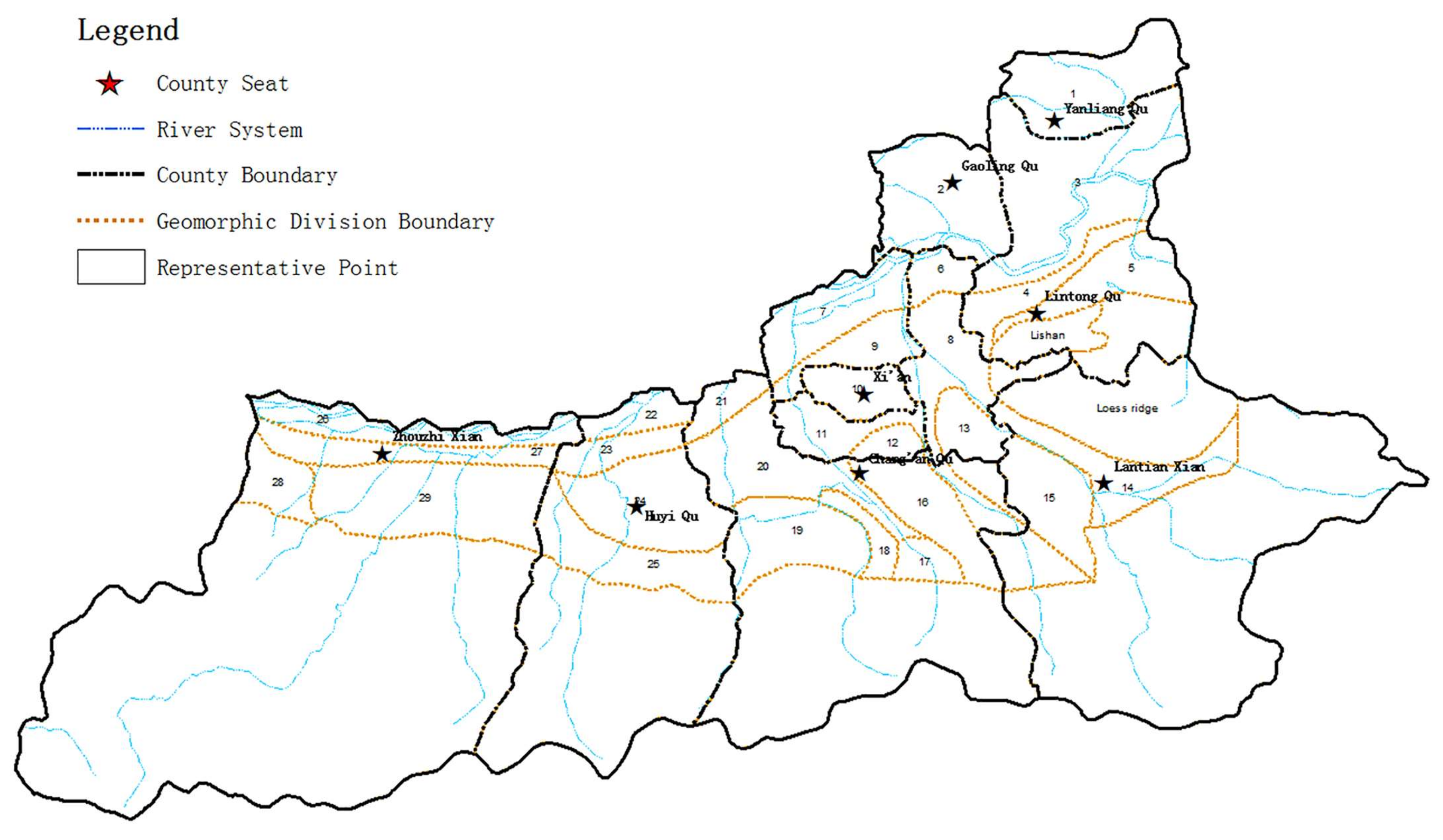
Based on the administrative divisions and geomorphological characteristics, the plain area of Xi’an was divided into 29 sub-areas, which were the basic units for groundwater overload evaluation. A representative point was selected in each zone for evaluation, as shown in
Figure 3.
The name, number, and landform of each zone are shown in
Table 2.
4.2. Establishment of the Evaluation Index System
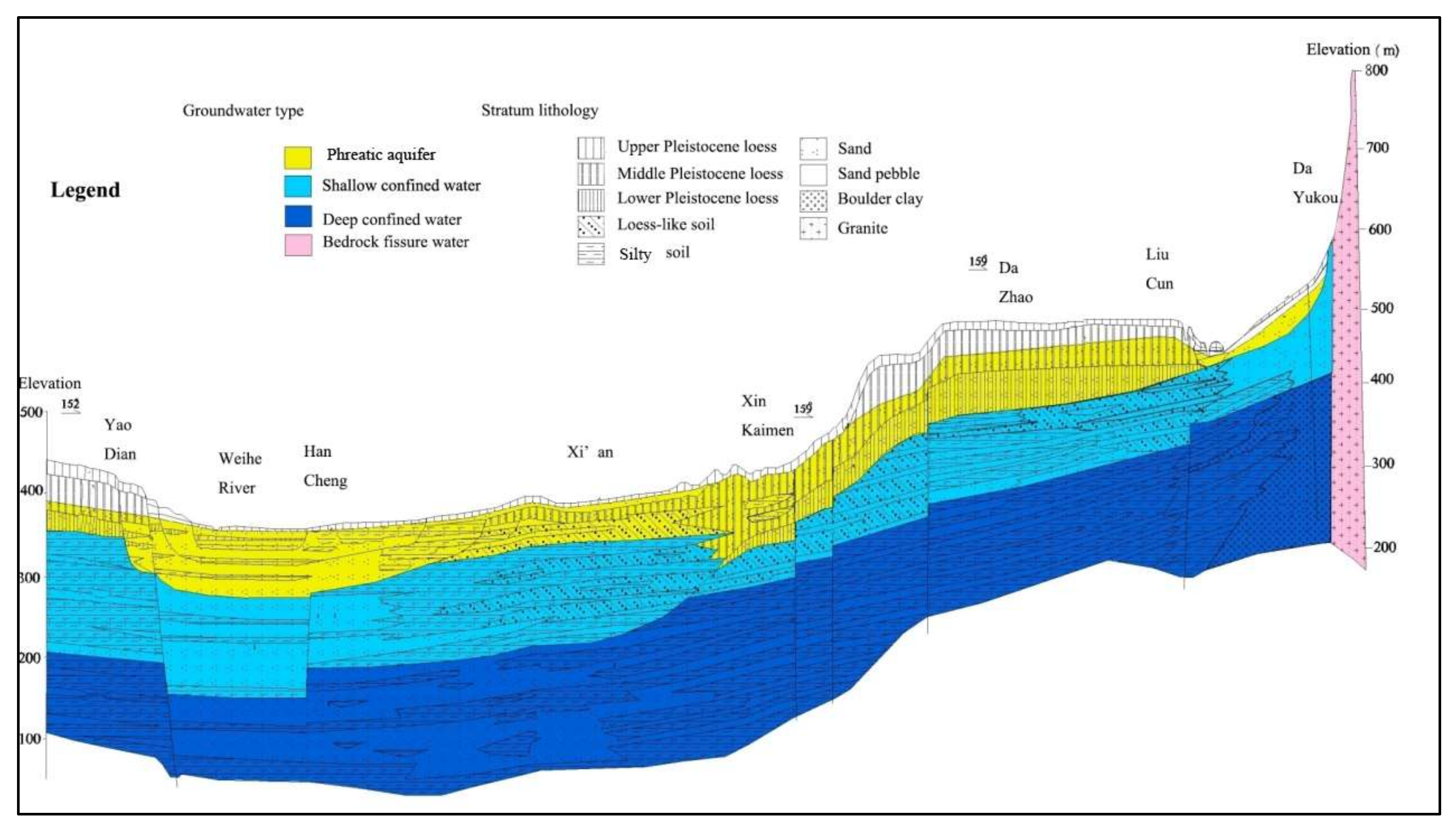
The traditional evaluation index of the carrying capacity of groundwater is considered based on the aspects of society, economy, and environment. This method has certain limitations and differences in the determination of the threshold of groundwater carrying capacity because the connection between surface water and groundwater is difficult to distinguish. We assumed that the bearing capacity of groundwater is the attribute of its storage medium-aquifer and groundwater. The population, economy, environment, and other indicators are only the external force of groundwater, and do not affect the carrying capacity of groundwater. For example, the load capacity of a car is only related to its performance, regardless of the object it carries. Therefore, in this study, all external indicators were unified into the external force of groundwater by the groundwater overexploitation index. The groundwater carrying capacity only considers the characteristics of the underground aquifer and the groundwater. According to the analysis of stratigraphic lithology, hydrogeological conditions, and recharge, runoff, and discharge conditions of the aquifer group in the second chapter of this paper, the evaluation indices of the carrying capacity of groundwater were determined as follows.
There were eight indices in total, including precipitation, buried depth of the phreatic water level, the permeability coefficient of phreatic aquifer, thickness of the phreatic aquifer, decline range of the phreatic water level, the permeability coefficient of the confined aquifer, the thickness of the confined aquifer, and buried depth of the confined water level. Among these, four indicators were time-relevant and required the value of the evaluation year and included precipitation, groundwater depth, groundwater level drop, and confined water depth. These accounted for 50% of the total number of water carrying capacity evaluation indices.
The relationship between each index and the carrying capacity of groundwater is described as follows:
Precipitation: higher general precipitation is associated with the greater recharge of phreatic and confined water and higher carrying capacity of groundwater.
Phreatic water level depth: lesser depth of the phreatic water level indicates that the precipitation recharge is more vulnerable and the carrying capacity is higher.
Permeability coefficient of phreatic aquifer: a higher permeability coefficient of the phreatic aquifer indicates faster water migration in the aquifer and a higher carrying capacity.
Phreatic aquifer thickness: a greater thickness of the phreatic aquifer indicates greater aquifer water storage and a higher bearing capacity.
Decline range of the phreatic water level: a smaller decline range of the phreatic water level indicates a higher quantity of water in the phreatic aquifer and a higher carrying capacity.
The permeability coefficient of confined aquifer: a higher permeability coefficient of the confined aquifer indicates a faster movement of water in the aquifer and a higher bearing capacity.
Confined aquifer thickness: a higher thickness of a confined aquifer indicates greater water storage capacity of the confined aquifer and a higher bearing capacity.
The buried depth of confined water level: a lesser buried depth of the confined water level indicates a lower water bearing capacity of the confined aquifer, greater water storage, and a higher bearing capacity.
4.3. Construction of the Probabilistic Neural Network Model
Based on the learning mechanism of the probabilistic neural network, the probabilistic neural network evaluation model of the groundwater carrying capacity was constructed, i.e., the normalized value of the evaluation index in the evaluation standard was taken as the input sample, and the corresponding level was taken as the output sample to form the evaluation standard sample mode. When evaluating, we only needed to input the normalized evaluation factor sample value as the input sample into the mature network to directly receive the evaluation results.
- (1)
Determination and normalization of the standard pattern P of network learning
Because the neural network has high accuracy in training and predicting [0, 1] data, the input data need to be normalized. There are two types of evaluation indicators, one is the larger, where the level of indicators is higher. The other is the smaller, but the level of indicators is higher. These indexes are normalized by the definition of relative membership degree in fuzzy mathematics [
31].
For the higher grade index, the relative membership degree of the maximum value max xij of index i in the original value set to the highest grade target was 1; the relative membership degree of the target value 0 to the highest level target was 0, which constituted the two poles of the reference continuum. The larger the level, the higher the relative membership degree of the target (referred to as the relative membership degree of the target) (also known as the normalized formula), i.e.,
For the index with a low level and a high level, the definition of relative membership degree was applied. The minimum value min xij of the index i in the original value set was taken as the relative membership degree l of the highest level target. When xij was substantially larger than min xij, the relative membership degree of the highest level target was approximately 0, which constituted the two poles of the reference continuum. The formula for the relative membership degree of the smaller level and the higher target were obtained as follows:
According to the standard model of probabilistic neural network learning, the standard limits of each index were established and normalized. After normalizing the standard limit of the ‘W–F extension law’, as shown in
Table 1, the standard mode of the probabilistic neural network learning, i.e., input vector P, was obtained. The normalized results of the standard limit of the groundwater index for Xi’an are shown in
Table 3.
- (2)
Determination of network target output vector T
According to the construction rules of the probabilistic neural network, the target output vector of the network is defined as . A row vector in is the response state of four neurons in the output layer of the network at four evaluation levels (VL, L, M, H) in the groundwater carrying capacity evaluation standard.
- (3)
Calculation of the probabilistic neural network
The probabilistic neural network model was calculated to compare the classification sample to be determined (unknown pattern) with the learning pattern sample (standard pattern) P to obtain the maximum response output.
The sample index values of the area to be evaluated were normalized, and the constructed probabilistic neural network model was used for learning to obtain the response output of the standard model with the maximum probability, i.e., the evaluation result of the carrying capacity of groundwater.
5. Evaluation Results
Based on the limit value of the groundwater carrying capacity evaluation index determined by the ‘W–F extension law’, the standard model of network learning was obtained after normalization.
Here,
represents the input vector, the number of elements of the input vector R = 5, and the number of radial basis function neurons Q = 4. The probabilistic neural network output layer for groundwater carrying capacity evaluation:
The evaluation results of groundwater carrying capacity are shown in the following figure. The five index values of the 29 zones were normalized and calculated by the probabilistic neural network model.
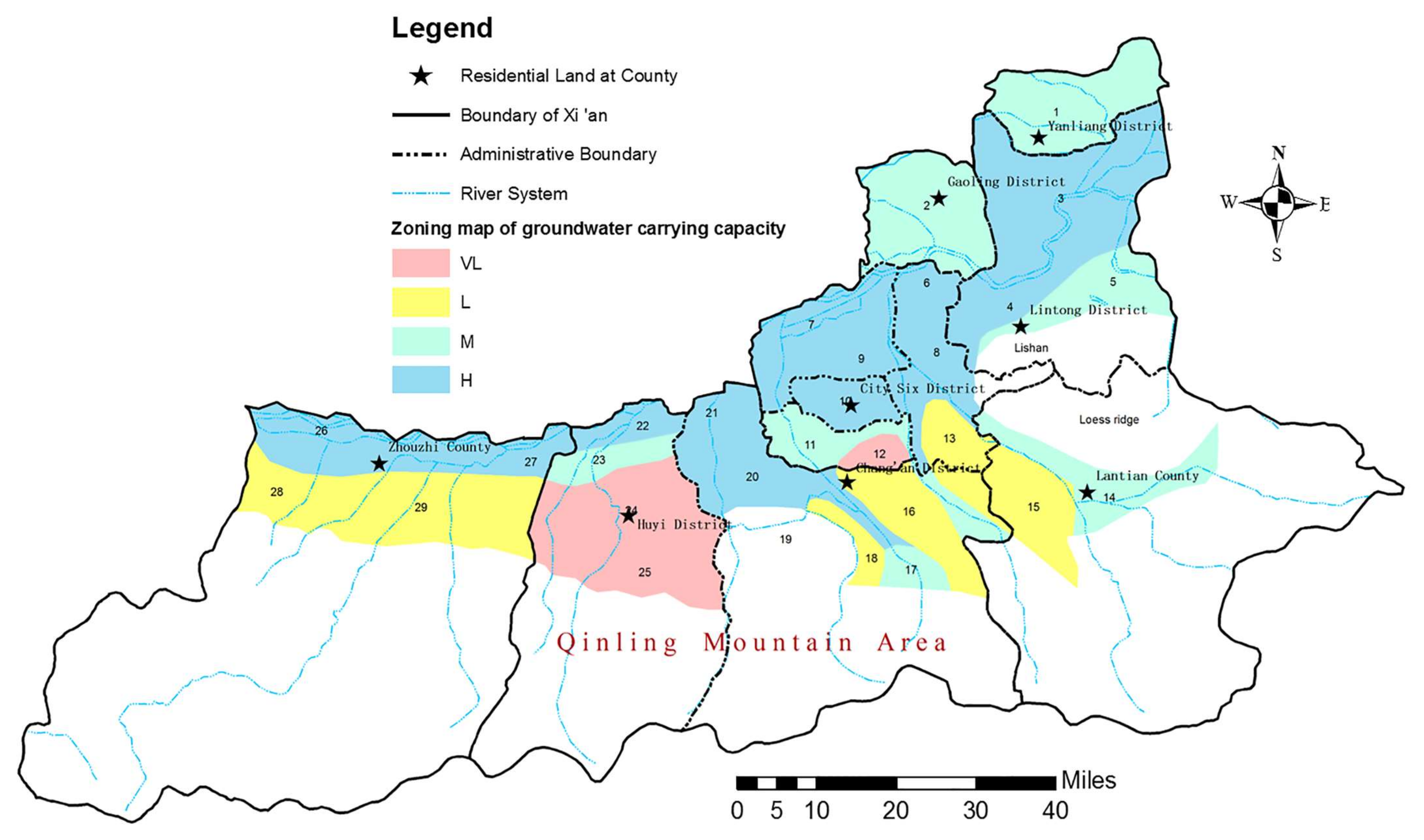
As shown in
Figure 4, the phreatic water carrying capacity in the plain area of Xi’an decreased from floodplain, first-order terrace, second-order terrace, third-order terrace, and alluvial fan to loess table source, and the water availability worsened. The characteristics of each area for which the phreatic water carrying capacity was evaluated are as follows:
Two areas had a very low water carrying capacity. The representative points of the partition were 12 and 25, which were located at Shaolingyuan in the sixth district of the city and the alluvial fan of the Huyi district, respectively. Shaolingyuan in the sixth district of the city was located in the source side area of the loess platform source. The buried depth of the phreatic water level was about 80 m, the thickness was about 40 m, and the permeability coefficient of the aquifer was about 1 m/d. Additionally, the phreatic water level decreased greatly (by about 32 m) from 2000 to 2018, which indicated the overexploitation of phreatic water in this area. The phreatic water level decreased further, and the quantity of phreatic water decreased. The depth of the phreatic water level of the alluvial fan in the Huyi district was about 40 m, and the thickness was about 15 m. From 2000 to 2018, the phreatic water level decreased by about 37 m, and thus, it was categorized as an area with very low groundwater bearing capacity; the quantity of water used from this source should be strictly controlled.
Six areas had a low groundwater carrying capacity, and the representative points 13, 15, 16, 18, 28, and 29 were located in Zhouzhi county, Chang’an district, the sixth district, and Bailuyuan, respectively. The permeability coefficient of the phreatic aquifer in the loess platform source area was about 1 m/d, and the representative points were 15, 16, 18, and 28. The depth of the phreatic water level was more than 80 m, and the thickness of the aquifer was 40–45 m. The phreatic water level decreased by 2–8 m from 2000 to 2018, and representative point 29 was the alluvial fan area of Zhouzhi county. The permeability coefficient of the phreatic aquifer was about 10 m/d, the buried depth of the phreatic water level was about 41 m, the thickness of the aquifer was about 10 m, and the decline in the phreatic water level from 2000 to 2018 was about 9 m. The quantity of groundwater utilized in a low carrying capacity area should be limited.
Seven areas with a medium carrying capacity of groundwater, and the representative points of 1, 2, 5, 11, 14, 17, and 23 were located in Huyi district, Chang’an district, the sixth district, Lantian county, Lintong district, Yanliang district, and Gaoling district, which were the first, second, and third terraces or alluvial fans. Representative points 1 and 2 in the study area were the first-order terraces. The buried depth of the phreatic water level was 13–20 m, and the drawdown of the phreatic water level was about 6–10 m. The indicators, such as water abundance and exploitation, were at a medium level in the evaluation area. The representative point 17 of the partition was the alluvial fan, which was positioned at the front edge of the loess platform in Chang’an district. The rest were located in the second and third terraces, and the water yield and exploitation of phreatic were at a medium level in the evaluation area. Areas with a medium carrying capacity of groundwater should plan groundwater usage to prevent overexploitation.
There were 12 high carrying capacity areas of groundwater, which were located in the floodplain or first-class terrace. The phreatic water supply conditions in this area were good, and the water availability was high. From 2000 to 2018, the phreatic water level did not change much, and the decline was small, about 0–9 m. The phreatic water level of the Chanba river and Fengzao river water sources decreased considerably, which were 21 m and 15 m, respectively. However, because of riverside mining, the large permeability coefficient of the phreatic aquifer (about 40–50 m/d), and the thickness of the aquifer (about 50–55 m), we considered that recharging the aquifer would be easy and categorized the region as a high carrying capacity area of groundwater. In the high bearing capacity area, groundwater should not be overexploited, and the use should be determined based on the relationship between the current water level and the ecological water level of groundwater.