Working Mode Identification Method for High Arch Dam Discharge Structure Based on Improved Wavelet Threshold–EMD and RDT Algorithm
Abstract
:1. Introduction
2. Basic Theory
2.1. Improved Wavelet Threshold–EMD Hybrid Algorithm for High Arch Dam Noise Reduction
2.2. Modal Parameter Identification of High Arch Dam Discharge Structures Based on Improved HHT–RDT Algorithm
2.3. Recognition Process Based on Improved Wavelet Threshold–EMD and RDT Algorithm
3. Application Case
3.1. Engineering Data
3.2. Improved Wavelet Threshold–EMD Hybrid Algorithm for Signal Noise Reduction
3.3. Modal Identification of Working Parameters of High Arch Dam Discharge Structures
4. Conclusions
- An improved wavelet threshold–EMD hybrid algorithm is proposed for noise reduction pretreatment on measured vibration response data of high arch dams. The improved wavelet threshold algorithm was adapted to overcome the defect of soft and hard threshold function selection, which can effectively eliminate the high-frequency white noise and reduce the influence of the modal aliasing. Then, EMD further eliminates the low-frequency flow noise and white noise, improving the accuracy of filtering and noise reduction.
- An improved wavelet threshold–EMD and RDT algorithm is proposed for working mode identification of high arch dam discharge structures under the working environment load excitation. The proposed method avoids the complicated system ordering process and accurately identifies the modal parameters of high arch dam discharge structures. This method has a simple principle and does not require solving large matrices during calculation. The result has strong robustness and high identification accuracy.
- The engineering examples show that the proposed method can accurately extract the work characteristic information of structures, has good noise reduction capabilities, and has high recognition accuracy. Therefore, this method eases the working modal parameter identification of high arch dam discharge structures and can be used for working modal recognition of other large frequency-intensive structures.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, H.; Wang, Y.; Wei, B. Inversion algorithm for the whole prototype dynamic displacement field of a high arch dam based on limited measuring points. J. Vib. Control. 2017, 23, 3431–3447. [Google Scholar] [CrossRef]
- Chengye, L.; Wei, L.; Bin, M.; Mingfu Song. Research on modal parameter identification method of high arch dam based on improved HHT. J. Hydroelectr. Eng. 2012, 31, 48–55. [Google Scholar]
- Cheng, L.; Tong, F. Application of Blind Source Separation Algorithms and Ambient Vibration Testing to the Health Monitoring of Concrete Dams. Math. Probl. Eng. 2016, 4, 1–15. [Google Scholar] [CrossRef] [Green Version]
- Bao, Y.; Xia, H.; Bao, Z.; Ke, S.; Li, Y. Structural Damage Identification of Pipe Based on GA and SCE-UA Algorithm. Math. Probl. Eng. 2013, 2013, 9. [Google Scholar] [CrossRef] [Green Version]
- Li, H.; Wang, G.; Wei, B.; Zhong, Y.; Zhan, L. Dynamic inversion method for the material parameters of a high arch dam and its foundation. Appl. Math. Model. 2019, 71, 60–76. [Google Scholar] [CrossRef]
- Wei, B.; Xie, B.; Li, H.; Zhong, Z.; You, Y. An improved Hilbert–Huang transform method for modal parameter identification of a high arch dam. Appl. Math. Model. 2021, 91, 297–310. [Google Scholar] [CrossRef]
- Menghui, X.; Nan, J. Dynamic load identification for interval structures under a presupposition of ‘being included prior to being measured. Appl. Math. Model. 2020, 85, 107–123. [Google Scholar]
- Wei, P.; Li, Q.; Sun, M.; Huang, J. Modal identification of high-rise buildings by combined scheme of improved empirical wavelet transform and Hilbert transform techniques. J. Build. Eng. 2022, 63, 105443. [Google Scholar] [CrossRef]
- Shangqing, Z.; Jiuzhang, L. Modal Test Analysis of Tied Arch Bridge Based on Random Subspace Method. Munic. Technol. 2015, 33, 38–41. [Google Scholar]
- Loh, C.H.; Wu, T.C. System identification of Fei-Tsui arch dam from forced vibration and seismic response data. J. Earthq. Eng. 2000, 4, 511–537. [Google Scholar] [CrossRef]
- Xueyuan, N.; Hua, D. Discussion on Modal Parameter Identification Method Based on Random Decreasing Technology. Mech. Des. 2012, 29, 1–5. [Google Scholar]
- Chun, R.; Cheng Cheng, Z.; Qi Feng, L. Application of HHT Method in Time Domain Identification of Structural Modal Parameters. J. Yangtze Univ. 2008, 5, 115–118, 414. [Google Scholar]
- Feldman, M. Time-varying vibration decomposition and analysis based on the Hilbert transform. J. Sound Vib. 2005, 295, 518–530. [Google Scholar] [CrossRef]
- Huokun, L.; Jijian, L. Opperational Modal Parameter Identification of High Arch Dam Under flood discharge exciting Based on Frequency Domain Decomposition Method. J. Vib. Shock. 2008, 27, 149–153. [Google Scholar]
- Li, H.; Liu, B.; Huang, W.; Liu, H.; Wang, G. Vibration load identification in the time-domain of high arch dam under discharge excitation based on hybrid LSQR algorithm. Mechanic 2020, 177, 109193. [Google Scholar] [CrossRef]
- Pengming, T.; Junyi, L.; Feng, Z. Application of Random Decrement Method in Identification of Working Modal Parameters. Mech. Electr. Eng. Technol. 2012, 41, 105–108. [Google Scholar]
- Wenge, T.; Xiaobing, Z. Working Mode Recognition Based on HVD and RDT. J. Guangxi Univ. 2018, 43, 132–140. [Google Scholar]
- Jianwei, Z.; Lianghuan, Z.; Qi, J.; Yu, Z.; Jia, G. Identification of working modal parameters of high dam discharge structure based on HHT. Vib. Meas. Diagn. 2015, 35, 777–783, 804. [Google Scholar]
- He, X.H.; Hua, X.G.; Chen, Z.Q.; Huang, F.L. EMD-based random decrement technique for modal parameter identification of an existing railway bridge. Eng. Struct. 2011, 33, 1348–1356. [Google Scholar] [CrossRef]
- Frank Pai, P.; Palazotto, A.N. HHT-based nonlinear signal processing method for parametric and non-parametric identification of dynamical systems. Int. J. Mech. Sci. 2008, 50, 1619–1635. [Google Scholar] [CrossRef]
- Jianping, H.; Lin, L.; Hongtao, W.; Wei, Q. Modal parameter identification based on Hilbert-Huang transform and random decrement technique. World Earthq. Eng. 2011, 27, 72–77. [Google Scholar]
- Jinyuan, T.; Weitao, C.; Siyu, C.; Wei, Z. A new wavelet threshold function and its application in vibration signal denoising analysis. J. Vib. Shock. 2009, 28, 118–121. [Google Scholar]
- Zhisong, L. Signal Denoising Method Based on Wavelet Analysis. J. Zhejiang Ocean. Univ. 2011, 30, 150–154. [Google Scholar]
- Xiuping, L.; Wei, Y.; Lili, H.; Junfeng, J.; Jian, X.; Zebin, S.; Haifeng, S. X-ray pulsar signal de-noising for impulse noise using wavelet packet. Aerosp. Sci. Technol. 2017, 64, 147–153. [Google Scholar] [CrossRef]
- Wenwen, Z.; Xingwen, C. A New EMD Denoising Method. Electron. Technol. 2008, 21, 30–32, 36. [Google Scholar]
- Dybała, J.; Zimroz, R. Rolling bearing diagnosing method based on Empirical Mode Decomposition of machine vibration signal. Appl. Acoust. 2014, 77, 195–203. [Google Scholar] [CrossRef]
- Chengye, L.; Jijian, L.; Wei, L.; Bin, M. Improvement of Joint Filtering Method of EMD and Wavelet Threshold and Its Application in Vibration Analysis of Discharge Structure. J. Vib. Shock. 2013, 32, 63–70, 110. [Google Scholar]
- Jintao, Y.; Shuyan, Z.; Wei, W. Denoising of Transmitted Signal Based on Empirical Mode Decomposition and Wavelet Transform. J. Harbin Inst. Technol. 2011, 43, 88–92. [Google Scholar]
- Aijun, H.; Jingjing, S.; Ling, X. Modal aliasing problem in empirical mode decomposition. Vib. Test. Diagn. 2011, 43, 429–434. [Google Scholar]
- Jianwei, Z.; Qi, J.; Yu, Z.; Lianghuan, Z.; Jia, G. A Signal Denoising Method Suitable for Vibration Analysis of Discharge Structures. J. Vib. Shock. 2015, 34, 179–184. [Google Scholar]
- Zhi, C.; Feng, H.; Xiaolong, Z.; Xu, J.; Zailong, H. Wavelet-experience mode decomposition method for trend term modulation for atmospheric dry length profile denoising. Acta Opt. Sin. 2017, 37, 15–26. [Google Scholar]
- Wei, B.W.; Yuan, D.Y.; Li, H.K.; Xu, Z. Combination forecast model for concrete dam displacement considering residual correction. Struct. Health Monit. 2017, 18, 232–244. [Google Scholar] [CrossRef]
- Wei, B.W.; Yuan, D.Y.; Li, H.K.; Li, L. Modified hybrid forecast model considering cjhaotic residual errors for dam deformation. Struct. Control. Health Monitor. 2018, 25, e2188. [Google Scholar] [CrossRef]
- Wei, L.; Xiaohui, C.; Haijie, M. Research on adaptive determination of decomposition layer in wavelet threshold denoising algorithm. Comput. Simul. 2009, 26, 311–313, 336. [Google Scholar]
- Yang, J.; Lia, P.; You, Y.; Dian, X. An improved EMD method for modal identification and a combined static-dynamic method for damage detection. J. Sound Vib. 2018, 28, 242–260. [Google Scholar] [CrossRef]
- Qinwei, R.; Wei, L.; Ce, S.; Hongzhi, K. Research on EMD dense modal identification and its application in power plant buildings. J. Hydroelectr. Eng. 2017, 36, 103–113. [Google Scholar]
- Mert, A.; Akan, A. Detrended fluctuation thresholding for empirical mode decomposition based denoising. Digit. Signal Proc. 2014, 32, 48–56. [Google Scholar] [CrossRef]
- Wenping, H.; Qiong, W.; Haiying, C.; Wen, Z. Comparison of different filtering methods for denoising in detrended wave analysis. Acta Phys. Sin. 2011, 60, 029203. [Google Scholar]
- Fubin, L.; Xiangming, G. Hurst Exponent Estimation Based on EEMD and DFA. Meas. Control. Technol. 2013, 32, 98–101. [Google Scholar]
- Jijian, L.; Hunkun, L.; Jianwei, Z. Hydraulic structure vibration mode ERA recognition method based on singular entropy fixed-stage noise reduction. Chin. Sci. 2008, 38, 1398–1413. [Google Scholar]
- Wen, Y.; Guoming, L.; Wei, L. Modal analysis of nozzle concrete gravity dam based on strong earthquake record. Earthq. Eng. Eng. Vib. 2014, 34, 25–33. [Google Scholar]
- Shengkui, D.; Deqiang, Z.; Jian, L. Structural modal parameter identification based on ITD method. J. Civ. Eng. Manag. 2012, 29, 15–19. [Google Scholar]
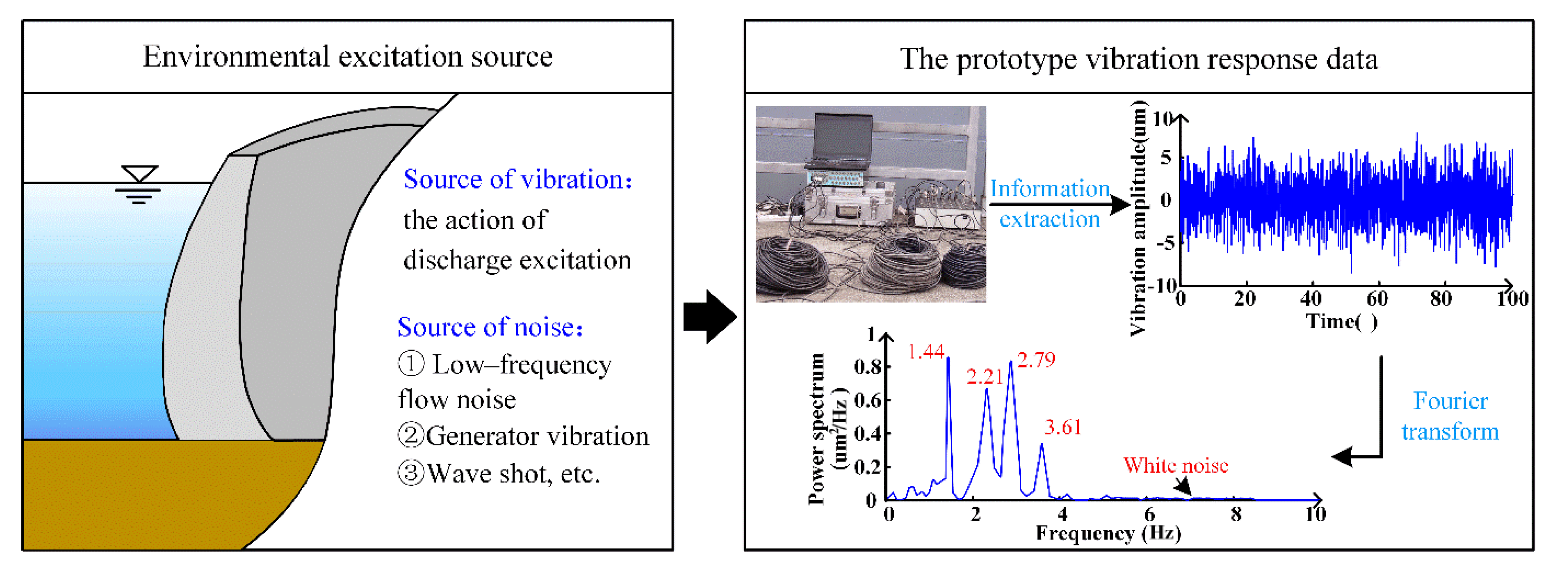









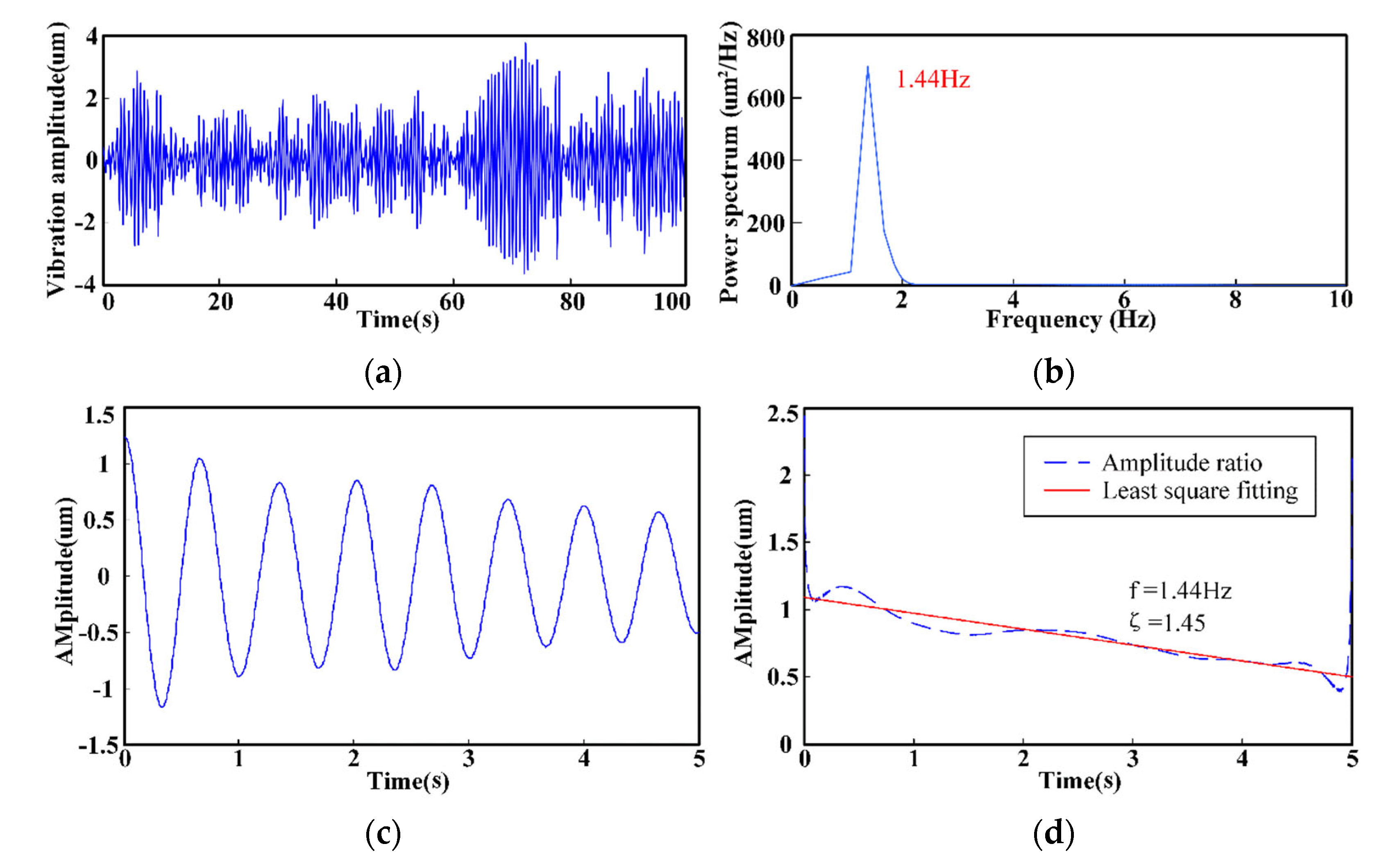
| Condition | Spillway Opening | Upstream Water Level (m) | Downstream Water Level (m) |
|---|---|---|---|
| 1 | Fourth surface spillway and first tunnel spillway | 1196.00 | 1014.36 |
| 2 | Third, fourth surface spillway and first tunnel spillway | 1196.01 | 1014.50 |
| Modal | Natural Frequency/Hz | Damping Ratio/% | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Order | B2 | B3 | B4 | B8 | B2 | B3 | B4 | B8 | |
| 1 | 1.44 | 1.44 | 1.44 | 1.43 | 1.45 | 1.79 | 1.51 | 1.69 1.91 | |
| 2 | 1.52 | 1.53 | 1.52 | 1.53 | 1.54 | 1.08 | 1.26 | 1.35 | |
| 3 | 2.21 | 2.19 | 2.19 | 2.20 | 1.45 | 1.28 | 2.24 | 1.46 | |
| 4 | 2.80 | 2.81 | 2.78 | 2.81 | 1.48 | 1.46 | 2.17 | 1.28 | |
| 5 | 3.58 | 3.60 | 3.59 | 3.61 | 1.31 | 3.47 | 4.08 | 1.79 | |
| 6 | 4.32 | 4.31 | 4.32 | 4.28 | 4.38 | 4.96 | 6.5 | 5.6 | |
| 7 | 4.90 | 4.90 | 4.92 | 4.91 | 2.18 | 1.93 | 3.67 | 2.38 | |
| 8 | 5.15 | 5.12 | 5.20 | 5.21 | 2.86 | 5.5 | 2.87 | 6.72 | |
| 9 | 7.24 | 7.28 | 7.30 | 7.26 | 7.67 | 7.16 | 8.12 | 7.47 | |
| 10 | 9.67 | 9.69 | 9.58 | 9.52 | 4.79 | 6.45 | 6.45 | 5.34 | |
| Modal Order | Method in the Study/Hz | ERA/Hz | ARX/Hz | ITD/Hz |
|---|---|---|---|---|
| 1 | 1.44 | 1.45 | 1.42 | 1.43 |
| 2 | 1.52 | 1.53 | 1.47 | 1.51 |
| 3 | 2.21 | 2.22 | 2.14 | 2.08 |
| 4 | 2.80 | 2.87 | 2.81 | 2.79 |
| 5 | 3.58 | 3.74 | 3.68 | 3.63 |
| 6 | 4.32 | 4.38 | 4.40 | 4.32 |
| 7 | 4.9 | 4.82 | 4.71 | 4.85 |
| 8 | 5.15 | 5.09 | 5.03 | / |
| 9 | 7.24 | 7.36 | 6.98 | 7.01 |
| 10 | 9.67 | 9.52 | 9.16 | / |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Y.; You, Z.; Wei, B. Working Mode Identification Method for High Arch Dam Discharge Structure Based on Improved Wavelet Threshold–EMD and RDT Algorithm. Water 2022, 14, 3735. https://doi.org/10.3390/w14223735
Guo Y, You Z, Wei B. Working Mode Identification Method for High Arch Dam Discharge Structure Based on Improved Wavelet Threshold–EMD and RDT Algorithm. Water. 2022; 14(22):3735. https://doi.org/10.3390/w14223735
Chicago/Turabian StyleGuo, Yingjia, Zongzhe You, and Bowen Wei. 2022. "Working Mode Identification Method for High Arch Dam Discharge Structure Based on Improved Wavelet Threshold–EMD and RDT Algorithm" Water 14, no. 22: 3735. https://doi.org/10.3390/w14223735








