Numerical Investigation on Influence of Number of Bubbles on Laser-Induced Microjet
Abstract
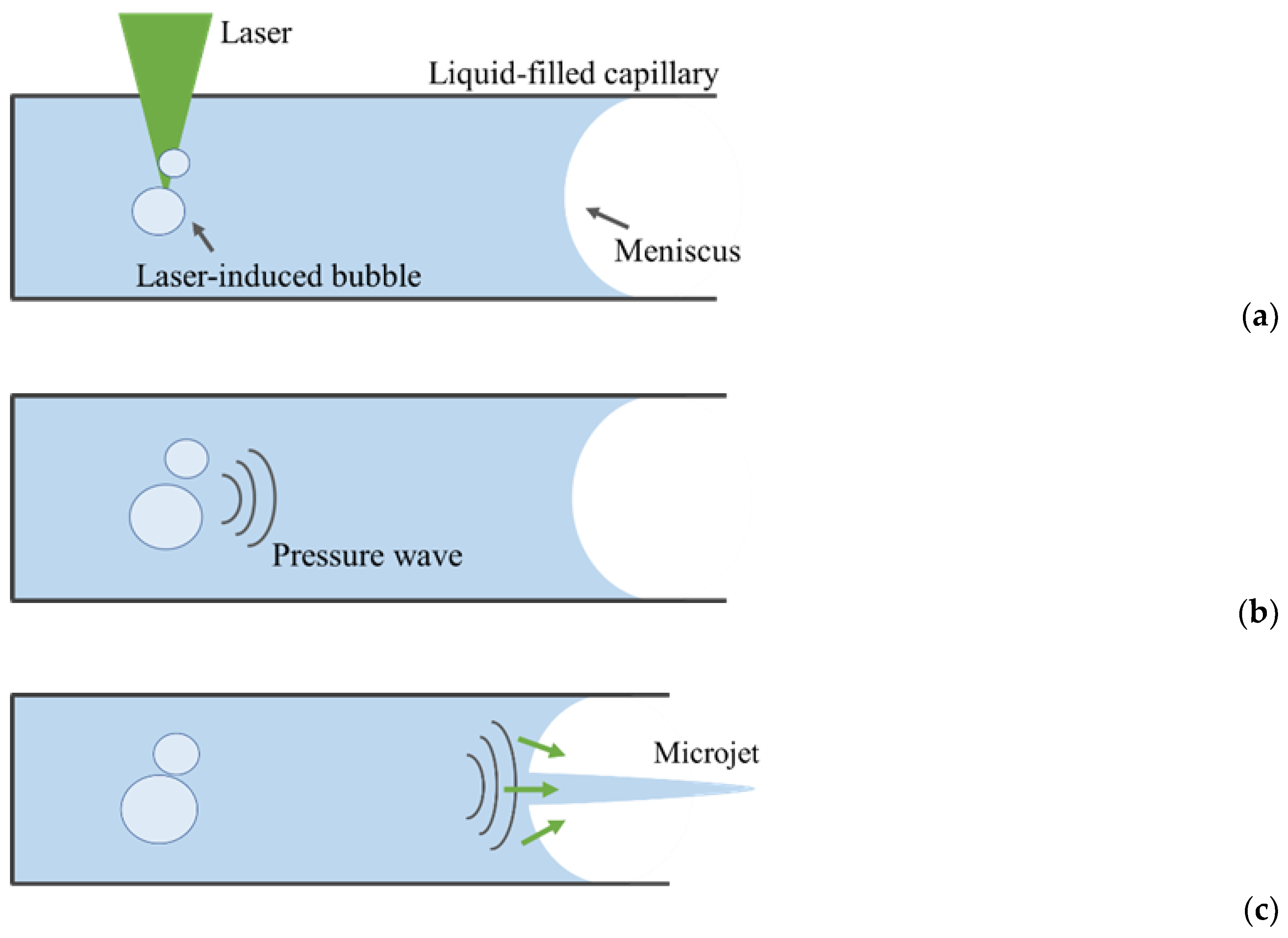
:1. Introduction
2. Computational Methods
2.1. Governing Equations
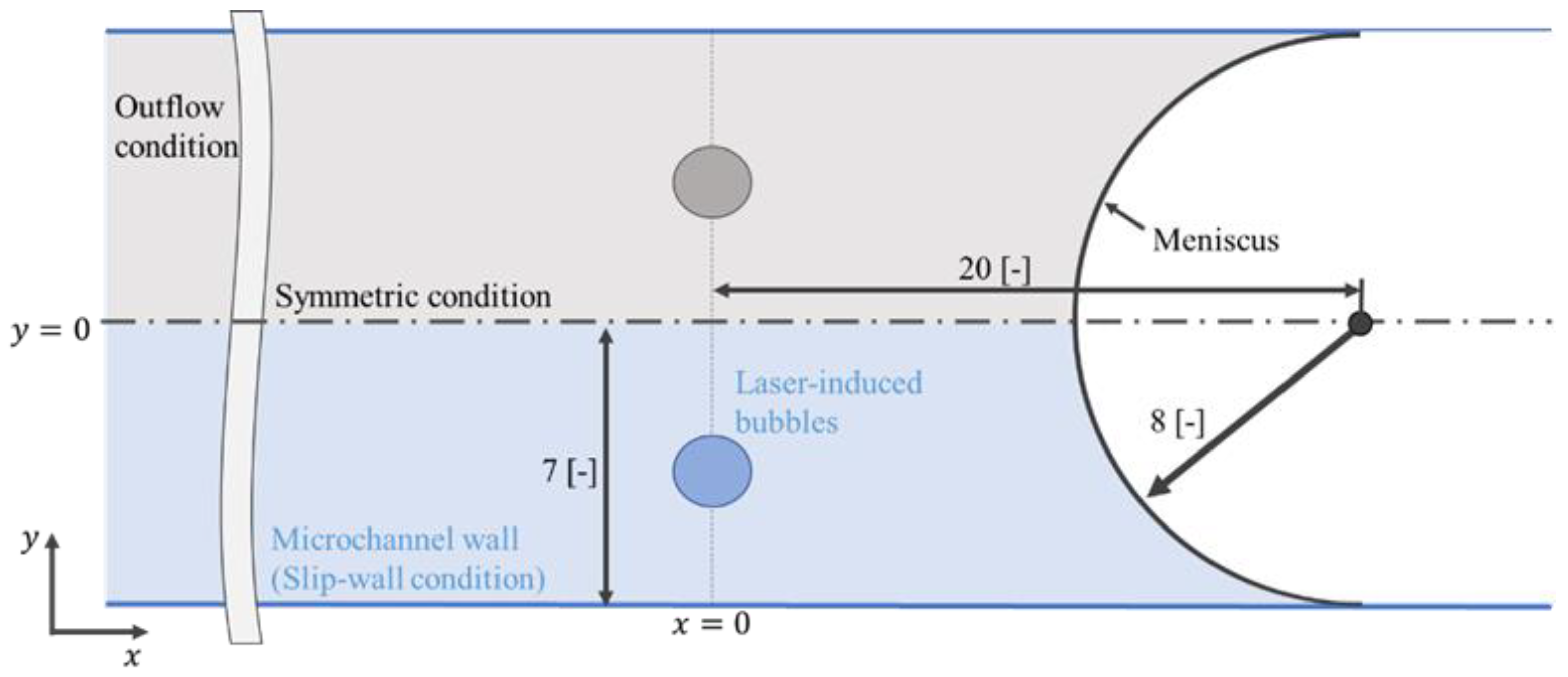
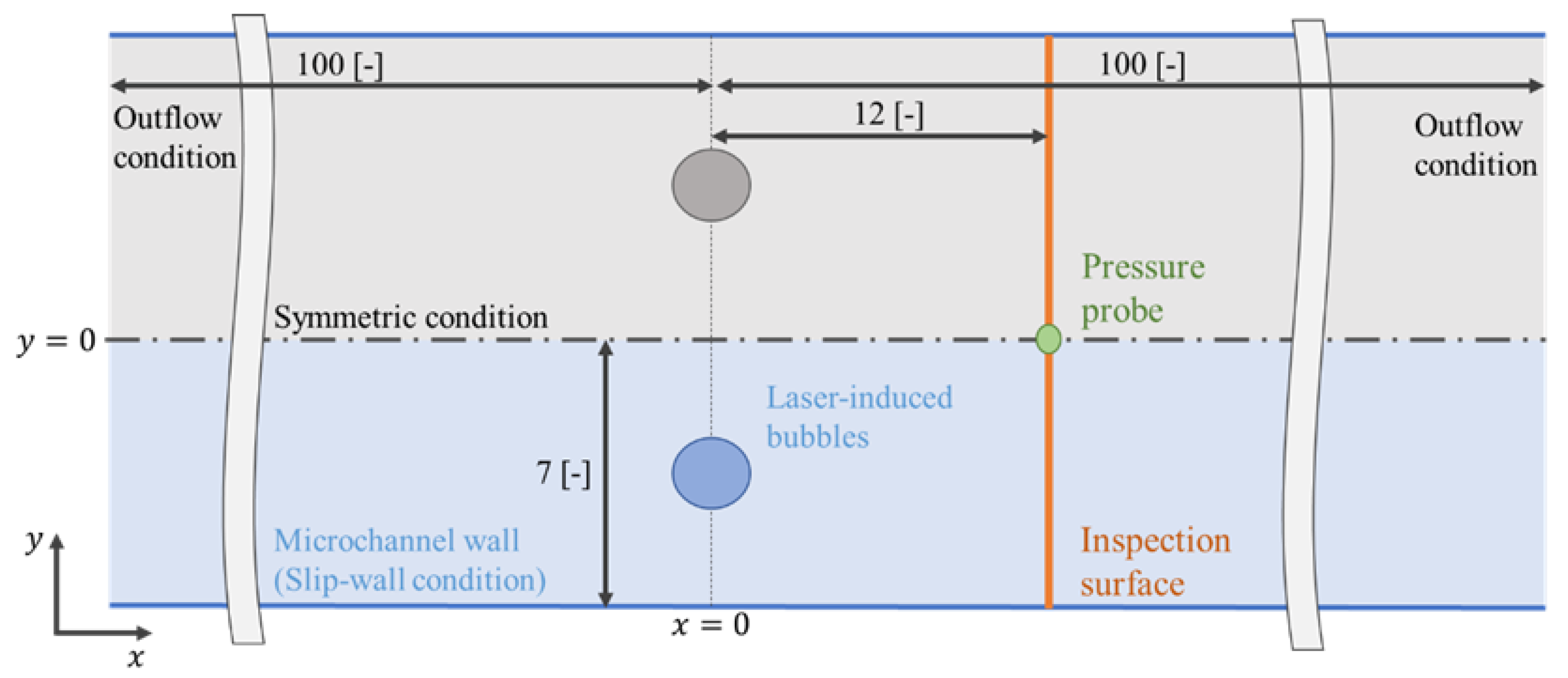
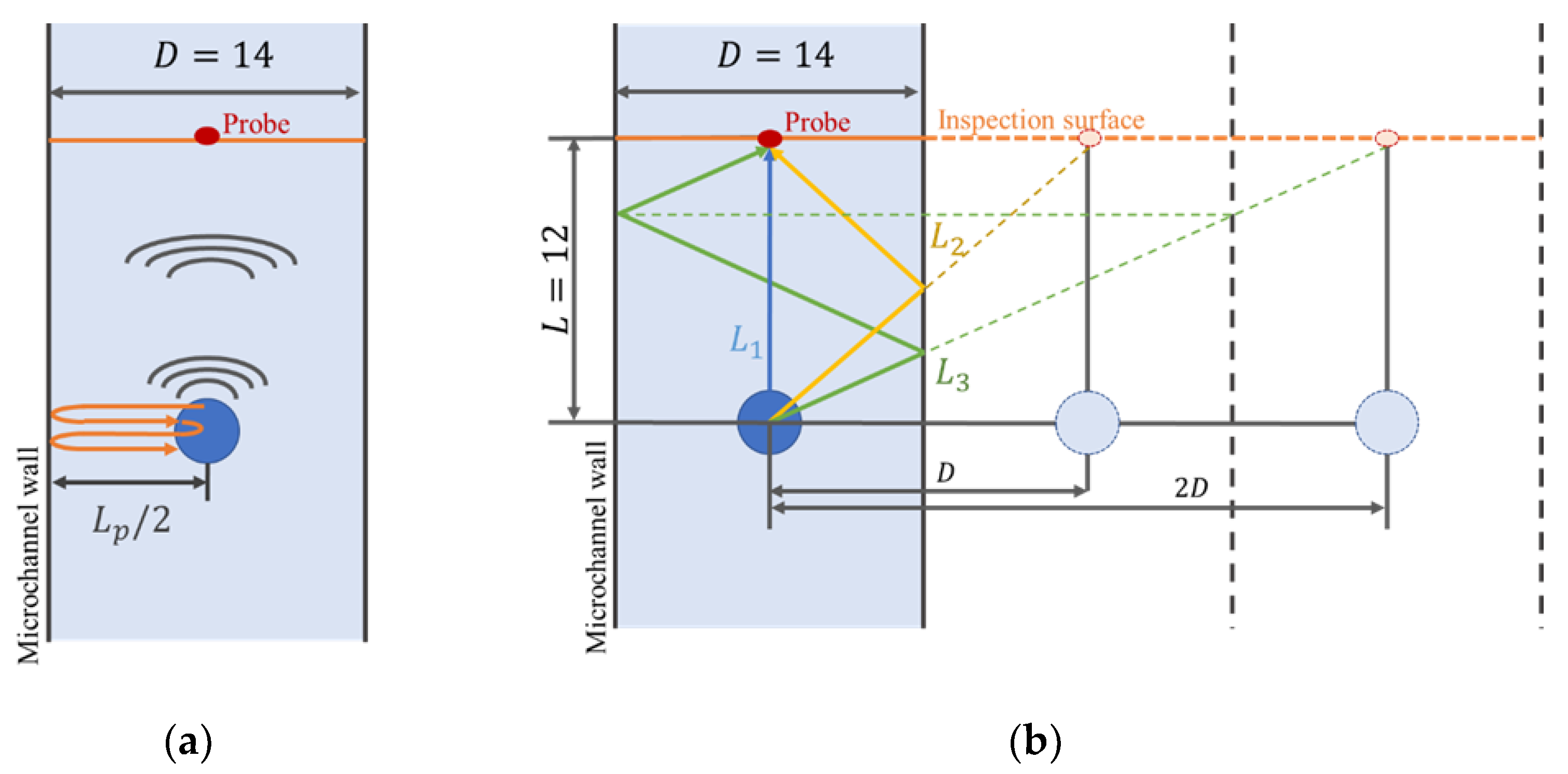
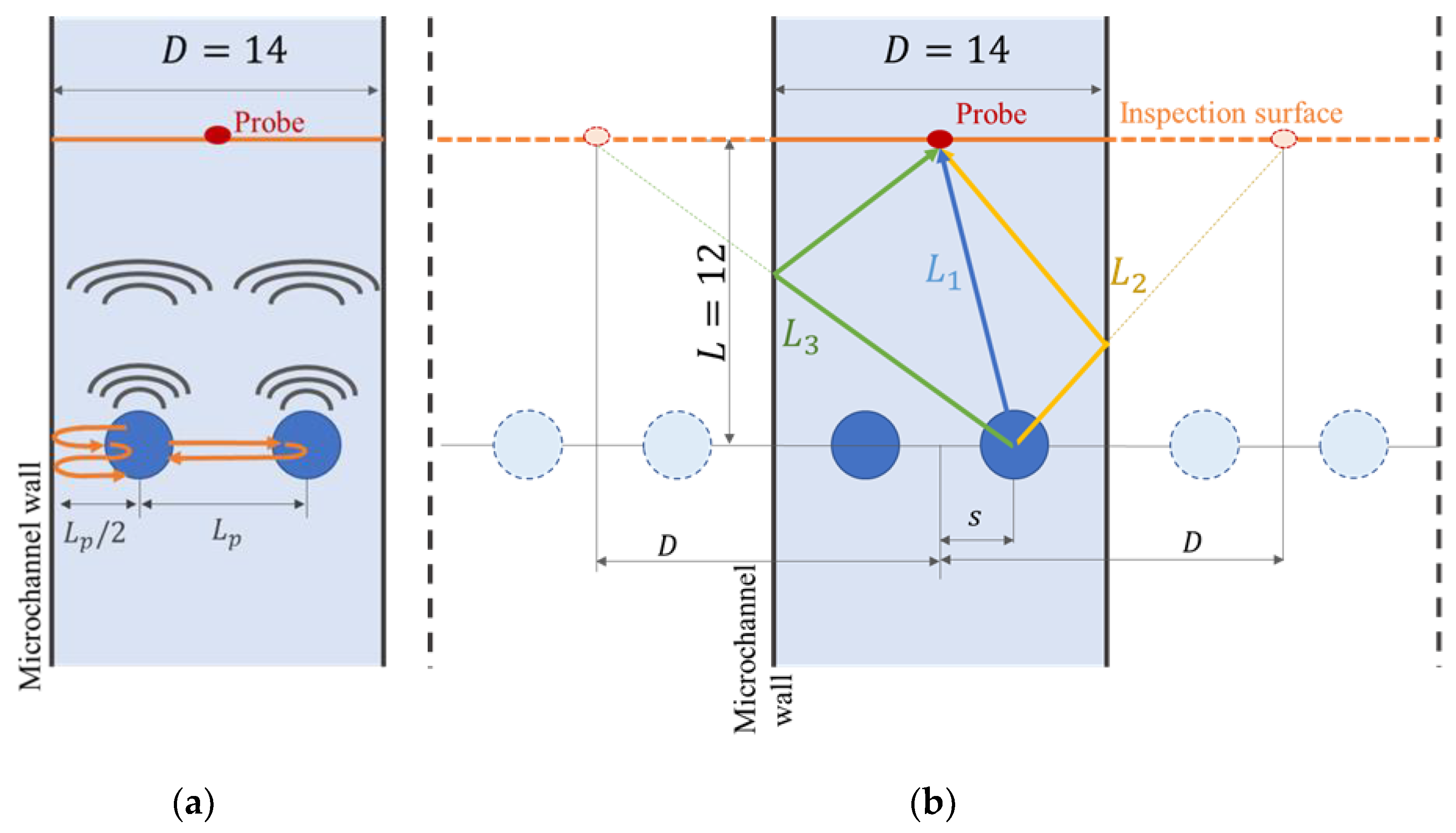
2.2. Simulation Settings and Conditions
2.3. Numerical Schemes
- THINC-MUSCL3
- MP-WENO5-JS
3. Result and Discussion
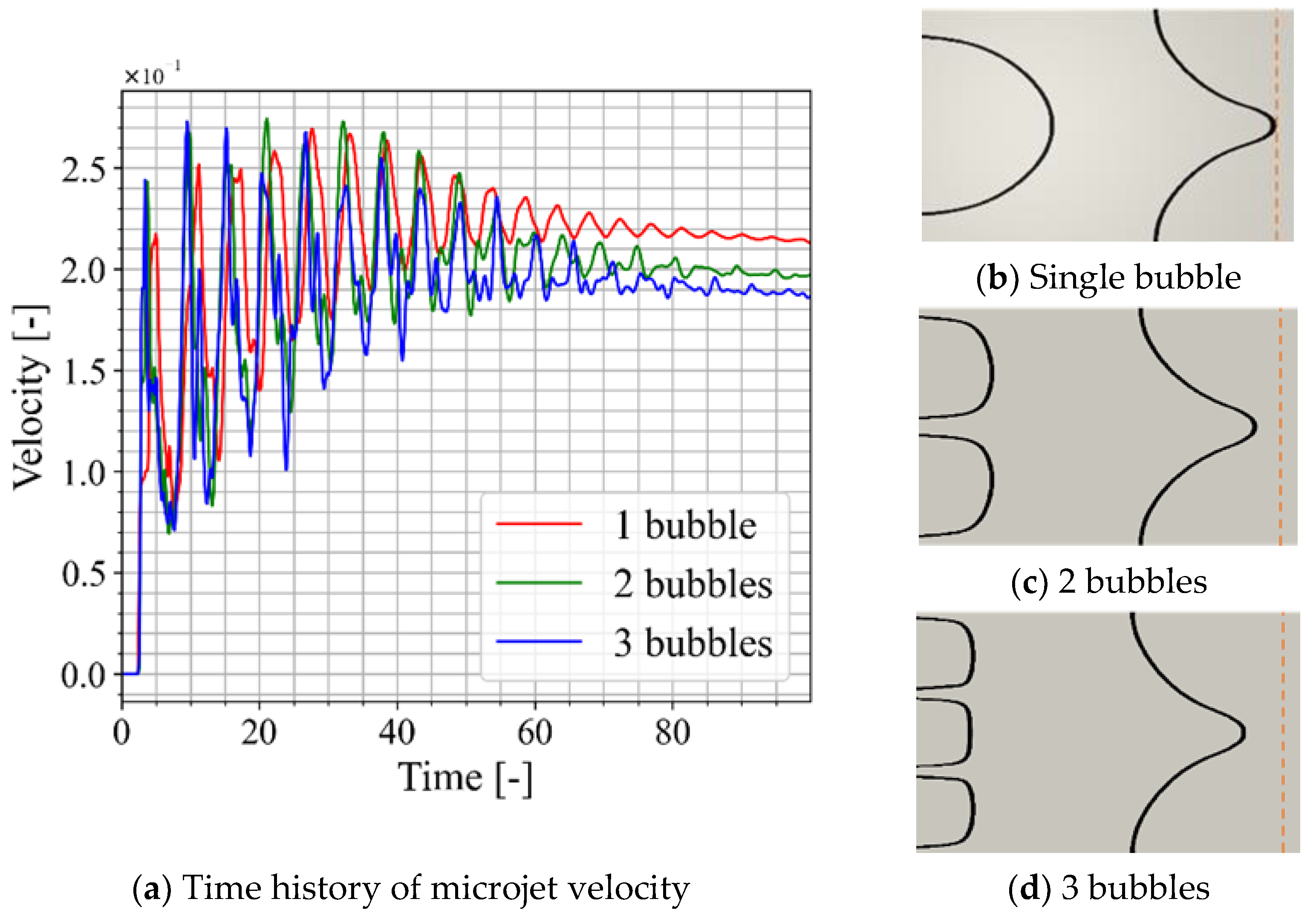
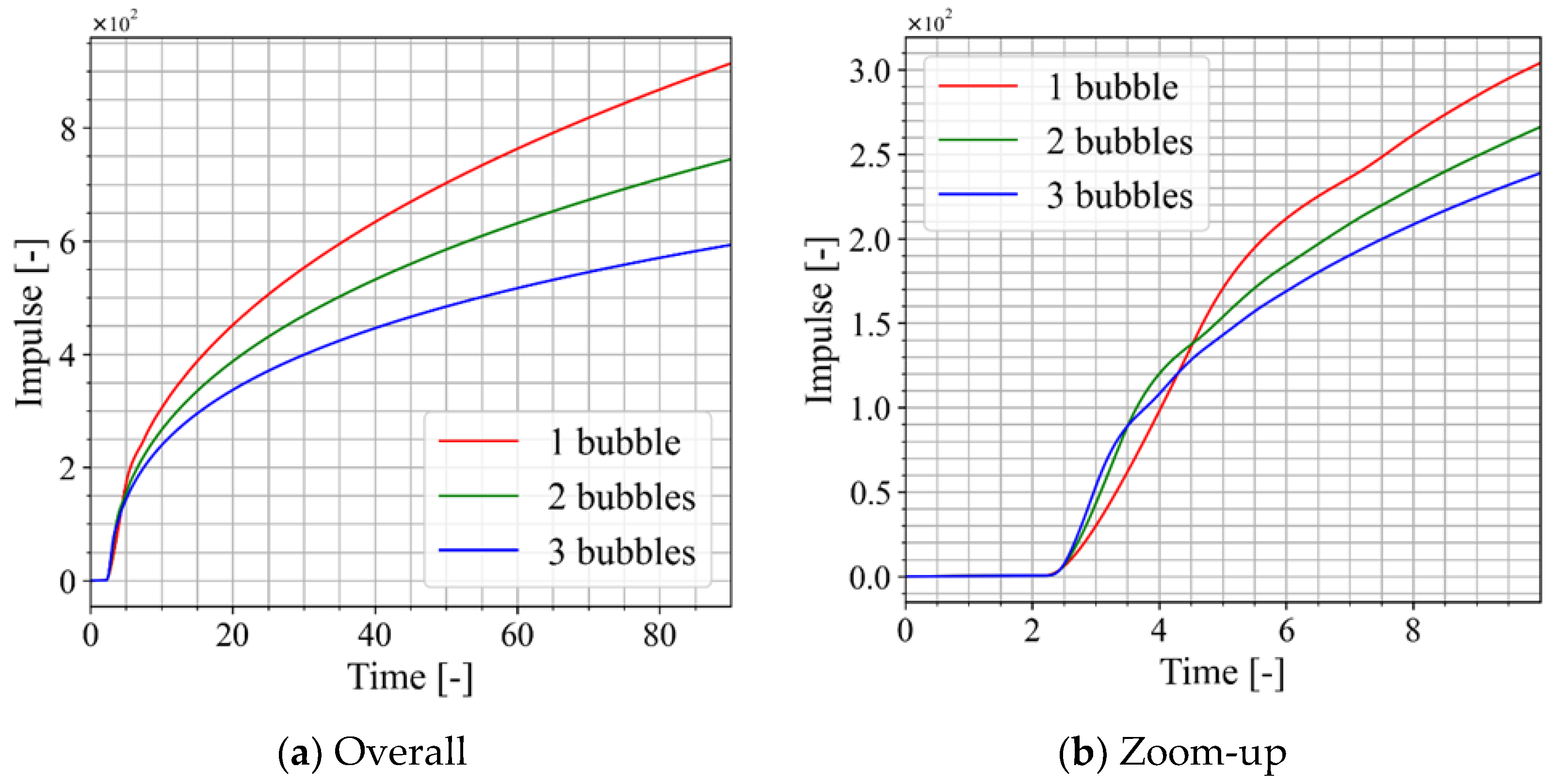
3.1. Microjet Evolution and Time History of Impulse
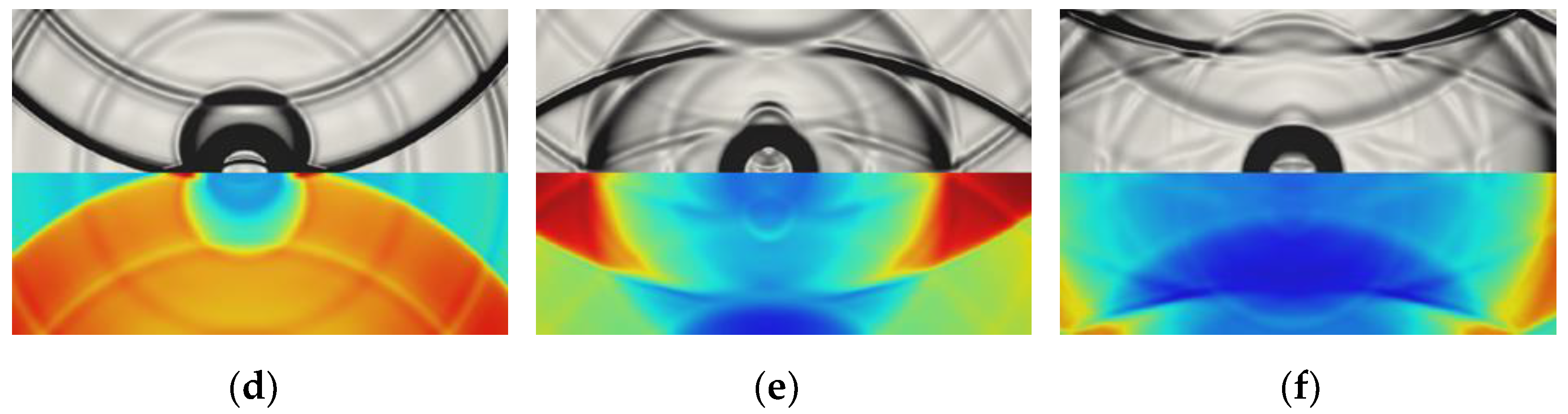
3.2. Pressure Field Evolution around a Single Bubble
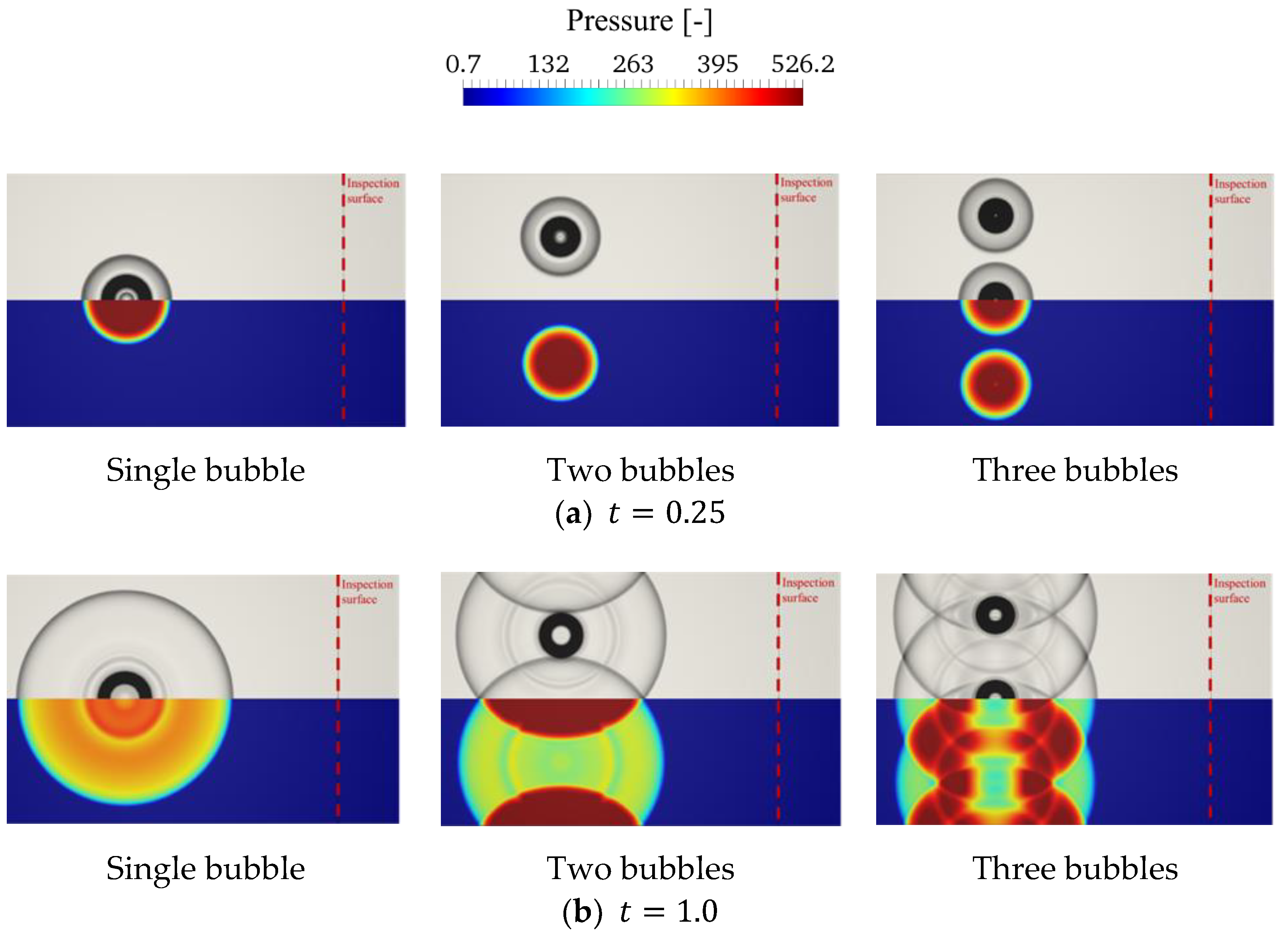
3.3. Pressure Field Evolution around Multi-Bubbles
3.4. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Solver Varidation

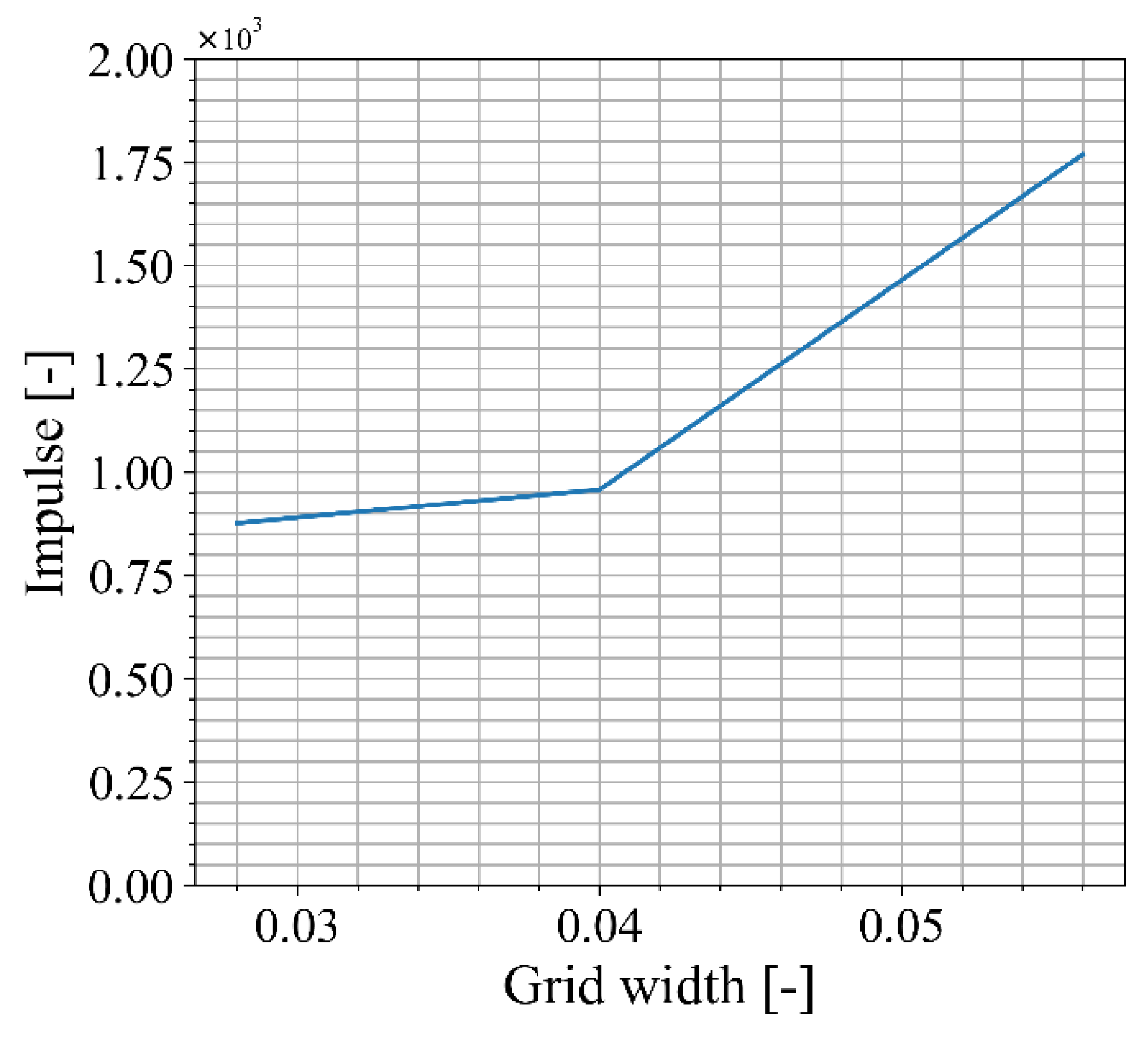
Appendix B. Grid Independence Study
References
- Tagawa, Y.; Oudalov, M.; Visser, C.W.; Peters, I.R.; Meer, D.; Sun, C.; Prosperetti, A.; Lohse, D. Highly focused supersonic microjets. Phys. Rev. X 2012, 2, 31002. [Google Scholar] [CrossRef] [Green Version]
- Antkowiak, A.; Bremond, N.; Le Dizès, S.; Villermaux, E. Short-term dynamics of a density interface following an impact. J. Fluid Mech. 2007, 577, 241–250. [Google Scholar] [CrossRef] [Green Version]
- Zeff, B.W.; Kleber, B.; Fineberg, J.; Lathrop, D.P. Singularity dynamics in curvature collapse and jet eruption on a fluid surface. Nature 2000, 403, 401–404. [Google Scholar] [CrossRef]
- Duchemin, L.; Popinet, S.; Josserand, C.; Zaleski, S. Jet formation in bubbles bursting at a free surface. Phys. Fluids 2002, 14, 3000. [Google Scholar] [CrossRef]
- Bergmann, R.; van der Meer, D.; Gekle, S.; Lohse, D. Controlled impact of a disk on a water surface: Cavity dynamics. J. Fluid Mech. 2009, 633, 381–409. [Google Scholar] [CrossRef] [Green Version]
- Tagawa, Y.; Oudalov, N.; El Ghalbzouri, A.; Sun, C.; Lohse, D. Needle-free injection into skin and soft matter with highly focused microjets. Lab Chip 2013, 13, 1357–1363. [Google Scholar] [CrossRef] [Green Version]
- Kiyama, A.; Endo, N.; Kawamoto, S.; Katsuta, C.; Oida, K.; Tanaka, A.; Tagawa, Y. Visualization of penetration of a high-speed focused microjet into gel and animal skin. J. Vis. 2019, 22, 449–457. [Google Scholar] [CrossRef] [Green Version]
- Krizek, J.; Delrot, P.; Moser, C. Repetitive regime of highly focused liquid microjets for needle-free injection. Sci. Rep. 2020, 10, 5067. [Google Scholar] [CrossRef] [Green Version]
- Miyazaki, Y.; Usawa, M.; Kawai, S.; Yee, J.; Muto, M.; Tagawa, Y. Dynamic mechanical interaction between injection liquid and human tissue simulant induced by needle-free injection of a highly focused microjet. Sci. Rep. 2021, 11, 14544. [Google Scholar] [CrossRef]
- Delrot, P.; Modestino, M.A.; Gallaire, F.; Psaltis, D.; Moser, C. Inkjet printing of viscous monodisperse microdroplets by laser-induced flow focusing. Phys. Rev. Appl. 2016, 6, 24003. [Google Scholar] [CrossRef]
- Xiong, S.; Chin, L.K.; Ando, K.; Tandiono, T.; Liu, A.Q.; Ohl, C.D. Droplet generation via a single bubble transformation in a nanofluidic channel. Lab Chip 2015, 15, 1451–1457. [Google Scholar] [CrossRef] [PubMed]
- Peter, I.R.; Tagawa, Y.; Oudalov, N.; Sun, C.; Prosperetti, A.; Lohse, D.; van der Meer, D. Highly focused supersonic microjets: Numerical simulations. J. Fluid Mech. 2013, 719, 587–605. [Google Scholar] [CrossRef] [Green Version]
- Hayasaka, K.; Kiyama, A.; Tagawa, Y. Effects of pressure impulse and peak pressure of a shock wave on microjet velocity in a microchannel. Microfluid Nanofluid 2017, 21, 116. [Google Scholar] [CrossRef] [Green Version]
- Vogel, A.; Noack, J.; Nahen, K.; Theisen, D.; Busch, S.; Parliz, U.; Hammer, D.X.; Noojin, G.D.; Rockwell, B.A.; Birngruber, R. Energy balance of optical breakdown in water at nanosecond to femtosecond time scales. Appl. Phys. B 1999, 68, 271–280. [Google Scholar] [CrossRef]
- Kodama, T.; Hamblin, M.R.; Doukas, A.G. Cytoplasmic molecular delivery with shock waves: Importance of impulse. Biophys. J. 2000, 79, 1821–1832. [Google Scholar] [CrossRef] [Green Version]
- Sankin, G.N.; Simmons, W.N.; Zhu, S.L.; Zhong, P. Shock wave interaction with laser-generated single bubbles. Phys. Rev. Lett. 2005, 95, 34501. [Google Scholar] [CrossRef]
- Klaseboor, E.; Fong, S.W.; Turangan, C.K.; Khoo, B.C.; Szeri, A.J.; Calvisi, M.L.; Sankin, G.N.; Zhong, P. Interaction of lithotripter shockwaves with single inertial cavitation bubbles. J. Fluid Mech. 2007, 593, 33–56. [Google Scholar] [CrossRef]
- Ando, K.; Liu, A.-Q.; Ohl, C.-D. Homogeneous nucleation in water in microfluidic channels. Phys. Rev. Lett. 2012, 109, 44501. [Google Scholar] [CrossRef]
- Quinto-Su, P.A.; Ando, K. Nucleating bubble clouds with a pair of laser-induced shocks and bubbles. J. Fluid Mech. 2013, 733, R3. [Google Scholar] [CrossRef]
- Hsiao, C.-T.; Choi, J.-K.; Singh, S.; Chahine, G.L.; Hay, T.A.; Ilinskii, Y.A.; Zabolotskaya, E.A.; Hamilton, M.F.; Sankin, G.; Yuan, F.; et al. Modelling single- and tandem-bubble dynamics between two parallel plates for biomedical applications. J. Fluid Mech. 2013, 716, 137–170. [Google Scholar] [CrossRef]
- Supponen, O.; Obreschkow, D.; Kobel, P.; Tinguely, M.; Dorsaz, N.; Farhat, M. Shock waves from non-spherical cavitation bubbles. Phys. Rev. Fluids 2017, 2, 93601. [Google Scholar] [CrossRef] [Green Version]
- Beig, S.A. A Computational Study of the Inertial Collapse of Gas Bubbles Near a Rigid Surface. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2018. [Google Scholar]
- Kyriazis, N.; Koukouvinis, P.; Gavaises, M. Numerical investigations on bubble-induced jetting and shock wave focusing: Application on a needle-free injection. Proc. R. Soc. A Math. Phys. Eng. Sci. 2019, 475, 20180548. [Google Scholar] [CrossRef] [PubMed]
- Kapila, A.K.; Menikoff, R.; Bdzil, J.B.; Son, S.F.; Stewart, D.S. Two-phase modeling of deflagration-to-detonation transition in granular materials: Reduced equations. Phys. Fluids 2001, 13, 3002–3024. [Google Scholar] [CrossRef]
- Allaire, G.; Clerc, S.; Kokh, S. A five-equation model for the simulation of interfaces between compressible fluids. J. Comput. Phys. 2002, 181, 577–616. [Google Scholar] [CrossRef] [Green Version]
- Shukla, R.K.; Pantano, C.; Freund, J.B. An interface capturing method for the simulation of multi-phase compressible flows. J. Comput. Phys. 2010, 229, 7411–7439. [Google Scholar] [CrossRef]
- Daramizadeh, A.; Ansari, M.R. Numerical simulation of underwater explosion near air–water free surface using a five-equation reduced model. Ocean Eng. 2015, 110, 25–35. [Google Scholar] [CrossRef]
- Rasthofer, U.; Wermelinger, F.; Hadijdoukas, P.; Koumoutsakos, P. Large Scale Simulation of Cloud Cavitation Collapse. Procedia Comput. Sci. 2017, 108, 1763–1772. [Google Scholar] [CrossRef]
- Garrick, D.P.; Hagen, W.A.; Regele, J.D. An interface capturing scheme for modeling atomization in compressible flows. J. Comput. Phys. 2017, 344, 260–280. [Google Scholar] [CrossRef]
- Yu, J.; Liu, J.; He, B.; Li, H.; Xie, T.; Pei, D. Numerical research of water jet characteristics in underwater explosion based on compressible multicomponent flows. Ocean Eng. 2021, 242, 110135. [Google Scholar] [CrossRef]
- Baer, M.R.; Nunziato, J.W. A two-phase mixture theory for the deflagration-to-detonation transition (ddt) in reactive granular materials. Int. J. Multiph. Flow 1986, 12, 861–889. [Google Scholar] [CrossRef]
- Tiwari, A.; Freund, J.B.; Pantano, C. A diffuse interface model with immiscibility preservation. J. Comput. Phys. 2013, 252, 290–309. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmidmayer, K.; Bryngelson, S.H.; Colonius, T. An assessment of multicomponent flow models and interface capturing schemes for spherical bubble dynamics. J. Comput. Phys. 2020, 402, 109080. [Google Scholar] [CrossRef] [Green Version]
- Saurel, R.; Petitpas, F.; Berry, R.A. Simple and efficient relaxation methods for interfaces separating compressible fluids, cavitating flows and shocks in multiphase mixtures. J. Comput. Phys. 2009, 228, 1678–1712. [Google Scholar] [CrossRef]
- Métayer, O.L.; Saurel, R. The Noble-Abel Stiffened-Gas equation of state. Phys. Fluids 2016, 28, 46102. [Google Scholar] [CrossRef] [Green Version]
- Saurel, R.; Métayer, O.L.; Massoni, J.; Gavrilyuk, S. Shock jump relations for multiphase mixtures with stiff mechanical relaxation. Shock Waves 2007, 16, 209–232. [Google Scholar] [CrossRef]
- Gutiérrez-Hernández, U.J.; Colle, F.D.; Ohl, C.-D.; Quinto-Su, P.A. Transient time-delay focusing of shock waves in thin liquids. J. Fluid. Mech. 2021, 910, A27. [Google Scholar] [CrossRef]
- Tian, B.; Toro, E.F.; Castro, C.E. A path-conservative method for a five-equation model of two-phase flow with an HLLC-type Riemann solver. Comput. Fluids 2011, 46, 122–132. [Google Scholar] [CrossRef]
- van Leer, B. Towards the ultimate conservative difference scheme. V. A second-order sequel to Godunov’s method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Roe, P.L. Characteristic-based schemes for the Euler equations. Annu. Rev. Fluid Mech. 1986, 18, 337–365. [Google Scholar] [CrossRef]
- Skyue, K.M.; Xiao, F. An Eulerian interface sharpening algorithm for compressible two-phase flow: The algebraic THINC approach. J. Comput. Phys. 2014, 268, 326–354. [Google Scholar]
- Jiang, G.-S.; Shu, C.-W. Efficient Implementation of Weighted ENO Schemes. J. Comput. Phys. 1996, 126, 202–228. [Google Scholar] [CrossRef]
- Balsara, D.S.; Shu, C.-W. Monotonicity Preserving Weighted Essentially Non-oscillatory Schemes with Increasingly High Order of Accuracy. J. Comput. Phys. 2000, 160, 405–452. [Google Scholar] [CrossRef] [Green Version]
- Coralic, V.; Colonius, T. Finite-volume WENO scheme for viscous compressible multicomponent flows. J. Comput. Phys. 2014, 274, 95–121. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tagawa, Y.; Yamamoto, S.; Hayasaka, K.; Kameda, M. On pressure impulse of a laser-induced underwater shock wave. J. Fluid Mech. 2016, 808, 5–18. [Google Scholar] [CrossRef] [Green Version]
- Cocchi, J.P.; Saurel, R.; Loraud, J.C. Treatment of interface problems with Godunov-type schemes. Shock Waves 1996, 5, 347–357. [Google Scholar] [CrossRef]
- Garrick, D.P.; Owkes, M.; Regele, J.D. A finite-volume HLLC-based scheme for compressible interfacial flows with surface tnsion. J. Comput. Phys. 2007, 339, 46–67. [Google Scholar] [CrossRef]






| Number of Bubbles | 1 | 2 | 3 |
|---|---|---|---|
| Positions [-] |
| Times [-] | ||||
|---|---|---|---|---|
| Simulation Results (Figure 4) | 2.9 | 2.6 | 3.7 | 6.2 |
| Results of Equations (26) and (27) | 2.9 | 2.5 | 3.9 | 6.4 |
| Times [-] | ||||
|---|---|---|---|---|
| Simulation Results (Figure 4) | 1.4 | 2.6 | 3.2 | 4.3 |
| Results of Equation (26) and Equation (27) | 1.5 | 2.6 | 3.3 | 4.5 |
| Times [-] | ||||
|---|---|---|---|---|
| Simulation Results (Figure 4) | 0.9 | 2.4 | 2.6 | 3.0 |
| Results of Equation (26) and Equation (27) | 1.0 | 2.5 | 2.6 | 3.1 |
| Number of Bubbles | 1 | ||
|---|---|---|---|
| Maximum Pressure [-] | 2.9 | 2.6 | 3.7 |
| Time at the Maximum Pressure [-] | 2.9 | 2.5 | 3.9 |
| Number of Bubbles | 1 | 2 | 3 |
|---|---|---|---|
| Time [-] | 2.5 | 1.0 | 0.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ishikawa, T.; Nishida, H.; Tagawa, Y. Numerical Investigation on Influence of Number of Bubbles on Laser-Induced Microjet. Water 2022, 14, 3707. https://doi.org/10.3390/w14223707
Ishikawa T, Nishida H, Tagawa Y. Numerical Investigation on Influence of Number of Bubbles on Laser-Induced Microjet. Water. 2022; 14(22):3707. https://doi.org/10.3390/w14223707
Chicago/Turabian StyleIshikawa, Tatsumasa, Hiroyuki Nishida, and Yoshiyuki Tagawa. 2022. "Numerical Investigation on Influence of Number of Bubbles on Laser-Induced Microjet" Water 14, no. 22: 3707. https://doi.org/10.3390/w14223707






