Application of Particle Trace Morphology and Sensitivity Analysis in Delineation of Drinking Water Protection Zone in the Luan River, North China
Abstract
:1. Introduction
2. Materials and Methods
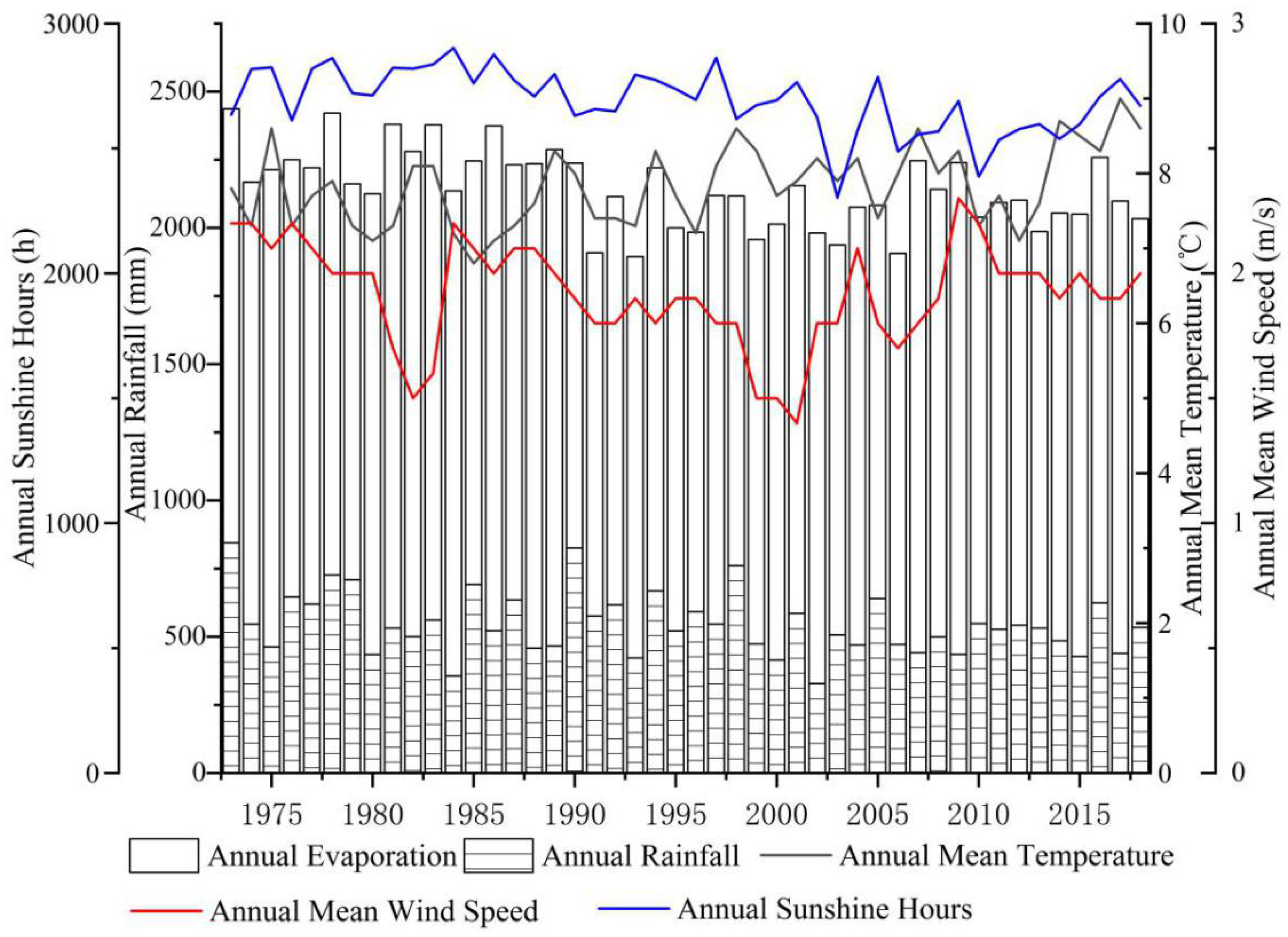
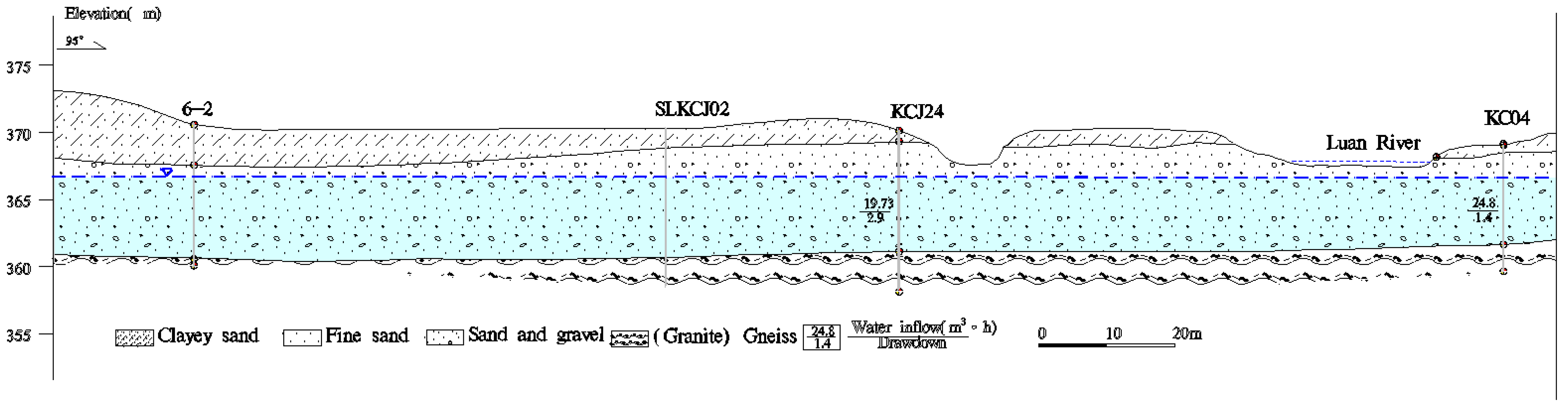
2.1. Geography and Hydrogeology of the Study Area
2.2. Methodology
2.2.1. Data Sources
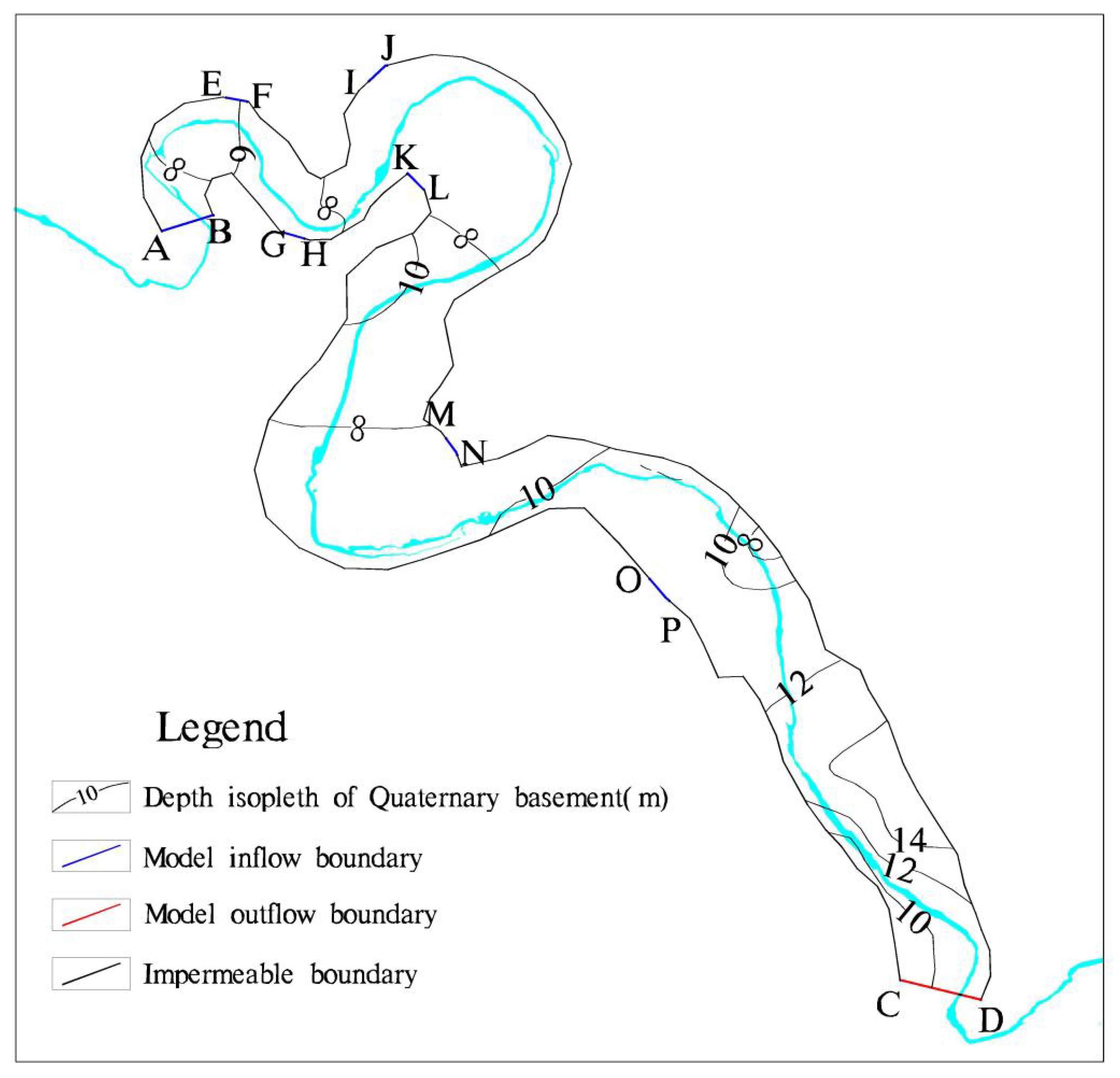
2.2.2. Hydrogeological Conceptual Model
2.2.3. The Governing Groundwater Flow
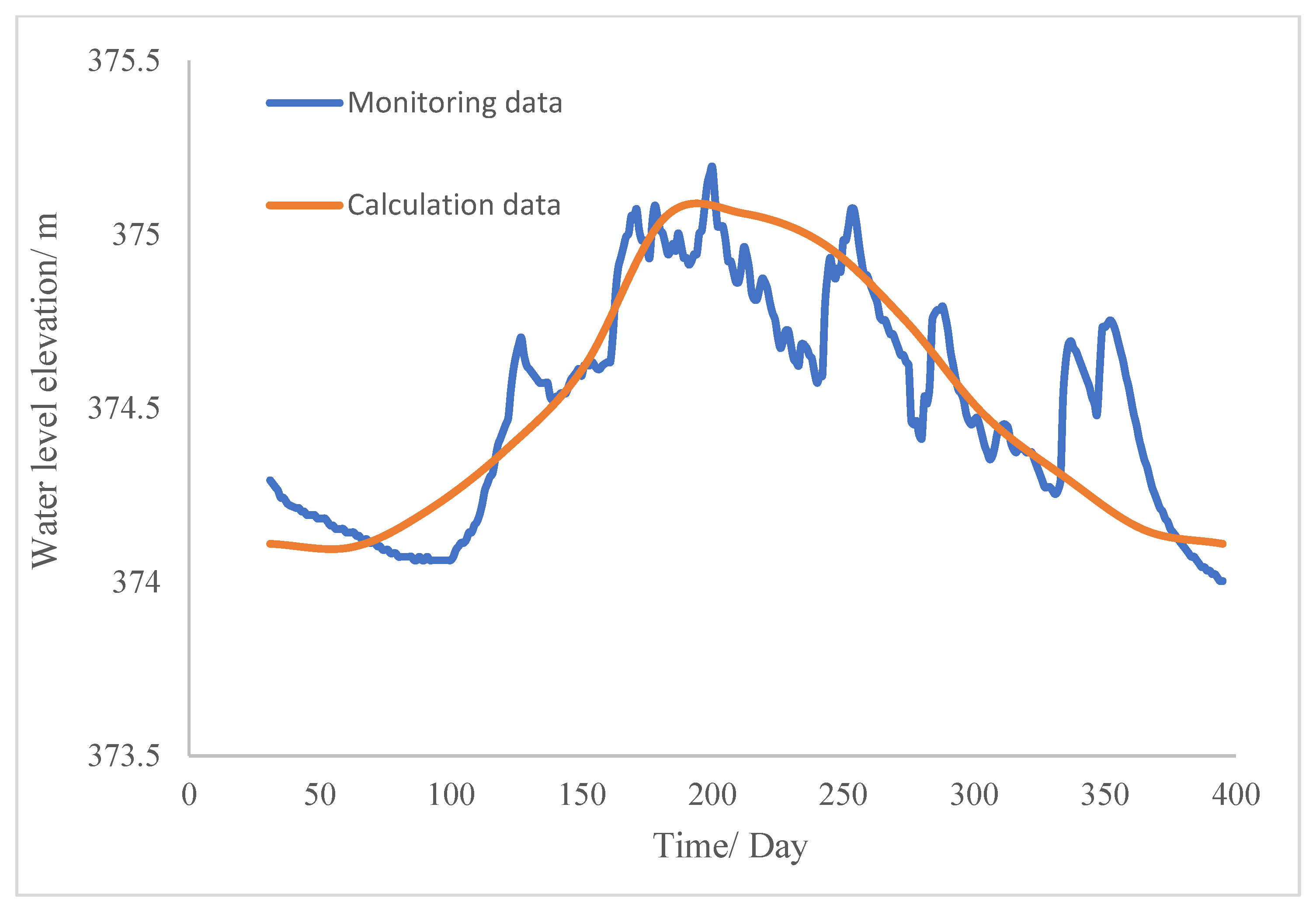
2.2.4. Model Input
2.2.5. Model Output
2.2.6. Demarcation of Groundwater Protection Zones
2.2.7. Sensitivity Analysis
3. Results and Discussion
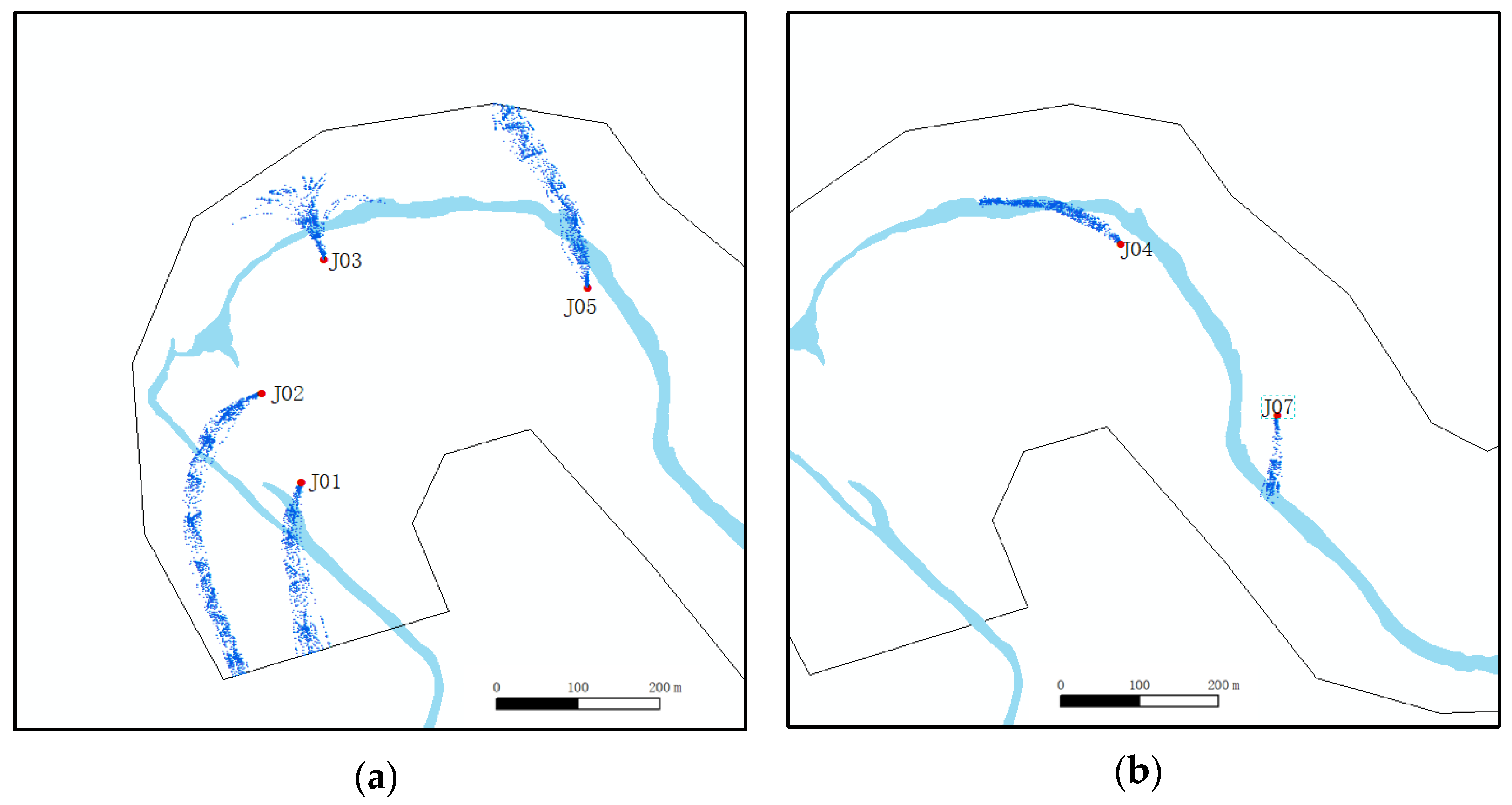
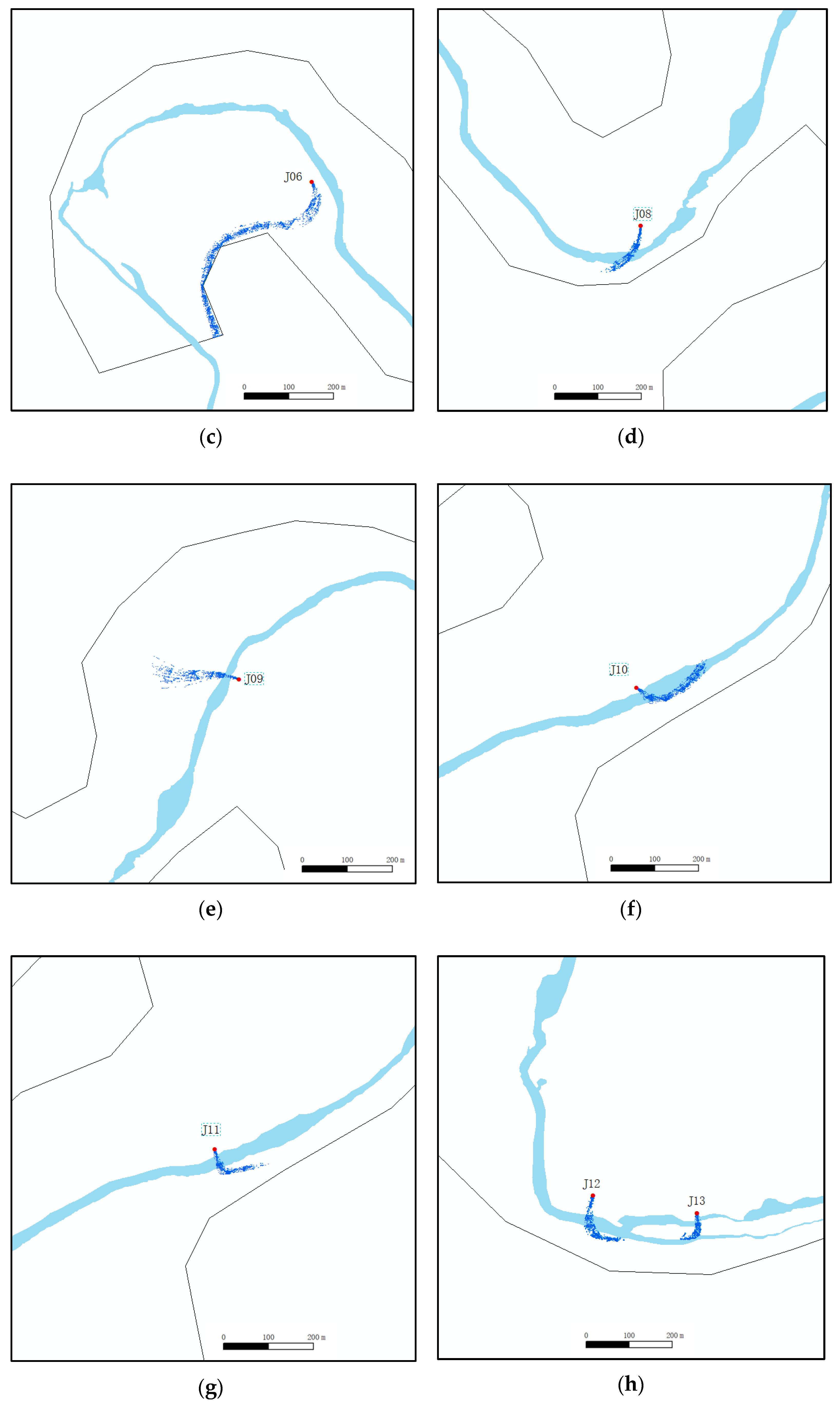
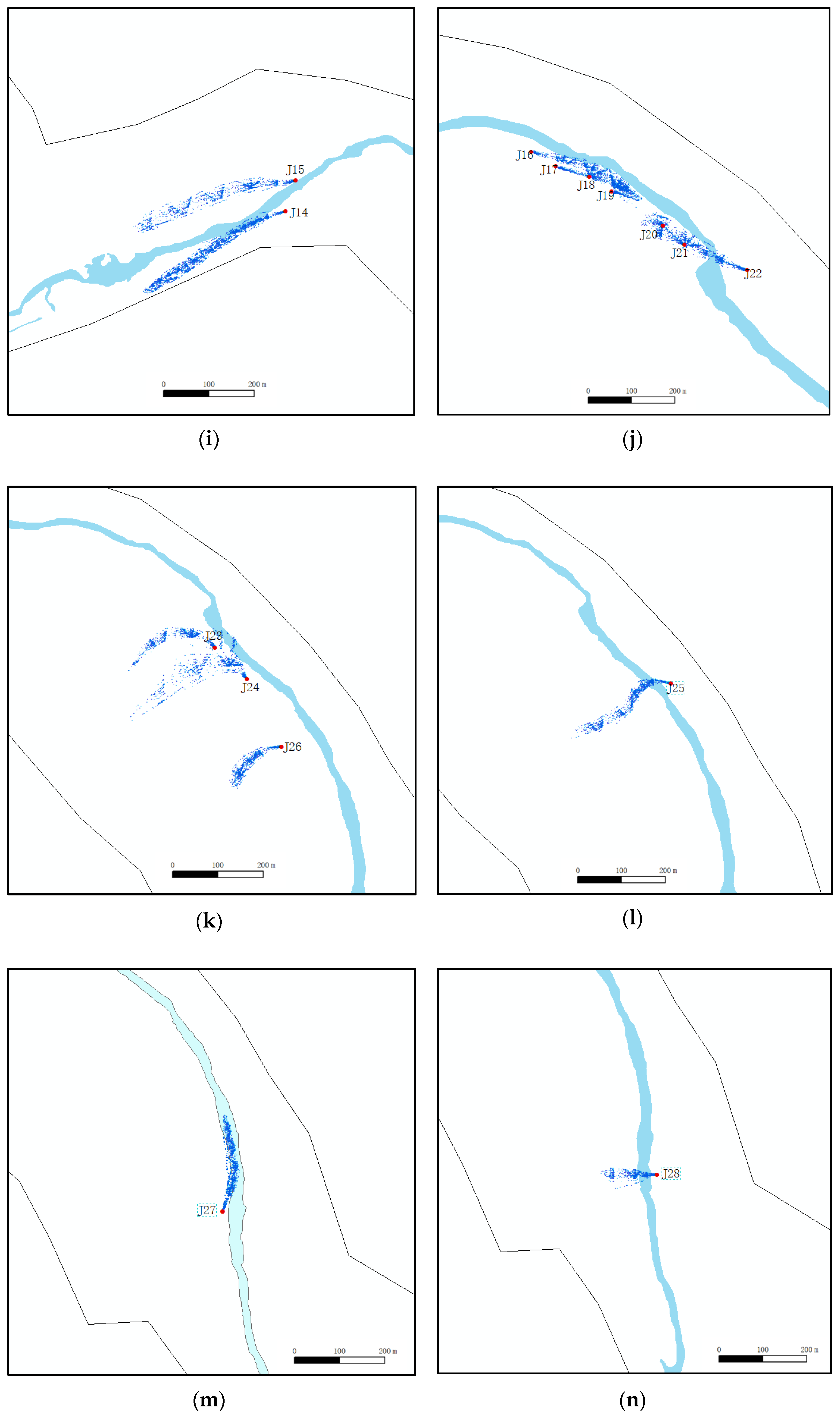
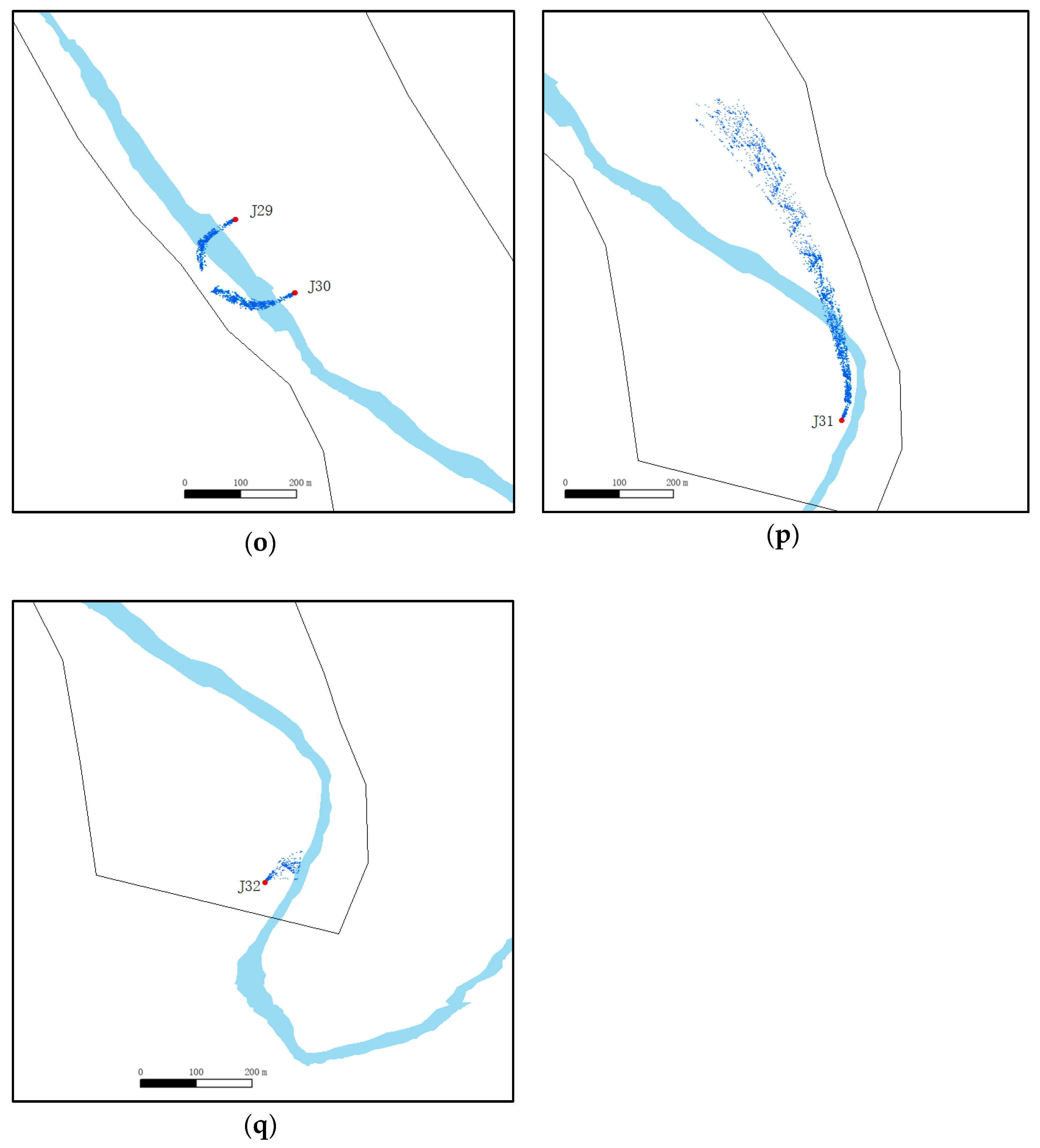
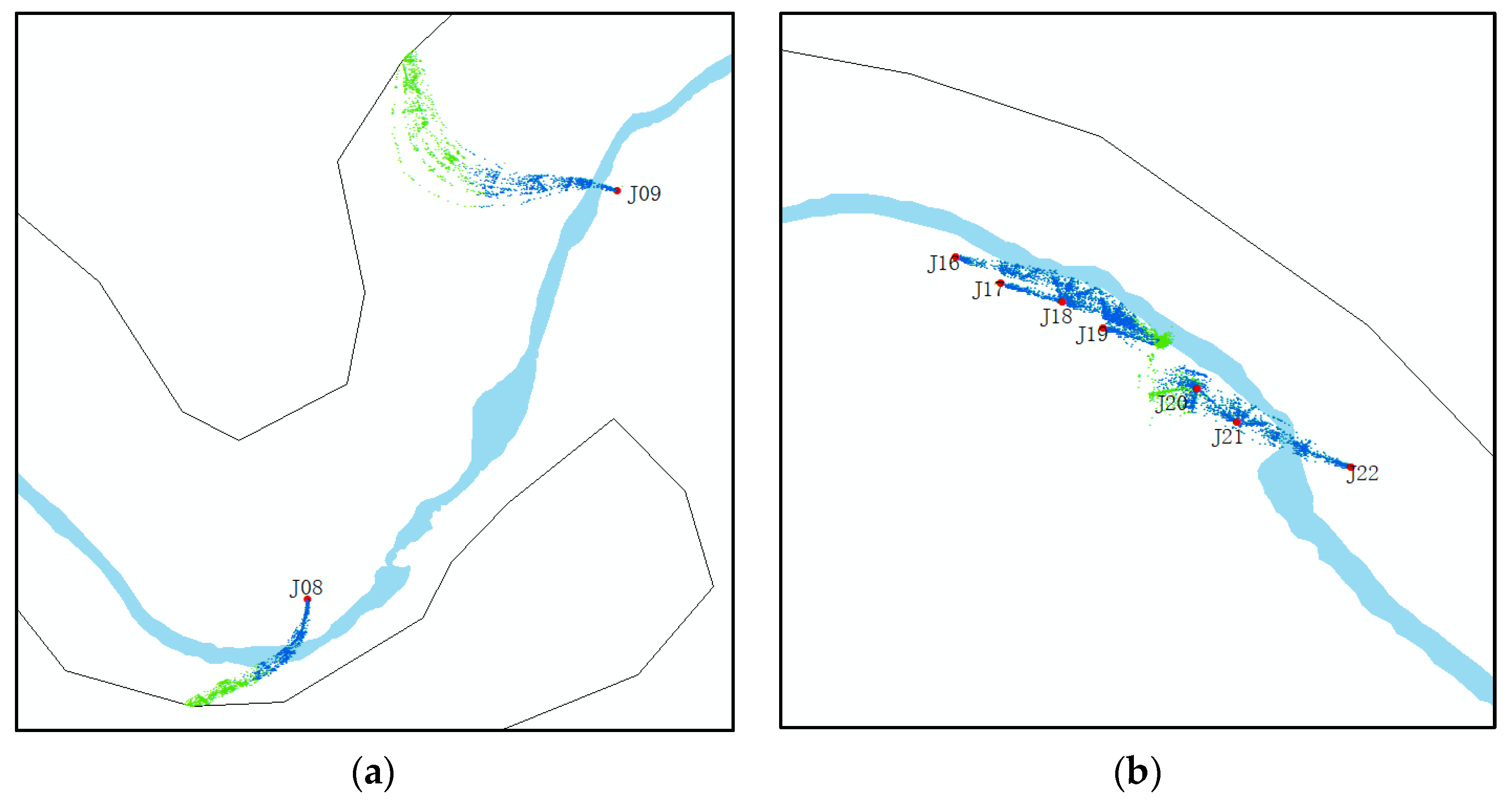
3.1. Particle Trace Characteristics
3.2. Protection Area Division and Sensitivity Analysis
3.2.1. Groundwater Protection Zones
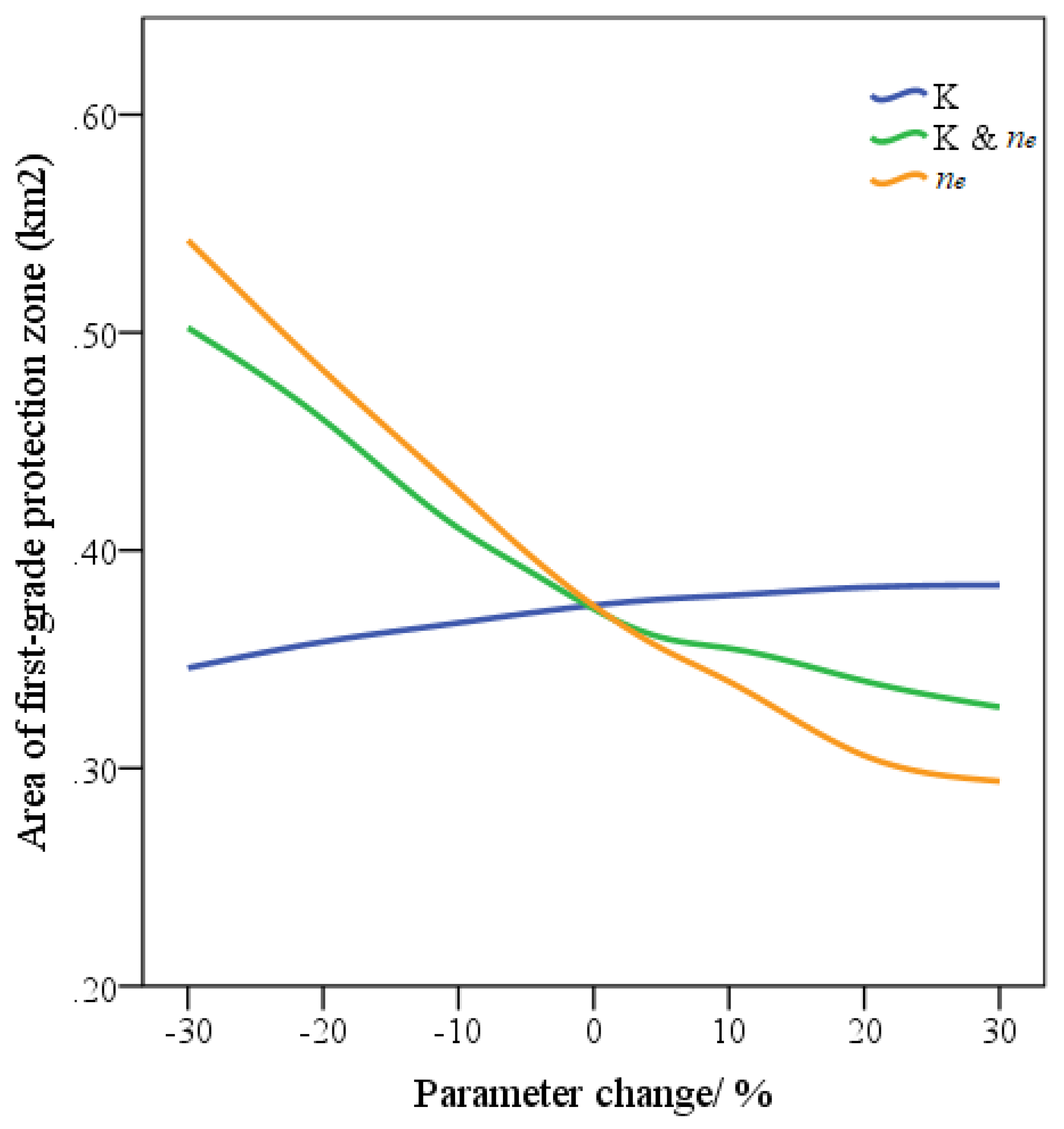
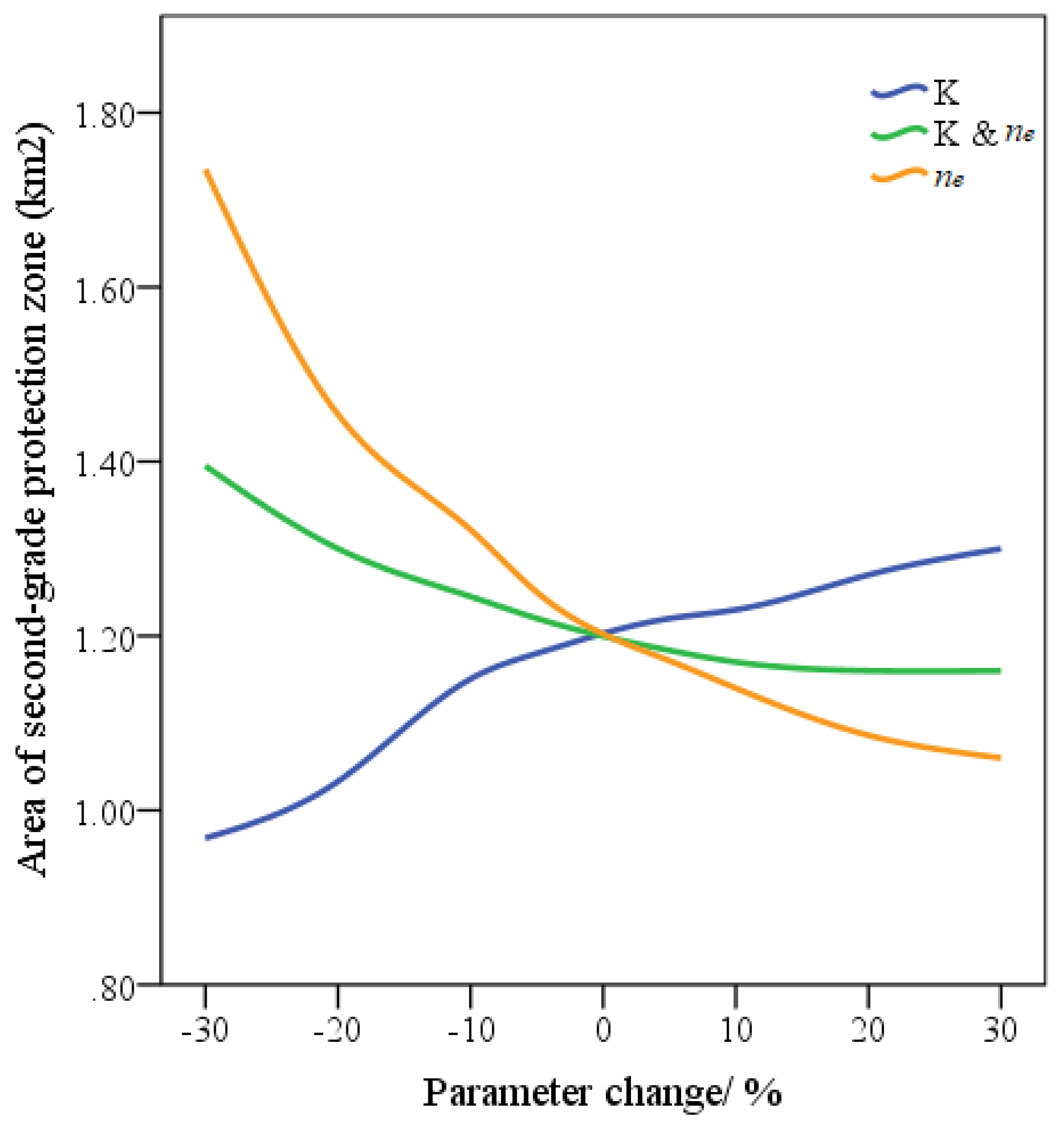
3.2.2. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, X.; Wang, W.; Zhang, C. An analysis of the exploitation scheme and groundwater resources of a well field at the riverside based on the Combination of Analytical and numerical Method. China Rural. Water Hydropower 2021, 2, 95–101. [Google Scholar]
- Wen, X.; Cheng, Y.; Zhang, J.; Hua, D. Ecological function zoning and protection of groundwater in Asia. J. Groundw. Sci. Eng. 2021, 9, 359–368. [Google Scholar]
- Zhu, Y.; Zhai, Y.; Teng, Y.; Wang, G.; Du, Q.; Wang, J.; Yang, G. Water supply safety of riverbank filtration wells under the impact of surface water-groundwater interaction: Evidence from long-term field pumping tests. Sci. Total Environ. 2020, 711, 135141. [Google Scholar] [CrossRef] [PubMed]
- Ray, C. Worldwide potential of riverbank filtration. Clean Technol. Environ. Policy 2008, 10, 223–225. [Google Scholar] [CrossRef]
- Liu, P. Uncertainty on Numerical Simulation of Groundwater Flow in the Riverside Well Field. J. Jilin Univ. Earth Sci. Ed. 2008, 106, 751–752. [Google Scholar]
- Zhou, Y.; Parvez, S.; Nico, M. Analysis of travel time; sources of water and well protection zones with groundwater models. J. Groundw. Sci. Eng. 2015, 3, 363–374. [Google Scholar]
- Expósito, J.L.; Esteller, M.V.; Paredes, J.; Rico, C.; Franco, R. Groundwater protection using vulnerability maps and Wellhead protection area (WHPA): A Case Study in Mexico. Water Resour. Manag. 2010, 24, 4219–4236. [Google Scholar] [CrossRef] [Green Version]
- Li, J. Establishment and Protection of Drinking Water Source Protection Zone in Germany. Prog. Geogr. 1988, 17, 88–97. [Google Scholar]
- Jiang, G.; Teng, M. Partitioning Method of The Groundwater Wellhead Protection Zone. Saf. Environ. Eng. 2016, 23, 36–39. [Google Scholar]
- EPA440/5-93-001; Guidelines for Delineation of Wellhead Protection Areas. US Environmental Protection Agency: Washington, DC, USA, 1993.
- Fifth Session of the Standing Committee of the Sixth National People’s Congress of the People’s Republic of China. In Water Pollution Prevention and Control Law of the People’s Republic of China; Law Press: Beijing, China, 1984.
- Dušan, P.; Dragoljub, B.; Bojan, H.; Dragan, P. Numerical modeling and simulation of the effectiveness of groundwater source protection management plans: Riverbank filtration case study in Serbia. Water 2022, 14, 1993. [Google Scholar]
- Zeferino, J.; Paiva, M.; Carvalho, M.D.R.; Carvalho, J.M.; Almeida, C. Long Term Effectiveness of Wellhead protective Areas. Water 2022, 14, 1063. [Google Scholar] [CrossRef]
- Amin, M.; Mohammad, N.; Mahdi, L.; Tafreshi, G.M. Determination of the travel time and path of pollution in Iranshahr aquifer by particle-tracking model. SN Appl. Sci. 2019, 1, 1616. [Google Scholar]
- Staboultzidis, A.; Dokou, Z.; Karatzas, G. Capture Zone Delineation and Protection Area Mapping in the Aquifer of Agia; Crete; Greece. Environ. Process. 2017, 4, 95–112. [Google Scholar] [CrossRef]
- Gurwin, J. Integration of numerical models and geoinformatic techniques in the delimitation of a protection zone for the Study on the characteristics of aquifer system in China. Geologos 2015, 21, 169–177. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Su, X.; Meng, X.; Du, S.; Meng, J. Global Sensitivity Analysis of Groundwater Flow Numerical Simulation Parameters Based on the Uniform Design. China Rural. Water Hydropower 2014, 8, 92–97. [Google Scholar]
- Tomer, T.; Katyal, D.; Joshi, V. Sensitivity analysis of groundwater vulnerability using DRASTIC method: A case study of National Capital Territory; Delhi; India-ScienceDirect. Groundw. Sustain. Dev. 2019, 9, 100271. [Google Scholar] [CrossRef]
- Khonok, A.; Tabrizi, M.; Babazadeh, H. Sensitivity analysis of water quality parameters related to flow changes in regulated rivers. Int. J. Environ. Sci. Technol. 2021, 7, 3001–3014. [Google Scholar] [CrossRef]
- Mckay, M.; Beckman, R.; Conover, W. A comparison of three methods for selecting values of input variables in the analysis of output from a Computer Code. J. Comput. Sci. Technol. 1999, 21, 239–245. [Google Scholar]
- Dennis, D. The Investigation of Groundwater Contamination in Wicomico County’s Morris Mill Community. J. Environ. Health 2016, 78, 16–25. [Google Scholar]
- Uys, L.; Hofmeyr, J.; Rohwer, J. Coupling Kinetic models and Advection-Diffusion equations. 2. Sensitivity analysis of an advection-diffusion-reaction model. J. Silico Plants 2021, 3, diab014. [Google Scholar] [CrossRef]
- Karunanidhi, D.; Aravinthasamy, P.; Subramani, T.; Kumar, D.; Setia, R. Investigation of health risks related with multipath entry of groundwater nitrate using Sobol sensitivity indicators in an urban-industrial sector of south India. Environ. Res. 2021, 200, 111726–111738. [Google Scholar] [CrossRef] [PubMed]
- Saravanan, R.; Balamurugan, R.; Karthikeyan, M.; Rajkumar, R.; Anuthaman, N.; Gopalakrishnan, A.N. Groundwater modeling and demarcation of groundwater protection zones for Tirupur Basin—A case study. J. Hydro-Environ. Res. 2011, 5, 197–212. [Google Scholar] [CrossRef]
- Li, X. Study on Wellhead Protection Area along the Yellow River in Zhengzhou by Numerical Simulation Method. Master’s Thesis, China University of Geosciences, Beijing, China, 2014. [Google Scholar]
- Ministry of Environmental Protection of the People’s Republic of China. Technical Guideline for Delineating Source Water Protection Areas: HJ338-2018; China Environmental Science Press: Beijing, China, 2018.
- Morris, M. Factorial sampling plans for preliminary computational experiments. Technometrics 1991, 33, 161–174. [Google Scholar] [CrossRef]
- Jin, M.; Tian, Y.; Michele, L.; Yu, J.; Zheng, C.-M. Global sensitivity analysis of LID facility model parameters based on Morris; Sobol and EFAST. China Rural Water Hydropower 2022, 6, 104–110. [Google Scholar]
- Zhang, H.; Wang, Z.; Wei, Q. Sensitivity analysis of particle tracking trace length and division of groundwater source protection area—An example of Ganhezi Well Field. South-North Water Transf. Water Sci. Technol. 2020, 18, 62–69. [Google Scholar]






| Equilibrium Terms | Budget (104 m3) | |
|---|---|---|
| Recharge items | Upstream lateral recharge | 98.5 |
| River recharge | 820 | |
| Irrigation + Precipitation—Evaporation | 26 | |
| Gully recharge | 145 | |
| Discharge items | River discharge | 186 |
| Artificial exploitation | 183 | |
| Downstream lateral discharge | 610 | |
| Equalization difference | 110.5 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Li, J.; Wang, W.; Cheng, Z. Application of Particle Trace Morphology and Sensitivity Analysis in Delineation of Drinking Water Protection Zone in the Luan River, North China. Water 2022, 14, 3702. https://doi.org/10.3390/w14223702
Li X, Li J, Wang W, Cheng Z. Application of Particle Trace Morphology and Sensitivity Analysis in Delineation of Drinking Water Protection Zone in the Luan River, North China. Water. 2022; 14(22):3702. https://doi.org/10.3390/w14223702
Chicago/Turabian StyleLi, Xiaoyuan, Jianxiu Li, Wenzhong Wang, and Zhongshuang Cheng. 2022. "Application of Particle Trace Morphology and Sensitivity Analysis in Delineation of Drinking Water Protection Zone in the Luan River, North China" Water 14, no. 22: 3702. https://doi.org/10.3390/w14223702





