Hydraulic Stimulation of Geothermal Reservoirs: Numerical Simulation of Induced Seismicity and Thermal Decline
Abstract
:1. Introduction
2. Materials and Methods
2.1. Thermo-Hydro-Mechanical 3D Model of Fault Reactivation
2.2. Flow and Heat Transport along Faults
2.3. Frictional Strength of Faults
2.4. Model Description and Parameters
3. Results
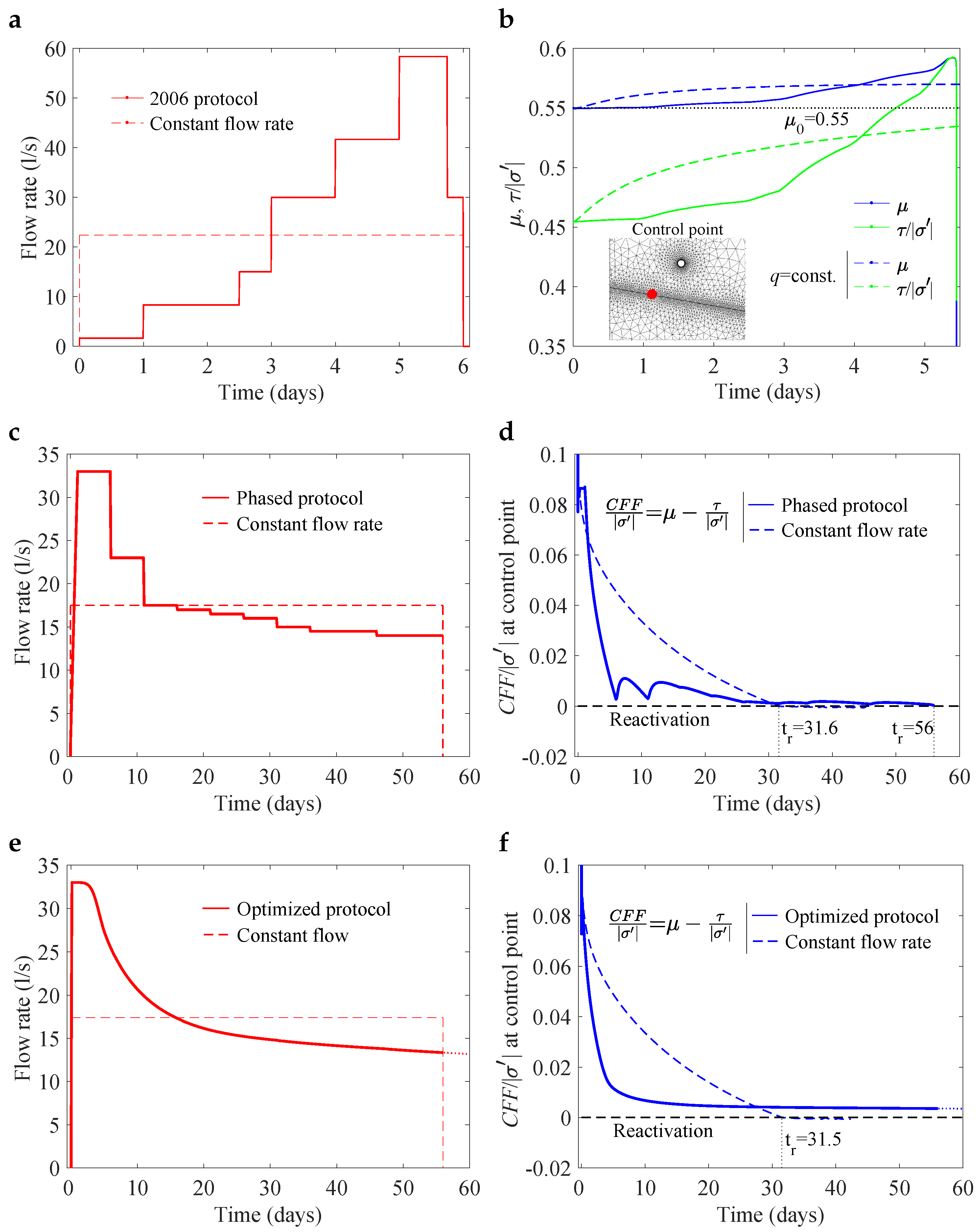
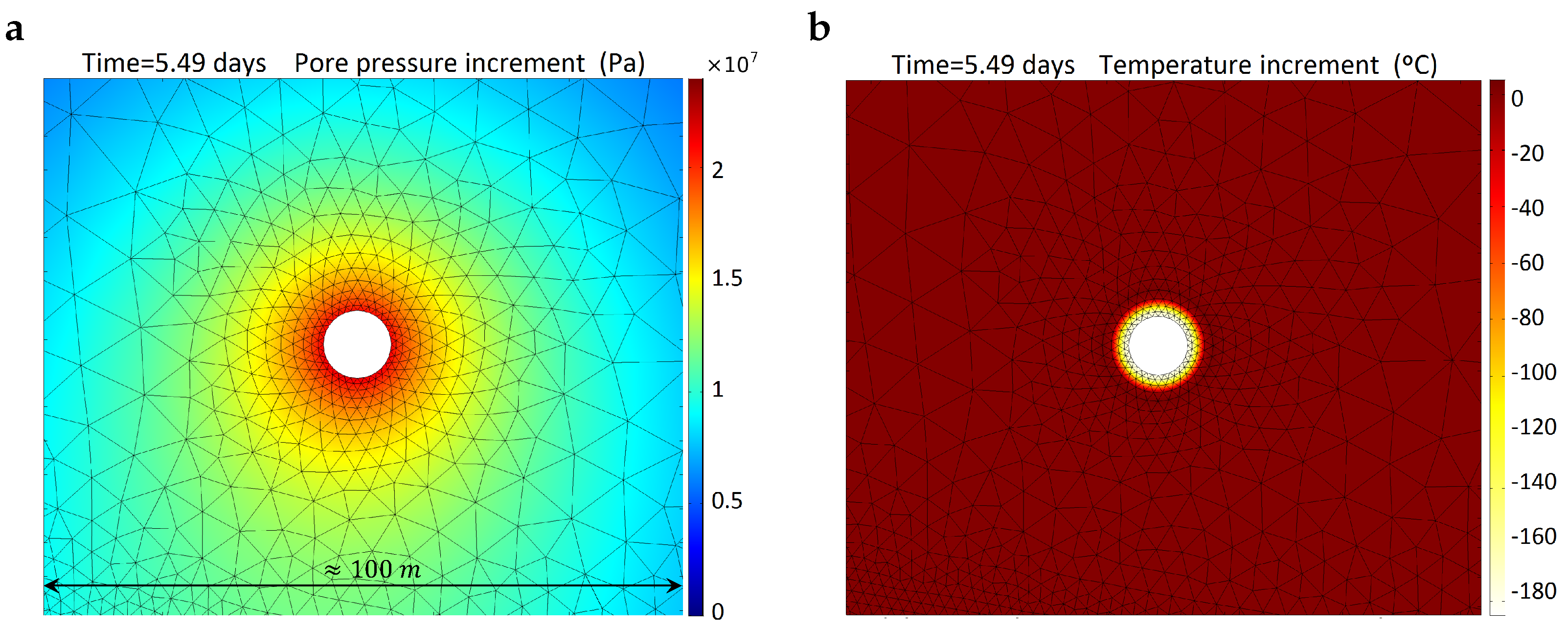
3.1. Fault Reactivation and Injection Design
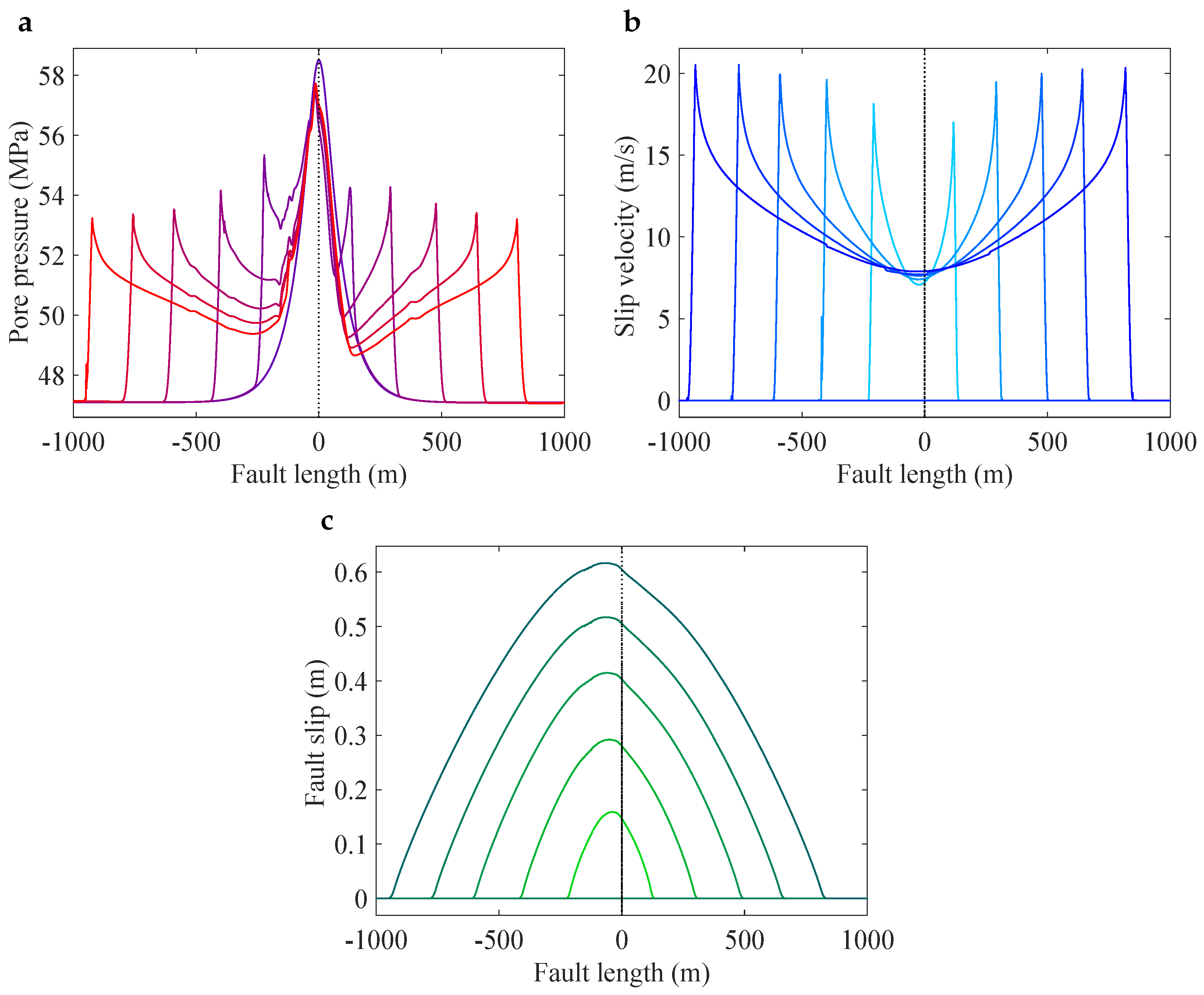
3.2. Seismic Rupture and Earthquake Magnitude
3.3. Permeability Enhancement
3.4. Long-Term Operation and Thermal Decline
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Colglazier, W. Sustainable development agenda: 2030. Science 2015, 349, 1048–1050. [Google Scholar] [CrossRef] [PubMed]
- Mahbaz, S.; Dehghani-Sanij, A.; Dusseault, M.; Nathwani, J. Enhanced and integrated geothermal systems for sustainable development of Canada’s northern communities. Sustain. Energy Technol. Assess. 2020, 37, 100565. [Google Scholar] [CrossRef]
- MIT Energy Initiative. The Future of Geothermal Energy: Impact of Enhanced Geothermal Systems (EGS) on the United States in the 21st Century; Massachusetts Institute of Technology: Cambridge, MA, USA, 2006. [Google Scholar]
- Kinney, C.; Dehghani-Sanij, A.; Mahbaz, S.; Dusseault, M.; Nathwani, J.; Fraser, R. Geothermal Energy for Sustainable Food Production in Canada’s Remote Northern Communities. Energies 2019, 12, 4058. [Google Scholar] [CrossRef] [Green Version]
- Soltani, M.; Moradi-Kashkooli, F.; Dehghani-Sanij, A.; Nokhosteen, A.; Ahmadi-Joughi, A.; Gharali, K.; Mahbaz, S.; Dusseault, M. A comprehensive review of geothermal energy evolution and development. Int. J. Green Energy 2019, 16, 971–1009. [Google Scholar] [CrossRef]
- Andrés, S.; Santillán, D.; Mosquera, J.; Cueto-Felgueroso, L. Thermo-Poroelastic Analysis of Induced Seismicity at the Basel Enhanced Geothermal System. Sustainability 2019, 11, 6904. [Google Scholar] [CrossRef] [Green Version]
- Santillan, D.; Mosquera, J.; Cueto-Felgueroso, L. Fluid-driven fracture propagation in heterogeneous media: Probability distributions of fracture trajectories. Phys. Rev. E 2017, 96, 053002. [Google Scholar] [CrossRef]
- Santillán, D.; Juanes, R.; Cueto-Felgueroso, L. Phase field model of hydraulic fracturing in poroelastic media: Fracture propagation, arrest, and branching under fluid injection and extraction. J. Geophys. Res. Solid Earth 2018, 123, 2127–2155. [Google Scholar] [CrossRef] [Green Version]
- Rinaldi, A.; Rutqvist, J.; Sonnenthal, E.; Cladouhos, T. Coupled THM Modeling of Hydroshearing Stimulation in Tight Fractured Volcanic Rock. Transp. Porous Med. 2014, 108, 131–150. [Google Scholar] [CrossRef] [Green Version]
- Rinaldi, A.; Rutqvist, J. Joint opening or hydroshearing? Analyzing a fracture zone stimulation at Fenton Hill. Geothermics 2019, 77, 83–98. [Google Scholar] [CrossRef] [Green Version]
- Giardini, D. Geothermal quake risks must be faced. Nature 2009, 462, 848–849. [Google Scholar] [CrossRef]
- Schultz, R.; Skoumal, R.; Brudzinski, M.; Eaton, D.; Baptie, B.; Ellsworth, W. Hydraulic Fracturing-Induced Seismicity. Rev. Geophys. 2020, 58, e2019RG000695. [Google Scholar] [CrossRef]
- Parker, R. The Rosemanowes HDR project 1983–1991. Geothermics 1999, 28, 603–615. [Google Scholar] [CrossRef]
- Pine, R.; Batchelor, A. Downward migration of shearing in jointed rock during hydraulic injections. Int. J. Rock. Mech. Min. Sci. Geomech. Abstr. 1984, 21, 249–263. [Google Scholar] [CrossRef]
- Häring, M.; Hopkirk, R. The Swiss Deep Heat Mining Project-The Basel Exploration Drilling. GHC Bull. 2002, 23, 31–33. [Google Scholar]
- Häring, M.; Schanz, U.; Ladner, F.; Dyer, B. Characterisation of the Basel 1 enhanced geothermal system. Geothermics 2008, 37, 469–495. [Google Scholar] [CrossRef]
- Baisch, S.; Vörös, R.; Weidler, R.; Wyborn, D. Investigation of Fault Mechanisms during Geothermal Reservoir Stimulation Experiments in the Cooper Basin, Australia. Bull. Seismol. Soc. Am. 2009, 99, 148–158. [Google Scholar] [CrossRef]
- Ellsworth, W.; Giardini, D.; Townend, J.; Ge, S.; Shimamoto, T. Triggering of the Pohang, Korea, Earthquake (Mw 5.5) by Enhanced Geothermal System Stimulation. Seismol. Res. Lett. 2019, 90, 1844–1858. [Google Scholar] [CrossRef]
- Chang, K.; Yoon, H.; Kim, Y.; Lee, M. Operational and geological controls of coupled poroelastic stressing and pore-pressure accumulation along faults: Induced earthquakes in Pohang, South Korea. Sci. Rep. 2020, 10, 2073. [Google Scholar] [CrossRef] [Green Version]
- Ziagos, J.; Phillips, B.; Boyd, L.; Jelacic, A.; Stillman, G.; Hass, E. A Technology Roadmap for Strategic Development of Enhanced Geothermal Systems. In Proceedings of the 38th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 11–13 February 2013. [Google Scholar]
- Minetto, R.; Montanari, D.; Planès, T.; Bonini, M.; Ventisette, C.; Antunes, V.; Lupi, M. Tectonic and Anthropogenic Microseismic Activity While Drilling Toward Supercritical Conditions in the Larderello-Travale Geothermal Field, Italy. J. Geophys. Res. Solid Earth 2020, 125, e2019JB018618. [Google Scholar] [CrossRef]
- Bagagli, M.; Kissling, E.; Piccinini, D.; Saccorotti, G. Local earthquake tomography of the Larderello-Travale geothermal field. Geothermics 2020, 83, 101731. [Google Scholar] [CrossRef]
- Rutqvist, J.; Jeanne, P.; Dobson, P.; Garcia, J.; Hartline, C.; Hutchings, L.; Singh, A.; Vasco, D.; Walters, M. The Northwest Geysers EGS Demonstration Project, California—Part2: Modeling and interpretation. Geothermics 2016, 63, 120–138. [Google Scholar] [CrossRef]
- Garcia, J.; Hartline, C.; Walters, M.; Wright, M.; Rutqvist, J.; Dobson, P.; Jeanne, P. The Northwest Geysers EGS Demonstration Project, California—Part 1: Characterization and reservoir response to injection. Geothermics 2016, 63, 97–119. [Google Scholar] [CrossRef] [Green Version]
- Kim, K.; Ree, J.; Kim, Y.; Kim, S.; Kang, S.; Seo, W. Assessing whether the 2017 Mw 5.4 Pohang earthquake in South Korea was an induced event. Science 2018, 360, 1007–1009. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Grigoli, F.; Cesca, S.; Rinaldi, A.; Manconi, A.; López-Comino, J.; Clinton, J.; Westaway, R.; Cauzzi, C.; Dahm, T.; Wiemer, S. The November 2017 Mw 5.5 Pohang earthquake: A possible case of induced seismicity in South Korea. Science 2018, 360, 1003–1006. [Google Scholar] [CrossRef] [Green Version]
- Hubbert, M.; Rubey, W. Role of fluid pressure in mechanics of overthrust faulting I. Mechanics of fluid-filled porous solids and its application to overthrust faulting. Geol. Soc. Am. Bull. 1959, 70, 115–166. [Google Scholar]
- Pampillón, P.; Santillán, D.; Mosquera, J.; Cueto-Felgueroso, L. Geomechanical Constraints on Hydro-Seismicity: Tidal Forcing and Reservoir Operation. Water 2020, 12, 2724. [Google Scholar] [CrossRef]
- Pampillón, P.; Santillán, D.; Mosquera, J.; Cueto-Felgueroso, L. Dynamic and Quasi-Dynamic Modeling of Injection-Induced Earthquakes in Poroelastic Media. J. Geophys. Res. Solid Earth 2018, 123, 5730–5759. [Google Scholar] [CrossRef]
- National Research Council. Induced Seismicity Potential in Energy Technologies; The National Academies Press: Washington, DC, USA, 2013. [Google Scholar]
- Ellsworth, W. Injection-Induced Earthquakes. Science 2013, 341, 1225942. [Google Scholar] [CrossRef]
- Brodsky, E.; Lajoie, L. Anthropogenic Seismicity Rates and Operational Parameters at the Salton Sea Geothermal Field. Science 2013, 341, 543–546. [Google Scholar] [CrossRef]
- Buijze, L.; van Bijsterveldt, L.; Cremer, H.; Paap, B.; Veldkamp, H.; Wassing, B.; van Wees, J.; van Yperen, J.; ter Heege, J.; Jaarsma, B. Review of induced seismicity in geothermal systems worldwide and implications for geothermal systems in the Netherlands. Neth. J. Geosci. 2019, 98, E13. [Google Scholar] [CrossRef] [Green Version]
- Horton, S. Disposal of hydrofracking waste fluid by injection into subsurface aquifers triggers earthquake swarm in central Arkansas with potential for damaging earthquake. Seismol. Res. Lett. 2012, 83, 250–260. [Google Scholar] [CrossRef] [Green Version]
- Juanes, R.; Hager, B.; Herzog, H. No geologic evidence that seismicity causes fault leakage that would render large-scale carbon capture and storage unsuccessful. Proc. Natl. Acad. Sci. USA 2012, 109, E3623. [Google Scholar] [CrossRef] [PubMed]
- Vilarrasa, V.; Carrera, J. Geologic carbon storage is unlikely to trigger large earthquakes and reactivate faults through which CO2 could leak. Proc. Natl. Acad. Sci. USA 2015, 112, 5938–5943. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- White, J.; Foxall, W. Assessing induced seismicity risk at CO2 storage projects: Recent progress and remaining challenges. Int. J. Greenh. Gas Control 2016, 49, 413–424. [Google Scholar] [CrossRef] [Green Version]
- Vilarrasa, V.; De Simone, S.; Carrera, J.; Villaseñor, A. Unraveling the causes of the seismicity induced by underground gas storage at Castor, Spain. Geophys. Res. Lett. 2021, 48, e2020GL092038. [Google Scholar] [CrossRef]
- Weingarten, M.; Ge, S.; Godt, J.; Bekins, B.; Rubinstein, J. High-rate injection is associated with the increase in U.S. mid-continent seismicity. Science 2015, 348, 1336–1340. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shirzaei, M.; Ellsworth, W.; Tiampo, K.; González, P.; Manga, M. Surface uplift and time-dependent seismic hazard due to fluid injection in eastern Texas. Science 2016, 353, 1416–1419. [Google Scholar] [CrossRef] [Green Version]
- McComas, K.; Lu, H.; Keranen, K.; Furtney, M.; Song, H. Public perceptions and acceptance of induced earthquakes related to energy development. Energy Policy 2016, 99, 27–32. [Google Scholar] [CrossRef]
- Mignan, A.; Karvounis, D.; Broccardo, M.; Wiemer, S.; Giardini, D. Including seismic risk mitigation measures into the Levelized Cost of Electricity in enhanced geothermal systems for optimal siting. Appl. Energy 2019, 238, 831–850. [Google Scholar] [CrossRef]
- Lee, K.; Ellsworth, W.; Giardini, D.; Townend, J.; Ge, S.; Shimamoto, T.; Yeo, I.; Kang, T.; Rhie, J.; Sheen, D.; et al. Managing injection-induced seismic risks. Science 2019, 364, 730–732. [Google Scholar] [CrossRef]
- McGarr, A. Maximum magnitude earthquakes induced by fluid injection. J. Geophys. Res. Solid Earth 2014, 119, 1008–1019. [Google Scholar] [CrossRef]
- Scholz, C. The Mechanics of Earthquakes and Faulting; Cambridge University Press: Cambridge, UK, 2002. [Google Scholar]
- Charlety, J.; Cuenot, N.; Dorbath, L.; Dorbath, C.; Haessler, H.; Frogneux, M. Large earthquakes during hydraulic stimulations at the geothermal site of Soultz-sous-Forêts. Int. J. Rock. Mech. Min. Sci. 2007, 44, 1091–1105. [Google Scholar] [CrossRef]
- Deichmann, N.; Giardini, D. Earthquakes Induced by the Stimulation of an Enhanced Geothermal System below Basel (Switzerland). Seismol. Res. Lett. 2009, 80, 784–798. [Google Scholar] [CrossRef]
- De Simone, S.; Carrera, J.; Vilarrasa, V. Superposition approach to understand triggering mechanisms of post-injection induced seismicity. Geothermics 2017, 70, 85–97. [Google Scholar] [CrossRef]
- Rutqvist, J.; Birkholzer, J.; Tsang, C.F. Coupled reservoir-geomechanical analysis of the potential for tensile and shear failure associated with CO2 injection in multilayered reservoir-caprock systems. Int. J. Rock. Mech. Min. Sci. 2008, 45, 132–143. [Google Scholar] [CrossRef] [Green Version]
- De Simone, S.; Vilarrasa, V.; Carrera, J.; Alcolea, A.; Meier, P. Thermal coupling may control mechanical stability of geothermal reservoirs during cold water injection. Phys. Chem. Earth 2013, 64, 117–126. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Olivella, S.; Carrera, J.; Rutqvist, J. Long term impacts of cold CO2 injection on the caprock integrity. Int. J. Greenh. Gas Control 2014, 24, 1–13. [Google Scholar] [CrossRef]
- Jacquey, A.; Cacace, M.; Blöcher, G.; Watanabe, N.; Huenges, E.; Scheck-Wenderoth, M. Thermo-poroelastic numerical modelling for enhanced geothermal system performance: Case study of the Groß Schönebeck reservoir. Tectonophysics 2016, 684, 119–130. [Google Scholar] [CrossRef]
- Rice, J. Heating and weakening of faults during earthquake slip. J. Geophys. Res. 2006, 111, B05311. [Google Scholar] [CrossRef] [Green Version]
- Dieterich, J.; Linker, F. Fault stability under conditions of variable normal stress. Geophys. Res. Lett. 1992, 19, 1691–1694. [Google Scholar] [CrossRef]
- Kilgore, B.; Beeler, N.; Lozos, J.; Oglesby, D. Rock friction under variable normal stress. J. Geophys. Res. Solid Earth 2017, 122, 7042–7075. [Google Scholar] [CrossRef]
- Dieterich, J. Modeling of rock friction: 1. Experimental results and constitutive equations. J. Geophys. Res. 1979, 84, 2161–2168. [Google Scholar] [CrossRef]
- Linker, F.; Dieterich, J. Effects of variable normal stress on rock friction: Observations and constitutive equations. J. Geophys. Res. 1992, 97, 4923–4940. [Google Scholar] [CrossRef]
- Wyss, R.; Link, K. Actual Developments in Deep Geothermal Energy in Switzerland. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Meier, P.; Alcolea Rodríguez, A.; Bethmann, F. Lessons Learned from Basel: New EGS Projects in Switzerland Using Multistage Stimulation and a Probabilistic Traffic Light System for the Reduction of Seismic Risk. In Proceedings of the World Geothermal Congress 2015, Melbourne, Australia, 19–25 April 2015. [Google Scholar]
- Gischig, V.; Wiemer, S. A stochastic model for induced seismicity based on non-linear pressure diffusion and irreversible permeability enhancement. Geophys. J. Int. 2013, 194, 1229–1249. [Google Scholar] [CrossRef] [Green Version]
- Mena, B.; Wiemer, S.; Bachmann, C. Building Robust Models to Forecast the Induced Seismicity Related to Geothermal Reservoir Enhancement. Bull. Seismol. Soc. Am. 2013, 103, 383–393. [Google Scholar] [CrossRef] [Green Version]
- Catalli, F.; Rinaldi, A.; Gischig, V.; Nespoli, M.; Wiemer, S. The importance of earthquake interactions for injection-induced seismicity: Retrospective modeling of the Basel Enhanced Geothermal System. Geophys. Res. Lett. 2016, 43, 4992–4999. [Google Scholar] [CrossRef] [Green Version]
- Andrés, S.; Santillán, D.; Mosquera, J.; Cueto-Felgueroso, L. Delayed weakening and reactivation of rate-and-state faults driven by pressure changes due to fluid injection. J. Geophys. Res. Solid Earth 2019, 124, 11917–11937. [Google Scholar] [CrossRef]
- Ungemach, P.; Antics, M. The Road Ahead Toward Sustainable Geothermal Development in Europe. In Proceedings of the World Geothermal Congress 2010, Bali, Indonesia, 25–29 April 2010. [Google Scholar]
- Gholizadeh Doonechaly, N.; Abdel Azim, R.; Rahman, S. Evaluation of recoverable energy potential from enhanced geothermal systems: A sensitivity analysis in a poro-thermo-elastic framework. Geofluids 2016, 16, 384–395. [Google Scholar] [CrossRef]
- Liu, G.; Zhou, C.; Rao, Z.; Liao, S. Impacts of fracture network geometries on numerical simulation and performance prediction of enhanced geothermal systems. Renew. Energy 2021, 171, 492–504. [Google Scholar] [CrossRef]
- Wu, X.; Yu, L.; Hassan, N.; Ma, W.; Liu, G. Evaluation and optimization of heat extraction in enhanced geothermal system via failure area percentage. Renew. Energy 2021, 169, 204–220. [Google Scholar] [CrossRef]
- Biot, M. General Theory of Three-Dimensional Consolidation. J. Appl. Phys. 1941, 12, 155–164. [Google Scholar] [CrossRef]
- Rice, J.; Cleary, M. Some basic stress diffusion solutions for fluid-saturated elastic porous media with compressible constituents. Rev. Geophys. 1976, 14, 227–241. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Santillán, D.; Mosquera, J. Stick-slip dynamics of flow-induced seismicity on rate and state faults. Geophys. Res. Lett. 2017, 44, 4098–4106. [Google Scholar] [CrossRef]
- Cueto-Felgueroso, L.; Vila, C.; Santillán, D.; Mosquera, J. Numerical Modeling of Injection-Induced Earthquakes Using Laboratory-Derived Friction Laws. Water Resour. Res. 2018, 54, 9833–9859. [Google Scholar] [CrossRef]
- Fourier, J. Théorie Analytique de la Chaleur; Chez Firmin Didot Pére et Fils: Paris, France, 1822. [Google Scholar]
- Andrés, S.; Dentz, M.; Cueto-Felgueroso, L. Multirate mass transfer approach for double-porosity poroelasticity in fractured media. Water Resour. Res. 2021, 57, e2021WR029804. [Google Scholar] [CrossRef]
- Jha, B.; Juanes, R. Coupled multiphase flow and poromechanics: A computational model of pore pressure effects on fault slip and earthquake triggering. Water Resour. Res. 2014, 50, 3776–3808. [Google Scholar] [CrossRef]
- Bowden, F.; Tabor, D. The Friction and Lubrication of Solids I; Clarendon Press: London, UK, 1950. [Google Scholar]
- Baumberger, T.; Caroli, C. Solid friction from stick-slip down to pinning and aging. Adv. Phys. 2006, 55, 279–348. [Google Scholar] [CrossRef] [Green Version]
- Barber, J. Multiscale Surfaces and Amontons’ Law of Friction. Tribol. Lett. 2013, 49, 539–543. [Google Scholar] [CrossRef]
- Ruina, A. Slip instability and state variable friction laws. J. Geophys. Res. 1983, 88, 10359–10370. [Google Scholar] [CrossRef]
- Tal, Y.; Hager, B.; Ampuero, J. The Effects of Fault Roughness on the Earthquake Nucleation Process. J. Geophys. Res. Solid Earth 2018, 123, 437–456. [Google Scholar] [CrossRef] [Green Version]
- Rice, J.; Lapusta, N.; Ranjith, K. Rate and state dependent friction and the stability of sliding between elastically deformable solids. J. Mech. Phys. Solids 2001, 49, 1865–1898. [Google Scholar] [CrossRef] [Green Version]
- Putelat, T.; Dawes, J.; Willis, J. On the microphysical foundations of rate-and-state friction. J. Mech. Phys. Solids 2011, 59, 1062–1075. [Google Scholar] [CrossRef]
- Hong, T.; Marone, C. Effects of normal stress perturbations on the frictional properties of simulated faults. Geochem. Geophys. Geosyst. 2005, 6, Q03012. [Google Scholar] [CrossRef] [Green Version]
- Perfettini, H.; Molinari, A. A micromechanical model of rate and state friction: 2. Effect of shear and normal stress changes. J. Geophys. Res. Solid Earth 2017, 122, 2638–2652. [Google Scholar]
- Rathbun, A.; Marone, C. Symmetry and the critical slip distance in rate and state friction laws. J. Geophys. Res. Solid Earth 2013, 118, 3728–3741. [Google Scholar] [CrossRef]
- Bhattacharya, P.; Rubin, A.; Bayart, E.; Savage, H.; Marone, C. Critical evaluation of state evolution laws in rate and state friction: Fitting large velocity steps in simulated fault gouge with time-, slip-, and stress-dependent constitutive laws. J. Geophys. Res. Solid Earth 2015, 120, 6365–6385. [Google Scholar] [CrossRef] [Green Version]
- Perfettini, H.; Schmittbuhl, J.; Rice, J.; Cocco, M. Frictional response induced by time-dependent fluctuations of the normal loading. J. Geophys. Res. 2001, 106, 13455–13472. [Google Scholar] [CrossRef]
- Hanks, T.; Kanamori, H. A moment magnitude scale. J. Geophys. Res. 1979, 84, 2348–2350. [Google Scholar] [CrossRef]
- Norbeck, J.; McClure, M.; Horne, R. Field observations at the Fenton Hill enhanced geothermal system test site support mixed-mechanism stimulation. Geothermics 2018, 74, 135–149. [Google Scholar] [CrossRef]
- Cacace, M.; Jacquey, A. Flexible parallel implicit modelling of coupled thermal-hydraulic-mechanical processes in fractured rocks. Solid Earth 2017, 8, 921–941. [Google Scholar] [CrossRef] [Green Version]
- COMSOL. COMSOL Multiphysics Structural Mechanics Module User’s Guide v5.2a; COMSOL: Stockholm, Sweden, 2016. [Google Scholar]
- Clark, C.; Harto, C.; Sullivan, J.; Wang, M. Water Use in the Development and Operation of Geothermal Power Plants; Agronne National Laboratory, U.S. Department of Energy: Lemont, IL, USA, 2011.
- Gischig, V.; Preisig, G. Hydro-Fracturing Versus Hydro-Shearing: A Critical Assessment of Two Distinct Reservoir Estimulation Mechanisms. In Proceedings of the 13th International Congress of Rock Mechanics, Montreal, QC, Canada, 10–13 May 2015. [Google Scholar]
- Deichmann, N.; Kraft, T.; Evans, K. Identification of faults activated during the stimulation of the Basel geothermal project from cluster analysis and focal mechanisms of the larger magnitude events. Geothermics 2014, 52, 84–97. [Google Scholar] [CrossRef]
- Alghannam, M.; Juanes, R. Understanding rate effects in injection-induced earthquakes. Nat. Commun. 2020, 11, 3053. [Google Scholar] [CrossRef] [PubMed]
- Riahi, A.; Damjanac, B. Numerical Study of Hydro-Shearing in Geothermal Reservoirs with a Pre-Existing Discrete Fracture Network. In Proceedings of the 38th Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 11–13 February 2013. [Google Scholar]
- Ye, Z.; Ghassemi, A. Injection-Induced Shear Slip and Permeability Enhancement in Granite Fractures. J. Geophys. Res. Solid Earth 2018, 123, 9009–9032. [Google Scholar] [CrossRef]
- Liu, R.; Huang, N.; Jiang, Y.; Jing, H.; Li, B.; Xia, Y. Effect of Shear Displacement on the Directivity of Permeability in 3D Self-Affine Fractal Fractures. Geofluids 2018, 2018, 9813846. [Google Scholar] [CrossRef]
- Gehne, S.; Benson, P. Permeability enhancement through hydraulic fracturing: Laboratory measurements combining a 3D printed jacket and pore fluid over-pressure. Sci. Rep. 2019, 9, 12573. [Google Scholar] [CrossRef] [Green Version]
- McDermott, C.; Randriamanjatosoa, A.; Tenzer, H.; Kolditz, O. Simulation of heat extraction from crystalline rocks: The influence of coupled processes on differential reservoir cooling. Geothermics 2006, 35, 321–344. [Google Scholar] [CrossRef]
- Koh, J.; Roshan, H.; Rahman, S. A numerical study on the long term thermo-poroelastic effects of cold water injection into naturally fractured geothermal reservoirs. Comput. Geotech. 2011, 38, 669–682. [Google Scholar] [CrossRef]
- De Simone, S.; Pinier, B.; Bour, O.; Davy, P. A particle-tracking formulation of advective–diffusive heat transport in deformable fracture networks. Comput. Geotech. 2021, 603, 127157. [Google Scholar] [CrossRef]
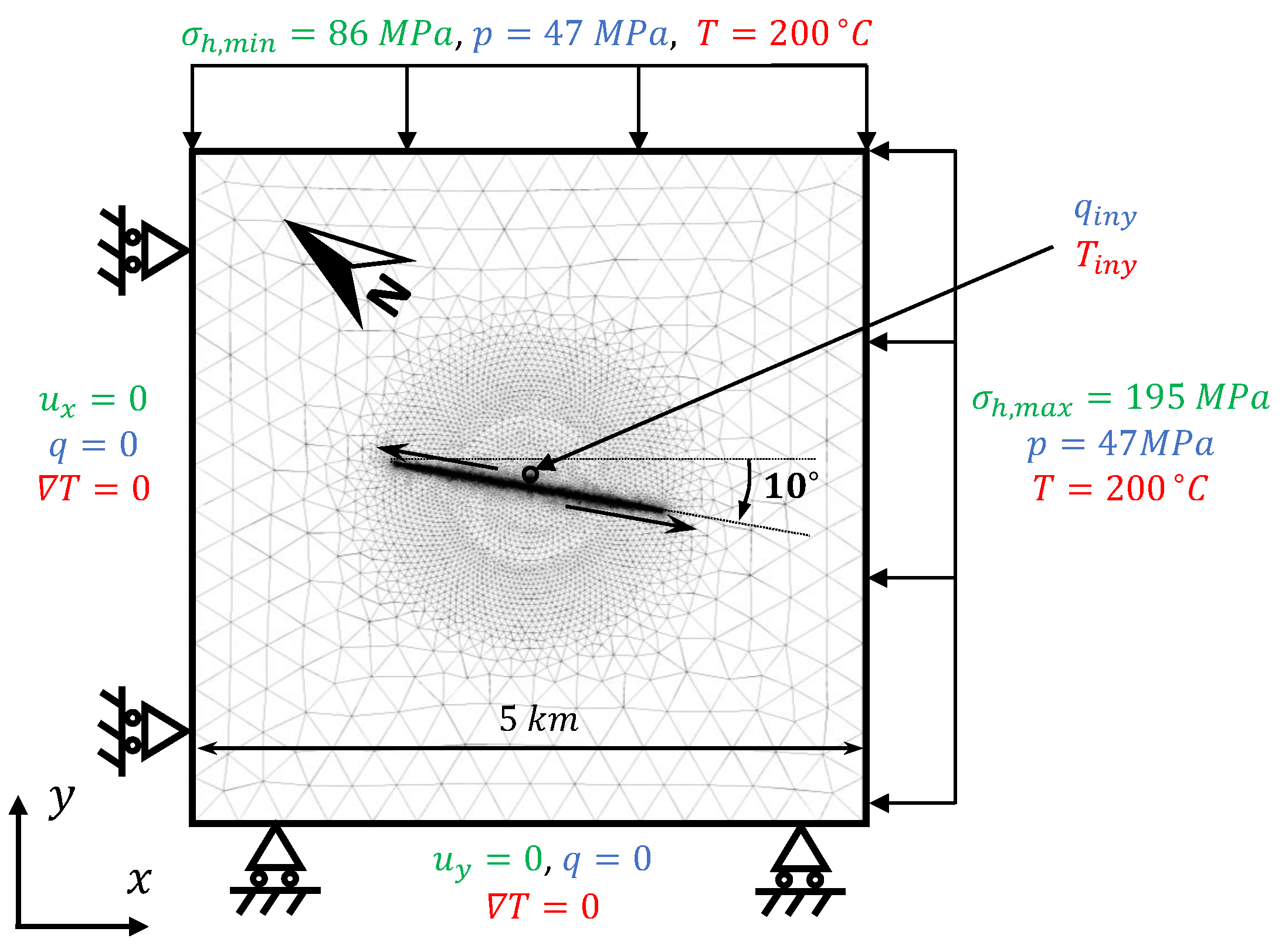
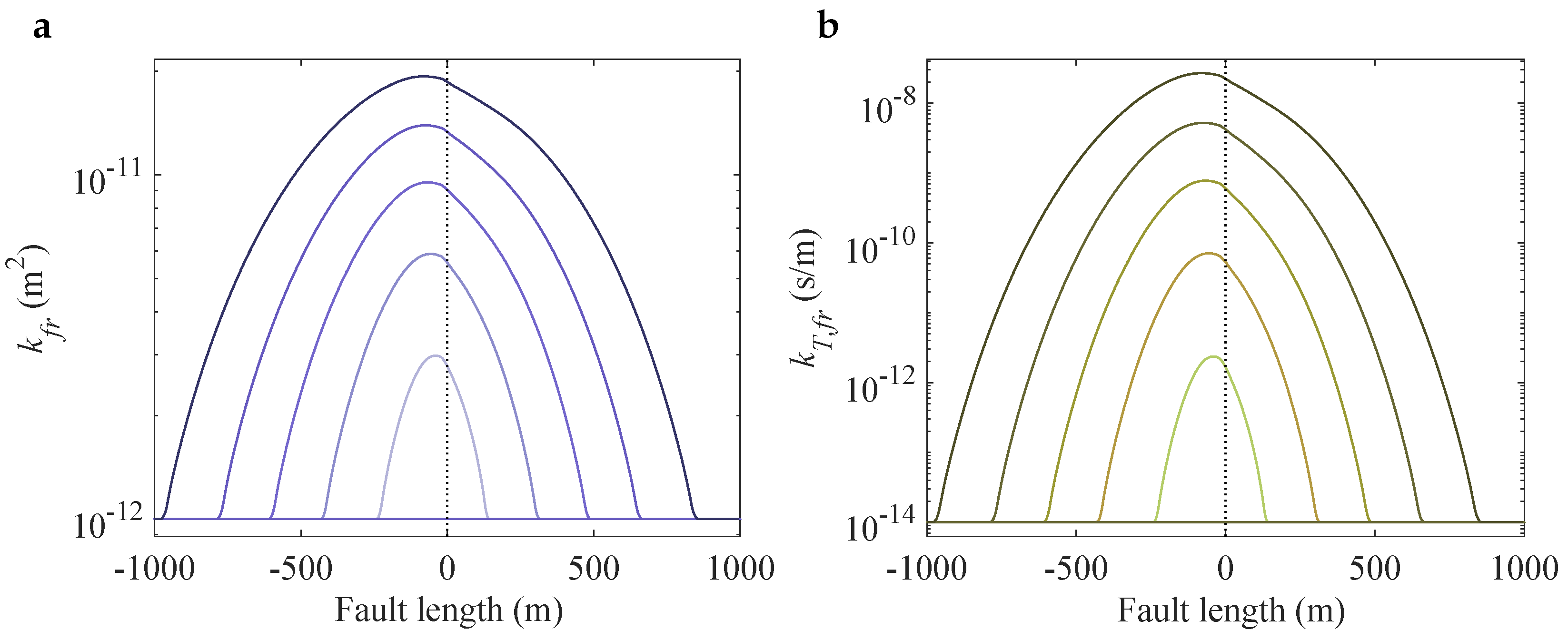
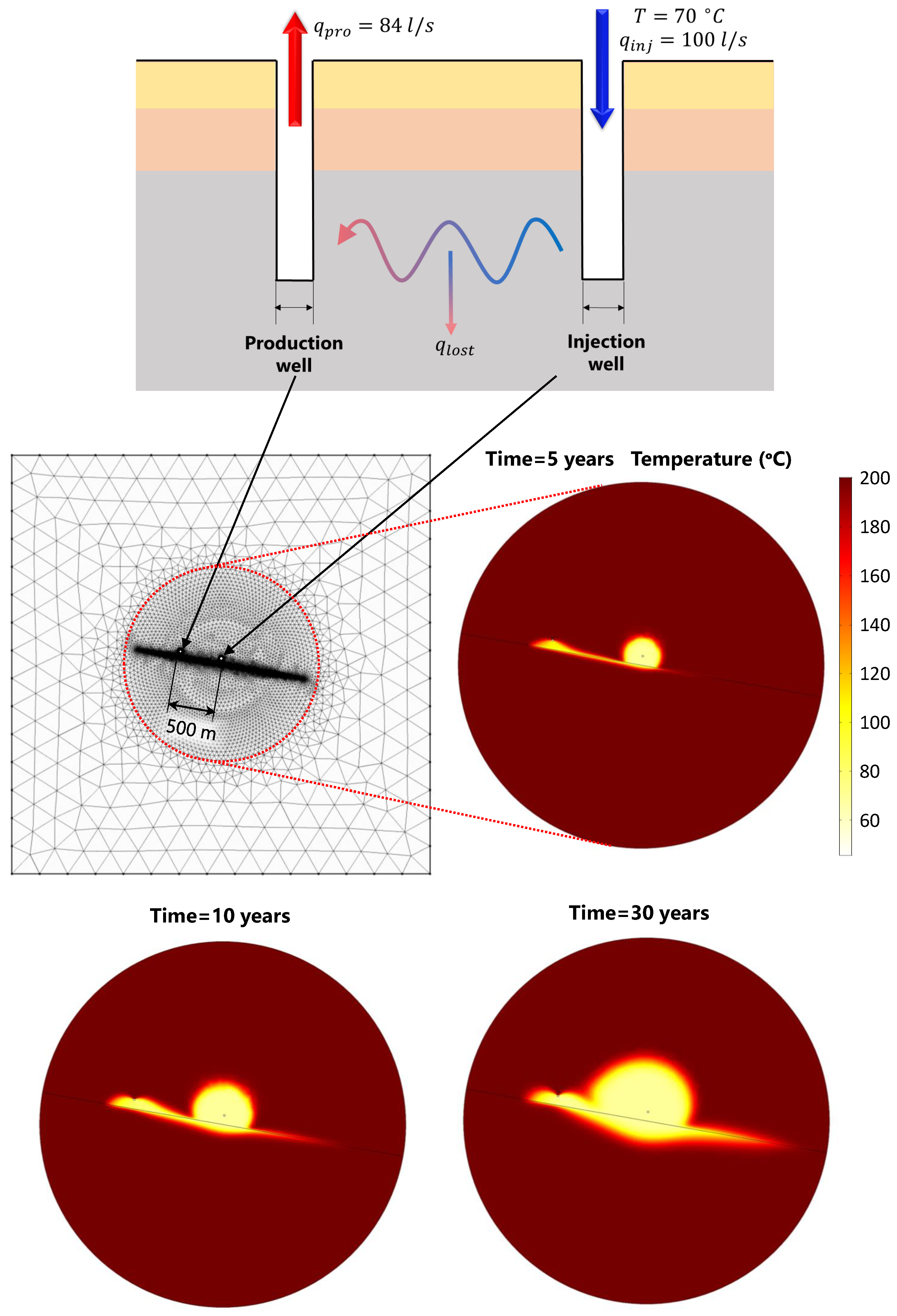
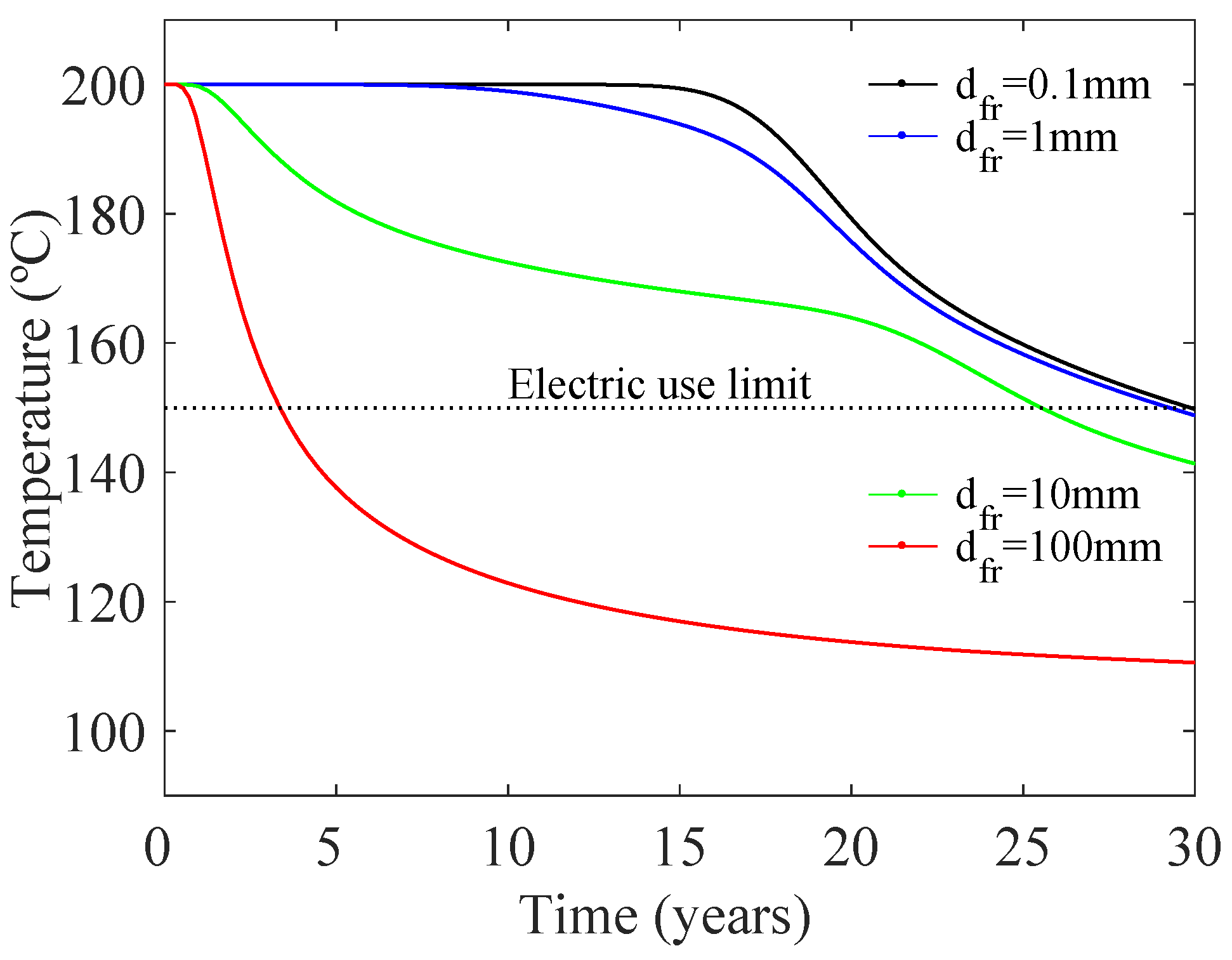
| Parameter | Value | Unit | Description |
|---|---|---|---|
| E | 20 | GPa | Young modulus of the rock |
| 0.25 | – | Poisson ratio of the rock | |
| 2700 | kg/m | Rock density | |
| 86 | MPa | Maximum principal stress | |
| 195 | MPa | Minimum principal stress | |
| 1000 | kg/m | Fluid density | |
| 0.00024 | Pa·s | Fluid viscosity | |
| 4 × 10 | Pa | Fluid compressibility | |
| k | 10 | m | Porous matrix permeability |
| 0.1 | – | Porosity | |
| 2.4 | W/(m·K) | Solid thermal conductivity | |
| 0.6 | W/(m·K) | Fluid thermal conductivity | |
| 800 | J/(kg·K) | Solid heat capacity | |
| 4200 | J/(kg·K) | Fluid heat capacity | |
| T | 473.15 | K | Natural temperature |
| 1 | – | Biot coefficient | |
| 8 × 10 | K | Thermal expansion coefficient | |
| 0.55 | – | Friction coefficient | |
| a | 0.005 | – | Direct effect parameter |
| b | 0.03 | – | Friction evolution parameter |
| 0.0007 | m | Characteristic slip distance | |
| 10 | m/s | Reference slip velocity | |
| 0.2 | – | Linker–Dieterich stressing rate coefficient |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andrés, S.; Santillán, D.; Mosquera, J.C.; Cueto-Felgueroso, L. Hydraulic Stimulation of Geothermal Reservoirs: Numerical Simulation of Induced Seismicity and Thermal Decline. Water 2022, 14, 3697. https://doi.org/10.3390/w14223697
Andrés S, Santillán D, Mosquera JC, Cueto-Felgueroso L. Hydraulic Stimulation of Geothermal Reservoirs: Numerical Simulation of Induced Seismicity and Thermal Decline. Water. 2022; 14(22):3697. https://doi.org/10.3390/w14223697
Chicago/Turabian StyleAndrés, Sandro, David Santillán, Juan Carlos Mosquera, and Luis Cueto-Felgueroso. 2022. "Hydraulic Stimulation of Geothermal Reservoirs: Numerical Simulation of Induced Seismicity and Thermal Decline" Water 14, no. 22: 3697. https://doi.org/10.3390/w14223697





