Predicting Chlorine and Trihalomethanes in a Full-Scale Water Distribution System under Changing Operating Conditions
Abstract
:1. Introduction
1.1. The Importance and Challenges of Predicting Free Chlorine Residual and THMs in Drinking Water Distribution Systems
1.2. Chlorine Prediction Models
1.3. THMs Prediction Models
1.4. Study Objectives and Approach
2. Materials and Methods
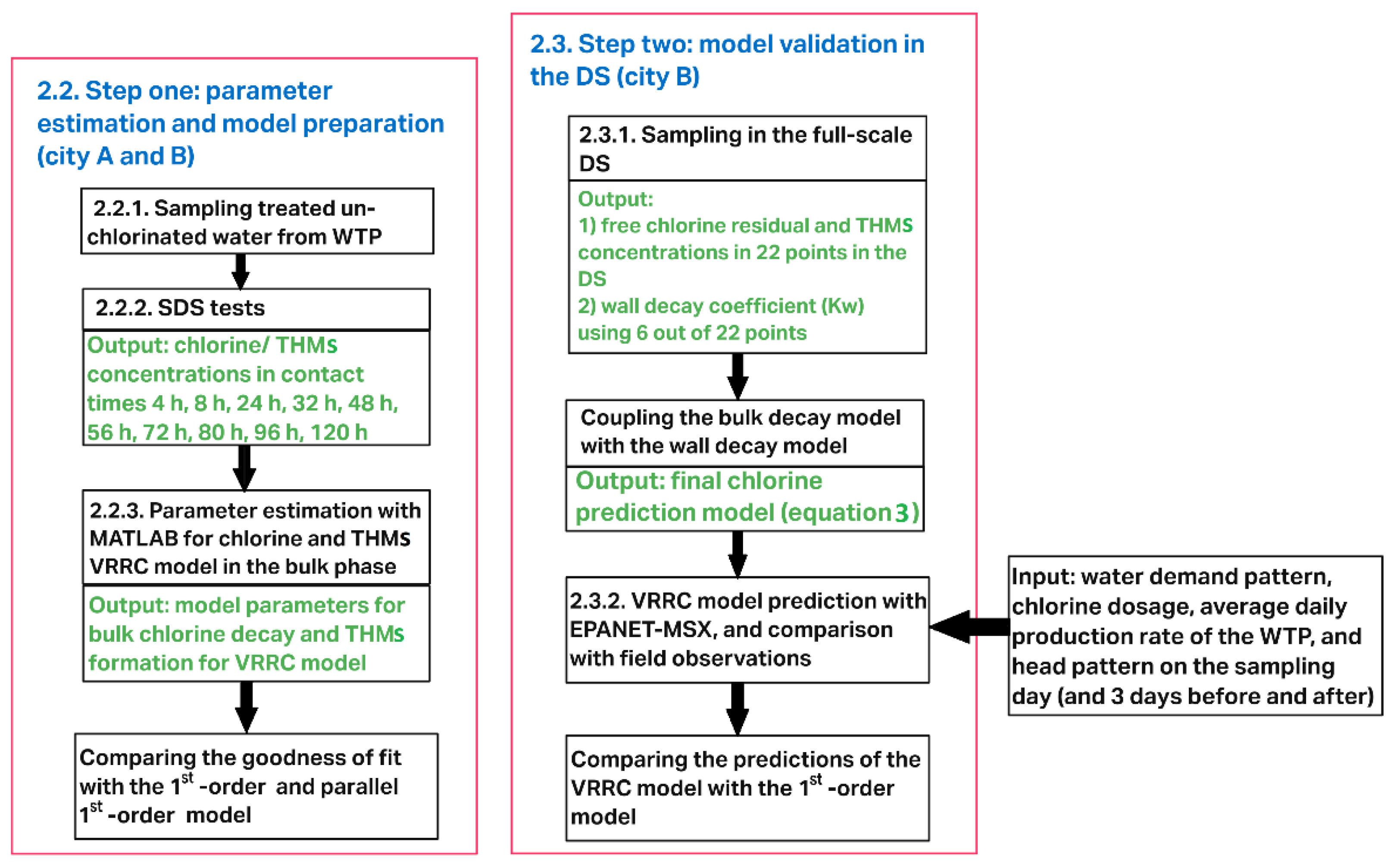
2.1. Chlorine and THMs Prediction in the DS: Overall Approach
2.2. Step One: Parameter Estimation and Model Preparation
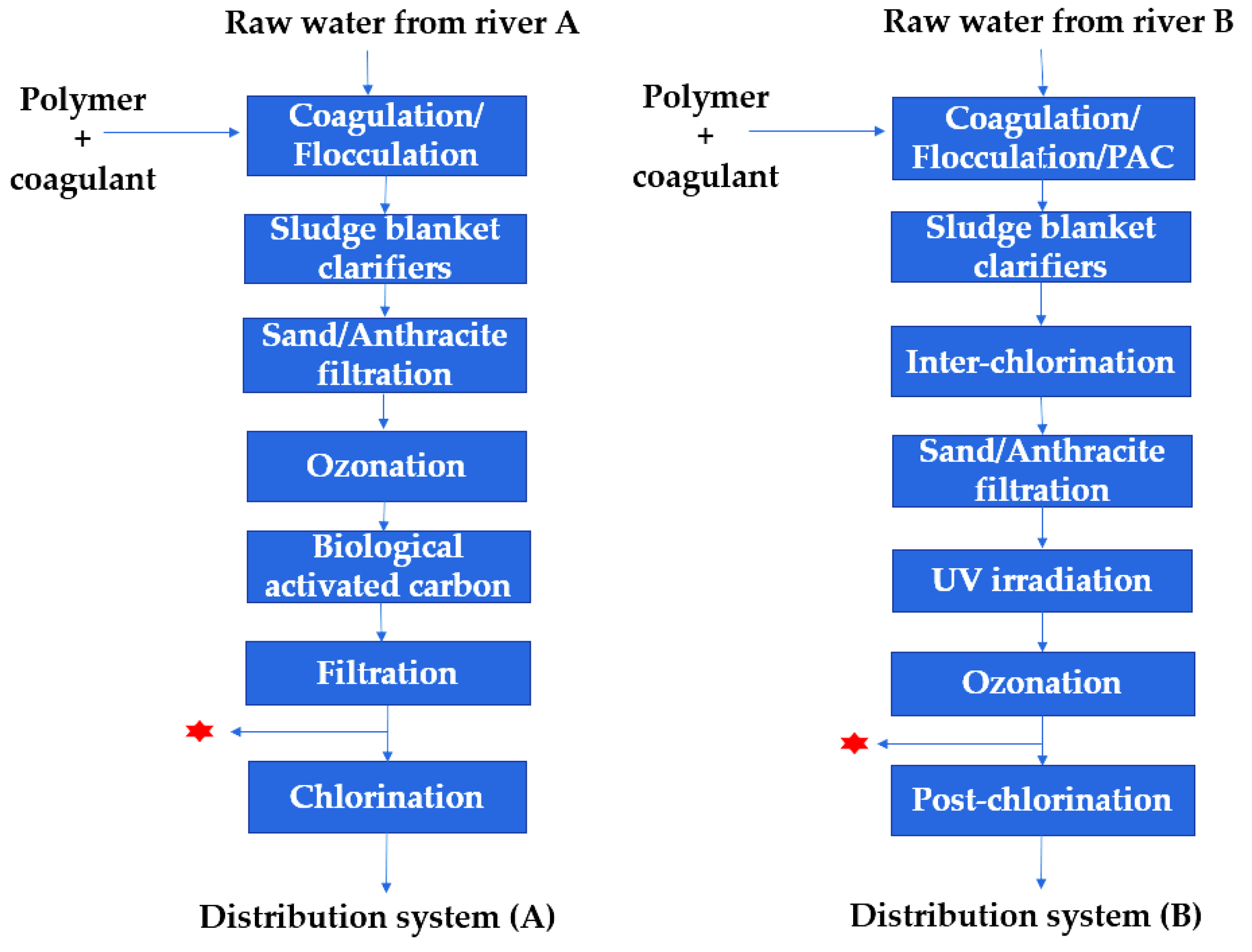
2.2.1. Sampling at WTP
2.2.2. Simulated Distribution Systems (SDS) Assays
2.2.3. VRRC Model Parameters Estimation
- VRRC-chlorine model
- VRRC-THMs model
2.3. Step Two: Model Prediction and Validation
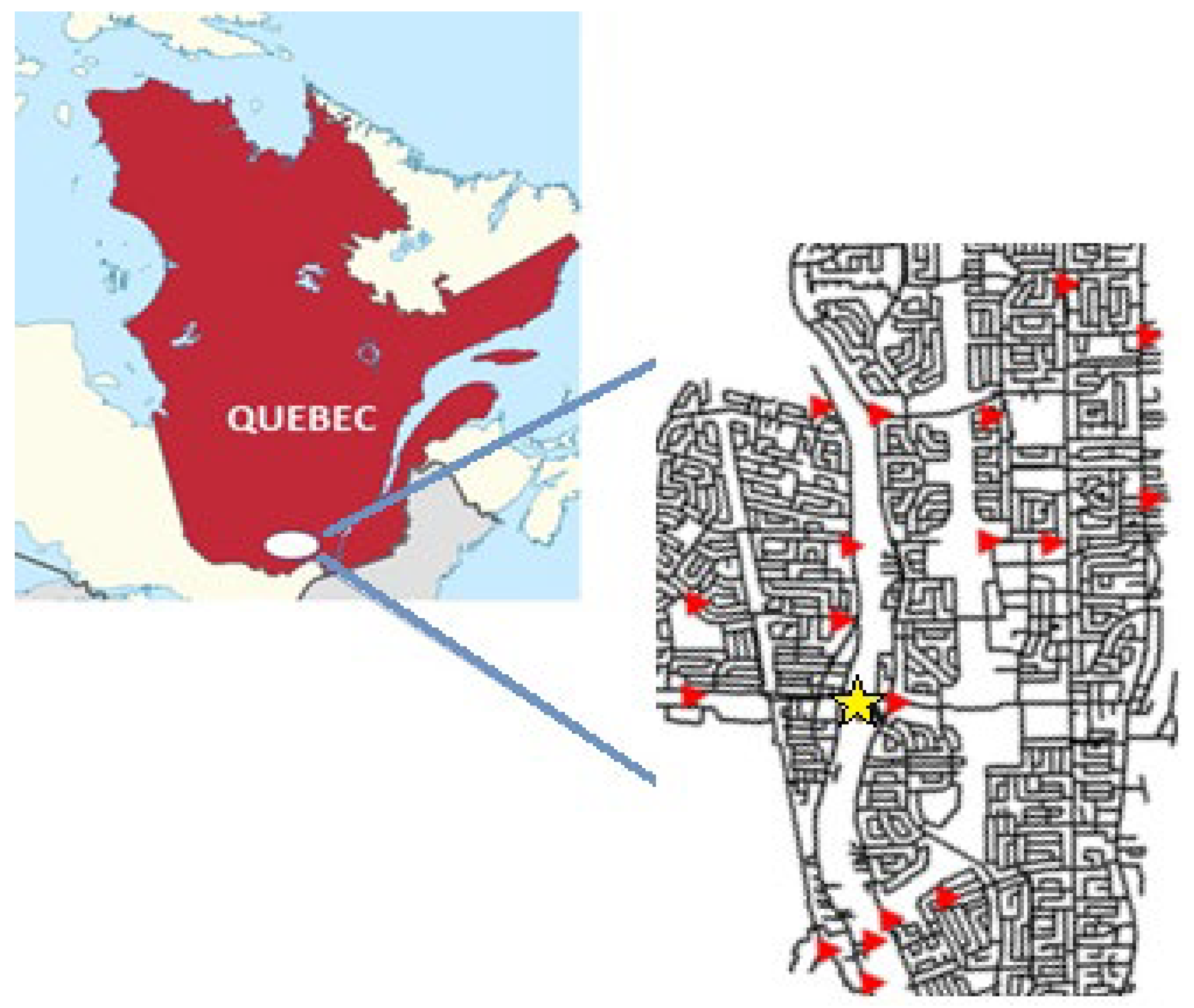
2.3.1. Sampling in Full-Scale DS
2.3.2. VRRC Model Prediction and Comparison with Field Observations
3. Results and Discussion
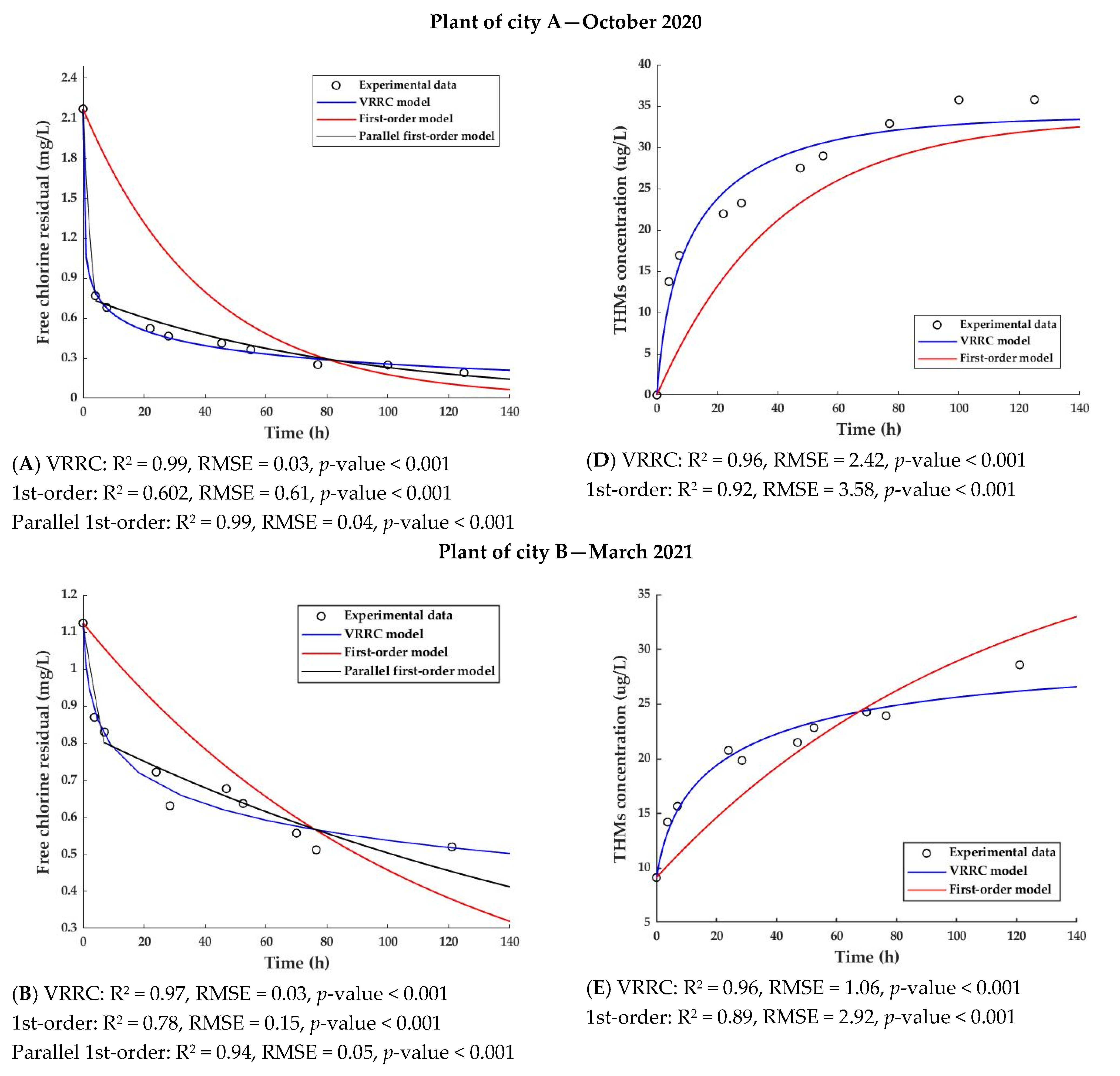
3.1. Parameter Estimation for the VRCC Model
3.2. Predicting Free Chlorine and THMs in the DS
3.2.1. Free Chlorine Prediction
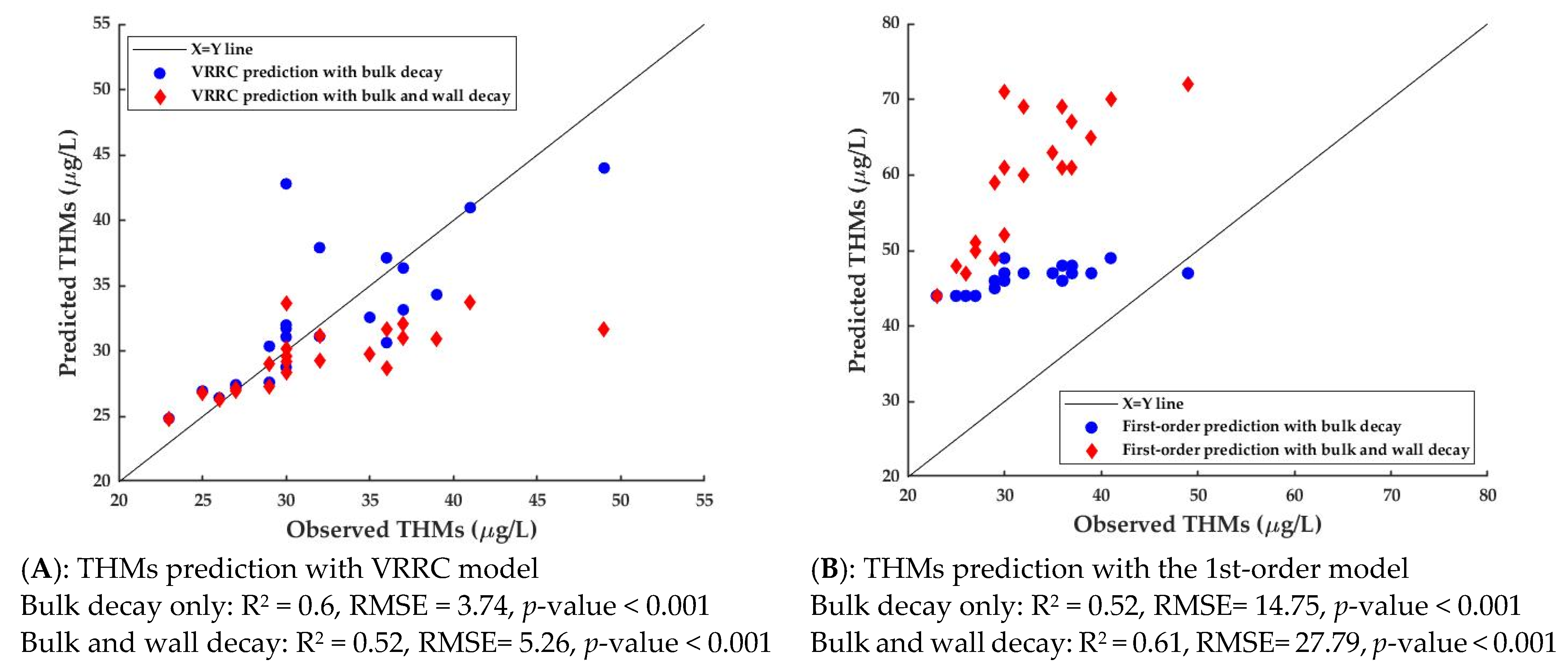
3.2.2. THMs Prediction
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Méité, L.; Fotsing, M.; Barbeau, B. Efficacy of ozone to reduce chlorinated disinfection by-products in Quebec (Canada) drinking water facilities. Ozone Sci. Eng. 2015, 37, 294–305. [Google Scholar] [CrossRef]
- Jonkergouw, P.M.R.; Khu, S.-T.; Savic, D.A.; Zhong, D.; Hou, X.Q.; Zhao, H.-B. A Variable Rate Coefficient Chlorine Decay Model. Environ. Sci. Technol. 2009, 43, 408–414. [Google Scholar] [CrossRef] [PubMed]
- Code of Federal Regulations (CFR). 40 CFR 141.72. National Primary Drinking Water Regulations, Subpart H—Filtration and Disinfection, Disinfection; U.S. Government: Washington, DC, USA, 2010; pp. 456–458. Available online: https://www.ecfr.gov/current/title-40/chapter-I/subchapter-D/part-141/subpart-H (accessed on 20 October 2022).
- Walski, T. Raising the bar on disinfectant residuals. World Water Mag. 2019, 42, 34–35. [Google Scholar]
- Rossman, L.A.; Brown, R.A.; Singer, P.C.; Nuckols, J.R. DBP formation kinetics in a simulated distribution system. Water Res. 2001, 35, 3483–3489. [Google Scholar] [CrossRef]
- Simard, A.; Pelletier, G.; Rodriguez, M. Water residence time in a distribution system and its impact on disinfectant residuals and trihalomethanes. J. Water Supply Res. Technol. 2011, 60, 375–390. [Google Scholar] [CrossRef]
- Sérodes, J.-B.; Rodriguez, M.J.; Li, H.; Bouchard, C. Occurrence of THMs and HAAs in experimental chlorinated waters of the Quebec City area (Canada). Chemosphere 2003, 51, 253–263. [Google Scholar] [CrossRef]
- Chhipi-Shrestha, G.; Rodriguez, M.; Sadiq, R. Unregulated disinfection By-products in drinking water in Quebec: A meta analysis. J. Environ. Manag. 2018, 223, 984–1000. [Google Scholar] [CrossRef]
- US Envionmental Protection Agency (USEPA). Stage 2 Disinfectants and Disinfection Byproducts Rule: A Quick Reference Guide For Schedule 4 Systems; USEPA: Cincinnati, OH, USA, 2006. Available online: https://nepis.epa.gov/Exe/ZyPDF.cgi?Dockey=P100A2D8.txt (accessed on 20 October 2022).
- US Envionmental Protection Agency. Comprehensive Disinfectants and Disinfection Byproducts Rules (Stage 1 and Stage 2): Quick Reference Guide; Systems DWRfSaPW; USEPA: Cincinnati, OH, USA, 2010. Available online: https://www.epa.gov/dwreginfo/stage-1-and-stage-2-disinfectants-and-disinfection-byproducts-rules (accessed on 20 October 2022).
- Tryby, M.E.; Boccelli, D.L.; Koechling, M.T.; Uber, J.G.; Summers, R.S.; Rossman, L.A. Booster chlorination for managing disinfectant residuals. J. Am. Water Work. Assoc. 1999, 91, 95–108. [Google Scholar] [CrossRef]
- Hua, P.; Vasyukova, E.; Uhl, W. A variable reaction rate model for chlorine decay in drinking water due to the reaction with dissolved organic matter. Water Res. 2015, 75, 109–122. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Sathasivan, A. Evaluation of suitable chlorine bulk-decay models for water distribution systems. Water Res. 2011, 45, 4896–4908. [Google Scholar] [CrossRef]
- Meng, F.; Liu, S.; Ostfeld, A.; Chen, C.; Burchard-Levine, A. A deterministic approach for optimization of booster disinfection placement and operation for a water distribution system in Beijing. J. Hydroinformatics 2013, 15, 1042–1058. [Google Scholar] [CrossRef]
- Al Heboos, S.; Licskó, I. Application and comparison of two chlorine decay models for predicting bulk chlorine residuals. Period. Polytech. Civ. Eng. 2017, 61, 7–13. [Google Scholar] [CrossRef] [Green Version]
- Hallam, N.; West, J.; Forster, C.; Powell, J.; Spencer, I. The decay of chlorine associated with the pipe wall in water distribution systems. Water Res. 2002, 36, 3479–3488. [Google Scholar] [CrossRef]
- García-Ávila, F.; Avilés-Añazco, A.; Ordoñez-Jara, J.; Guanuchi-Quezada, C.; del Pino, L.F.; Ramos-Fernández, L. Modeling of residual chlorine in a drinking water network in times of pandemic of the SARS-CoV-2 (COVID-19). Sustain. Environ. Res. 2021, 31, 1–15. [Google Scholar] [CrossRef]
- Fisher, I.; Kastl, G.; Sathasivan, A. New model of chlorine-wall reaction for simulating chlorine concentration in drinking water distribution systems. Water Res. 2017, 125, 427–437. [Google Scholar] [CrossRef]
- Clark, R.M. Chlorine Demand and TTHM Formation Kinetics: A Second-Order Model. J. Environ. Eng. 1998, 124, 16–24. [Google Scholar] [CrossRef]
- Boccelli, D.L.; Tryby, M.E.; Uber, J.G.; Summers, R. A reactive species model for chlorine decay and THM formation under rechlorination conditions. Water Res. 2003, 37, 2654–2666. [Google Scholar] [CrossRef]
- Gang, D.; Clevenger, T.E.; Banerji, S.K. Relationship of chlorine decay and THMs formation to NOM size. J. Hazard. Mater. 2003, 96, 1–12. [Google Scholar] [CrossRef]
- Deborde, M.; von Gunten, U. Reactions of chlorine with inorganic and organic compounds during water treatment—Kinetics and mechanisms: A critical review. Water Res. 2008, 42, 13–51. [Google Scholar] [CrossRef]
- Yang, X.; Shang, C.; Lee, W.; Westerhoff, P.; Fan, C. Correlations between organic matter properties and DBP formation during chloramination. Water Res. 2008, 42, 2329–2339. [Google Scholar] [CrossRef]
- Zhang, X.-L.; Yang, H.-W.; Wang, X.-M.; Fu, J.; Xie, Y.F. Formation of disinfection by-products: Effect of temperature and kinetic modeling. Chemosphere 2013, 90, 634–639. [Google Scholar] [CrossRef] [PubMed]
- Gallard, H.; von Gunten, U. Chlorination of phenols: Kinetics and formation of chloroform. Environ. Sci. Technol. 2002, 36, 884–890. [Google Scholar] [CrossRef] [PubMed]
- Hua, P. Variable Reaction Rate Models for Chlorine Decay and Trihalomethanes Formation in Drinking and Swimming Pool Waters; Technische Universität: Dresden, Germany, 2016; Available online: https://d-nb.info/1226430732/3 (accessed on 20 October 2022).
- Shang, F.; Uber, J.G.; Rossman, L.A.; Janke, R. EPANET Multi-Species Extension User’s Manual; Risk Reduction Engineering Laboratory, US Environmental Protection Agency: Cincinnati, OH, USA, 2008. [Google Scholar]
- American Public Health Association (APHA); American Water Works Association (AWWA); Water Environment Federation (WEF). Standard Methods for the Examination of Water and Wastewater; American Public Health Association: Washington, DC, USA, 2012. [Google Scholar]
- United States Envionmental Protection Agency (USEPA). Method 524.2. Measurement of Purgeable Organic Compounds in Water by Capillary Column Gas Chromatography/Mass Spectrometry; USEPA: Cincinnati, OH, USA, 1992; p. 43. Available online: https://settek.com/EPA-Method-524-2/ (accessed on 20 October 2022).
- Vasconcelos, J.J.; Rossman, L.A.; Grayman, W.M.; Boulos, P.F.; Clark, R.M. Kinetics of chlorine decay. J. Am. Water Work. Assoc. 1997, 89, 54–65. [Google Scholar] [CrossRef]
- Powell, J.C.; West, J.R.; Hallam, N.B.; Forster, C.F.; Simms, J. Performance of Various Kinetic Models for Chlorine Decay. J. Water Resour. Plan. Manag. 2000, 126, 13–20. [Google Scholar] [CrossRef]
- Shang, F.; Uber, J.G. Calibrating Pipe Wall Demand Coefficient for Chlorine Decay in Water Distribution System. J. Water Resour. Plan. Manag. 2007, 133, 363–371. [Google Scholar] [CrossRef]
- Rossman, L.A.; Clark, R.M.; Grayman, W.M. Modeling chlorine residuals in drinking-water distribution systems. J. Environ. Eng. 1994, 120, 803–820. [Google Scholar] [CrossRef]
- Rossman, L.A. EPANET Users Manual; USEPA: Cincinnati, OH, USA, 1994. Available online: https://nepis.epa.gov/Exe/ZyPURL.cgi?Dockey=3000349Y.TXT (accessed on 20 October 2022).
- Liu, Z.; Lompe, K.M.; Mohseni, M.; Bérubé, P.R.; Sauvé, S.; Barbeau, B. Biological ion exchange as an alternative to biological activated carbon for drinking water treatment. Water Res. 2020, 168, 115148. [Google Scholar] [CrossRef]
- McNeill, L.S.; Edwards, M. The importance of temperature in assessing iron pipe corrosion in water distribution systems. Environ. Monit. Assess. 2002, 77, 229–242. [Google Scholar] [CrossRef]
- Volk, C.; Dundore, E.; Schiermann, J.; Lechevallier, M. Practical evaluation of iron corrosion control in a drinking water distribution system. Water Res. 2000, 34, 1967–1974. [Google Scholar] [CrossRef]
- Kahil, M.A. Application of First Order Kinetics for Modeling Chlorine Decay in Water Networks. Int. J. Sci. Eng. Res. 2016, 7, 331–336. [Google Scholar]
- McGrath, J.; Maleki, M.; Bouchard, C.; Pelletier, G.; Rodriguez, M.J. Bulk and pipe wall chlorine degradation kinetics in three water distribution systems. Urban Water J. 2021, 18, 512–521. [Google Scholar] [CrossRef]
- Blokker, E.J.M.; Vreeburg, J.H.G.; Buchberger, S.G.; van Dijk, J.C. Importance of demand modelling in network water quality models: A review. Drink. Water Eng. Sci. 2008, 1, 27–38. [Google Scholar] [CrossRef]
- Koch, B.; Krasner, S.W.; Sclimenti, M.J.; Schimpff, W.K. Predicting the Formation of DBPs by the Simulated Distribution System. J. Am. Water Work. Assoc. 1991, 83, 62–70. [Google Scholar] [CrossRef]


| Water Source | DS Temperature (°C) | Ammonia Concentration (μg N/L) | DOC (mg C/L) | pH | Applied Dosage in the Lab (mg Cl2/L) |
|---|---|---|---|---|---|
| City A WTP (October 2020) 1 sample tested | 10 | 91 ± 5 | 2.10.03 | 7.10.03 | 2.170.03 |
| City B WTP (March 2021) 2 samples tested | 4 | <5 | 1.520.04 | 7.840.03 | 1.120.009 |
| City B WTP (October 2021) 3 samples tested | 17 | <5 | 1.680.04 | 7.820.02 | 2.00 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Absalan, F.; Hatam, F.; Barbeau, B.; Prévost, M.; Bichai, F. Predicting Chlorine and Trihalomethanes in a Full-Scale Water Distribution System under Changing Operating Conditions. Water 2022, 14, 3685. https://doi.org/10.3390/w14223685
Absalan F, Hatam F, Barbeau B, Prévost M, Bichai F. Predicting Chlorine and Trihalomethanes in a Full-Scale Water Distribution System under Changing Operating Conditions. Water. 2022; 14(22):3685. https://doi.org/10.3390/w14223685
Chicago/Turabian StyleAbsalan, Faezeh, Fatemeh Hatam, Benoit Barbeau, Michèle Prévost, and Françoise Bichai. 2022. "Predicting Chlorine and Trihalomethanes in a Full-Scale Water Distribution System under Changing Operating Conditions" Water 14, no. 22: 3685. https://doi.org/10.3390/w14223685





