Numerical Simulation of Debris Flow and Driftwood with Entrainment of Sediment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Computational Model
2.2.1. Debris-Flow Model
2.2.2. Bottom Shear-Stress of Debris Flow
2.2.3. Entrainment Erosion
2.3. Driftwood Generation Model
2.4. Calculation Procedure
2.5. Computational Conditions
3. Results
3.1. Model Reproducibility
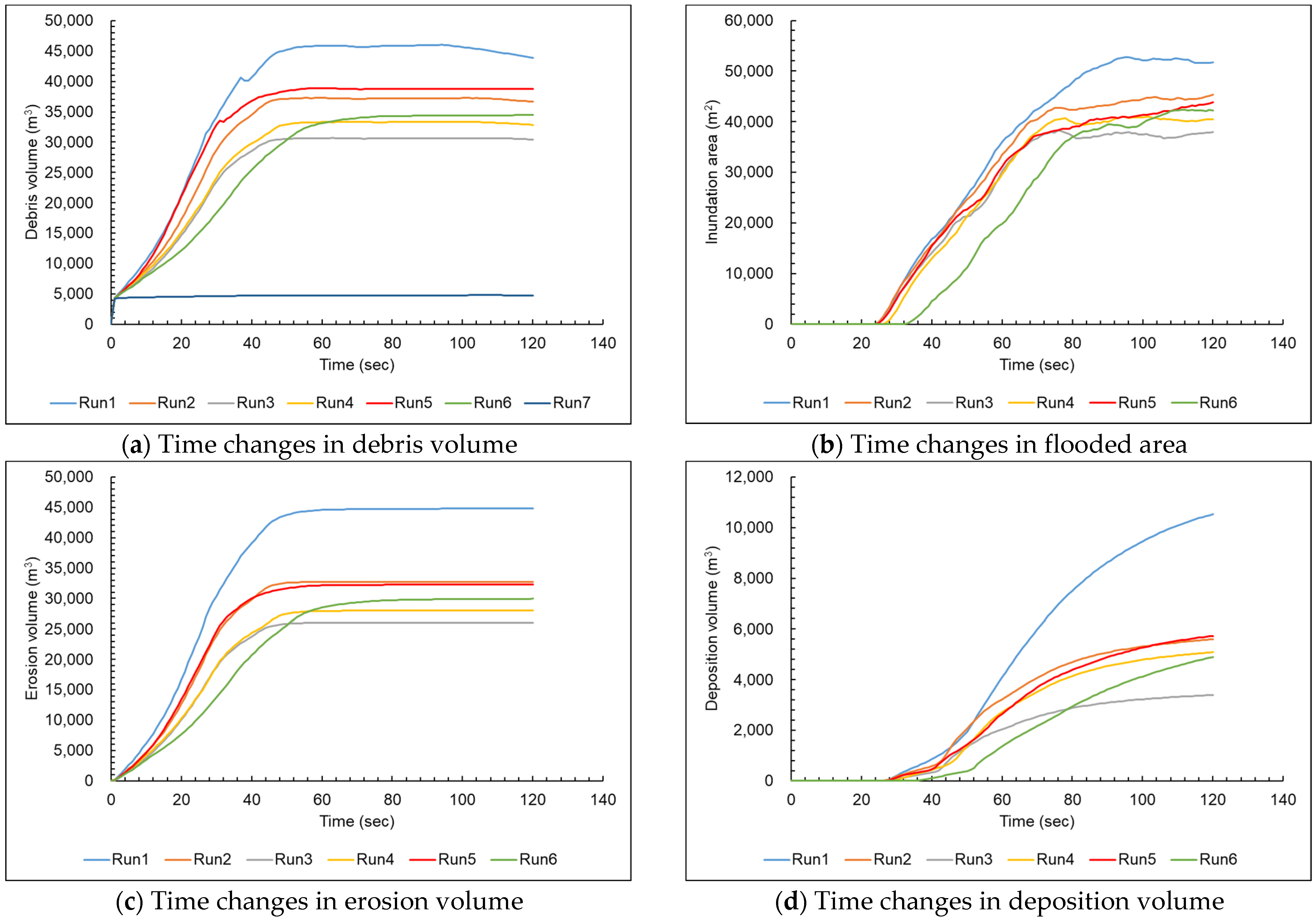
3.2. Time Changes in Simulation Results
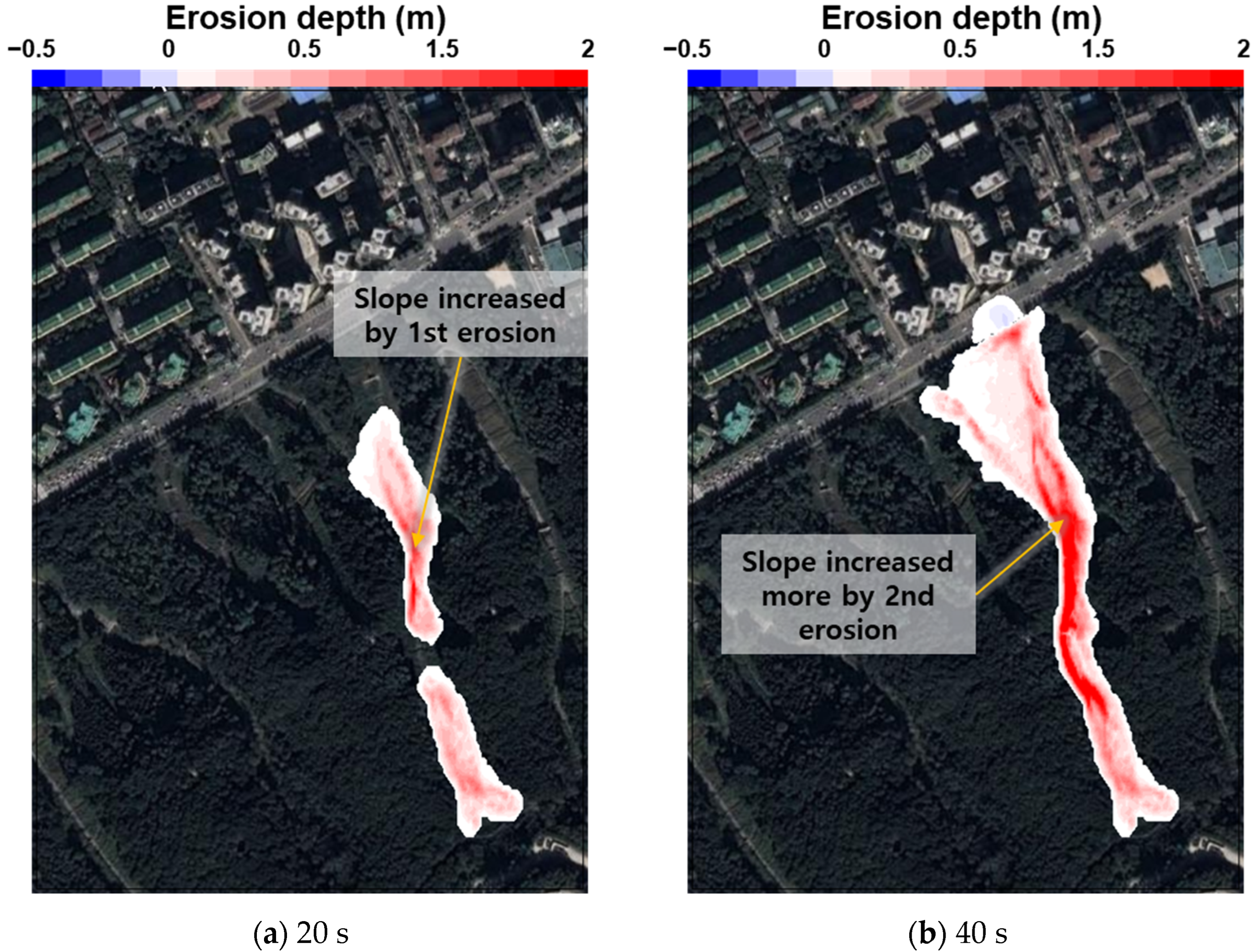
3.3. Final Patterns of Entrainment Erosion
4. Discussion
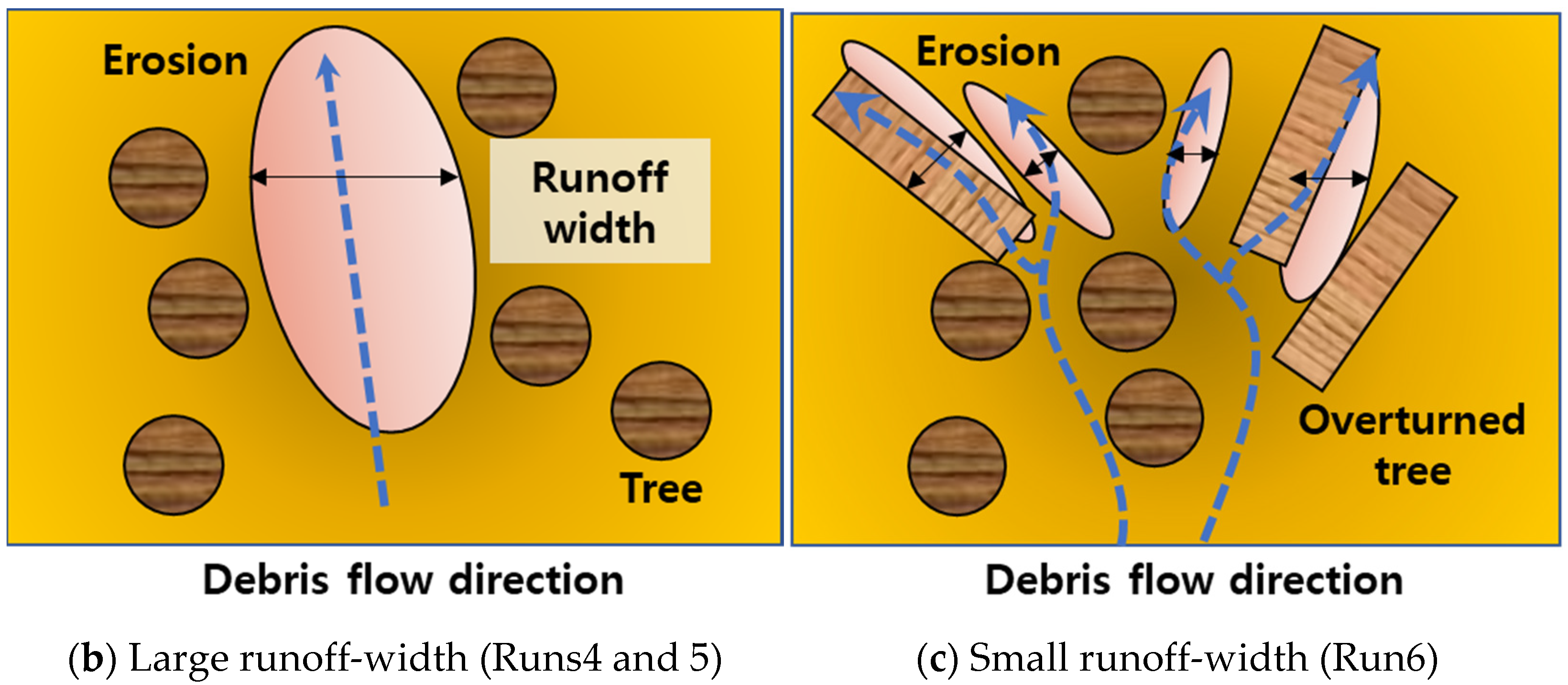
4.1. Patterns of Entrainment Erosion with Forest
4.2. Effect of Characterized Forest and Driftwood on Debris Flow
4.3. Vulnerability Analysis by Impulse Stress
4.4. Model Limits
4.4.1. Model Reproducibility
4.4.2. Model Sensitivity by Sediment Size
4.4.3. Applicability of Empirical Parameters
4.4.4. Two-Dimensional Plane Structured Flow of the Model
4.4.5. Wood Collision
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Korea Institute of Geoscience And Mineral Resources (KIGAM). Development of QRA system and damage mitigation technology of landslides. Research report, Office for Government Policy Coordination. KIGAM 2006, TRKO200500002717, 1–360. (In Korean) [Google Scholar]
- The Donga Ilbo. 2022. Available online: https://www.donga.com (accessed on 1 September 2022). (In Korean).
- Lee, M.; Kim, Y. Movement and deposition characteristics of debris flow according to rheological factors. J. Korean Soc. Agric. Eng. 2013, 29, 19–27. (In Korean) [Google Scholar]
- O’Brien, J.S.; Julien, P.Y. Physical properties and mechanics of hyper-concentrated sediment flows. In Proceedings of the Specialty Conference on Delineation of Landslide, Flash Flood and Debris Flow Hazard in Utah, Logan, UT, USA, 14–15 June 1984; Utah State University: Logan, UT, USA, 1985; pp. 260–279. [Google Scholar]
- Iverson, R.M.; Ried, M.E.; LaHusen, R.G. Debris-flow mobilization from landslides. Annu. Rev. Earth Planet. Sci. 1997, 25, 85–138. [Google Scholar] [CrossRef]
- Jeong, S. Rheological models for describing fine-laden debris flows: Grain-size effect. J. Korean Geotech. Soc. 2011, 27, 49–61. (In Korean) [Google Scholar] [CrossRef] [Green Version]
- Iverson, R.M. The debris-flow rheology myth. In Debris Flow Hazards Mitigation: Mechanics, Prediction and Assessment; Rickenmann, R., Chen, C.L., Eds.; Millpress: Bethlehem, PA, USA, 2003; pp. 303–314. [Google Scholar]
- O’Brien, J.S.; Julien, P.Y.; Fullerton, W.T. Two dimensional water flood and mudflow simulation. J. Hydraul. Engrg. ASCE 1993, 119, 244–261. [Google Scholar] [CrossRef]
- Beguería, S.; Van Asch, T.W.J.; Malet, J.-P.; Gröndahl, S. A GIS-based numerical model for simulating the kinematics of mud and debris flows over complex terrain. Nat. Hazards Earth Syst. Sci. 2009, 9, 1897–1909. [Google Scholar] [CrossRef] [Green Version]
- Blanc, T.; Pastor, M. Numerical simulation of debris flows with the 2D–SPH depth integrated model. In Proceedings of the EGU General Assembly Conference Abstracts, Vienna, Austria, 19–24 April 2009; p. 1978. [Google Scholar]
- Mergili, M.; Fellin, W.; Moreiras, S.M.; Stötter, J. Simulation of debris flows in the Central Andes based on open source GIS: Possibilities, limitations, and parameter sensitivity. Nat. Hazards 2012, 61, 1051–1081. [Google Scholar] [CrossRef] [Green Version]
- Imran, J.; Parker, G.; Locat, J.; Lee, H. 1D numerical model of muddy subaqueous and subaerial debris flows. J. Hydraul. Eng. ASCE 2000, 127, 959–968. [Google Scholar] [CrossRef]
- Shrestha, B.B.; Nakagawa, H.; Kawaike, K.; Baba, Y. Numerical simulation on debris-flow deposition and erosion processes upstream of a check dam with experimental verification. Annu. Disaster Prev. Res. Inst. 2008, 51, 613–624. [Google Scholar]
- D’Aniello, A.; Cozzolino, L.; Cimorelli, L.; Morte, R.D.; Pianese, D. A numerical model for the simulation of debris flow triggering, propagation and arrest. Nat. Hazards 2015, 75, 1403–1433. [Google Scholar] [CrossRef]
- Kim, S.; Paik, J.; Kim, K. Run-out modeling of debris flows in Mt. Umyeon using FLO-2D. J. Korean Soc. Civ. Eng. 2013, 33, 965–974. (In Korean) [Google Scholar]
- Hsu, S.M.; Chiou, L.B.; Lin, G.F.; Chao, C.H.; Wen, H.Y.; Ku, C.Y. Applications of simulation technique on debris-flow hazard zone delineation: A case study in Hualien County, Taiwan. Nat. Hazards Earth Syst. Sci. 2010, 10, 535–545. [Google Scholar] [CrossRef] [Green Version]
- Hussin, H.Y.; Quan Luna, B.; van Westen, C.J.; Christen, M.; Malet, J.-P.; van Asch, T.W.J. Parameterization of a numerical 2-D debris flow model with entrainment: A case study of the Faucon catchment, Southern French Alps. Nat. Hazards Earth Syst. Sci. 2012, 12, 3075–3090. [Google Scholar] [CrossRef] [Green Version]
- An, H.; Kim, M.; Lee, G.; Kim, Y.; Lim, H. Estimation of the area of sediment deposition by debris flow using a physical-based modeling approach. Quat. Int. 2019, 503, 59–69. [Google Scholar] [CrossRef]
- Lee, S.; An, H.; Kim, M.; Lim, H.; Kim, Y. A Simple Deposition Model for Debris Flow Simulation Considering the Erosion–Entrainment–Deposition Process. Remote Sens. 2022, 14, 1904. [Google Scholar] [CrossRef]
- Takahashi, T.; Nakagawa, H.; Harada, T.; Yamashiki, Y. Routing debris flows with particle segregation. J. Hydraul. Eng. ASCE 1992, 118, 1490–1507. [Google Scholar] [CrossRef]
- Shieh, C.L.; Jan, C.D.; Tsai, Y.F. A numerical simulation of debris flow and its application. Nat. Hazards 1996, 13, 39–54. [Google Scholar] [CrossRef]
- Ghilardi, P.; Natale, L.; Savi, F. Modeling debris flow propagation and deposition. Phys. Chem. Earth 2001, 26, 651–656. [Google Scholar] [CrossRef]
- Mambretti, S.; Larcan, E.; Wrachien, D.D. Theoretical and experimental analysis of debris flow: Rheology and two-phase modeling. Irrig. Drain. 2008, 57, 555–570. [Google Scholar] [CrossRef]
- Brufau, P.; Garcia-Navarro, P.; Ghilardi, P.; Natale, L.; Savi, F. 1D mathematical modelling of debris flow. J. Hydraul. Res. 2000, 38, 435–446. [Google Scholar] [CrossRef]
- Jan, C.D. A study on the numerical modeling of debris flow. In Proceedings of the 1997 1st International Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, San Francisco, CA, USA, 7–9 August 1997; pp. 717–726. [Google Scholar]
- Jin, M.; Fread, D.L. 1D routing of mud/debris flow using NWS FLDWAV model. In Proceedings of the First Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, San Francisco, CA, USA, 7–9 August 1997; pp. 687–696. [Google Scholar]
- Laigle, D.; Coussot, P. Numerical modeling of mudflows. J. Hydraul. Eng. 1997, 123, 617–623. [Google Scholar] [CrossRef]
- Locat, J. Normalized rheological behavior of fine muds and their flow properties in a pseudoplastic regime. In Proceedings of the First Conference on Debris-Flow Hazards Mitigation: Mechanics, Prediction, and Assessment, San Francisco, CA, USA, 7–9 August 1997; pp. 260–269. [Google Scholar]
- Takahashi, T. Debris Flow. Monograph Series of IAHR; Routledge & CRC Press Balkema: New York, NY, USA, 1991; pp. 1–165. [Google Scholar]
- Remaître, A.; Malet, J.-P.; Maquaire, O.; Ancey, C.; Locat, J. Flow behaviour and runout modelling of a complex debris flow in a clay-shale basin. Earth Surf. Process. Landf. 2005, 30, 479–488. [Google Scholar] [CrossRef]
- Shrestha, B.; Nakagawa, H.; Kawaike, K.; Baba, Y.; Zhang, H. Driftwood deposition from debris flows at slit-check dams and fans. Nat. Hazards 2012, 61, 577–602. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Bukcle, I. Coupled SPH–FEM modeling of tsunami-borne large debris flow and impact on coastal structures. J. Mar. Sci. 2021, 9, 1068. [Google Scholar] [CrossRef]
- Istrati, D.; Hasanpour, A. Advanced numerical modelling of large debris impact on piers during extreme flood events. In Proceedings of the 7th IAHR Europe Congress, Athens, Greece, 7–9 September 2022. [Google Scholar]
- Haehnel, R.B.; Daly, S.F. Maximum impact force of woody debris on floodplain structures. J. Hydraul. Eng. 2004, 130, 112–120. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D.; Bukcle, I. Multi-physics modeling of tsunami debris impact on bridge decks. In Proceedings of the 3rd International Conference on Natural Hazards & Infrastructure, Athens, Greece, 5–7 July 2022. [Google Scholar]
- Oudenbroek, K.; Naderi, N.; Bricker, J.D.; Yang, Y.; Van der Veen, C.; Uijttewaal, W.; Moriguchi, S.; Jonkman, S.N. Hydrodynamic and debris-damming failure of bridge decks and piers in steady flow. Geosciences 2018, 8, 409. [Google Scholar] [CrossRef] [Green Version]
- Istrati, D.; Hasanpour, A.; Buckle, I. Numerical investigation of tsunami-borne debris damming loads on a coastal bridge. In Proceedings of the 17 World Conference on Earthquake Engineering, Sendai, Japan, 13–18 September 2020. [Google Scholar]
- Ruiz-Villanueva, V.; Bladé, E.; Sánchez-Juny, M.; Marti-Cardona, B.; Díez-Herrero, A.; Bodoque, J.M. Two-dimensional numerical modeling of wood transport. J. Hydroinform. 2014, 16, 1077–1096. [Google Scholar] [CrossRef]
- Ruiz-Villanueva, V.; Gamberini, C.; Bladé, E.; Stoffel, M.; Bertoldi, W. Numerical Modeling of Instream Wood Transport, Deposition, and Accumulation in Braided Morphologies Under Unsteady Conditions: Sensitivity and High-Resolution Quantitative Model Validation. Water Resour. Res. 2020, 56, e2019WR026221. [Google Scholar] [CrossRef]
- Kang, T.; Kimura, I.; Shimizu, Y. Numerical simulation of large wood deposition patterns and responses of bed morphology in a braided river using large wood dynamics model. Earth Surf. Process. Landf. 2020, 45, 962–977. [Google Scholar] [CrossRef]
- Kang, T.; Kimura, I.; Onda, S. Application of Computational Modeling for Large Wood Dynamics with Collisions on Moveable Channel Beds. Adv. Water Resour. 2021, 152, 103912. [Google Scholar] [CrossRef]
- Persi, E.; Petaccia, G.; Sibilla, S.; Brufau, P.; García-Navarro, P. Calibration of a dynamic Eulerian-lagrangian model for the computation of wood cylinders transport in shallow water flow. J. Hydroinf. 2019, 21, 164–179. [Google Scholar] [CrossRef]
- Leonardi, A. Numerical simulation of debris flow and interaction between flow and obstacle via DEM. Doctoral Dissertation, ETH Zurich, Zürich, Switzerland, 2015. [Google Scholar]
- Nakagawa, H.; Takahashi, T.; Ikeguchi, M. Driftwood behavior by overland flood flows. J. Hydrosci. Hydraul. Eng. JSCE 1994, 12, 31–39. (In Japanese) [Google Scholar]
- Nakagawa, H.; Inoue, K.; Ikeguchi, M.; Tsubono, T. Behavior of driftwood and the process of its damming up. J. Hydrosci. Hydraul. Eng. JSCE 1995, 13, 55–67. (In Japanese) [Google Scholar]
- Gotoh, H.; Sakai, T.; Hayashi, M. Lagrangian model of drift-timbers induced flood by using moving particle semi-implicit model. J. Hydrosci. Hydraul. Eng. JSCE 2002, 20, 95–102. [Google Scholar]
- Ikari, H.; Gotoh, H.; Sumi, T. Computational mechanics of a blocking of gateless bottom outlet by drift woods. Annu. J. Hydraul. Eng. JSCE 2006, 50, 793–798, (In Japanese with English abstract). [Google Scholar] [CrossRef]
- Shimizu, Y.; Osada, K. Numerical simulation on the driftwood behavior in open-channel flows by using distinct element method. In Proceedings of the 8th International Conference on Hydro-Science and Engineering (ICHE-8), Nagoya, Japan, 9–11 September 2008. [Google Scholar]
- Eggertsson, O. Mackenzie river driftwood—A dendrochronological study. Arctic 1994, 47, 128–136. [Google Scholar] [CrossRef] [Green Version]
- Braudrick, C.A.; Grant, G.E.; Ishikawa, Y.; Ikeda, H. Dynamics of wood transport in streams: A flume experiment. Earth Surf. Process. Landf. 1997, 22, 669–683. [Google Scholar] [CrossRef]
- Abbe, T.B.; Montgomery, D.R. Patterns and processes of wood debris accumulation in the Queets river basin, Washington. Geomorphology 2003, 51, 81–107. [Google Scholar] [CrossRef]
- Comiti, F.; Andreoli, A.; Lenzi, M.A.; Mao, L. Spatial density and characteristics of woody debris in five mountain rivers of the Dolamites (Italian Alps). Geomorphology 2006, 78, 44–63. [Google Scholar] [CrossRef]
- Bochhiola, D.; Rulli, M.C.; Rosso, R. Transport of large woody debris in the presence of obstacles. Geomorphology 2006, 76, 166–178. [Google Scholar] [CrossRef]
- Rickenmann, D.; Laigle, D.; McArdell, B.W.; Hübl, J. Comparison of 2D debris-flow simulation models with field events. Comput. Geosci. 2006, 10, 241–264. [Google Scholar] [CrossRef] [Green Version]
- Crosta, G.B.; Imposimato, S.; Roddeman, D. Numerical modelling of entrainment/ deposition in rock and debris-avalanches. Eng. Geol. Mech. Veloc. Large Landslides 2009, 109, 135–145. [Google Scholar] [CrossRef]
- D’Ambrosio, D.; Di Gregorio, S.; Iovine, G. Simulating debris flows through a hexagonal cellular automata model: SCIDDICA S3–hex. Nat. Hazards Earth Syst. Sci. 2003, 3, 545–559. [Google Scholar] [CrossRef] [Green Version]
- Medina, V.; Hürlimann, M.; Bateman, A. Application of FLATModel, a 2D finite volume code, to debris flows in the northeastern part of the Iberian Peninsula. Landslides 2008, 5, 127–142. [Google Scholar] [CrossRef]
- Hungr, O.; McDougall, S. Two numerical models for landslide dynamic analysis. Comput. Geosci. 2009, 35, 978–992. [Google Scholar] [CrossRef]
- Pastor, M.; Haddad, B.; Sorbino, G.; Cuomo, S.; Drempetic, V. A depth-integrated, coupled SPH model for flow-like landslides and related phenomena. Int. J. Numer. Anal. Methods Geomech. 2009, 33, 143–172. [Google Scholar] [CrossRef]
- Shimizu, Y.; Suzuki, E.; Kawamura, S.; Inoue, T.; Iwasaki, T.; Hamaki, M.; Omura, K.; Kakegawa, E. Nays2D Flood solver manual. Int. River Interface Coop. 2015. [Google Scholar]
- International River Interface Cooperative (iRIC). 2022. Available online: http://i-ric.org/en (accessed on 1 September 2022).
- Seoul City. Research contract report: Addition and Complement causes survey of Mt, vol.2011 Woomyeon landslide. Res. Rep. 2014, 51-6110000-000649-01, 1–46. (In Korean) [Google Scholar]
- Yonhapnews. 2011. Available online: https://www.yna.co.kr (accessed on 1 September 2022). (In Korean).
- Sisain. 2011. Available online: https://www.sisain.co.kr (accessed on 1 September 2022). (In Korean).
- Kang, T.; Kimura, I. Computational modeling for large wood dynamics with root wad and anisotropic bed friction in shallow flows. Adv. Water Resour. 2018, 121, 419–431. [Google Scholar] [CrossRef]
- Kimura, I.; Kitanozo, K. Effects of the driftwood Richardson number and applicability of a 3D-2D model to heavy wood jamming around obstacles. Environ. Fluid Mech. 2020, 20, 503–525. [Google Scholar] [CrossRef]
- Hasanpour, A.; Istrati, D. Reducing extreme flooding loads on essential facilities via elevated structures. In Proceedings of the ASCE Lifelines Conference, Los Angeles, CA, USA, 31 January–4 February 2022. [Google Scholar]
- United States Department of Agriculture. Wood Handbook; Department of Agriculture: Washington, DC, USA, 2010. [Google Scholar]
- National Geographic Information Institute (NGII). Mt. Umyon Digital Topographical Map 2022. Available online: https://www.ngii.go.kr (accessed on 1 September 2022). (In Korean)









| Parameter | Value (Unit) | Parameter | Value (Unit) |
|---|---|---|---|
| Initial debris flow volume | 4250 (m3) | Critical bending stress of wood breaking | 45 (MPa) |
| Advection of concentration | Upwind | Critical bending stress of wood deformation | 8 (MPa) |
| Turbulence model | Zero equation | Advection of flow | TVD-MUSCL |
| Computational domain | 0.6 (width) 0.8 (length) (km2) | Uniform grid size | 3 3 (m2) |
| Resolution of topography | 1 1 (m2) | Manning roughness coefficient | 0.04 (s/m1/3) |
| Angle of repose | 25 (degree) | Simulation time | 120 (s) |
| Density of water | 1000 (kg/m3) | Density of forest of study area | 6000 (0.06 m2) |
| Density of tree | 800 (kg/m3) | Mean stem-length of wood | 10.3 (m) |
| Static-friction coefficient of driftwood | 0.9 | Mean stem-diameter of wood | 0.28 (m) |
| Rolling friction coefficient of driftwood | 0.4 | Kinematic friction coefficient of driftwood | 0.6 |
| Concentration of sediment–water mixture | 0.4 | Max. concentration | 0.55 |
| Limitative concentration | 0.5 | Density of sediment | 2000 (kg/m3) |
| Time step | 0.01 (s) | Max. erosion depth | 3 (m) |
| Erosion ratio | 0.001 | Deposition ratio | 0.01 |
| No. | Sediment Size (mm) | Wood Diameter of Forest (m) | Driftwood Generation | Density of Forest (Tree Number/m2) | Remarks |
|---|---|---|---|---|---|
| Run1 | 0.75 | - | N | - | Small diameter |
| Run2 | 1 | - | N | - | Standard |
| Run3 | 1.25 | - | N | - | Large diameter |
| Run4 | 1 | 0.231 | Y | 0.06 | Run2 with driftwood |
| Run5 | 1 | 0.231 | Y | 0.3 | Forest density 5 |
| Run6 | 1 | 1.155 | Y | 0.06 | Stem diameter 5 |
| Run7 | 1 | - | N | - | No-entrainment erosion |
| Case | Impact Height (1) (m) | Inflowing Velocity (2) (m/s) | Final Debris Volume (3) (m3) | Driftwood Volume (m3) |
|---|---|---|---|---|
| Observation | 12.0 | 28.0 | 42,500 | - |
| Run1 | 5.3 | 16.5 | 43,892 | - |
| Run2 | 12.9 | 20.4 | 36,653 | - |
| Run3 | 12.4 | 22.1 | 30,403 | - |
| Run4 | 11.9 | 20.5 | 32,843 (32,041, without driftwood) | 802 |
| Run5 | 10.1 | 19.2 | 38,775 (35,591, without driftwood) | 3814 |
| Run6 | 8.5 | 20.1 | 34,441 | 0 |
| Run7 | 0.8 | 14.3 | 4775 | - |
| No. | Height Acc. (-) | Velocity Acc. (-) | Debris Vol. Acc. (-) | Mean Acc. Value (-) |
|---|---|---|---|---|
| Run1 | 0.44 | 0.59 | 0.97 | 0.67 |
| Run2 | 0.93 | 0.73 | 0.86 | 0.84 |
| Run3 | 0.97 | 0.79 | 0.72 | 0.82 |
| Run4 | 0.99 | 0.73 | 0.77 | 0.83 |
| Run5 | 0.84 | 0.69 | 0.91 | 0.81 |
| Run6 | 0.71 | 0.72 | 0.81 | 0.75 |
| Run7 | 0.07 | 0.51 | 0.11 | 0.23 |
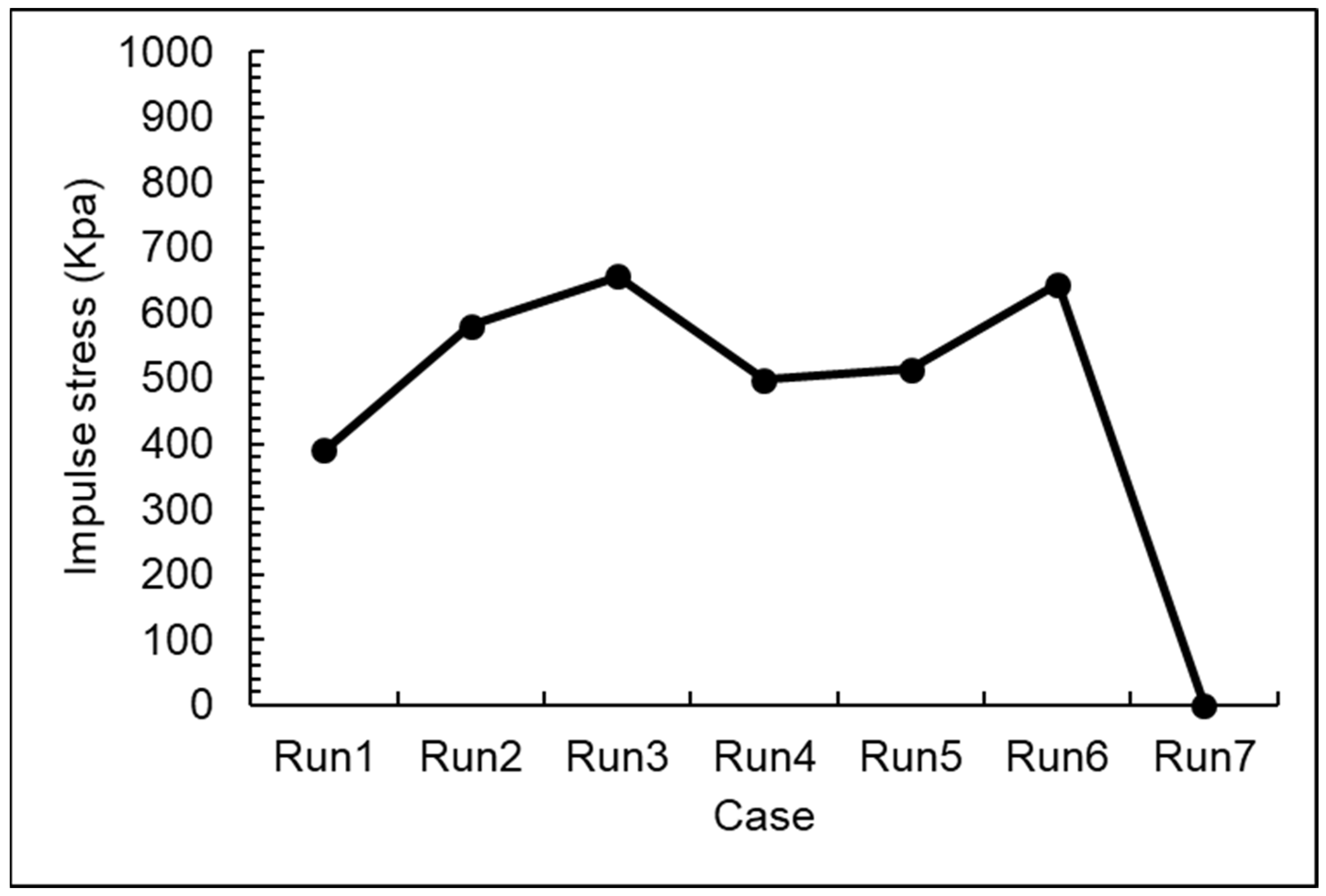
| No. | Concentration of Sediment–Water Mixture (m3/m3) | Impact Velocity at Target Area 1 (m/s) | Water Density (kg/m3) | Sediment Density (kg/m3) | Impulse Stress (kPa) |
|---|---|---|---|---|---|
| Run1 | 0.45 | 16.4 | 1000 | 2000 | 389.9 |
| Run2 | 0.48 | 19.8 | 1000 | 2000 | 580.2 |
| Run3 | 0.42 | 21.5 | 1000 | 2000 | 656.3 |
| Run4 | 0.47 | 18.4 | 1000 | 2000 | 497.6 |
| Run5 | 0.39 | 19.2 | 1000 | 2000 | 514.2 |
| Run6 | 0.49 | 20.8 | 1000 | 2000 | 644.6 |
| Run7 | 0 | 0.95 | 1000 | 2000 | 0.9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kang, T.; Jang, C.-L.; Kimura, I.; Lee, N. Numerical Simulation of Debris Flow and Driftwood with Entrainment of Sediment. Water 2022, 14, 3673. https://doi.org/10.3390/w14223673
Kang T, Jang C-L, Kimura I, Lee N. Numerical Simulation of Debris Flow and Driftwood with Entrainment of Sediment. Water. 2022; 14(22):3673. https://doi.org/10.3390/w14223673
Chicago/Turabian StyleKang, Taeun, Chang-Lae Jang, Ichiro Kimura, and Namjoo Lee. 2022. "Numerical Simulation of Debris Flow and Driftwood with Entrainment of Sediment" Water 14, no. 22: 3673. https://doi.org/10.3390/w14223673








