Multi-Step Ahead Probabilistic Forecasting of Daily Streamflow Using Bayesian Deep Learning: A Multiple Case Study
Abstract
:1. Introduction
2. Materials and Methods
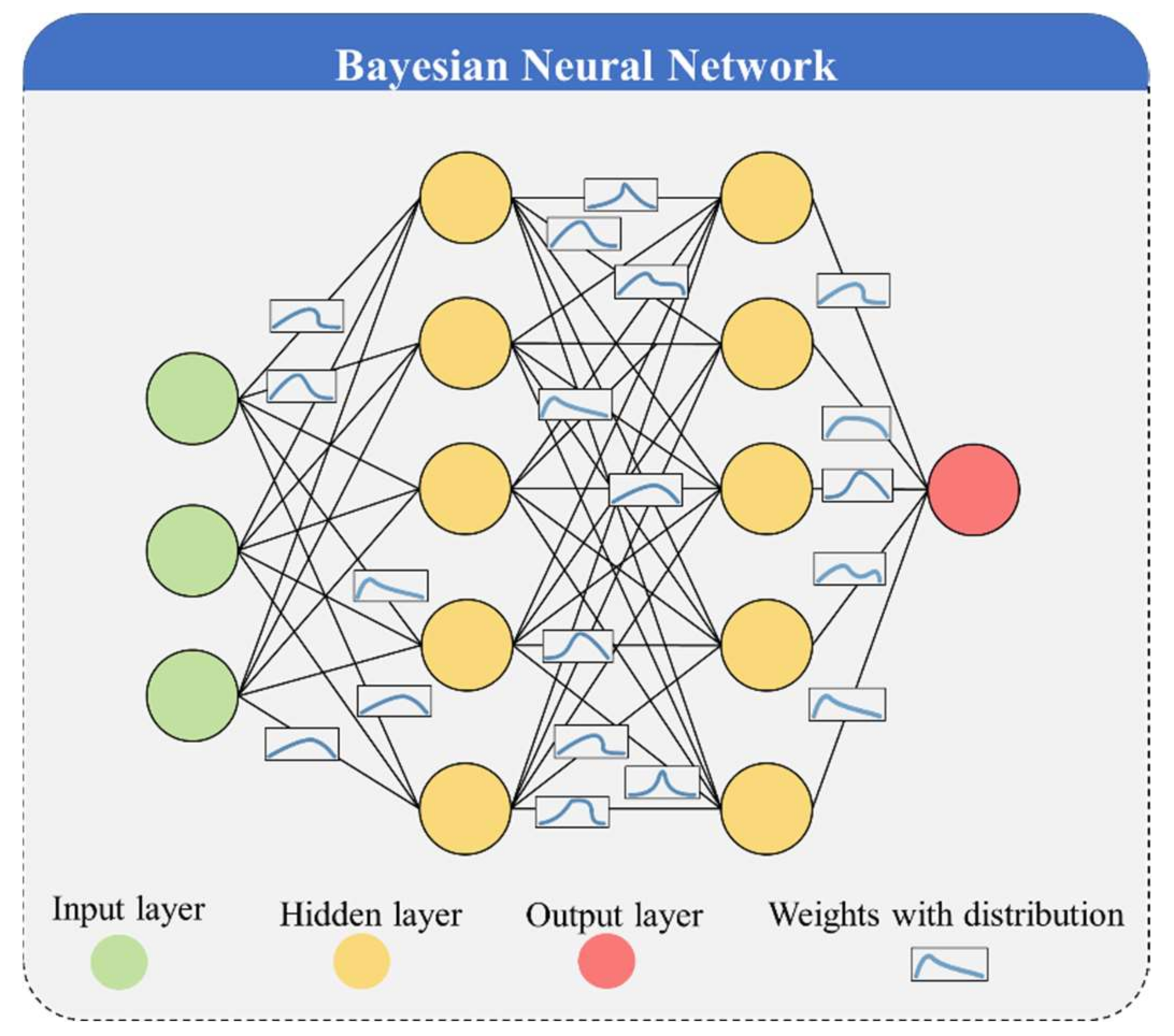
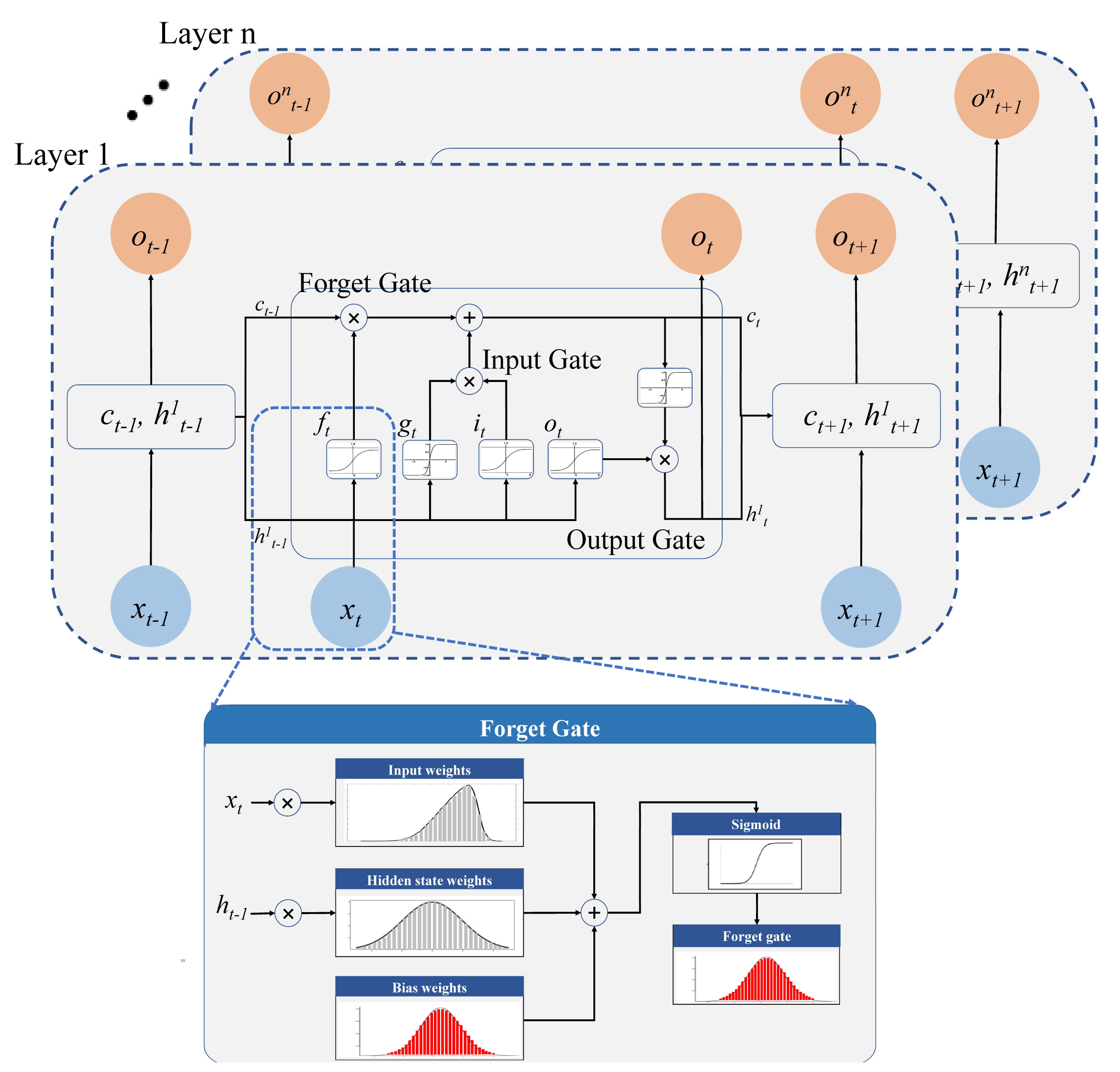
2.1. Bayesian Long Short-Term Memory (BLSTM)
2.1.1. Epistemic Uncertainty
2.1.2. Aleatoric Uncertainty
2.1.3. Combining Aleatoric and Epistemic Uncertainty
2.2. Performance Evaluation Metrics
- 1.
- Metric for Deterministic Forecasting
- 2.
- Metrics for Probabilistic Forecasting
3. Case Study
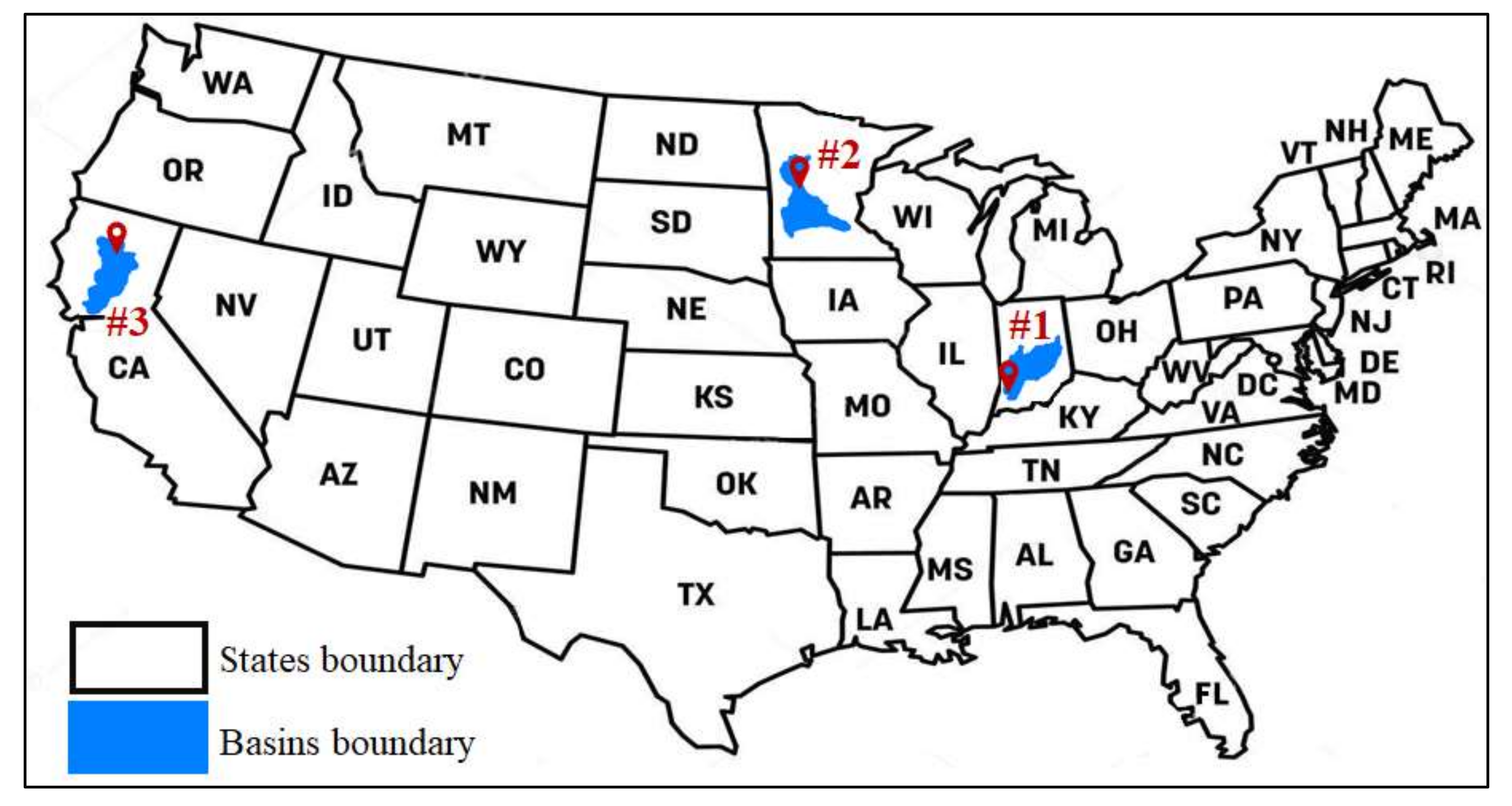
3.1. Study Area
3.2. Experiment Setup
4. Result and Discussion
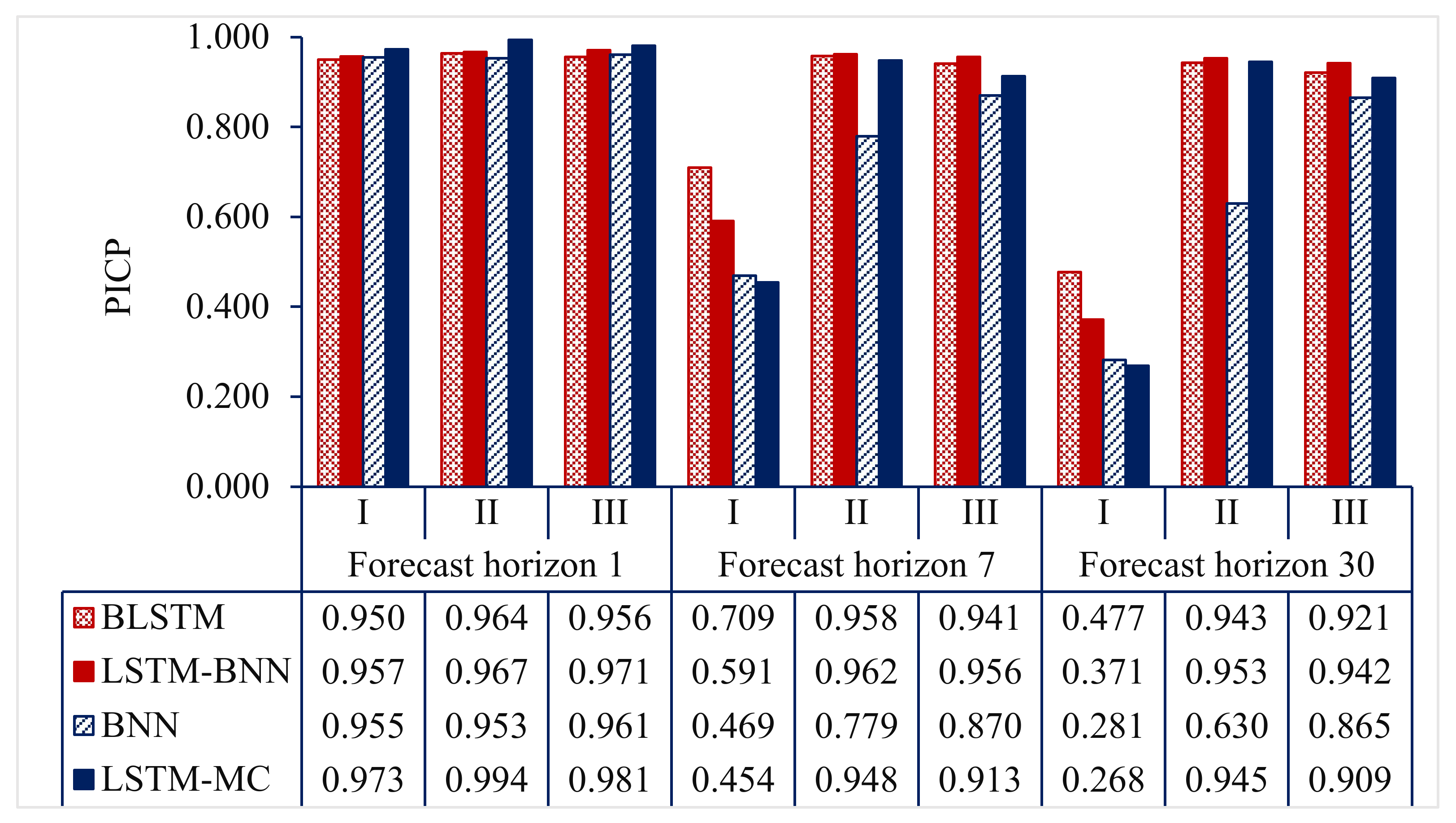
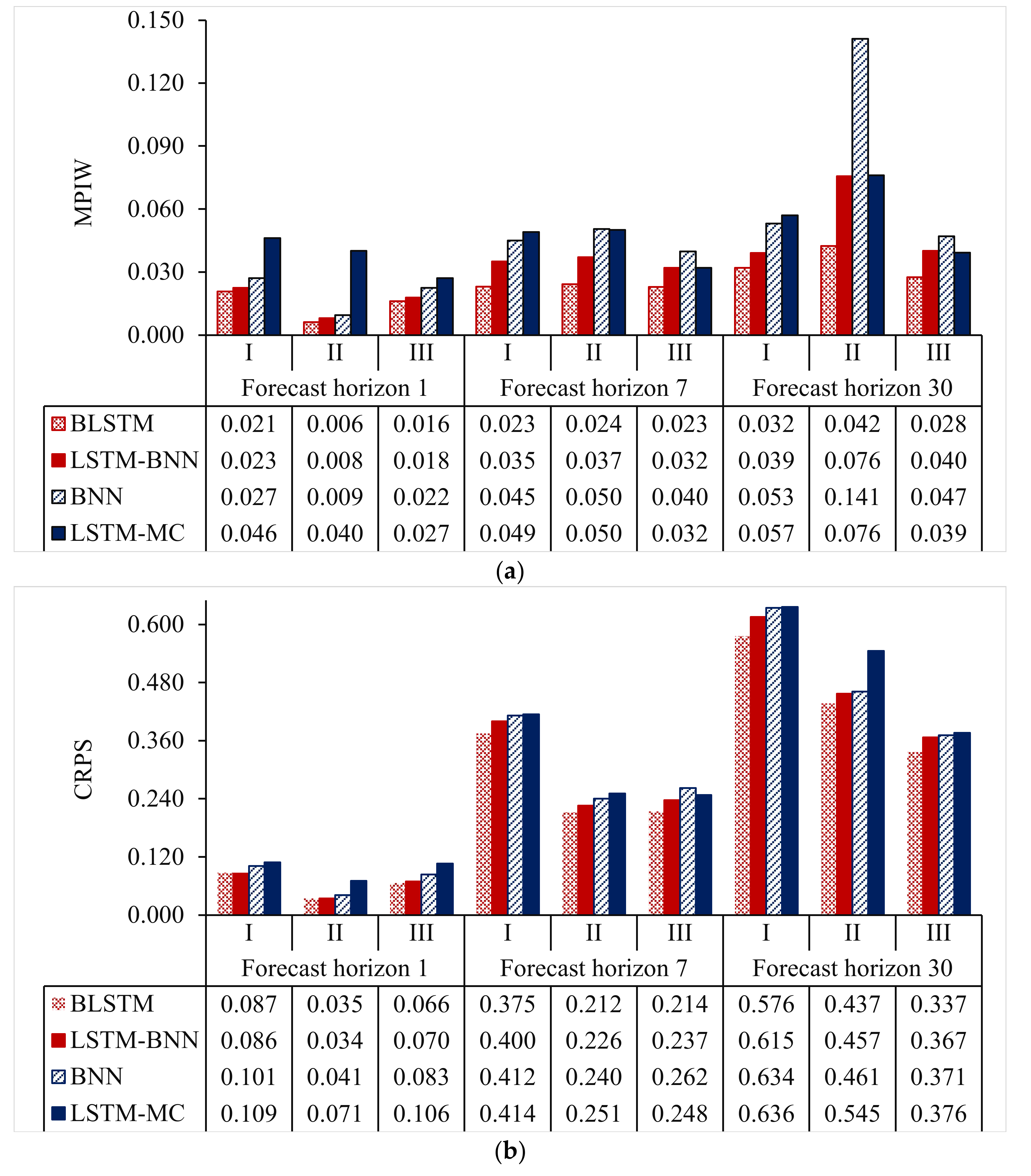
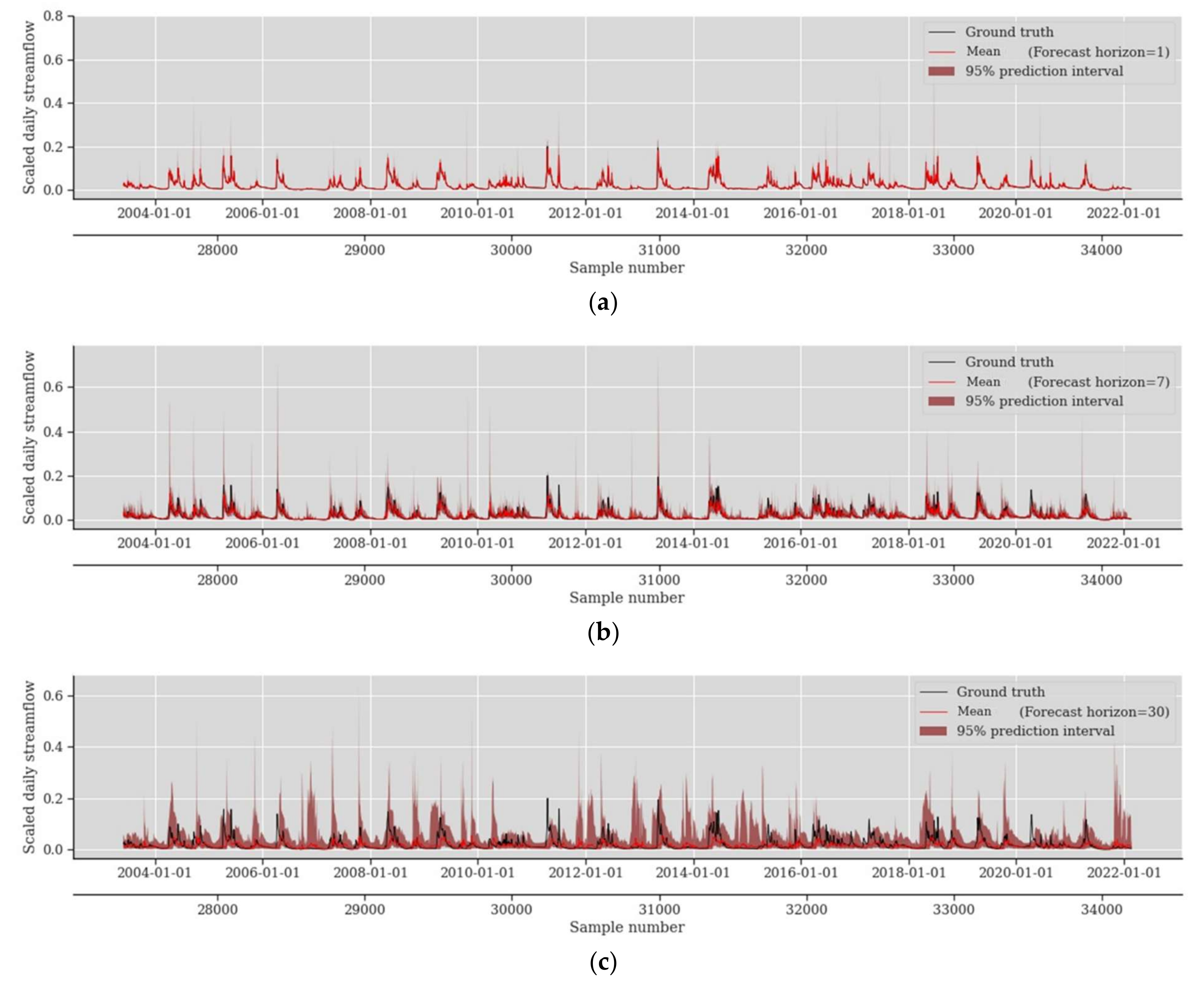
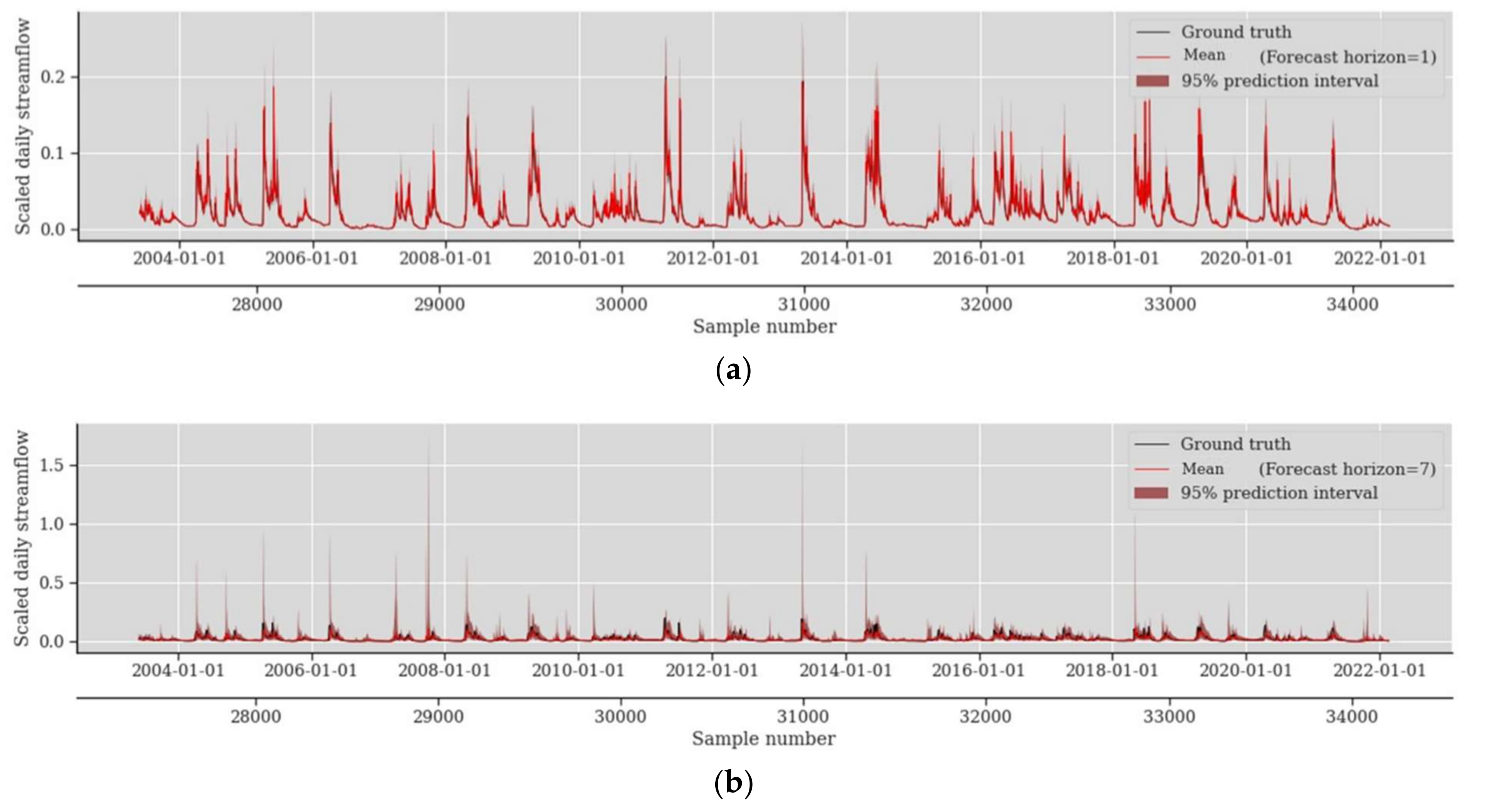
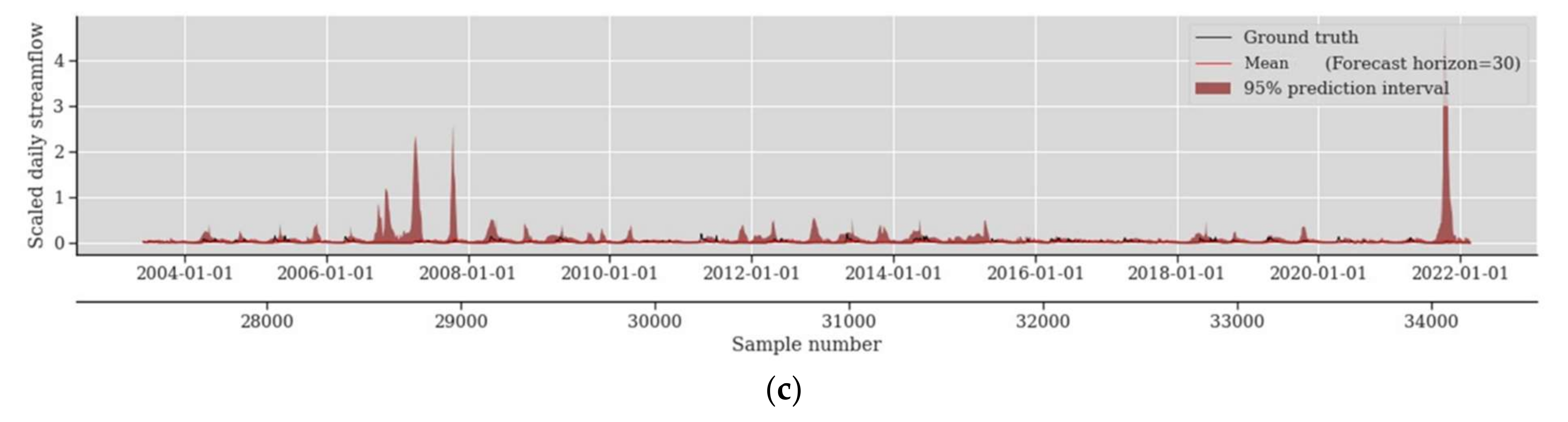
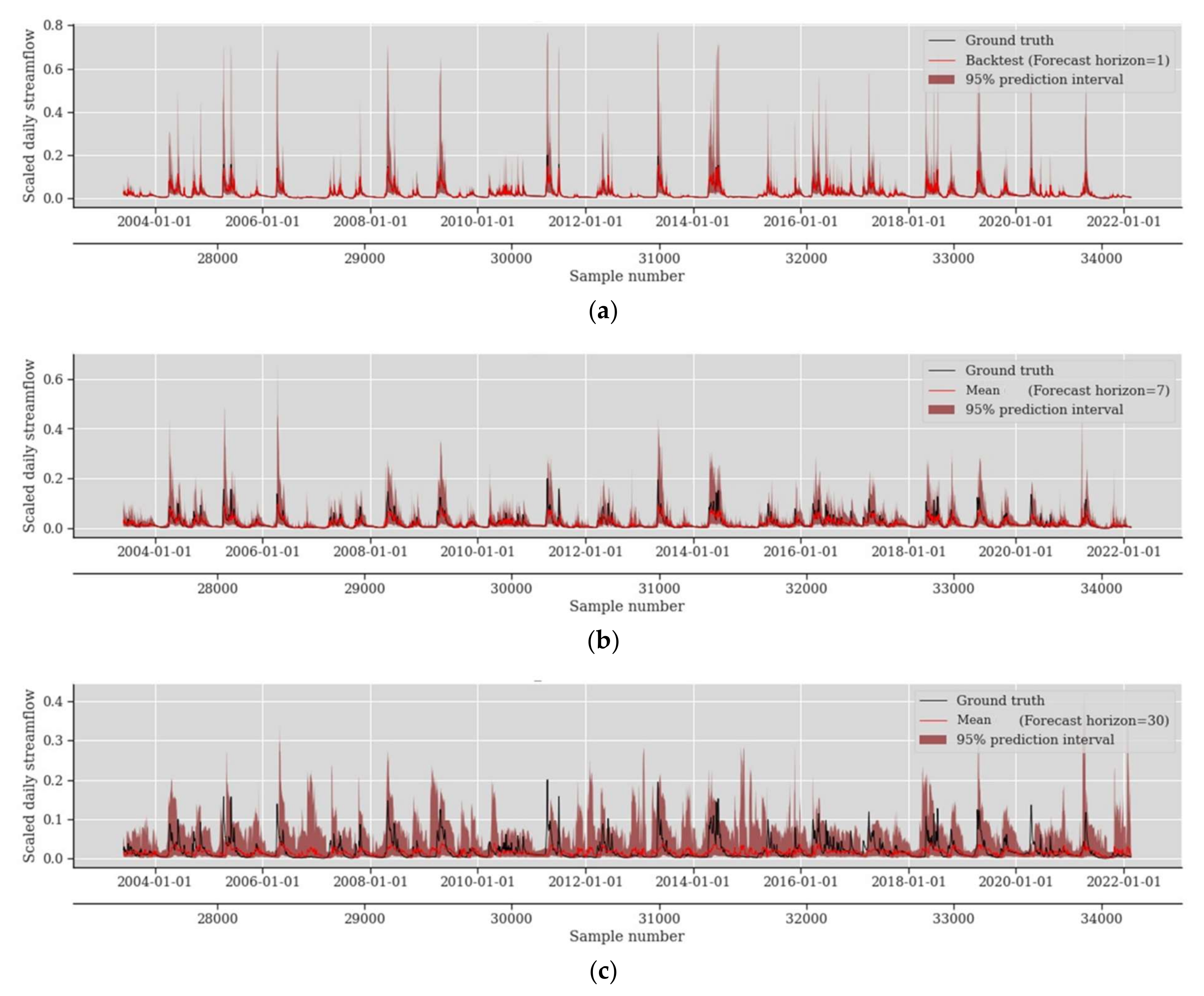
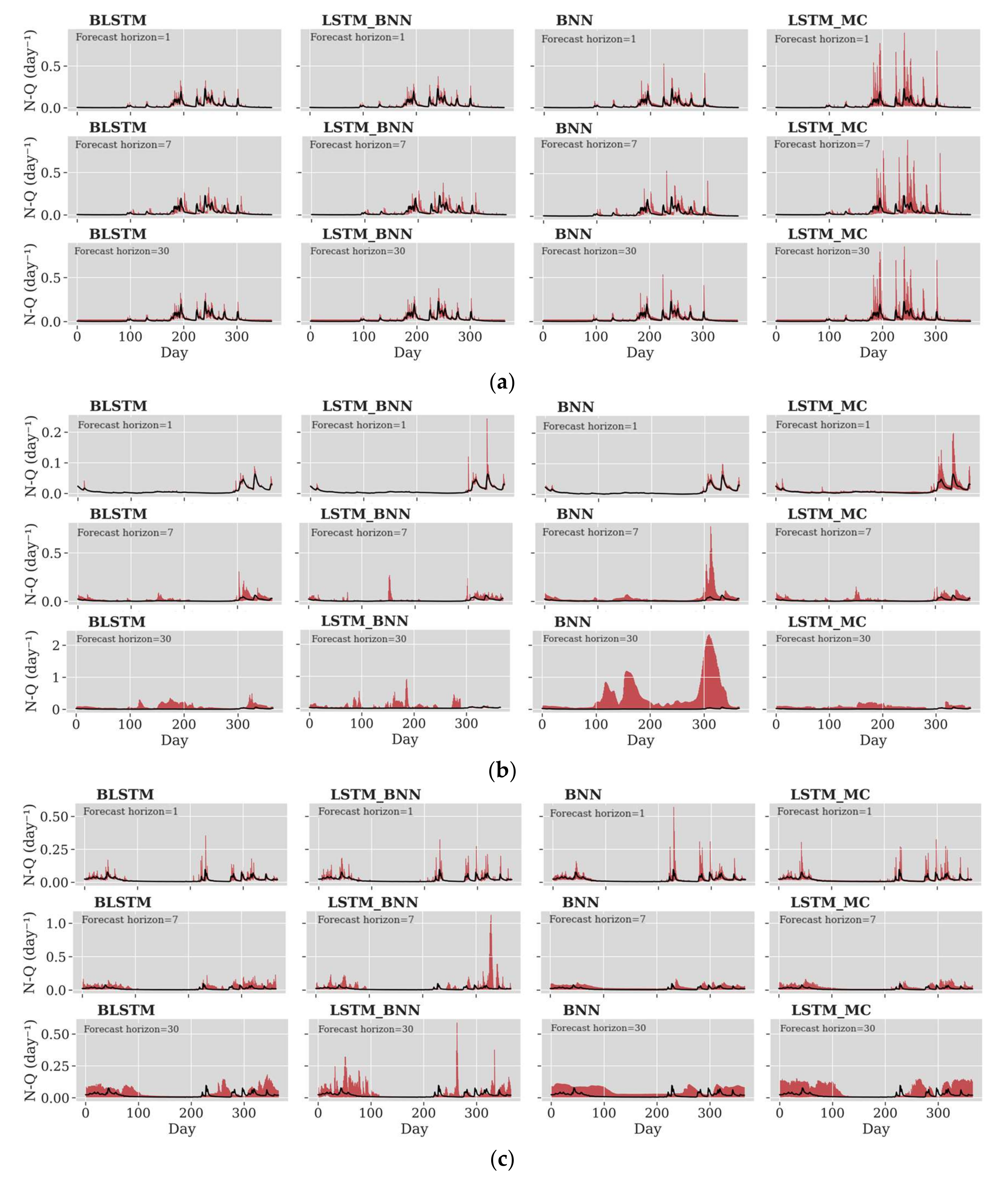
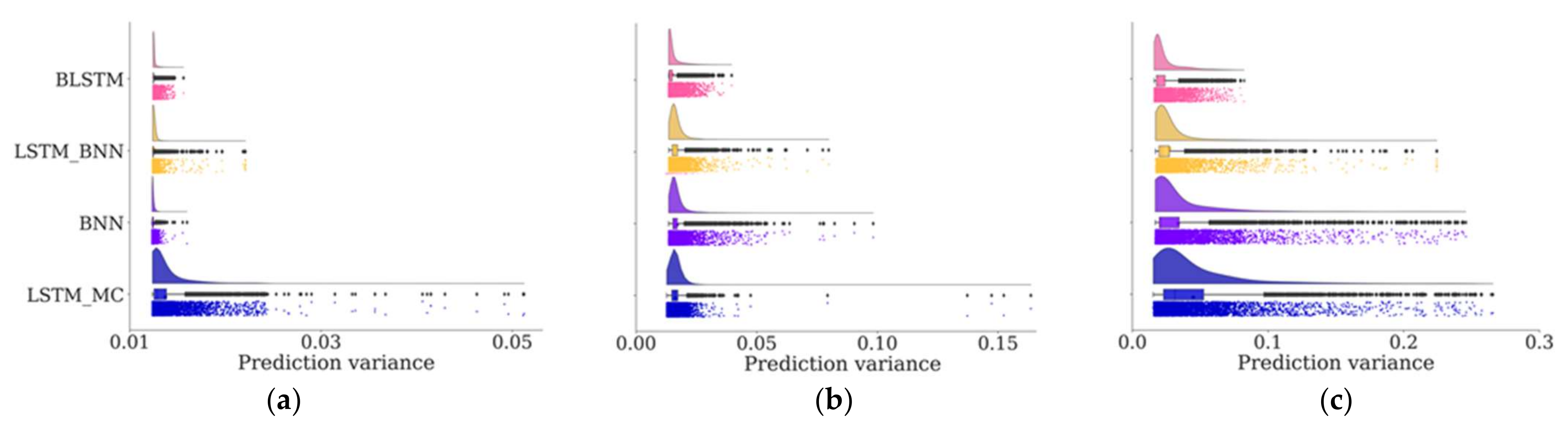
4.1. Probabilistic Prediction Performance Assessment
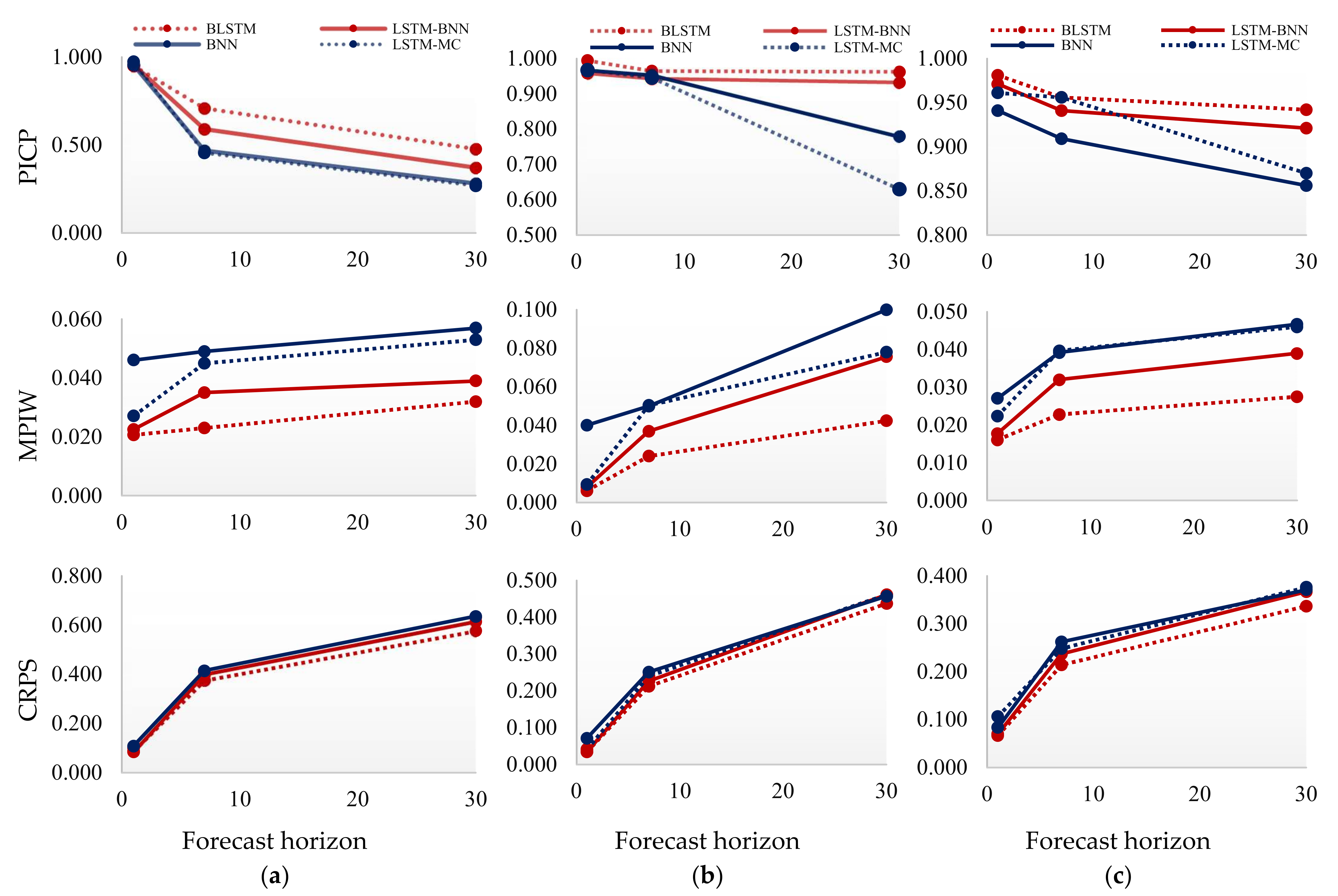
4.2. Impact of Forecast Horizon in Probabilistic Prediction Performance
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ghobadi, F.; Kang, D. Improving Long-Term Streamflow Prediction in a Poorly Gauged Basin Using Geo-Spatiotemporal Mesoscale Data and Attention-Based Deep Learning: A Comparative Study. J. Hydrol. 2022, 615, 128608. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, J.; Li, R.; Suo, X.; Lu, E.H. Medium and Long-Term Precipitation Prediction Using Wavelet Decomposition-Prediction-Reconstruction Model. Water Resour. Manag. 2022, 36, 971–987. [Google Scholar] [CrossRef]
- Dikshit, A.; Pradhan, B.; Santosh, M. Artificial Neural Networks in Drought Prediction in the 21st Century–A Scientometric Analysis. Appl. Soft Comput. 2022, 114, 108080. [Google Scholar] [CrossRef]
- Van den Hurk, B.J.J.M.; Bouwer, L.M.; Buontempo, C.; Döscher, R.; Ercin, E.; Hananel, C.; Hunink, J.E.; Kjellström, E.; Klein, B.; Manez, M.; et al. Improving Predictions and Management of Hydrological Extremes through Climate Services: Www.Imprex.Eu. Clim. Serv. 2016, 1, 6–11. [Google Scholar] [CrossRef]
- Lange, H.; Sippel, S. Machine Learning Applications in Hydrology BT—Forest-Water Interactions; Levia, D.F., Carlyle-Moses, D.E., Iida, S., Michalzik, B., Nanko, K., Tischer, A., Eds.; Springer International Publishing: Cham, Switzerland, 2020; pp. 233–257. ISBN 978-3-030-26086-6. [Google Scholar]
- Lin, Y.; Wang, D.; Wang, G.; Qiu, J.; Long, K.; Du, Y.; Xie, H.; Wei, Z.; Shangguan, W.; Dai, Y. A Hybrid Deep Learning Algorithm and Its Application to Streamflow Prediction. J. Hydrol. 2021, 601, 126636. [Google Scholar] [CrossRef]
- Hagen, J.S.; Leblois, E.; Lawrence, D.; Solomatine, D.; Sorteberg, A. Identifying Major Drivers of Daily Streamflow from Large-Scale Atmospheric Circulation with Machine Learning. J. Hydrol. 2021, 596, 126086. [Google Scholar] [CrossRef]
- Ren, K.; Wang, X.; Shi, X.; Qu, J.; Fang, W. Examination and Comparison of Binary Metaheuristic Wrapper-Based Input Variable Selection for Local and Global Climate Information-Driven One-Step Monthly Streamflow Forecasting. J. Hydrol. 2021, 597, 126152. [Google Scholar] [CrossRef]
- Tayerani Charmchi, A.S.; Ifaei, P.; Yoo, C.K. Smart Supply-Side Management of Optimal Hydro Reservoirs Using the Water/Energy Nexus Concept: A Hydropower Pinch Analysis. Appl. Energy 2021, 281, 116136. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H. A Review of Machine Learning Concepts and Methods for Addressing Challenges in Probabilistic Hydrological Post-Processing and Forecasting. arXiv 2022. [Google Scholar] [CrossRef]
- Ghimire, S.; Yaseen, Z.M.; Farooque, A.A.; Deo, R.C.; Zhang, J.; Tao, X. Streamflow Prediction Using an Integrated Methodology Based on Convolutional Neural Network and Long Short-Term Memory Networks. Sci. Rep. 2021, 11, 17497. [Google Scholar] [CrossRef]
- Klotz, D.; Kratzert, F.; Gauch, M.; Keefe Sampson, A.; Brandstetter, J.; Klambauer, G.; Hochreiter, S.; Nearing, G. Uncertainty Estimation with Deep Learning for Rainfall-Runoff Modeling. Hydrol. Earth Syst. Sci. 2022, 26, 1673–1693. [Google Scholar] [CrossRef]
- Papacharalampous, G.; Tyralis, H.; Langousis, A.; Jayawardena, A.W.; Sivakumar, B.; Mamassis, N.; Montanari, A.; Koutsoyiannis, D. Probabilistic Hydrological Post-Processing at Scale: Why and How to Apply Machine-Learning Quantile Regression Algorithms. Water 2019, 11, 2126. [Google Scholar] [CrossRef] [Green Version]
- Adnan, R.M.; Liang, Z.; Parmar, K.S.; Soni, K.; Kisi, O. Modeling Monthly Streamflow in Mountainous Basin by MARS, GMDH-NN and DENFIS Using Hydroclimatic Data. Neural Comput. Appl. 2021, 33, 2853–2871. [Google Scholar] [CrossRef]
- Apaydin, H.; Taghi Sattari, M.; Falsafian, K.; Prasad, R. Artificial Intelligence Modelling Integrated with Singular Spectral Analysis and Seasonal-Trend Decomposition Using Loess Approaches for Streamflow Predictions. J. Hydrol. 2021, 600, 126506. [Google Scholar] [CrossRef]
- Mehdizadeh, S.; Fathian, F.; Safari, M.J.S.; Adamowski, J.F. Comparative Assessment of Time Series and Artificial Intelligence Models to Estimate Monthly Streamflow: A Local and External Data Analysis Approach. J. Hydrol. 2019, 579, 124225. [Google Scholar] [CrossRef]
- Nanda, T.; Sahoo, B.; Chatterjee, C. Enhancing Real-Time Streamflow Forecasts with Wavelet-Neural Network Based Error-Updating Schemes and ECMWF Meteorological Predictions in Variable Infiltration Capacity Model. J. Hydrol. 2019, 575, 890–910. [Google Scholar] [CrossRef]
- Khosravi, K.; Golkarian, A.; Tiefenbacher, J.P. Using Optimized Deep Learning to Predict Daily Streamflow: A Comparison to Common Machine Learning Algorithms. Water Resour. Manag. 2022, 36, 699–716. [Google Scholar] [CrossRef]
- Xu, W.; Chen, J.; Zhang, X.J. Scale Effects of the Monthly Streamflow Prediction Using a State-of-the-Art Deep Learning Model. Water Resour. Manag. 2022, 36, 3609–3625. [Google Scholar] [CrossRef]
- Cheng, M.; Fang, F.; Kinouchi, T.; Navon, I.M.; Pain, C.C. Long Lead-Time Daily and Monthly Streamflow Forecasting Using Machine Learning Methods. J. Hydrol. 2020, 590, 125376. [Google Scholar] [CrossRef]
- Cui, Z.; Zhou, Y.; Guo, S.; Wang, J.; Xu, C.Y. Effective Improvement of Multi-Step-Ahead Flood Forecasting Accuracy through Encoder-Decoder with an Exogenous Input Structure. J. Hydrol. 2022, 609, 127764. [Google Scholar] [CrossRef]
- Yin, H.; Zhang, X.; Wang, F.; Zhang, Y.; Xia, R.; Jin, J. Rainfall-Runoff Modeling Using LSTM-Based Multi-State-Vector Sequence-to-Sequence Model. J. Hydrol. 2021, 598, 126378. [Google Scholar] [CrossRef]
- Kao, I.F.; Zhou, Y.; Chang, L.C.; Chang, F.J. Exploring a Long Short-Term Memory Based Encoder-Decoder Framework for Multi-Step-Ahead Flood Forecasting. J. Hydrol. 2020, 583, 124631. [Google Scholar] [CrossRef]
- Babaeian, E.; Paheding, S.; Siddique, N.; Devabhaktuni, V.K.; Tuller, M. Short- and Mid-Term Forecasts of Actual Evapotranspiration with Deep Learning. J. Hydrol. 2022, 612, 128078. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A Rainfall-Runoff Model With LSTM-Based Sequence-to-Sequence Learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Ferreira, L.B.; da Cunha, F.F. Multi-Step Ahead Forecasting of Daily Reference Evapotranspiration Using Deep Learning. Comput. Electron. Agric. 2020, 178, 105728. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F.; de Marinis, G. Stacked Machine Learning Algorithms and Bidirectional Long Short-Term Memory Networks for Multi-Step Ahead Streamflow Forecasting: A Comparative Study. J. Hydrol. 2022, 613, 128431. [Google Scholar] [CrossRef]
- Masrur Ahmed, A.A.; Deo, R.C.; Feng, Q.; Ghahramani, A.; Raj, N.; Yin, Z.; Yang, L. Deep Learning Hybrid Model with Boruta-Random Forest Optimiser Algorithm for Streamflow Forecasting with Climate Mode Indices, Rainfall, and Periodicity. J. Hydrol. 2021, 599, 126350. [Google Scholar] [CrossRef]
- Rahimzad, M.; Moghaddam Nia, A.; Zolfonoon, H.; Soltani, J.; Danandeh Mehr, A.; Kwon, H.H. Performance Comparison of an LSTM-Based Deep Learning Model versus Conventional Machine Learning Algorithms for Streamflow Forecasting. Water Resour. Manag. 2021, 35, 4167–4187. [Google Scholar] [CrossRef]
- Barzegar, R.; Aalami, M.T.; Adamowski, J. Coupling a Hybrid CNN-LSTM Deep Learning Model with a Boundary Corrected Maximal Overlap Discrete Wavelet Transform for Multiscale Lake Water Level Forecasting. J. Hydrol. 2021, 598, 126196. [Google Scholar] [CrossRef]
- Granata, F.; Di Nunno, F. Forecasting Evapotranspiration in Different Climates Using Ensembles of Recurrent Neural Networks. Agric. Water Manag. 2021, 255, 107040. [Google Scholar] [CrossRef]
- Zheng, Y.; Xie, Y.; Long, X. A Comprehensive Review of Bayesian Statistics in Natural Hazards Engineering. Nat. Hazards 2021, 108, 63–91. [Google Scholar] [CrossRef]
- Han, S.; Coulibaly, P. Bayesian Flood Forecasting Methods: A Review. J. Hydrol. 2017, 551, 340–351. [Google Scholar] [CrossRef]
- Costa, V.; Fernandes, W. Bayesian Estimation of Extreme Flood Quantiles Using a Rainfall-Runoff Model and a Stochastic Daily Rainfall Generator. J. Hydrol. 2017, 554, 137–154. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, X.; Fang, H.; Lai, R.; Zhang, Y.; Huang, L.; Liu, X. A Real-Time Probabilistic Channel Flood-Forecasting Model Based on the Bayesian Particle Filter Approach. Environ. Model. Softw. 2017, 88, 151–167. [Google Scholar] [CrossRef] [Green Version]
- Huang, Y.; Shao, C.; Wu, B.; Beck, J.L.; Li, H. State-of-the-Art Review on Bayesian Inference in Structural System Identification and Damage Assessment. Adv. Struct. Eng. 2019, 22, 1329–1351. [Google Scholar] [CrossRef]
- Goodarzi, L.; Banihabib, M.E.; Roozbahani, A.; Dietrich, J. Bayesian Network Model for Flood Forecasting Based on Atmospheric Ensemble Forecasts. Nat. Hazards Earth Syst. Sci. 2019, 19, 2513–2524. [Google Scholar] [CrossRef] [Green Version]
- Bai, H.; Li, G.; Liu, C.; Li, B.; Zhang, Z.; Qin, H. Hydrological Probabilistic Forecasting Based on Deep Learning and Bayesian Optimization Algorithm. Hydrol. Res. 2021, 52, 927–943. [Google Scholar] [CrossRef]
- Zhu, S.; Luo, X.; Yuan, X.; Xu, Z. An Improved Long Short-Term Memory Network for Streamflow Forecasting in the Upper Yangtze River. Stoch. Environ. Res. Risk Assess. 2020, 34, 1313–1329. [Google Scholar] [CrossRef]
- Gude, V.; Corns, S.; Long, S. Flood Prediction and Uncertainty Estimation Using Deep Learning. Water 2020, 12, 884. [Google Scholar] [CrossRef] [Green Version]
- Althoff, D.; Rodrigues, L.N.; Bazame, H.C. Uncertainty Quantification for Hydrological Models Based on Neural Networks: The Dropout Ensemble. Stoch. Environ. Res. Risk Assess. 2021, 35, 1051–1067. [Google Scholar] [CrossRef]
- Li, D.; Marshall, L.; Liang, Z.; Sharma, A. Hydrologic Multi-Model Ensemble Predictions Using Variational Bayesian Deep Learning. J. Hydrol. 2022, 604, 127221. [Google Scholar] [CrossRef]
- He, Y.; Fan, H.; Lei, X.; Wan, J. A Runoff Probability Density Prediction Method Based on B-Spline Quantile Regression and Kernel Density Estimation. Appl. Math. Model. 2021, 93, 852–867. [Google Scholar] [CrossRef]
- Lu, D.; Konapala, G.; Painter, S.L.; Kao, S.C.; Gangrade, S. Streamflow Simulation in Data-Scarce Basins Using Bayesian and Physics-Informed Machine Learning Models. J. Hydrometeorol. 2021, 22, 1421–1438. [Google Scholar] [CrossRef]
- Sun, M.; Zhang, T.; Wang, Y.; Strbac, G.; Kang, C. Using Bayesian Deep Learning to Capture Uncertainty for Residential Net Load Forecasting. IEEE Trans. Power Syst. 2020, 35, 188–201. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Gan, D.; Sun, M.; Zhang, N.; Lu, Z.; Kang, C. Probabilistic Individual Load Forecasting Using Pinball Loss Guided LSTM. Appl. Energy 2019, 235, 10–20. [Google Scholar] [CrossRef] [Green Version]
- Toubeau, J.F.; Bottieau, J.; Vallee, F.; De Greve, Z. Deep Learning-Based Multivariate Probabilistic Forecasting for Short-Term Scheduling in Power Markets. IEEE Trans. Power Syst. 2019, 34, 1203–1215. [Google Scholar] [CrossRef]
- Wang, H.; Yi, H.; Peng, J.; Wang, G.; Liu, Y.; Jiang, H.; Liu, W. Deterministic and Probabilistic Forecasting of Photovoltaic Power Based on Deep Convolutional Neural Network. Energy Convers. Manag. 2017, 153, 409–422. [Google Scholar] [CrossRef]
- Xu, L.; Hu, M.; Fan, C. Probabilistic Electrical Load Forecasting for Buildings Using Bayesian Deep Neural Networks. J. Build. Eng. 2022, 46, 103853. [Google Scholar] [CrossRef]
- Van der Meer, D.W.; Shepero, M.; Svensson, A.; Widén, J.; Munkhammar, J. Probabilistic Forecasting of Electricity Consumption, Photovoltaic Power Generation and Net Demand of an Individual Building Using Gaussian Processes. Appl. Energy 2018, 213, 195–207. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Q.; Singh, V.P. Univariate Streamflow Forecasting Using Commonly Used Data-Driven Models: Literature Review and Case Study. Hydrol. Sci. J. 2018, 63, 1091–1111. [Google Scholar] [CrossRef]
- Lange, H.; Sippel, S. Machine Learning Applications in Hydrology. In Forest-Water Interactions; Ecological Studies, Volume 240; Springer: Cham, Switzerland, 2020; pp. 233–257. [Google Scholar]
- Abdul Kareem, B.; Zubaidi, S.L.; Ridha, H.M.; Al-Ansari, N.; Al-Bdairi, N.S.S. Applicability of ANN Model and CPSOCGSA Algorithm for Multi-Time Step Ahead River Streamflow Forecasting. Hydrology 2022, 9, 171. [Google Scholar] [CrossRef]
- Wegayehu, E.B.; Muluneh, F.B. Short-Term Daily Univariate Streamflow Forecasting Using Deep Learning Models. Adv. Meteorol. 2022, 2022, 1860460. [Google Scholar] [CrossRef]
- Kendall, A.; Gal, Y. What Uncertainties Do We Need in Bayesian Deep Learning for Computer Vision? Adv. Neural Inf. Process. Syst. 2017, 2017, 5575–5585. [Google Scholar] [CrossRef]
- Blundell, C.; Cornebise, J.; Kavukcuoglu, K.; Wierstra, D. Weight Uncertainty in Neural Networks. arXiv 2015. [Google Scholar] [CrossRef]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Li, G.; Yang, L.; Lee, C.G.; Wang, X.; Rong, M. A Bayesian Deep Learning RUL Framework Integrating Epistemic and Aleatoric Uncertainties. IEEE Trans. Ind. Electron. 2021, 68, 8829–8841. [Google Scholar] [CrossRef]
- Bernardo, J.M.; Smith, A.F.M. Bayesian Theory; Wiley Blackwell: Hoboken, NJ, USA, 2008; ISBN 9780470316870. [Google Scholar]
- Runnalls, A.R. Kullback-Leibler Approach to Gaussian Mixture Reduction. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 989–999. [Google Scholar] [CrossRef] [Green Version]
- Jospin, L.V.; Buntine, W.; Boussaid, F.; Laga, H.; Bennamoun, M. Hands-on Bayesian Neural Networks–A Tutorial for Deep Learning Users. IEEE Comput. Intell. Mag. 2020, 17, 29–48. [Google Scholar] [CrossRef]
- Gal, Y.; Ghahramani, Z. Dropout as a Bayesian Approximation: Representing Model Uncertainty in Deep Learning. 33rd Int. Conf. Mach. Learn. ICML 2016, 3, 1651–1660. [Google Scholar] [CrossRef]
- Gal, Y. Uncertainty in Deep Learning. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2016. [Google Scholar]
- Abdar, M.; Pourpanah, F.; Hussain, S.; Rezazadegan, D.; Liu, L.; Ghavamzadeh, M.; Fieguth, P.; Cao, X.; Khosravi, A.; Acharya, U.R.; et al. A Review of Uncertainty Quantification in Deep Learning: Techniques, Applications and Challenges. Inf. Fusion 2021, 76, 243–297. [Google Scholar] [CrossRef]
- Jian, X.; Wolock, D.M.; Lins, H.F.; Henderson, R.J.; Brady, S.J. Streamflow—Water Year 2021: U.S. Geological Survey Fact Sheet 2022–3072; USGS: Reston, VA, USA, 2022. [Google Scholar]
- Chen, R.; Cao, J.; Zhang, D. Probabilistic Prediction of Photovoltaic Power Using Bayesian Neural Network-LSTM Model. In Proceedings of the 2021 IEEE 4th International Conference on Renewable Energy and Power Engineering (REPE), Beijing, China, 9–11 October 2021; pp. 294–299. [Google Scholar] [CrossRef]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Salakhutdinov, R. Dropout: A Simple Way to Prevent Neural Networks from Overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Fortunato, M.; Blundell, C.; Vinyals, O. Bayesian Recurrent Neural Networks. arXiv 2019. [Google Scholar] [CrossRef]
- Ketkar, N. Introduction to Keras. In Deep Learning with Python; Ketkar, N., Ed.; Apress: Berkeley, CA, USA, 2017; pp. 97–111. ISBN 978-1-4842-2766-4. [Google Scholar]
- Abadi, M.; Barham, P.; Chen, J.; Chen, Z.; Davis, A.; Dean, J.; Devin, M.; Ghemawat, S.; Irving, G.; Isard, M.; et al. TensorFlow: A System for Large-Scale Machine Learning. In Proceedings of the 12th USENIX Symposium on Operating Systems Design and Implementation (OSDI 16), Savannah, GA, USA, 2–4 November 2016; pp. 265–283. [Google Scholar]
- PyTorch Documentation—PyTorch 1.13 Documentation. Available online: https://pytorch.org/docs/stable/index.html (accessed on 7 November 2022).


| Field | Probabilistic Method | Base Models | Posterior Approximation * | Evaluation Metrics | Ref. | ||
|---|---|---|---|---|---|---|---|
| VI | MCM | Deterministic | Probabilistic | ||||
| Streamflow | LSTM-HetGP | ANN, HetGP, GLM, LSTM | - | - | NSE, RMSE, MRE, MSLE | percentage of coverage (POC) and the average interval width (AIW) | [39] |
| Flood | LSTM | ARIMA | - | - | RMSE, MAE | [40] | |
| Streamflow | LSTM with multiparameter ensemble and dropout ensemble | _ | - | ✓ | PBIAS, MARE, RMSE, NSE, KGE | POC, average width (AW), average interval score (AIS) | [41] |
| Streamflow | Variational Bayesian Long Short-Term Memory network (VB-LSTM) | Bayesian model Averaging (BMA) | ✓ | - | MAE | CRPS | [42] |
| Runoff | XGBoost (XGB) and Gaussian process regression (GPR) with Bayesian optimization algorithm (BOA) | GBR, LGB, CNN, LSTM, ANN, SVR, QR, GPR—combined with GPR | - | - | RMSE, MAPE, R2 | Coverage probability, Mean width percentage, Suitability metric, CRPS | [38] |
| Runoff | B-spline quantile regression model combined with kernel density estimation | QR, QRNN | - | - | RMSE, R2, Qr | PICP, PINAW, CRPS | [43] |
| Streamflow | Bayesian LSTM model | physics-based hydrologic model (Precipitation-Runoff Modeling System) | - | ✓ | NSE, RMSE-observations standard deviation ratio (RSR) | [44] | |
| Criteria | Case Study 1 | Case Study 2 | Case Study 3 |
|---|---|---|---|
| No. Samples | 27,146 | 34,205 | 22,645 |
| Mean (m3/s) | 58 | 30 | 31 |
| Std (m3/s) | 90 | 51 | 42 |
| Min (m3/s) | 2.5 | 0.6 | 3 |
| 25% (m3/s) | 13 | 4 | 9 |
| 50% (m3/s) | 31 | 11 | 20 |
| 75% (m3/s) | 64 | 32 | 36 |
| Max (m3/s) | 1654 | 702 | 1274 |
| Case Study. No. | Station ID | G-Name | Elev. (m) | Drainage Area (km2) | Lon. (°) | Lat. (°) | Period |
|---|---|---|---|---|---|---|---|
| 1 | 03364000 | EAST FORK WHITE RIVER AT COLUMBUS, IN | 183.8 | 4421 | 85°55′32″ | 39°12′00″ | 1948–2022 |
| 2 | 05131500 | LITTLE FORK RIVER AT LITTLEFORK, MN | 330.3 | 4403 | 93°32′57″ | 48°23′45″ | 1928–2022 |
| 3 | 11368000 | MCCLOUD R AB SHASTA LK CA | 335.3 | 1564 | 122°13′07″ | 40°57′30″ | 1945–2007 |
| Forecast Horizon = 1 | Forecast Horizon = 7 | Forecast Horizon = 30 | |||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Model | Metric | Case I | Case II | Case III | Case I | Case II | Case III | Case I | Case II | Case III | |||||||||
| BLSTM | PICP | 0.950 |  | 0.964 |  | 0.956 |  | 0.709 |  | 0.958 |  | 0.941 |  | 0.477 |  | 0.943 |  | 0.921 |  |
| MPIW | 0.021 |  | 0.006 |  | 0.016 |  | 0.023 |  | 0.024 |  | 0.023 |  | 0.032 |  | 0.042 |  | 0.028 |  | |
| CRPS | 0.087 |  | 0.035 |  | 0.066 |  | 0.375 |  | 0.212 |  | 0.214 |  | 0.576 |  | 0.437 |  | 0.337 |  | |
| LSTM-BNN | PICP | 0.957 |  | 0.967 |  | 0.971 |  | 0.591 |  | 0.962 |  | 0.956 |  | 0.371 |  | 0.953 |  | 0.942 |  |
| MPIW | 0.023 |  | 0.008 |  | 0.018 |  | 0.035 |  | 0.037 |  | 0.032 |  | 0.039 |  | 0.076 |  | 0.040 |  | |
| CRPS | 0.086 |  | 0.034 |  | 0.070 |  | 0.400 |  | 0.226 |  | 0.237 |  | 0.615 |  | 0.457 |  | 0.367 |  | |
| BNN | PICP | 0.955 |  | 0.953 |  | 0.961 |  | 0.496 |  | 0.779 |  | 0.870 |  | 0.281 |  | 0.630 |  | 0.865 |  |
| MPIW | 0.027 |  | 0.009 |  | 0.022 |  | 0.045 |  | 0.050 |  | 0.040 |  | 0.053 |  | 0.141 |  | 0.047 |  | |
| CRPS | 0.101 |  | 0.041 |  | 0.083 |  | 0.412 |  | 0.240 |  | 0.262 |  | 0.634 |  | 0.461 |  | 0.371 |  | |
| LSTM-MC | PICP | 0.973 |  | 0.994 |  | 0.981 |  | 0.454 |  | 0.948 |  | 0.913 |  | 0.268 |  | 0.945 |  | 0.909 |  |
| MPIW | 0.046 |  | 0.040 |  | 0.027 |  | 0.049 |  | 0.050 |  | 0.032 |  | 0.057 |  | 0.076 |  | 0.039 |  | |
| CRPS | 0.109 |  | 0.071 |  | 0.106 |  | 0.414 |  | 0.251 |  | 0.248 |  | 0.636 |  | 0.545 |  | 0.376 |  | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ghobadi, F.; Kang, D. Multi-Step Ahead Probabilistic Forecasting of Daily Streamflow Using Bayesian Deep Learning: A Multiple Case Study. Water 2022, 14, 3672. https://doi.org/10.3390/w14223672
Ghobadi F, Kang D. Multi-Step Ahead Probabilistic Forecasting of Daily Streamflow Using Bayesian Deep Learning: A Multiple Case Study. Water. 2022; 14(22):3672. https://doi.org/10.3390/w14223672
Chicago/Turabian StyleGhobadi, Fatemeh, and Doosun Kang. 2022. "Multi-Step Ahead Probabilistic Forecasting of Daily Streamflow Using Bayesian Deep Learning: A Multiple Case Study" Water 14, no. 22: 3672. https://doi.org/10.3390/w14223672






