An Improved Combination Model for the Multi-Scale Prediction of Slope Deformation
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data Source
2.3. Multiple Linear Regression Model
2.4. Multiple Nonlinear Regression Model
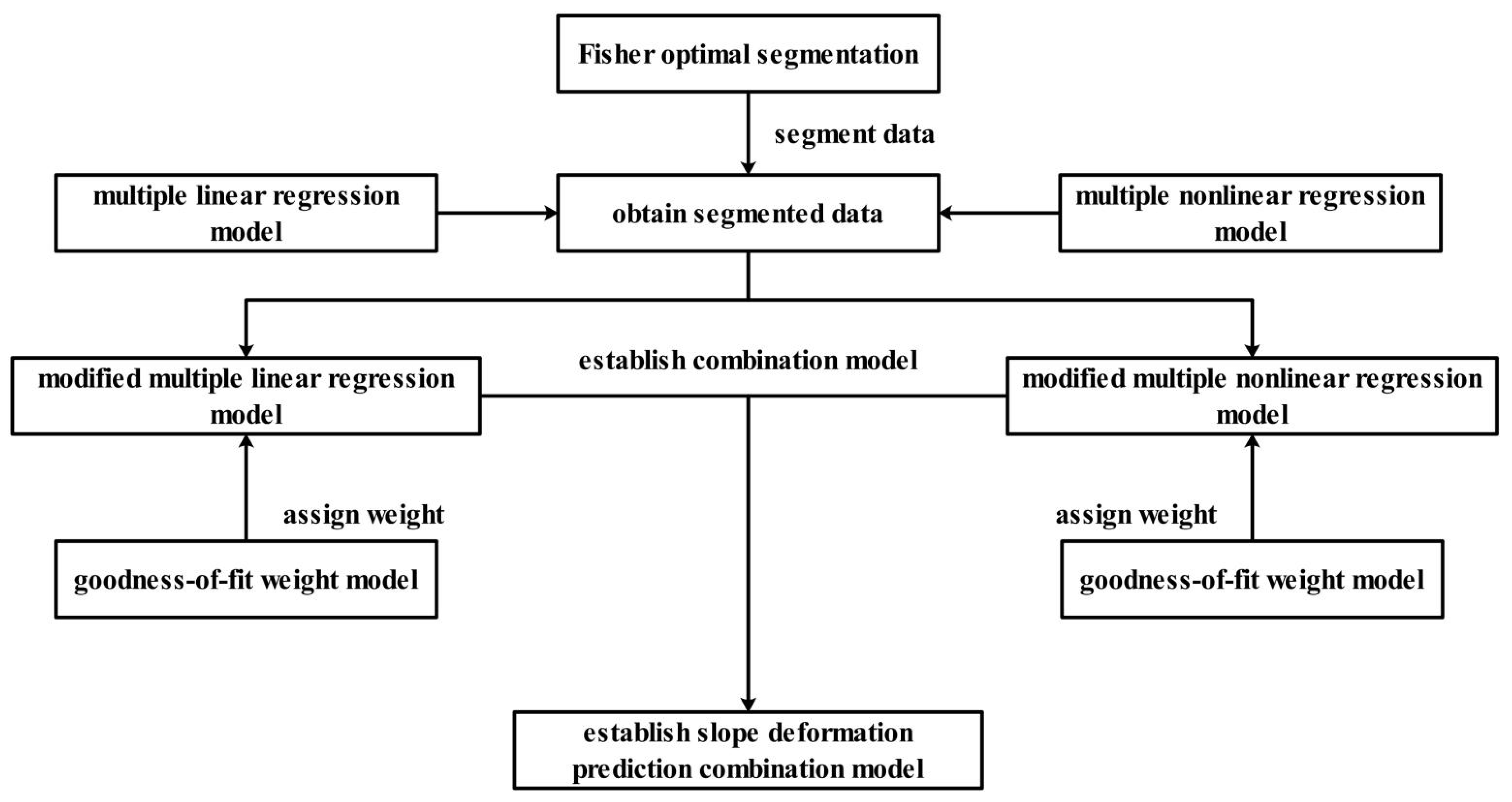
2.5. Modified Deformation Prediction Combination Model Based on GFW-Fisher Optimal Segmentation Method
2.6. Model Accuracy Evaluation
3. Results and Discussion
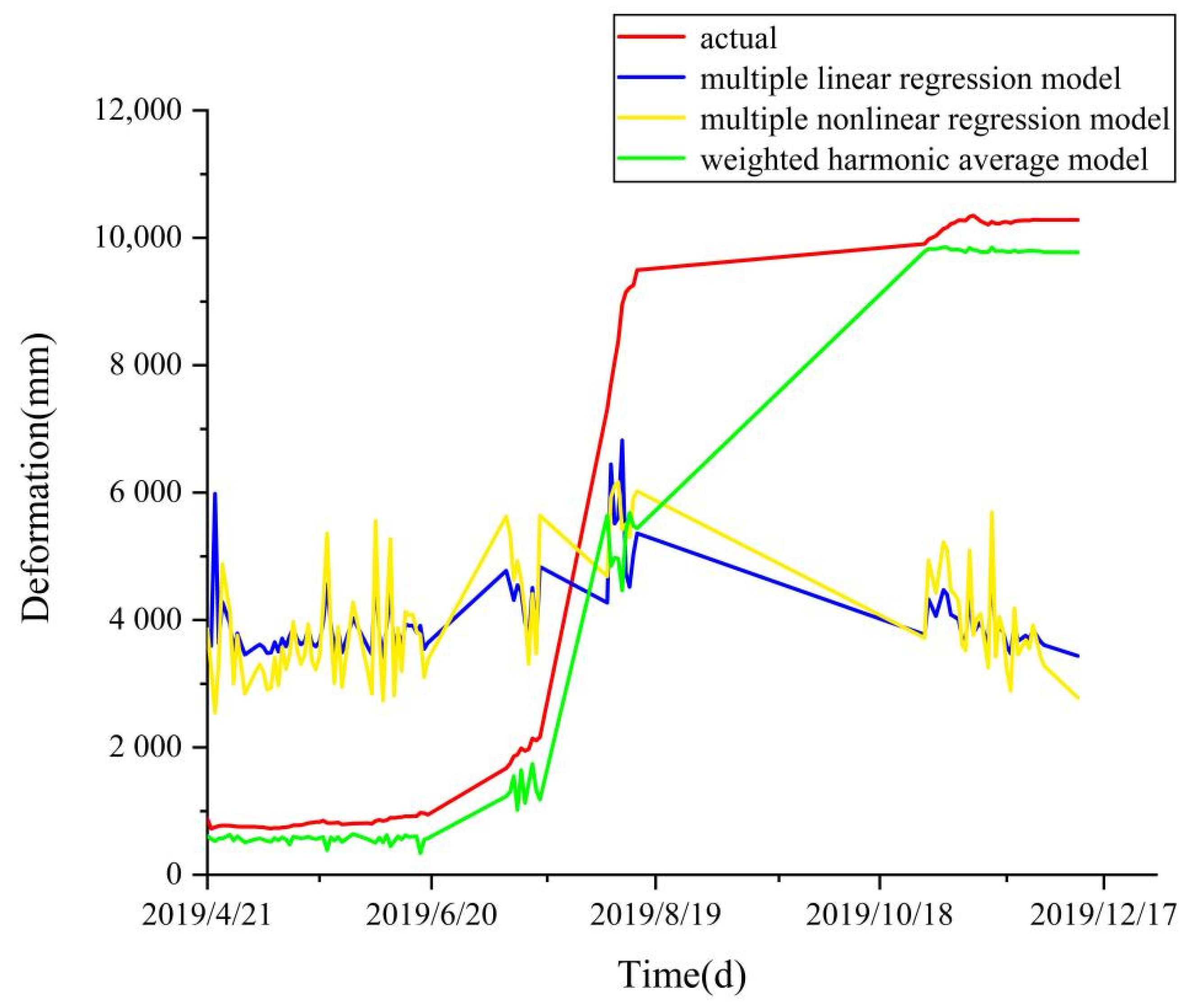
3.1. Slope Deformation Prediction Results
3.2. The Results of Accuracy Evaluation
3.3. Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singh, P.; Gupta, A.; Singh, M. Hydrological inferences from watershed analysis for water resource management using remote sensing and GIS techniques. Egypt. J. Remote Sens. Space Sci. 2014, 17, 111–121. [Google Scholar] [CrossRef] [Green Version]
- Salifu, E.; MacLachlan, E.; Iyer, K.R.; Knapp, C.W.; Tarantino, A. Application of microbially induced calcite precipitation in erosion mitigation and stabilisation of sandy soil foreshore slopes; a preliminary investigation. Eng. Geol. 2016, 201, 96–105. [Google Scholar] [CrossRef] [Green Version]
- Zhong, B.; Peng, S.; Zhang, Q.; Ma, H.; Cao, S. Using an ecological economics approach to support the restoration of collapsing gullies in southern China. Land Use Policy 2013, 32, 119–124. [Google Scholar] [CrossRef]
- Zhang, X.; Nie, J.; Cheng, C.; Xu, C.; Zhou, L.; Shen, S.; Pei, Y. Natural and Socioeconomic Factors and Their Interactive Effects on House Collapse Caused by Typhoon Mangkhut. Int. J. Disaster Risk Sci. 2021, 12, 121–130. [Google Scholar] [CrossRef]
- Che, A.; Yang, H.; Wang, B.; Ge, X. Wave propagations through jointed rock masses and their effects on the stability of slopes. Eng. Geol. 2016, 201, 45–56. [Google Scholar] [CrossRef]
- Cheng, M.; Hoang, N. A Swarm-Optimized Fuzzy Instance-based Learning approach for predicting slope collapses in mountain roads. Knowl.-Based Syst. 2015, 76, 256–263. [Google Scholar] [CrossRef]
- Dick, G.J.; Eberhardt, E.; Cabrejo-Liévano, A.G.; Stead, D.; Rose, N.D. Development of an early-warning time-of-failure analysis methodology for open-pit mine slopes utilizing ground-based slope stability radar monitoring data. Can. Geotech. J. 2015, 52, 515–529. [Google Scholar] [CrossRef]
- Xu, J.; Li, H.; Du, K.; Yan, C.; Zhao, X.; Li, W.; Xu, X. Field investigation of force and displacement within a strata slope using a real-time remote monitoring system. Environ. Earth Sci. 2018, 77, 1–11. [Google Scholar] [CrossRef]
- He, Z.; Xie, M.; Huang, Z.; Lu, G.; Yan, B.; Wang, J. Method to Realize the Tilt Monitoring and Instability Prediction of Hazardous Rock on Slopes. Adv. Civ. Eng. 2021, 2021, 1–14. [Google Scholar] [CrossRef]
- Mazzanti, P.; Bozzano, F.; Cipriani, I.; Prestininzi, A. New insights into the temporal prediction of landslides by a terrestrial SAR interferometry monitoring case study. Landslides 2015, 12, 55–68. [Google Scholar] [CrossRef]
- Li, M.; Zhang, L.; Ding, C.; Li, W.; Luo, H.; Liao, M.; Xu, Q. Retrieval of historical surface displacements of the Baige landslide from time-series SAR observations for retrospective analysis of the collapse event. Remote Sens. Environ. 2020, 240, 111695. [Google Scholar] [CrossRef]
- Dong, M.; Wu, H.; Hu, H.; Azzam, R.; Zhang, L.; Zheng, Z.; Gong, X. Deformation Prediction of Unstable Slopes Based on Real-Time Monitoring and DeepAR Model. Sensors 2020, 21, 14. [Google Scholar] [CrossRef]
- Jiang, S.; Lian, M.; Lu, C.; Gu, Q.; Ruan, S.; Xie, X. Ensemble Prediction Algorithm of Anomaly Monitoring Based on Big Data Analysis Platform of Open-Pit Mine Slope. Complexity 2018, 2018, 1–13. [Google Scholar] [CrossRef]
- Hu, B.; Su, G.; Jiang, J.; Sheng, J.; Li, J. Uncertain Prediction for Slope Displacement Time-Series Using Gaussian Process Machine Learning. IEEE Access 2019, 7, 27535–27546. [Google Scholar] [CrossRef]
- Zhang, Y.-G.; Tang, J.; He, Z.-Y.; Tan, J.; Li, C. A novel displacement prediction method using gated recurrent unit model with time series analysis in the Erdaohe Landslide. Nat. Hazards 2021, 10, 783–813. [Google Scholar] [CrossRef]
- Khajehzadeh, M.; Taha, M.R.; Keawsawasvong, S.; Mirzaei, H.; Jebeli, M. An Effective Artificial Intelligence Approach for Slope Stability Evaluation. IEEE Access 2022, 10, 5660–5671. [Google Scholar] [CrossRef]
- Zhao, X.; Ye, S. Space reconstruction of audiovisual media based on artificial intelligence and virtual reality. J. Intell. Fuzzy Syst. 2021, 40, 7285–7296. [Google Scholar] [CrossRef]
- Zhang, H.; Nguyen, H.; Bui, X.-N.; Pradhan, B.; Asteris, P.G.; Costache, R.; Aryal, J. A generalized artificial intelligence model for estimating the friction angle of clays in evaluating slope stability using a deep neural network and Harris Hawks optimization algorithm. Eng. Comput. 2021, 1–14. [Google Scholar] [CrossRef]
- Huang, Y.; Han, X.; Zhao, L. Recurrent neural networks for complicated seismic dynamic response prediction of a slope system. Eng. Geol. 2021, 289, 106198. [Google Scholar] [CrossRef]
- Elsheikh, A.H.; Panchal, H.; Ahmadein, M.; Mosleh, A.O.; Sadasivuni, K.K.; Alsaleh, N.A. Productivity forecasting of solar distiller integrated with evacuated tubes and external condenser using artificial intelligence model and moth-flame optimizer. Case Stud. Therm. Eng. 2021, 28, 101671. [Google Scholar] [CrossRef]
- Yang, B.; Yin, K.; Lacasse, S.; Liu, Z. Time series analysis and long short-term memory neural network to predict landslide displacement. Landslides 2019, 16, 677–694. [Google Scholar] [CrossRef]
- Ozsen, H. Monitoring unstable slopes in an open pit lignite mine using ARIMA. J. S. Afr. Inst. Min. Metall. 2020, 120, 173–180. [Google Scholar] [CrossRef]
- Gong, C.; Lei, S.; Bian, Z.; Tian, Y.; Zhang, Z.; Guo, H.; Zhang, H.; Cheng, W. Using time series InSAR to assess the deformation activity of open-pit mine dump site in severe cold area. J. Soil. Sediment. 2021, 21, 3717–3732. [Google Scholar] [CrossRef]
- Momeni, E.; Yarivand, A.; Dowlatshahi, M.B.; Armaghani, D.J. An efficient optimal neural network based on gravitational search algorithm in predicting the deformation of geogrid-reinforced soil structures. Transp. Geotech. 2021, 26, 100446. [Google Scholar] [CrossRef]
- Barvor, Y.J.; Bacha, S.; Qingxiang, C.; Zhao, C.S.; Siddique, M. Surface mines composite slope deformation mechanisms and stress distribution. Min. Miner. Depos. 2020, 14, 1–16. [Google Scholar] [CrossRef]
- Deng, L.; Smith, A.; Dixon, N.; Yuan, H. Machine learning prediction of landslide deformation behaviour using acoustic emission and rainfall measurements. Eng. Geol. 2021, 293, 106315. [Google Scholar] [CrossRef]
- Li, L.; Qiang, Y.; Li, S.; Yang, Z. Research on Slope Deformation Prediction Based on Fractional-Order Calculus Gray Model. Adv. Civ. Eng. 2018, 2018, 1–9. [Google Scholar] [CrossRef]
- Bacha, S.; Barvor, Y.J.; Qingxiang, C.; Zhao, C.S.; Wang, M. Influence of composite slope geometrical parameters on soft rock slope stability. Min. Miner. Depos. 2020, 14, 112–119. [Google Scholar] [CrossRef]
- Abdellah, W.R.; Hussein, M.Y.; Imbabi, S.S. Rock slope stability analysis usingshear strength reduction technique (SSRT)–Case histories. Min. Miner. Depos. 2020, 14, 16–24. [Google Scholar] [CrossRef]
- Jiang, N.; Li, H.; Zhou, J. Quantitative hazard analysis and mitigation measures of rockfall in a high-frequency rockfall region. Bull. Eng. Geol. Environ. 2021, 80, 3439–3456. [Google Scholar] [CrossRef]
- Luo, D.; Li, H.; Wu, Y.; Li, D.; Yang, X.; Yao, Q. Cloud model-based evaluation of landslide dam development feasibility. PLoS ONE 2021, 16, e0251212. [Google Scholar] [CrossRef]
- Jiang, F.; Dai, X.; Xie, Z.; Xu, T.; Yin, S.; Qu, G.; Yang, S.; Zhang, Y.; Yang, Z.; Xu, J.; et al. Flood inundation evolution of barrier lake and evaluation of regional ecological spatiotemporal response-a case study of Sichuan-Tibet region. Environ. Sci. Pollut. Res. 2022, 29, 71290–71310. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Ma, S.; Qiu, X.; Shi, J.; Zhang, X.; Chen, F. Microblog Topic-Words Detection Model for Earthquake Emergency Responses Based on Information Classification Hierarchy. Int. J. Environ. Res. Public Health 2021, 18, 8000. [Google Scholar] [CrossRef] [PubMed]
- Sun, X.; Guo, L. Crustal velocity, density structure, and seismogenic environment in the southern segment of the North-South Seismic Belt, China. Earthq. Sci. 2021, 34, 471–488. [Google Scholar] [CrossRef]
- Lv, M.; Ding, Z.; Xu, X. Seismogenic environments of earthquakes on the southeastern margin of the Tibetan Plateau revealed by double-difference tomography. Tectonophysics 2022, 843, 229603. [Google Scholar] [CrossRef]
- Lu, X.; Cheng, Q.; Xu, Z.; Xiong, C. Regional seismic-damage prediction of buildings under mainshock-aftershock sequence. Front. Eng. Manag. 2021, 8, 122–134. [Google Scholar] [CrossRef]
- Jiang, P.; Li, R.; Liu, N. A novel composite electricity demand forecasting framework by data processing and optimized support vector machine. Appl. Energ. 2020, 260, 114243. [Google Scholar] [CrossRef]
- Zhang, L.; Cai, X.; Wang, Y.; Wei, W.; Liu, B.; Jia, S.; Pang, T.; Bai, F.; Wei, Z. Long-term ground multi-level deformation fusion and analysis based on a combination of deformation prior fusion model and OTD-InSAR for longwall mining activity. Meas. J. Int. Meas. Confed. 2020, 161, 107911. [Google Scholar] [CrossRef]
- Ottaviani, M.F.; Marco, A.D. Multiple Linear Regression Model for Improved Project Cost Forecasting. Procedia Comput. Sci. 2022, 196, 808–815. [Google Scholar] [CrossRef]
- Babar, I.; Ayed, H.; Chand, S.; Suhail, M.; Khan, Y.A.; Marzouki, R. Modified Liu estimators in the linear regression model: An application to Tobacco data. PLoS ONE 2021, 16, e0259991. [Google Scholar] [CrossRef] [PubMed]
- Yang, K.; Musselman, K.N.; Rittger, K.; Margulis, S.A.; Painter, T.H.; Molotch, N.P. Combining ground-based and remotely sensed snow data in a linear regression model for real-time estimation of snow water equivalent. Adv. Water Resour. 2022, 160, 104075. [Google Scholar] [CrossRef]
- Tang, S.; Li, T.; Guo, Y.; Zhu, R.; Qu, H. Correction of various environmental influences on Doppler wind lidar based on multiple linear regression model. Renew. Energy 2022, 184, 933–947. [Google Scholar] [CrossRef]
- Roozbeh, M.; Babaie-Kafaki, S.; Aminifard, Z. A nonlinear mixed-integer programming approach for variable selection in linear regression model. Communications in statistics. Simul. Comput. 2021, 1–12, ahead of print. [Google Scholar] [CrossRef]
- Jahangir, H.; Bagheri, M.; Delavari, S.M.J. Cyclic Behavior Assessment of Steel Bar Hysteretic Dampers Using Multiple Nonlinear Regression Approach. Iranian journal of science and technology. Trans. Civ. Eng. 2021, 45, 1227–1251. [Google Scholar]
- Cepowski, T.; Chorab, P.; Łozowicka, D. Application of an Artificial Neural Network and Multiple Nonlinear Regression to Estimate Container Ship Length Between Perpendiculars. Pol. Marit. Res. 2021, 28, 36–45. [Google Scholar] [CrossRef]
- Zhang, K.; Li, W.; Han, Y.; Geng, Z.; Chu, C. Production capacity identification and analysis using novel multivariate nonlinear regression: Application to resource optimization of industrial processes. J. Clean. Prod. 2021, 282, 124469. [Google Scholar] [CrossRef]
- Basco, R.; Hair, J.F.; Ringle, C.M.; Sarstedt, M. Advancing family business research through modeling nonlinear relationships: Comparing PLS-SEM and multiple regression. J. Fam. Bus. Strategy 2022, 13, 100457. [Google Scholar] [CrossRef]
- Kun, Z.; Weibing, F. Prediction of China’s Total Energy Consumption Based on Bayesian ARIMA-Nonlinear Regression Model. IOP conference series. Earth Environ. Sci. 2021, 657, 12056. [Google Scholar]
- Zhang, W.; Xiao, R.; Shi, B.; Zhu, H.-H.; Sun, Y.-J. Forecasting slope deformation field using correlated grey model updated with time correction factor and background value optimization. Eng. Geol. 2019, 260, 105215. [Google Scholar] [CrossRef]
- Cai, M.; Koopialipoor, M.; Armaghani, D.J.; Pham, B.T. Evaluating Slope Deformation of Earth Dams Due to Earthquake Shaking Using MARS and GMDH Techniques. Appl. Sci. 2020, 10, 1486. [Google Scholar] [CrossRef] [Green Version]
- Tan, X.L. Combinatorial Method of Deformation Prediction Based on Multipoint Monitoring for Large Slope and Its Engineering Application. J. Yangtze River Sci. Res. Inst. 2014, 31, 143–148. [Google Scholar]
- Du, S.; Zhang, J.; Deng, Z.; Li, J. A New Approach of Geological Disasters Forecasting using Meteorological Factors based on Genetic Algorithm Optimized BP Neural Network. Elektron. Ir Elektrotechnika 2014, 20, 57–62. [Google Scholar] [CrossRef]



| Spatial and Scale | Intervals | Weights of Multiple Linear Regression Model | Weights of Multiple Nonlinear Regression Model |
|---|---|---|---|
| Deformation prediction at point scales with 100 grids | The first interval | 0.594 | 0.406 |
| The second interval | 0.205 | 0.795 | |
| The third interval | 0.813 | 0.187 | |
| The forth interval | 0.322 | 0.678 | |
| Deformation prediction at linear scales with 100 grids | The first interval | 0.256 | 0.744 |
| The second interval | 0.090 | 0.910 | |
| The third interval | 0.369 | 0.631 | |
| The forth interval | 0.415 | 0.585 | |
| Deformation prediction at surface scales with 100 grids | The first interval | 0.198 | 0.802 |
| The second interval | 0.060 | 0.940 | |
| The third interval | 0.440 | 0.560 | |
| The forth interval | 0.076 | 0.924 | |
| Deformation prediction at point scales with 200 grids | The first interval | 0.426 | 0.574 |
| The second interval | 0.228 | 0.772 | |
| The third interval | 0.330 | 0.670 | |
| The forth interval | 0.654 | 0.346 | |
| Deformation prediction at linear scales with 200 grids | The first interval | 0.184 | 0.816 |
| The second interval | 0.358 | 0.642 | |
| The third interval | 0.454 | 0.546 | |
| The forth interval | 0.312 | 0.688 | |
| Deformation prediction at surface scales with 200 grids | The first interval | 0.727 | 0.273 |
| The second interval | 0.117 | 0.883 | |
| The third interval | 0.366 | 0.634 | |
| The forth interval | 0.366 | 0.634 |
| Spatial Scale | Linear Combination Model | Weighted Geometric Average Model | Weighted Harmonic Average Model |
|---|---|---|---|
| Point scale | 0.89 | 0.88 | 0.83 |
| Linear scale | 0.77 | 0.79 | 0.84 |
| Surface scale | 0.93 | 0.93 | 0.95 |
| Spatial Scale | Linear Combination Model | Weighted Geometric Average Model | Weighted Harmonic Average Model |
|---|---|---|---|
| Point scale | 0.88 | 0.87 | 0.88 |
| Linear scale | 0.94 | 0.94 | 0.94 |
| Surface scale | 0.95 | 0.95 | 0.96 |
| Model | RMSE | MAE | Relative Error |
|---|---|---|---|
| Multiple linear regression model | 20.91% | 19.52% | 96.33% |
| Multiple nonlinear regression model | 20.74% | 19.14% | 94.47% |
| Linear combination model | 5.62% | 3.14% | 4.33% |
| Weight geometric average model | 5.62% | 3.12% | 4.33% |
| Weight harmonic average model | 5.57% | 3.11% | 3.98% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Lei, T.; Qin, J.; Wang, J.; Wang, W.; Chen, D.; Qian, G.; Lu, J. An Improved Combination Model for the Multi-Scale Prediction of Slope Deformation. Water 2022, 14, 3667. https://doi.org/10.3390/w14223667
Li X, Lei T, Qin J, Wang J, Wang W, Chen D, Qian G, Lu J. An Improved Combination Model for the Multi-Scale Prediction of Slope Deformation. Water. 2022; 14(22):3667. https://doi.org/10.3390/w14223667
Chicago/Turabian StyleLi, Xiangyu, Tianjie Lei, Jing Qin, Jiabao Wang, Weiwei Wang, Dongpan Chen, Guansheng Qian, and Jingxuan Lu. 2022. "An Improved Combination Model for the Multi-Scale Prediction of Slope Deformation" Water 14, no. 22: 3667. https://doi.org/10.3390/w14223667









