Discrete Element Simulation of the Road Slope Considering Rainfall Infiltration
Abstract
:1. Introduction
2. Materials and Methods
2.1. Moisture Diffusion Model
2.2. Strength Calculation between Particles
- (1)
- Samples are taken at the slope site, and 5–10 groups of samples with different water content are designed;
- (2)
- An indoor direct shear test is conducted for each group of experiments. The vertical pressure is divided into 50 kPa, 100 kPa and 200 kPa. The horizontal shear stress is applied under different vertical pressures to obtain the shear stress at failure;
- (3)
- A numerical model is established in PFC to simulate the direct shear test. Based on the water content grouping in step (1) and the shear strength obtained in step (2), the numerical simulation inversion can obtain the mapping relationship between the water content and friction coefficient;
- (4)
- Draw curves. Take the water content as the abscissa and the friction coefficient as the ordinate;
- (5)
- Fit the curve. A mathematical equation is obtained, which takes the water content as independent variable and friction coefficient as dependent variable;
- (6)
- Based on the fitting equation, the program in PFC is used to map the moisture transfer and friction coefficient of the particles.
2.3. Strength Calculation between Particles
3. Application
3.1. Study Area
3.2. Slope Model and Boundary Conditions
3.3. Parameter Calibration
4. Results and Discussion
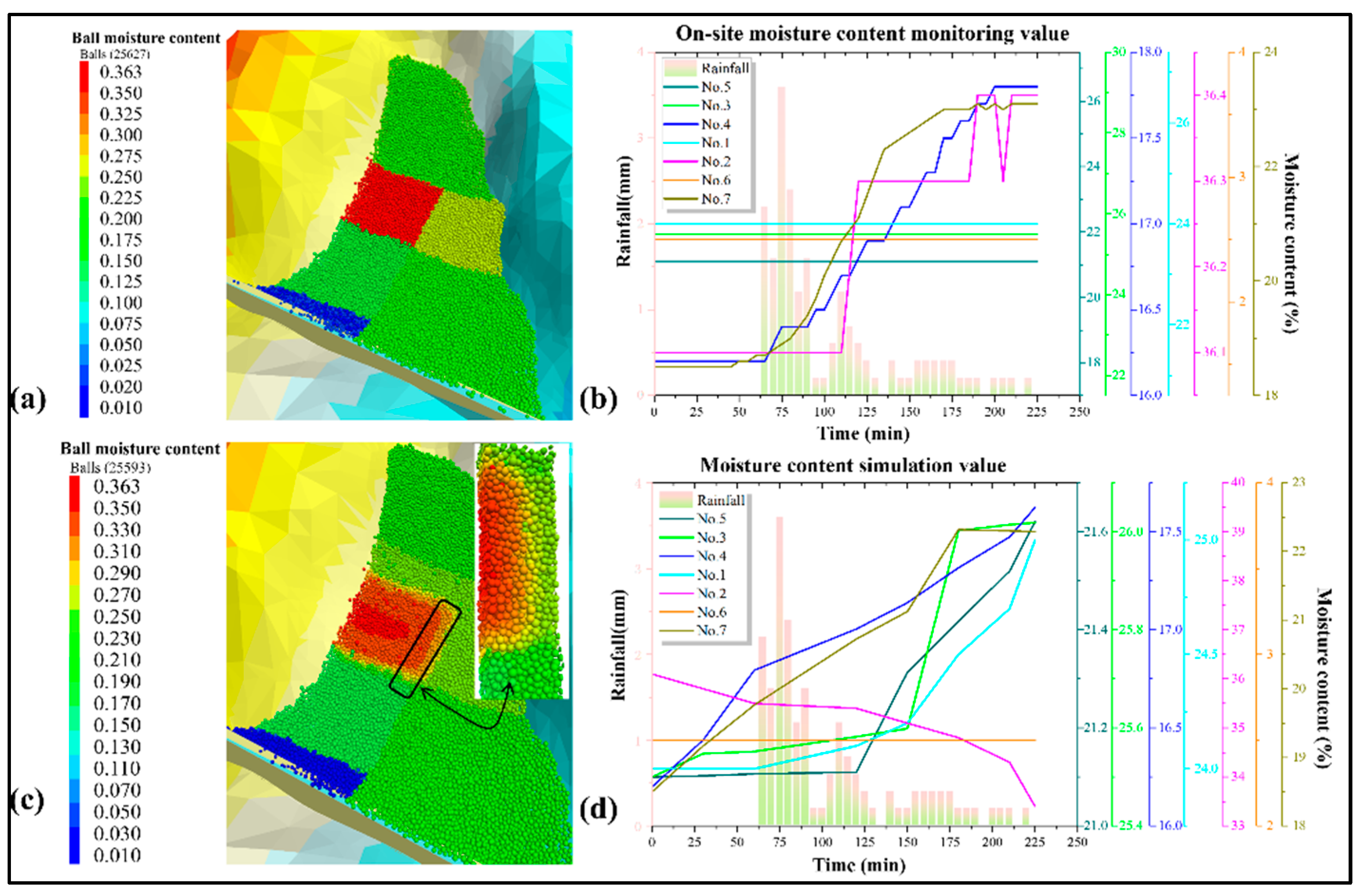
4.1. Comparison of Moisture Content
4.2. Earth Pressure Comparison
4.3. Highlights and Prospects
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharma, R.H.; Shakya, N.M. Rain induced shallow landslide hazard assessment for ungauged catchments. Hydrogeol. J. 2008, 16, 871–877. [Google Scholar] [CrossRef]
- Chenguang, W.U.; Meng, L.U.; Jie, Z.; Jiang, Z. Probabilistic Prediction of Rain-Induced Landslide Travel Distance. J. Eng. Geol. 2019, 27, 164–171. [Google Scholar]
- Bhardwaj, A.; Wasson, R.J.; Ziegler, A.D.; Chow, W.T.L.; Sundriyal, Y.P. Characteristics of rain-induced landslides in the Indian Himalaya: A case study of the Mandakini Catchment during the 2013 flood. Geomorphology 2019, 330, 100–115. [Google Scholar] [CrossRef]
- Cho, S.E. Stability analysis of unsaturated soil slopes considering water-air flow caused by rainfall infiltration. Eng. Geol. 2016, 211, 184–197. [Google Scholar] [CrossRef]
- Damiano, E.; Greco, R.; Guida, A.; Olivares, L.; Picarelli, L. Investigation on rainwater infiltration into layered shallow covers in pyroclastic soils and its effect on slope stability. Eng. Geol. 2017, 220, 208–218. [Google Scholar] [CrossRef]
- Zhang, J.; Zhu, D.; Zhang, S. Shallow slope stability evolution during rainwater infiltration considering soil cracking state. Comput. Geotech. 2020, 117, 103285. [Google Scholar] [CrossRef]
- Li, Q.; Song, D.; Yuan, C.; Nie, W. An image recognition method for the deformation area of open-pit rock slopes under variable rainfall. Measurement 2022, 188, 110544. [Google Scholar] [CrossRef]
- Morbidelli, R.; Saltalippi, C.; Flammini, A.; Govindaraju, R.S. Role of slope on infiltration: A review. J. Hydrol. 2018, 557, 878–886. [Google Scholar] [CrossRef]
- Li, M.; Zhang, X.; Yang, Z.; Yang, T.; Pei, X. The rainfall erosion mechanism of high and steep slopes in loess tablelands based on experimental methods and optimized control measures. Bull. Eng. Geol. Environ. 2020, 79, 4671–4681. [Google Scholar] [CrossRef]
- Tan, W.; Huang, Q.; Chen, X. Physical Model Test on the Interface of Loess Fill Slope. Land 2022, 11, 1372. [Google Scholar] [CrossRef]
- Wang, H.; Jiang, Z.; Xu, W.; Wang, R.; Xie, W. Physical model test on deformation and failure mechanism of deposit landslide under gradient rainfall. Bull. Eng. Geol. Environ. 2022, 81, 66. [Google Scholar] [CrossRef]
- Li, Q.; Geng, J.; Song, D.; Nie, W.; Saffari, P.; Liu, J. Automatic recognition of erosion area on the slope of tailings dam using region growing segmentation algorithm. Arab. J. Geosci. 2022, 15, 438. [Google Scholar] [CrossRef]
- Zhu, W.; Ren, M.; Dai, F.; Zhang, P.; Wang, L.; Liu, H.; Jia, H.; Wang, X. Prediction and Early Warning of Mining-induced Disasters Based on Combined In-situ Monitoring and Numerical Simulation. Met. Mine 2020, 52, 151–162. [Google Scholar]
- Su, Z.; Wang, G.; Wang, Y.; Luo, X.; Zhang, H. Numerical simulation of dynamic catastrophe of slope instability in three Gorges reservoir area based on FEM and SPH method. Nat. Hazards 2022, 111, 709–724. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Q.; Zhang, N.; Jin, Y.; Qin, H.; Ding, J. Slope failure of biotreated sand embankments under rainfall conditions: Experimental investigation and numerical simulation. Bull. Eng. Geol. Environ. 2020, 79, 4683–4699. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, Z. Numerical analysis of an expansive subgrade slope subjected to rainfall infiltration. Bull. Eng. Geol. Environ. 2021, 80, 5481–5491. [Google Scholar] [CrossRef]
- Elkamhawy, E.; Wang, H.; Zhou, B.; Yang, Z. Failure mechanism of a slope with a thin soft band triggered by intensive rainfall. Environ. Earth Sci. 2018, 77, 340. [Google Scholar] [CrossRef]
- Joe, E.J.; Ali, N.; Jusoh, S.N. Numerical modelling of coupled seepage-deformation subjected to rainfall infiltration in unsaturated slope. World J. Eng. 2020, 17, 867–875. [Google Scholar] [CrossRef]
- Tian, Y.; Wu, Y.; Lin, J.; Li, X.; Xu, D.; Zhou, F.; Feng, Q. Characterization of the Erosion Damage Mechanism of Coal Gangue Slopes through Rainwater Using a 3D Discrete Element Method: A Case Study of the Guizhou Coal Gangue Slope (Southwestern China). Appl. Sci. 2022, 12, 8548. [Google Scholar] [CrossRef]
- Chang, W.; Wang, P.; Wang, H.; Chai, S.; Yu, Y.; Xu, S. Simulation of the Q2 loess slope with seepage fissure failure and seismic response via discrete element method. Bull. Eng. Geol. Environ. 2021, 80, 3495–3511. [Google Scholar] [CrossRef]
- Hu, J.; Ma, T.; Ma, K. DEM-CFD simulation on clogging and degradation of air voids in double-layer porous asphalt pavement under rainfall. J. Hydrol. 2021, 595, 126028. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, B.; Wu, C.; Chen, K. Macro and micro analysis on coal-bearing soil slopes instability based on CFD-DEM coupling method. PLoS ONE 2021, 16, e0257362. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Chen, J.; Zhou, F.; Bao, Y.; Yan, J.; Zhang, Y.; Li, Y.; Gu, F.; Wang, Q. Combined numerical investigation of the Gangda paleo landslide runout and associated dam breach flood propagation in the upper Jinsha River, SE Tibetan Plateau. Landslides 2022, 19, 941–962. [Google Scholar] [CrossRef]
- Wang, Y.; Chai, J.; Xu, Z.; Qin, Y.; Wang, X. Numerical Simulation of the Fluid–Solid Coupling Mechanism of Internal Erosion in Granular Soil. Water 2020, 12, 137. [Google Scholar] [CrossRef] [Green Version]
- Jiang, W.-Z.; Tan, Y.; Cao, Y.-C. Numerical Analyses of Erosion in Sand-Gravel Mixtures Caused by Buried Defective Pipeline under Intense Rainfall. In Geo-Extreme; American Society of Civil Engineers: Reston, VA, USA, 2021; pp. 150–159. [Google Scholar]
- Hung, C.; Liu, C.-H.; Chang, C.-M. Numerical Investigation of Rainfall-Induced Landslide in Mudstone Using Coupled Finite and Discrete Element Analysis. Geofluids 2018, 2018, 9192019. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Fu, Z.; Gao, A.; Wen, Z. Particle Flow Code Method-Based Meso-scale Identification for Seepage Failure of Soil Levee. Transp. Porous Med. 2017, 119, 311–336. [Google Scholar] [CrossRef]
- Su, H.; Li, H.; Zhang, L.; Wen, Z. Particle flow code method-based seepage behavior analysis and control effect evaluation for soil levee. Eng. Comput. 2020, 36, 97–114. [Google Scholar] [CrossRef]
- Li, W.C.; Li, H.J.; Dai, F.C.; Lee, L.M. Discrete element modeling of a rainfall-induced flowslide. Eng. Geol. 2012, 149, 22–34. [Google Scholar] [CrossRef]
- Yang, G.; Qin, Y.; Jiang, W.; Liang, F.; Xiang, X. Characteristics and particle flow simulation of failure mechanism of Ludaping landslide in Renhuai red bed area, China. Arab. J. Geosci. 2022, 15, 1237. [Google Scholar] [CrossRef]
- Lo, C.-M.; Lee, C.-F.; Huang, W.-K. Failure mechanism analysis of rainfall-induced landslide at Pingguang stream in Taiwan: Mapping, investigation, and numerical simulation. Environ. Earth Sci. 2016, 75, 1422. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, B.; Yang, Z.; Ji, E. Numerical Study on Vertical and Horizontal Seepage Deformation of Silty Soil. IOP Conf. Ser. Earth Environ. Sci. 2019, 304, 052099. [Google Scholar] [CrossRef]
- Su, Y.; Lan, S.M.; Xu, L.; Ding, J.H. Simulation of Progressive Failure Process in Rainfall-Induced Landslides. Adv. Mater. Res. 2014, 1065, 63–66. [Google Scholar] [CrossRef]
- Li, X.; Lu, Y.; Wu, Y. Application of CFD—DEM coupling method in seepage—induced ground subsidence. J. Shanghai Univ. Nat. Sci. Ed. 2020, 26, 842–852. [Google Scholar]
- Liu, J.; Liu, Y.; Hu, Q. Stability of embankment slope subjected to rainfall infiltration considering both runoff-underground seepage and fluid-solid coupling. Rock Soil Mech. 2010, 31, 903–910. [Google Scholar]
- Itasca PFC (Particle Flow Code) Version 5.0; Itasca Consulting Group Inc.: Chicago, IL, USA, 2014.
- Weng, M.-C.; Lin, M.-L.; Lo, C.-M.; Lin, H.-H.; Lin, C.-H.; Lu, J.-H.; Tsai, S.-J. Evaluating failure mechanisms of dip slope using a multiscale investigation and discrete element modelling. Eng. Geol. 2019, 263, 105303. [Google Scholar] [CrossRef]
- Whitaker, S. Flow in porous media I: A theoretical derivation of Darcy’s law. Transp. Porous Med. 1986, 1, 3–25. [Google Scholar] [CrossRef]
- Tran, K.M.; Bui, H.H.; Nguyen, G.D. DEM modelling of unsaturated seepage flows through porous media. Comp. Part. Mech. 2022, 9, 135–152. [Google Scholar] [CrossRef]
- Tran, K.M.; Bui, H.H.; Nguyen, G.D. A hybrid discrete-continuum approach to model hydro-mechanical behaviour of soil during desiccation. arXiv 2021, arXiv:2106.04676. [Google Scholar]
- Gili, J.A.; Alonso, E.E. Microstructural deformation mechanisms of unsaturated granular soils. Int. J. Numer. Anal. Meth. Geomech. 2002, 26, 433–468. [Google Scholar] [CrossRef] [Green Version]
- Hillel, D. Water Flow in Saturated Soil. In Introduction to Environmental Soil Physics; Elsevier: Amsterdam, The Netherlands, 2003; pp. 127–148. [Google Scholar]
- Van Genuchten, M.T. A Closed-form Equation for Predicting the Hydraulic Conductivity of Unsaturated Soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef] [Green Version]
- Berg, P. Long-term simulation of water movement in soils using mass-conserving procedures. Adv. Water Resour. 1999, 22, 419–430. [Google Scholar] [CrossRef]
- Wang, X.; Xiao, L.; Zhao, J.; Ye, S.; Wei, J.; Huang, X. Analysis of the formation mechanism of a landslide in the lacustrine sediment of the Diexi ancient dammed lake in the upper reaches of the Minjiang River. Bull. Eng. Geol. Environ. 2022, 81, 339. [Google Scholar] [CrossRef]
- Pan, Y.-W.; Su, H.-K.; Liao, J.-J.; Huang, M.-W. Reconstruction of Rainfall-induced Landslide Dam by Numerical Simulation—The Barrier Lake in Taimali River as an Example. In Proceedings of the ISRM International Symposium—8th Asian Rock Mechanics Symposium, Sapporo, Japan, 14–16 October 2014. [Google Scholar]
- Brooks, R.H.; Corey, A.T. Properties of Porous Media Affecting Fluid Flow. J. Irrig. Drain. Div. 1966, 92, 61–88. [Google Scholar] [CrossRef]
- Xie, W.; Nie, W.; Saffari, P.; Robledo, L.F.; Descote, P.-Y.; Jian, W. Landslide hazard assessment based on Bayesian optimization–support vector machine in Nanping City, China. Nat. Hazards 2021, 109, 931–948. [Google Scholar] [CrossRef]
- Li, X.; Li, Q.; Hu, Y.; Chen, Q.; Peng, J.; Xie, Y.; Wang, J. Study on Three-Dimensional Dynamic Stability of Open-Pit High Slope under Blasting Vibration. Lithosphere 2022, 2021, 6426550. [Google Scholar] [CrossRef]
- Ajamzadeh, M.R.; Sarfarazi, V.; Haeri, H.; Dehghani, H. The effect of micro parameters of PFC software on the model calibration. Smart Struct. Syst. 2018, 22, 643–662. [Google Scholar]
- Wu, H.; Dai, B.; Zhao, G.; Chen, Y.; Tian, Y. A Novel Method of Calibrating Micro-Scale Parameters of PFC Model and Experimental Validation. Appl. Sci. 2020, 10, 3221. [Google Scholar] [CrossRef]
- Ren, J.; Xiao, M.; Liu, G. Rock Macro–Meso Parameter Calibration and Optimization Based on Improved BP Algorithm and Response Surface Method in PFC 3D. Energies 2022, 15, 6290. [Google Scholar] [CrossRef]
- Xia, L.; Zeng, Y. Parametric study of smooth joint parameters on the mechanical behavior of transversely isotropic rocks and research on calibration method. Comput. Geotech. 2018, 98, 1–7. [Google Scholar] [CrossRef]
- Zhai, S.; Zhan, J.; Ba, Y.; Chen, J.; Li, Y.; Li, Z. PFC model parameter calibration using uniform experimental design and a deep learning network. IOP Conf. Ser. Earth Environ. Sci. 2019, 304, 032062. [Google Scholar] [CrossRef] [Green Version]
- Su, H.; Li, H.; Hu, B.; Yang, J. A Research on the Macroscopic and Mesoscopic Parameters of Concrete Based on an Experimental Design Method. Materials 2021, 14, 1627. [Google Scholar] [CrossRef] [PubMed]







| Parameters | Definition | Parameter Value |
|---|---|---|
| Radius (m) | 0.25–0.4 | |
| Density (kg/m3) | 1600 | |
| Tangential stiffness (Pa) | 5 × 107 | |
| Normal stiffness (Pa) | 5 × 107 | |
| Saturated volume moisture content | 0.4 | |
| Residual moisture content | 0.008 | |
| Saturated permeability coefficient | 2.46 × 10−6 | |
| α, m, n | Fitting parameters | 1.76, 4.53, 0.22 |
| Rainfall Time | Rainfall Duration | Moisture Content Monitoring Point | No.1 | No.2 | No.3 | No.4 | No.5 | No.6 | No.7 |
|---|---|---|---|---|---|---|---|---|---|
| 27 April 2022 | 21 mm/4 h | Field monitoring (%) | 24.00 | 36.40 | 25.50 | 17.80 | 21.20 | 2.50 | 20.30 |
| Numerical simulation (%) | 25.00 | 33.37 | 26.02 | 17.62 | 21.62 | 2.50 | 22.29 | ||
| Relative error * (%) | 4.17 | 8.32 | 2.04 | 1.01 | 1.98 | 0 | 9.8 |
| Value | Monitoring Data | Simulated Data | Relative Error * | ||||
|---|---|---|---|---|---|---|---|
| This Model | Saturated Water Content Model | Seepage Force Model | This Model | Saturated Water Content Model | Seepage Force Model | ||
| Start value | 3.99667 | 3.99639 | 3.99857 | 3.99667 | 11.5% | 17.82% | 38.99% |
| Peak value | 4.02214 | 4.01891 | 4.02858 | 4.01221 | |||
| Difference value | 0.02547 | 0.02252 | 0.03001 | 0.01554 | |||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, X.; Nie, W.; Li, Q.; Geng, J.; Zhou, T.; Yuan, C. Discrete Element Simulation of the Road Slope Considering Rainfall Infiltration. Water 2022, 14, 3663. https://doi.org/10.3390/w14223663
Gu X, Nie W, Li Q, Geng J, Zhou T, Yuan C. Discrete Element Simulation of the Road Slope Considering Rainfall Infiltration. Water. 2022; 14(22):3663. https://doi.org/10.3390/w14223663
Chicago/Turabian StyleGu, Xiao, Wen Nie, Qihang Li, Jiabo Geng, Tao Zhou, and Canming Yuan. 2022. "Discrete Element Simulation of the Road Slope Considering Rainfall Infiltration" Water 14, no. 22: 3663. https://doi.org/10.3390/w14223663








