A Dynamically Dimensioned Search Allowing a Flexible Search Range and Its Application to Optimize Discrete Hedging Rule Curves
Abstract
:1. Introduction
- The DDS has constant specified-search boundaries of decision variables until the optimization is terminated.
- If the two decision variables are under an inequality constraint, the DDS-FSR can exclude infeasible areas for the decision variable by converting the upper or lower boundary for the decision variable to the current best solution for the other decision variable.
2. Methods
2.1. Discrete Hedging Rules
- Normal: Release the monthly planned municipal water supply;
- Caution: Release the monthly contracted water supply with local governments/industrial complexes, etc.;
- Alert: Release the monthly actual usage surveyed on last year basis among the contractual water supply;
- Severe: Release 80% of the monthly actual usage.
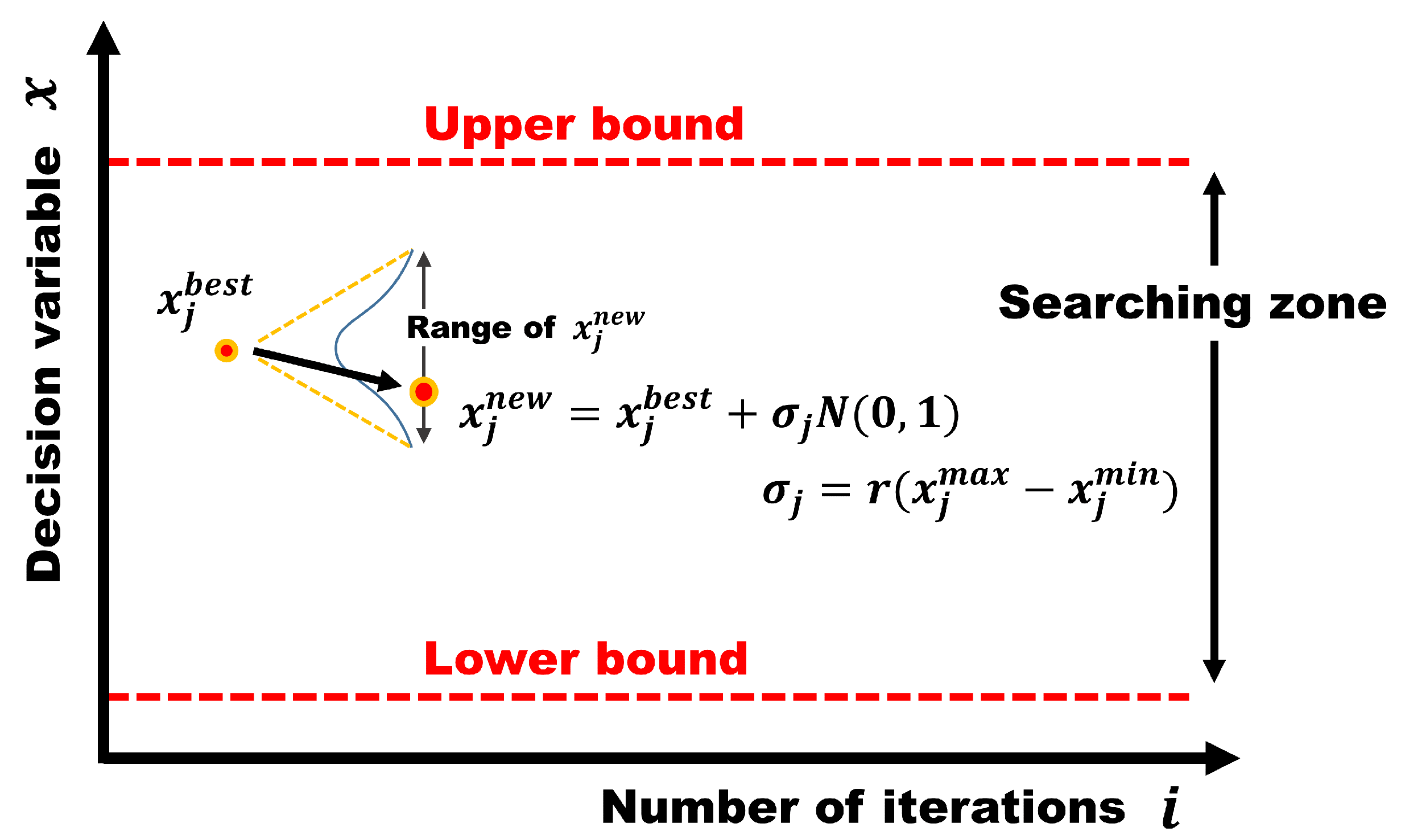
2.2. Dynamically Dimensioned Search Allowing a Flexible Search Range
2.3. Reservoir Simulation and Optimization Model
- 1.
- The sum of water supply shortage for the total period T;
- 2.
- The penalty term to restrain the reversal of trigger volumes in drought phase severity;
- 3.
- The penalty term to restrain water supply failures within the optimization period.
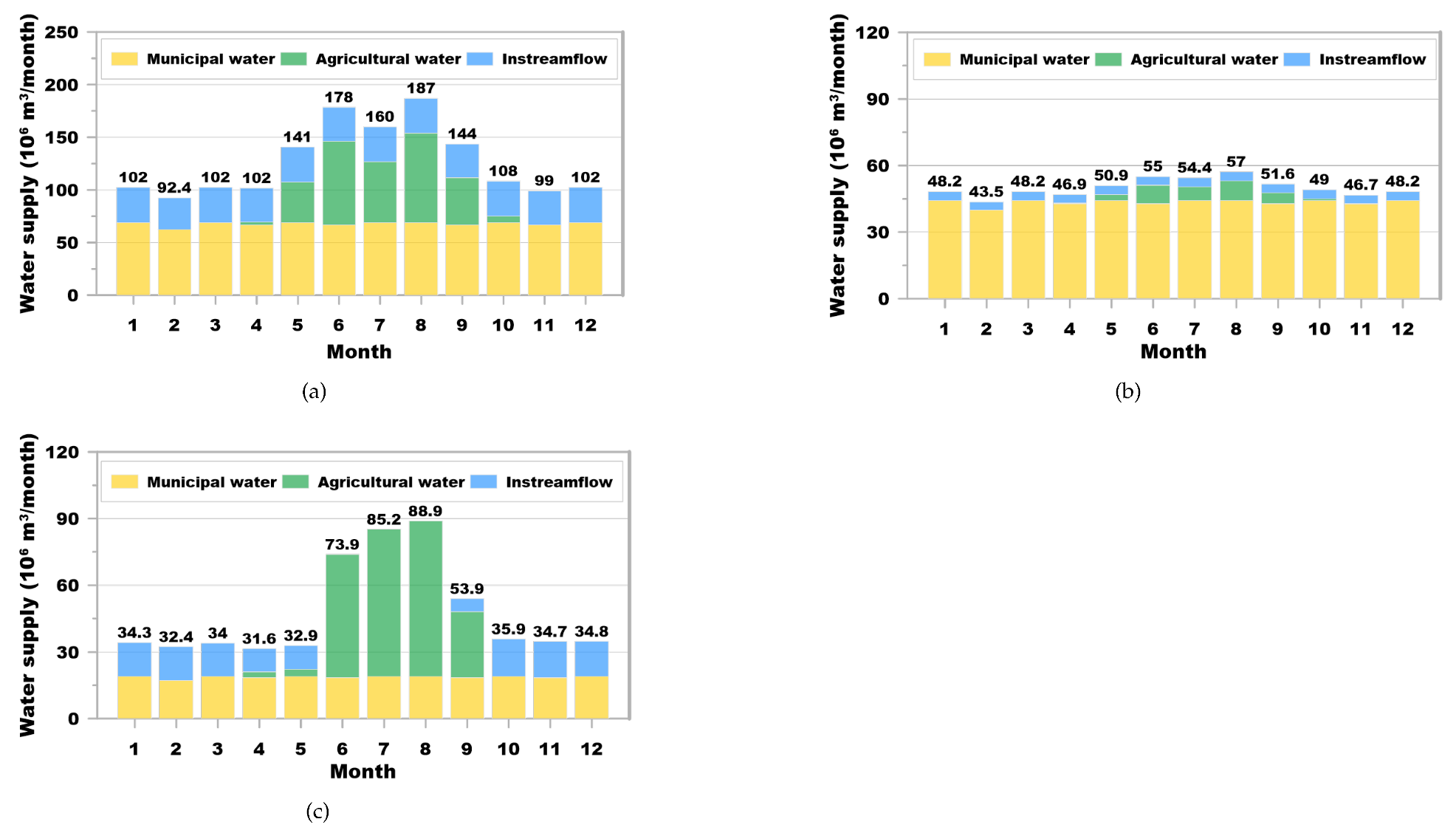
3. Study Area and Data
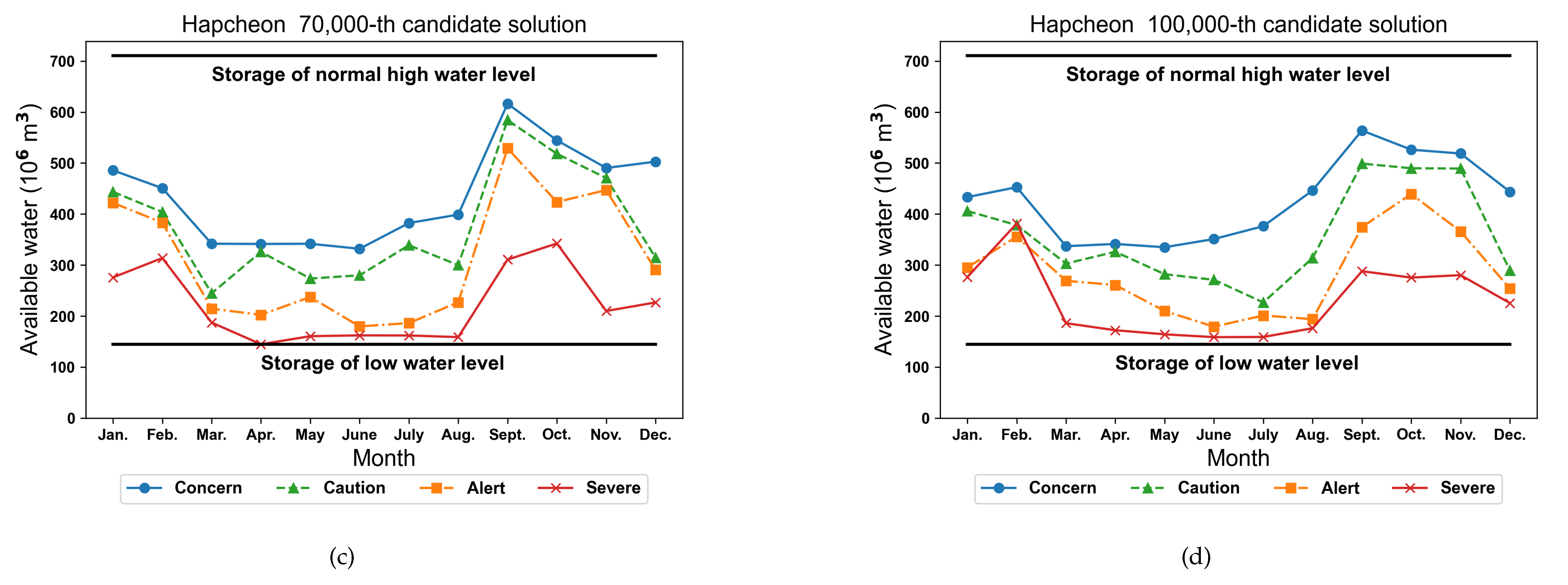
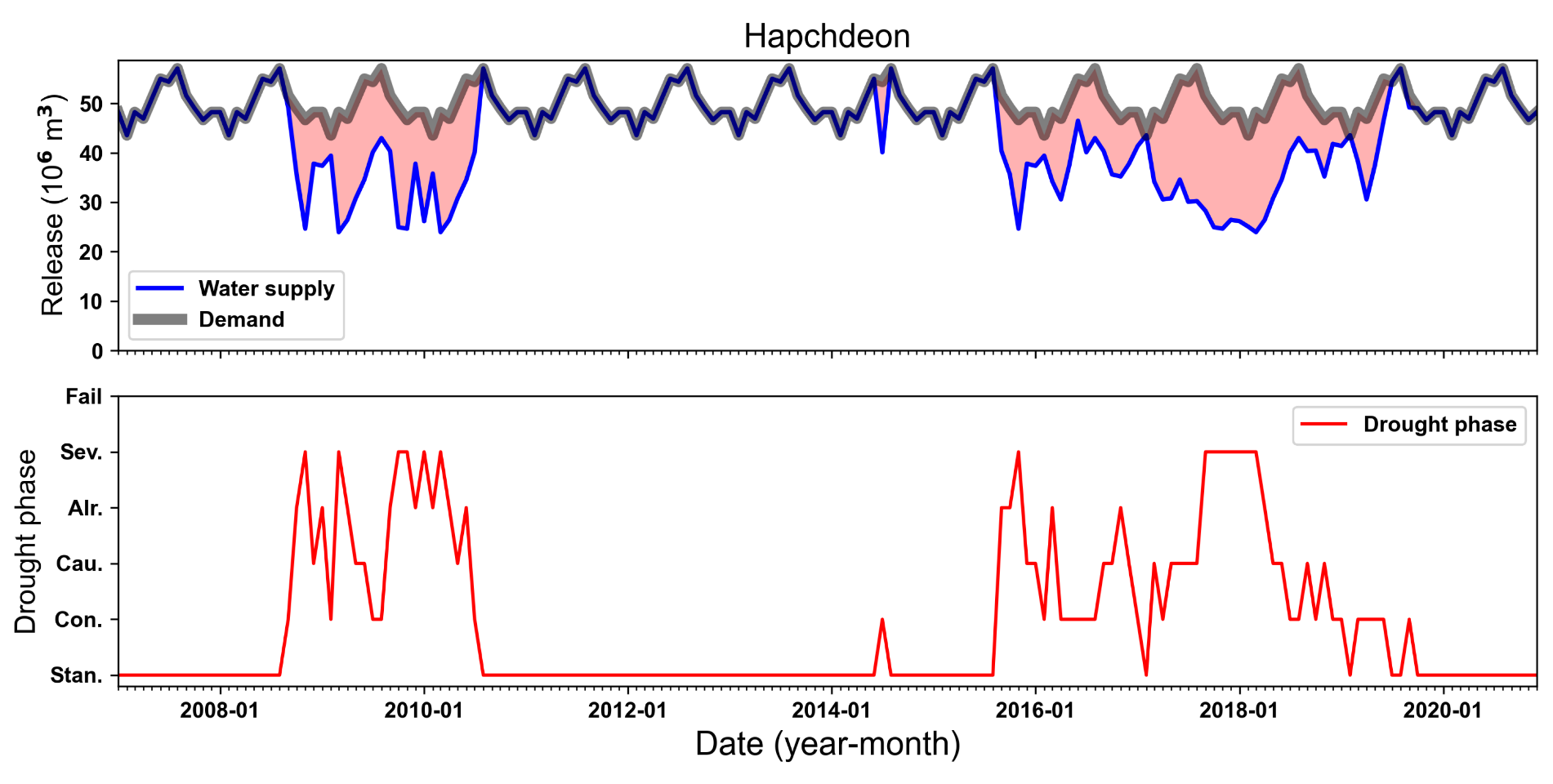
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
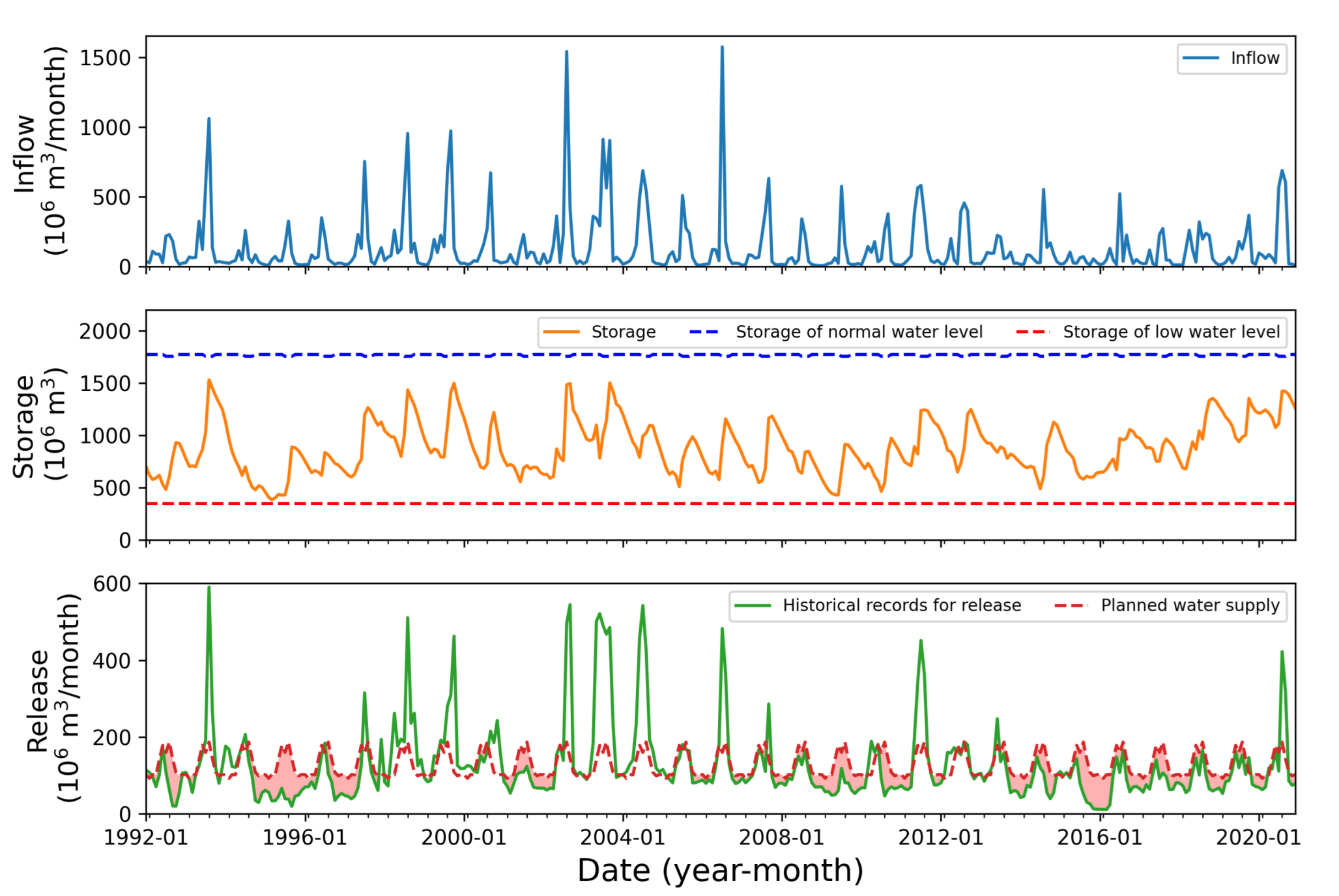
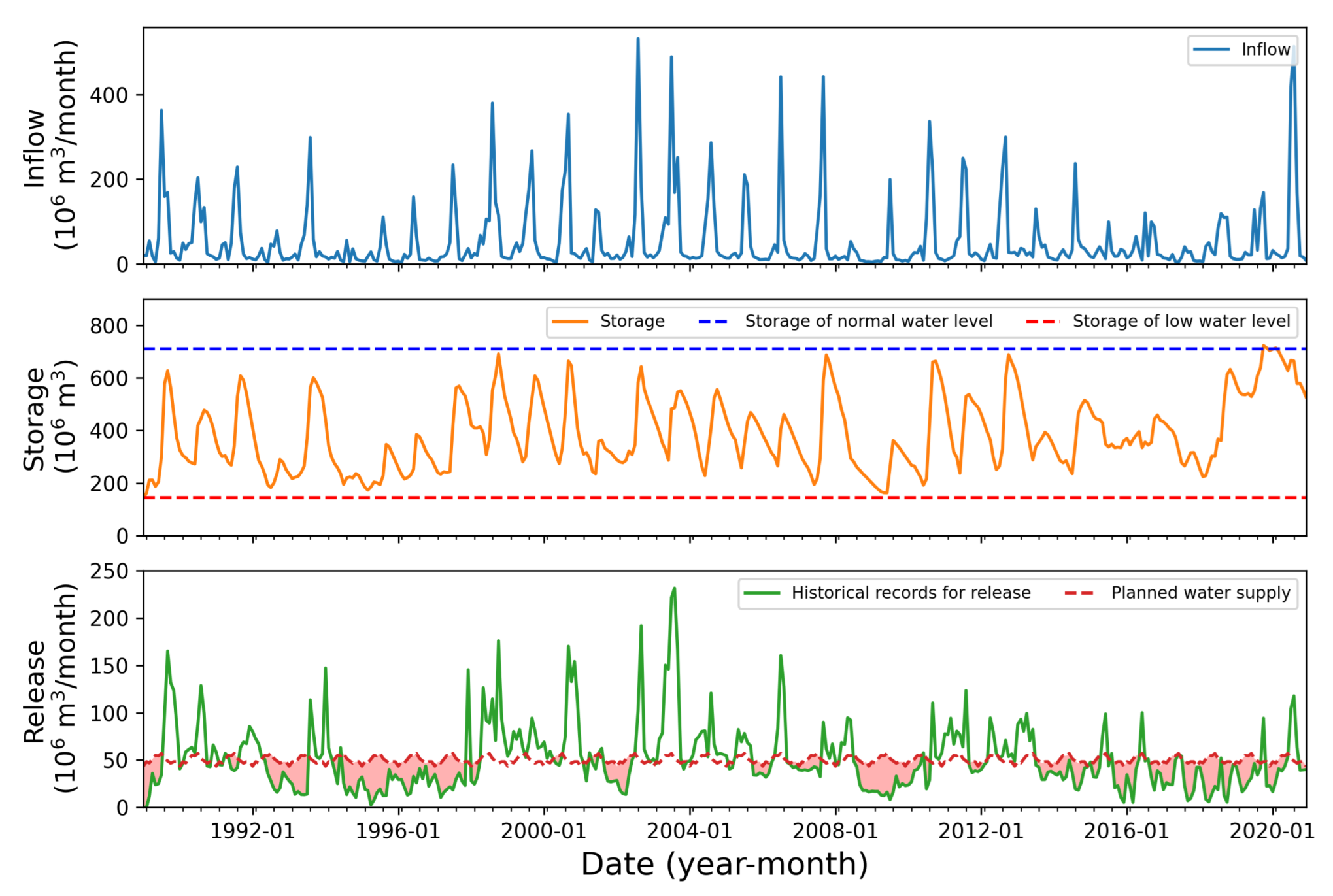
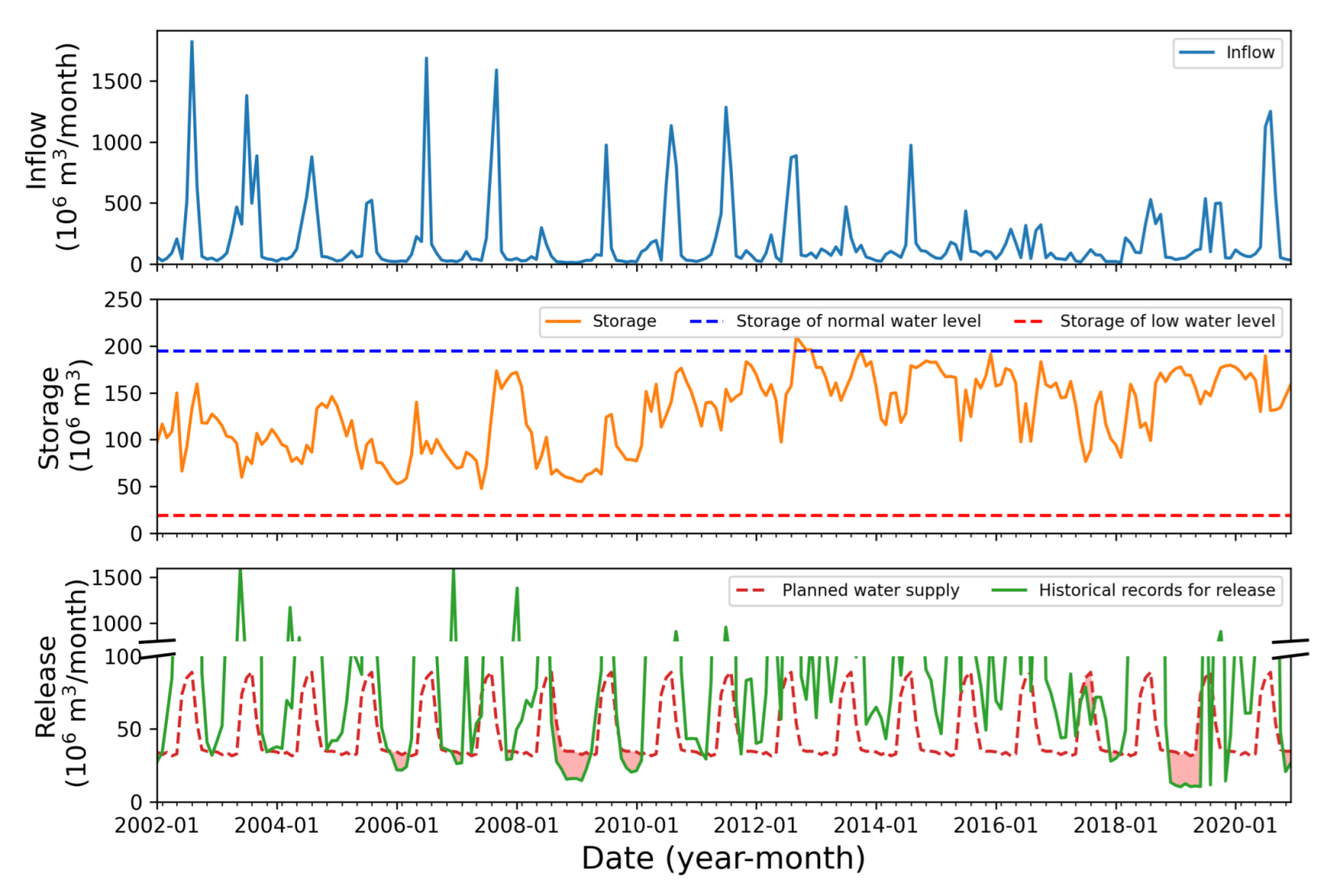
Appendix A. The Historical and Reservoir Operation Records for Andong-Imha, Hapcheon, and Namgang Reservoirs
References
- IPCC. Summary for Policymakers. In Climate Change 2007: The Physical Science Basis; Contribution of Working Group to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change; Technical Report; Cambridge University Press: Cambridge, UK, 2007. [Google Scholar]
- Adeloye, A.J.; Dau, Q.V. Hedging as an adaptive measure for climate change induced water shortage at the Pong reservoir in the Indus Basin Beas River, India. Sci. Total. Environ. 2019, 687, 554–566. [Google Scholar] [CrossRef] [PubMed]
- Hashimoto, T.; Stedinger, J.R.; Loucks, D.P. Reliability, resiliency, and vulnerability criteria for water resource system performance evaluation. Water Resour. Res. 1982, 18, 14–20. [Google Scholar] [CrossRef] [Green Version]
- Zeng, X.; Hu, T.; Guo, X.; Li, X. Water Transfer Triggering Mechanism for Multi-Reservoir Operation in Inter-Basin Water Transfer-Supply Project. Water Resour. Manag. 2014, 28, 1293–1308. [Google Scholar] [CrossRef]
- Spiliotis, M.; Mediero, L.; Garrote, L. Optimization of Hedging Rules for Reservoir Operation During Droughts Based on Particle Swarm Optimization. Water Resour. Manag. 2016, 30, 5759–5778. [Google Scholar] [CrossRef]
- Shiau, J.T.; Lee, H.C. Derivation of optimal hedging rules for a water-supply reservoir through compromise programming. Water Resour. Manag. 2005, 19, 111–132. [Google Scholar] [CrossRef]
- Tu, M.Y.; Hsu, N.S.; Yeh, W.W.G. Optimization of Reservoir Management and Operation with Hedging Rules. J. Water Resour. Plan. Manag. 2003, 129, 86–97. [Google Scholar] [CrossRef]
- Tu, M.Y.; Hsu, N.S.; Tsai, F.T.C.; Yeh, W.W.G. Optimization of Hedging Rules for Reservoir Operations. J. Water Resour. Plan. Manag. 2008, 134, 3–13. [Google Scholar] [CrossRef]
- You, J.Y.; Cai, X. Hedging rule for reservoir operations: 1. A theoretical analysis. Water Resour. Res. 2008, 44, w01415. [Google Scholar] [CrossRef]
- You, J.Y.; Cai, X. Hedging rule for reservoir operations: 2. A numerical model. Water Resour. Res. 2008, 44, W01416. [Google Scholar] [CrossRef]
- Eum, H.I.; Kim, Y.O.; Palmer, R.N. Optimal Drought Management Using Sampling Stochastic Dynamic Programming with a Hedging Rule. J. Water Resour. Plan. Manag. 2011, 137, 113–122. [Google Scholar] [CrossRef]
- Zhao, J.; Cai, X.; Wang, Z. Optimality conditions for a two-stage reservoir operation problem. Water Resour. Res. 2011, 47, W08503. [Google Scholar] [CrossRef]
- Jin, Y.; Lee, S. Comparative Effectiveness of Reservoir Operation Applying Hedging Rules Based on Available Water and Beginning Storage to Cope with Droughts. Water Resour. Manag. 2019, 33, 1897–1911. [Google Scholar] [CrossRef]
- Hınçal, O.; Altan-Sakarya, A.B.; Ger, A.M. Optimization of Multireservoir Systems by Genetic Algorithm. Water Resour. Manag. 2011, 25, 1465–1487. [Google Scholar] [CrossRef]
- Taghian, M.; Rosbjerg, D.; Haghighi, A.; Madsen, H. Optimization of Conventional Rule Curves Coupled with Hedging Rules for Reservoir Operation. J. Water Resour. Plan. Manag. 2014, 140, 693–698. [Google Scholar] [CrossRef]
- Chu, J.; Peng, Y.; Ding, W.; Li, Y. A Heuristic dynamically dimensioned search with sensitivity information (HDDS-S) and application to river basin management. Water 2015, 7, 2214–2238. [Google Scholar] [CrossRef] [Green Version]
- Yin, X.A.; Mao, X.F.; Pan, B.Z.; Zhao, Y.W. Suitable range of reservoir storage capacities for environmental flow provision. Ecol. Eng. 2015, 76, 122–129. [Google Scholar] [CrossRef]
- Anand, J.; Gosain, A.K.; Khosa, R. Optimisation of Multipurpose Reservoir Operation by Coupling Soil and Water Assessment Tool (SWAT) and Genetic Algorithm for Optimal Operating Policy (Case Study: Ganga River Basin). Sustainability 2018, 10, 1660. [Google Scholar] [CrossRef] [Green Version]
- Felfelani, F.; Movahed, A.J.; Zarghami, M. Simulating hedging rules for effective reservoir operation by using system dynamics: A case study of dez Reservoir, Iran. Lake Reserv. Manag. 2013, 29, 126–140. [Google Scholar] [CrossRef] [Green Version]
- Ahmadianfar, I.; Adib, A.; Taghian, M. Optimization of Fuzzified Hedging Rules for Multipurpose and Multireservoir Systems. J. Hydrol. Eng. 2016, 21, 05016003. [Google Scholar] [CrossRef]
- Cheng, W.M.; Huang, C.L.; Hsu, N.S.; Wei, C.C. Risk analysis of reservoir operations considering short-term flood control and long-term water supply: A case study for the Da-Han Creek basin in Taiwan. Water 2017, 9, 424. [Google Scholar] [CrossRef]
- Gomes, L.S.; Maia, A.G.; de Medeiros, J.D.F. Fuzzified hedging rules for a reservoir in the Brazilian semiarid region. Environ. Chall. 2021, 4, 100125. [Google Scholar] [CrossRef]
- Shih, J.S.; Revelle, C. Water supply operations during drought: A discrete hedging rule. Eur. J. Oper. Res. 1995, 82, 163–175. [Google Scholar] [CrossRef]
- Kim, J.H.; Myung, H. Evolutionary Programming Techniques for Constrained Optimization Problems. IEEE Trans. Evol. Comput. 1997, 1, 129–140. [Google Scholar] [CrossRef]
- Laisupannawong, T.; Intiyot, B.; Jeenanunta, C. Mixed-integer linear programming model and heuristic for short-term scheduling of pressing process in multi-layer printed circuit board manufacturing. Mathematics 2021, 9, 653. [Google Scholar] [CrossRef]
- Shiau, J.T. Optimization of Reservoir Hedging Rules Using Multiobjective Genetic Algorithm. J. Water Resour. Plan. Manag. 2009, 135, 355–363. [Google Scholar] [CrossRef]
- Tolson, B.A.; Asadzadeh, M.; Maier, H.R.; Zecchin, A. Hybrid discrete dynamically dimensioned search (HD-DDS) algorithm for water distribution system design optimization. Water Resour. Res. 2009, 45, W12416. [Google Scholar] [CrossRef]
- Kang, T.; Lee, S. Modification of the SCE-UA to Include Constraints by Embedding an Adaptive Penalty Function and Application: Application Approach. Water Resour. Manag. 2014, 28, 2145–2159. [Google Scholar] [CrossRef]
- Lee, S.; Kang, T. Analysis of Constrained Optimization Problems by the SCE-UA with an Adaptive Penalty Function. J. Comput. Civ. Eng. 2016, 30, 04015035. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Duan, Q.; Sorooshian, S.; Gupta, V. Effective and Efficient Global Optimization for Conceptual Rainfall-Runoff Models. Water Resour. Res. 1992, 28, 1015–1031. [Google Scholar] [CrossRef]
- Tolson, B.A.; Shoemaker, C.A. Dynamically dimensioned search algorithm for computationally efficient watershed model calibration. Water Resour. Res. 2007, 43, W01413. [Google Scholar] [CrossRef] [Green Version]
- Qin, H.; Liu, Z.; Zhang, S.; Wen, A. Routing and wavelength assignment based on genetic algorithm. IEEE Commun. Lett. 2002, 6, 455–457. [Google Scholar] [CrossRef]
- Bhanja, U.; Mahapatra, S.; Roy, R. An evolutionary programming algorithm for survivable routing and wavelength assignment in transparent optical networks. Inf. Sci. 2013, 222, 634–647. [Google Scholar] [CrossRef]
- Zakouni, A.; Luo, J.; Kharroubi, F. Solving the static manycast RWA problem in optical networks using evolutionary programming. In International Conference on Intelligent Computing; Springer: Cham, Switzerland, 2016; Volume 9772, pp. 147–157. [Google Scholar] [CrossRef]
- Nelder, J.A.; Mead, R. A Simplex Method for Function Minimization. Comput. J. 1965, 7, 308–313. [Google Scholar] [CrossRef]
- Nezhad, O.B.; Najarchi, M.; NajafiZadeh, M.M.; Hezaveh, S.M.M. Developing a shuffled complex evolution algorithm using a differential evolution algorithm for optimizing hydropower reservoir systems. Water Supply 2018, 18, 1081–1092. [Google Scholar] [CrossRef] [Green Version]
- Majeed, K.; Qyyum, M.A.; Nawaz, A.; Ahmad, A.; Naqvi, M.; He, T.; Lee, M. Shuffled Complex Evolution-Based Performance Enhancement and Analysis of Cascade Liquefaction Process for Large-Scale LNG Production. Energies 2020, 13, 2511. [Google Scholar] [CrossRef]
- Chu, W.; Gao, X.; Sorooshian, S. A Solution to the Crucial Problem of Population Degeneration in High-Dimensional Evolutionary Optimization. IEEE Syst. J. 2011, 5, 362–373. [Google Scholar] [CrossRef] [Green Version]
- Chu, W.; Gao, X.; Sorooshian, S. A new evolutionary search strategy for global optimization of high-dimensional problems. Inf. Sci. 2011, 181, 4909–4927. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Duan, Q.; Gong, W.; Ye, A.; Di, Z.; Miao, C. An evaluation of adaptive surrogate modeling based optimization with two benchmark problems. Environ. Model. Softw. 2014, 60, 167–179. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Li, D. Chaotic Dynamically Dimensioned Search Algorithm. IEEE Access 2020, 8, 152474–152499. [Google Scholar] [CrossRef]
- Kang, S.; Lee, S.; Kang, T. Development and Application of Storage-Zone Decision Method for Long-Term Reservoir Operation Using the Dynamically Dimensioned Search Algorithm. Water Resour. Manag. 2017, 31, 219–232. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Suganthan, P.N. Ensemble of Constraint Handling Techniques. IEEE Trans. Evol. Comput. 2010, 14, 561–579. [Google Scholar] [CrossRef]
- Yeniay, Ö. Penalty Function Methods for Constrained Optimization with Genetic Algorithms. Math. Comput. Appl. 2005, 10, 45–56. [Google Scholar] [CrossRef] [Green Version]
- Michalewicz, Z.; Janikow, C.Z. GENOCOP: A Genetic Algorithm for Numerical Optimization Problems with Linear Constraints. J. Commun. ACM 1996, 175–201. [Google Scholar] [CrossRef]
- Coello, C.A.C. Theoretical and numerical constraint-handling techniques used with evolutionary algorithms: A survey of the state of the art. Comput. Methods Appl. Mech. Eng. 2002, 191, 1245–1287. [Google Scholar] [CrossRef]
- Jin, Y.; Lee, S. An Additional Water Supply Method from Upstream Dams to Lessen Water Supply Shortage at Downstream Control Points Using a Heuristic Method. Korean Soc. Hazard Mitig. 2017, 17, 507–514. [Google Scholar] [CrossRef]
- Jin, Y.; Lee, S. Determination of hedging rule curves to mitigate water supply deficit for a single dam using dynamically dimensioned search method. In Proceedings of the European Water Resources Association EWRA, Madrid, Spain, 25–29 June 2019; pp. 41–42. [Google Scholar]
- Bellman, R.; Kalaba, R. A mathematical theory of adaptive control processes. Proc. Natl. Acad. Sci. USA 1959, 45, 1288–1290. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bellman, R. Dynamic programming. Science 1966, 153, 34–37. [Google Scholar] [CrossRef]
- Mendes, R.; Kennedy, J.; Neves, J. The fully informed particle swarm: Simpler, maybe better. IEEE Trans. Evol. Comput. 2004, 8, 204–210. [Google Scholar] [CrossRef]
- Lund, J.R. Developing Seasonal and Long-Term Reservoir System Operation Plans Using HEC-PRM; Technical Report; Hydrologic Engineering Center, U.S. Army Corps of Engineers: Davis, CA, USA, 1996.
- Griffin, J.D.; Kolda, T.G. Nonlinearly Constrained Optimization Using Heuristic Penalty Methods and Asynchronous Parallel Generating Set Search. Appl. Math. Res. Express 2010, 2010, 36–62. [Google Scholar] [CrossRef]
- Costa, M.F.P.; Rocha, A.M.A.C.; Fernandes, E.M.G.P. Penalty-Based Heuristic DIRECT Method for Constrained Global Optimization; Springer: Cham, Switzerland, 2020; pp. 538–551. [Google Scholar]

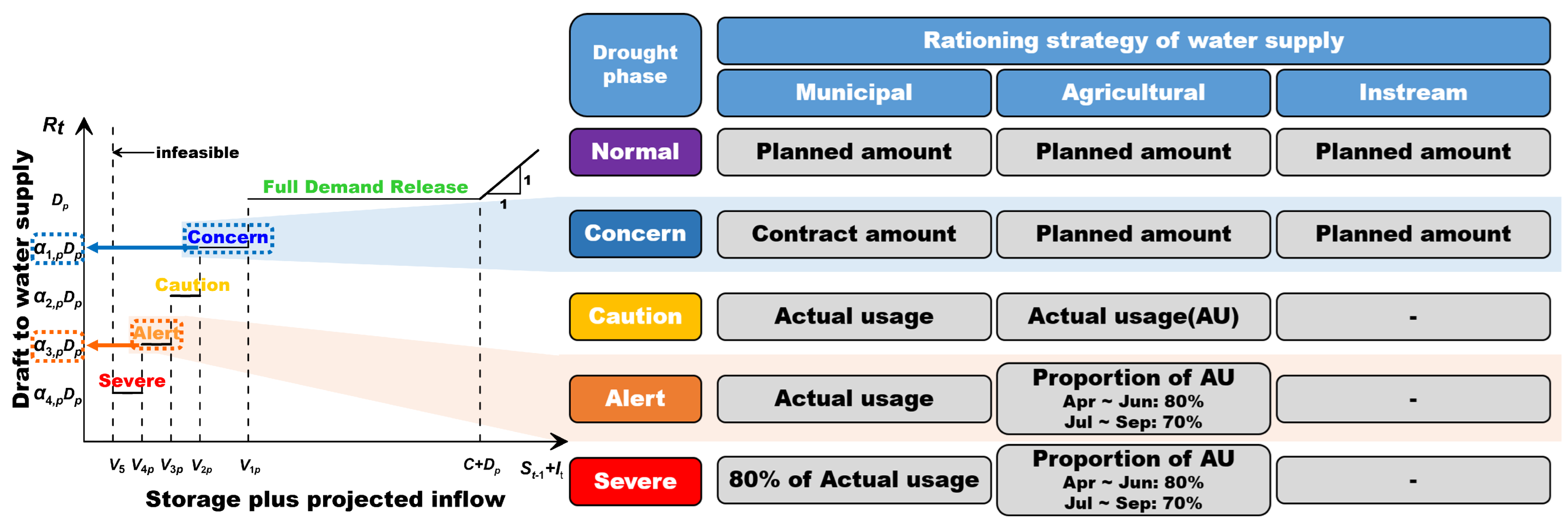






| Classification | Simulation Model | ||
|---|---|---|---|
| Drought Phases | Condition | Release | |
| Release determination | Normal | ||
| Concern | |||
| Caution | |||
| Alert | |||
| Severe | |||
| Fail | |||
| Reservoir | Watershed Area (km2) | Annual Average Inflow ( m3) | Storage of Normal High Water Level ( m3) | Storage of Low-Water Level ( m3) | Active Capacity ( m3) |
|---|---|---|---|---|---|
| AD-IH | 2945 | 1613 | 1772 | 351.0 | 1421 |
| HC | 925.0 | 637.4 | 724.1 | 151.0 | 599.0 |
| NG | 2285 | 2105 | 182.4 | 16.15 | 166.3 |
| Month | Andong-Imha | Hapcheon | Namgang | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| January | 0.74 | 0.41 | 0.41 | 0.33 | 0.86 | 0.77 | 0.77 | 0.54 | 0.74 | 0.29 | 0.29 | 0.23 | ||
| February | 0.75 | 0.42 | 0.42 | 0.34 | 0.91 | 0.82 | 0.82 | 0.58 | 0.75 | 0.28 | 0.28 | 0.22 | ||
| March | 0.74 | 0.42 | 0.42 | 0.34 | 0.79 | 0.71 | 0.71 | 0.50 | 0.74 | 0.30 | 0.30 | 0.24 | ||
| April | 0.76 | 0.43 | 0.43 | 0.34 | 0.65 | 0.56 | 0.56 | 0.39 | 0.73 | 0.39 | 0.37 | 0.25 | ||
| May | 0.83 | 0.40 | 0.38 | 0.32 | 0.74 | 0.61 | 0.61 | 0.42 | 0.73 | 0.40 | 0.38 | 0.24 | ||
| June | 0.89 | 0.35 | 0.33 | 0.28 | 0.85 | 0.63 | 0.63 | 0.44 | 0.88 | 0.88 | 0.73 | 0.11 | ||
| July | 0.86 | 0.34 | 0.33 | 0.27 | 0.74 | 0.55 | 0.55 | 0.39 | 0.89 | 0.89 | 0.66 | 0.09 | ||
| August | 0.88 | 0.28 | 0.27 | 0.22 | 0.75 | 0.53 | 0.53 | 0.37 | 0.90 | 0.90 | 0.66 | 0.09 | ||
| September | 0.85 | 0.34 | 0.33 | 0.27 | 0.95 | 0.78 | 0.78 | 0.55 | 0.84 | 0.73 | 0.56 | 0.14 | ||
| October | 0.78 | 0.42 | 0.42 | 0.34 | 0.83 | 0.73 | 0.73 | 0.51 | 0.75 | 0.28 | 0.28 | 0.22 | ||
| November | 0.77 | 0.45 | 0.45 | 0.36 | 0.84 | 0.75 | 0.75 | 0.53 | 0.75 | 0.28 | 0.28 | 0.22 | ||
| December | 0.74 | 0.43 | 0.43 | 0.34 | 0.87 | 0.78 | 0.78 | 0.55 | 0.74 | 0.29 | 0.29 | 0.23 | ||
| Reservoir | Optimization Period | Total Water Supply Shortage ( ) |
|---|---|---|
| AD-IH | January 1992∼ December 2020 | 9481 |
| HC | January 1989∼ December 2020 | 4562 |
| NG | January 2002∼ December 2020 | 765 |
| Case | Maximum Number of Function Evaluations (m) | Neighborhood Perturbation Size (r) |
|---|---|---|
| 1 | 100,000 | 0.2 |
| 2 | 100,000 | 0.1 |
| 3 | 50,000 | 0.2 |
| 4 | 50,000 | 0.1 |
| 5 | 20,000 | 0.2 |
| 6 | 20,000 | 0.1 |
| 7 | 10,000 | 0.2 |
| 8 | 10,000 | 0.1 |
| Trigger Volume | DDS-FSR | DDS | |||
|---|---|---|---|---|---|
| Lower Bound | Upper Bound | Lower Bound | Upper Bound | ||
| S-NHWL | S-LWL | S-NHWL | |||
| S-LWL | |||||
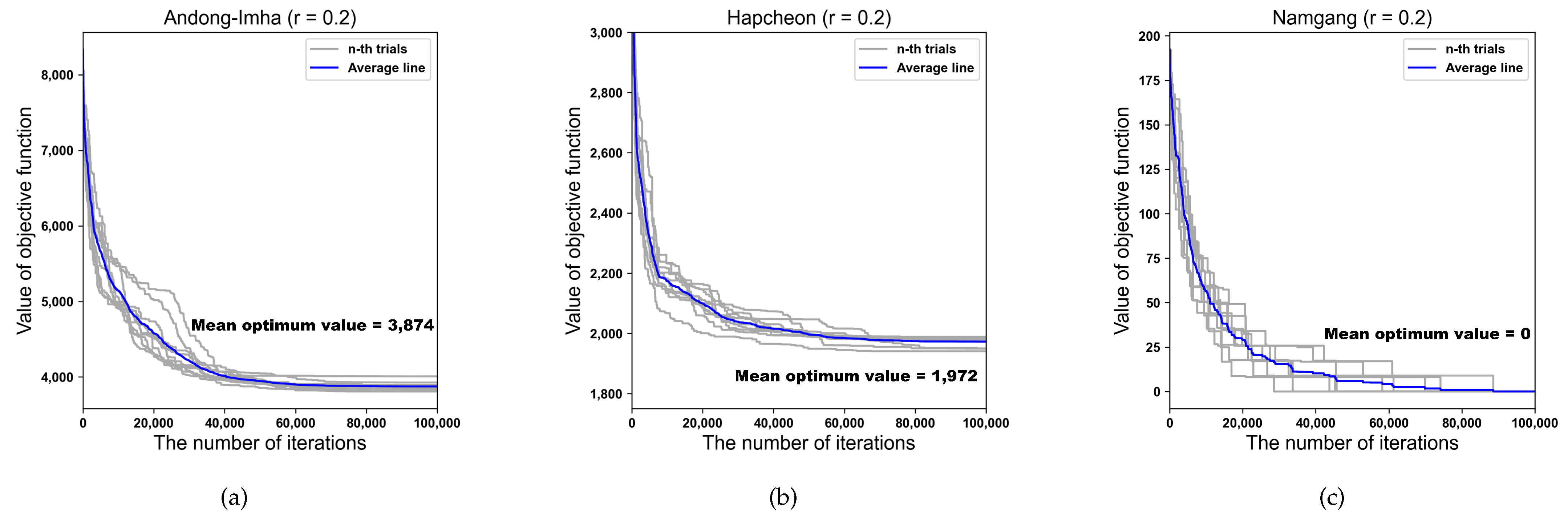
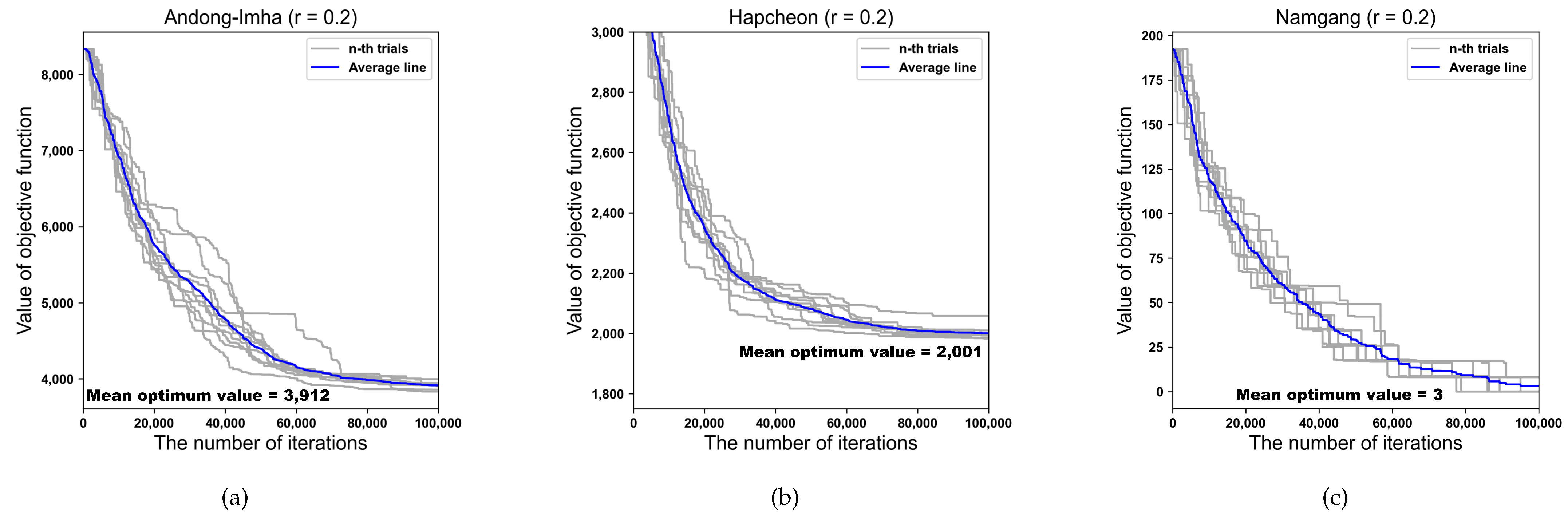
| Case | Reservoir | DDS | DDS-FSR | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Best | Mean | Worst | St. Dev | Best | Mean | Worst | St. Dev | |||
| 1 | AD-IH | 3831 | 3912 | 3996 | 43 | 3806 | 3874 | 4008 | 56 | |
| HC | 1983 | 2001 | 2058 | 21 | 1941 | 1972 | 1988 | 18 | ||
| NG | 0 | 3 | 8 | 4 | 0 | 0 | 0 | 0 | ||
| 2 | AD-IH | 3814 | 3887 | 3964 | 48 | 3803 | 3859 | 3907 | 32 | |
| HC | 1948 | 1985 | 2047 | 24 | 1959 | 1995 | 2079 | 33 | ||
| NG | 0 | 2 | 9 | 4 | 0 | 1 | 9 | 3 | ||
| 3 | AD-IH | 3935 | 4058 | 4345 | 111 | 3843 | 3885 | 3990 | 43 | |
| HC | 1984 | 2025 | 2192 | 59 | 1953 | 1987 | 2030 | 23 | ||
| NG | 8 | 15 | 26 | 7 | 0 | 5 | 9 | 4 | ||
| 4 | AD-IH | 3876 | 3993 | 4202 | 91 | 3836 | 3891 | 3935 | 29 | |
| HC | 1955 | 2006 | 2111 | 42 | 1979 | 2000 | 2028 | 18 | ||
| NG | 0 | 8 | 17 | 6 | 0 | 1 | 8 | 2 | ||
| 5 | AD-IH | 3948 | 4361 | 4867 | 330 | 3964 | 4132 | 4673 | 238 | |
| HC | 2014 | 2072 | 2155 | 44 | 1975 | 2027 | 2112 | 47 | ||
| NG | 17 | 28 | 43 | 8 | 9 | 19 | 26 | 5 | ||
| 6 | AD-IH | 3978 | 4366 | 6072 | 583 | 3902 | 4088 | 4537 | 186 | |
| HC | 1983 | 2056 | 2196 | 60 | 1998 | 2045 | 2175 | 51 | ||
| NG | 8 | 18 | 34 | 9 | 0 | 11 | 26 | 8 | ||
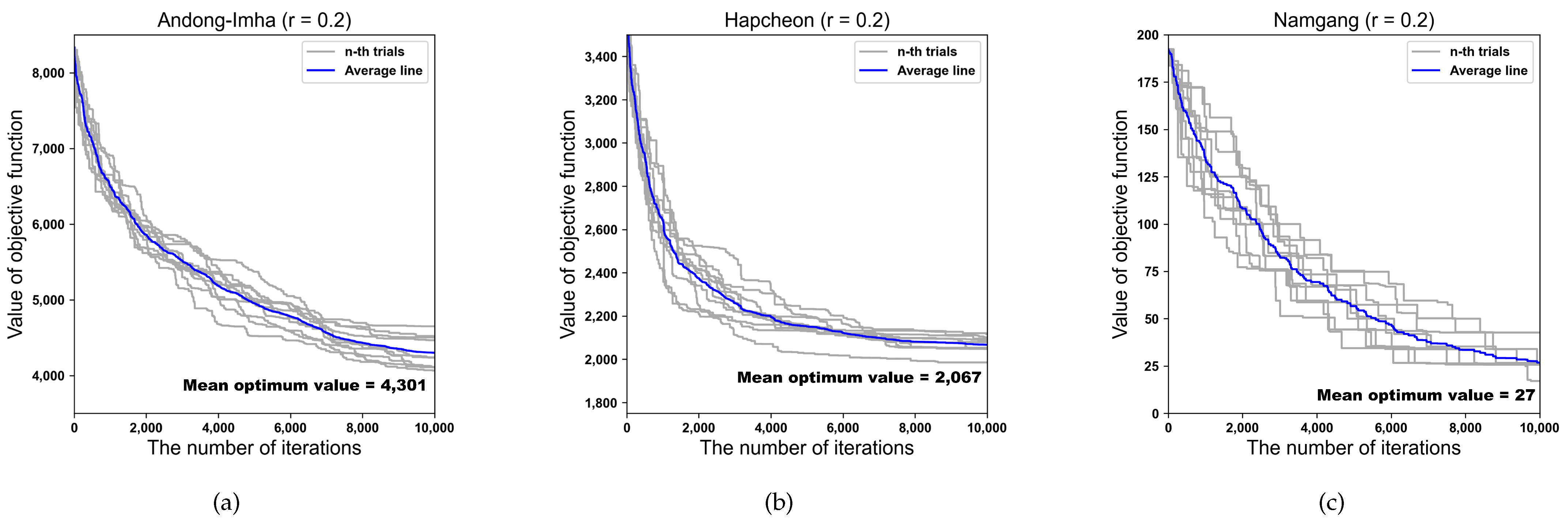
| 7 | AD-IH | 4337 | 4814 | 6510 | 590 | 4066 | 4301 | 4650 | 202 | |
| HC | 2016 | 2157 | 2451 | 126 | 1985 | 2067 | 2116 | 36 | ||
| NG | 25 | 40 | 59 | 12 | 17 | 27 | 43 | 6 | ||
| 8 | AD-IH | 4193 | 4568 | 4977 | 254 | 4040 | 4450 | 4893 | 207 | |
| HC | 2022 | 2078 | 2190 | 59 | 2017 | 2073 | 2179 | 45 | ||
| NG | 18 | 36 | 51 | 10 | 17 | 27 | 42 | 8 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, Y.; Lee, S.; Kang, T.; Kim, Y. A Dynamically Dimensioned Search Allowing a Flexible Search Range and Its Application to Optimize Discrete Hedging Rule Curves. Water 2022, 14, 3633. https://doi.org/10.3390/w14223633
Jin Y, Lee S, Kang T, Kim Y. A Dynamically Dimensioned Search Allowing a Flexible Search Range and Its Application to Optimize Discrete Hedging Rule Curves. Water. 2022; 14(22):3633. https://doi.org/10.3390/w14223633
Chicago/Turabian StyleJin, Youngkyu, Sangho Lee, Taeuk Kang, and Yeulwoo Kim. 2022. "A Dynamically Dimensioned Search Allowing a Flexible Search Range and Its Application to Optimize Discrete Hedging Rule Curves" Water 14, no. 22: 3633. https://doi.org/10.3390/w14223633






